Vorlesung 3 - IKP, TU Darmstadt

Moderne Experimente
der Kernphysik
Wintersemester 2011/12
Vorlesung 03 – 31.10.2011
Moderne Experimente der Kernphysik | Prof. Thorsten Kröll | Vorlesung 3
31.10.2011
1
- Gammaspektroskopie Elektromagnetische Zerfälle angeregter Kernzustände
Programm
• Gammaübergänge zwischen Kernniveaus
- Erhaltungsgrößen
- Winkelverteilungen
- Linearpolarisation
• Übergangswahrscheinlichkeiten
- reduzierte Matrixelemente
- Weisskopf-Abschätzung
• Wechselwirkungsprozesse mit Materie
• Gammadetektoren
- Szintillationsdetektoren
- Germaniumdetektoren
- 4π-Spektrometer
- „Gamma-Ray Tracking“
z
Elektromagnetische Übergänge zwischen zwei Kernzuständen | i ⟩, | f ⟩
z
Erhaltungsgrößen: Energie :
E f = Ei − hω
r
r r
Drehimpuls : J f = J i + l
M f = Mi + μ
Parität :
π f = π i ⋅π γ
Ei
Ji, Mi , πi
|i⟩
ℓ, μ, π
Ef
Jf, Mf, πf
|f⟩
Energie
Angeregte Kernzustände - Gammazerfall 1
z
Der Drehimpuls ℓ der Gammastrahlung (des Photons) wird auch die
Multipolordnung der Strahlung genannt
– Strahlungsfeld wird in Kugelflächenfunktionen entwickelt
– z.B. erzeugt ein schwingender Dipol ein Dipolfeld (Hertzscher Dipol)
z
Man unterscheidet zwischen elektrischer und magnetischer Strahlung,
was von der Natur des emittierenden Multipols abhängt:
– Schwingende Ladungsverteilung
→ elektrische Strahlung (E)
– Schwingende Stromverteilung
→ magnetische Strahlung (M)
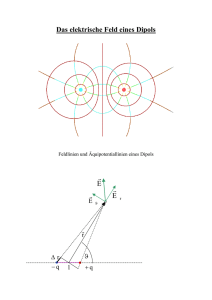
Klassischer Dipolstrahler
Elektrischer Dipol
Magnetischer Dipol
Elektromagnetische Wellen - Hertzscher Dipol
Poynting-Vektor
(
r 1 r r
S=
E×B
μ0
)
• Richtung des
Energieflusses
• Betrag der
Leistungsdichte
Strahlungsfeld eines Dipols
Einheit:
J/m2/s = W/m2
Bei hohen Frequenzen „lösen“ sich die Felder
vom Dipol ab, elektromagnetische Wellen werden
abgestrahlt.
John Henry Poynting (1852-1914)
6
Strahlungscharakteristik eines Hertzschen Dipols
E nach „oben“
(positive z-Achse)
E nach unten
(negative z-Achse)
Farbintensität |E|
Poynting-Vektor
7
Angeregte Kernzustände - Gammazerfall 2
z
Auswahlregeln:
– Aufgrund der Eigenschaften der Kugelflächenfunktionen ergeben
sich für die Multipolstrahlung folgende Auswahlregeln:
π i = ( −1)l π f
für (Eℓ)-Strahlung
π i = ( −1)l+1π f
für (Mℓ)-Strahlung
Angeregte Kernzustände - Gammazerfall 3
z
Warum sind in der Tabelle nur die niedrigsten Multipole angegeben?
Betrachte die Emission eines Photons (masseloses Teilchen, Spin=1)
mit einer Einheit Drehimpuls (ħ):
Emission im Abstand x
h = x× p = x
Eγ
c
⇒x=
hc
=D
Eγ
hc 197 MeV ⋅ fm
=
≈ 200 fm >> R Kern
Für Kerne ist Eγ ~ 1 MeV D =
Eγ
1 MeV
Hieraus folgt:
• Die Wahrscheinlichkeit für Emission von Photonen mit Drehimpuls ℓ
nimmt rapide mit wachsendem Drehimpuls ab!
• In Atomen (ähnliche Größenverhältnisse) führt dies dazu, dass es fast
ausschließlich Dipolstrahlung bei Hüllenübergängen gibt.
• Im Kern dominieren niedrige Multipole wobei auch ℓ = 2 meistens noch
konkurrieren kann und auch ℓ =3,4 vorkommen können (jedoch selten)
Winkelverteilung 1
Emittierte Intensität (Poynting-Vektor Z) als
Funktion des Winkels zur Quantisierungsachse:
1
{1 − P2 (cosθ )}
4π
1
Z1±1 (θ ) =
1 + 12 P2 (cos θ )
4π
r
r r
2
Z lμ (θ) = E × B ∝ Ylμ (θ, φ)
Z10 (θ ) =
{
Ylm (Kugelflächenfunktionen):
Eigenfunktionen zu Drehimpulsquantenzahlen (lm)
Erwartungswert ein Photon (lm)
bei Winkel (θ,φ) zu finden
Dipol (ℓ=1)
}
Quadrupol (ℓ=2)
1
1 + 75 P2 (cos θ ) − 127 P4 (cos θ )
4π
1
Z 2±1 (θ ) =
1 + 145 P2 (cos θ ) + 87 P4 (cos θ )
4π
1
Z 2± 2 (θ ) =
1 − 75 P2 (cos θ ) − 72 P4 (cos θ )
4π
Z 20 (θ ) =
{
}
{
}
{
}
Winkelverteilung hängt nicht vom Azimuthalwinkel ab!
l
Isotrope Winkelverteilung, wenn alle μ gleich häufig sind:
∑ Z lμ (θ ) =
μ =− l
2l + 1
4π
Winkelverteilung 2
Zusammenfassen der Terme Pk(cos θ):
l = 1:
W (θ ) = 1 + A2 P2 (cosθ )
l = 2 : W (θ ) = 1 + A2 P2 (cosθ ) + A4 P4 (cosθ )
...
Die experimentellen Werte für A2 und A4 hängen ab von:
• Bevölkerung der magnetischen Unterzustände Mi des zerfallenden Niveaus
Sind alle Mi mit gleicher Wahrscheinlichkeit besetzt, ist die Verteilung
isotrop
l,μ
• Das Gewicht des Anteils J i , M i ⎯⎯→
J f ,M f
ist gegeben durch den Clebsch-Gordan-Koeffizienten
Ji M i l μ J f M f
• Mögliche Multipolkomponenten im Übergang:
Multipolmischung, z.B. E2 und M1 für einen Übergang ΔJ = ±1 oder 0
ohne Änderung der Parität
Winkelverteilung 3
Die Messung der Winkelverteilung erlaubt die Bestimmung der Multipolarität ℓ:
Beispiel für einen 6+ → 4+ (E2) Quadrupolübergang
• Anpassung der Koeffizienten
A2 und A4 an exp. Daten
• Vergleich mit den theoretischen Werten
A2 = 0,347(16)
A4 = −0,166(23)
Elektrischer oder magnetischer Charakter kann nicht durch Messung der
Winkelverteilung bestimmt werden!!!
→ Messung der Linearpolarisation
Q
ua
nt
is
ie
ru
ng
s
ac
hs
e
z
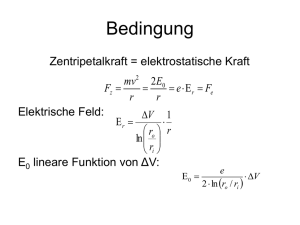
Linearpolarisation – Definition
Die von Propagationsrichtung r
(=Poynting-Vektor) und elektrischem
Feld E aufgespannte Ebene
heißt Polarisationsebene
Grad der Polarisation ist definiert als:
(
(
)
)
(
(
W θ , γ = 0o − W θ , γ = 90o
P(θ ) =
W θ , γ = 0o + W θ , γ = 90o
Bei Emission unter Θ=90º
steht der elektrische Feldvektor E entweder senkrecht (γ=90°) oder parallel
(γ=0°) zur Quantisierungsachse z.
)
)
Polarisation und Comptonstreuung
Klein-Nishina-Formel:
dσ r ⎛⎜ Eγ ' ⎞⎟
=
dΩ 2 ⎜⎝ Eγ ⎟⎠
2
e
2
⎡ Eγ ' Eγ
⎤
2
2
+
− 2 sin ϑ cos γ ⎥
⎢
⎢⎣ Eγ Eγ '
⎥⎦
γ
Comptonstreuung bevorzugt Streuung in Ebene senkrecht zum E-Vektor!
Aus der Messung einer bevorzugten Richtung bzw. einer
Asymmetrie in der Comptonstreuung kann man auf die
Polarisation zurückschließen
Polarisation – Messung der Asymmetrie 1
(
(
)
)
(
(
W θ , γ = 0o − W θ , γ = 90o
P(θ ) =
W θ , γ = 0o + W θ , γ = 90 o
)
)
A(θ ) =
N ⊥ − N ||
N ⊥ + N||
= Q(Eγ )⋅ P(θ )
Q: Polarisations-Sensitivität
N ⊥ = W (θ , γ = 0o )⋅
dσ
dσ
(
(
ϑ , ϕ = 90o ) + W (θ , γ = 90o ) ⋅
ϑ , ϕ = 0o )
dΩ
dΩ
Zählraten für
Streuung senkrecht
und parallel zur
dσ
dσ
Emissionsebene
ϑ , ϕ = 0o + W θ , γ = 90o ⋅
ϑ , ϕ = 90o
N || = W θ , γ = 0o ⋅
dΩ
dΩ
(
)
(
)
(
)
(
)
Polarisation – Messung der Asymmetrie 2
Compton-Streuung bevorzugt
Streuung in Ebene senkrecht
zum E-Vektor!
Magnetische Strahlung:
E steht senkrecht zur Emissionsebene
N|| > N ⊥ ⇒ A(θ ) =
N ⊥ − N||
N ⊥ + N||
<0
Elektrische Strahlung:
E steht parallel zur Emissionsebene
N|| < N ⊥ ⇒ A(θ ) =
N ⊥ − N||
N ⊥ + N||
>0
A(θ)
Übergangswahrscheinlichkeiten 1
Abgestrahlte Leistung einer klassischen Multipolantenne:
8π (l + 1)c ⎛ ω ⎞
P (σl ) =
⎟
2 ⎜
l[(2l + 1)!!] ⎝ c ⎠
2 l+2
M σ2l
Quantenmechanik: Übergangswahrscheinlichkeit
Ti → f
P(σl )
8π (l + 1)c ⎛ hω ⎞
≡
=
⎜
⎟
2
hω
h
c
l[(2l + 1)!!] hc ⎝
⎠
8π (l + 1)c ⎛ Eγ ⎞
⎜⎜ ⎟⎟
=
2
l[(2l + 1)!!] hc ⎝ hc ⎠
2 l +1
2 l +1
i Mˆ (σl, μ ) f
2
i Mˆ (σl, μ ) f
2
Übergangswahrscheinlichkeit enthält wichtige Information über die
Wellenfunktionen von Ausgangszustand |i> und Endzustand |f>!!!
Übergangswahrscheinlichkeiten 2
Ti→ f
8π (l + 1) ⎛ Eγ ⎞
=
⎟⎟
2 ⎜
⎜
h
c
l[(2l + 1)!!] h ⎝ ⎠
2 l+1
J i mi Mˆ (σl, μ ) J f m f
2
• Wir kennen üblicherweise weder den magnetischen Unterzustand des
Anfangszustandes noch den des Endzustandes!!
• Daher wird über alle magnetischen Unterzustände des Ausgangszustandes
gemittelt und über die magnetischen Unterzustände des Endzustandes summiert:
Wigner-Eckart-Theorem:
Faktorisierung in Matrixelement, das von Orientierung unabhängig ist,
und Clebsch-Gordan-Koeffizient, der die Drehimpulskopplung beinhaltet:
ji mi Oˆ lμ j f m f =
ji mi lμ j f m f
1442443
ji Oˆ l j f
Clebsch −Gordan − Koeffizient
Reduzierte
Übergangsstärke
oder
-wahrscheinlichkeit
B (σl, J i → J f ) ≡
=
1
∑
2 J i + 1 mi , m f , μ
1
2Ji +1
Reduziertes
Matrixelement
J i mi Mˆ (σl, μ ) J f m f
J i Mˆ (σl ) J f
2
2
Übergangswahrscheinlichkeiten 3
Ti → f
8π (l + 1) ⎛ Eγ ⎞
⎜ ⎟⎟
=
2 ⎜
l[(2l + 1)!!] h ⎝ hc ⎠
2 l +1
B (σl, J i → J f )
Zusammenhang zwischen Übergangswahrscheinlichkeit und reduziertem
Matrixelement bzw. reduzierter Übergangswahrscheinlichkeit:
Ti → f (σl ) = Const ⋅ Eγ
2 l +1
⋅ B (σl, J i → J f )
T(σℓ) in [s-1]
Eγ in [MeV]
B(Eℓ) in [e2fm2ℓ]
B(Mℓ) in [μN2 fm2ℓ-2]
Messung von Übergangswahrscheinlichkeiten
Messgröße beim Zerfall von angeregten Zuständen:
Lebensdauer τ ≡
Zerfallsgesetz:
1
λ
=
1
Ti→ f
dn
= −λ ⋅ n (t )
dt
bzw. Halbwertszeit
T1/ 2 =
ln 2
λ
= τ ln 2
n (t ) = n0 ⋅ e − λt
Aus der Messung der Halbwertszeit eines Zustandes erfährt man etwas über
die Matrixelemente, die diesen Zustand mit anderen Zuständen verbindet.
Diese Matrixelemente geben wiederum Aufschluss über die Wellenfunktion der
beteiligten Zustände.
Näheres zur experimentellen Methoden zur Bestimmung von Lebensdauern
→ Kapitel „Lebensdauermessung“
Alternativ lassen sich reduzierte Matrixelemente auch aus Anregungswahrscheinlichkeiten in Coulombanregung bestimmen
Näheres dazu → Kapitel „ Coulombanregung“
Weisskopfabschätzung 1
Betrachte Anregung eines Nukleons in einen Schalenmodellzustand:
J i Mˆ (σl ) J f = ℜl ⋅ ji er lYl j f
{ 142
4 43
4
Radial
Integral
Winkel − Integral
Beispiel: elektrische Multipolstrahlung:
Winkel −Integral
6444
4744448
2 e2
1
1
B (El, J i → J f ) = (2l + 1) J i 2 l0 J f 2
⋅ ℜ2l
4π
• Der Winkelanteil ist exakt berechenbar (unabhängig vom verwendeten Potential)
• Radialanteil müsste für jeden Zustand / Potential genau berechnet werden
Einfachste Alternative (Abschätzung nach Weisskopf)
• Winkelanteil =1
• Annahme einer konstanten Radialwellenfunktion
im Kern:
ℜWl =
l
3
3
(
R0l =
1,2 fm ⋅ A1 / 3 )
l+3
l+3
Weisskopfabschätzung 2
2
elektrische Multipolstrahlung:
1 ⎛ 3 ⎞ 2 2l
⋅⎜
BW (El, J i → J f ) =
⎟ e R0
4π ⎝ l + 3 ⎠
magnetische Multipolstrahlung:
10 ⎛ 3 ⎞ 2 2 l−2
B (Ml, J i → J f ) = ⋅ ⎜
⎟ μ N R0
π ⎝l+2⎠
2
W
Man vergleicht oft gemessene Übergangsmatrixelemente mit der
Weisskopfabschätzung. Das Resultat wird in sog. Weisskopf-Einheiten
(Weisskopf-Units W.U.) angegeben.
Weisskopfabschätzung 3
Halbwertszeiten nach der Weisskopfabschätzung
inkl.
Konversion
Wechselwirkung von Gammaquanten
mit Materie
Messung von Gammastrahlung
z
Gammastrahlung wird in einem Detektor über eine Wechselwirkung
mit dem Detektormaterial nachgewiesen
z
Wechselwirkungsarten von Gammastrahlung mit Materie
– Photoeffekt
– Compton-Streuung
– Paarbildung
Nachweis von Gammastrahlung – Photoeffekt
•
•
•
Direkte Absorption eines Photons durch ein atomares Elektron mit
anschließender Emission des Elektrons
Nicht möglich für freie Elektronen!
Rückstossimpuls wird vom Atom aufgenommen
E = hν − B.E .
... Röntgen-Quant
wird auch gemessen
→ E = hν
Wirkungsquerschnitt:
σ Photo
Z 4 −5
≅ const. × 7 / 2
Eγ
Absorptionskanten
= Bindungsenergie
der Hüllenelektronen
Nachweis von Gammastrahlung – Compton-Streuung 1
Elastische Streuung des
Gammaquants an einem
(freien) Elektron
Wellenlängendifferenz:
λ '−λ = λC (1 − cosθ )
Compton-Wellenlänge des Elektrons:
h
2πhc 6,28 ⋅197 MeV ⋅ fm
λC =
=
=
≈ 2400 fm
2
me c me c
0,511 MeV
E0 = me c 2 = 511 keV
Nachweis von Gammastrahlung – Compton-Streuung 2
Restenergie des gestreuten
Gamma-Photons:
Eγ ' =
Eγ ⋅ me c 2
me c + Eγ (1 − cos θ )
2
Energiespektrum
der Elektronen
Maximale Energie des
gestreuten Elektrons:
( )
T e−
max
=
2 Eγ2
me c 2 + 2 Eγ
Prinzipielle Form des Spektrums
Nachweis von Gammastrahlung – Compton-Streuung 3
Wirkungsquerschnitt der Comptonstreuung
Klein-Nishina Formel:
2
2
⎞
⎛
(
)
Γ
−
1
1
cos
θ
dσ re2
2
⎜1 + cos θ +
⎟
=
2 ⎜
1 + Γ(1 − cos θ ) ⎟⎠
dΩ 2 [1 + Γ(1 − cos θ )] ⎝
„klassischer Elektronenradius“
Γ=
Eγ
me c 2
e2
re =
≈ 2.818 fm
2
4πε 0 me c
Die Klein-Nishina-Formel wird noch modifiziert, wenn die Linearpolarisation
der Strahlung mit berücksichtigt wird.
Nachweis von Gammastrahlung – Compton-Streuung 3
⎧1 + Γ ⎡ 2(1 + Γ ) 1
1 + 3Γ ⎫
⎤ 1
− ln (1 + 2Γ )⎥ +
σ C = 2π r ⎨ 2 ⎢
ln(1 + 2Γ ) −
2⎬
Γ
Γ
+
Γ
Γ
1
2
2
(
)
+
Γ
1
2
⎣
⎦
⎩
⎭
2
e
Γ=
Winkelverteilung
Eγ
me c 2
Nachweis von Gammastrahlung – Paarbildung
Umwandlung eines Photons in ein
Elektron-Positron-Paar
• Minimale Energie des Photons:
2mec2 = 1,022 MeV
• Kern muss Rückstoss aufnehmen
Wirkungsquerschnitt:
σ paar
⎡ 7 ⎛ 2 Eγ
⎞ 109 ⎤
= 4 Z α r ⎢ ⎜⎜ ln
− f ( Z ) ⎟⎟ −
⎥
2
m
c
54
9
e
⎠
⎦
⎣ ⎝
2
2
e
f(Z): Coulomb-Korrektur
α=1/137 : Feinstrukturkonstante
Nachweis von Gammastrahlung
– Totaler Wirkungsquerschnitt 1
Grosses Z des Materials ⇔ grosser WQ für Photoeffekt
Nachweis von Gammastrahlung
– Totaler Wirkungsquerschnitt 2
Wesentlicher Energiebereich für viele Kernstrukturuntersuchungen
Nachweis von Gammastrahlung – Form des Spektrums 1
Nachweis von Gammastrahlung – Form des Spektrums 2
Nachweis von Gammastrahlung – Form des Spektrums 3
Eγ = 766 keV
Eγ = 1779 keV