Schulcurriculum LUG Mathematik Klasse 5 u. 6 - Ludwig
Werbung
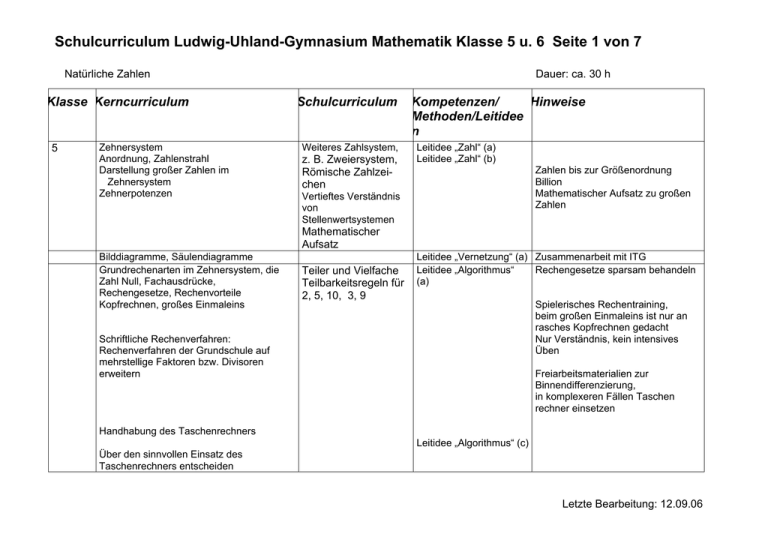
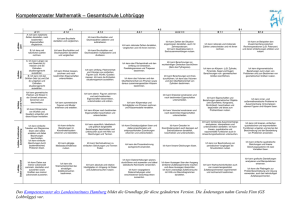
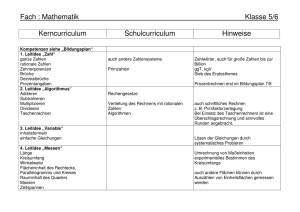
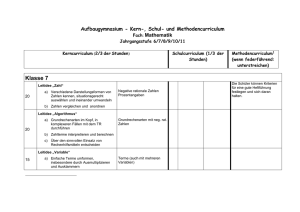
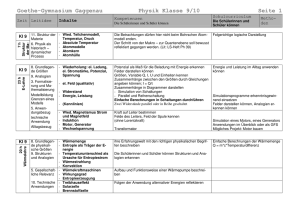
Schulcurriculum Ludwig-Uhland-Gymnasium Mathematik Klasse 5 u. 6 Seite 1 von 7 Natürliche Zahlen Klasse Kerncurriculum 5 Zehnersystem Anordnung, Zahlenstrahl Darstellung großer Zahlen im Zehnersystem Zehnerpotenzen Dauer: ca. 30 h Schulcurriculum Weiteres Zahlsystem, z. B. Zweiersystem, Römische Zahlzeichen Kompetenzen/ Hinweise Methoden/Leitidee n Leitidee „Zahl“ (a) Leitidee „Zahl“ (b) Zahlen bis zur Größenordnung Billion Mathematischer Aufsatz zu großen Zahlen Vertieftes Verständnis von Stellenwertsystemen Mathematischer Aufsatz Bilddiagramme, Säulendiagramme Grundrechenarten im Zehnersystem, die Zahl Null, Fachausdrücke, Rechengesetze, Rechenvorteile Kopfrechnen, großes Einmaleins Teiler und Vielfache Teilbarkeitsregeln für 2, 5, 10, 3, 9 Leitidee „Vernetzung“ (a) Zusammenarbeit mit ITG Rechengesetze sparsam behandeln Leitidee „Algorithmus“ (a) Spielerisches Rechentraining, beim großen Einmaleins ist nur an rasches Kopfrechnen gedacht Nur Verständnis, kein intensives Üben Schriftliche Rechenverfahren: Rechenverfahren der Grundschule auf mehrstellige Faktoren bzw. Divisoren erweitern Freiarbeitsmaterialien zur Binnendifferenzierung, in komplexeren Fällen Taschen rechner einsetzen Handhabung des Taschenrechners Leitidee „Algorithmus“ (c) Über den sinnvollen Einsatz des Taschenrechners entscheiden Letzte Bearbeitung: 12.09.06 Schulcurriculum Ludwig-Uhland-Gymnasium Mathematik Klasse 5 u. 6 Seite 2 von 7 Runden, Überschlagsrechnungen Zahlenausdrücke ohne und mit Klammern Vertiefende Übungen Leitidee „Algorithmus“ (d) Leitidee „Zahl“ (c) Leitidee „Algorithmus“ (b) Variable, einfache Gleichungen Leitidee „Variable“ (a), (b) Geometrische Grunderfahrungen Klasse Kerncurriculum 5 Runden ausführlich, Überschlag sparsam Auch Übertragen eines Zahlenausdrucks in verbale Form und umgekehrt Lösen auch durch systematisches Probieren Dauer: 20 h Schulcurriculum Kompetenzen/ Hinweise Methoden/Leitideen Geometrische Grundobjekte Parallelität, Orthogonalität Abstände Spiegeln an Gerade Symmetrie Rechteck, Quadrat Parallelogramm, Dreieck Quadratisches Gitter Quader, Würfel Oberfläche, Kante, Ecke, Diagonale, Netz, Pentominos; Bauen Schrägbild mit „EFFEKT“- Baukasten Leitidee „Raum und Form“ (a),(b) Leitidee „Raum und Form“ (a)– c) Leitidee „Raum und Form“ (b) Leitidee „Raum und Form“ (c), (d) Leitidee „Raum und Form“ (a)– (c) Leitidee „Vernetzung“ (a) Leitidee „Raum und Form“ (a), (b) Leitidee „Raum und Form“ (a)- (c), (e) Leitidee „Vernetzung“ (a) Begriffe, wo immer möglich, durch altersgemäßes Hantieren erschließen Freiarbeitsmaterial: Nagelbretter Kreatives Entwerfen und Gestalten Koordinatensystem Eigenständiges Entdecken von Eigenschaften Vertiefung der Raumanschauung, Verbalisieren, Verwenden von Fachausdrücken Letzte Bearbeitung: 12.09.06 Schulcurriculum Ludwig-Uhland-Gymnasium Mathematik Klasse 5 u. 6 Seite 3 von 7 : Mathematik in der Praxis: Größen Klasse 5 Kerncurriculum Maßeinheiten von Längen, Massen, Zeitspannen, Dauer: 25 h Schulcurriculum Themenorientierung Kompetenzen/ Hinweise Methoden/Leitideen Leitidee „Messen“ (a)-(d) Flächeninhalten, Rauminhalten Umwandlung, Maße schätzen und bestimmen Rechnen mit Größen Umfang und Flächeninhalt von Rechtecken Oberflächen- und Rauminhalt von Quadern Sachaufgaben Maßstäbliches Zeichnen Leitidee „Modellieren“ (b) Leitidee „Messen“ (b)-(d) Leitidee „Variable“ (c) Leitidee „Funktionaler Zusammenhang“ (a), (b) Leitidee „Messen“ (b)-(d) Leitidee „Variable“ (c) Leitidee „Funktionaler Zusammenhang“ (a), (b) Leitidee „Messen“ (b) Leitidee „Variable“ (a), (b) Leitidee „Modellieren“ (b), (d) Leitidee „Vernetzung“ (a)(d) Leitidee „Modellieren“ (a) Bruch- und Kommaschreibweise nur so weit in Sachaufgaben sinnvoll Lesen von Fahrplänen. Nachdruck auf die Umrechnungszahlen legen und häufig üben. Empfehlung: Hier Taschenrechner einführen Leitidee „Vernetzung“ (a) : Letzte Bearbeitung: 12.09.06 Schulcurriculum Ludwig-Uhland-Gymnasium Mathematik Klasse 5 u. 6 Seite 4 von 7 Bruchzahlen (Teil 1) Klasse 5 Kerncurriculum Brüche Erweitern und Kürzen Darstellung am Zahlenstrahl, Gleichheit, Größer-Relation Addition und Subtraktion von Brüchen Dauer: 15 h Schulcurriculum Kompetenzen/ Hinweise Methoden/Leitideen Prozent Leitidee „Zahl“ (a) Leitidee „Zahl“ (a) Leitidee „Zahl“ (b) Leitidee „Zahl“ (b) Leitidee „Algorithmus“ (a) Bruchzahlen (Teil 2) Klasse 6 Kerncurriculum Multiplikation und Division von Brüchen Rechengesetze und ihre Begründung Rechenvorteile Bruchzahlen zunächst in Größenbereichen veranschaulichen Binnendifferenzierung in der Übungsphase (Freiarbeitsmaterial), in komplexeren Fälle Taschenrechner einsetzen Dauer: 30 h Schulcurriculum Kompetenzen/ Hinweise Methoden/Leitideen Leitidee „Algorithmus“ (a) Binnendifferenzierung in der Übungsphase (Freiarbeitsmaterial) Selbstvertrauen durch Erfolgserlebnisse fördern, in komplexeren Fälle Taschenrechner einsetzen (c) (b) Zahlterme Dezimalbrüche Umwandlung der Bruchschreibweise in Dezimalschreibweise und umgekehrt Leitidee „Zahl“ (a) Einfache Beispiele genügen. Freiarbeitsmaterial vorhanden Letzte Bearbeitung: 12.09.06 Schulcurriculum Ludwig-Uhland-Gymnasium Mathematik Klasse 5 u. 6 Seite 5 von 7 Rechnen mit abbrechenden Dezimalbrüchen Leitidee „Algorithmus“(a)(d) Rationale Zahlen Klasse 6 Dauer: 30 h Kerncurriculum Schulcurriculum Kompetenzen/ Methoden/Leitideen Zahlbereichserweiterung Leitidee „Zahl“ (a) Zahlengerade, Anordnung Betrag Rechnen mit rationalen Zahlen Anwendungen Leitidee „Zahl“ (b) Winkel und Kreis Klasse 6 Hinweise Dieses Kapitel am Ende von 6 unterrichten Leitidee „Algorithmus“ (a)-(c) Leitidee „Modellieren“ (b) Leitidee „Vernetzung“ (a)-(d) Dauer: 25 h Kerncurriculum Winkel Winkelmessung, auch Schätzen Scheitelwinkel, Nebenwinkel, Winkelhalbierende Punktspiegelung Kreis, Kreisteile Zahl π Kreisfläche; Kreisumfang Umfang und Flächeninhalt von Parallelogramm und Dreieck Schulcurriculum Kompetenzen/ Hinweise Methoden/Leitideen Leitidee „Raum und Form“ (a)-(c) Leitidee „Messen“ (a)-(c) Leitidee „Raum und Form“ (a)-(c) Leitidee „Raum und Form“ (a)-(c) Leitidee „Messen“ Leitidee „Messen“ (a)-(d) Leitidee „Variable“ (c) Leitidee „Funktionaler Zusammenhang“ (a),(b) Letzte Bearbeitung: 12.09.06 Schulcurriculum Ludwig-Uhland-Gymnasium Mathematik Klasse 5 u. 6 Seite 6 von 7 Mathematik in der Praxis: Sachrechnen Klasse 6 Kerncurriculum Runden von Dezimalzahlen Überlegungen zur Genauigkeit Überschlagsrechnungen Systematische Bestimmung von Anzahlen Häufigkeitsverteilungen und ihre Darstellung Urliste Anteile, auch in Prozent Häufigkeitstabelle, Diagramm Mittelwert Dauer:25 h Schulcurriculum Kompetenzen/ Hinweise Methoden/Leitideen Verwendung realitätsnaher Daten; auch selbständiges Erheben, Sammeln und Auswerten z.B. aus der Tagespresse oder bei einem Lerngang Leitidee „Algorithmus“ (d) Angabe des Intervalls, das zu einer gerundeten Zahl gehört Auch für Summe und Produkt Leitidee „Zahl“ (a) Leitidee „Vernetzung“ (a)(d) Leitidee „Modellieren“ (b) Ausgehend von Zufallsexperimenten können hier Vorerfahrungen aus dem Bereich der Stochastik vermittelt werden (s. auch Buch Elemente 1, S. 99/100) Leitidee „Daten und Zufall“ z.B. im Zusammenhang mit dem Schulweg oder dem Freizeitverhalten (a),(b) Leitidee „Zahl“ (a) Leitidee „Vernetzung“ (a)(d) Auch Kreisdiagramme Typische Darstellungsfehler bzw. Übertreibungen beim Diagramm Letzte Bearbeitung: 12.09.06 Schulcurriculum Ludwig-Uhland-Gymnasium Mathematik Klasse 5 u. 6 Seite 7 von 7 Dreisatzaufgaben Leitidee „Funktionaler Zusammenhang“ (a),(b) Interpretation von Graphen, auch entsprechende Grafiken aus Zeitungen Erklären, wie die Änderung einer Größe sich auf die andere auswirkt Ergebnisse sinnvoll runden,durch Schätzen auf Brauchbarkeit überprüfen. Der Dreisatz sollte wie im Buch in Spalten geschrieben werden: Leitidee „Modellieren“ (d) Größe 1 Leitidee „Modellieren“ (c),(d) 5 1 7 Größe 2 15 3 21 Grund: Das (gedachte) Gleichheitszeichen soll vermieden werden. Sachaufgaben Aufstellen und Interpretieren von Termen Interpretation von Graphen Leitidee „Variable“ (a),(b) Leitidee „Modellieren“ (b),(d) Leitidee „Vernetzung“ (a)(d) Einsatz von Freiarbeitsmaterialien Beispiele aus verschiedenen Bereichen; auch: Versprachlichen eines Terms Einfache Situationen mithilfe von Termen und Gleichungen darstellen, durch systematisches Probieren lösen. Dieses Kapitel nicht separat unterrichten. „Modellieren “ a, „Vernetzung“ d Es eignen sich auch entsprechende Graphiken aus Zeitungen Letzte Bearbeitung: 12.09.06