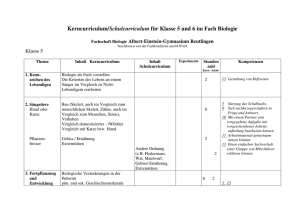
Kl. 7-10 - Liebfrauenschule Sigmaringen
Werbung
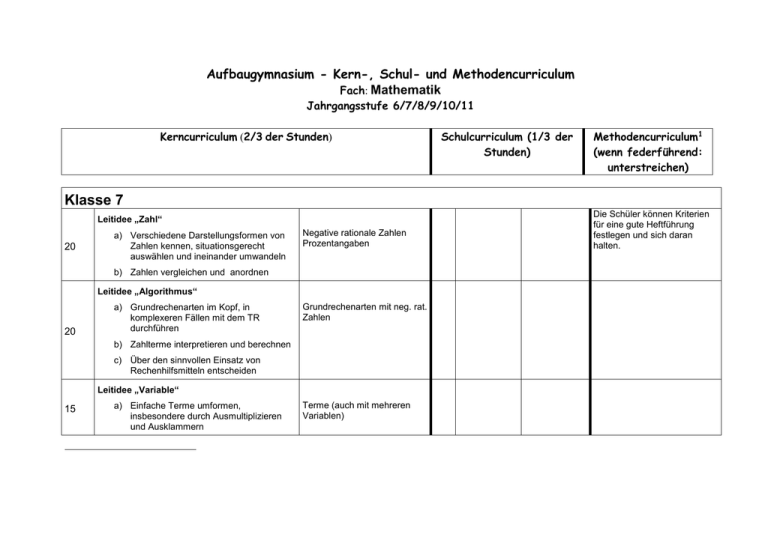
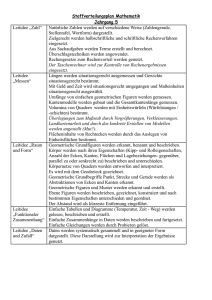
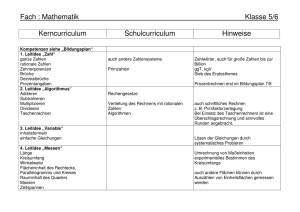
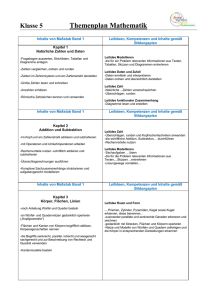
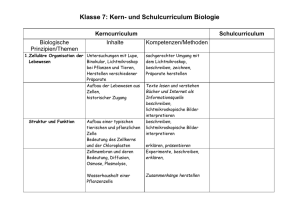
Aufbaugymnasium - Kern-, Schul- und Methodencurriculum Fach: Mathematik Jahrgangsstufe 6/7/8/9/10/11 Kerncurriculum (2/3 der Stunden) Schulcurriculum (1/3 der Stunden) Methodencurriculum1 (wenn federführend: unterstreichen) Klasse 7 Leitidee „Zahl“ 20 a) Verschiedene Darstellungsformen von Zahlen kennen, situationsgerecht auswählen und ineinander umwandeln Negative rationale Zahlen Prozentangaben b) Zahlen vergleichen und anordnen Leitidee „Algorithmus“ 20 a) Grundrechenarten im Kopf, in komplexeren Fällen mit dem TR durchführen Grundrechenarten mit neg. rat. Zahlen b) Zahlterme interpretieren und berechnen c) Über den sinnvollen Einsatz von Rechenhilfsmitteln entscheiden Leitidee „Variable“ 15 a) Einfache Terme umformen, insbesondere durch Ausmultiplizieren und Ausklammern Terme (auch mit mehreren Variablen) Die Schüler können Kriterien für eine gute Heftführung festlegen und sich daran halten. Std. Kerncurriculum Kompetenzen Inhalte Std. Schulcurriculum Kompetenzen Inhalte b) Größengleichungen umformen Leitidee „Messen“ a) Die Struktur und den Gebrauch von Maßsystemen verstehen 20 b) Geeignete Maßgrößen und Einheiten nutzen, um Situationen zu beschreiben und zu untersuchen Flächeninhalte von: Rechteck, Parallelogramm, Dreieck und Kreis c) Maße schätzen und bestimmen Leitidee „Raum und Form“ a) Eigenschaften ebener geometrischer Figuren erkennen und begründen 20 b) Ebene Figuren mit vorgegebenen Eigenschaften darstellen c) Ebene Figuren abbilden 10 Achsen- und Punktspiegelung Winkel an Parallelen Seiten und Winkel im Dreieck Abstände Ortslinien einfache Dreieckskonstruktionen Leitidee „Funktionaler Zusammenhang“ 10 a) Abhängigkeiten dynamisch deuten, d.h. erklären, wie die Änderung einer Größe sich auf die andere auswirkt Leitidee „Daten und Zufall“ 15 a) Daten systematisch sammeln, anordnen und übersichtlich darstellen b) Daten bewerten und aus ihnen Schlüsse ziehen Tabellenkalkulation 7 Einfache Zufallsversuche, Durchschnitte Die Schüler können Daten der Solar-AG in Diagrammen darstellen und interpretieren Methoden Kerncurriculum Kompetenzen Std. Inhalte Klasse 8 Leitidee „Zahl“ 12 a) Verschiedene Darstellungsformen von Zahlen kennen, situationsgerecht auswählen und ineinander umwandeln Prozentangaben b) Zahlen vergleichen und anordnen Leitidee „Algorithmus“ 20 a) Gleichungen und Ungleichungen erkennen sowie rechnerisch und grafisch lösen b) Lineare Gleichungssysteme rechnerisch und grafisch lösen Lineare Gleichungen und Ungleichungen mit einer Variablen Lineare Gleichungssysteme (2x2) c) Über den sinnvollen Einsatz von Rechenhilfsmitteln entscheiden Leitidee „Variable“ 18 a) Einfache Terme umformen, insbesondere durch Ausmultiplizieren und Ausklammern Terme (auch mit mehreren Variablen) Binomische Formeln b) Größengleichungen umformen Leitidee „Raum und Form“ a) Eigenschaften ebener geometrischer Figuren erkennen und begründen 20 b) Ebene Figuren mit vorgegebenen Eigenschaften darstellen Inkreis und Umkreis von Dreiecken kongruente Figuren Einfache Dreieckskonstruktionen, auch c) Kongruenz von Dreiecken erkennen und Bestimmung wahrer Größen anwenden bei Strecken und Flächen Kongruenzsätze Std. Schulcurriculum Kompetenzen Inhalte Methoden Kerncurriculum Kompetenzen Std. Inhalte Std. Klasse 9 Leitidee „Funktionaler Zusammenhang“ a) Funktionale Zusammenhänge erkennen und darstellen 25 Proportionalität lineare Funktionen b) Kennzeichnende Eigenschaften von Funktionen kennen und sachgerecht nutzen c) Funktionen dynamisch deuten Leitidee „Vernetzung“ a) Verschiedene Darstellungsformen einer Funktion ineinander übersetzen 15 b) Algebraische und geometrische Fragestellungen in geeigneten Fällen ineinander überführen und ggf. auf diesem Weg lösen Übersetzung von Darstellungsformen verbal, Tabelle, Term, Graph Leitidee „Modellieren“ 10 a) Inner- und außermathematische Sachverhalte mit Hilfe von Tabellen, Termen oder Graphen beschreiben und umgekehrt Tabellen, Terme und Graphen in Bezug auf einen Sachverhalt interpretieren b) mit Prozentangaben sicher umgehen Interpretation von Graphen und einfachen Termen (Methodencurriculum) Aufstellen von Termen Prozentrechnung 10 Schulcurriculum Kompetenzen Inhalte Methoden Std. Kerncurriculum Kompetenzen Inhalte Std. Schulcurriculum Kompetenzen Inhalte Leitidee „Zahl“ 20 a) Die Unvollständigkeit von Zahlbereichen verstehen und aufzeigen Reelle Zahlen Quadratwurzeln b) Zahlbereiche unterscheiden, Zahlen diesen zuordnen c) Zahlterme vereinfachen Leitidee „Algorithmus“ 16 10 a) Gleichungen und Ungleichungen erkennen sowie manuell, grafisch, und mit Hilfe des GTR lösen Leitidee „Variable“ a) Terme umformen und vereinfachen Leitidee „Raum und Form“ 16 a) Figuren zentrisch strecken, Eigenschaften der zentr. Streckung kennen und anwenden Quadratische Gleichungen Einfache Wurzeln mit Variablen vereinfachen F zentrische Streckung; Strahlensätze Satz des Pythagoras b) grundlegende Sätze zur Berechnung von Strecken-längen kennen und anwenden Leitidee „Funktionaler Zusammenhang“ 20 a) Funktionale Zusammenhänge erkennen und darstellen Proportionalität b) Kennzeichnende Eigenschaften von Funktionen kennen und sachgerecht nutzen Quadratische Funktionen Potenzfunktionen mit natürlichen Hochzahlen c) Funktionen dynamisch deuten Leitidee „Daten und Zufall“ 16 a) den Begriff Wahrscheinlichkeit Wahrscheinlichkeitsverteilung; Pfadregeln Auch LGS (3x4) Methoden Std. Kerncurriculum Kompetenzen Inhalte verstehen b) Wahrscheinlichkeiten bei mehrstufigen Zufalls-experimenten berechnen Leitidee „Vernetzung“ a) Verschiedene Darstellungsformen einer Funktion ineinander übersetzen 12 b) Algebraische und geometrische Fragestellungen in geeigneten Fällen ineinander überführen und ggf. auf diesem Weg lösen Übersetzung von Darstellungsformen verbal, Tabelle, Term, Graph Leitidee „Modellieren“ 10 a) Inner- und außermathematische Sachverhalte mit Hilfe von Tabellen, Termen oder Graphen beschreiben und umgekehrt Tabellen, Terme und Graphen in Bezug auf einen Sachverhalt interpretieren Interpretation von Graphen und einfachen Termen (vgl. Methodencurriculum) Aufstellen von Termen Std. Schulcurriculum Kompetenzen Inhalte Methoden Kerncurriculum Kompetenzen Std. Inhalte Klasse 10 Leitidee „Zahl“ a) Besondere Darstellungsformen von reellen Zahlen und anwenden 16 b) Objekte und Verknüpfungen zur rechnerischen Behandlung geometrischer Fragestellungen kennen und einsetzen Potenzen mit rationalen Hochzahlen Normdarstellung Logarithmus Leitidee „Variable“ a) Einfache Terme umformen 12 b) Elementare Gleichungen lösen Rechenregeln für Potenzen und Logarithmen (zur Lösung einfacher Gleichungen) Leitidee „Messen“ Raum- und Oberflächeninhalt Inhaltsformeln einfacher Körper von Prisma und Zylinder kennen und mithilfe der Ideen „Zerlegung“ und „Annäherung“ einsichtig machen Umfang und Inhalt von Figuren; auch durch b) Maße von Figuren und Körpern Kreisbögen begrenzt abschätzen und mithilfe der Zusammengesetzte Körper Formelsammlung berechnen Pyramide, Kegel a) 20 Leitidee „Raum und Form“ a) Seitenlängen und Winkelweiten am rechtwinkligen Dreieck berechnen 20 b) Grundlegende Sätze zur Berechnung von Streckenlängen kennen und anwenden Berechnen von Streckenlängen und Inhalten bei Körpern sin ( ) , cos ( ) , tan ( ) Std. Schulcurriculum Kompetenzen Inhalte Methoden Std. Kerncurriculum Kompetenzen Inhalte Leitidee „Funktionaler Zusammenhang“ 16 a) Über Grundkompetenzen im Umgang mit Potenzfunktionen mit ganzen und einfachen rationalen Funktionen verfügen Hochzahlen Einfache Exponentialfunktionen Leitidee „Vernetzung“ a) Verschiedene Darstellungsformen einer Funktion ineinander übersetzen 12 b) Algebraische und geometrische Fragestellungen in geeigneten Fällen ineinander überführen und ggf. auf diesem Weg lösen Übersetzung von Darstellungsformen: verbal, Tabelle, Term , Graph c) Den GTR als Hilfsmittel einsetzen Leitidee „Modellieren“ 16 a) einen Sachverhalt auf angemessene Weise math. Beschreiben. Eine zugehörige Problemstellung im gewählten math. Modell lösen und die Ergebnisse auf die Ausgangssituation übertragen, interpretieren und überprüfen b) Wachstumsvorgänge durch diskrete Modelle beschreiben und interpretieren c) Das Änderungsverhalten von Größen analytisch beschreiben und interpretieren Proportionalität; lineares , natürliches und beschränktes Wachstum Std. Schulcurriculum Kompetenzen Inhalte Methoden Kerncurriculum Kompetenzen Std. Inhalte Std. Schulcurriculum Kompetenzen Inhalte Methoden Klasse 11 Leitidee „Zahl“ 12 a) Objekte und Verknüpfungen zur rechnerischen Behandlung geom. Fragestellungen kennen und einsetzen Vektoren, Linearkombination Leitidee „Algorithmus“ 22 a) LGS lösen LGS (3x3 ; 3x2) b) Einfache Funktionen ableiten Ableitung von xn ( n aus N) und 1/x Ableitungsregeln für Potenz, Summe und konstanter Faktor c) Werte iterativ berechnen Fördermaßnahmen für Quereinsteiger von RS Leitidee „Raum und Form“ 14 a) Geometrische Objekte im Raum analytisch beschreiben und ihre Lagebeziehungen analysieren Leitidee „Funktionaler Zusammenhang“ a) Grundkompetenzen im Umgang mit Funktionen haben b) Funktionen auf lokale und globale Eigenschaften untersuchen 28 c) Wirkungen von Parametern in Funktionen verstehen Ortsvektor, Geradengleichung Eigenschaften von Funktionen: Nullstellen, Extremstellen, Monotonie, Ganzrat. Funktionen x x k (k 1;2) ; x a x x sin( x) ; x cos(x) d) Das Änderungsverhalten von Funktionen Verschobene und gestreckte Graphen qualitativ beschreiben Änderungsrate und Ableitung Ableitungsfunktion Geraden, Punkt-SteigungsForm, Zwei-Punkte-Form Tangente und Normale Fördermaßnahmen für Quereinsteiger von RS Std. Kerncurriculum Kompetenzen Inhalte Leitidee „Daten und Zufall“ 20 a) Wahrscheinlichkeiten von Ereignissen berechnen b) Erwartungswert einer Zufallsvariablen verstehen und berechnen 12 b) Math. Denken und Modellieren in außermathematischen Gebieten wie Kunst, Naturwissenschaften und Gesellschaft anwenden c) Grundlegende Problemlösetechniken kennen und anwenden Unabhängigkeit von Ereignissen, Binomialverteilung, Erwartungswert Umgang mit Hilfsmitteln wie Formelsammlung, GTR, Software, elektronischen Medien, Internet Problemlösetechniken Leitidee „Modellieren“ 12 a) einen Sachverhalt auf angemessene Weise math. beschreiben. Eine zugehörige Problemstellung im gewählten math. Modell lösen und die Ergebnisse auf die Ausgangssituation übertragen, interpretieren und überprüfen Methoden 10 Leitidee „Vernetzung“ a) Hilfsmittel effizient einsetzen Std. Schulcurriculum Kompetenzen Inhalte Simulation dynamischer Vorgänge Momentane Änderungsrate von Größen Fördermaßnahmen für Quereinsteiger von RS