Grundlagen der Ökonomie Übungen - Franz Sinabell

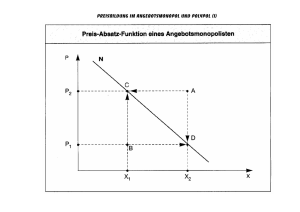
G r u n d l a g e n
d e r
Ö k o n o m i e
Ü b u n g e n
Franz Sinabell, WIFO, [email protected]
Problemstellungen 11. Jänner 2011
1. Aufgabe
Gegeben ist folgende Nachfragefunktion: q = 100 – 2 p
a) Zeichnen Sie die Nachfrage- und Grenzerlösfunktion! Berechnen Sie die Gesamt- und
Grenzerlösfunktion!
b) Welche Werte nimmt die Preiselastizität der Nachfrage im Punkt mit dem Maximum der
Gesamterlösfunktion an?
c) Wie viel von dem Gut wird abgesetzt, wenn der Preis p = 30 Geldeinheiten ist? Wie hoch ist der
Umsatz bei dieser Menge?
2. Aufgabe
Hinweise zur Terminologie:
Totalkosten (=Gesamtkosten) TK; Englisch TC total costs
Durchschnittskosten DK, Englisch AC average costs
Fixkosten FK, Englisch FC fixed costs
Variable Kosten VK, Englisch VC variable costs
Grenzkosten GK, English MC marginal costs
Gesamterlös (Gesamtumsatz), English TR total revenue
Grenzerlös (Grenzumsatz), Englisch MR marginal revenue
Gegeben sind Fixkosten (FK) und variable Kosten VK eines Monopolisten:
FK = 250 und VK = q + 0,000125 * q2
Gegeben ist die relevante Nachfragefunktion: q = 20000 – 4000 * p
a) Ermitteln und zeichnen Sie in einer Abbildung: Gesamterlös-, Gesamtkosten- und
Gewinnfunktion ein!
b) Zeichnen Sie in einer zweiten Abbildung Grenzkosten und Nachfragefunktion!
c) Berechnen Sie die Menge, bei der der Gewinn maximiert wird!
Welchen Preis legt der Monopolist fest bzw. wieviel Ware setzt der Monopolist ab, um den
Gewinn zu maximieren?
d) Wie hoch ist die Summe aus Produzentenrente und Konsumentenrente
1
Nehmen Sie nun an, es handelt sich nicht um ein Monopol, sondern um ein Polypol:
a) Welche Menge wird im Polypol abgesetzt?
b) Wie hoch ist der Preis im Polypol?
c) Wie hoch ist die Summe aus Konsumentenrente und Produzentenrente im Polypol?
3. Aufgabe
Die Amoroso-Robinson-Relation beschreibt in der Mikroökonomie die Beziehung zwischen Preis,
Grenzumsatz und Preiselastizität der Nachfrage. Sie kann abgeleitet werden aus dem folgenden
Zusammenhang: MR = p + p (1/η).
Wobei: MR = marginal revenue Grenzerlös (=Grenzumsatz), p = Preis, η = Preiselastizität der
Nachfrage.
Versetzen Sie sich in die Lage eines Anbieters, der den Preis seiner Ware fixieren kann, ohne
Konkurrenz fürchten zu müssen. Die Ware kostet ihm im Einkauf 15 Euro und η = -1,5.
a) Welchen Verkaufspreis legt der Anbieter fest?
b) Unter welcher Bedingung beträgt der Verkaufspreis 15 Euro?
4. Aufgabe
Gegeben folgende Kostenfunktion in Abhängigkeit vom Output y:
TK (y) = a . y 1/α + FK
[Summe aus variablen Kosten a . y 1/α und Fixkosten FK]
TK ... Totalkosten (= Gesamtkosten)
y ... Output
Die Parameter betragen:
1)
a = 0,0050363
α = 0,375
FK = 300
Ermitteln Sie analytisch:
Grenzkostenfunktion
durchschnittliche variable Kosten
2)
Führen Sie in einem Tabellenkalkulation eine Wertetabelle aus mit folgendem Inhalt:
Als unabhängige Variable Output (y) von 5 bis 125 in Schritten von 5 Einheiten
und davon abhängig folgende Größen:
Fixkosten
Totalkosten
2
Grenzkosten
var.Kosten
Ø Totalkosten
Ø Fixkosten
Ø variable Kosten
Jede Einheit des Outputs erzielt einen Preis von py=25 Geldeinheiten. Ermitteln Sie:
Grenzerlös
Gesamterlös
Gewinn
Schicken Sie das Tabellenblatt an [email protected].
5. Aufgabe
Gegeben sind folgende Produktionsparameter:
Produktionsfunktion Weizen in t je Hektar: y = 1 + 0,09 * N – 0,0004 * N2
Emissionsfunktion mg Nitrat im Grundwasser: z = 0,1 N + 0,007 * N2
Preis Stickstoffdünger pN = 0,45 Euro/kg
Preis Weizen pW = 150 Euro/t
Fixkosten je Hektar: 360 Euro
1)
Ermitteln Sie analytisch:
Profitfunktion
Gesamtkostenfunktion TK und Grenzkostenfunktion dTK/dy
Grenzertragsfunktion dy/dN
2)
Erstellen Sie eine Wertetabelle zu unterschiedlichen Weizenpreisen; fertigen Sie eine
Zeichnung davon an!
pW
pN
100
125
150
175
0,45
0,45
0,45
0,45
DüngerMenge
N
Weizenertrag
t/ha
3
Gewinn ∏
Emission
3)
4)
Erstellen Sie eine Wertetabelle zu unterschiedlichen Düngerpreisen; fertigen Sie eine
Zeichnung davon an!
pW
pN
150
150
150
150
0,30
0,45
0,75
1,25
DüngerMenge
N
Weizenertrag
t/ha
Gewinn ∏
Emission
Wie viel darf gedüngt werden, dass der Grenzwert von 45 mg Nitrat im Grundwasser nicht
überschritten wird?
a)
Bei welchem Düngerpreis ist dies der Fall, wenn pw = 150 Euro / t
b)
Bei welchem Weizenpreis ist dies der Fall, wenn pN = 4,5 Euro / kg
4