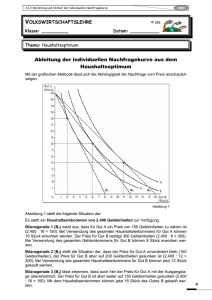
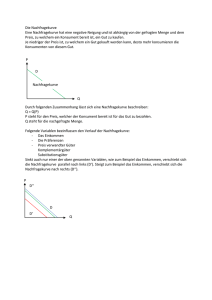
Ableitung der individuellen Nachfragekurve aus dem
Werbung

3.2.2 Herleitung und Verlauf der individuellen Nachfragekurve VOLKSWIRTSCHAFTSLEHRE Klasse: __________ © SEI Datum: ___________ Thema: Haushaltsoptimum Ableitung der individuellen Nachfragekurve aus dem Haushaltsoptimum Aus unserer Lebenserfahrung wissen wir bereits, dass die Preise der Wirtschaftsgüter und die Nachfrage nach diesen Gütern in einem bestimmten Zusammenhang stehen. Ein sparsamer Verbraucher wird, falls er genügend Zeit hat, regelmäßig die Preise in den verschiedenen Geschäften vergleichen, um sein Haushaltsgeld (sein Budget) zu schonen. Die Nachfrage nach einem Gut lässt sich aus den Gossen’schen Gesetzen ableiten. Denn Geld ist aus der Sicht des wirtschaftenden Menschen ebenfalls ein Gut, weil ihm der Besitz von Geld Nutzen stiftet. Die Hergabe von Geld bedeutet Nutzenverzicht, die Einnahme von Geld Nutzengewinn. Der private Haushalt maximiert seinen Nutzen dann, wenn sich beim Kauf eines Gutes der dadurch entstehende Nutzengewinn und der durch die Hergabe des Geldes hervorgerufene Nutzenverlust ausgleichen. Je teurer eine Ware ist, desto mehr „tut es einem Haushalt weh“, noch einen zusätzlichen Geldschein hergeben zu müssen. Der Haushalt wird also im Normalfall weniger von dem begehrten Gut kaufen wollen als bisher, wenn dessen Preis steigt. Im Extremfall wird er ganz auf den Kauf verzichten. Das Gleiche gilt natürlich auch im umgekehrten Sinne. Beispiel: Die Nutzentabelle auf der Folgeseite zeigt die „Bedürfnisstruktur“ der ferienhungrigen Frau Hella Bronn, die stets das gleiche Reiseziel aufsucht. Hat sie z. B. 1.000,00 Euro auf dem Konto und macht sie zwei Ferienreisen, hat sie einen Gesamtnutzen von 21 Nutzeneinheiten (NE). Kann sie z. B. drei Reisen bei einem Barvermögen von 1.000,00 Euro machen, so steigt ihr Nutzen auf insgesamt 23,5 NE. Eine weitere Reise bringt ihr bei gleichem Geldvermögen nur noch einen Nutzenzuwachs (Grenznutzen) von 1,5 (= Erstes Gossen’sches Gesetz). Mehr Geld (bei gleicher Anzahl von Ferienreisen) bringt Frau Bronn ebenfalls einen (abnehmenden) zusätzlichen Nutzen. Zum Beispiel hat sie bei einer Ferienreise und einem Barvermögen von 5.000,00 Euro einen Nutzen von 29 NE. Die Kombination 6.000,00 Euro und eine Ferienreise hat für sie ein Nutzenniveau von 30. Aus der Nutzentabelle lässt sich entnehmen, dass es verschiedene Kombinationen von Geld einerseits und Ferienreisen andererseits gibt, die Frau Bronn den gleichen Nutzen stiften. Dies gilt z. B. für die Kombinationen 9.000,00 Euro auf dem Konto und eine Ferienreise, 4.000,00 Euro auf dem Konto und zwei Ferienreisen, 3.000,00 Euro auf dem Konto und drei Ferienreisen sowie 2.000,00 Euro und sechs Ferienreisen. Diese Kombinationen sind für Frau Bronn völlig gleichwertig, also indifferent. Verbindet man die Kombinationen gleichen Nutzens, erhält man die so genannten Indifferenzkurven. Je höher das Versorgungsniveau ist, desto höher ist der Gesamtnutzen, den Frau Bronn hat. Die Nutzentabelle zeigt z. B., dass für Frau Bronn 3.000,00 Euro und eine Ferienreise einen Gesamtnutzen von 26 NE haben, während ihr der Besitz von 4.000,00 Euro und der Genuss zweier Ferienreisen einen Gesamtnutzen von 33 NE bringen. Für welche Kombination sich Frau Bronn entscheidet, hängt unter sonst gleichen Bedingungen vom Preis der Ferienreisen ab. Hat Frau Bronn z. B. ein Budget von 10.000,00 Euro zur Verfügung und kostet eine Ferienreise 1.000,00 Euro, so kann sie z. B. 10.000,00 Euro behalten und überhaupt nicht in die Ferien fahren. Sie kann aber auch das ganze Geld ausgeben und 10 Ferienreisen machen. Schließlich kann sie auch andere Kombinationen dazwischen wählen, z. B. sechs Ferienreisen machen und 4.000,00 Euro behalten. Alle theoretisch möglichen Kombinationen werden durch die Bilanzgerade 1 angezeigt. (Praktisch sind die Kombinationen begrenzt, weil die Ferienreisen nicht beliebig teilbar sind.) Handelt Frau Bronn nach dem ökonomischen Prinzip, wird sie die Kombination wählen, die ihr den höchsten Nutzen bringt. Dies ist bei folgender Kombination der Fall: Sie macht vier Ferienreisen und behält 6.000,00 Euro. Jede andere Kombination bringt ihr einen geringeren Gesamtnutzen. Um es nochmals zu sagen: Frau Bronn fragt bei einem Reisepreis von 1.000,00 Euro vier Ferienreisen nach. Steigt indessen der Reisepreis z. B. auf 1.666,67 Euro, kann sie nur noch entweder sechs Reisen bezahlen oder – im anderen Extremfall – 10.000,00 Euro behalten. Alle dazwischen liegenden Kombinationen werden durch die Bilanzgerade 2 angezeigt. 1 Um noch ein Beispiel zu zeigen: Steigt der Preis für eine Reise auf 3.000,00 Euro, kann Frau Bronn z. B. drei Reisen machen und 1.000,00 Euro behalten oder eine Reise machen und 7.000,00 Euro auf ihrem Konto lassen. Alle erdenklichen Kombinationen liegen auf der Bilanzgerade 3. (Wobei man natürlich bedenken muss, dass die Reisen nicht beliebig teilbar sind.) Die Kombination, die Frau Bronn den höchsten Nutzen bringt, ist fol- 3.2.2 Herleitung und Verlauf der individuellen Nachfragekurve gende: Sie macht zwei Reisen zu je 3.000,00 Euro und lässt 4.000,00 Euro auf dem Konto. Jede andere Kombination weist einen niedrigeren Gesamtnutzen als 33 NE auf. Nunmehr lässt sich aus der Tabelle die individuelle Nachfragekurve von Frau Bronn ableiten. Unter sonst gleichen Bedingungen fragt Frau Bronn wie folgt nach: Preis einer Ferienreise Zahl der nachgefragten Reisen 1.000,00 Euro 4 1.666,67 Euro 3 3.000,00 Euro 2 Nutzentabelle (Die Zahlen zeigen die unterschiedlichen Gesamtnutzen bei verschiedenen Geld-GüterKombinationen.) bei B1 Bilanzgerade einem Preis von 1.000,00 Euro je Reise bei B2 Bilanzgerade einem Preis von 1.666,67 Euro je Reise bei B3 Bilanzgerade einem Preis von 3.000,00 Euro je Reise nutzenmaximale Geld-GüterKombinationen bei unterschiedlichen Preisen N Nachfragekurve 2