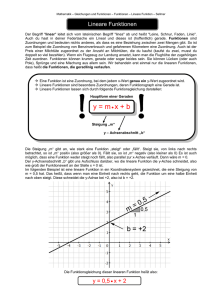
Vorläufige Version der ersten beiden Kapitel des geänderten Skripts

Universität
Stuttgart
Vorlesung Mathematik für Informatiker
und Softwaretechniker I, WS 2006/2007
Prof. Dr. Anna-Margarete Sändig
Berichte aus dem Institut für
Angewandte Analysis und Numerische
Simulation
Vorlesungsskript 2006/xxx
Universität Stuttgart
Vorlesung Mathematik für Informatiker
und Softwaretechniker I, WS 2006/2007
Prof. Dr. Anna-Margarete Sändig
Berichte aus dem Institut für
Angewandte Analysis und Numerische
Simulation
Vorlesungsskript 2006/xxx
Institut für Angewandte Analysis und Numerische Simulation (IANS)
Fakultät Mathematik und Physik
Fachbereich Mathematik
Pfaffenwaldring 57
D-70 569 Stuttgart
E-Mail: [email protected]
WWW: http://preprints.ians.uni-stuttgart.de
ISSN 1611-4176
c Alle Rechte vorbehalten. Nachdruck nur mit Genehmigung des Autors.
Inhaltsverzeichnis
1 Grundlagen
1.1 Aussagenlogik . . . . . . . . . . .
1.2 Mengen, Relationen, Abbildungen
1.3 Zahlenmengen . . . . . . . . . . .
1.4 Gruppen, Ringe, Körper . . . . .
.
.
.
.
.
.
.
.
7
7
17
33
51
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
2 Lineare Algebra
2.1 Vektorräume . . . . . . . . . . . . . . . .
2.2 Lineare Abbildungen von Vektorräumen
2.3 Matrizen . . . . . . . . . . . . . . . . . .
2.4 Lineare Gleichungssysteme . . . . . . . .
2.5 Determinante einer Matrix . . . . . . . .
2.6 Eigenwerte und Diagonalisierbarkeit . . .
2.7 Skalarprodukt . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
63
. 63
. 80
. 84
. 99
. 113
. 124
. 138
5
.
.
.
.
Kapitel 1
Grundlagen
In diesem Kapitel werden Grundbegriffe wie Aussage, Menge, Relation, Abbildung, Zahlenmengen, Gruppe, Ring und Körper eingeführt. Zusammenhänge werden erläutert, einige
Eigenschaften werden bewiesen und Beispiele illustrieren die Begriffe. Als Literatur wird
empfohlen [3, Kapitel 1-4,7] und [5, Kapitel 1-5]
1.1
Aussagenlogik
Ich beginne mit einem Zitat aus [3].
Ohne Aussagenlogik keine Schaltkreise und ohne Schaltkreise keine Computer.“
”
Was verstehen wir unter einer Aussage? Sie sollte in einer Sprache formuliert werden können
und eindeutig als wahr oder falsch identifizierbar sein. Die Bewertung wahr“ oder falsch“
”
”
entspricht bei Schaltkreisen der Zuordnung 1 oder 0.
Definition 1.1. Eine Aussage ist ein Satz in einer Sprache, der entweder wahr (w) oder
falsch (f) ist.
Bemerkung: Diese Definition besagt, dass eine zweiwertige Logik (Aristotelische Logik,
tertium non datur) benutzt wird. Außerdem wird angenommen, dass intuitiv klar ist, wann
eine Aussage wahr ist. Eine rigorose Definition eines Wahrheitsbegriffes in einer Sprache
ist sehr kompliziert. Ein Konzept dazu wurde von Tarski ([9]) 1933 entwickelt.
Beispiele:
(i) Was studierst Du?“ Dieser Satz ist keine Aussage
”
(ii) 11 ist eine Primzahl.“ Dieser Satz ist eine wahre Aussage.
”
(iii) Meine Mutter ist jünger als ich.“ Dieser Satz ist eine falsche Aussage.
”
Wir können neue Aussagen erzeugen, indem wir Abbildungen und Verknüpfungen von Aussagen einführen. Die Werte der Abbildungen bzw. Verknüpfungen können in sogenannten
Wahrheitstafeln beschrieben werden.
7
8
KAPITEL 1. GRUNDLAGEN
1. Fall: Abbildung einer Aussage
Wir gehen von einer Aussage A aus. Die Abbildung r ordne der Aussage A die Aussage r(A)
zu. In der entsprechenden Wahrheitstafel werden die Wahrheitswerte w und f eingetragen:
A
w
f
r1 (A)
w
f
r2 (A)
f
w
r3 (A)
w
w
r4 (A)
f
f
Es gibt 4 verschiedene Möglichkeiten die Wahrheitswerte der Bilder ri (A) zu beschreiben.
Wir sehen uns die Abbildung r2 genauer an.
Definition 1.2 (Negation). Als Negation einer Aussage A bezeichnen wir die Aussage
¬A (sprich: nicht A“), die den Wahrheitswert f annimmt, wenn A wahr ist und den
”
Wahrheitswert w annimmt, wenn A falsch ist.
Beispiele
• Die Aussage A laute: Die Kreide ist weiß.“ Die Negation ist: Die Kreide ist nicht
”
”
weiß.“
• Die Aussage A laute: 1 = 2.“ Die Negation ist: 1 6= 2.“
”
”
2. Fall: Verknüpfung von zwei Aussagen
Wir betrachten zwei Aussagen A und B und wollen diese zu einer Aussage C verknüpfen.
Wir schreiben
R(A, B) = C.
Alle möglichen Verknüpfungen Ri (A, B), i = 1, . . . , 16, können mit Hilfe von Wahrheitstafeln beschrieben werden:
A B
w w
w f
f w
f f
R1 (A, B)
w
w
w
w
R2 (A, B)
w
w
w
f
...
...
...
...
...
R16 (A, B)
f
f
f
f
Wir sehen uns auch hier einige Verknüpfungen etwas genauer an, die Konjunktion, die
Disjunktion, die Implikation und die Äquivalenz:
A
B
w
w
f
f
w
f
w
f
Konjunktion
A∧B
w
f
f
f
Disjunktion
A∨B
w
w
w
f
Implikation
A⇒B
w
f
w
w
Äquivalenz
A⇔B
w
f
f
w
Tabelle 1.1: Konjunktion, Disjunktion, Implikation und Äquivalenz
9
1.1. AUSSAGENLOGIK
Zunächst wird die Konjunktion durch eine Definition eingeführt.
Definition 1.3 (Konjunktion (und)). Die Verknüpfung der Aussagen A und B durch das
logische und“ nennen wir Konjunktion:
”
R(A, B) = A ∧ B.
Sie ist nur dann wahr, wenn beide Aussagen wahr sind.
Umgangssprachlich entspricht die Konjunktion dem Ausdruck sowohl als auch“. In Schalt”
kreisen sind sie durch eine Reihenschaltung von A und B realisiert und das Zeichen & wird
benutzt.
Die Disjunktion entspricht dem oder“, mindestens eine Aussage muss wahr sein, damit
”
die Verknüpfung wahr ist. Die entsprechende Definition lautet:
Definition 1.4 (Disjunktion (oder)). Die Verknüpfung der Aussagen A und B durch das
logische oder“ nennen wir Disjunktion:
”
R(A, B) = A ∨ B.
Die Disjunktion ist wahr, wenn mindestens eine der beiden Aussagen wahr ist, sonst ist sie
falsch. Sie wird durch eine Parallelschaltung in Schaltkreisen realisiert und das Symbol ≥
wird benutzt.
Definition 1.5 (Implikation (Folgerung)). Die Verknüpfung der Aussagen A und B durch
eine logische Folgerung, nennen wir Implikation:
R(A, B) = (A ⇒ B).
Sie ist nur dann falsch, wenn A wahr und B falsch ist.
Die Implikation tritt sehr häufig in Programmiersprachen auf: If [true], then ...
Sie ist auch in der Mathematik sehr wichtig, um aus wahren Aussagen neue wahre Aussagen
herzuleiten. Dies wird in Formulierungen wenn ... , dann“ ausgedrückt.
”
Beispiel
Wenn f im Punkt x0 differenzierbar ist, dann ist f im Punkt x0 stetig.
A = {f ist im Punkt x0 differenzierbar}
B = {f ist im Punkt x0 stetig}.
Die Aussage A ⇒ B besagt:
A ist hinreichende Bedingung für B,
B ist notwendige Bedingung für A.
10
KAPITEL 1. GRUNDLAGEN
Beispiel:
Nicht jede stetige Funktion ist differenzierbar. A kann falsch sein, trotzdem ist B wahr.
Ein weiteres Beispiel aus dem täglichen Leben:
nass} .
Wenn es regnet, dann |ist die Straße
{z
| {z }
B
A
A ist hinreichend für B, aber nicht notwendig, d.h. B ; A. Die Straße kann auch anders
nass geworden sein. Ist die Straße nicht nass, dann regnet es auch nicht.
Definition 1.6 (Äquivalenz (Gleichwertigkeit)). Die Verknüpfung der Aussagen A und B
durch eine logische Folgerung in beiden Richtungen wird Äquivalenz genannt
R(A, B) = (A ⇔ B) = C.
C ist wahr, falls A und B gleiche Wahrheitswerte besitzen.
In der Mathematik wird die Äquivalenz durch die Formulierungen ... genau dann, wenn
”
...“ ausgedrückt.
Beispiel:
A ist eine gerade Zahl, genau dann, wenn A durch 2 teilbar ist.
Theorem 1.7. Es gilt:
(A ⇒ B) ∧ (B ⇒ A) ⇔ (A ⇔ B).
Beweis:
Wir sehen uns die Wahrheitstafel an:
A
w
w
f
f
B
w
f
w
f
A⇒B
w
f
w
w
B⇒A
w
w
f
w
(A ⇒ B) ∧ (B ⇒ A)
w
f
f
w
Bemerkung: Die folgenden Verknüpfungen XOR (exklusives or), NOR (not or) und
NAND (not and) werden häufig benutzt
A
B
w
w
f
f
w
f
w
f
¬(A ⇔ B)
XOR
f
w
w
f
¬(A ∧ B)
NAND
f
w
w
w
¬(A ∨ B)
NOR
f
f
f
w
11
1.1. AUSSAGENLOGIK
Mathematische Beweise
Mathematische Sätze werden mit unterschiedlichen Beweistechniken bewiesen. Um zu zeigen, dass aus der Aussage A die Aussage B folgt (A ⇒ B) können wir einen direkten,
indirekten oder Widerspruchsbeweis führen. Die Äquivalenz dieser Beweistechniken wird
durch folgenden Satz beschrieben
Theorem 1.8. Es gilt:
A ⇒ B ⇔ (¬B ⇒ ¬A) ⇔ ¬(A ∧ (¬B)).
Beweis: Wir betrachten die Wahrheitstafel:
A
w
w
f
f
B
w
f
w
f
A⇒B
w
f
w
w
¬A
f
f
w
w
¬B
f
w
f
w
¬B ⇒ ¬A
w
f
w
w
¬(A ∧ (¬B))
w
f
w
w
Wir erläutern die Beweistechniken.
1. Direkter Beweis
A sei wahr. Wir zeigen (evtl. schrittweise), A ⇒ B ist wahr. Damit ist auch B wahr.
2. Indirekter Beweis
A sei wahr. Wir nehmen an ¬B sei wahr. Wir zeigen ¬B ⇒ ¬A ist wahr. Damit ist ¬A
wahr, was nicht sein kann.
3. Widerspruchsbeweis
A sei wahr. Wir zeigen, dass A ∧ (¬B) falsch ist, d.h. diese Aussage ist ein Widerspruch.
Daher muss ¬(A ∧ (¬B)) wahr sein.
Beispiel
Man zeige: Aus {|x − 1| < 1} = A folgt {x < 2} = B für eine feste reelle Zahl x.
1. Direkter Beweis.
Fall a) Es sei x ≥ 1. Dann ist |x − 1| = x − 1 < 1 und x < 2.
Fall b) Es sei x < 1. Dann ist x < 1 < 2.
2. Indirekter Beweis.
Es gelte ¬B = {x ≥ 2}. Dann ist |x − 1| = x − 1 ≥ 1, d.h. ¬B ⇒ ¬A.
3. Widerspruchsbeweis.
Die Aussage A ∧ (¬B) = {|x − 1| < 1} ∧ {x ≥ 2} ist falsch, da in diesem Fall |x − 1| =
12
KAPITEL 1. GRUNDLAGEN
x − 1 ≥ 1 ist.
Reduktion der Verknüpfungen auf ¬, ∧, ∨
Wir haben in Satz 1.8 gesehen, dass (A ⇒ B) ⇔ ¬(A ∧ (¬B)) ist, d.h. dass die Implikation
durch die Verknüpfungen ¬, ∧ ersetzt werden kann. Dies gilt auch für die Äquivalenz
(A ⇔ B) ⇔ (A ⇒ B) ∧ (B ⇒ A).
Die Frage tritt auf: Können wir alle 16 Möglichkeiten der Verknüpfungen von 2 Aussagen
auf logische Ausdrücke in denen nur ¬, ∧, ∨ auftreten, zurückführen?
Theorem 1.9. Jede Verknüpfung von 2 Aussagen kann durch logische Ausdrücke, in denen
nur ¬, ∧, ∨ auftreten, erzeugt werden.
Beweis: Es gibt 16 verschiedene Möglichkeiten, wie die Wahrheitswerte einer Verknüpfung
angeordnet sind. 8 davon werden durch Negation erzeugt. Von den verbleibenden 8 sind
5 durch Disjunktion (A ∧ B), Konjunktion (A ∨ B), Implikationen (A ⇒ B, B ⇒ A) und
Äquivalenz (A ⇔ B) erklärt. Die restlichen 3 sind:
A B
w w
w f
f w
f f
A ∨ (¬B ∨ B)
w
w
w
w
A = A ∧ (¬B ∨ B)
w
w
f
f
B = B ∧ (¬A ∨ A)
w
f
w
f
In der obigen Wahrheitstafel haben wir sogenannte Tautologien benutzt.
Definition 1.10. Eine logische Aussage ist eine Tautologie, falls sie stets wahr ist. Tritt
nur der Wert falsch auf, wird sie Widerspruch genannt.
Beispiele:
¬B ∨ B ist eine Tautologie, ¬B ∧ B ist ein Widerspruch.
Folgende Rechenregeln können leicht verifiziert werden:
(1) De Morgan’sche Regeln (Augustus de Morgan(1806-1871))
¬(A ∧ B) = ¬A ∨ ¬B ,
¬(A ∨ B) = ¬A ∧ ¬B .
(1.1)
(1.2)
A ∨ (B ∧ C) = (A ∨ B) ∧ (A ∨ C) ,
A ∧ (B ∨ C) = (A ∧ B) ∨ (A ∧ C) .
(1.3)
(1.4)
(2) Distributivgesetze
13
1.1. AUSSAGENLOGIK
(3) Transitivität der Implikation
(A ⇒ B) ∧ (B ⇒ C) ⇒ (A ⇒ C).
(1.5)
Aus den Morgan’schen Regeln und Satz 1.9 folgt
Theorem 1.11. Jede Verknüpfung von 2 Aussagen kann durch logische Ausdrücke, in
denen nur ¬, ∨ bzw. ∧ auftreten, erzeugt werden.
Quantoren
In der Mathematik benutzt man auch die Symbole
∀: für alle (Elemente),
∃: es existiert ein (Element),
∃ !: es existiert genau ein (Element).
Beispiele
• (∀ x ∈ N : x2 ∈ N) bedeutet: für alle x aus der Menge der natürlichen Zahlen N gilt,
dass x2 aus N ist.
• (∃x ∈ N : x ≤ 4) bedeutet: es existiert ein x aus N mit der Eigenschaft, dass x ≤ 4
ist.
• (∃ !x ∈ N : x − 1 = 5) bedeutet: es gibt genau ein x ∈ N, so dass x − 1 = 5 ist.
Negation von Aussagen, die Quantoren enthalten
Sei A = A(x) eine Aussage, die sich auf Elemente x aus einer Menge M bezieht.
Die Negation der Aussage
∀ x aus M :
A(x) ist wahr
(1.6)
∃ x aus M :
A(x) ist falsch.
(1.7)
lautet:
Die Negation der Aussage
∃ x aus M : A(x) ist wahr
(1.8)
∀ x aus M : A(x) ist falsch.
(1.9)
lautet:
14
KAPITEL 1. GRUNDLAGEN
Logische Ausdrücke und Schaltkreise
In der Hardware-Entwicklung wird vorgegeben, welche Werte durch einen Schaltkreis realisiert werden sollen, d.h. die Wahrheitstafel ist damit festgelegt. Dann wird der Schaltkreis
entworfen, der zu diesem Ergebnis führt. Dabei soll eine möglichst optimale“ Schaltung
”
gefunden werden.
Als Beispiel sehen wir uns einen Multiplexer an.
x
m
Eingang
y
Ausgang
z
Abbildung 1.1: Multiplexer
z wählt aus, welche Daten weitergeleitet werden, z heißt Steuergröße. Die Steuerregel laute:
Falls z wahr ist, dann soll x übertragen werden, falls z falsch ist, dann soll y übertragen
werden. Die Wahrheitstafel für den Multiplexer lautet also:
z
w
w
w
w
f
f
f
f
x
w
w
f
f
w
w
f
f
y
w
f
w
f
w
f
w
f
m
w
w
f
f
w
f
w
f
z ∧ x ∧ y = A1
z ∧ x ∧ (¬y) = A2
¬z ∧ x ∧ y = A3
¬z ∧ ¬x ∧ y = A4
Wir konstruieren den entsprechenden logischen Ausdruck. Dazu sehen wir uns die Zeilen an, in denen m den Wert w annimmt und verbinden die logischen Ausdrücke durch
Konjunktionen. Der Ausgang m ist durch den Wert w belegt, falls
A = A1 ∨ A2 ∨ A3 ∨ A4
wahr ist. Durch Nachprüfen kann man sich überzeugen, dass alle Ai , i = 1, 2, 3, 4, in den
übrigen Fällen den Wert f annehmen und damit A den Wert f besitzt. A stellt also den
15
1.1. AUSSAGENLOGIK
logischen Ausdruck dar, der den Ausgang m beschreibt.
Mit Hilfe der Rechenregel (1.4) kann A vereinfacht werden. Dazu setzen wir z ∧ x = p,
¬z ∧ y = q und erhalten:
A
=
(1.4)
=
=
(p ∧ y) ∨ (p ∧ ¬y) ∨ (q ∧ x) ∨ (q ∧ ¬x)
(p ∧ (y ∨ ¬y)) ∨ (q ∧ (x ∨ ¬x))
p ∨ q = (z ∧ x) ∨ (¬z ∧ y).
(1.10)
A ist durch eine entsprechende Schaltung realisierbar. Wir führen dazu den Negator, die
Parallel- und Reihenschaltung als Bausteine ein.
• Negator: x wird in ¬x umgewandelt.
• Reihenschaltung: Die Eingänge x und y gehen in a = x ∧ y über.
• Parallelschaltung: Die Eingänge x und y gehen in a = x ∨ y über.
Diese Bausteine werden schematisch wie folgt dargestellt.
x
y
¬x
x
Negator
&
x
a
y
≥1
a
Parallelschaltung
Reihenschaltung
Der folgende Schaltkreis entspricht dem logischen Ausdruck A.
Bemerkung: Es können sehr viel mehr Eingänge auftreten, der Multiplexer wird dann
x
&
≥1
y
m
&
z
komplizierter. Im Allgemeinen ist das Konstruieren einer optimalen Schaltung ein schwieriges Problem.
16
KAPITEL 1. GRUNDLAGEN
Übungsaufgaben
Aufgabe 1.1 (von Ralf Schindler aus DMV-Mitteilungen 14-3/2006)
Drei Logiker sitzen auf Stühlen hintereinander. Der hinterste sieht die beiden vorderen, der mittlere
sieht nur den vordersten, und der vorderste sieht niemanden. Alle drei wissen, dass sie jeweils einen Hut
aus der Garderobe eines Theaters aufgesetzt bekommen haben, und sie wissen, dass diese Garderobe
fünf Hüte zur Verfügung stellt: zwei rote und drei schwarze.
Nun wird der hinterste Logiker gefragt, ob er seine Hutfarbe kenne. Er sagt NEIN. Dann wird der
mittlere das gleiche gefragt. Auch er sagt NEIN. Schließlich wird der vorderste gefragt. Was antwortet
er?
Aufgabe 1.2 (von Ralf Schindler aus DMV-Mitteilungen 14-3/2006)
Wieder haben die drei Logiker jeweils einen Hut aus derselben Garderobe auf dem Kopf. Ihnen wurden
die Augen verbunden, als man sie ihnen aufsetzte. Nun stehen sie zu dritt in einem Zimmer, die
Augenbinden werden ihnen gleichzeitig abgenommen, jeder von ihnen sieht die beiden anderen.
Sie sollen sich zu Wort melden, wenn sie wissen, welchen Hut sie selbst aufhaben. Sie sind schnelle
Denker, und sie denken genau gleich schnell. Nach drei Sekunden melden sie sich exakt gleichzeitig
zu Wort. Wie sind die Hutfarben verteilt?
Aufgabe 1.3
Die Studierenden Angelika, Bernd, Cornelia und Dieter haben sich zu einer Arbeitsgruppe zusammengefunden, die sich einmal in der Woche in einem Raum an der Universität trifft, um die MathematikÜbungsblätter zu bearbeiten.
Allerdings haben sie dabei mit einigen Schwierigkeiten zu kämpfen:
• Nur Cornelia und Dieter haben einen Schlüssel zum Arbeitsraum. Ein Treffen kann nur stattfinden, wenn einer der beiden da ist.
• Angelika hat kein eigenes Auto und wohnt auf dem Land mit sehr schlechter öffentlicher Verkehrsanbindung. Sie wird deshalb von Bernd abgeholt und kann also nur da sein wenn auch
Bernd da ist.
• Bernd und Cornelia sind Geschwister und pflegen ihre kranke Großmutter. Sie können nicht
beide gleichzeitig da sein.
An einem Nachmittag, kam die Arbeitsgruppe nicht zum Bearbeiten der Aufgaben, da lange darüber
diskutiert wurde, warum Bernd morgens so sauer auf Dieter war, dass er gesagt hat: Wenn Dieter
”
heute Nachmittag kommt, komme ich nicht.“
Wer war an diesem Nachmittag an der Diskussion beteiligt?
Aufgabe 1.4
Überprüfen Sie sowohl durch Umformung, als auch mit Hilfe einer Wahrheitswerttabelle, ob die Ausdrücke
• (A ∨ B) ⇒ (¬A ∨ B) ∧ (A ⇒ ¬A)
• A ⇒ (B ⇒ C) ⇔ (A ∧ B) ⇒ C
stets wahr sind.
17
1.2. MENGEN, RELATIONEN, ABBILDUNGEN
Aufgabe 1.5
Formulieren Sie jede der folgenden Aussagen mit Hilfe von Quantoren, und geben Sie ihre Verneinung
und ihren Wahrheitswert an:
A: Es gibt m, n ∈ N, für die m + n ∈ N und m − n ∈ N .
B: Die Gleichung m2 = n − 5 besitzt für jedes m ∈ N eine Lösung n ∈ N .
C: Jedes gerade n ∈ N kann als Summe zweier Quadratzahlen geschrieben werden.
1.2
Mengen, Relationen, Abbildungen
Wir beschäftigen uns zunächst mit Mengen.
Mengen
Bei der Einführung der Quantoren hatten wir bereits von Mengen gesprochen. Wir geben
jetzt eine Definition an, die vom Begründer der Mengenlehre, Georg Cantor (1845 - 1918),
stammt.
Definition 1.12. Unter einer Menge M verstehen wir jede Zusammenfassung von bestimmten wohlunterschiedenen Objekten der Anschauung oder des Denkens, welche die
Elemente von M genannt werden, zu einem Ganzen.
Kurz: Eine Menge M ist eine Sammlung von Objekten (Elementen).
Gehört ein Element x zur Menge M, dann schreiben wir x ∈ M, gehört ein Element x
nicht zur Menge M, dann wird dies durch x ∈
/ M ausgedrückt.
Mengen können wie folgt beschrieben werden:
• explizit, durch Aufzählen der Elemente, die in geschweiften Klammern gesetzt werden, z.B.
M = {1, 2, 3} = {3, 2, 1}, M = {1, 2, {1, 2}},
• durch Eigenschaften, z.B.
M = {n ∈ N : n ist gerade},
M = {n ∈ N : n < 10}.
Beispiele für Zahlenmengen
N = {1, 2, 3, . . . }
Menge der natürlichen Zahlen,
Z = {. . . , −2, −1, 0, 1, 2, . . . } Menge der ganzen Zahlen,
a
Menge der rationalen Zahlen.
Q = { : a ∈ Z ∧ b ∈ N}
b
∅ ist die leere Menge. Diese Menge enthält kein Element.
(1.11)
(1.12)
18
KAPITEL 1. GRUNDLAGEN
Vergleich von Mengen
Gleichheit: Zwei Mengen M1 und M2 sind gleich, wenn sie die gleichen Elemente enthalten, d.h.
x ∈ M1 ⇔ x ∈ M2 .
Teilmengen: M1 ist Teilmenge von M2 , geschrieben als M1 ⊆ M2 , falls für alle x ∈ M1
x ∈ M1 ⇒ x ∈ M2
gilt. Falls M1 6= M2 dann ist M1 eine echte Teilmenge von M2 , geschrieben als M1 ⊂ M2 .
M2 wird auch Obermenge von M1 genannt.
Beispiele
• Es ist N ⊂ Z.
• Sei M eine beliebige Menge, dann ist ∅ ⊆ M.
Verknüpfungen von Mengen
Seien M1 und M2 zwei Mengen. Die Menge
M1 ∪ M2 = {x : x ∈ M1 ∨ x ∈ M2 } heißt Vereinigung von M1 und M2 ,
M1 ∩ M2 = {x : x ∈ M1 ∧ x ∈ M2 } heißt Durchschnitt von M1 und M2 ,
M1 \ M2 = {x : x ∈ M1 ∧ x ∈
/ M2 } heißt Differenz von M1 und M2 .
Falls M2 ⊆ M1 ist, dann heißt M1 \ M2 auch Komplement von M2 in M1 und wir schreiben
M1 \ M2 = M2c . Der obere Index bezieht sich somit auf die Obermenge M1 .
M1 und M2 heißen disjunkt, falls M1 ∩ M2 = ∅ gilt.
Potenzmenge
Für jede Menge M können wir eine neue Menge bilden, die als Elemente alle Teilmengen
von M besitzt.
Definition 1.13. Die Potenzmenge P(M) einer Menge ist die Menge aller Teilmengen von
M.
Beispiel
Es sei M = {1, 2, 3}. Dann ist
P(M) = {∅, {1}, {2}, {3}, {1, 2}, {1, 3}, {2, 3}, {1, 2, 3}}.
Wir sehen, die Menge M, die aus 3 Elementen besteht, besitzt eine Potenzmenge, die aus
8 Elementen besteht. Es gilt allgemein.
19
1.2. MENGEN, RELATIONEN, ABBILDUNGEN
Theorem 1.14. Die Potenzmenge einer Menge M von n Elementen besitzt 2n Elemente.
Beweis: Diese Aussage kann durch vollständige Induktion bewiesen werden (Übung)
Rechengesetze
Theorem 1.15. Für eine Menge M und S, T, V ∈ P(M) gelten folgende Rechengesetze.
Kommutativität:
S ∪ T = T ∪ S,
S ∩ T = T ∩ S.
Assoziativität:
(S ∪ T ) ∪ V
(S ∩ T ) ∩ V
= S ∪ (T ∪ V ),
= S ∩ (T ∩ V ).
Distributivität:
S ∪ (T ∩ V ) = (S ∪ T ) ∩ (S ∪ V ),
S ∩ (T ∪ V ) = (S ∩ T ) ∪ (S ∩ V ).
De Morgan’sche Regeln:
(S ∩ T )c = S c ∪ T c
(S ∪ T )c = S c ∩ T c .
(1.13)
(1.14)
Weitere Rechengesetze:
S ∪ ∅ = S,
S ∩ ∅ = ∅,
S ∪ M = M,
S ∩ M = S,
S ∪ S = S,
S ∩ S = S,
c
S ∪ S = M,
S ∩ S c = ∅,
M c = ∅,
∅c = M,
(S \ T ) \ V = S \ (T ∪ V ),
S \ (T \ V ) = (S \ T ) ∪ (S ∩ V ),
S ∪ (T \ V ) = S ∪ T \ (V \ S), S ∩ (T \ V ) = S ∩ T \ (S ∩ V ).
Bemerkung: Wir hatten bereits die DeMorganschen Regeln (1.1) und (1.2) eingeführt.
Die Negation entspricht der Komplementärbildung, die Vereinigung dem logischen oder“ ,
”
der Durchschnitt dem logischen und“ . Wir zeigen mit Hilfe von (1.2), dass
”
(S ∪ T )c = S c ∩ T c
(1.15)
20
KAPITEL 1. GRUNDLAGEN
gilt.
Wir betrachten die Aussagen A = {x ∈ S}, B = {x ∈ T }. Dann wird die rechte Seite von
(1.15)
{x ∈ S c ∩ T c }
=
(1.2)
=
{x 6∈ S} ∩ {x 6∈ T } = ¬A ∧ ¬B
¬(A ∨ B) = {x 6∈ (S ∪ T )} = {x ∈ (S ∪ T )c } .
Kartesisches Produkt
Die Verknüpfung zweier Mengen zu einer Produktmenge spielt eine wichtige Rolle bei der
Einführung von Relationen.
Definition 1.16. Das kartesische Produkt M1 × M2 zweier Mengen M1 und M2 ist die
Menge aller geordneten Paare (m1 , m2 ) mit m1 ∈ M1 und m2 ∈ M2 :
M1 × M2 = {(m1 , m2 ) : m1 ∈ M1 , m2 ∈ M2 }.
Entsprechend ist
M1 × · · · × Mr = {(m1 , m2 , . . . , mr ) : mj ∈ Mj , 1 ≤ j ≤ r},
wobei (m1 , m2 , . . . , mr ) ein geordnetes r-Tupel ist.
Beispiel
Wir betrachten das kartesische Produkt zweier Intervalle,
M1 = [1, 2] = {x ∈ R : 1 ≤ x ≤ 2},
M2 = [3, 5] = {y ∈ R : 3 ≤ y ≤ 5}.
Es ist M1 × M2 = {(x, y) : 1 ≤ x ≤ 2 ∧ 3 ≤ y ≤ 5} ein Rechteck (siehe Abbildung 1.2).
y
5
3
1111
0000
0000
1111
0000
1111
0000
1111
0000
1111
0000
1111
1 2
x
Abbildung 1.2: M1 × M2
1.2. MENGEN, RELATIONEN, ABBILDUNGEN
21
Relationen
Die Elemente einer gegebenen Menge können eine oder mehrere Eigenschaften besitzen.
Sehen wir z.B. die Menge der Studenten in diesem Hörsaal an. Wir können die Merkmale
größer oder kleiner gleich als 1.80 m, weiblich oder männlich, Einkommen kleiner gleich
oder größer als 300 Euro, Brille oder nicht Brille jedem Studenten zuordnen.
Wir stellen damit eine Relation (Beziehung) zwischen der Menge der Studenten M und
einer Menge N von Merkmalen auf, was der Anlage einer Datenbank entspricht. Bemerkung:
Tabellen (Datenbanken), in denen Informationen aufgelistet sind, entsprechen Relationen.
Die Relationen sind Teilmengen von M1 ×· · ·×Mr , wobei r z.B. die Anzahl der Spalten der
Tabellen sind und Mi die Elemente enthalten, die in den Spalten auftreten. Um Informationen zu extrahieren oder neue zu gewinnen, können mengentheoretische Verknüpfungen
herangezogen werden, z.B. für Teilmengen R1 und R2 von M1 × · · · × Mr ist erklärt:
1. R1 ∪ R2 (R1 UNION R2 ) erzeugt alle Tupel, die in R1 oder R2 vorkommen,
2. R1 \ R2 (R1 MINUS R2 ) enthält alle Tupel, die in R1 aber nicht in R2 vorkommen,
3. R1 × R2 (R1 TIMES R2 ) ist das kartesische Produkt.
Beispiel
Es sei M = {1, 2, 3, 4} eine Menge von 4 Studenten, N = {a, b, c} eine Menge von 3 Merkmalen. Eine Relation zwischen M und N kann sein
x∈M
1
1
2
3
3
4
y∈N
a
b
a
b
c
c
(x, y) ∈ M × N
(1, a)
(1, b)
(2, a)
(3, b)
(3, c)
(4, c)
d.h. Student 1 besitzt die Merkmale a und b, Student 2 das Merkmal a, Student 3 die
Merkmale b und c und Student 4 das Merkmal c. Dies kann auch folgendermaßen dargestellt
werden.
Die dicken runden Punkte kennzeichnen die obige Relation. Sie bilden eine Teilmenge von
M × N.
Definition 1.17 (Relation). Eine Teilmenge R des kartesischen Produkts M × N der
Mengen M und N heißt binäre Relation. Eine n-näre Relation zwischen den Mengen
M1 , M2 , . . . , Mn ist eine Teilmenge des kartesischen Produkts M1 × M2 × · · · × Mn
R ⊆ M1 × M2 × · · · × Mn .
22
KAPITEL 1. GRUNDLAGEN
y
c
1
0
0
1
0
1
1
0
0
1
0
1
1
0
0
1
1
0
0
1
b
1
0
0
1
1
0
0
1
0
1
1
0
0
1
1
0
0
1
0
1
a
1
0
0
1
1
0
0
1
1
0
0
1
0
1
1
0
0
1
0
1
1
2
3
4
11111111111111 x
00000000000000
Abbildung 1.3: Merkmalsverteilung
In unserem obigen Beispiel ist R eine binäre Relation
R = {(1, a), (1, b), (2, a), (3, b), (3, c), (4, c)}.
Aus gegebenen Relationen können neue durch Durchschnittsbildung, Vereinigungen, Differenzen, u.s.w. erzeugt werden. Eine weitere Möglichkeit ist die Komposition.
Definition 1.18 (Komposition). Seien R ⊆ M1 × M2 , S ⊆ M2 × M3 binäre Relationen.
Dann ist die Komposition S ◦ R eine Relation auf M1 × M3 , die durch
S ◦ R = {(m1 , m3 ) ∈ M1 × M3 : ∃ m2 ∈ M2 sodass (m1 , m2 ) ∈ R, (m2 , m3 ) ∈ S ist}
gegeben ist.
Bemerkung:
S ◦ R bedeutet: zuerst R dann S ausführen, d.h. von rechts nach links die Relationen
abarbeiten.
23
1.2. MENGEN, RELATIONEN, ABBILDUNGEN
Beispiel
Wir betrachten eine Familie im eigentlichen Sinne und die Mengen
M1 = {m11 , m12 , m13 } = {männliche Personen, deren Alter ≥ 30 ist},
M2 = {m21 , m22 , m23 , m24 } = {männliche Personen, deren Alter < 30 ist},
M3 = {m31 , m32 , m33 , m34 } = {weibliche Personen, deren Alter < 30 ist}.
Wir sehen uns die Relation
Vater von“ an:
”
R = {(m11 , m21 ), (m11 , m23 ), (m12 , m24 )} ⊂ M1 × M2 ,
d.h. m11 hat die Söhne m21 und m23 , m12 hat den Sohn m24 . Weiterhin sehen wir uns die
Relation verheiratet mit “ an
”
S = {(m21 , m32 ), (m24 , m33 )} ⊂ M2 × M3 ,
d.h. der Sohn m21 ist mit m32 verheiratet, der Sohn m24 ist mit m33 verheiratet.
Dann ist
S ◦ R = {(m11 , m32 ), (m12 , m33 )} ⊂ M1 × M3
die Relation Schwiegervater von “ . Die verbindenden Elemente wären die Söhne m21 und
”
m24 .
Definition 1.19 (Inverse Relation). Ist R ⊆ M × N eine binäre Relation, dann nennen
wir
R−1 = {(y, x) ∈ N × M : (x, y) ∈ M × N}
die zu R inverse Relation.
Beispiel
Es sei R = {(x, y) ∈ R × R : x ≥ y} (siehe Abbildung 1.4). Dann ist R−1 = {(y, x) ∈
R × R : y ≤ x} (siehe Abbildung 1.5).
y
R
x≥y
x
R−1
x≥y
x
Abbildung 1.4: Die Menge R
y
Abbildung 1.5: Die Menge R−1
Es ist
R−1 ◦ R = {(x, x), x ∈ R} ,
R ◦ R−1 = {(y, y), y ∈ R} .
24
KAPITEL 1. GRUNDLAGEN
Definition 1.20. Sei M eine Menge. Wir nennen die Relation
IM = {(x, x), x ∈ M} ⊆ M × M
die identische Relation oder Identität in M.
Achtung! Es gilt nicht für jede Relation R ⊆ M × N, dass
R−1 ◦ R = IM
R ◦ R−1 = IN
ist. Dazu betrachten wir ein Beispiel:
Sei M = N = {1, 2}, R = {(1, 1), (1, 2), (2, 1), (2, 2)}. Es ist R−1 = R und R−1 ◦ R =
R ◦ R = R 6= IM .
Äquivalenz- und Ordnungsrelationen
Wir betrachten spezielle binäre Relationen R ⊂ M × M.
Definition 1.21. Die Relation R ⊂ M × M heißt
• reflexiv, falls für alle x ∈ M (x, x) ∈ R ist,
• symmetrisch, falls aus (x, y) ∈ R folgt (y, x) ∈ R,
• antisymmetrisch, falls aus (x, y) ∈ R ∧ (y, x) ∈ R folgt x = y,
• transitiv, falls für (x, y) ∈ R und (y, z) ∈ R gilt (x, z) ∈ R.
Definition 1.22 (äquivalenzrelation). Eine reflexive, symmetrische und transitive Relation
R ⊂ M × M heißt äquivalenzrelation. Für (x, y) ∈ R schreibt man x ∼ y.
Beispiel
Es sei M = Z die Menge der ganzen Zahlen. Weiterhin sei R = {(x, y) ∈ Z × Z : x ≡
y mod 5}. Hierbei bedeutet, dass zwei ganze Zahlen x und y kongruent modulo einer
natürlichen Zahl m sind, falls m ein Teiler der Differenz x − y ist (also x − y = qm ist,
wobei q ∈ Z beliebig ist).
Wir überprüfen die obigen Eigenschaften.
• Reflexivität:
Es ist x ≡ x mod 5, denn x − x = 0 · 5.
• Symmetrie:
Es sei x ≡ y mod 5, d.h. x − y = q · 5. Daraus folgt y − x = −q · 5 und y ≡ x mod 5.
1.2. MENGEN, RELATIONEN, ABBILDUNGEN
25
• Transitivität:
Es sei x ≡ y mod 5 und y ≡ z mod 5. Dann ist x − y = q1 · 5 und y − z = q2 · 5.
Daraus folgt
x − z = x − y + (y − z) = (q1 + q2 ) · 5 = q · 5.
Durch eine äquivalenzrelation kann man die Menge M in zueinander disjunkte Teilmengen,
die Äquivalenzklasse genannt werden, zerlegen. Dabei gehören die Elemente x und y, für
die (x, y) ∈ R, bzw. für die x ∼ y ist, zu einer Klasse.
Definition 1.23 (Äquivalenzklasse). Für x ∈ M nennen wir die Menge
R[x] = {y ∈ M : x ∼ y}
die Äquivalenzklasse von x bezüglich der äquivalenzrelation R.
Beispiel
Im obigen Beispiel ist
R[0] = {y ∈ Z : y = x − q5, x = 0, q ∈ Z}
= {. . . , −10, −5, 0, 5, 10, . . . }
R[1] = {. . . , −9, −4, 1, 6, 11, . . . }
R[2] = {. . . , −8, −3, 2, 7, 12, . . . }
R[3] = {. . . , −7, −2, 3, 8, 13, . . . }
R[4] = {. . . , −6, −1, 4, 9, 14, . . . }.
Damit ist Z = R[0] ∪ R[1] ∪ · · · ∪ R[4] und R[i] ∩ R[j] = ∅ für i 6= j, i, j ∈ {0, 1, 2, 3, 4}.
Die Zahlen i mit i ∈ {0, 1, 2, 3, 4} heißen Repräsentanten von R[i].
Die Menge Z ist damit in 5 disjunkte Teilmengen zerlegt worden, allgemeiner spricht man
von einer Partition {R[i]}i=0,1,...,4 von Z.
Definition 1.24 (Partition einer Menge M). Eine Menge von Teilmengen {Mi ⊂ M}i∈I
mit Mi ∩ Mj = ∅ für alle i, j ∈ I, i 6= j, nennen wir Partition von M falls
[
Mi = M
i∈I
ist.
Bemerkung:
Die Indexmenge I kann aus endlich vielen oder unendlich vielen Elementen bestehen. So
kann z.B. die Menge der natürlichen Zahlen N wie folgt dargestellt werden
N=
∞
[
{i}.
i=1
26
KAPITEL 1. GRUNDLAGEN
Theorem 1.25. Jede äquivalenzrelation R ⊂ M × M erzeugt eine Partition von M, jede
Partition bestimmt eine äquivalenzrelation.
Es wird empfohlen, den Beweis als Übung auszuführen.
Beispiel
Sei M die Menge aller Wörter. Wir führen in M folgende äquivalenzrelation ein: zwei
Wörter sind äquivalent, falls sie den gleichen Anfangsbuchstaben besitzen. Dadurch wird
eine Partition erzeugt.
Ordnungsrelation
Die äquivalenzrelation kann auch als Gleichheitsrelation“ angesehen werden. Ordnungs”
relationen sollten Vergleiche wie ≤ “ bzw. ≥ “ ermöglichen.
”
”
Definition 1.26 (Ordnungsrelation). Eine reflexive, antisymmetrische und transitive Relation R ⊂ M × M heißt Ordnungsrelation. Wir schreiben in diesem Fall
(x, y) ∈ R als x ≤ y.
Beispiele
1◦ Sei M die Menge der natürlichen Zahlen N und R = {(n1 , n2 ) : n1 ≤ n2 }. Dann gilt
• (n1 , n1 ) ∈ R,
• (n1 , n2 ) ∈ R ∧ (n2 , n1 ) ∈ R, d.h. n1 ≤ n2 ∧ n2 ≤ n1 , dann ist n1 = n2 ,
• (n1 , n2 ) ∈ R ∧ (n2 , n3 ) ∈ R, d.h. n1 ≤ n2 , n2 ≤ n3 , dann ist n1 ≤ n3 und
(n1 , n3 ) ∈ R.
n2
R
1 2 3 4 5
n1
Abbildung 1.6: Die Relation R = {(n1 , n2 ) : n1 ≤ n2 }
1.2. MENGEN, RELATIONEN, ABBILDUNGEN
27
2◦ Sei M = N × N = N2 . Für zwei Elemente x = (x1 , x2 ), y = (y1 , y2 ) ∈ N2 sei folgende
Relation definiert:
R = {(x, y) : x1 ≤ y1 }.
Diese Relation ist keine Ordnungsrelation, da sie nicht antisymmetrisch ist:
(x, y) ∈ R ∧ (y, x) ∈ R
bedeutet x1 = y1 , aber nicht x = y.
Wir führen in N2 eine lexikographische Ordnungsrelation ein:
Rlex = {(x, y) : x1 ≤ y1 ∧ falls x1 = y1 , dann x2 ≤ y2 }.
Es gilt tatsächlich:
• (x, x) ∈ Rlex .
• Seien (x, y) ∈ Rlex ∧ (y, x) ∈ Rlex . Dann ist y1 = x1 und x2 ≤ y2 ∧ y2 ≤ x2 ,
woraus x = y folgt.
• Seien (x, y) ∈ Rlex ∧ (y, z) ∈ Rlex . Es ist x1 ≤ y1 ≤ z1 . Falls x1 = y1 = z1 ,
dann ist x2 ≤ y2 ≤ z2 , also x2 ≤ z2 und somit (x, z) ∈ Rlex .
Somit ist diese lexikographische Ordnungsrelation im mathematischen Sinn wohl definiert.
Abbildungen
Seinen M und N Mengen. Wir führen den Begriff einer Abbildung von Elementen x ∈ M
auf Elemente y ∈ N ein.
Definition 1.27 (Abbildungen). Die Zuordnungsvorschrift f , die Elemente x ∈ M eindeutig auf Elemente y ∈ N abbildet, heißt Abbildung. Es wird kurz geschrieben
f : M → N (f bildet M in N ab),
x → f (x) = y (jedem x ∈ M wird eindeutig ein Element f (x) = y ∈ N zugeordnet).
M heißt Definitionsbereich von f , N heißt Wertebereich von f ,
f (M) = {y ∈ N : ∃x ∈ M : f (x) = y} ist das Bild von M;
f −1 (Y ) = {x ∈ M : f (x) ∈ Y ⊂ N} ist das Urbild einer Menge Y ⊂ f (M).
Bemerkung:
Sind M = N = R die Mengen der reellen Zahlen, dann bezeichnet man f auch als Funktion.
Der Graph einer Abbildung ist eine spezielle Relation.
Definition 1.28. Der Graph G = G(f ) ⊂ M × N einer Abbildung f : M → N ist durch
G = G(f ) = {(x, y) ∈ M × N, y = f (x)}
gegeben.
28
KAPITEL 1. GRUNDLAGEN
Beispiel
Es sei M = N = R die Menge der reellen Zahlen und
f : R → R,
f : x → x2
die Funktion f (x) = x2 . Der Graph G = G(f ) = {(x, y) ∈ R × R = R2 : y = x2 } ist in
Abbildung 1.7 dargestellt.
y
4
3.5
3
2.5
2
1.5
1
0.5
−2
−1
1
2
x
Abbildung 1.7: f (x) = x2
Definition 1.29. Die Abbildung f : M → N heißt surjektiv, falls f (M) = N ist, kurz:
f ist eine Abbildung von M auf N.
Die Abbildung f : M → N heißt injektiv, falls gilt: f (x1 ) = f (x2 ) ⇔ x1 = x2 , d.h. f ist
eine eineindeutige Abbildung von M auf f (M) ⊂ N.
Die Abbildung f : M → N heißt bijektiv, falls sie sowohl injektiv als auch surjektiv ist.
Bemerkungen 1.36
1◦ Eine bijektive Abbildung f zwischen M und N wird kurz geschrieben als f : M ↔ N.
2◦ Für injektive Abbildungen f : M → N wird eine inverse Abbildung f −1 : f (M) → M
durch
f −1 (f (x)) = f −1 ◦ f (x) = x ∀ x ∈ M ,
f (f −1 (y)) = f ◦ f −1 (y) = y ∀ y ∈ f (M)
eingeführt.
Beispiel
Die obige Abbildung f : R → R, f (x) = x2 , ist weder surjektiv noch injektiv.
29
1.2. MENGEN, RELATIONEN, ABBILDUNGEN
Mächtigkeit von Mengen
Besitzen zwei Mengen endlich viele Elemente, so können wir durch die Anzahl der Elemente
ihre Mächtigkeit definieren, d.h. wir können sofort sehen, ob sie gleich groß (gleich mächtig)
sind oder nicht. Bei Mengen, die unendlich viele Elemente enthalten, ist das schwieriger.
Betrachten wir z.B. N und die Teilmenge Nger = {n ∈ N : n gerade}. Beide enthalten
unendlich viele Elemente; sind diese Mengen N und Nger gleich mächtig?
Definition 1.30. Zwei Mengen A und B heißen gleich groß oder gleich mächtig, falls es
eine bijektive Abbildung f : A ↔ B gibt.
Die Menge A heißt endlich, falls es ein n ∈ N und eine Bijektion f : A → {1, 2, . . . , n}
gibt, oder A = ∅ ist.
A heißt unendlich, falls A nicht endlich ist.
A heißt abzählbar unendlich, falls A gleich mächtig zu N ist.
A heißt überabzählbar, falls A unendlich und nicht abzählbar unendlich ist.
Beispiel
1◦ Die Menge der geraden natürlichen Zahlen ist gleichmächtig zu N:
f : Nger ↔ N,
1
f : m = 2n →
2
1
m
= n.
2
2
N
N
f −1
f
2
3
4
Nger
Abbildung 1.8: f (m) =
2
3
4
Nger
Abbildung 1.9: f −1 (n) = 2n
m
2
2◦ Z ist gleichmächtig zu N. Eine Bijektion wäre
(
2m
falls m > 0,
f : Z ↔ N, f (m) =
−2m + 1 falls m ≤ 0.
Es ist
f
−1
(n) =
n
2
−(n−1)
2
falls n gerade
falls n ungerade .
30
KAPITEL 1. GRUNDLAGEN
−1
0 1 2 3
00000000000000000000000
11111111111111111111111
0000000000000
1111111111111
0000−2
1111
1111111111111111111111111111111
0000000000000000000000000000000
00000000000000000000000
11111111111111111111111
0000000000000
1111111111111
00000000000000000000000
11111111111111111111111
0000000000000
1111111111111
00000000000000000000000
11111111111111111111111
0000000000000
1111111111111
00000000000000000000000
11111111111111111111111
0000000000000
1111111111111
00000000000000000000000
11111111111111111111111
0000000000000
1111111111111
1111111111111111111111111111111
0000000000000000000000000000000
00000000000000000000000
11111111111111111111111
0000000000000
1111111111111
12 34 5 6
Abbildung 1.10: Zuordnungsvorschrift f (m)
3◦ N × N und N sind gleichmächtig. Wir schreiben die Paare (n1 , n2 ) aus N × N folgendermaßen auf:
(1, 1)
(2, 1)
(3, 1)
(4, 1)
..
.
(1, 2)
ւ
ւ
ւ
(2, 2)
(3, 2)
(1, 3)
ւ
ւ
(4, 2)
..
.
(2, 3)
(1, 4) . . .
ւ
(2, 4) . . .
(3, 3)
(3, 4) . . .
(4, 3)
..
.
(4, 4) . . .
..
.
Dies ergibt ein zweidimensionales Nummerierungsschema.
n2
n1
1
2
3
4
5
6
..
.
1
2
3
4
5
6
1 2 4 7 11
3 5 8 12 17
6 9 13 18
10 14 19
15 20
21
16
...
Die Nummerierung ist eineindeutig. Dieses Vorgehen wird Cantorsches Diagonalverfahren genannt. Durch sie wird eine bijektive Abbildung f : N × N ↔ N erzeugt.
4◦ Die Menge der rationalen Zahlen ist abzählbar unendlich. Um dies zu zeigen, betrachten wir zunächst, ähnlich wie bei den ganzen Zahlen, eine Bijektion f1 :
a
f1 : Q ↔ Q+ = { , a ∈ N, b ∈ N, a und b teilerfremd}.
b
1.2. MENGEN, RELATIONEN, ABBILDUNGEN
31
Danach bilden wir Q+ injektiv in N × N durch f2 ab:
a
f2 ( ) = (a, b).
b
Da a und b teilerfremd sind, ist die Bildmenge f2 (Q+ ) eine echte Teilmenge von N×N.
Es ist leicht zu sehen, dass f2 (Q+ ) abzählbar ist, indem wir bei der Nummerierung
durch das Cantorsche Diagonalverfahren, die Paare überspringen, bei denen Zähler
und Nenner nicht teilerfremd sind.
Durch diese Nummerierung haben wir eine bijektive Abbildung von f3 : f2 (Q+ ) ↔ N
beschrieben.
Fügen wir die Abbildungen f1 , f2 , f3 nacheinander aus, erhalten wir, dass
f = f3 ◦ f2 ◦ f1 : Q ↔ N
die gesuchte bijektive Abbildung ist.
32
KAPITEL 1. GRUNDLAGEN
Übungsaufgabe
Aufgabe 2.1
Vereinfachen Sie die folgende Schaltung:
&
A
&
≥1
≥1
B
C
≥1
&
&
Aufgabe 2.2
Untersuchen Sie, ob die Differenzbildung von Mengen assoziativ ist, indem Sie die Vereinigung und
den Schnitt von A \ (B \ C) und (A \ B) \ C bilden.
Aufgabe 2.3
Entscheiden Sie, ob es sich bei den folgenden Relationen auf der Menge aller jetzt lebenden Menschen
um Äquivalenzrelationen handelt.
a) (a, b) ∈ R, wenn a und b gemeinsame Großeltern haben.
b) (a, b) ∈ R, wenn a in einer Entfernung von weniger als 100km von b lebt.
c) (a, b) ∈ R, wenn a und b denselben Vater haben.
Falls es sich um eine Äquivalenzrelation handelt, ist ein Vertreter aus jeder Äquivalenzklasse anzugeben.
Aufgabe 2.4
Wie viele Relationen gibt es zwischen zwei jeweils dreielementigen Mengen A und B? Wie viele davon
sind Abbildungen und wie viele der Abbildungen sind surjektiv?
Aufgabe 2.5
Zeigen Sie für eine Abbildung f : A −→ B und Teilmengen C, C1 , C2 ⊆ A bzw. D ⊆ B:
a) f (C1 ∩ C2 ) ⊆ f (C1 ) ∩ f (C2 ). Geben Sie ein Beispiel für f (C1 ∩ C2 ) 6= f (C1 ) ∩ f (C2 ).
b) f (C1 ∪ C2 ) = f (C1 ) ∪ f (C2 ).
c) f −1 (f (C)) ⊇ C. Geben Sie ein Beispiel für f −1 (f (C)) 6= C.
d) f (f −1 (D)) ⊆ D. Geben Sie ein Beispiel für f (f −1 (D)) 6= D.
33
1.3. ZAHLENMENGEN
1.3
Zahlenmengen
Wir haben bereits in vorangegangenen Abschnitten von den Mengen der natürlichen, ganzen, rationalen und reellen Zahlen gesprochen.
Insbesondere die rationalen und reellen Zahlen können im Allgemeinen nur näherungsweise
mit Hilfe von Stellenwertsystemen (endliche Darstellung!) auf dem Computer realisiert werden. über diese Realisierung werden wir später sprechen. Wir sehen uns zunächst an, wie
die Zahlenmengen N, Z, Q und R eingeführt werden können.
Natürliche Zahlen, vollständige Induktion
In der Mathematik werden aus gegebenen Aussagen mit Hilfe logischer Schlussfolgerungen
neue Aussagen gewonnen, die Sätze. Dieser Prozess muss irgendwann beginnen. Am Anfang
müssen Tatsachen stehen, die als wahr angenommen werden, ohne dass diese bewiesen
werden. Diese Grundtatsachen nennt man Axiome.
Giuseppe Peano (1858-1932) hat 1889 das folgende Axiomensystem aufgestellt, wodurch
natürliche Zahlen charakterisiert werden.
Definition 1.31 (Peano-Axiome). Die natürlichen Zahlen bilden eine Menge N, auf der
eine Abbildung f , die jedem n einen Nachfolger zuordnet;
f :N→N
erklärt ist, die folgende Eigenschaften besitzt:
(N1) ∃ !1 ∈ N : 1 ∈
/ f (N), d.h. es existiert genau eine Zahl, die nicht Nachfolger einer
anderen Zahl ist.
(N2) Die Abbildung f ist injektiv, d.h. aus
f (n1 ) = f (n2 ) folgt n1 = n2 .
(N3) Ist M ⊆ N und gilt
a) 1 ∈ M,
b) aus n ∈ M folgt f (n) ∈ M,
dann ist M = N.
Bemerkung:
• Die Zahl 1 ist die kleinste natürliche Zahl. Das ist Konvention. Man könnte auch mit
der 0 beginnen. Um die 0 einzubeziehen führt man N0 = N ∪ {0} ein.
• Das Axiom (N3) wird auch Induktionsaxiom genannt. Es bildet die Grundlage für
ein Beweisverfahren, das vollständige Induktion genannt wird.
34
KAPITEL 1. GRUNDLAGEN
Theorem 1.32 (Vollständige Induktion). Für n ∈ N sei A = A(n) eine Aussage. Es gelte
• A(1) ist wahr (Induktionsanfang),
• Für alle n ∈ N gilt: Ist A(n) wahr, so folgt auch, dass A(n + 1) wahr ist (Induktionsschritt).
Dann ist auch A(n) wahr für alle n ∈ N (Induktionsschluss).
Beweis
Sei M = {n ∈ A(n) : A(n) ist wahr}. Die Eigenschaften a) und b) des Axioms (N3) sind
erfüllt. Daher ist M = N.
Beispiel
Man beweise: Es sei q 6= 1. Dann ist für alle n ∈ N
q0 + q1 + · · · + qn =
1 − q n+1
.
1−q
(1.16)
Beweis
Wir betrachten die Aussage
1 − q n+1
0
1
n
.
A(n) : q + q + · · · + q =
1−q
• Die Aussage A(1) : q 0 + q 1 = 1 + q =
1−q 2
1−q
ist wahr.
• Es sei A(n) wahr. Dann gilt
1 − q n+1 + (1 − q)q n+1
1 − q n+1
+ q n+1 =
1−q
1−q
1 + (−1 + 1 − q)q n+1
=
1−q
n+2
1−q
,
=
1−q
was bedeutet, dass A(n + 1) wahr ist.
35
1.3. ZAHLENMENGEN
Teilbarkeit und Primzahlen
Der Begriff
Teiler“ einer ganzen Zahl ist aus der Schule bekannt.
”
Definition 1.33. Sei n ∈ Z, m ∈ N. Die Zahl m heißt Teiler von n, in Zeichen m|n, wenn
∃ k ∈ Z : km = n.
In diesem Fall heißt n teilbar durch m.
Es gilt:
• Die Zahl 0 ist durch alle m teilbar.
• Ist m|n1 , m|n2 dann folgt m|(n1 + n2 ).
Definition 1.34. Sei a ∈ Z. Die Menge aller Teiler ist
D(a) = {d ∈ N : d|a}.
Seien a, b ∈ Z. Die Menge aller gemeinsamen Teiler von a und b ist
D(a, b) = D(a) ∩ D(b).
Die Zahl
ggT(a, b) := max{d ∈ D(a) ∩ D(b)}
heißt größter gemeinsamer Teiler von a und b.
Beispiel
Sei a = 30 und b = 24. Dann ist
D(30) = {1, 2, 3, 5, 6, 10, 15, 30},
D(24) = {1, 2, 3, 4, 6, 8, 12, 24}.
Weiterhin ist D(30, 24) = D(30)∩D(24) = {1, 2, 3, 6} und somit ist der größte gemeinsame
Teiler von 30 und 24:
ggT(30, 24) = 6.
Berechnung des größten gemeinsamen Teilers
Wir gehen vom Teilen“ mit Rest aus. Sind a und b ∈ N, a > b. Dann gibt es natürliche
”
Zahlen q, r mit 0 ≤ r < b und
a = qb + r.
Beispiel
36
KAPITEL 1. GRUNDLAGEN
Wie bei dem vorherigen Beispiel sei a = 30 und b = 24. Es gilt
30 = 1 · 24 + 6.
Hilfe
Seien a ∈ N und b ∈ N und a = qb + r. Dann ist
D(a, b) = D(b, r),
ggT(a, b) = ggT(b, r).
(1.17)
(1.18)
Beweis
Ist d ∈ D(a, b), d.h. d|a ∧ d|b, dann gilt d|r mit r = a − qb. Damit ist d ∈ D(b, r). Umgekehrt, sei d ∈ D(b, r) d.h. d|b ∧ d|r. Dann ist d|a und d ∈ D(a, b). Daher gilt (1.17) und
(1.18).
Euklidischer Algorithmus zur Berechnung von ggT(a, b)
Starte mit (a, b).
1. Teste, ob b|a.
2. Wenn ja: D(a, b) = D(b) und ggT(a, b) = b; Stopp.
3. Wenn nein: Teile mit Rest a = qb + r, 0 < r < b. Zurück zum Anfang mit dem Paar
(b, r).
Beispiele
Berechne ggT(30, 24).
1. Gilt 24|30 ? Nein. Daraus folgt 30 = 1 · 24 + 6.
2. Gilt 6|24 ? Ja. Daraus folgt ggT(30, 24) = 6.
Berechne ggT(210, 25).
1. Gilt 25|210 ? Nein. Daraus folgt 210 = 8 · 25 + 10.
2. Gilt 10|25 ? Nein. Daraus folgt 25 = 2 · 10 + 5.
3. Gilt 5|10 ? Ja. Daraus folgt ggT(210, 25) = 5.
37
1.3. ZAHLENMENGEN
Dieses Vorgehen kann allgemein folgendermaßen beschrieben werden.
Seien a ∈ N und b ∈ N, a > b. Dann existieren eindeutig bestimmte Zahlen r0 , r1 , . . . , rk+2 ∈
N mit
r0 = a = q1 r1 + r2 ,
0 < r2 < r1 = b,
r1 = b = q2 r2 + r3 ,
0 < r3 < r2 ≤ b − 1,
..
.
rk = qk+1 rk+1 + rk+2 , 0 < rk+2 < rk+1 ,
rk+1 = qk+2 rk+2 + 0.
Es ist ggT(a, b) = rk+2 , da D(r0 , r1 ) = D(r1 , r2 ) = · · · = D(rk+1, rk+2 ) = D(rk+2).
Das Flussbild dieses Algorithmus ist in Abbildung 1.11 dargestellt.
Start
(a, b)
a = bq + r
r=0?
Ja
b = ggT(a, b)
Nein
(b, r)
Stopp
Abbildung 1.11: Berechnung von ggT(a, b), a > b.
38
KAPITEL 1. GRUNDLAGEN
Primzahlen
Definition 1.35. Eine natürliche Zahl p ≥ 2 heißt Primzahl, falls
D(p) = {1, p}
ist.
Lemma 1.36. Jede natürliche Zahl n ≥ 2 ist ein Produkt von Primzahlen.
Beweis Vollständige Induktion.
Wir betrachten die Aussage A(n) n ist Produkt von Primzahlen“ .
”
Induktionsanfang: A(2) ist wahr.
Induktionsannahme: A(n) sei wahr für n ≥ 3.
Induktionsschluss: Wir zeigen A(n + 1) ist wahr.
Wir unterscheiden die Fälle
a) n + 1 sei prim, d.h. n + 1 = p.
b) n+1 ist nicht prim, d.h. n+1 = n1 ·n2 mit n1 < n+1, n2 < n+1. Nach Induktionsannahme ist n + 1 = n1 · n2 = p1 . . . pk1 q1 . . . qk2 , wobei pi , qj , i = 1, . . . , k1 , j = 1, . . . , k2
Primzahlen sind.
Der folgende Satz wird als Übungsaufgabe empfohlen.
Theorem 1.37 (Fundamentalsatz der Arithmetik). Jede natürliche Zahl n ≥ 2 lässt sich
bis auf die Reihenfolge der Faktoren auf genau eine Weise als Produkt von Primzahlen
schreiben.
Theorem 1.38 (Satz von Euklid). Es gibt unendlich viele Primzahlen.
Beweis
Wir nehmen an, es gäbe r verschiedene Primzahlen p1 , p2 , . . . , pr . Wir konstruieren weitere
Primzahlen. Dazu zerlegen wir die Zahl p1 p2 . . . pr + 1 in Primfaktoren
p1 p2 . . . pr + 1 = q1 q2 . . . qs .
Wir zeigen durch einen Widerspruchsbeweis, dass pi 6= qj ist für 1 ≤ i ≤ r, 1 ≤ j ≤ s.
Wäre für ein i = i0 und ein j = j0 pi0 = qj0 , dann wäre pi0 |q1 . . . qs und damit
pi0 |(p1 . . . pr + 1). Es würde folgen, dass pi0 |1, was nicht sein kann. Daher sind q1 , . . . , qs
weitere Primzahlen, die wir der Liste p1 , p2 , . . . , pr hinzufügen können.
39
1.3. ZAHLENMENGEN
Rationale und reelle Zahlen
Wir erinnern zunächst an die Menge der rationalen Zahlen Q und führen die Menge der
reellen Zahlen R ein, indem wir diese Mengen beschreiben, aber nicht alle technischen
Details ausführen. In der Mathematik führt man die Menge der reellen Zahlen mit Hilfe
Dedekindscher Schnitte oder mit Intervallschachtelung ein, die in Q definiert werden. Eine weitere Möglichkeit wäre, die Menge der reellen Zahlen durch ein Axiomensystem zu
beschreiben. Wir gehen hier einen anderen Weg und führen, etwas weniger mathematisch
rigoros Q und R so ein, wie sie historisch entstanden sind.
Mit Hilfe der Peano-Axiome können in N eine Addition, Multiplikation und eine Ordnungsrelation eingeführt werden. Die Umkehrung dieser Rechenoperationen, die Subtraktion und
Division ist nicht immer möglich. Um diese ausführen zu können, wird die Menge der ganzen Zahlen Z und die Menge der rationalen Zahlen Q eingeführt:
N ⊂ Z ⊂ Q.
Die Menge Q hat folgende Eigenschaften:
1. Die Menge Q ist total geordnet, d.h. für je zwei verschiedene rationale Zahlen a und
b lässt sich angeben, welche die kleinere ist.
2. Die Menge Q ist in sich überall dicht, d.h. zwischen je zwei verschiedenen rationalen
Zahlen a und b liegt mindestens eine weitere rationale Zahl c. Daher liegen zwischen
zwei verschiedenen rationalen Zahlen unendlich viele weitere rationalen Zahlen.
3. Die Rechenoperationen Addition, Subtraktion, Multiplikation und Division (außer
durch 0) sind in Q ausführbar.
4. Jede rationale Zahl lässt sich in Form eines endlichen oder unendlichen periodischen
Dezimalbruches darstellen.
Die Menge der rationalen Zahlen reicht jedoch nicht aus, um die gesamte
Zahlengerade zu
a n
a
n
füllen. So ist das Potenzieren von rationalen Zahlen q = b , q = b = q · · · · · q, n ∈ N
in Q definiert, die inverse Operation, das Wurzelziehen, liefert jedoch nicht immer eine
rationale Zahl.
Beispiel
√
√
Die Ausdrücke 2 und 3 10 sind keine rationalen Zahlen.√
Wir führen einen Widerspruchsbeweis um zu zeigen, dass 2 keine rationale Zahl ist. Dazu
betrachten wir die Aussagen
√
A = {x = 2}, B = {x ist nicht rational}.
Wir behaupten, dass die Aussage {A ⇒ B} wahr ist, d.h. die Aussage A ∧ ¬B ist falsch.
Die Aussage ¬B lautet: x ist rational, genauer: x = ab , wobei a und b teilerfremd sind. Die
Aussage
√ a
A ∧ ¬B = x = 2 ∧ x = (teilerfremd)
b
40
KAPITEL 1. GRUNDLAGEN
liefert
√ √
a2
2 2 = 2 , 2b2 = a2 .
b
2
Damit ist a eine ganze Zahl und a muss gerade sein. Wir setzen a = 2k und erhalten
2b2 = 4k 2 und somit ist b2 = 2k 2 gerade. Es folgt, dass b gerade ist und 2 Teiler von a
und b ist. Dies ist ein Widerspruch und ¬ (A ∧ ¬B) ist wahr, was äquivalent dazu ist, dass
A ⇒ B wahr ist.
Die Einführung irrationaler Zahlen gestattet es, jedem Punkt der Zahlengeraden eine reelle
Zahl zuzuordnen. Dabei ist eine Zahl irrational, wenn sie sich durch einen nichtperiodischen
unendlichen Dezimalbruch darstellen lässt.
Wir können jetzt die Menge der reellen Zahlen R einführen:
R = Q ∪ {irrationale Zahlen}.
Die Menge R ist nicht abzählbar.
Theorem 1.39. Das Intervall I = {x ∈ R : 0 < x < 1} ist überabzählbar und damit ist R
überabzählbar.
Beweis
Wir nehmen an, dass f : I → N bijektiv sei, d.h. wir können die Elemente aus I durchnummerieren x1 , x2 , x3 , . . . , xn , . . . .
Sei in der Dezimaldarstellung
(n) (n)
(n)
xn = 0, a−1 a−2 . . . a−n . . . .
(1.19)
Wir setzen
(
(n)
6 0,
0 falls a−n =
bn =
(n)
1 falls a−n = 0
(1)
und betrachten das Element y = 0, b1 b2 b3 . . . . Es ist y 6= x1 , da b1 6= a−1 ist; y 6= x2 ,
(2)
da b2 6= a−1 ist; usw. Das Element y = 0, b1 b2 b3 . . . gehört also nicht zu der Menge der
Elemente xn , die durch (1.19) beschrieben werden. Dieser Widerspruch besagt, dass I nicht
abzählbar ist.
Haupteigenschaften der reellen Zahlen
1. Die Menge der reellen Zahlen ist total geordnet.
2. Die Menge der rationalen Zahlen Q ist dicht in R, d.h. sei r ∈ R, dann gilt: Für alle
ε > 0 existiert ein q = q(ε) ∈ Q : |q − r| < ε.
41
1.3. ZAHLENMENGEN
3. Die Menge der reellen Zahlen ist stetig (ein Kontinuum), d.h. jeder Punkt der Zahlengeraden entspricht einer reellen Zahl.
4. Die arithmetischen Operationen (Addition, Subtraktion, Multiplikation, Division –
außer durch 0 –) sind mit reellen Zahlen stets ausführbar und ergeben wieder eine
reelle Zahl. Das Potenzieren ist in R stets ausführbar, wobei das Wurzelziehen im
Bereich R+ = {x ∈ R : x ≥ 0} definiert ist.
Um Wurzeln aus negativen Zahlen zu definieren, muss die Menge der komplexen Zahlen
eingeführt werden.
Übersicht, welche Rechenoperationen in den einzelnen Zahlenmengen ausgeführt
werden können
N
Addition, Multiplikation
Z
zusätzlich: Subtraktion
Q
zusätzlich: Division
0 1 2 3
−2 −1 0 1 2
0 abzählbar, unendlich
0 überabzählbar
· z = (a, b)
R
zusätzlich: Wurzelziehen
√
n
b, b ≥ 0,
C
zusätzlich: Wurzelziehen
√
n
−b
Gauß’sche Zahlenebene
Die Menge der komplexen Zahlen C
Die Einführung der komplexen Zahlen ist notwendig, um Nullstellen von Polynomen bestimmen, bzw. Wurzeln aus negativen reellen Zahlen ziehen zu können.
42
KAPITEL 1. GRUNDLAGEN
Definition 1.40. Sei R die Menge der reellen Zahlen. Die Menge der komplexen Zahlen C entspricht dem kartesischen Produkt R × R = R2 , in der folgende Addition und
Multiplikation eingeführt sind:
z1 + z2 = (a1 + a2 , b1 + b2 ),
z1 · z2 = (a1 , b1 ) · (a2 , b2 ) = (a1 a2 − b1 b2 , a1 b2 + a2 b1 ),
wobei z1 = (a1 , b1 ) ∈ R2 , z2 = (a2 , b2 ) ∈ R2 sind.
Bemerkung:
Die Menge der reellen Zahlen kann als Teilmenge von C aufgefasst werden. Sei R∗ = {z ∈
C : z = (a, 0)}. Dann ist die folgende Abbildung f : R → R∗ bijektiv, d.h.
a ∈ R ⇔ z = (a, 0) := a.
(1.20)
Wir führen die imaginäre Einheit ein:
i = (0, 1).
Es gilt
(1.20)
i2 = (0, 1)(0, 1) = (0 − 1, 0) = (−1, 0) = −1
√
und es wird kurz geschrieben i = −1.
Theorem 1.41. Für jede komplexe Zahl z ∈ C ist
z = (a, b) = a + ib.
Beweis
Wir haben
a + ib = (a, 0) + (b, 0)(0, 1) = (a, 0) + (0, b) = (a, b).
Definition 1.42. Sind a und b reelle Zahlen und ist z = a + ib, dann heißt z̄ := a − ib
die konjugiert komplexe Zahl zu z. Die Zahlen a = Re(z), b = Im(z) werden Realteil bzw.
Imaginärteil von z genannt.
Komplexe Zahlen können in der Gauß’schen Zahlenebene dargestellt werden.
Theorem 1.43. Sind z und w komplexe Zahlen, dann gilt
a) z + w = z̄ + w̄,
43
1.3. ZAHLENMENGEN
Im z
b
(a, b) = z
|z|
|z̄|
Re z
a
(a, −b) = z̄
Abbildung 1.12: Gauß’sche Zahlenebene
b) z · w = z̄ · w̄,
c) z + z̄ = 2Re(z), z − z̄ = 2iIm(z),
d) z · z̄ ist eine reelle nichtnegative Zahl.
Der Beweis wird als Übung empfohlen (siehe auch Abbildung 1.12).
Definition 1.44. Der Betrag von z = a + ib ∈ C ist definiert als:
√
1
|z| := (z · z̄) 2 = a2 + b2 .
Es ist |z| = |z̄|.
Trigonometrische Darstellung der komplexen Zahlen
Die komplexen Zahlen z = a + ib mit |z| = 1 liegen auf dem Einheitskreis.
Daher gilt a = cos ϕ und b = sin ϕ. Der Winkel ϕ = arg(z) wird als Argument von z
bezeichnet. In diesem Fall ist
z = cos ϕ + i sin ϕ.
Sei nun z 6= (0, 0) ein Element aus C. Es ist |z| =
6 0. Die komplexe Zahl w =
Betrag |w| = 1 und daher ist
w = cos ϕ + i sin ϕ und
z = |z| (cos ϕ + i sin ϕ) .
z
|z|
besitzt den
(1.21)
Schreibt man |z| = r erhält man die trigonometrische Darstellung der komplexen Zahl z
z = r (cos ϕ + i sin ϕ) .
44
KAPITEL 1. GRUNDLAGEN
b
1
(a, b) = z
ϕ
a
Abbildung 1.13: Einheitskreis
b
r = |z|
ϕ
Dabei ist cos ϕ =
√ a
, sin ϕ
a2 +b2
=
(a, b) = z
a
√ b
.
a2 +b2
Beispiele
Es ist
π + i sin
,
2 2
π √
π
+ i sin
.
z = 1 + i = 2 cos
4
4
z = i = cos
π Zahlendarstellung mit g-adischen Brüchen
Wir betrachten eine natürliche Zahl n ∈ N. Sie lässt sich als Summe von Potenzen der Zahl
10 darstellen
n = a0 · 100 + a1 · 101 + a2 · 102 + · · · + aN · 10N ,
0 ≤ ai ≤ 9, aN 6= 0 .
Beispiel
Die Zahl 2006 lässt sich darstellen als
2006 = 6 · 100 + 0 · 101 + 0 · 102 + 2 · 103 .
45
1.3. ZAHLENMENGEN
Die Zifferndarstellung besteht darin, die Koeffizienten in umgekehrter Reihenfolge anzuordnen:
n = aN aN −1 . . . a0 .
(1.22)
Etwas schwieriger ist es, eine reelle Zahl als Zehnerpotenzen darzustellen. Wir beschreiben
diese Dezimaldarstellung als Algorithmus:
Sei x ∈ R. Wir finden ein y ∈ Z mit
y ≤ x < y + 1.
Falls y = x ist, dann ist der Algorithmus beendet und wir schreiben x = ±aN aN −1 . . . a0 wie
in (1.22). Falls nicht, wird das Intervall [y, y +1) in 10 Teilintervalle Ia−1 , a−1 ∈ {0, 1, . . . , 9}
mit gleicher Länge zerlegt. Wir betrachten das Teilintervall Ia−1 , das x enthält, d.h.
r1 = y + a−1 · 10−1 ≤ x < y + (a−1 + 1)10−1 = r2 .
Falls x = y + a−1 · 10−1 , dann ist der Algorithmus beendet; falls nicht, wird das Intervall
[r1 , r2 ) in 10 Teilintervalle gleichmäßig zerlegt und das Teilintervall Ia−2 , a−2 ∈ {0, 1, . . . , 9}
betrachtet, das x enthält. Dieser Prozess wird so oft wiederholt, bis es entweder ein Intervall gibt, dessen linker Randpunkt gleich x ist (endlicher Dezimalbruch) oder er hat kein
endliches Ende (unendlicher Dezimalbruch). Wir schreiben
x = y, a−1a−2 a−3 · · · = ±aN aN −1 . . . a0 , a−1 a−2 a−3 . . .
(1.23)
Es gilt folgende Vereinbarung:
Ist a−i = 9 für alle i : i ≥ i0 und a−i0 +1 6= 9, dann schreiben wir
x = y, a−1 . . . a−i0 +1 999 . . .
= y, a−1 . . . (a−i0 +1 + 1).
(1.24)
Beispiele
Es ist
0, 9999 . . . = 1,
3, 264999 . . . = 3, 265.
Mit dieser Konvention sind zwei reelle Zahlen gleich, wenn ihre Ziffern gleich sind.
g-adische Darstellung von reellen Zahlen
Neben der Dezimaldarstellung (1.23) von reellen Zahlen, die auf der Darstellung durch
Zehner-Potenzen beruht, können auch andere Ziffernbasen verwandt werden.
Sei g ∈ N, g ≥ 2.
46
KAPITEL 1. GRUNDLAGEN
Theorem 1.45. Jede natürliche Zahl n ∈ N lässt sich eindeutig in der Form
n = ng =
N
X
i=0
ai g i = a0 g 0 + a1 g 1 + · · · + aN g N ,
aN 6= 0,
ai ∈ {0, 1, . . . , g − 1},
darstellen. Die Ziffern ai , i = 0, . . . , N, können mit Hilfe eines Divisionsalgorithmus berechnet werden. Die Zifferndarstellung lautet
n = ng = aN aN −1 . . . a0 .
Beweis
Wir zeigen zunächst die Eindeutigkeit.
Es gelte
n = a0 g 0 + a1 g 1 + · · · + aN g N = b0 g 0 + b1 g 1 + · · · + bM g M ,
ai , bj ∈ {0, 1, . . . , g − 1}, i = 0, . . . , N, j = 0, 1, . . . , M.
M ≥ N,
(1.25)
(1.26)
Dann ist
a0 − b0 = b1 g 1 + · · · + bM g M − a1 g 1 + · · · + aN g N
= g b1 − a1 + · · · + (bN − aN ) g N −1 + bN +1 g N + · · · + bM g M −1
= gk,
mit k = b1 − a1 + · · · + (bN − aN ) g N −1 + bN +1 g N + · · · + bM g M −1 ∈ Z.
Wegen (1.26) ist
−g < a0 − b0 = gk < g
und k = 0. Es folgt a0 = b0 .
In (1.25) ziehen wir a0 = b0 auf beiden Seiten ab und dividieren durch g. Es folgt analog,
dass a1 = b1 ist und schließlich dass ai = bi für i = 1, . . . , N und bN +1 = · · · = bM = 0
sind. Durch die Bedingung aN 6= 0 ist N eindeutig bestimmt.
2. Schritt: Existenzbeweis durch Konstruktion
0◦ Es existiert ein N ∈ N, so dass
g N ≤ n < g N +1
ist. Wir bestimmen dieses N und führen danach folgenden Divisionsalgorithmus aus.
1◦ Teile n durch g N (Teilen mit Rest):
n = aN g N + rN ,
mit 0 ≤ rN < g N , 0 < aN ≤ g − 1.
2◦ Teile rN durch g N −1 :
rN = aN −1 g N −1 + rN −1 ,
mit 0 ≤ rN −1 < g N −1 , 0 ≤ aN −1 ≤ g − 1.
47
1.3. ZAHLENMENGEN
3◦ Teile rN −1 durch g N −2 :
rN −1 = aN −2 g N −2 + rN −2 , mit 0 ≤ rN −2 < g N −2 , 0 ≤ aN −2 ≤ g − 1,
..
.
r2 = a1 g 1 + r1 , mit 0 ≤ r1 < g ,
r1 = a0 .
Bemerkung:
Im Schritt 1◦ ist aN > 0 wegen g N ≤ n. Für i ∈ {1, 2, . . . , N −1} ist auch ai = 0 zugelassen,
da nicht immer g i ≤ ri+1 ist.
Beispiele
Wir stellen die Zahl 2006 dar, indem wir N bestimmen und den Divisionsalgorithmus
ausführen.
g=2:
210 < 2006 < 211 , N = 10
20062 = 0 · 20 + 1 · 21 + 1 · 22 + 0 · 23 + 1 · 24
+0 · 25 + 1 · 26 + 1 · 27 + 1 · 28 + 1 · 29 + 1 · 210
= 11111010110
g=4:
45 < 2006 < 46 , N = 5
20064 = 2 · 40 + 1 · 41 + 1 · 42 + 3 · 43 + 3 · 44 + 1 · 45
= 133112
g = 16 : 162 < 2006 < 163 , N = 2
200616 = 2 · 160 + 7 · 161 + 7 · 161
= 772
Bemerkung:
Um im Hexadezimalsystem die Zahlen
darzustellen, verwendet man die Buchstaben
10, 11,
A, B,
12, 13, 14,
C, D, E,
15
F.
Die Darstellung der reellen Zahlen im g-adischen Ziffernsystem folgt dem Algorithmus, der
zuvor für g = 10 erklärt wurde.
Wir erhalten das Ergebnis: Jede reelle Zahl x lässt sich eindeutig im g-adischen Ziffern-
48
KAPITEL 1. GRUNDLAGEN
system darstellen:
x = xg = ±aN aN −1 . . . a0 , a−1 a−2 . . . ,
N
x = aN g + aN −1 g
∞
X
=
a−j g −j .
N −1
0
aN 6= 0,
+ · · · + a0 g + a−1 g −1 + a−2 g −2 + . . .
(1.27)
j=−N
Dabei vereinbaren wir, wie zuvor, dass
a−j = g − 1 für alle j ≥ j0 , a−j0 +1 < g − 1 ,
verboten ist (vergleiche mit (1.24)) und setzen
± aN aN −1 . . . a0 , a−1 a−2 . . . a−j0 +1 (g − 1)(g − 1)(g − 1) . . .
= ±aN aN −1 . . . a0 , a−1 a−2 . . . (a−j0 +1 + 1) .
Bemerkung: Die Babylonier benutzten 1600 v. Chr. ein Zahlensystem mit g = 60, die
Mayas hatten 665 n. Chr. ein Zahlensystem mit g = 20.
Zahlendarstellung im Computer
Die Darstellung der ganzen Zahlen im Computer erfolgt zumeist für g = 2, d.h. in einem
binären Stellenwertsystem. Es können nur Zahlen einer endlichen Länge L benutzt werden. Daher können nur maximal 2L verschiedene Zahlen als Bitmuster dargestellt werden.
Außerdem muss das Vorzeichen berücksichtigt werden [3, S.49].
Bitmuster:
L
z }| {
000 . . . 000 ∼
= 0,
000 . . . 001 ∼
= 1,
∼
000 . . . 010 = 2,
..
.
111 . . . 111 ∼
=
L−1
X
i=0
2i = 1 + 2 + 22 + · · · + 2L−1 =
1 − 2L
= 2L − 1.
1−2
Die Bitmuster können addiert und subtrahiert werden.
Rationale Zahlen können durch Multiplikation der Bitmuster mit dem Faktor 2−k erfasst werden (Festpunkt-Zahlensystem) oder der Skalierungsfaktor wird variabel gehalten
(Gleitpunkt-Zahlensystem). Numerische Berechnungen, die eine Vielzahl von Gleitpunktoperationen benötigen, können beträchtliche Fehler aufweisen. Ursache können Rundungsfehler sein, wie sie bei Subtraktion entstehen. Das Assoziativgesetz ist im Gleitkommasystem (festes L) verletzt.
49
1.3. ZAHLENMENGEN
Beispiel (Dezimalsystem , siehe [3, S.53])
x = 0.23371258 · 10−4 ,
y = 0.33678429 · 102 ,
z = −0.33677811 · 102 .
Das exakte Ergebnis lautet x + y + z = 0.641371258 · 10−3.
Durch Rundung erhalten wir
x + (y + z) = 0.23371258 · 10−4
+ 0.00000618 · 102
≈ 0.02337126 · 10−3
+ 0.618
· 10−3
= 0.64137126 · 10−3 ,
(x + y) + z ≈ (0.00000023 · 102
+ 0.33678429 · 102 )
+z
= 0.33678452 · 102
− 0.33677811 · 102
= 0.00000641 · 102 = 0.641 · 10−3 .
Die Kunst der Numerik besteht darin, diese Fehler klein zu halten.
Übungsaufgaben
Aufgabe 3.1
Zeigen Sie mit Hilfe von vollständiger Induktion: Die Potenzmenge P(M ) einer Menge M mit n
Elementen hat 2n Elemente.
Aufgabe 3.2
Pascalsches Dreieck und Binomischer Satz.
Für ganze Zahlen n ≥ k ≥ 0 ist der Binomialkoeffizient durch
n(n − 1)(n − 2) . . . (n − k + 1)
n!
n
=
,
:=
k
(n − k)!k!
k(k − 1)(k − 2) . . . 2 · 1
(lies: n über k) definiert, wobei n! = 1 · 2 · · · (n − 1)n und 0! = 1 ist.
1
1
1
a) Betrachten Sie das Pascalsche Dreieck
1
1
1
3
4
5
1
2
1
3
6
10
1
4
10
1
5
1
50
KAPITEL 1. GRUNDLAGEN
Das Dreieck hat am Rand Einsen und die inneren Zahlen sind die Summe der beiden darüber
liegenden Zahlen. Zeigen Sie durch vollständige Induktion nach n, dass die k-te Zahl der n-ten
Zeile durch den Binomialkoeffizienten ( nk ) gegeben ist, wobei die Nummerierung von n und k
bei 0 startet.
b) Zeigen Sie für a, b ∈ R den Binomischen Satz
(a + b)n =
n X
n
k=0
k
an−k bk .
Aufgabe 3.3
a) Bestimmen Sie ggT(a, b) von den Paaren a = 3267 , b = 8877 und a = 5161 , b = 6817 durch
Ausführen des Euklidischen Algorithmus auf dem Papier.
b) Bestimmen Sie ggT(a, b) von den Paaren a = 123454321, b = 2222222222 und a = 1122334455,
b = 6677889900 wahlweise auf Papier oder mit Hilfe eines (selbst geschriebenen) Programms.
Das Programm ist ggf. mit anzugeben.
c) Finden Sie eine Folge an , n ≥ 1 , von ganzen Zahlen, so dass der Euklidische Algorithmus
genau n Schritte zur Berechnung des ggT(an+1 , an ) benötigt.
Hinweis: Starten Sie mit einer beliebigen Zahl a1 und finden Sie mit Hilfe des Algorithmus eine
passende Zahl a2 .
Aufgabe 3.4
Beweisen Sie die folgenden Summenformeln mit vollständiger Induktion.
a)
n
X
k=1
n(n + 1)
,
k=
2
n
X
(2k − 1) = n2 ,
b)
c)
n
X
k2 =
k=1
k=1
n(n + 1)(2n + 1)
.
6
Aufgabe 3.5
Die Fibonacci-Zahlen Fn , n ∈ N0 , sind definiert durch
F0 = 0,
F1 = 1,
Fn+2 = Fn + Fn+1 .
Bestimmen Sie F7 und zeigen Sie die folgenden Beziehungen:
a)
n
X
k=0
Fk = Fn+2 − 1
b)
n
X
k=0
Fk2 = Fn Fn+1
51
1.4. GRUPPEN, RINGE, KÖRPER
1.4
Gruppen, Ringe, Körper
Die Menge der komplexen Zahlen wurde eingeführt, indem wir im R2 = R × R eine Addition und eine Multiplikation von zwei Elementen definiert hatten. Die Addition und
Multiplikation sind Beispiele für Verknüpfungen, die folgendermaßen definiert werden.
Definition 1.46. Sei M eine Menge. Eine Abbildung
f : M × M → M,
(m1 , m2 ) → m = m1 ∗ m2
heißt Verknüpfung. Eine Verknüpfung heißt assoziativ, wenn gilt
(m1 ∗ m2 ) ∗ m3 = m1 ∗ (m2 ∗ m3 ) ∀ m1 , m2 , m3 ∈ M.
Sie heißt kommutativ, wenn
m1 ∗ m2 = m2 ∗ m1
∀ m1 , m2 ∈ M
gilt. Ein Element e ∈ M heißt neutral, falls gilt
e ∗ m = m ∗ e = m ∀ m ∈ M.
Beispiele
1◦ Sei M = P(X) die Potenzmenge einer Menge X. Die Abbildungen Vereinigung “
”
und Durchschnitt “
”
f : M × M → M, g : M × M → M,
f : U ∪ V = W,
g : U ∩ V = W, U, V ⊂ M
sind kommutative und assoziative Verknüpfungen.
Das neutrale Element für f ist die leere Menge ∅; das neutrale Element für g ist die
Menge X.
2◦ In der Informatik wird folgende Situation betrachtet:
Gegeben ist eine endliche Menge M, ein sogenanntes Alphabet. Über M wurden
Bitstrings“ betrachtet, das sind endliche Folgen von Elementen aus M. Genauer,
”
falls
u : N→M
n → u(n) = un ∈ M ,
dann ist ein string = string(u, k) = {u(1), . . . , u(k)} = u(1) . . . u(k) eine Folge der
Länge k bzw. ein Wort der Länge k. Als Verknüpfung zweier strings“ (u(1) . . . u(k))
”
und (v(1) . . . v(l)) wird die Verkettung (Konkatenation) eingeführt:
(u(1) . . . u(k)) ∗ (v(1) . . . v(l) = (w(1) . . . w(k + l)) = (u(1) . . . u(k)v(1) . . . v(l)) ,
52
KAPITEL 1. GRUNDLAGEN
wobei
w(i) =
u(i)
für 1 ≤ i ≤ k
v(i − k) für k + 1 ≤ i ≤ k + l
ist.
Dies ist eine assoziative Verknüpfung in der Menge M ∗ aller strings.
3◦ Wir betrachten die Menge der rationalen Zahlen Q und die Abbildungen Addition
und Multiplikation:
f : Q × Q → Q, g : Q × Q → Q,
f (a, b) = a + b, g(a, b) = a · b.
Das neutrale Element für die Addition ist die Null, für die Multiplikation die Eins.
Definition 1.47 (Halbgruppe, Monoid). Eine Menge G mit einer assoziativen Verknüpfung
∗“ heißt Halbgruppe, geschrieben als (G, ∗).
”
Eine Halbgruppe heißt Monoid, falls ein eindeutig bestimmtes neutrales Element e ∈ G
existiert mit
e∗g =g∗e=g
∀g ∈ G.
Wir schreiben (G, ∗, e) für das Monoid.
Ist die Verknüpfung ∗“ zusätzlich kommutativ, so heißt G ein kommutatives Monoid.
”
Um Gruppen einzuführen, benötigen wir den Begriff der Invertierbarkeit eines Elementes
aus einem Monoid.
Definition 1.48 (inverses Element,Gruppe). Ist (G, ∗, e) ein Monoid, so ist g ∈ G invertierbar in G, falls ein Element g −1 ∈ G existiert mit
g ∗ g −1 = g −1 ∗ g = e .
Man nennt g −1 Inverse (inverses Element) zu g.
Ein Monoid (G, ∗, e) heißt Gruppe, wenn jedes g ∈ G invertierbar ist. Ist außerdem die
Verknüpfung ∗“ kommutativ, dann heißt (G, ∗, e) abelsche Gruppe. Hat eine Gruppe
”
endlich viele Elemente, dann sprechen wir von einer endlichen Gruppe.
Beispiele
0◦ Fügen wir im obigen Beispiel 2◦ das leere Wort als neutrales Element in M ∗ hinzu,
so erhalten wir ein Monoid.
1◦ Die natürlichen Zahlen bilden eine Halbgruppe mit der Multiplikation oder der Addition.
53
1.4. GRUPPEN, RINGE, KÖRPER
2◦ Z, Q, R und C sind Gruppen bezüglich der Addition; Q+ = {x ∈ Q : x > 0} ist eine
Gruppe bezüglich der Multiplikation.
3◦ Die endliche Menge G = {−1, +1} ist ebenfalls eine Gruppe bezüglich der Multiplikation in Z.
4◦ Permutationsgruppen
Etwas ausführlicher betrachten wir Permutationsgruppen. Es sei M eine Menge und
S(M) folgende Menge von Abbildungen von M in M:
S(M) = {f : M ↔ M, f bijektiv}.
Die Verknüpfung in S(M) sei die Komposition
f ∗ g = f ◦ g.
Das neutrale Element ist die identische Abbildung e
e : M → M,
e : m → m, ∀ m ∈ M.
Da f bijektiv ist, existiert die inverse Abbildung f ◦ f −1 = f −1 ◦ f = e. Daher ist
(S(M), ◦, e) eine Gruppe.
Als Spezialfall betrachten wir: Sn = S({1, 2, 3, . . . , n}). Sn heißt auch symmetrische
Gruppe auf n Elementen. Diese Gruppe hat n! Elemente, die Permutationen genannt
werden. Dieser Beweis ist als Übung empfohlen.
Beispiel
Wir betrachten
S3 = S({1, 2, 3}).
Die möglichen Permutationen können folgendermaßen beschrieben werden:
1
2
3
.
f (1) f (2) f (3)
Es ergeben sich 3! = 6 Permutationen:
1
1 2 3
, f2 =
ˆ
f1 = e=
ˆ
1
1 2 3
1
1 2 3
, f5 =
ˆ
f4 =
ˆ
3
2 3 1
1
2 3
, f3 =
ˆ
2
3 2
1
2 3
, f6 =
ˆ
3
1 2
2 3
,
1 3
2 3
.
2 1
5◦ Gruppe der Restklassen
Wir hatten in der Menge der ganzen Zahlen eine Äquivalenzrelation eingeführt (kongruent modulo m, m ∈ N)
a ∼ b ⇔ a ≡ b modulo m ⇔ a − b = qm,
q ∈ Z.
54
KAPITEL 1. GRUNDLAGEN
Dadurch erhalten wir eine Partition von Z, deren m Elemente die Äquivalenzklassen
sind.
Die Äquivalenzklasse von a ∈ Z wird auch Restklasse von a modulo m genannt
R[a] = {b ∈ Z : b ∼ a},
= a + mZ.
Das Element a heißt Vertreter bzw. Repräsentant der Restklasse. Die Menge aller
Restklassen {R[0], R[1], . . . R[m − 1]} wird mit
Z/mZ
bezeichnet. Auf Z/mZ kann eine Addition ⊕ und eine Multiplikation ⊙ definiert
werden:
R[a] ⊕ R[b] = R[a + b],
R[a] ⊙ R[b] = R[ab].
Beispiel
Es sei m = 2, dann gibt es zwei Restklassen:
R[0] = {b ∈ Z : 0 − b = 2q, q ∈ Z}
= {. . . , −4, −2, 0, 2, 4, 6, . . . } ganze gerade Zahlen,
R[1] = {b ∈ Z : 1 − b = 2q, q ∈ Z}
= {. . . , −3, −1, 0, 1, 3, 5, . . . } ganze ungerade Zahlen.
Es ist e = R[0] das neutrale Element bezüglich der Addition und e = R[1] das
neutrale Element bezüglich der Multiplikation. Insbesondere haben wir:
R[0] ⊕ R[1] = R[1],
R[0] ⊕ R[0] = R[0],
R[1] ⊕ R[1] = R[2] = R[0],
R[0] ⊙ R[0] = R[0],
R[0] ⊙ R[1] = R[0],
R[1] ⊙ R[1] = R[1],
d.h.
d.h.
d.h.
d.h.
d.h.
d.h.
gerade Zahl + ungerade Zahl = ungerade Zahl,
gerade Zahl + gerade Zahl = gerade Zahl,
ungerade Zahl + ungerade Zahl = gerade Zahl,
gerade Zahl · gerade Zahl = gerade Zahl,
gerade Zahl · ungerade Zahl = gerade Zahl,
ungerade Zahl · ungerade Zahl = ungerade Zahl.
Die Menge (Z/mZ, ⊕) ist eine Gruppe; die Menge ((Z/mZ)\{R[0]}, ⊙) ist eine Gruppe, falls m eine Primzahl ist.
Bemerkung:
Die Verknüpfungen in endlichen Gruppen kann man in Verknüpfungstafeln aufschreiben:
55
1.4. GRUPPEN, RINGE, KÖRPER
∗
a1
a1
a1 ∗ a1
..
.
a2
···
an ∗ a1
···
a2
..
.
an
···
···
an
a1 ∗ an
an ∗ an
So können wir die Gruppe G = {−1, +1, ·, 1 = e} in Beispiel 3◦ durch folgende Verknüpfungstafel beschreiben.
·
-1
+1
-1 -1
1 -1
-1 1
In Beispiel 5◦ kann (Z/4Z, ⊕, e = R[0]) durch die Verknüpfungstafel charakterisiert werden
⊕
R[0]
R[1]
R[2]
R[3]
R[0]
R[0]
R[1]
R[2]
R[3]
R[1]
R[1]
R[2]
R[3]
R[0]
R[2]
R[2]
R[3]
R[0]
R[1]
R[3]
R[3]
R[0]
R[1]
R[2]
Wir erhalten
(R[0])−1 = R[0], (R[1])−1 = R[3], (R[2])−1 = R[2], (R[3])−1 = R[1] .
Definition 1.49 (Ring). Eine Menge mit zwei Verknüpfungen + “ und · “ und den
”
”
Eigenschaften:
1. (M, +) ist abelsche Gruppe mit dem neutralen Element e+ ,
· “ ist assoziativ, es gibt ein neutrales Element e· ,
”
3. (a + b) · c = a · c + b · c, c · (a + b) = c · a + c · b für alle a, b, c ∈ M,
2. die Verknüpfung
4. e+ 6= e· .
heißt Ring.
Beispiele für Ringe sind: Z und Z/pZ, wobei p eine Primzahl ist.
Definition 1.50 (Körper). Sei M ein Ring. Ist M kommutativ bezüglich der Multiplikation
und M\{e+ } eine Gruppe unter der Verknüpfung · “, dann heißt M Körper.
”
Beispiele
Q, R und C sind Körper.
56
KAPITEL 1. GRUNDLAGEN
Abbildungen von Monoiden und Gruppen
Wir haben bisher Relationen, insbesondere 0 und Graphen von Abbildungen als Teilmengen
des kartesischen Produktes M1 × M2 × · · · × Mr von Mengen Mi , i = 1, . . . , r, betrachtet.
Falls zwischen den Mengen Mi Verknüpfungen erklärt sind, dann sollten diese auch auf die
Relationen übertragbar sein.
Definition 1.51 (Strukturerhaltende Relation). Seien (G1 , ∗1 ) und (G2 , ∗2 ) Halbgruppen.
Die Relation
R ⊂ G1 × G2
heißt strukturerhaltend, falls für (a1 , a2 ) ∈ R und (b1 , b2 ) ∈ R folgt, dass (a1 ∗1 b1 , a2 ∗2 b2 ) ∈
R ist.
Wenn die Relation R ein Graph G(f ) einer Abbildung
f : G1 → G2
ist, lautet die obige Definition: für (a1 , f (a1 )) ∈ G(f ) und (b1 , f (b1 )) ∈ G(f ) soll gelten
(a1 ∗1 b1 , a2 ∗2 b2 ) ∈ G(f ), d.h. es muss sein, dass
f (a1 ) ∗2 f (b1 ) = f (a1 ∗1 b1 ) ∀a1 , b1 ∈ G1
(1.28)
ist. In diesem Fall heißt die Abbildung strukturerhaltend.
Beispiele:
1◦ Sei (G1 , ∗1 ) = (G2 , ∗2 ) = (R, +) und f : R → R. f ist strukturerhaltend, falls
f (a1 + b1 ) = f (a1 ) + f (b1 ) für alle a1 , b1 ∈ R ist.
Dies ist zum Beispiel für f (x) = ax, a ist eine feste reelle Zahl, erfüllt.
2◦ Sei (G1 , ∗1 ) = (G2 , ∗2 ) = (C, ·) und f : C → C. f ist strukturerhaltend, falls
f (z1 · z2 ) = f (z1 ) · f (z2 ) ∀ z1 , z2 ∈ C
ist. Dies ist für f (z) = z 2 erfüllt.
Der Begriff der strukturerhaltenden Abbildung wird etwas verschärft, wenn wir uns auf
Monoide und Gruppen beschränken. In diesem Fall existieren in G1 und G2 neutrale Elemente, die durch die Abbildung f ineinander überführt werden sollen.
Definition 1.52 (Monoid- und Gruppenhomomorphismus). Seien (G1 , ∗1 , e1 ) und (G2 , ∗2 , e2 )
Monoide bzw. Gruppen. Eine Abbildung f : G1 → G2 heißt Monoidhomomorphismus bzw.
Gruppenhomomorphismus, falls
f (a1 ∗1 b1 ) = f (a1 ) ∗2 f (b1 ) für alle a1 , b1 ∈ G1 ,
f (e1 ) = e2 .
Ein bijektiver Homomorphismus wird Isomorphismus genannt.
(1.29)
(1.30)
1.4. GRUPPEN, RINGE, KÖRPER
57
Im vorherigen Beispiel 1◦ ist die Abbildung f : R → R, f (x) = ax, a 6= 0, ein Isomorphismus.
Wir werden im Weiteren den Begriff einer Untergruppe benötigen.
Definition 1.53 (Untergruppe). Sei (G, ∗, e) eine Gruppe. Eine nichtleere Teilmenge U
von G heißt Untergruppe von G, falls
a, b ∈ U ⇒ a ∗ b ∈ U ,
e∈U,
−1
a∈U ⇒a ∈U.
(1.31)
(1.32)
(1.33)
Beispiele:
1◦ Wir betrachten die Gruppe (Q, +, 0). Dann ist (Z, +, 0) eine Untergruppe.
2◦ Seien (G1 , ∗1 , e1 ) und (G2 , ∗2 , e2 ) zwei Gruppen und f : G1 → G2 ein Gruppenhomomorphismus. Dann sind ker f ⊂ G1 und im f ⊂ G2 Untergruppen. Was ker f und
im f bedeuten, wird durch folgende Definition geklärt.
Definition 1.54 (Kern und Bild). Sei f : G1 → G2 . Dann ist
Kern(f ) = ker(f ) = {a1 ∈ G1 : f (a1 ) = e2 }
der Kern von f ,
Bild(f ) = im(f ) = {b2 ∈ G2 : ∃a1 ∈ G1 mit f (a1 ) = b2 }
das Bild von f .
Bemerkung: Mit unseren früheren Bezeichnungen können wir schreiben:
ker f = Urbild {e2 } = f −1 ({e2 })
im f = f (G1 ) .
Lemma 1.55. Sei f : G1 → G2 ein Gruppenhomomorphismus. Dann sind ker f und im f
Untergruppen von G1 bzw. G2 .
Beweis
Wir überprüfen die Eigenschaften (1.31), (1.32) und (1.33) unter Beachtung von (1.29)
und (1.30). Die genaue Ausführung wird als 0 empfohlen.
Beispiele:
1◦ Es sei f : R → R, f (x) = ax, a 6= 0, (R, +, 0). Dann ist ker f = {0}, im f = R.
58
KAPITEL 1. GRUNDLAGEN
2◦ Für f : R → R, f (x) = x(1 − x), R = (R, +, 0) haben wir ker f = {0, 1}, im f = R.
In diesem Beispiel ist f kein Gruppenhomomorphismus
Wir betrachten jetzt folgende Aufgabenstellung:
Für einen gegebenen Gruppenhomomorphismus f : G1 → G2 führe man eine Partition von
G1 ein, so dass f zu einem Ismorphismus wird.
Eine Partition von G1 wird durch eine Äquivalenzrelation in G1 erzeugt. Wir betrachten
die folgende Äquivalenzrelation:
a1 ∼f b1 :⇔ f (a1 ) = f (b1 ) .
(1.34)
Durch überprüfen der Reflexivität, Symmetrie und Transitivität überzeugen wir uns, dass
(1.34) tatsächlich eine Äquivalenzrelation ist.
Weiterhin folgt aus (1.29) sofort die Eigenschaft
a1 ∼f b1 ∧ c1 ∼f d1 ⇒ a1 ∗1 c1 ∼f b1 ∗1 d1 .
(1.35)
Damit ist die Äquivalenzrelation (1.34) strukturerhaltend. In diesem Fall spricht man auch
von einer Kongruenzrelation.
Durch (1.34) zerfällt G1 in einer Menge von Restklassen
{[a1 ] : a1 ∈ G1 }, mit [a1 ] = {b1 ∈ G1 : f (a1 ) = f (b1 )}
(1.36)
Insbesondere ist
(1.30)
[e1 ] = {b1 ∈ G1 : f (e1 ) = e2 = f (b1 )} = ker f .
(1.37)
Die Verknüpfung von Restklassen kann man folgendermaßen definieren
[a1 ] ∗1 [b1 ] := [a1 ∗1 b1 ] .
(1.38)
Aufgrund von (1.35) ist (1.38) wohl definiert.
Wir können zeigen, dass die Menge der Restklassen (1.36) mit der Verknüpfung (1.38) und
dem Element [e1 ] eine Gruppe bildet, die auch Faktorgruppe G1 /ker f genannt wird. Dass
diese Bezeichnung gerechtfertigt ist, besagt folgender Satz.
Theorem 1.56. Sei f : G1 → G2 ein Gruppenhomomorphismus. (G1 , ∗1 , e1 ) und (G2 , ∗2 , e2 )
seien die entsprechenden Gruppen. Dann ist
G1 /kerf = ({[a1 ]}a1 ∈G1 , ∗1 , [e1 ])
eine Gruppe, die auch Faktorgruppe genannt wird.
Beweis: Wegen
[a1 ] ∗1 ([a2 ] ∗1 [a3 ]) = [a1 ∗1 (a2 ∗1 a3 )] = [(a1 ∗1 a2 ) ∗1 a3 ]
= ([a1 ] ∗1 [a2 ]) ∗1 [a3 ]
1.4. GRUPPEN, RINGE, KÖRPER
59
ist die Klassenverknüpfung (1.38) assoziativ. Da
[a1 ] ∗1 [e1 ] = [a1 ∗1 e1 ] = [a1 ]
und
[e1 ] ∗1 [a1 ] = [e1 ∗1 a1 ] = [a1 ]
ist, ist [e1 ] tatsächlich das neutrale Element. Schließlich gilt
[a1 ]−1 := [a−1
1 ],
da
[a1 ]−1 ∗1 [a1 ] = [a1 ] ∗1 [a1 ]−1 = [e1 ] .
60
KAPITEL 1. GRUNDLAGEN
Es folgt unmittelbar der Homomorphiesatz für Gruppen:
Theorem 1.57. Sei f : G1 → G2 ein Homomorphismus zwischen den Gruppen (G1 , ∗1 , e1 )
und (G2 , ∗2 , e2 ). Dann ist die Faktorgruppe G1 /ker f isomorph zur Untergruppe im f ⊂ G2 .
Kurz:
G1 /ker f ∼
= im f .
Beweis
Die Abbildung
F : G1 /kerf → imf
[a1 ] → f (a1 )
ist bijektiv. Außerdem ist F ein Homomorphismus, d.h die Eigenschaften (1.29) und (1.30)
gelten.
F ([a1 ] ∗1 [b1 ])
=
(1.29) für f
F ([e1 ])
=
=
F [a1 ∗1 b1 ] = f (a1 ∗1 b1 )
f (a1 ) ∗2 f (b1 ) = F [a1 ] ∗2 F [b1 ] ,
f (e1 ) = e2 .
Übungsaufgaben
Aufgabe 4.1
Prüfen Sie, ob die Zahlen
√
3
3,
rational sind.
√
3+
√ 2
5 ,
√
√
√ 4
√ 2
2 + 3 + 10
2− 3
Aufgabe 4.2
Zeigen Sie, dass R und C gleichmächtig sind.
Hinweis: Verwenden Sie die Darstellung der reellen Zahlen als nicht-abbrechende Dezimalzahlen.
Aufgabe 4.3
Berechnen Sie Betrag und Argument der folgenden komplexen Zahlen
√
a) z = 2 + 2 3 i ,
c) z = (4 − 2i) (1 + 3i) ,
b) z = (1 + i) + (1 + i)2 + (1 + i)3 + (1 + i)4 ,
√
√
(−1 + i 3)13 ( 3 + i)2
√
d) z =
.
(1 + i 3)11
1.4. GRUPPEN, RINGE, KÖRPER
61
Aufgabe 4.4
Bestimmen Sie die trigonometrische Darstellung des Produkts z1 z2 zweier komplexer Zahlen z1 =
a1 + ib1 , z2 = a2 + ib2 und vergleichen Sie Betrag und Winkel mit denen der ursprünglichen Zahlen.
Was fällt auf?
Hinweis:
cos(ϕ + ϑ) = cos ϕ cos ϑ − sin ϕ sin ϑ
sin(ϕ + ϑ) = sin ϕ cos ϑ + cos ϕ sin ϑ
62
KAPITEL 1. GRUNDLAGEN
Kapitel 2
Lineare Algebra
In der linearen Algebra werden lineare Räume (Vektorräume) beschrieben und lineare Abbildungen in diesen Räumen untersucht. Vektoren werden verwendet, um die Lage und
Bewegung von Punkten in der Ebene bzw. in drei oder n-dimensionalen Räumen zu beschreiben. Sie treten in vielen Anwendungen, z.B. in der Computer-Graphik, ComputerTomographie, in der Strömungs- und Festkörpermechanik (Kräfte, Geschwindigkeiten, Felder) in der Elektromechanik, Meteorologie, usw. auf.
In diesem Kapitel werden Vektorräume eingeführt, lineare Abbildungen zwischen verschiedenen Vektorräumen beschrieben und in Form linearer Gleichungssysteme untersucht. Dazu
werden grundlegende Begriffe wie lineare Unabhängigkeit, Basis, Dimension, Matrix und
Determinante eingeführt. Weiterhin werden Eigenwerte, Eigenvektoren und Diagonalisierbarkeit von Matrizen behandelt, sowie Vektorräume mit Skalarprodukt untersucht. Als
Literatur wird empfohlen [3, Kapitel 5], [4], [5, Kapitel 6-10], [8, 2. Teil].
2.1
Vektorräume
Wir erinnern zunächst an das kartesische Produkt R2 = R×R, bzw. Rn = R
| ×R×
{z· · · × R}
n−mal
als Mengen geordneter Paare (x1 , x2 ) bzw. geordneter n-Tupel x = (x1 , x2 , . . . , xn ),
xi ∈ R, i = 1, 2, . . . , n. In Rn kann eine Addition definiert werden:
x + y = (x1 , x2 , . . . , xn ) + (y1 , y2 , . . . , yn ) = (x1 + y1 , x2 + y2 , . . . , xn + yn ),
die (Rn , +) zu einer kommutativen Gruppe macht. Das neutrale Element ist 0 = (0, 0, . . . , 0),
das inverse Element zu x ist −x = (−x1 , −x2 , . . . , −xn ).
Weiterhin kann die Multiplikation auf Rn mit skalaren“ Elementen α ∈ R eingeführt
”
werden
αx = α(x1 , x2 , . . . , xn ) := (αx1 , . . . , αxn ).
63
64
KAPITEL 2. LINEARE ALGEBRA
Es gilt für α, β ∈ R:
α(x + y) = αx + αy,
(αβ)x = α(βx),
(α + β)x = αx + βx.
Diese Verknüpfungen (Addition in Rn und Multiplikation auf Rn mit skalaren Elementen
aus einem Zahlenkörper) motivieren die Definition eines Vektorraums, der auch linearer
Raum genannt wird.
Definition 2.1. Sei K ein Körper, dessen neutrales Element bezüglich der Multiplikation
mit 1 bezeichnet wird. V sei eine Menge mit einer Verknüpfung +“ :V × V → V , so dass
”
(V, +) eine kommutative Gruppe ist.
Die Verbindung von K und V sei durch eine Multiplikation
K × V → V,
(α, x) → αx
beschrieben, wobei für alle α, β ∈ K und für alle x, y die folgenden Eigenschaften gelten:
(αβ)x = α(βx),
1x = x,
(α + β)x = αx + βx,
α(x + y) = αx + αy.
(2.1)
(2.2)
(2.3)
(2.4)
Dann heißt V Vektorraum bzw. linearer Raum über dem Körper K, kurz K-Vektorraum
geschrieben. Die Elemente von V heißen Vektoren. Ist K = R, bzw. K = C, dann spricht
man von reellen bzw. komplexen Vektorräumen.
Beispiele
1◦ Rn mit K = R, Qn mit K = Q und Cn mit K = C sind Vektorräume, ebenso Cn mit
K = R.
2◦ Sei M = {f : R → R} die Menge aller Abbildungen (Funktionen) von R in R. Durch
die Verknüpfungen
(f + g)(x) :=f (x) + g(x) ∀ f, g ∈ M, ∀ x ∈ R,
(αf )(x) := αf (x)
∀ f ∈ M, ∀ α, x ∈ R
wird die Menge M zu einem reellen Vektorraum.
Definition 2.2. Sei V ein K-Vektorraum. Eine nichtleere Teilmenge V0 ⊆ V heißt Teilvektorraum oder Untervektorraum falls gilt:
1. Sind x, y Elemente aus V0 , dann ist auch x+y ∈ V0 , d.h. V0 ist bezüglich der Addition
in V abgeschlossen.
65
2.1. VEKTORRÄUME
2. Ist x ∈ V0 , dann ist auch αx ∈ V0 für alle α ∈ K, d.h. V0 ist unter der Multiplikation
mit Skalaren abgeschlossen, insbesondere gilt 0 ∈ V0 .
Beispiel
V = R2 ist ein R-Vektorraum, M = R × {0} ⊂ R × R ist Teilvektorraum, d.h.
R = {(a, 0) : a ∈ R} ⊂ {(a, b) : a ∈ R, b ∈ R}.
Lineare Abhängigkeit, Basen
Im Vektorraum V waren die Addition und die Multiplikation mit Skalaren“ aus dem
”
Körper K definiert. Diese Verknüpfungen können auf endlich viele Elemente in Form einer
Linearkombination übertragen werden.
Definition 2.3. Sei V ein Vektorraum über dem Körper K. M ⊂ V sei eine Teilmenge.
Ein Element x ∈ V heißt Linearkombination von Elementen aus M, falls es eine endliche
Menge Mx ⊂ M gibt, so dass x in der Gestalt
X
αm m
x=
m∈Mx
mit αm ∈ K, darstellbar ist.
Span(M) = {x ∈ V : x ist Linearkombination von Elementen aus M} heißt der von M
aufgespannte Teilvektorraum von V . Span(M) wird auch lineare Hülle von M genannt.
Wir überzeugen uns davon, dass Span(M) ein Vektorraum über K ist. Dazu zeigen wir
zunächst folgendes Lemma.
Lemma 2.4. Sei V ein Vektorraum über dem Körper K, α ∈ K und x ∈ V . Dann ist
αx = 0 genau dann, wenn α = 0 oder x = 0 ist.
Beweis
a) Wir nehmen an, dass α = 0 oder x = 0 ist. Aus α = 0 folgt für ein β ∈ K
βx = (β + 0)x = βx + 0x, also ist 0x = 0 das neutrale Element. Aus x = 0 folgt,
αy = α(0 + y) = α0 + αy. Damit ist α0 = 0.
b) Es sei αx = 0 und α 6= 0. Dann ist x = 1 · x = (α−1 α)x = α−1 (αx) = 0. Es sei αx = 0
und x 6= 0. Wäre α 6= 0, dann existiert α−1 mit α−1 (αx) = α−1 0 = 0 = x, was zu
einem Widerspruch führt.
Lemma 2.5. Für M 6= ∅ ist Span(M) ist ein K-Teilvektorraum von V .
66
KAPITEL 2. LINEARE ALGEBRA
Beweis
Die Addition, die in V erklärt ist, gilt auch für Elemente (x, y) ∈ Span(M) × Span(M):
X
X
βm m
αm m +
x+y =
m∈Mx
=
X
m∈My
γm m.
m∈Mx ∪My
Die Addition ist kommutativ.
Das neutrale Element
0 = 0m,
m∈M
befindet sich in Span(M) nachP
Lemma 2.4.
Ist x ∈ Span(M), d.h. x =
m∈Mx αm m, dann ist das inverse Element bezüglich der
Addition
X
(−αm )m
x−1 =
m∈Mx
ebenfalls in Span(M).
Die Eigenschaften (2.1)-(2.4) gelten.
Beispiele
1◦ Wir betrachten den Vektorraum R3 = R × R × R. Die Menge M besteht aus 2
Dreiertupeln
M = {(1, 0, 0), (0, 1, 0)}.
Dann ist
Span(M) = {x = (x1 , x2 , x3 ) : x = α(1, 0, 0) + β(0, 1, 0) = (α, β, 0), α, β ∈ R},
d.h. Span(M) ⊂ R3 beschreibt eine Ebene, die durch die Vektoren (3er-Tupel)
(1, 0, 0), (0, 1, 0) aufgespannt wird, siehe Abbildung 2.1.
2◦ Wir betrachten wieder den Vektorraum R3 und die Menge
M = {(1, 0, 0), (−1, 0, 0)}.
Dann ist
Span(M) = {x = (x1 , x2 , x3 ) ∈ R3 : x = (α, 0, 0), α ∈ R},
d.h. Span(M) stimmt mit der x1 -Achse überein, siehe Abbildung 2.2.
Im ersten Beispiel waren die Elemente von M linear unabhängig, im 2. Beispiel linear
abhängig. Die lineare Unabhängigkeit von Elementen einer Menge M wird wie folgt definiert.
67
2.1. VEKTORRÄUME
x3
x2
Span(M)
x1
Abbildung 2.1: x1 − x2 -Ebene
Definition 2.6. Sei V ein K-Vektorraum. Eine Menge M ⊂ V besteht aus linear unabhängigen Elementen, falls für jede endliche nichtleere Teilmenge M̃ ⊂ M gilt:
Aus
X
αm m = 0, αm ∈ K
(2.5)
m∈M̃
folgt αm = 0 für alle m ∈ M̃ .
Ist M eine endliche Menge, dann braucht in (2.5) nur M̃ = M betrachtet werden.
Wir sehen uns die vorherigen Beispiele an.
1◦ Es sei
M = {(1, 0, 0), (0, 1, 0)}.
Wir betrachten die Linearkombination (2.5)
X
αm m = (α1 , α2 , 0) = 0 = (0, 0, 0).
m∈M
Es folgt α1 = α2 = 0.
2◦ Es sei
M = {(1, 0, 0), (−1, 0, 0)}.
Die Linearkombination (2.5) lautet
α(1, 0, 0) + β(−1, 0, 0) = (α − β, 0, 0) = (0, 0, 0),
woraus α = β folgt.
68
KAPITEL 2. LINEARE ALGEBRA
x3
1111111111
0000000000
00000
11111
0000000000
1111111111
00000
11111
0000000000
1111111111
00000
11111
0000000000
1111111111
00000
11111
0000000000
1111111111
00000
11111
0000000000
1111111111
00000
11111
Span(M)
0000000000
1111111111
00000
11111
0000000000
1111111111
00000
11111
0000000000
1111111111
00000
11111
0000000000
1111111111
00000
11111
0000000000
1111111111
00000
11111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
0000000000
1111111111
x2
x1
Abbildung 2.2: Span(M)
Definition 2.7. Eine Menge B ⊂ V heißt Basis des Vektorraums V , falls B aus linear
unabhängigen Elementen besteht und
Span(B) = V
ist.
Beispiel
1◦ Im Rn bildet die Menge der Vektoren
B = {(1, 0, . . . , 0), (0, 1, 0, . . . , 0), . . . , (0, 0, . . . , 1)}
eine Basis, aus Einheitsvektoren, die sehr häufig betrachtet und im Folgenden Standardbasis genannt wird.
2◦ Im R2 bilden die Vektoren
B = {(a, b), (−b, a)} (a, b) 6= (0, 0)
eine Basis.
Wir zeigen, dass B aus linear unabhängigen Vektoren besteht. Sei
α(a, b) + β(−b, a) = (αa − βb, αb + βa) = (0, 0).
69
2.1. VEKTORRÄUME
Dann muss
αa − βb = 0,
αb + βa = 0
(2.6)
(2.7)
ist. Durch Einsetzen von α in (2.7) erhalten wir
sein. Es folgt aus (2.6), dass α = βb
a
= 0 folgt.
β(b2 + a2 ) = 0, woraus β = 0 und schließlich α = βb
a
Weiterhin enthält Span(B) die Einheitsvektoren (1, 0) und (0, 1), durch die der ganze
Raum R2 aufgespannt wird.
Theorem 2.8. Sei B ⊂ V eine Basis des K-Vektorraums V . Jedes x ∈ V kann eindeutig
als
X
x=
αe e
e∈B
mit αe ∈ K, e ∈ B, αe 6= 0 nur für endlich viele e ∈ B, dargestellt werden.
Beweis
Es sei
x=
X
αe e =
e∈B
Dann ist
0=
X
e∈B
X
βe e.
e∈B
(αe − βe )e.
Wegen der linearen Unabhängigkeit der Elemente e ∈ B folgt
αe = βe .
Die Elemente αe ∈ K heißen Koordinaten von x bezüglich der Basis B.
Beispiel
1◦ Wir betrachten den Rn und schreiben die Elemente (n-Tupel) des kartesischen Produktes in Spaltenform
 
x1
 x2 
 
x =  ..  .
.
xn
70
KAPITEL 2. LINEARE ALGEBRA
Sei B die Standardbasis im Rn
   
 

0 
0
1


   
0



1
0
 
   

0
0 0
B =  , ,...,  .
 .. 
 ..   .. 




 . 
. .




 0
1 
0
(2.8)
Dann ist x folgenderweise darstellbar
 
 
 
 
0
0
1
x1
0
1
0
 x2 
 
 
 
 
 
 
 
 
x =  x3  = x1 0 + x2 0 + · · · + xn 0 ,
 .. 
 .. 
 .. 
 .. 
.
.
.
.
1
0
0
xn
d.h. xi ist die i-te Koordinate bezüglich der Standardbasis.
2◦ Koordinatendarstellung zu zwei unterschiedlichen Basen
Wir betrachten die Basis

 
  
4
4
1 






−2
1
2 
B1 =
,
,


1
−2
2
und die Basis
     
3
2 
 1





2
1
3  .
B2 =
,
,


3
2
1


14
Wir stellen den Vektor  11  in der Standardbasis als Linearkombination von
11
Elementen aus B1 bzw. B2 dar:
 




   
14
4
4
1
1
11







= 1
−2
+ 1
1
+ 6
2
=
1 
11 standard
1
−2
2
6
 
 
    B1
1
3
2
1
= 1  2  + 3  1  + 2  3 = 3  .
3
2
1
2 B
2
71
2.1. VEKTORRÄUME
Lemma 2.9 (Austausch eines Basiselements). Sei B ⊂ V eine Basis des K-Vektorraums
V . Wir betrachten ein Element e0 ∈ B und ein Element f0 6= 0 aus V mit der Darstellung
X
f0 =
αe e, αe0 =
6 0.
(2.9)
e∈B
Dann ist auch B̂ = (B \ {e0 }) ∪ {f0 } eine Basis.
Beweis
a) Wir zeigen zunächst, dass B̂ aus linear unabhängigen Elementen besteht. Dazu betrachten wir die Gleichung
X
βe e = 0.
(2.10)
βf0 f0 +
e∈B
e6=e0
Mit der Darstellung (2.9) erhalten wir
X
X
X
(βf0 αe + βe )e = 0.
βe e = βf0 αe0 e0 +
αe e) +
βf0 (αe0 e0 +
e∈B
e6=e0
e∈B
e6=e0
e∈B
e6=e0
Da die Elemente e ∈ B linear unabhängig sind, folgt
βf0 αe0 = 0,
βf0 αe + βe = 0 für e 6= e0 .
Da αe0 6= 0 ist, muss βf0 = 0 sein und daher βe = 0 für e 6= e0 . Damit verschwinden
alle Koeffizienten in (2.10).
b) Wir zeigen, dass jedes x ∈ V Linearkombination von Elementen aus B̂ ist. Aus der
Darstellung (2.9) von f0 folgt
X
αe0 e0 = f0 −
αe e,
e∈B
e6=e0
e0 =
X αe
f0
−
e.
αe0 e∈B αe0
(2.11)
e6=e0
Sei x beliebig aus V . Die Darstellung von x bezüglich der Basis B lautet
X
γe e.
x = γe0 e0 +
e∈B
e6=e0
Unter der Beachtung von (2.11) erhalten wir daraus eine Darstellung bezüglich der
Basis B̂:
X
γ e0
γ e0
γe −
f0 +
αe e.
x=
αe0
αe0
e∈B
e6=e0
72
KAPITEL 2. LINEARE ALGEBRA
Lemma 2.10 (Austausch von k Basiselementen). Sei V ein K-Vektorraum mit der Basis
B. Seien f1 , . . . , fk linear unabhängige Elemente aus V , fi 6= 0, i = 1, . . . , k. Dann gibt es
e1 , . . . , ek Elemente aus B, so dass auch
B̂ = (B \ {e1 , . . . , ek }) ∪ {f1 , . . . , fk }
eine Basis ist.
Beweis
Das Element f1 besitzt eine Darstellung bezüglich B:
X
f1 =
αe e 6= 0.
e∈B
Es gibt ein Element e1 ∈ B, so dass αe1 6= 0 ist. Daher ist nach Lemma 2.9 B̂ = (B \
{e1 }) ∪ f1 eine Basis. Nun betrachten wir f2 ∈ V und ein Element e2 ∈ B̂ ∩ B, so dass
X
f2 =
βê ê und βe2 6= 0
ê∈B̂
ist. Ein solches Element e2 muss existieren, da die fi , i = 1, . . . , k, linear unabhängig sind.
Diesen Prozess setzen wir fort und erhalten die Behauptung.
Beispiel: Austausch von k-Basisvektoren Wir betrachten den R4 mit der Standardbasis S = {e1 , e2 , e3 , e4 }. Wir wollen e1 , e2 und e3 durch die Vektoren
 
 
 
0
1
1
1
0
1
 
 

f1 = 
1 , f2 = 1 , f3 = 1 .
0
0
0
ersetzen. Es ist
       
0
0
1
1
1 0 1 0
      
f1 = 
1 = 0 + 0 + 1 = 1e1 + 1e2 + 1e3 + 0e4 .
0
0
0
0
Wir ersetzen e2 durch f1 . Das ist möglich, da
schwindet. Damit wird
   
1
1


   
0 1
,
B1 = 

0 1



0
0
(2.12)
der Koeffizient vor e2 in (2.12) nicht ver-
 
0
0

,
1
0
 
0 

0

,
0


1
73
2.1. VEKTORRÄUME
eine neue Basis. Wir betrachten jetzt f2 :
     
0
1
1
0 0 0
    
f2 = 
1 = 0 + 1 = 1e1 + 0f1 + 1e3 + 0e4 .
0
0
0
Wir ersetzen e2 durch f2 und erhalten die Basis B2 :
     
1
1
1


     
1
0
 ,   , 0
B2 = 

0 1 1



0
0
0
 
0 

0


,  .
0 


1
Nun sehen wir uns f3 an:
   
 
1
1
0
0 1
1
   

f3 = 
1 = − 0 + 1 = −1e1 + 1f1 + 0f2 + 0e4 .
0
0
0
Es ist nur sinnvoll, e1 durch f3 zu ersetzen (Koeffizient 6= 0). Damit ist die gewünschte
Basis
       
0 
1
1


 0

1 1 0 0








B3 =   ,   ,   ,   .
0 
1
1
1





1
0
0
0
Aus Lemma 2.10 folgt der Satz:
Theorem 2.11. Sei V ein K-Vektorraum mit einer Basis von n Elementen. Jede weitere
Basis besitzt ebenfalls n Elemente.
Beweis
Seien B = {e1 , . . . , en } und B̂ = {ê1 , . . . , êm } zwei Basen. Wir nehmen an, dass m > n ist.
Nach Lemma 2.10 ist jedoch {ê1 , . . . , ên } bereits eine Basis und die Menge B̂ wäre linear
abhängig. Dies ist ein Widerspruch und m muss gleich n sein.
Existenz von Basen
In unseren Beispielen hatten wir bisher gegebene Basen betrachtet. Erinnern wir uns an
den Vektorraum
V = {f : f : R → R},
so sieht man nicht unmittelbar, dass in diesem Raum eine Basis existiert. Die Frage nach
der Existenz von Basen ist also durchaus sinnvoll.
74
KAPITEL 2. LINEARE ALGEBRA
Es gilt: Jeder Vektorraum besitzt eine Basis. Um dies zu beweisen benötigt man Axiome
aus der Mengenlehre. Wir verzichten hier auf den Beweis und verweisen auf [2, S. 261].
Jedoch können wir in sogenannten endlich erzeugten “ Vektorräumen leicht eine Basis
”
konstruieren.
Definition 2.12. Ein Vektorraum V heißt endlich erzeugt, wenn es endlich viele Elemente
v1 , . . . , vn ∈ V gibt, so dass
Span({v1 , . . . , vn }) = V
ist.
Theorem 2.13. Jeder endlich erzeugte Vektorraum V besitzt eine Basis.
Beweis
Wir wählen aus der Menge {v1 , . . . , vn } eine größte Teilmenge aus, die linear unabhängig
ist. Dies sei B = {v1 , . . . , vr }, r ≤ n. B ist Basis von V .
Da wir festgestellt haben, dass jeder Vektorraum eine Basis besitzt, können wir jetzt definieren, was wir unter der Dimension eines Vektorraums verstehen. Dazu bemerken wir,
dass zwei Basen in V stets die gleiche Mächtigkeit besitzen.
Definition 2.14.
1) v = {0} besitzt die Dimension 0.
2) Besitzt V 6= {0} eine Basis aus n Elementen, dann hat V die Dimension n, d.h.
dimV = n.
3) Besitzt V eine unendliche Basis, dann ist V unendlich-dimensional. Wir schreiben
dimV = ∞.
Wir können also kurz formulieren:
Ist V 6= {0}, dann ist die Dimension von V gleich der Anzahl der Basiselemente.
Vektorrechnung im Rn
In diesem Abschnitt gehen wir auf die geometrische Veranschaulichung der Rechenoperatoren, Koordinatendarstellung und der Beschreibung von Geraden und Ebenen im Rn ein,
indem wir die Darstellung durch Pfeile benutzen.
Es sei V = Rn der n-dimensionale Vektorraum mit der bereits zu Beginn dieses Abschnittes
eingeführten Addition und der Multiplikation mit Skalaren aus K = R.
Wir betrachten die Standardbasis B. Die Koordinatendarstellung eines Elements (Vektors)
75
2.1. VEKTORRÄUME
aus V lautet also
 
0
0
.
.
.
 
ei = 1 ← i-te Stelle.
.
 .. 
 
0
0


x1
n
 ..  X
xi ei ,
x= . =
xn
i=1
(2.13)
Die geometrische Darstellung des Elements x erfolgt im R2 und R3 auch durch den sogenannten Ortsvektor ~x, einem Pfeil vom 0-Element (Nullpunkt) zum x-Element (Punkt x).
x3
~x
~y
x
x2
x1
Abbildung 2.3: Ortsvektor ~x und freier Vektor ~y
Die Ortsvektoren können im Rn durch Drehungen und Verschiebungen bewegt werden. Der
Anfangspunkt eines solchen entstandenen freien “ Vektors braucht also nicht im Null”
punkt zu liegen. Um eine bijektive Abbildung zwischen der Menge der freien Vektoren“
”
und der Koordinatendarstellung (2.13) zu erhalten, wird eine Äquivalenzrelation in der
Menge der freien Pfeilvektoren “ eingeführt:
”
Zwei freie Vektoren ~x und ~y sind äquivalent, falls Länge und Richtung der entsprechenden
Pfeile übereinstimmen (siehe Abbildung 2.4).
Wir können stets einen Vertreter der Äquivalenzklasse finden, dessen Ausgangspunkt im
Nullpunkt liegt und der durch den Index 0 gekennzeichnet wird. Damit wird die Menge
der Äquivalenzklassen der freien Pfeilvektoren auf den R2 oder den R3 bijektiv abgebildet.
Dies sei durch die Abbildung
f : {Äquivalenzklassen freier Vektoren} → Rn ,
n = 2, 3
realisiert. Wir beschreiben Summe und Differenz zweier freier Pfeilvektoren.
Die Summe zweier freier Pfeilvektoren ~x und ~y (o.B.d.A. Endpunkt von ~x=Ausgangspunkt
von ~y ) ist der Pfeilvektor, der vom Ausgangspunkt von ~x zum Endpunkt von ~y führt.
76
KAPITEL 2. LINEARE ALGEBRA
Abbildung 2.4: äquivalente freie Pfeilvektoren
~y
~x
~x + ~y
Abbildung 2.5: Addition zweier freier Pfeilvektoren
Wir überzeugen uns, dass für die bijektive Abbildung f : {Äquivalenzklassen freier Vektoren} →
R2 gilt
f (~x + ~y ) = f (~x) + f (~y) = x + y.
Dazu betrachten wir die zu ~x und ~y äquivalenten Ortsvektoren ~x0 , ~y0 deren Ausgangspunkt
der Nullpunkt ist. Dann ist ~x0 + ~y0 der Ortsvektor zu x + y (siehe Abbildung 2.6).
x2
~y
~x0 = ~x
(x1 + y1 , x2 + y2 )
~x + ~y
~y0
x1
Abbildung 2.6: Ortsvektor zu x + y
Die Differenz zweier freier Pfeilvektoren ist durch
~x − ~y = ~x + (−~y )
erklärt (siehe Abbildung 2.7).
Die Multiplikation eine Pfeilvektors ~x mit α ∈ R ergibt einen Pfeilvektor, dessen Länge das
|α|-fache der Länge von ~x beträgt. Seine Richtung stimmt mit der Richtung von ~x überein,
falls α > 0 ist; für α < 0 ist sie entgegengesetzt.
77
2.1. VEKTORRÄUME
−~y
(~x − ~y )0
~x0
−~y0
0
~x − ~y
~y0
Abbildung 2.7: Differenz zweier freier Vektoren
α~x
~x
−|α|~x
α~x
0<α<1
α>1
α<0
Abbildung 2.8: Multiplikation eines Pfeilvektors mit einem Skalar
Geraden und Ebenen im Rn
Wir beschreiben zunächst Geraden im Rn .
Definition 2.15. Die Teilmenge G ⊂ Rn ist eine Gerade, wenn es Elemente x, y ∈ Rn
gibt, so dass
G = {z ∈ Rn : ∃ α ∈ R, so dass z = x + αy}.
Diese Darstellung heißt Parameterdarstellung (α ∈ R ist der Parameter). Ist x = 0, so ist
G eine Gerade durch den Nullpunkt.
Eine Gerade, die durch die Punkte x und y verläuft hat die Parameterdarstellung
G = {z ∈ Rn : ∃ α ∈ R, so dass z = x + α(y − x)}.
Diese Definition gilt auch in allgemeinen Vektorräumen V , d.h. eine Gerade ist durch zwei
Vektoren x und y eindeutig bestimmt. Bei der Definition von Ebenen werden wir auf drei
Vektoren zurückgreifen.
78
KAPITEL 2. LINEARE ALGEBRA
G
~x0
~y0
Abbildung 2.9: Parameterdarstellung der Geraden G
~y − ~x
~x
G
~y
Abbildung 2.10: Gerade durch x und y
Definition 2.16. Eine Teilmenge E ⊂ Rn nennen wir Ebene, wenn es drei Vektoren
u, v, w ∈ Rn gibt, mit
E = {x ∈ Rn : ∃ α, β ∈ R, so dass x = u + αv + βw}.
Dies ist ebenfalls eine Parameterdarstellung.
Eine Ebene, die durch die Punkte u, v, w verläuft, hat die Darstellung
E = {x ∈ Rn : ∃ α, β ∈ R, so dass x = u + α(v − u) + β(w − u)}.
Es ist


u
x = u + α(v − u) + β(w − u) = v


w
für α = β = 0,
für α = 1, β = 0,
für α = 0, β = 1.
79
2.1. VEKTORRÄUME
x3
E
~v
w
~
~u
x2
x1
Abbildung 2.11: Ebene durch u, v, w
Übungsaufgaben
Aufgabe 5.1
Sei V = R × R+ = {(x, y) : x ∈ R, y ∈ R, y > 0}, sowie
⊕ : V × V → V , (x1 , y1 ) ⊕ (x2 , y2 ) = (x1 + x2 , y1 · y2 ) und
⊙ : R × V → V , α ⊙ (x, y) = (αx, y α ). Prüfen Sie, ob dadurch ein reeller Vektorraum definiert
wird.
Aufgabe 5.2
Geben Sie alle Möglichkeiten an, aus den 5 Vektoren
1
1
1
−3
2
,
,
,
,
0
−1
1
3
0
eine Basis für R2 auszuwählen und stellen Sie den Vektor
5
3
in jeder der Basen dar.
Aufgabe 5.3
Die Bernsteinpolynome
bnk (x)
=
n
k
xk (1 − x)n−k ,
k = 0, . . . , n
bilden eine Basis des Vektorraums der Polynome vom Grad ≤ n ,
(
)
n
X
Pn = p(x) =
αk xk , αk ∈ R .
k=0
Überprüfen Sie dies für den Fall n = 3 und stellen Sie die Polynome p0 (x) = 1 und p3 (x) = x3 in
dieser Basis dar.
80
KAPITEL 2. LINEARE ALGEBRA
2.2
Lineare Abbildungen von Vektorräumen
Sind Elemente, Geraden bzw. Ebenen in einem Vektorraum gegeben, so können wir sie bewegen bzw. verkleinern oder vergrößern, indem wir eine Verschiebung (Translation), eine
Drehung (Rotation), eine Streckung oder Stauchung bzw. Scherung vornehmen. Drehungen, Stauchungen oder Streckungen und Scherungen können durch lineare Abbildungen
beschrieben werden.
Wir beginnen mit der Definition einer linearen Abbildung.
Definition 2.17. Seien V und W K-Vektorräume. Eine Abbildung f
f :V →W
heißt linear, falls gilt
• f (x + y) = f (x) + f (y) für alle x, y ∈ V , kurz: f ist additiv.
• f (αx) = αf (x) für alle α ∈ K und x ∈ V , kurz: f ist homogen.
Damit ist f eine strukturerhaltende Abbildung, f (0V ) = 0W . Die Menge aller linearen
Abbildungen von V in W wird als L(V, W ) bezeichnet.
Beispiele
1◦ Es sei V = W = R2 . Die Abbildung f : R2 → R2 ,
x1
−x2
f
=
x2
x1
ist linear. Geometrisch beschreibt f eine Drehung nach links“ um 90◦ (siehe Ab”
bildung 2.12).
x2
(x1 , x2 )
(−x2 , x1 )
11111111111111x
00000000000000
1
Abbildung 2.12: Drehung um 90◦
2.2. LINEARE ABBILDUNGEN VON VEKTORRÄUMEN
81
x3
(x1 , x2 , x3 )
(x1 , x2 )
x2
x1
Abbildung 2.13: Projektion auf die x1 x2 -Ebene
2◦ Es sei V = R3 , W = R2 . Die Abbildung f : R3 → R2
 
x1
x1
f x2  =
x2
x3
ist eine Projektion (siehe Abbildung 2.13), f ist linear.
3◦ Es sei V = R2 , W = R3 . Wir betrachten zwei feste Elemente u und v ∈ W . Wir
betrachten die Abbildung
f : V → W,
x1
f
= x1 u + x2 v.
x2
Die Abbildung f ist linear, das Bild beschreibt eine Ebene durch den Nullpunkt.
4◦ Es sei V = W = R, f : V → W, f (x) = ax + b, wobei a und b feste reelle Zahlen sind
und a 6= 0, b 6= 0. Die Abbildung f ist nicht linear:
f (x + y) = a(x + y) + b 6= f (x) + f (y) = a(x + y) + 2b.
x1
x1
◦
2
5 Es sei V = W = R , f : V → W, f
=
. Die Abbildung f ist nicht linear
x2
x22
αx1
x1
αx1
f (αx) = f
6= αf
=
α2 x22
x2
αx22
für α 6= 0, α 6= 1.
6◦ Es sei V = W = Rn , f : V → W ,




α1 x1
x1
 α2 x2 
 x2 




f  ..  = f 
..  ,

 . 
. 
αn xn
xn
αi > 0 .
82
KAPITEL 2. LINEARE ALGEBRA
Diese Abbildung ist linear und beschreibt die Streckung bzw. Stauchung der einzelnen
Komponenten um den Faktor αi .
Wir charakterisieren jetzt Vektorräume, die als
gleich“ angesehen werden können.
”
Definition 2.18. Seien V und W K-Vektorräume. Eine bijektive lineare Abbildung
f : V → W heißt Isomorphismus. Zwei K-Vektorräume V und W heißen isomorph
(geschrieben als V ∼
= W ), falls es einen Isomorphismus f : V → W gibt.
Beispiel
Sei V ein n-dimensionaler K-Vektorraum mit der Basis B = {e1 , . . . , en }. Jedes x ∈ V ist
eindeutig darstellbar als
n
n
X
X
αi (x)ei .
x=
αi ei =
i=1
i=1
Die Abbildung


α1 (x)


f : V → K n , f (x) =  ... 
αn (x)
(2.14)
ist ein Isomorphismus. Dieser Isomorphismus heißt Koordinatendarstellung zur Basis
B. Lineare Abbildungen f sind durch ihre Werte auf einer Basis vollständig bestimmt.
Dies wird durch nachfolgendes Lemma genauer ausgedrückt.
Lemma 2.19. Seien V und W K-Vektorräume und B ⊂ V eine Basis. Jedem e ∈ B sei
durch die lineare Abbildung f ein Element ê ∈ W zugeordnet. f ist eindeutig bestimmt,
d.h. es gibt genau eine lineare Abbildung
f :V →W
mit
f (e) = ê.
Beweis
Jedes x ∈ V hat die Darstellung
x=
X
αe e,
e∈B
αe = αe (x) ∈ K,
wobei nur endlich viele αe (x) 6= 0 sind. Für eine beliebige lineare Abbildung f : V → W
gilt
!
X
X
f (x) = f
αe (x)e =
αe (x)f (e).
(2.15)
e∈B
e∈B
2.2. LINEARE ABBILDUNGEN VON VEKTORRÄUMEN
83
P
Sei f (e) = ê. Dann ist f (x) :=
e∈B αe (x)ê für alle x ∈ V . Für jede weitere lineare
Abbildung g : V → W mit g(e) = ê gilt (2.15)
X
g(x) =
αe (x)ê
e∈B
und damit muss f = g sein.
Theorem 2.20. Wir betrachten die K-Vektorräume V und W und eine lineare Abbildung
f : V → W . Dann sind die Mengen
im(f ) = f (V ) = {f (x) : x ∈ V } ⊂ W,
ker(f ) = {x ∈ V : f (x) = 0} ⊂ V
(Bildmenge, image)
(Kern, kernel)
Teilvektorräume.
Beweis
Wir müssen zeigen, dass im(f ) und ker(f ) bezüglich der Addition und der Multiplikation
mit Skalaren abgeschlossen sind. Wir sehen uns zunächst im(f ) an. Seien w1 , w2 ∈ im(f ).
Es gibt Elemente x1 und x2 ∈ V , so dass w1 = f (x1 ) und w2 = f (x2 ) ist. Da f linear ist,
gilt
w1 + w2 = f (x1 ) + f (x2 ) = f (x1 + x2 ) ∈ im(f ).
Weiterhin ist für ein w = f (x) ∈ W :
αw = αf (x) = f (αx) ∈ im(f ).
Für ker(f ) werden analoge Überlegungen ausgeführt.
Die Dimensionen der Teilvektorräume im(f ) und ker(f ) hängen wie folgt zusammen:
Theorem 2.21 (Dimensionssatz). Sei V ein n-dimensionaler und W ein beliebiger KVektorraum; f : V → W eine lineare Abbildung. Dann ist
n = dim(V ) = dim(ker(f )) + dim(im(f )).
Beweis
Nach Lemma 2.10 über den Austausch von Basisvektoren ist stets eine solche Basis
B = {e1 , e2 , . . . , er , er+1 , . . . , en }
von V wählbar, dass
Bker(f ) = {e1 , e2 , . . . , er },
r ≤ n,
84
KAPITEL 2. LINEARE ALGEBRA
Basis von ker(f ) ist. Wegen der Linearität von f ist
im(f ) = Span{f (er+1 ), . . . , f (en )}.
Wir zeigen, dass die Elemente f (er+1 ), . . . , f (en ) linear unabhängig sind und damit eine
Basis von im(f ) bilden. Dazu betrachten wir eine verschwindende Linearkombination
!
n−r
n−r
X
X
αr+j f (er+j ) = f
0=
αr+j er+j .
j=1
j=1
Pn−r
Damit ist j=1
αr+j er+j aus ker(f ) und kann als Linearkombination der Basiselemente
e1 , . . . , er dargestellt werden,
n−r
X
αr+j er+j =
j=1
r
X
βi ei .
i=1
Es folgt, dass
r
X
i=1
βi ei −
n−r
X
αr+j er+j = 0
j=1
ist. Da B = {e1 , . . . , en } aus linear unabhängigen Elementen besteht, müssen die Koeffizienten αr+j = 0 für j = 1, . . . , n − r sein.
Folgerung
Ein Isomorphismus zwischen zwei n-dimensionalen Vektorräumen bildet Basen aufeinander
ab. Umgekehrt, falls f Basen zweier n-dimensionaler Räume aufeinander abbildet, dann
ist f ein Isomorphismus (ker(f ) = {0}).
Bezeichnung: Sei f ∈ L(V, W ). V, W K-Vektorräume. Wir bezeichnen als Rang von f
dim(im(f )) = dim(f (V )) = Rang(f ).
2.3
Matrizen
Wir hatten lineare Abbildungen eines K-Vektorraums V in den K-Vektorraum W im
vorherigen Abschnitt betrachtet. Wir betrachten jetzt endlichdimensionale K-Vektorräume
V und W ; {v 1 , . . . , v s } sei Basis von V , {w 1 , . . . , wr } sei Basis von W . Sei f eine lineare
Abbildung von V in W . Es gibt eindeutig bestimmt Zahlen aij ∈ K, die die Koordinaten
der Basisdarstellung von f (v j ) sind:
f (v j ) =
r
X
i=1
aij wi ,
j = 1, . . . , s.
(2.16)
85
2.3. MATRIZEN
Nach Lemma 2.19 ist die lineare Abbildung f durch die Elemente aij ∈ K, 1 ≤ i ≤ r, 1 ≤
j ≤ s eindeutig bestimmt. Wir ordnen die Menge {aij } 1≤i≤r in Form einer Matrix an.
1≤j≤s
Definition 2.22. Sei K ein Körper, r, s
rechteckiges Schema

a11
a21

A =  ..
 .
ar1
∈ N und aij ∈ K, 1 ≤ i ≤ r, 1 ≤ j ≤ s. Ein

a12 . . . a1s
a22 . . . a2s 

..
..
.. 
.
.
. 
ar2 . . . ars
heißt (r × s) Matrix über K. A besitzt r Zeilen und s Spalten.
  Der erste Index ist der
a1j
a2j 
 
Zeilenindex, der zweite der Spaltenindex. Die Vektoren  ..  heißen Spaltenvektoren,
 . 
arj
j = 1, . . . , s. Die Vektoren (ai1 , . . . , ais ), i = 1, . . . , r, heißen Zeilenvektoren.
Aus den obigen überlegungen folgt:
Lemma 2.23. Sei V ein s-dimensionaler K-Vektorraum mit der Basis {v1 , . . . , vs } und W
ein r-dimensionaler K-Vektorraum mit der Basis {w1 , . . . , wr }. Jeder linearen Abbildung
f : V → W wird durch (2.16) eine eindeutig bestimmte Matrix A = (aij ) 1≤i≤r zugeordnet.
1≤j≤s
Umgekehrt wird durch eine gegebene r × s Matrix A durch (2.16) eine lineare Abbildung
f : V → W definiert. Dabei sind die Spaltenvektoren von (aij ) die Koordinatenvektoren
der Bilder der Basisvektoren von V .
Beispiele
1◦ Wir betrachten den R2 mit der Standardbasis und die lineare Abbildung f : R2 → R2
mit
x2
x1
.
=
f
−x1
x2
Die Gleichungen (2.16) lauten
1
0
1
0
f
=
=0
−1
,
0
−1
0
1
0
1
1
0
f
=
=1
+0
.
1
0
0
1
Damit ist a11 = 0, a21 = −1, a12 = 1, a22 = 0 und
0 1
.
A=
−1 0
86
KAPITEL 2. LINEARE ALGEBRA
Bemerkung: Eine Drehung um den Winkel ϑ nach links kann mit Hilfe der Matrix
cos ϑ sin ϑ
A=
sin ϑ cos ϑ
beschrieben werden.
2◦ Es sei V = R3 , W = R2 mit den entsprechenden Standardbasen. Wir betrachten die
Projektion
 
x1
x1


f x2 =
.
x2
x3
Wir sehen uns die Gleichungen (2.16) an:
 
1
0
1
1


,
+0
f 0 =
=1
1
0
0
0
 
0
0
1
0
,
+1
f 1 =
=0
1
0
1
0
 
0
0
1
0
f 0 =
=0
+0
.
0
0
1
1
Die entsprechende (2 × 3) Matrix A lautet
1 0 0
.
A=
0 1 0
1
0
3 Es sei V = R mit der Standardbasis und W = R , versehen mit der Basis
,
.
1
1
Sei wie in Beispiel 2◦
 
x1
x1


f x2 =
.
x2
x3
Dann ist
 
1
1
1
0


f 0 =
=1
−1
,
0
1
1
0
 
0
0
1
0
,
+1
f 1 =
=0
1
1
1
0
 
0
0
1
0
f 0 =
=0
+0
0
1
1
1
◦
3
2
87
2.3. MATRIZEN
und somit
Â =
1 0 0
.
−1 1 0
Dieses Beispiel zeigt, dass A und Â verschieden sind und somit von der Wahl der
Basen abhängen.
Das Bild eines allgemeinen Vektors
Bisher hatten wir uns angesehen, wohin die Basisvektoren durch eine lineare Abbildung
abgebildet werden. Wir sehen uns jetzt das Bild eines beliebigen Elementes v ∈ V an. Es
ist
!
!
s
r
r
s
s
s
X
X
X
X
X
(2.16) X
f (v) = f
αj v j =
αj f (v j ) =
αj
aij wi =
aij αj w i .
j=1
j=1
j=1
i=1
i=1
j=1
 
α1
 .. 
Damit werden die Koordinaten  .  bezüglich der Basis {v 1 , . . . , v s } auf die Koordinaten
αs
Ps
j=1 a1j αj


..
Ps .
j=1
arj αj
 
β1
  .. 
=.

(2.17)
βr
bezüglich der Basis {w1 , . . . , w r } abgebildet.
In (2.17) treten die Einträge aij der (r × s) Matrix A auf. Wir schreiben


Ps

a11 . . . a1s  
a
α
α
1j
j
1
j=1
a21 . . . a2s 


  .. 

..
A α =  ..
:=

.


..
..
.
P
 .

.
.
s
αs
j=1 arj αj
ar1 . . . ars
 
β1
 .. 
=  .  = β.
βr
(2.18)
Wir haben damit eine Matrix-Vektor Multiplikation eingeführt, indem wir rechnen:
1. Koordinate des Bildvektors = 1. Zeile der Matrix mal “ Vektor,
”
2. Koordinate des Bildvektors = 2. Zeile der Matrix mal “ Vektor,
”
..
.
r. Koordinate des Bildvektors = r. Zeile der Matrix mal “ Vektor.
”
Hierbei bedeutet mal “ das Produkt der Zeilenvektoren der Matrix mit dem Spaltenvek”
tor α, was dem Skalarprodukt zweier Vektoren entspricht.
88
KAPITEL 2. LINEARE ALGEBRA
Bemerkung:
Sind V = K s und W = K r mit der Standardbasis versehen, dann ist
s
X
f (x) = f
j=1
xj ej
!
=
r
s
X
X
i=1
aij xj
j=1
!
ei = Ax.
(2.19)
In diesem Fall identifizieren wir f mit A und schreiben f = fA .
Beispiele
1◦ Wir sehen uns das erste vorherige Beispiel an:
x1
x2
f
=
.
x2
−x1
In der Standardbasis ist
α1
0
1
x1
=
+ x2
= x1
α2
1
0
x2
und
β1
0
1
x2
.
=
− x1
= x2
β2
1
0
−x1
0 1
erhalten wir
Mit Hilfe der Matrix A =
−1 0
β1
x2
x1
0 1
x1
.
=
=
= Ax =
f
β2
−x1
x2
−1 0
x2
2◦ Wir betrachten die lineare Abbildung f : R2 → R3 , wobei in R2 und R3 die Standardbasen betrachtet werden,


x1 + 2x2
x1
= 3x1 + 4x2  .
f
x2
5x1 + 6x2
Sie kann durch eine (3 × 2) Matrix A dargestellt werden


1 2 x
f (x) = Ax = 3 4 1 .
x2
5 6
89
2.3. MATRIZEN
Produkt von Matrizen
Man kann in natürlicher Weise ein Produkt von Matrizen erklären. Sei K ein Körper und
f : K s → K r , g : K r → K t lineare Abbildungen. Die Komposition
g ◦ f : Ks → Kt
ist linear. Zu f gehöre die (r × s) Matrix A = (aij ), zu g die (t × r) Matrix B = (bkl ). Dann
soll das Produkt von BA die zu g ◦ f gehörige (t × s) Matrix sein. Nach (2.18) erhalten
wir (man beachte, dass (x1 , . . . , xs ) = (α1 , . . . , αs ) ist)

Ps
j=1 a1j xj


..
f (x) = f (x1 , . . . , xs ) = Ax = 
 = y,
.
Ps
j=1 arj xj

Pr
l=1 b1l yl


..
g(y) = g(y1, . . . , yr ) = By = 
.
Pr .
l=1 btl yl
Für die Komposition gilt:
(g ◦ f )(x) = g(
s
X
a1j xj , . . . ,
j=1
Ps
j=1
j=1 (
wobei C die Einträge

=
Ps
Pr
j=1 (
ckj =
s
X
l=1 (b1l

arj xj ) = 
l=1 b1l alj )xj
..
Pr.
l=1 btl alj )xj
r
X
bkl alj ,
l=1
Pr

Pr
l=1 (btl
Ps
j=1 alj xj )
..
.
P
s
j=1 alj xj )




 = BAx = Cx,
1 ≤ k ≤ t, 1 ≤ j ≤ s
besitzt.
Die Multiplikation zweier Matrizen ist also folgendermaßen definiert:
Sei A eine (r × s) Matrix, B eine (t × r) Matrix. Dann ist das Produkt BA = C eine (t × s)
Matrix, deren Einträge
ckj =
r
X
bkl alj
l=1
(Produkt der k-ten Zeile von B mit der j-ten Spalte von A) sind:
B
A = C,
(t × r) (r × s) (t × s)
(2.20)
90
KAPITEL 2. LINEARE ALGEBRA



b11 . . . b1r 


..
..  a11 . . . a1j . . . a1s
 ..
c11 . . . c1s
.
.  a

 .

  21 . . . a2j . . . a2s   ..
. 
bk1 . . . bkr   ..
..  =  . ckj ..  .
..
..
..
 .

. 
.
.
.
..
..   .
 ..
ct1 . . . cts
.
.
ar1 . . . arj . . . ars
bt1 . . . btr
Produkt zweier Vektoren
Als Spezialfall erhalten wir für das Produkt eines Zeilenvektors = Matrix (1×r), mit einem
Spaltenvektor, Matrix (r × 1), eine (1 × 1) Matrix, also einen Skalar:
 
a1
r


a2  X
b1 b2 . . . br  ..  =
bi ai = c.
 .  i=1
ar
Dieses Produkt wird auch als Skalarprodukt zweier Vektoren im Rr bezeichnet.
Produkt einer Matrix mit einem Vektor
Durch die Formel (2.18) wurde bereits die Matrix-Vektor Multiplikation eingeführt. Sie
kann auch als Spezialfall der Matrizenmultiplikation (2.20) aufgefasst werden.
Sei B eine (t × r) Matrix und A eine (r × 1) Matrix (Spaltenvektor). Dann ist
B
A = C
(t × r) (r × 1) (t × 1)
ein Spaltenvektor ((t × 1) Matrix). Ausführlich geschrieben, heißt das

 a    Pr

1
b11 . . . b1r
c1
i=1 b1i ai
..   .  
..
..  
..
 ..

.   ..  
.
. 
.
 .



P

 ..     r

b
a
c
.
=
=
bk1 . . . bkr  



 .   k   i=1 ki i 
 .



.
.
.
.

 ..
..
..   ..   ..  
.

.
Pr .
bt1 . . . btr
ct
ar
i=1 bti ai
Die lineare Gruppe der Matrizen, inverse Matrizen
Wir haben gesehen, dass lineare Abbildungen f : K s → K r (wähle z.B. K = R) durch
(r×s) Matrizen darstellbar sind. Weiterhin haben wir eine Verknüpfung, die Multiplikation
von (t × r) Matrizen mit (r × s) Matrizen, eingeführt.
Wir klären nun, ob die Menge der linearen Abbildungen von K s → K r , bzw. die Menge
der Matrizen M(K, r × s) ein Vektorraum oder sogar eine multiplikative Gruppe ist.
91
2.3. MATRIZEN
Lemma 2.24. Die Menge der linearen Abbildungen von K s in K r , bzw. die Menge der
Matrizen M(K, r × s) ist ein Vektorraum mit der Addition
(f + g)(x) = f (x) + g(x) ∀ x ∈ K s ,
A + B := (aij + bij ) 1≤i≤r
1≤j≤s
und der Multiplikation mit Elementen aus K:
(αf )(x) :=αf (x) ∀ x ∈ K s ,
αA :=(αaij ) 1≤i≤r .
1≤j≤s
Das neutrale Element bezüglich der Addition ist die Nullabbildung f (x) = 0 für alle x ∈ K s ,
bzw. die Nullmatrix A = (aij = 0) 1≤i≤r .
1≤j≤s
Wir sehen uns jetzt etwas genauer die Multiplikation in M(K, r × s) an:
Zunächst stellen wir fest. Die Komposition von Abbildungen
f : K s → K r , g : K r → K t, h : K t → K l
ist assoziativ
h ◦ (g ◦ f ) = (h ◦ g) ◦ f.
Daraus folgt, dass das Produkt von Matrizen A ∈ M(K, r × s), B ∈ M(K, t × r), C ∈
M(K, l × t) assoziativ ist,
C(BA) = (CB)A.
Um das Produkt in M(K, r × s) definieren zu können, nehmen wir an, dass r = s ist. Dann
sind AB und BA für A, B ∈ M(K, r × r) definiert. Jedoch ist die Multiplikation nicht
immer kommutativ, d.h. es gibt Beispiele mit
AB 6= BA.
Beispiel
Es sei r = 2, A =
0 0
0 1
. Dann
,B=
0 1
0 0
0
0 1
AB =
0
0 0
0
0 0
BA =
0
0 1
ist
0
0
=
0
1
0
1
=
0
0
1
,
0
0
.
0
Ein neutrales Element bezüglich der Multiplikation existiert in M(K, r × r). Es ist die
Einheitsmatrix


1 0 ... 0
.. 
 .. . . .
.
.
Er =  .
.
. . .. 
 ..
. .
0 ... 0 1
92
KAPITEL 2. LINEARE ALGEBRA
Definition 2.25 (invertierbare Matrix). Man nennt eine Matrix A ∈ M(K, r × r) invertierbar, falls es eine Matrix A−1 ∈ M(K, r × r) gibt, so dass
A−1 A = AA−1 = Er
ist. A−1 heißt inverse Matrix zu A.
Nicht alle Matrizen sind invertierbar.
Beispiel
b11 b12
0 1
−1
. Dann müsste gelten
und A =
Sei r = 2, A =
b21 b22
0 0
b11 b12
0 1
0 b11
1 0
=
=
b21 b22
0 0
0 b21
0 1
und
was nicht sein kann.
0 1
b11 b12
b21 b22
1 0
=
=
,
0 0
b21 b22
0
0
0 1
Lemma 2.26. A ist invertierbar genau dann, wenn die lineare Abbildung f : K r → K r
fA (x) = Ax
bijektiv ist, d.h. ker fA = ker A = {0} ist.
Beweis
a) Wir nehmen an, dass A−1 existiert. Falls Ax = 0 ist, folgt
A−1 Ax = x = A−1 0 = 0
und ker A = {0}.
b) Wir nehmen an, dass ker A = {0} ist. Nach dem Dimensionssatz 2.21 ist
r = dim(ker fA ) + dim(im fA )
und daher r = dim(im fA ).
Damit ist die Gleichung Ax = b für alle b aus K r eindeutig lösbar, d.h. die inverse
lineare Abbildung fA−1 existiert, d.h.
fA−1 ◦ fA (x) = x = fA ◦ fA−1 (x).
Die fA−1 zugeordnete Matrix ist A−1 .
93
2.3. MATRIZEN
Lemma 2.27. Die invertierbaren Matrizen aus M(K, r × r) bilden eine Gruppe bezüglich
der Multiplikation mit dem neutralen Element Er . Diese Gruppe heißt lineare Gruppe
GLr (K).
Der Beweis dieses Lemmas besteht darin, die Gruppenaxiome zu überprüfen. Es muss u.a.
gezeigt werden: Falls A, B ∈ GLr (K), dann ist auch AB ∈ GLr (K) und
(AB)−1 = B −1 A−1 .
Bemerkung: Die Berechnung von inversen Matrizen ist keine einfache Aufgabe. Wir werden hierzu einen Algorithmus kennen lernen.
Wir fassen folgende Rechengesetze für Matrizen, die von ihrer Größe her zusammenpassen,
zusammen:
A+B
(A + B)C
(AB)C
AB
= B + A,
= AC + BC,
= A(BC),
6= BA (im Allgemeinen).
Basiswechsel, Koordinatentransformation
Am Beginn dieses Abschnittes hatten wir lineare Abbildungen eines K-Vektorraumes V
mit der Basis {v 1 , . . . , vr } in den K-Vektorraum W mit der Basis {w1 , w2 , . . . , w s } betrachtet. Wir betrachten nun einen Basiswechsel in V , d.h. in V = W seien die Basen
B1 = {v 1 , . . . , vr } und B2 = {w1 , . . . , w r } gegeben und wir möchten die lineare Abbildung beschreiben, die den Übergang zwischen den Basen angibt.
Für ein beliebiges v ∈ V gilt
v=
r
X
αi v i =
i=1
r
X
βi wi .
(2.21)
i=1
Sei HB1 die (r × r) Matrix, die aus den Spaltenvektoren v 1 , . . . , vr besteht und HB2 die
(r × r) Matrix, die die Spaltenvektoren w 1 , . . . , wr besitzt. Dann können wir (2.21) schreiben als
v = HB1 α = HB2 β,
(2.22)


 
α1
β1
 .. 
 .. 
wobei α =  . , β =  .  sind.
αr
βr
(2.22) liefert uns die Koordinatentransformation
α = HB−11 HB2 β,
β = HB−12 HB1 α.
(2.23)
94
KAPITEL 2. LINEARE ALGEBRA
Ist insbesondere B1 = {e1 , . . . , er } die Standardbasis, dann ist HB1 = E = Er und
α = HB2 β,
β = HB−12 α.
(2.24)
(2.25)
Beispiel
Sei V = W = R2 . Wir wollen die
von der Standardbasis
Koordinatentransformation
2 1
1
2
und
beschreiben. Es ist HB2 =
,
B1 = {e1 , e2 } in die Basis B2 =
1 3
3
1
3 −1
, wovon man sich durch Nachrechnen überzeugen kann.
HB−12 = 51
−1 2
Somit wird ein v ∈ V , zunächst in der Standardbasis gegeben, in der Basis B2 folgendermaßen dargestellt
(2.22)
1
2
x1
+ β2
= x1 e1 + x2 e2 = β1
v=
3
1
x2
1
1
2
1
+ (−x1 + 2x2 )
.
= (3x1 − x2 )
1
3
5
5
Hier haben wir die Gleichung (2.25) benutzt:
1
1 3 −1
x1
β1
(3x1 − x2 )
5
= 1
=
.
x2
β2
(−x1 + 2x2 )
5 −1 2
5
Der Rang einer Matrix
Der Rang einer linearen Abbildung f : V → W war bereits eingeführt worden:
Rang f = dim(im f ) = dim(f (V )).
Zu jeder Matrix A = (aij ) ∈ M(K, r × s) gibt es eine lineare Abbildung fA , so dass gilt
Ps
j=1 a1j xj
fA : K s → K r ,

x → fA (x) = Ax = 
Damit können wir definieren
Ps
..
.
j=1
arj xj


.
Rang A := Rang(fA ).
Lemma 2.28. Der Rang einer Matrix ist gleich der maximalen Anzahl linear unabhängiger
Spaltenvektoren von A. Man spricht kurz vom Spaltenrang.
95
2.3. MATRIZEN
Beweis
Es ist


a11 x1 + a12 x2 + · · · + a1s xs
a21 x1 + a22 x2 + · · · + a2s xs 


Ax = 

..


.
ar1 x1 + ar2 x2 + · · · + ars xs
 
 
 
a1s
a12
a11
a2s 
a22 
a21 
 
 
 
= x1  ..  + x2  ..  + · · · + xs  .. 
 . 
 . 
 . 
ars
ar2
ar1
und daher
im fA = Span(Spaltenvektoren),
dim(im fA ) = maximale Anzahl linear unabhängiger Spaltenvektoren von A
= Spaltenrang.
Beispiele

1
◦

1 Für A = 0
0

1
2◦ Für A = 0
2

1 1
1 1 ist Rang A = 3.
0 1

0 1
1 1 ist Rang A = 2.
0 2
Es gilt jedoch überraschend:
Lemma 2.29. Der Rang einer Matrix A ist gleich der maximalen Anzahl linear unabhängiger Zeilenvektoren, kurz als Zeilenrang bezeichnet.
Beweis
A hat r Zeilenvektoren {z1 , . . . , zr } der Länge s. Die maximale Anzahl der linear unabhängigen Zeilenvektoren sei r0 ≤ r. Wir bezeichnen sie mit
bj = (bj1 , . . . , bjs ),
1 ≤ j ≤ r0 .
Die Zeilenvektoren z i , i = 1, . . . , r, lassen sich als Linearkombination der bj darstellen
z i = ki1 b1 + ki2 b2 + · · · + kir0 br0
= (ki1 b11 + ki2 b21 + · · · + kir0 br0 1 , . . . , ki1 b1s + · · · + kir0 br0 s ).
(2.26)
96
KAPITEL 2. LINEARE ALGEBRA
Wir betrachten in jedem Zeilenvektor z i , i = 1, . . . , r, den l-ten Eintrag, 1 ≤ l ≤ s. Dann
lautet (2.26):
a1l = k11 b1l + · · · + k1r0 br0 l
..
.
ail = ki1 b1l + · · · + kir0 br0 l
..
.
arl = kr1 b1l + · · · + krr0 br0 l .
Damit ist jeder Spaltenvektor in der Form
 
 


a1l
k11
k1r0
 .. 
 .. 
 .. 
 . 
 . 
 . 
 
 


 ail  = b1l  ki1  + · · · + br0 l  kir0 
 . 
 . 
 . 
 .. 
 .. 
 .. 
arl
kr1
krr0
darstellbar. Es folgt, dass
Rang A = Spaltenrang ≤ r0 = Zeilenrang
ist. Das gleiche Verfahren können wir anwenden, indem wir die Zeilenvektoren durch Spaltenvektoren ersetzen. Es gilt dann
r0 = Zeilenrang ≤ Spaltenrang = Rang A.
Damit erhalten wir, dass Spaltenrang = Zeilenrang ist und damit
Rang A = maximale Anzahl der linear unabhängigen Spaltenvektoren
= maximale Anzahl der linear unabhängigen Zeilenvektoren.
(2.27)
97
2.3. MATRIZEN
Übungsaufgaben
Aufgabe 6.1
Untersuchen Sie, ob die durch
a) f (z) = (2 + i)z
b) f (z) = Im(iz)
c) f (z) = z̄
gegebenen Selbstabbildungen von C homogen bzw. additiv sind.
d) f (z) = max{Re(z), Im(z)}
Aufgabe 6.2
Die folgenden linearen Abbildungen p 7−→ q bilden Polynome vom Grad ≤ m auf Polynome vom Grad
≤ n ab. Bestimmen Sie die Matrixdarstellungen bezüglich der Monombasis {1, x, x2 , x3 , . . . , xn } .
a) m = n = 2,
q(x) = p(x + 1)
b) m = n − 2 = 2,
c) m = n/2 = 2,
q(x) = (x2 + 1)p(x)
q(x) = p(x2 + 1)
Aufgabe 6.3
Gegeben seien folgende Matrizen:
1 −2
A=
,
−2 4

 
4
E=
D =  5 ,
6
B
1
1
4
8 6
,
=
4 3

2
3
1
3 ,
−5 −2
C=
1 7 −1

,

1 2 3 4
F =  −1 0 0 4 
5 7 3 1
Welche Produkte sind möglich? Berechnen Sie diese.
Aufgabe 6.4
In den abgebildeten Matrizen

∗ ∗
0 ∗
A=
0 0
0 0
sind mit ∗ die von Null


0 0
0 0
∗ 0
∗ 0
 B=
0 ∗
∗ ∗
0 ∗
0 0
verschiedenen Einträge


0 0
0 0
0 0
0 0
 C=
0 0
0 0
∗ 0
0 0
Geben Sie an, in welchen Positionen die Matrixprodukte
AB, BC, (A + B)2 , C 2
ungleich Null sein können.
gekennzeichnet.

∗ ∗
0 ∗

0 0
0 0
98
KAPITEL 2. LINEARE ALGEBRA
Aufgabe 6.5
Geben Sie an, welche der abgebildeten Figuren durch eine lineare Abbildung ineinander überführt
werden können. Geben Sie die Abbildung dann jeweils in Matrix-Form an. (Der markierte Punkt ist
jeweils (0, 0)).
(2, 2)
(2, 2)
(2, 1)
(1, 2)
(3, 2)
(4, 0)
(2, −1)
Aufgabe 6.6
Welche Dimension hat der von den Vektoren


 
1+i
1
 2i 
 0 


v2 = 
v1 = 
 1 ,
 1 ,
1
0
(1, 0)


−i
 1−i 

v3 = 
 0 ,
1+i
aufgespannte Unterraum U von V = C4 ? Geben Sie eine Basis für U an.


0
 1+i 

v4 = 
 0 
i
Aufgabe 6.7
Bestimmen Sie die Matrizen für den Basiswechsel
     
     
2
2 
2
2 
 −1
 1
B =  2  , −1 ,  2  ←→ B̂ = 0 , 1 , 2




2
2
−1
0
0
1
und stellen Sie die Vektoren mit den Koordinaten (3, 0, 4) jeweils bezüglich der anderen Basis dar.
Aufgabe 6.8
Bestimmen Sie Rang A der folgenden reellen Matrix:

2 1
0 1
A=
1 1
−1 2
4
2
3
3

−3
−1

−2
−1
Hinweis: Addiert man zu einer Zeile eine Linerkombination aus den anderen Zeilen, ändert sich der
Rang nicht.
2.4. LINEARE GLEICHUNGSSYSTEME
2.4
99
Lineare Gleichungssysteme
Die Theorie der linearen Abbildungen, die wir in den Abschnitten 2.2 und 2.3 kennen
gelernt haben, findet eine schöne Anwendung bei der Lösung linearer Gleichungssysteme.
Definition 2.30. Unter einem linearen Gleichungssystem mit s Unbekannten und r Gleichungen verstehen wir das System
a11 x1 + a12 x2 + · · · + a1s xs = b1
a21 x1 + a22 x2 + · · · + a2s xs = b2
..
.
ar1 x1 + ar2 x2 + · · · + ars xs = br ,
(2.28)
wobei die Koeffizientenmatrix A = (aij ) 1≤i≤r ∈ M(K, r×s) (K ist ein Körper, z.B. K = R)
1≤j≤s
und die rechte Seite
 
b1
 .. 
b =  .  ∈ Kr
br
 
x1
 .. 
gegeben sind. Gesucht ist die Lösungsmenge L aller Vektoren x =  .  ∈ K s , die allen
xs
Gleichungen (2.28) genügen.
Das Gleichungssystem (2.28) kann kürzer als
Ax = b
(2.29)
geschrieben werden. Ist b = 0, dann spricht man von einem homogenen Gleichungssystem,
Ax = 0,
für b 6= 0 von einem inhomogenen Gleichungssystem.
Die Existenz und Eindeutigkeit der Lösungen des Gleichungssystems (2.28) wird durch
folgenden Lösbarkeitssatz beschrieben.
Theorem 2.31 (Existenz- und Eindeutigkeit für r × s Systeme).
1. Das Gleichungssystem (2.28) ist genau dann lösbar, wenn b im Bild der linearen
Abbildung
fA : K s → K r , x → fA (x) = Ax
liegt, d.h.
Rang A = Rang(A|b),
100
KAPITEL 2. LINEARE ALGEBRA
wobei A|b die erweiterte (r × (s + 1)) Koeffizienten-Matrix ist:


a11 . . . a1s b1

..
..  .
A|b =  ...
.
. 
ar1 . . . ars bs
2. Das Gleichungssystem (2.28) ist für alle b ∈ K r lösbar, falls gilt
Rang A = r.
3. Ist das Gleichungssystem (2.28) lösbar für ein b ∈ K r , dann ist eine Lösung x
eindeutig bestimmt, falls gilt
Rang A = s.
Beweis.
zu 1. Das Bild der linearen Abbildung fA ist
im(fA ) = {b ∈ K r : ∃ x ∈ K s mit Ax = b}.
Nach Lemma 2.28 ist
im(fA ) = Span{linear unabhängige Spaltenvektoren von A}.
Daher muss eine gegeben rechte Seite b von (2.28) durch eine Linearkombination der
linear unabhängigen Spaltenvektoren von A darstellbar sein, woraus
Rang A = Rang(A|b)
folgt.
zu 2. In diesem Fall ist im(fA ) = K r .
zu 3. Nach dem Dimensionssatz 2.21 ist
s = dim(ker fA ) + Rang A.
Ist Rang A = s, dann ist dim(ker fA ) = 0 und ker fA = {0}. Daraus folgt die Eindeutigkeit.
Conclusion 2.32. Falls r > s, dann ist (2.28) nicht für alle b ∈ K r lösbar, falls r < s, dann
besitzt (2.28) keine eindeutig bestimmte Lösung.
Im Fall r = s kann man die eindeutige Lösbarkeit einfacher charakterisieren.
2.4. LINEARE GLEICHUNGSSYSTEME
101
Theorem 2.33 (Eindeutige Lösbarkeit von (r × r) Systemen). Sei A eine (r × r) Matrix.
Dann sind folgende Aussagen äquivalent.
(i) A ist invertierbar, d.h. A−1 existiert.
(ii) Für alle b ∈ K r ist Ax = b eindeutig lösbar.
(iii) Das homogene Gleichungssystem Ax = 0 besitzt nur die triviale Lösung x = 0.
Beweis. Wir zeigen (i) ⇒ (ii) ⇒ (iii) ⇒ (i).
a) Es gelte (i). Wir betrachten das System Ax = b. Dann ist
A−1 Ax = x = A−1 b
und (ii) ist gezeigt.
b) Es gelte (ii). Dann besitzt auch das homogene System Ax = 0 nur eine Lösung
x = 0.
c) Es gelte (iii). Nach dem Dimensionssatz 2.21 ist
r = dim(ker fA ) + Rang A = Rang A.
Aus Satz 2.31, Aussagen 2 und 3 folgt, dass (2.28) für jede rechte Seite eindeutig
lösbar ist. Damit muss
x = A−1 b
sein und (i) gilt.
Das Gaußsche Eliminationsverfahren
Nach den theoretischen Sätzen 2.31 und 2.33 wenden wir uns jetzt einem praktischen
Lösungsweg zu, der von Carl Friedrich Gauß (1777 - 1855) vorgeschlagen wurde. Dabei
wird die erweiterte Koeffizientenmatrix (A|b) in eine Matrix besonders einfacher Gestalt,
in eine sogenannte Zeilenstufenmatrix, umgewandelt. Aus der Zeilenstufenmatrix lässt sich
die Lösung leicht gewinnen, der Rang kann abgelesen werden und es ist damit zu sehen,
ob das Gleichungssystem überhaupt eine Lösung besitzt.
Die Umwandlung der erweiterten Koeffizientenmatrix in eine Zeilenstufenform erfolgt durch
elementare Zeilenoperationen. Dabei verstehen wir unter einer Zeilenstufenmatrix folgendes:
102
KAPITEL 2. LINEARE ALGEBRA
Definition 2.34. Sei A = (aij ) ∈ M(K, r × s). Sei Ii die Anzahl der von links gezählten
aufeinander folgenden Nullen der i-ten Zeile:
(
max{I : ai1 = ai2 = · · · = aiI = 0} (1 ≤ i ≤ r),
Ii =
0
falls ai1 6= 0.
Ist I1 < I2 < · · · < Ir oder I1 < I2 < · · · < It < It+1 = · · · = Ir = s für ein t < r (d.h. ab
der (t + 1)-ten Zeile treten nur Nullzeilen auf), dann heißt A Zeilenstufenmatrix.
Beispiele:


1 0 1 0
1◦ A = 0 0 0 2 ist Zeilenstufenmatrix. Es ist I1 = 0, I2 = 3, I3 = 4.
0 0 0 0


1 1 0 0
2◦ A = 0 0 1 1  ist keine Zeilenstufenmatrix, denn I1 = 0, I2 = 2, I3 = 2.
0 0 2 3
Hat die Koeffizientenmatrix eines linearen Gleichungssystems Zeilenstufenform, dann kann
die Lösungsmenge explizit angegeben werden:
1. In den Zeilen, wo nur Nullen stehen, müssen die Einträge von b verschwinden, sonst
existiert keine Lösung. Diese können dann gestrichen werden.
2. In den verbleibenden Zeilen beginnen wir dann mit der t-ten Zeile, t ≤ r, mit I1 <
I2 < · · · < It 6= s, It+1 = s. Die Zeilengleichung lautet
X
atj xj = bt .
(2.30)
It <j≤s
Hier ist atj
angeben.

xIt +1


6 0 für j = It + 1 und wir können alle Lösungen der Form  ... 
=
xs

3. Wir setzen eine dieser Lösungen in die (t − 1)-te Zeilengleichung ein
X
a(t−1)j xj = bt−1 .
(2.31)
It−1 <j≤s
Wegen It−1 < It ist (2.31) eine Gleichung zur Bestimmung der noch freien Unbekannten xIt−1 +1 , . . . , xIt .
103
2.4. LINEARE GLEICHUNGSSYSTEME


xIt−1 +1
 .. 
 . 


 x 
4. Die Vektoren  It  werden in die (t − 2)-te Zeilengleichung eingesetzt. Daraus
 xIt +1 
 . 
 .. 
xs
wird der Vektor


xIt−2 +1
 .. 
 . 


 xIt−1 


xIt−1 +1 
 . 
 .. 


 x 
 It 
x

 It +1 
 . 
 .. 
xs
gewonnen.
5. Dieser Prozess wird fortgesetzt, bis die erste Zeile erreicht ist. Daraus erhalten wir
eine Lösung x.
Beispiel:
Wir betrachten das Gleichungssystem
 



 x1
b1
1 1 1 1  
x2  
b2  .
Ax = 0 0 0 2 
x3  =
b3 = 0
0 0 0 0
x4
Erster Schritt (Wegstreichen der Nullzeilen).
Durch Wegstreichen der Nullzeile erhalten wir
 
x1
b
x2 
1 1 1 1 


= 1 .
Âx =


b2
x3
0 0 0 2
x4
Zweiter Schritt.
Wir betrachten die zweite Zeile (t = 2). Es ist I2 = 3
a24 x4 = 2x4 = b2 ⇒ x4 =
b2
.
2
(2.32)
104
KAPITEL 2. LINEARE ALGEBRA
Dritter Schritt.
Einsetzen von x4 in die erste Zeilengleichung
x1 + x2 + x3 +
b2
= b1
2
ergibt
x1 + x2 + x3 = b1 −
Damit ist
(2.33)
b2
.
2
b2
− x2 − x3
2
 


b1 − b22 − 1
b1 − b22 − 1
,


0
1
1
0
x1 = b1 −
und
sind Lösungen von (2.33).
Es folgt, dass

 

b1 − b22 − 1
b1 − b22 − 1

 

0
1

,


 

1
0
b2
2
Lösungen von Ax = b sind.
(2.34)
b2
2
Die Frage ob wir alle Lösungen von Ax = b erfasst haben, diskutieren wir später. Wir
erklären jetzt, was wir unter elementaren Zeilenoperationen verstehen, die eine Matrix A
in eine Zeilenstufenform überführen.
Definition 2.35. Sei A|b die erweiterte Matrix zum Gleichungssystem
Ax = b.
Elementare Zeilenumformungen von A|b sind:
• Vertauschungen von Zeilen,
• Multiplikation von Zeilen mit α ∈ K\{0},
• Addition einer α- fachen Zeile zu einer andere Zeile.
Wir sehen sofort: die Lösungsmenge L des linearen Gleichungssystems ändert sich nicht
durch Anwendung elementarer Zeilenumformungen. So ist z.B. x Lösung von Ax = b,
genau dann falls x Lösung des folgende Gleichungsystems ist:
s
X
aij xj = bi ,
1 ≤ i ≤ r, i 6= l,
j=1
s
X
j=1
(alj + αakj )xj = bl + αbk .
105
2.4. LINEARE GLEICHUNGSSYSTEME
Lemma 2.36 (Gauß Elimination). Jede Matrix A ∈ M(K, r × s) lässt sich durch endlich
viele elementare Zeilenoperationen auf Zeilenstufenform bringen.
Beweis.
1.Schritt: Erzeugen von a11 6= 0.
Wir dürfen annehmen, dass die erste Spalte von A mindestens ein Element 6= 0 enthält
(sonst gehen wir zur ersten Spalte, die von Null verschieden ist, über). Durch Vertauschen
der Zeilen erreichen wir, dass a11 6= 0 ist.
2. Schritt: Erzeugen von Nullen (außer a11 ) in der ersten Spalte.
Wir bestimmen Elemente αi ∈ K, so dass gilt
αi a11 + ai1 = 0,
2 ≤ i ≤ r.
Durch addieren des αi -fachen der ersten Zeile zur i-ten Zeile erhalten wir


a11
a12
...
a1s
 0 α2 a12 + a22 . . . α2 a1s + a2s 


 ..
.
..
..
..
 .

.
.
.
0 αr a12 + ar2 . . . αr a1s + ars
(2.35)
(2.36)
3. Schritt: Erzeugen von Nullen in der zweiten Spalten von (2.36).
Wir unterscheiden 2 Fälle:
Sind alle Einträge unter a12 in der zweiten Spalte von (2.36) Null, so gehen wir zur 3.
Spalte über.
Ist zumindest ein Eintrag unter a12 in der zweiten Spalte von (2.36) nicht Null, so setzen
wir ihn durch Vertauschen der Zeilen unter a12 . Dann gehen wir wie oben vor. Wir erhalten


a11
a12
a13 . . .
a1s
 0 α2 a12 + a22 . . . . . . α2 a1s + a2s 


0

0
∗ ...
∗


0
.
0
∗
.
.
.
∗


 ..

..
..
 .

.
.
0
0
... ...
∗
Dieses Verfahren wird so oft angewandt, bis die Zeilenstufenform erreicht ist.
Beispiel
Wir betrachten die
erweiterte “ Matrix
”

1 0
 −1 3
2 1
0
2
−2

2
0 .
1
(2.37)
106
KAPITEL 2. LINEARE ALGEBRA
a11 ist von Null verschieden. Wir bestimmen α2 und α3 :
a21
= 1,
α2 a11 + a21 = 0 ⇒ α2 = −
a11
a31
α3 a11 + a31 = 0 ⇒ α3 = −
= −2.
a11
Damit erhalten wir nach Addition des α2 -fachen der ersten Zeile zur zweiten Zeile und des
α3 -fachen der ersten Zeile zur dritten Zeile


2
1 0 0
 0 3 2
2 .
0 1 −2 −3
Wir bestimmen jetzt eine Zahl µ, so dass gilt
1
µ=− ,
3
Zeile zur dritten Zeile:

2
0 0
3 2
2 .
8
0 − 3 − 11
3
µ3 + 1 = 0,
und addieren das µ-fache der zweiten

1
 0
0
Die Lösungsmenge von (2.37)
(2.38)

   
1 0 0
x1
2
−1 3 2  x2  = 0
2 1 −2
x3
1
stimmt mit der Lösungsmenge von (2.38)
  


x1
2
1 0 0
0 3 2  x2  =  2 
x3
− 11
0 0 − 83
3
(2.39)
überein. Wir erhalten sofort aus (2.39)
   
x1
2
x2  = − 1  .
4
11
x3
8
Remark 2.37.
(i) Das Gaußsche Eliminationsverfahren, das eine Matrix in eine Zeilenstufenmatrix
überführt, liefert gleichzeitig den Rang einer Matrix.
Der Rang einer Zeilenstufenmatrix ist gleich der Anzahl der Zeilen, die einen von
Null verschiedenen Eintrag enthalten.
(ii) Außerdem gilt: Der Rang einer Matrix ändert sich nicht bei elementaren Zeilenoperationen. Diese Aussage folgt aus Lemma 2.29.
2.4. LINEARE GLEICHUNGSSYSTEME
107
Die vollständige Lösung linearer Gleichungssysteme
Wir diskutieren jetzt, wie man die vollständige Lösungsmenge eines linearen Gleichungssystem
Ax = b, A ∈ M(K, r × s), b ∈ K r
beschreiben kann.
Theorem 2.38. Sei x0 ∈ K s eine spezielle Lösung von Ax = b. Jede Lösung x von
Ax = b hat die Gestalt
x = y + x0 ,
wobei y ∈ ker(A) = {y : Ay = 0} ist.
Kurz ausgedrückt: {x ∈ K s : Ax = b} = L = {x0 + y : Ay = 0}.
Beweis.
a) Seien x und x′ ∈ L. Dann ist A(x − x′ ) = 0, d.h. x ist darstellbar als
x = x − x′ + x′ = y + x0 ,
y = x − x′ ∈ ker A,
x′ = x0 ist Lösung von Ax0 = b.
b) Sei x = y + x0 . Dann ist
Ax = Ay + Ax0 = 0 + b = b.
Wir beschreiben nun, wie man vorgehen kann, um die vollständige Lösung eines Gleichungssystems Ax = b zu erhalten.
1. Bringe A|b in eine Zeilenstufenform.
2. Prüfe ob Rang(A) = Rang(A|b) ist.
Falls nein, dann existiert keine Lösung. Falls ja, konstruiere aus der Zeilenstufenmatrix eine spezielle Lösung x0 .
3. Bestimme ker(A). Es ist nach der Dimensionsformel 2.21 dim(ker(A)) = s − Rang A.
Aus der Zeilenstufenform von A kann die Basis von ker(A) bestimmt werden.
Beispiel
Wir sehen uns noch einmal das Beispiel (2.32) an:
x1 + x2 + x3 + x4 = b1
2x4 = b2 .
108
KAPITEL 2. LINEARE ALGEBRA
1.Schritt: Zeilenstufenform von A|b.
Es ist
1 1 1 1 b1
A|b =
0 0 0 2 b2
und damit liegt bereits eine Zeilenstufenmatrix vor.
2.Schritt: Rangbestimmung und Konstruktion einer speziellen Lösung.
Es ist Rang A = Rang A|b = 2. Somit ist

b1 −
 0
x0 = 
 0
b2
2
b2
2
eine spezielle Lösung der inhomogenen Gleichung.




3. Schritt: Berechnung von ker A.
Wir sehen, dass dim(ker(A)) = s − Rang A = 4 − 2 = 2 ist. Daher müssen wir zwei linear
unabhängige Lösungen von
x1 + x2 + x3 + x4 = 0
2x4 = 0
bestimmen. Da x4 = 0 sein muss, folgt x1 + x2 + x3 = 0. Es sind z.B.
 
 
1
1
0
−1

 
y1 = 
 0  , y 2 = −1
0
0
zwei linear unabhängige Lösungen.
Die Menge aller Lösungen ist
  
 
b1 −
1
1
0  0
−1

  
x = c1 
 0  + c2 −1 +  0
b2
0
0
2
b2
2


,

wobei c1 und c2 beliebige Konstanten aus K sind. Für c1 = 0, c2 = −1 und für c1 =
−1, c2 = 0 erhalten wir die Lösungen (2.34).
Berechnung inverser Matrizen
Wir betrachten ein r × r Gleichungssystem Ax = b. In Satz 2.33 wurde geklärt, wann eine
inverse Matrix A−1 existiert (ker A = {0}). In diesem Fall besitzt Ax = b eine eindeutig
bestimmte Lösung
x = A−1 b.
109
2.4. LINEARE GLEICHUNGSSYSTEME
Ist A−1 bekannt, dann kann die Lösung x für beliebige rechte Seiten b durch MatrixVektor-Multiplikation berechnet werden. Um A−1 zu berechnen, könnte man folgendermaßen vorgehen:
Bestimme eine Matrix B ∈ M(K, r × r), so dass
BA = Er
ist. Dies führt zu einem Gleichungssystem von r 2 Gleichungen zur Bestimmung der r 2
Unbekannten (bij ) 1≤i≤r . Wir können aber auch das Gaußsche Eliminationsverfahren an1≤j≤r
wenden, um effizienter zum Ziel zu kommen. Sei A eine (r × r)-Matrix mit Rang(A) = r.
1.Schritt
Wir betrachten die erweiterte (r × 2r)-Matrix
(A|Er )
und bringen diese durch elementare Zeilenumformungen
erhalten

c1
∗

.
.
(SA|S) = 
.
S
0
cr
auf eine Zeilenstufenform. Wir


,
wobei S eine Matrix ist, die die Zeilenumformungen beschreibt. Da Rang(A) = r ist,
müssen alle Diagonalelemente ci 6= 0 sein.
2.Schritt
Wir multiplizieren die Matrix SA|S mit der Diagonalmatrix
 −1

c1
0


..
C=
,
.
−1
0
cr
d.h. die i-te Zeile wird mit c−1
multipliziert. Wir erhalten
i


1
∗


..
(CSA|CS) = 
.
CS  .
0
1
(2.40)
3.Schritt
Wir bringen CSA durch elementare Zeilenoperationen in die Einheitsmatrix Er , d.h. es
existiert eine Matrix Ŝ mit ŜCSA = Er . Es wird
(ŜCSA|ŜCS) = (Er |ŜCS)
und ŜCS = A−1 .
Zusammenfassend können wir diesen Prozess folgendermaßen beschreiben:
110
KAPITEL 2. LINEARE ALGEBRA
Transformieren wir A durch elementare Zeilenoperationen in Er , dann wird aus Er die
inverse Matrix A−1
(A|Er )
↓ Zeilenoperationen
(Er |A−1 ).
Beispiel
Sei A = (aij ) 1≤i≤2 eine (2 × 2)-Matrix mit Rang 2, d.h. A−1 existiert.
1≤j≤2
1.Schritt
Wir betrachten die erweiterte (2 × 4)-Matrix
a11 a12
A|E2 =
a21 a22
1
0
0
1
.
Wir nehmen an, dass a11 6= 0 und bringen A|E2 in eine Zeilenstufenform. Wir bestimmen
nach (2.35) α2 so, dass
a21
α2 a11 + a21 = 0, α2 = −
a11
ist. Durch Addition des α2 -fachen der 1. Zeile zur 2. Zeile erhalten wir
1
0
a11
a12
.
SA|S =
0 −a21 a12a11+a22 a11 − aa21
1
11
(2.41)
Wir können annehmen, dass a11 a22 − a12 a21 = D 6= 0 ist, sonst wäre Rang A 6= 2.
2.Schritt
Die Matrix C lautet:
C=
1
a11
0
0
a11
D
.
Nach Multiplikation von (2.41) mit C ergibt sich
CSA|CS =
1
0
a12
a11
1
1
a11
− aD21
0
a11
D
.
(2.42)
3.Schritt
1 aa12
11
in die Einheitsmatrix, indem wir das − aa12
Wir bringen
-fache der 2. Zeile zur 1.
11
0 1
Zeile addieren. Dann ist
1 0 a111 + aa1211aD21 − aD12
,
ŜCSA|ŜCS =
a11
− aD21
0 1
D
2.4. LINEARE GLEICHUNGSSYSTEME
111
und
12 a21
1 D+aa11
−a12
A =
−a21
a11
D
1
a22 −a12
=
.
D −a21 a11
a11 a12
Wir fassen zusammen: Sei A =
. Ist D = a11 a22 − a12 a21 =
6 0, dann existiert die
a21 a22
inverse Matrix und es ist
1
a22 −a12
−1
.
(2.43)
A =
D −a21 a11
−1
Übungsaufgaben
Aufgabe 7.1
Bestimmen Sie alle Lösungen des linearen

(t − 1)2

1
2
in Abhängigkeit des Parameters t ∈ R .
Gleichungssystems

  
1 t
x1
0
1 0   x2  =  0 
3 1
t
x3
Aufgabe 7.2
Lösen Sie das lineare Gleichungssystem




1 1/2 1/3
11/6
 1/2 1/3 1/4  x =  13/12 
1/3 1/4 1/5
47/60
näherungsweise mit der Gauß-Elimination, indem Sie nach jeder Operation das Ergebnis auf drei
signifikante Stellen runden (1/3 ≈ 0.333 , 12.784 ≈ 12.8) . Vergleichen Sie das Ergebnis mit der
exakten Lösung x = (1, 1, 1)⊤ .
Aufgabe 7.3
Mit reellen Parametern α und β liegt folgendes lineares Gleichungssystem vor:
αx1 − 2x2
= 4
−x1 − x2 + 2x3 = β
x1 + x2 − x3 = 0
Für welches α = α0 ist die Lösbarkeit des Gleichungssystems von β abhängig?
Für welches β = β0 besitzt das Gleichungssystem für alle α eine Lösung?
Bestimmen Sie für die Parameter α0 und β0 alle Lösungen des Gleichungssystems.
Aufgabe 7.4
112
KAPITEL 2. LINEARE ALGEBRA
Die Veränderung der Matrix A und der rechten Seite b bei einem Gauß-Eliminations-Schritt zur Lösung
eines linearen Gleichungssystems Ax = b kann auch als Matrix-Multiplikation geschrieben werden. D.h.
die Matrix Aneu und der Vektor bneu entstehen mit Hilfe einer Matrix T (k, l) , k > l als
Aneu = T (k, l)A ,
bneu = T (k, l)b ,
wobei die Matrix T (k, l) von zwei Parametern (k, l) abhängt, die die Position des Elements in A
angeben, das eliminiert werden soll. Außerdem werden ggf. noch Matrizen P (k, l) benötigt, die die
Zeilen k und l der Matrix A vertauschen.
Geben Sie die Matrizen P (k, l) und T (k, l) in Abhängigkeit der Einträge der Matrix A an.
(freiwillig) Schreiben Sie ein Programm, dass die Gauß-Elimination mit Hilfe von Matrix-Multiplikationen
durchführt (ggf. müssen Sie dazu ein Unterprogramm schreiben, dass eine Matrix-Multiplikation
durchführt).
113
2.5. DETERMINANTE EINER MATRIX
2.5
Determinante einer Matrix
Bei der Berechnung der Inversen einer (2 × 2)-Matrix hat sich die Zahl D = a11 a22 − a12 a21
als wichtige Größe herausgestellt. Es wird sich erweisen, dass sie die Determinante der
Matrix A ist.
Determinanten werden für quadratische Matrizen folgendermaßen definiert.
Definition 2.39. Eine Abbildung f von M(K, r × r) → K, f : A → f (A) = det A heißt
Determinante, falls folgende Eigenschaften gelten:
(D1) det ist linear in den Zeilenvektoren, d.h. seien z 1 , . . . , z r die Zeilenvektoren von A, b
ein beliebiger Zeilenvektor und α, β ∈ K. Dann ist

.





z1
z1

 .. 

 .. 

 . 

 . 






 z k−1 
z k−1 
z k−1 






det αz k + βb = α det  z k  + β det  b 






 z k+1 
z k+1 
z k+1 






..

 ... 

 ... 
.
zr
zr
zr
z1
..
.
(D2) det A ändert bei Vertauschung zweier Zeilen von A das Vorzeichen, d.h.

 

z1
z1
 .. 
 .. 
.
.
 
 
zj 
z k 
.
 
 = − det  ...  .
.
det 
.
 
 
z 
z 
 k
 j
.
.
 .. 
 .. 
zr
zr
(D3) det Er = 1.
Lemma 2.40. Es gilt:
(D4) Sind zwei Zeilenvektoren gleich, so ist det A = 0.
(D5) Addition einer α-fachen Zeile zu einer anderen Zeile, ändert die Determinanten
nicht.
114
KAPITEL 2. LINEARE ALGEBRA
Beweis. (D4) Es sei z j = z k , k 6= j. Dann ist

 

 
z1
z1
z1
 .. 
 .. 
 .. 
.
.
.
 
 
 
z j 
z k 
z k 
.
 .  (D2)
 
 = det  ..  = − det  ...  = − det A,
.
det A = det 
.
 
 
 
z 
z 
z 
 k
 j
 j
.
.
.
 .. 
 .. 
 .. 
zr
zr
zr
woraus det A = 0 folgt.
(D5) Es ist
 
z1


.

z1
 .. 


..


z j 
.


 .  (D4)

 (D1)

det z k + αz j  = det A + α det 
 ..  = det A.


.


..


z j 
.
 .. 
zr
zr
Remark 2.41. Die Addition des α-fachen der j-ten Zeile zur k-ten Zeile (k 6= j) kann durch
Multiplikation mit einer Matrix
j − te Spalte
↓


1 0
0
 ...





α 1
S(α, k, j) = 
 ← k − te Zeile


..

. 
0
1


α für i = k, l = j,
Sil = 1 für i = l,


0 sonst
(2.44)
115
2.5. DETERMINANTE EINER MATRIX
beschrieben werden. Es ist nämlich


 a11
1 0
0  .
 ...
  ..



 aj1
α 1
S(α, k, j)A = 


 ak1
.
..   .

 ..
0
1
ar1


z1
..


.




= z k + αz j  .


..


.
zr

. . . a1r
.. 
. 

. . . akr 

. . . ajr 
.. 
. 
. . . arr
Lemma 2.42. Besitzt A ∈ M(K, r × r) Zeilenstufenform, dann ist
det A = a11 a22 · · · arr .
Beweis. Da A eine (r × r)-Matrix ist, hat A die Gestalt


a11
∗


..
A=
,
.
0
arr
wobei in der Diagonale auch Nullen stehen können.
1.Fall
Wir nehmen an, dass A nicht invertierbar ist, d.h. Rang(A) < r. Daher muss mindestens
die r-te Zeile aus Nullen bestehen, d.h. arr = 0.
Nach (D5) können wir zur letzten Zeile eine andere addieren und erhalten 2 gleiche Zeilen.
(D4) liefert uns die Aussage, dass in diesem Fall det A = 0 ist.
2.Fall
Es sei Rang(A) = r, d.h. A ist invertierbar. In diesem Fall müssen alle Diagonalelemente
ungleich Null sein. Durch Addition von α-fachen Zeilen zur darüberliegenden Zeile erhalten
wir eine Diagonalform Â


a11
0


..
Â = 
.
.
0
arr
Es ist

1
0
0 a22
(D5)
(D1)

det A = det Â = a11 det  . .

.
0
arr


(D3)
 (D1)
 = a11 a22 · · · arr det Er = a11 a22 · · · arr .

116
KAPITEL 2. LINEARE ALGEBRA
Beispiele
1◦ Wir betrachten
a11 a12
.
A=
a21 a22
Es sei a11 6= 0. Die Zeilenstufenform von A lautet
a11
a12
.
Ã =
a12 + a22
0 − aa21
11
Es ist nach (D1) und Lemma 2.42
a12
det A = det Ã = a11 − a21 + a22 = a11 a22 − a12 a21 = D (Vergleiche S. 110).
a11
2◦ Sei S(α, k, j) durch (2.44) gegeben. Dann ist
det S(α, k, j) = 1.
(2.45)
1.Fall: i < l. Dann liegt der Eintrag Sil = α in der oberen Dreiecksmatrix.
2.Fall: i > l. Sil = α befindet sich in der unteren Dreiecksmatrix und kann durch
Addition des α-fachen der l-ten Zeile zur i-ten Zeile zu Null gemacht werden.
Conclusion 2.43. Folgende Aussagen sind für Matrizen A ∈ M(K, r × r) äquivalent:
det A = 0 ⇔ Rang A < r ⇔ A ist nicht invertierbar
⇔ die Zeilen bzw. Spalten von A sind linear abhängig.
Offen ist bisher, ob die Determinante eindeutig bestimmt ist. Das folgende Lemma beantwortet diese Frage.
Lemma 2.44. Es gibt höchstens eine Determinante zu einer Matrix A ∈ M(K, r × r).
Beweis. Da durch Addition einer α-fachen Zeile zu einer anderen Zeile stets erreicht werden
kann, dass die entstehende Matrix Ã Zeilenstufenform hat und nach (D1)
det A = det Ã
ist, folgt aus Lemma 2.42 die Behauptung.
Achtung!
Es gibt Beispiele, dass det(A + B) 6= det A + det B ist.
0
1 2
,B =
A=
−2
2 1
Sei
0
.
0
2.5. DETERMINANTE EINER MATRIX
117
Es ist
1 2
= −3,
det A = det
0 −3
det B = 0.
Jedoch erhalten wir
1 2
det(A + B) = det
= 1 6= −3 + 0.
0 1
Für das Produkt zweier Matrizen gilt jedoch:
Lemma 2.45. Seien A, B ∈ M(K, r × r), dann gilt
(D6)
det(AB) = det A det B.
Beweis.
1. Fall
A sei nicht invertierbar,d.h. fA : K r → fA (K r ) K r . Damit erhalten wir: fA ◦ FB = fAB :
K r → fA (fB (K r )) K r . Es folgt, dass AB nicht invertierbar ist.
2. Fall
A sei invertierbar. Wir können A nach (D1) durch Multiplikation mit einer Matrix S, die
durch Multiplikation von Matrizen der Form S(α, k, j) (siehe Formel (2.44)) entsteht, in
Diagonalform bringen, wobei
det(SA) = â11 · · · ârr = det A
ist. Hierbei wurde genutzt, dass det S = 1 nach (2.45) und daher gilt in diesem speziellen
Fall (D6). Weiterhin ist
det(AB) = det(SAB) = det((SA)B)



â11
0
b11 . . . b1r

  ..
.. 
..
..
= det 
 .
.
. 
.
br1 . . . brr
0
ârr


â11 b11 . . . â11 b1r
 ..
..
.. 
= det  .
.
. 
ârr br1 . . . ârr brr
(D1)
= â11 â22 · · · ârr det B = det A det B.
118
KAPITEL 2. LINEARE ALGEBRA
Berechnung von Determinanten
Wir haben bereits gesehen, dass Determinanten von (2 × 2)-Matrizen folgendermaßen berechnet werden können:
a11 a12
= a11 a22 − a12 a21 .
det
a21 a22
Die Determinanten von (3 × 3) Matrizen können ebenfalls durch Transformation in eine
Zeilenstufenmatrix und nach Lemma 2.42 berechnet werden (Regel von Sarrus):


a11 a12 a13
det a21 a22 a23 
a31 a32 a33
= a11 a22 a33 + a12 a23 a31 + a13 a21 a32 − a13 a22 a31 − a12 a21 a33 − a11 a23 a32 .
(2.46)
Es gibt ein Verfahren, wie man die Berechnung der Determinante einer (r × r) Matrix auf
die Berechnung von Determinanten von ((r − 1) × (r − 1)) Matrizen zurückführen kann.
Um dies zu erläutern, führen wir folgende Bezeichnung ein:
Es sei A eine (r × r) Matrix


a11 . . . a1r

..
..  .
A =  ...
.
. 
ar1 . . . arr
Aij sei die ((r − 1) × (r − 1)) Matrix, die durch Streichen der i-ten Zeile und der j-ten
Spalte von A entsteht.
Weiterhin sei Ãij die Matrix, in der die i-te Zeile von A durch den j-ten Einheitsvektor
(0, . . . , 1, . . . , 0) ersetzt wird,




Ãij = 


a11
..
.
0
..
.
ar1
j-te Spalte
↓

. . . a1j . . . a1r
..
.. 
.
. 

. . . 1 . . . 0  ← i-te Zeile,
..
.. 
.
. 
. . . arj . . . arr
d.h. aij wird durch 1 ersetzt, sonst stehen Nullen in der i-ten Zeile.
Lemma 2.46. Es ist
det(Ãij ) = (−1)i+j det Aij .
Beweis.
1. Fall
119
2.5. DETERMINANTE EINER MATRIX
Es sei i = j = 1. Es gilt, dass
Rang(A11 ) = Rang(Ã11 ) − 1
ist. Es ist nämlich
A11


a22 . . . a2r

..  ,
..
=  ...
. 
.
ar2 . . . arr
Ã11

1 
0




.

= 
A11 
∗
Durch Addition von Vielfachen der ersten Zeile von Ã11 zu den anderen Zeilen können wir
erreichen, dass aus Ã11
1 0
˜
Ã11 =
0 A11
wird und
Rang(Ã11 ) = Rang(Ã˜11 ) = Rang(A11 ) + 1
gilt. Damit erhalten wir
det A11 = 0 ⇔ det Ã11 = 0.
Ist det A11 6= 0, so können wir A11 in Diagonalform bringen


â22
0


..
SA11 = Â11 = 
.
.
0
ârr
Wir betrachten
S̃ Ã11
wobei S̃ =
1 0
∗ S


1 0
0
0
∗ â22
0


=
..  ,
.
.
∗
. . 
∗ 0 . . . ârr
ist. Wir erhalten auch in diesem Fall
det A11 = â22 · · · · · ârr = det S̃ Ã11
(2.45),(D6)
=
1 · â22 · · · · · ârr = det Ã11 .
2. Fall
i und j seien beliebig.
Wir bringen die 1, die am Platz ij von Ãij steht, durch Vertauschen benachbarter Zeilen
in die Diagonale. Dies liefert nach (D2) den Faktor (−1)|i−j| = (−1)i+j . Dann gehen wir
analog zum 1. Fall vor.
120
KAPITEL 2. LINEARE ALGEBRA
Theorem 2.47 (Entwicklungssatz von Laplace). Sei A eine (r × r) Matrix. Es ist
det A =
r
X
(−1)i+j aij det Aij ,
(2.47)
j=1
wobei i ∈ {1, . . . , r} ist. (2.47) wird als Entwicklung nach der i-ten Zeile bezeichnet.
Beweis. Wir können die Matrix A folgendermaßen schreiben:

  
z1
z1
..

 ..  
.

. 

  
a
(1,
0,
.
.
.
,
0)
+
·
·
·
+
a
(0,
0,
.
.
.
,
1)
z
A =  i  =  i1
.
ir

. 
..

 ..  
.
zr
zr
Nach (D1) gilt
det A = ai1 det Ãi1 + · · ·+ air det Ãir
Lemma 2.46
=
ai1 (−1)i+1 det Ai1 + · · ·+ air (−1)i+r det Air .
Beispiel


2 0 4
Sei A =  5 3 1.
−1 0 1
a) Druch kreuzweises Rechnen (Regel von Sarrus (2.46)) erhalten wir
det A = 6 + 12 = 18.
b) Entwicklung nach der ersten Zeile liefert:
3 1
5 1
5 3
det A = 2 det
+ 0 det
+ 4 det
0 1
−1 1
−1 0
= 2 · 3 + 4 · 3 = 18.
c) Entwicklung nach der zweiten Spalte (siehe Lemma 2.50) liefert
2 4
det A = 3 det
−1 1
= 3 · 6 = 18.
121
2.5. DETERMINANTE EINER MATRIX
Die transponierte Matrix
Bei der Rangbestimmung haben wir gesehen, dass Rang A = Zeilenrang A = Spaltenrang A
ist. Es tritt die Vermutung auf, dass wir die Determinanten von A auch durch Entwicklung
nach Spalten berechnen können. Dies wird tatsächlich möglich sein.
Wir führen dazu die zu A transponierte Matrix A⊤ ein.
Definition 2.48. Sei A eine (r × s) Matrix, A = (aij ) 1≤i≤r . Die zu A transponierte Matrix
1≤j≤s
ist eine (s × r) Matrix und durch
A⊤ = (aji ) 1≤j≤s
1≤i≤r
gegeben.
Beispiele
1. Sei A =
1 2 0 0
. Dann ist
0 3 1 1

1

2
A⊤ = 
0
0
 
a1
 .. 
2. Für A =  .  gilt
ar

0
3
.
1
1
A⊤ = (a1 , . . . , ar ).
Lemma 2.49. Es ist
(AB)⊤ = B ⊤ A⊤ .
P
Beweis. Es gilt AB = (cik ), wobei cik = rj=1 aij bjk (i-te Zeile von A mal k-te Spalte von
B) ist. Andererseits ist (AB)⊤ = (cki ) mit
cki =
=
r
X
j=1
r
X
akj bji
(k-te Zeile von A mal i-te Spalte von B)
bij ajk
(i-te Zeile von B ⊤ mal k-te Spalte von A⊤ ).
j=1
Somit gilt (AB)⊤ = B ⊤ A⊤ .
Lemma 2.50. Sei A eine (r × r) Matrix. Dann ist
122
KAPITEL 2. LINEARE ALGEBRA
a) det(A) = det A⊤ ,
P
b) det A = ri=1 (−1)i+j aij det Aij , wobei j ∈ {1, 2, . . . , r} ist. (Entwicklung nach der
j-ten Spalte)
Beweis.
a) 1. Fall: Es sei det A = 0. Dann folgt Rang(A) < r und Rang(A⊤ ) < r (nach (2.27))
und damit det A⊤ = 0.
2. Fall: Es sei det A 6= 0.
Dann können wir durch Zeilenumformungen erreichen, dass


â11
0


..
det A = det(SA) = det 
.
.
0
ârr
(2.48)
Hierbei ist S das Produkt von Matrizen der Form S(α, k, j), die durch (2.44) gegeben
(2.45)
sind. Da det S(α, k, j) = det S(α, k, j)⊤
= 1 gilt und nach Lemma 2.45 und
Lemma 2.49
det S = det S ⊤ = 1
folgt, erhalten wir
(2.48)
det A = det(SA) = det(SA)⊤
b) Diese Eigenschaft folgt aus a).
Lemma 2.45
=
det A⊤ det S ⊤ = det A⊤ .
123
2.5. DETERMINANTE EINER MATRIX
Übungsaufgaben
Aufgabe 8.1
Berechnen Sie für

 
0 2 3
0



A = (a1 , a2 , a3 ) = 2 1 2 , b = 1 , A1 = (b, a2 , a3 ) , A2 = (a1 , b, a3 ) , A3 = (a1 , a2 , b)
3 2 0
9

(a1 , a2 , a3 sind die Spaltenvektoren von A) die Determinanten α = det(A), x1 = det(A1 ), x2 =
det(A2 ) und x3 = det(A3 ).
Berechnen Sie außerdem A(x1 , x2 , x3 )⊤ − αb .
Aufgabe 8.2
Berechnen Sie für die Matrizen


1 2 0
A =  3 0 4 ,
0 5 6


1 0 2
B= 3 0 6 
4 0 8
det(A) und det(B). Bestimmen Sie auch die Werte der Ausdrücke
det(A−1 ) , det (AB) , det A⊤ A−1 , Rang A⊤ AB ,
Rang B ⊤ A⊤ A .
Aufgabe 8.3
Zur Transformation eines linearen Gleichungssystems Ax = b mit n Zeilen auf Zeilenstufenform können
auch andere Matrizen verwendet werden.
Bei der Givens-Rotation werden zur Elimination des Eintrags an der Stelle (k, l) der Matrix A Matrizen
G(k, l) verwendet, die sich nur an vier Stellen von der (n × n)-Einheitsmatrix En unterscheiden und
zwar
G(k, l)k,k = G(k, l)l,l = c , G(k, l)l,k = −G(k, l)k,l = s ,
wobei c und s so gewählt sind, dass die Determinante der Matrix det(G(k, l)) = 1 ist.
Wie müssen c und s in Abhängigkeit der Einträge der Matrix A gewählt werden, damit der Eintrag
(k, l) in der Matrix Aneu = G(k, l) · A verschwindet?
(freiwillig) Verändern Sie Ihr Programm aus der letzten Aufgabe so, dass die Zeilenstufenform mit
Hilfe von Givens-Rotationen erzeugt wird.
Aufgabe 8.4
Gegeben seien die

2
 1

A=
 3
 −3
7
Matrizen
0
4
6
5
11

0 −3
0
0
1 −2 

5×5
1 −1
2 
∈R
2 −1
0 
4
1
1
a) Berechnen Sie det(A).
und




B=


b) Zeigen Sie, dass det(B) = (a + (n − 1)b) (a − b)n−1 .
b ···
b ···
.. ..
.
.
b ··· b
a
b ··· b
b
a b
b a
.. . .
.
.
b
b
..
.




 ∈ Rn×n .

b 
a
124
2.6
KAPITEL 2. LINEARE ALGEBRA
Eigenwerte und Diagonalisierbarkeit
Im vorigen Abschnitt hatten wir lineare Gleichungssysteme
Ax = b
betrachtet. Dabei konnten wir durch elementare Zeilenumformungen erreichen, dass das
Gleichungssystem eine Diagonalform annimmt. Wir sehen uns jetzt die Diagonalisierbarkeit einer gegebenen Matrix A an, die durch Darstellung der Matrix in einer geeigneten
Basis charakterisiert wird. Zunächst erinnern wir uns an die Darstellung linearer Abbildungen durch Matrizen, die von der Wahl der Basis abhängt (siehe Abschnitt 2.3).
Sei f eine lineare Abbildung, die einen r-dimensionalen Vektorraum V in sich selbst abbildet:
f : V → V, dim V = r.
Sei {v1 , . . . , vr } eine Basis von V . Es gibt eindeutig bestimmte Zahlen aB
ij ∈ K, so dass
f (v j ) =
r
X
aB
ij v i
(2.49)
i=1
ist. Die Matrix AB = (aB
ij ) charakterisiert die Abbildung f : V → V , siehe (2.18). In der
Standardbasis haben wir, siehe (2.19),
f (x) = fA (x) = Ax ∀x ∈ V = K r .
(2.50)
AB hängt von der Wahl der Basis ab. Die Diagonalisierbarkeit ist äquivalent dazu, eine
Basis zu finden, in der AB Diagonalform besitzt. In diesem Fall ist
f (v j ) = aB
jj v j .
(2.51)
Es wird sich erweisen, dass eine solche Basis durch sogenannte Eigenvektoren erzeugt werden kann.
Definition 2.51. Sei K = R oder C und V ein r-dimensionaler K-Vektorraum. Sei
f : V → V eine lineare Abbildung. Eine Zahl λ ∈ K heißt Eigenwert (kurz EW) von f ,
falls es ein v ∈ V \ {0} gibt mit
f v = λv.
(2.52)
Jedes v ∈ V \ {0}, das (2.52) genügt, heißt Eigenvektor von f (kurz EV) zum Eigenwert λ.
Ein Paar {λ, v}, wobei λ Eigenwert ist und v der zugehörigen Eigenvektor, wird Eigenpaar
genannt.
Bemerkung. Sei (e1 , . . . , er ) die Standardbasis in K r und A die durch (2.49) bzw. (2.19)
zugeordnete Matrix zu f = fA . Ersetzt man in der Definition 2.51 f durch A, erhält man
die Begriffe Eigenwert bzw. Eigenvektor einer Matrix.
2.6. EIGENWERTE UND DIAGONALISIERBARKEIT
125
Definition 2.52. Sei K = R oder C und V ein r-dimensionaler K-Vektorraum. Sei A eine
(r × r) Matrix. Eine Zahl λ ∈ K heißt Eigenwert von A, falls es ein x ∈ V \ {0} gibt mit
Ax = λx.
(2.53)
Jedes x ∈ V \ {0}, das (2.53) genügt, heißt Eigenvektor von A zum Eigenwert λ.
Wir führen jetzt den Begriff eines Eigenraumes und des Spektrums einer linearerAbbildung
ein.
Definition 2.53.
(i) Sei f wie in der Definition 2.51 gegeben und λ ∈ K ein Eigenwert von f . Der lineare
Teilraum
Eλ = {v ∈ V : f (v) = λv} = ker(f − λ id),
wobei id die identische Abbildung ist, id v = v, wird Eigenraum zum Eigenwert λ
genannt. Die Dimension des Eigenraums, dim Eλ , heißt geometrische Vielfachheit
des Eigenwertes λ.
(ii) Die Teilmenge
σ(f ) = {λ ∈ K : λ ist Eigenwert von f } ⊂ K
heißt Spektrum von f .
Diese Definitionen können auch auf Matrizen A, die durch lineare Abbildungen fA dargestellt werden, übertragen werden.
Für die Berechnung der Eigenwerte einer Matrix A ist folgender Satz grundlegend.
Theorem 2.54. Die Zahl λ ist genau dann Eigenwert von A, falls gilt
det(A − λE) = 0.
Beweis.
a) Es sei λ Eigenwert von A. Dann gibt es ein v 6= 0, so dass
Av − λv = (A − λE)v = 0
ist, d.h. ker(A − λE) 6= {0}, (A − λE) ist nicht invertierbar und aus Folgerung 2.43
erhalten wir
det(A − λE) = 0.
b) Es sei det(A − λE) = 0. Dann ist ker(A − λE) 6= {0} und es existiert ein v 6= 0, so
dass
Av = λv
ist.
126
KAPITEL 2. LINEARE ALGEBRA
Das charakteristische Polynom
Es ist


a11 − λ
a12
...
a1r
 a21
a22 − λ . . .
a2r 


det(A − λE) = det  ..
..
..
..  = P (λ),
 .
.
.
. 
ar1
...
arr−1 arr − λ
wobei P (λ) ein Polynom in λ ist. P (λ) wird charakteristisches Polynom genannt.
Damit ist λ genau dann ein Eigenwert von A, falls λ Nullstelle von P (λ) ist. Weiterhin
kann A (bzw. fA ) höchstens r Eigenwerte besitzen. Führen wir einen Basiswechsel durch,
so dass die Standardbasis im K r in eine Basis B aus r Eigenvektoren überführt wird,
B = {v 1 , . . . , vr }, dann wird die zugehörige Matrix AB nach (2.49) Diagonalform besitzen.
Dies wird später gezeigt und motiviert folgende Definition.
Definition 2.55. A (bzw. fA ) heißt diagonalisierbar, falls V = K r eine Basis besitzt, die
nur aus Eigenvektoren besteht.
Bemerkung: In Lemma 2.61 wird gezeigt: Ist A diagonalisierbar, dann existiert eine
Matrix H deren Spalten die Eigenvektoren sind, so dass


λ1
0


..
H −1AH = 

.
0
λr
ist. λ1 , . . . , λr sind die Eigenwerte von A.
Beispiele
0
0 1
. Die Abbildung Ax =
(i) Wir betrachten die Matrix A =
1
1 0
beschreibt die Spiegelung an der Diagonale in der x1 − x2 -Ebene.
−λ 1
= λ2 − 1 = 0,
det(A − λE) = det
1 −λ
x2
x1
1
=
x1
x2
0
Es ist
falls λ = ±1 ist.
Wir betrachten zunächst den Eigenwert λ1 = 1. Es ist
−1 1
x1
−x1 + x2
0
=
=
,
1 −1
x2
x1 − x2
0
1
ein Eigenvektor. Entsprechend gilt für den
falls x1 = x2 ist. Damit ist v 1 =
1
Eigenwert λ2 = −1
0
x1 + x2
x1
1 1
,
=
=
0
x1 + x2
x2
1 1
127
2.6. EIGENWERTE UND DIAGONALISIERBARKEIT
1
falls x1 = −x2 ist. Es folgt, dass v 2 =
ein Eigenvektor ist. Die Eigenvektoren
−1
v 1 und v 2 sind linear unabhängig. Man betrachte
1 1
det
= −2 6= 0.
1 −1
Führen wir im R2 die Basis B = {v 1 , v 2 } der Eigenvektoren ein, so erhalten wir nach
(2.49)
Av 1 =
B
v 1 = f (v 1 ) = aB
11 v 1 + a21 v 2
B
Av 2 = −v 2 = f (v 2 ) = aB
12 v 1 + a22 v 2 .
B
B
B
Da die Basisdarstellung eindeutig ist, ergibt sich aB
11 = 1, a21 = 0, a12 = 0, a22 = −1
und damit ist
1 0
.
A =
0 −1
B
0 1
. A beschreibt eine Spiegelung an der Achse x1 = x2 und eine
(ii) Es sei A =
0 0
anschließende Projektion auf die x1 -Achse:
x2
x1
0 1
.
=
Ax =
0
x2
0 0
Wir erhalten
−λ 1
det(A − λE) = det
= λ2 = 0,
0 −λ
falls λ = 0 ist. Wir bestimmen die zugehörigen Eigenvektoren. Es ist
x2
x1
0 1
= 0.
=
(A − 0λ)x =
0
x2
0 0
1
ein Eigenvektor, jedoch kann ein einzelner Eigenvektor keine Basis
Damit ist
0
im R2 bilden.
(iii) Wir sehen uns die Drehmatrix (Drehung um den Winkel φ) an:
cos φ − sin φ
.
A=
sin φ cos φ
Es ist
cos φ − λ − sin φ
det(A − λE) = det
sin φ
cos φ − λ
Die Wurzeln sind λ1,2
= (cos φ − λ)2 + (sin φ)2 = λ2 − 2λ cos φ + 1.
p
= cos φ ± −(sin φ)2 . Wir erhalten
128
KAPITEL 2. LINEARE ALGEBRA
– Für K = R:
Ist sin φ 6= 0, dann existiert kein reeller Eigenwert. Ist sin φ = 0, dann ist
A = ±E.
– Für K = C:
Es treten die Eigenwerte λ1,2 = cos φ ± i sin φ auf. Ist sin φ 6= 0, dann sind sie
voneinander verschieden. Wir bestimmen in diesem Fall die komplexen Eigenvektoren.
Für λ1 = cos φ + i sin φ muss gelten
− i sin φ − sin φ
z1
0
=
.
sin φ
− i sin φ
z2
0
Damit erhalten wir für z1 = a1 + i b1 , z2 = a2 + i b2 :
− sin φ(i z1 + z2 ) = 0,
sin φ(z1 − i z2 ) = 0,
woraus
a1 + i b1 − i(a2 + i b2 ) = 0,
a1 + b2 = 0,
b1 − a2 = 0
1+i
folgt. Damit ist v 1 =
ein Eigenvektor.
1−i
Für λ2 = cos φ − i sin φ muss gelten
0
z1
i sin φ − sin φ
.
=
0
z2
sin φ i sin φ
und analog zu oben erhalten wir, dass
1+i
v2 =
−1 + i
ein entsprechender Eigenvektor ist.
Bemerkung: Die lineare Abbildung f bzw. die Matrix A bilden Eigenräume in sich ab.
2.6. EIGENWERTE UND DIAGONALISIERBARKEIT
129
Diagonalisierbarkeit
Wir müssen also die Fragen nach der Existenz einer Basis, die nur aus Eigenvektoren
besteht, diskutieren. Wir sehen uns zunächst die lineare Unabhängigkeit von Eigenvektoren
an, die zu verschiedenen Eigenwerten gehören.
Theorem 2.56. Sei V ein K-Vektorraum, f : V → V . Seien λ1 , . . . , λk ∈ K verschiedene
Eigenwerte zu f , v 1 , . . . , v k dazugehörige Eigenvektoren. Dann sind {v 1 , . . . , v k } linear
unabhängig.
Beweis. Der Beweis erfolgt durch eine vollständige Induktion nach k ∈ N:
1. Es sei k = 1. Dann ist v 1 6= 0 und die Menge {v 1 } besteht aus linear unabhängigen
Vektoren (Induktionsanfang).
2. Die Aussage gelte für (k − 1) verschiedene Eigenwerte (Induktionsannahme).
3. Wir zeigen, die Aussage gilt für k verschiedene Eigenwerte (Induktionsschritt).
Wären {v 1 , . . . , v k } linear abhängig, dann lässt sich einer der Vektoren, sagen wir
v 1 , durch die anderen ausdrücken
v 1 = µ2 v 2 + · · · + µk v k ,
µi ∈ K.
(2.54)
Wir betrachten die Eigenwertgleichung:
λ1 v 1 = λ1 µ2 v 2 +· · ·+λ1µk v k = f (v 1 ) = f (µ2 v 2 +· · ·+µk v k ) = µ2 λ2 v 2 +· · ·+µk λk v k .
Daraus folgt
0 = µ2 (λ2 − λ1 )v 2 + · · · + µk (λk − λ1 )v k .
Aus der Induktionsannahme erhalten wir, dass gilt
µi (λi − λ1 ) = 0 für i = 2, . . . , k.
Da λi 6= λj ist, muss µi = 0 für i = 2, . . . , k sein. Der Eigenvektor v 1 ist durch (2.54)
gegeben und daher muss er der Nullvektor sein, was nicht sein kann.
Conclusion 2.57. Sei V endlichdimensional, dim V = r, f : V → V eine lineare Abbildung.
Besitzt f (bzw. fA ) r verschiedene Eigenwerte, d.h. σ(f ) = {λ1 , . . . , λr }, dann ist f bzw.
die zu fA gehörige Matrix A diagonalisierbar. In diesem Fall ist dim(Eλi ) = 1, i = 1, . . . , r.
Die Matrix im Beispiel (i) S. 118 ist damit diagonalisierbar.
Ist die Anzahl verschiedener Eigenwerte kleiner als r, dann kann die Diagonalisierbarkeit
bei genügender Anzahl von Eigenvektoren ebenfalls garantiert werden. Es gilt offensichtlich:
Theorem 2.58. Folgende Aussagen sind äquivalent.
1. fA bzw. A seien diagonalisierbar.
Pk
2.
i=1 dim(Eλi ) = r, wobei λ1 , . . . , λk , k ≤ r, verschiedene Eigenwerte sind.
130
KAPITEL 2. LINEARE ALGEBRA
Diagonalisierbarkeit und charakteristisches Polynom
Wir charakterisieren nun die Diagonalisierbarkeit mit Hilfe des charakteristischen Polynoms
P (λ) = det(A − λE).
Jede Nullstelle von P (λ) ist Eigenwert von A. Wir wissen, dass auch mehrfache Nullstellen
auftreten können.
Definition 2.59. Es sei
P (λ) = det(A − λE) = (λ1 − λ)n1 · · · · · (λk − λ)nk ,
d.h. die Nullstelle λi besitze die Vielfachheit ni . Die Zahl ni heißt algebraische Vielfachheit
des Eigenwertes λi .
Theorem 2.60. [?, S.235] Sei f : V = K r → V = K r eine lineare Abbildung. Folgende
Aussagen sind äquivalent:
(i) fA (bzw. A) ist diagonalisierbar.
(ii) P (λ) zerfällt über K in Linearfaktoren (es treten nicht notwendig r verschiedene
Nullstellen = Eigenwerte auf, siehe oben). Für jede Nullstelle λi gilt, dass die geometrische Vielfachheit (dim(Eλi )) mit der algebraischen Vielfachheit von λi übereinstimmt, i = 1, 2, . . . , k.
Beweis. Hier wird nur eine Skizze des Beweises angegeben.
• Es wird benutzt, dass für einen Eigenwert λ gilt
geometrische Vielfachheit von λ ≤ algebraische Vielfachheit von λ.
• Außerdem besagt, der Fundamentalsatz der Algebra, dass für K = C gilt
k
X
algebraische Vielfachheit (λi ) = r.
i=1
Diagonalisierung
Wir beschreiben jetzt den Prozess, wie man Matrizen diagonalisiert.
1.Schritt:
Berechnung der Eigenwerte λi , i = 1, 2, . . . , k, der Matrix A durch Bestimmen der Nullstellen des charakteristischen Polynoms P (λ) = det(A − λE) = 0.
131
2.6. EIGENWERTE UND DIAGONALISIERBARKEIT
2.Schritt:
Berechnung zugehöriger Eigenvektoren v i durch Lösung der Gleichungssysteme
(A − λi E)v i = 0.
Beachte, dass die v i nicht eindeutig bestimmt sind.
3.Schritt:
Prüfen, ob
4.Schritt:
Pk
i=1
dim(Eλi ) = r ist.
Bilde


AB = H −1 AH = D = 
λ1
0
..
.
0
λr


,
(2.55)
wobei die Matrix H als Spaltenvektoren die Eigenvektoren besitzt und die Eigenwerte λi
einfach oder mehrfach, gemäß ihrer geometrischen Vielfachheit, auftreten.
Wir erläutern den Schritt 4:
Wir nummerieren die verschiedenen Eigenpaare in der Form (λ1 , v 1 ), . . . , (λk , v k ), wobei
nicht alle λi verschieden sein müssen. Die Menge B = {v 1 , . . . , v r } der Eigenvektoren ist
die gewünschte Basis, in der AB Diagonalform besitzt. Wir überzeugen uns davon:
Die Koordinatentransformation von der Standardbasis {e1 , . . . , er } in die Basis B = {v1 , . . . , v r }
wird nach (2.22) durch die Matrix HB2 = HB = H, deren Spalten die Eigenvektoren
v 1 , . . . , v r sind, realisiert. Insbesondere ist v i = Hei .
Lemma 2.61. Es ist


λ1
0


..
AB = H −1AH = D = 
.
.
0
λr
(2.56)
Beweis. Die Eigenwertgleichung liefert
Av i = λi v i ,
i = 1, 2, . . . , r.
Die v i lassen sich darstellen als v i = Hei . Wir setzen v i in (2.57) ein und erhalten:
AHei = λi Hei = Hλiei .
Daraus folgt
H −1 AHei = λi ei ,
H −1AH = D.
(2.57)
132
KAPITEL 2. LINEARE ALGEBRA
Mit Hilfe der Beziehung (2.49) folgt AB = D. Es ist nämlich
fA (v j ) = Av j =
r
X
aB
ij v j = λj v j ,
j = 1, . . . , r.
i=1
Da die Koordinatendarstellung bezüglich der Basis {v 1 , . . . , v r } eindeutig ist, folgt
(
0 für i =
6 j,
aB
ij =
λj für i = j.
Wir erhalten, dass AB = (aB
ij ) 1≤i≤r = D ist.
1≤j≤r
Remark 2.62. Die Gleichung (2.56) kann auch durch direktes Nachrechnen von
AH = HD
unter Beachtung von (2.57) verifiziert werden.
Jordansche Normalform
Wie wir im Beispiel (ii) im letzten Abschnitt gesehen haben, kann es durchaus sein, dass
nicht genügend viele Eigenvektoren existieren, d.h.
geometrische Vielfachheit von λ < algebraische Vielfachheit von λ.
In diesem Fall ist fA nicht diagonalisierbar. Trotzdem kann man in diesem Fall noch eine Jordansche Normalform von fA bzw. der Matrix A konstruieren, in der anstelle der
Diagonalelemente einfache Blockmatrizen (Jordan-Matrizen) treten.
Definition 2.63. Sei λ ∈ K. Die (j × j) Matrix
heißt Jordan-Matrix.

λ
0
.

Jj (λ) =  ..
.
 ..
0

1 0 ... 0
λ 1 . . . 0
.. . . . . .. 
.
. .
.


..
..
. 1
.
0 0 ... λ
2.6. EIGENWERTE UND DIAGONALISIERBARKEIT
133
Theorem 2.64. [4, S. 268] Sei f = fA : V = K r → V = K r , fA (x) = Ax eine lineare
Abbildung deren charakteristisches Polynom in Faktoren zerfällt,
P (λ) = det(A − λE) = (λ1 − λ)n1 · · · · · (λk − λ)nk ,
wobei λ1 , . . . , λk verschiedene Eigenwerte von fA bzw. A sind. Dann gibt es eine Basis B
in K r in der die zu f gehörige Matrix AB die Form


Jn11 (λ1 ) . . .
...
...
...
...
0


..
..
..


.
.
.


.
.


..
..
Jn1l1 (λ1 )




.
.
..


.
.
(2.58)
.
.
.




.
.
..
..


Jnk1 (λk )




..
..
..
.


.
.
0
...
...
...
...
. . . Jnklk (λk )
Pi
nij = ni , i = 1, . . . , k, n1 + n2 + · · · + nk = r und die Anzahl li der
besitzt. Dabei ist lj=1
Jordanblöcke zum Eigenwert λi ist gleich seiner geometrischen Vielfachheit.
Bemerkungen: Die Jordanformen AB sind nicht eindeutig bestimmt, da die Reihenfolge
der Eigenwerte und die Anordnung der Jordanblöcke nicht festgelegt wurde. Ausserdem ist
die Kenntnis der geometrischen und algebraischen Vielfachheiten nicht immer ausreichend,
um die Jordanform zu beschreiben. Man betrachte z.B. eine 4 × 4 Matrix, die nur einen
Eigenwert mit der geometrischen Vielfachheit 2 besitzt.
Sind alle Jordan-Matrizen eindimensional, dann hat A Diagonalform.
Ist z.B. r = 2 und liegt nur ein Eigenwert λ1 vor, dann gibt es zwei Fälle:
• Ist die geometrische Vielfachheit von λ1 gleich 2, dann treten zwei 1 × 1 Jordanblöcke
auf und AB besitzt Diagonalform.
• Ist die geometrische Vielfachheit von λ1 gleich 1, dann tritt ein 2 × 2 Jordanblock
auf und AB besitzt (echte) Jordanform.
Beispiele
0 1
. A besitzt einen Eigen1. Im Beispiel (ii) des vorherigen Abschnittes war A =
0 0
wert λ1 = 0 mit geometrischer Vielfachheit 1 und algebraischer Vielfachheit 2. Daher
ist A nicht diagonalisierbar. In diesem speziellen Fall existiert eine Jordanform AB ,
die mit A übereinstimmt.
2. Wir betrachten die Matrix


0 1 3
A =  0 0 0 .
0 5 1
134
KAPITEL 2. LINEARE ALGEBRA
Es ist


−λ 1
3
0  = (1 − λ)λ2 ,
det(A − λE) = det  0 −λ
0
5 1−λ
d.h. n1 = 1, n2 = 2.
Die Eigenwerte sind λ1 = 1 und λ2 = 0. Wir betrachten zunächst den Eigenwert
λ1 = 1 und berechnen dazu einen Eigenvektor v 1 = (x1 , x2 , x3 )⊤ :

    

−1 1 3
x1
0
−x1 + x2 + 3x3
,
−x2
(A − E)v 1 =  0 −1 0 x2  = 0 = 
0
5 0
x3
0
5x2
woraus z.B. folgt
Wir erhalten
 
3

v 1 = 0 .
1
dim(Eλ1 ) = 1 = n1 .
Nun sehen wir uns den Eigenwert λ2 = 0 an und berechnen Eigenvektoren aus

    

0 1 3
x1
0
x2 + 3x3
.
0
(A − 0E)v 2 = 0 0 0 x2  = 0 = 
0 5 1
x3
0
5x2 + x3
 
1

Damit ist 0 = v 2 ein Eigenvektor und dim(Eλ2 ) = 1 < n2 .
0
Die Matrix A ist daher nicht diagonalisierbar. Da n11 = 1 und n21 = 2 ist ihre
Jordansche Normalform


1 0 0
AB = 0 0 1 .
(2.59)
0 0 0
 
3
Wir beschreiben eine Basis, in der AB gegeben ist. Zu den Eigenvektoren v 1 = 0
1
 
1
und v 2 = 0 ist ein weiterer Basisvektor v 3 zu konstruieren. Dazu sehen wir uns
0
die Gleichungen (2.49) und (2.50) an. Es soll gelten:
B
B
fA (v 3 ) = Av 3 = aB
13 v 1 + a23 v 2 + a33 v 3
= 0v 1 + 1v 2 + 0v 3
2.6. EIGENWERTE UND DIAGONALISIERBARKEIT
und damit
Wir erhalten
135

 
  

0 1 3
v3,1
1
v3,2 + 3v3,3
0 0 0 v3,2  = 1v 2 = 0 = 
.
0
0 5 1
v3,3
0
5v3,2 + v3,3

0

1 
.
v 3 =  − 14
5
14
Eine Basis in der A eine Jordan-Normalform AB besitzt, lautet
    

1
0 
 3
1 
.
B = 0 , 0 ,  − 14


5
1
0
14
3. Die (6 × 6)-Matrix A besitze zwei 3-fache Eigenwerte λ1 = 1 und λ2 = 2. Es sei
dim Eλ1 = 2 und dim Eλ2 = 1. Dann lautet eine Jordansche Normalform von A:


1 0 0 0 0 0
0 1 1 0 0 0


0 0 1 0 0 0


0 0 0 2 1 0 .


0 0 0 0 2 1
0 0 0 0 0 2
In diesem Fall ist in (2.58) n11 = 1, n12 = 2 und n21 = 3.
Remark 2.65. Der Algorithmus, der im 2. Beispiel zur Bestimmung des fehlenden Basisvektors v 3 geführt hat, kann allgemein beschrieben werden. Hier betrachten wir folgenden
Fall: Sei fA eine gegebene lineare Abbildung von V = K k in V = K k ,


λ 1
0
 .. . . . . . . .. 
.
.
B
A = .
(2.60)

.
. . 1
 ..
0
λ
ein k × k Jordanblock zum Eigenwert λ mit dim Eλ = 1. v 1 ∈ Eλ sei ein bekannter
Eigenvektor zu λ. Die restlichen k − 1 Basisvektoren v 2 , . . . , v k können Schritt für Schritt
aus folgenden Gleichungssystemen bestimmt werden, indem (2.49) und (2.60) verwendet
werden:
k
X
2. Spalte von (2.60)
fA (v 2 ) = Av 2 =
aB
=
1v 1 + λv 2 .
ij v i
i=1
Damit ist das Gleichungssystem
(A − λE)v 2 = v 1
(2.61)
136
KAPITEL 2. LINEARE ALGEBRA
zu lösen. Nehmen wir an, dass v 1 , . . . , v j−1 bekannt seien. Dann gilt für v j
fA (v j ) = Av j =
k
X
aB
ij v i
j−Spalte von (2.60)
=
v j−1 + λv j
i=1
und daraus folgt
(A − λ)v j = v j−1 .
Übungsaufgaben
Aufgabe 9.1
Bestimmen Sie die Eigenwerte und Eigenvektoren der Matrix


3 −1 −1
A =  −1
3
1 
−1
1
5
und transformieren Sie A auf Diagonalform.
Aufgabe 9.2
Die symmetrische Matrix A habe die Eigenwerte
λ1 = 1,
λ2 = −1,
λ3 = 2
und die dazugehörigen Eigenvektoren
 
 
 
1
1
−1
v1 =  0  , v2 = 1 , v3 =  2  .
−1
1
−1
a) Berechnen Sie A.
b) Berechnen Sie A−1 , det(A), Rang(A).
c) Lösen Sie Ax = (0, 1, 0)⊤ .
Aufgabe 9.3
Bestimmen Sie die

6
A= 8
2
Jordan–Normalformen JA ,


−2 3
3
−2 15  ,
B= 2
4
−1 8
JB und JC für die Matrizen



1 1 1
2 4
0 2 
und
C= 0 1 1 .
0 0 1
2 3
Aufgabe 9.4
Die Matrix A ∈ C4×4 besitze genau zwei Eigenwerte, λ und µ.
Geben Sie alle Matrizen an, die als Jordansche Normalform von A in Frage kommen. Läßt sich die
Jordansche Normalform von A allein mit Hilfe der algebraischen und geometrischen Vielfachheiten der
Eigenwerte bestimmen?
137
2.6. EIGENWERTE UND DIAGONALISIERBARKEIT
Aufgabe 9.5
Berechnen Sie für die Matrix

2
 0
A=
 0
0

0 1−α 1−α
2 α−1 α−1 
,
0 α2 + 4 α2 − 4 
0 α2 − 4 α2 + 4
α ∈ R.
die Eigenwerte in Abhängigkeit von α und geben Sie an, für welche α die Matrix diagonalisierbar ist.
138
2.7
KAPITEL 2. LINEARE ALGEBRA
Skalarprodukt
Wir betrachten in diesem Abschnitt abstrakte Vektorräume, die in Abschnitt 2.1 eingeführt wurden. Sie können endlich oder unendlichdimensional sein, ihre Elemente können
z.B. Zahlentupel, Abbildungen oder Funktionen sein. In Vektorräumen mit Skalarprodukt
können geometrische Größen, wie Betrag und Winkel eingeführt werden, wie sie in endlichdimensionalen Vektorräumen bekannt sind. Damit ist auch der Begriff der Orthogonalität
zweier Elemente eines abstrakt definierten Vektorraumes V wohldefiniert.
Definition 2.66. Es sei V ein K-Vektorraum, K = R oder K = C. Eine Abbildung
V × V → K,
(x, y) → hx, yi,
heißt Skalarprodukt auf V , falls die folgenden Eigenschaften für alle x, y, z ∈ V, α, β ∈ K
gelten:
(S1) hx, xi ≥ 0,
hx, xi = 0 ⇔ x = 0,
(S2) hx, yi = hy, xi für K = R
hx, yi = hy, xi für K = C,
(S3) hαx + βy, zi = αhx, zi + βhy, zi.
Aus diesen Eigenschaften folgt:
• hx, αyi = ᾱhx, yi,
• hx, y + zi = hx, yi + hx, zi.
Beispiele
(i) Die Standard-Skalarprodukte auf Rn oder Cn sind:
   
x1
y1
n
X
 ..   .. 
hx, yiRn = h .  ,  . i =
xi yi ,
i=1
xn
yn
   
w1
z1
n
X
 ..   .. 
zi w̄i .
hz, wiCn = h .  ,  . i =
i=1
wn
zn
(ii) Wir betrachten im Rn ein weiteres Skalarprodukt hx, yiA = hAx, yiRn , wobei A eine
Diagonalmatrix mit positiven Einträgen (aii > 0, i = 1, . . . , n) ist. Wir überprüfen
die Eigenschaften (S1), (S2) und (S3):
P
(S1) Es gilt hx, xiA = ni=1 aii x2i ≥ 0 und hx, xiA = 0 ⇔ x = 0.
139
2.7. SKALARPRODUKT
(S2) Es gilt hx, yiA =
(S3) Es gilt:
Pn
i=1
aii xi yi = hy, xiA =
Pn
hαx + βy, ziA = hA(αx + βy), zi
=α
n
X
aii xi zi + β
i=1
aii yi xi .
i=1
Rn
=
n
X
aii (αxi + βyi)zi
i=1
n
X
aii yi zi
i=1
= αhx, ziA + βhy, ziA .
(iii) Sei V := {f : [a, b] → C, f ist stetig}. Durch
Z b
hf, gi =
f (x)ḡ(x)dx
a
ist ein Skalarprodukt definiert.
Aus den Eigenschaften (S1), (S2) und (S3) kann man eine wichtige Abschätzung folgern,
die Cauchy-Schwarzsche Ungleichung:
Theorem 2.67. In einem K-Vektorraum, K = R oder K = C, mit einem Skalarprodukt
gilt die Abschätzung
p
p
(2.62)
|hx, yi| ≤ hx, xi hy, yi.
Beweis. Es ist im C-Vektorraum für einen Wert λ ∈ C
hx + λy, x + λyi = hx, xi + λhy, xi + λ̄hx, yi + |λ|2 hy, yi ≥ 0.
(2.63)
in (2.63). Wir
Wir nehmen an, dass y 6= 0 sei, also hy, yi > 0 ist und wählen λ = − hx,yi
hy,yi
erhalten
hx, yihy, xi hy, xihx, yi |hx, yi|2
−
+
hy, yi ≥ 0,
hx, xi −
hy, yi
hy, yi
hy, yi2
woraus
hx, xihy, yi ≥ |hx, yi|2
und schließlich (2.62) folgt.
Norm (Betrag)
Nun sind wir in der Lage, die Länge (Betrag) eines Elements im abstrakten Vektorraum
V mit Skalarprodukt zu definieren.
Theorem 2.68. Sei V ein K-Vektorraum, K = R oder K = C, mit Skalarprodukt. Dann
ist für jedes Element x ∈ V eine Norm (Betrag)
p
kxk = hx, xi
definiert, die folgende Eigenschaften für alle x, y ∈ V, α ∈ K besitzt:
140
(N1) kxk ≥ 0,
KAPITEL 2. LINEARE ALGEBRA
kxk = 0 ⇔ x = 0,
(N2) kαxk = |α|kxk,
(N3) kx + yk ≤ kxk + kyk.
Beweis. (N1) und (N2) sind offensichtlich und wir sehen uns nur die Dreiecksungleichung
(N3) an:
kx + yk2 = |hx + y, x + yi| = |hx, xi + hy, xi + hx, yi + hy, yi|
(2.62)
≤ kxk2 + 2kykkxk + kyk2 = (kxk + kyk)2 .
Remark 2.69. Ein K-Vektorraum, in dem eine Abbildung k · k : V → R definiert ist, die
den Axiomen (N1), (N2) und (N3) genügt, heißt normierter Raum.
Winkel und Orthogonalität
Wir können auch einen Winkel φ ∈ [0, π] zwischen zwei Elementen x 6= 0 und y 6= 0 in
einem abstrakten Vektorraum V mit Skalarprodukt einführen:
hx, yi
cos φ =
.
(2.64)
kxkkyk
(2.62)
|hx,yi|
≤ 1, ist diese Definition sinnvoll. Aus der Beziehung (2.64) folgt
Da cos φ = kxkkyk
unmittelbar die Erklärung, wann zwei Elemente x und y zueinander orthogonal sind.
Definition 2.70. Zwei Elemente x und y aus einem K-Vektorraum, K = R oder K = C,
sind orthogonal (x⊥y), falls gilt
hx, yi = 0.
Conclusion 2.71. Nur das Nullelement ist orthogonal zu allen Elementen aus V .
Definition 2.72. Eine Menge von Elementen (vi )i∈I ⊆ V mit vi 6= 0 heißt Orthogonalsystem, falls vi ⊥vj für i 6= j ist. Wir sprechen von einem Orthonormalsystem, falls
(
0 für i 6= j,
hvi , vj i = δij =
1 für i = j
ist. Ist ein Orthonormalsystem Basis in V , so sprechen wir von einer Orthonormalbasis.
Remark 2.73.
• Es gilt der verallgemeinerte Satz vom Pythagoras für ein Orthogonalsystem aus n
Elementen:
kx1 + · · · + xn k2 = kx1 k2 + · · · + kxn k2 .
• Ein Orthogonalsystem besteht aus linear unabhängigen Vektoren. Ein System aus
linear unabhängigen Vektoren, kann orthonormiert werden (Gram-Schmidtsches Orthogonalisierungsverfahren, siehe Übungsaufgabe 10.3).
141
2.7. SKALARPRODUKT
Lineare orthogonale Abbildungen (orthogonale Matrizen)
Wir charakterisieren lineare Abbildung (Matrizen) eines abstrakten Vektorraumes V in
V , die sich aus Spiegelungen und Drehungen zusammensetzen. Es sollen also Winkel und
Beträge erhalten bleiben.
Definition 2.74. Sei V ein K-Vektorraum, K = R oder K = C, mit Skalarprodukt. Eine
lineare Abbildung f : V → V , heißt orthogonal, falls für alle v und w aus V gilt
hv, wi = hf (v), f (w)i.
(2.65)
Conclusion 2.75. Es ist für alle v aus V für eine orthogonale Abbildung f
kvk = kf (v)k.
Der Winkel zwischen zwei Elementen v und w ∈ V bleibt erhalten:
Winkel zwischen v und w = Winkel zwischen f (v) und f (w).
Weiterhin ist eine orthogonale Abbildung injektiv.
Endlichdimensionale Vektorräume und orthogonale Matrizen
Wir betrachten jetzt endlichdimensionale Vektorräume V , dim V = r, mit Skalarprodukt.
In V sei eine Orthonormalbasis, B = {v 1 , . . . , v r }, gegeben:
hv i , v j i = δij
i, j = 1, . . . , r.
Wir wissen, dass eine lineare Abbildung f durch eine Matrix A bezüglich dieser Basis
dargestellt werden kann (vergleiche dazu (2.49), (2.50)). Wir charakterisieren die Matrizen,
die zu linearen orthogonalen Abbildungen gehören.
Lemma 2.76. Sei V = Rr ein Vektorraum mit Skalarprodukt und orthogonaler Basis.
Matrizen A, die zu linearen orthogonalen Abbildungen fA : V → V , fA (x) = Ax, gehören,
haben die Eigenschaft, dass
A⊤ = A−1
ist. Solche Matrizen heißen orthogonale Matrizen.
Beweis. Für eine orthogonale Basis {v 1 , . . . , v r } gilt:
hx, yi = h
Daher ist
r
X
i=1
(2.65)
xi v i ,
r
X
j=1
yj v j i =
r
X
i=1
xi yi = x⊤ y
für alle x, y ∈ V.
hx, yi = hAx, Ayi = (Ax)⊤ Ay = x⊤ A⊤ Ay = hx, A⊤ Ayi.
142
KAPITEL 2. LINEARE ALGEBRA
Es folgt, dass
hx, (A⊤ A − E)yi = 0 für alle x und y aus V ist,
und daher muss nach Folgerung 2.71
A⊤ A = E
(2.66)
sein. Wir müssen noch zeigen, dass AA⊤ = E ist.
Da V endlichdimensional ist und eine orthogonale Abbildung stets injektiv ist, liegt in
diesem Fall eine bijektive Abbildung vor und A−1 existiert. Für A−1 gilt
hA−1 z, A−1 wi = hAA−1 z, AA−1 wi = hz, wi für alle z, w ∈ V,
(2.67)
d.h. A−1 ist ebenfalls eine orthogonale Matrix. Jetzt können wir zeigen, dass auch A⊤ diese
Eigenschaft besitzt. Seien x und y beliebig aus V . Es existieren z und w aus V , so dass
x = Az, y = Aw sind. Wir erhalten
(2.66)
(2.67)
hA⊤ x, A⊤ yi = hA⊤ Az, A⊤ Awi = hz, wi = hA−1 x, A−1 yi = hx, yi.
Da
hA⊤ x, A⊤ yi = (A⊤ x)⊤ A⊤ y = x⊤ AA⊤ y = hx, AA⊤ yi = hx, yi
ist, gilt
AA⊤ = E
und zusammen mit (2.66) folgt A⊤ = A−1 .
Conclusion 2.77. Spalten und Zeilen einer orthogonalen Matrix sind jeweils orthonormale
Systeme.
Remark 2.78. Liegt ein C-Vektorraum vor, dann spricht man von unitären Matrizen, falls
A−1 = Ā⊤
ist.
Beispiele
• Für jedes α ∈ R sei
cos α − sin α
A(α) =
.
sin α cos α
A(α) beschreibt bezüglich der Standardbasis im R2 eine Drehung um den Winkel α.
Es ist
cos α sin α
⊤
A (α) =
− sin α cos α
und
1 0
A (α)A(α) =
.
0 1
⊤
143
2.7. SKALARPRODUKT
• Die Matrix
cos α sin α
B(α) =
sin α − cos α
ist ebenfalls orthogonal. Sie stellt eine Drehspiegelung dar. Es ist
sin α
0
cos α
1
.
=
, B(α)
=
B(α)
− cos α
1
sin α
0
Hauptachsentransformation
Wir hatten bereits gesehen, siehe (2.56), falls eine (r × r)-Matrix r Eigenvektoren besitzt,
dann können wir A diagonalisieren, indem wir


λ1 0 . . . 0
 0 λ2 . . . 0 


H −1AH = D =  ..
..  ,
..
.
. .
0 . . . . . . λr
bilden. Die Zahlen λi sind die Eigenwerte von A und H besitzt die Eigenvektoren als
Spaltenvektoren. Betrachten wir ein orthonormales System von Eigenvektoren, dann ist
H −1 = H ⊤ und
H ⊤ AH = D.
Diese Transformation wird auch Hauptachsentransformation genannt.
Übungsaufgaben
Aufgabe 10.1
Für welche Werte λ und µ in R ist hx, yiA = hAx, yiR2 mit
1 λ
A=
µ 1
ein Skalarprodukt auf R2 ?
Aufgabe 10.2
Zeigen Sie:
a) | ka − ck − kb − ck |≤ ka − bk
b) | ka − bk − kc − dk |≤ ka − ck + kb − dk
Aufgabe 10.3
Schmidt’sches Orthonormalisierungsverfahren.
Zu jeder Menge linear unabhängiger Vektoren {v1 , . . . , vn } gibt es ein Orthonormalsystem {w1 , . . . , wn }
mit
Span{v1 , . . . , vk } = Span{w1 , . . . , wk } ,
für alle 1 ≤ k ≤ n
144
KAPITEL 2. LINEARE ALGEBRA
Man beweist diese Aussage mit Induktion über n:
Ist n = 1, so ist
v1
w1 =
kv1 k
ein Orthonormalsystem mit Span{v1 } = Span{w1 }.
Für n = 2 setzt man w̃2 = v2 + αw1 und bestimmt α so, dass w̃2 ⊥ w1 :
0 = hw̃2 , w1 i = hv2 , w1 i + αhw1 , w1 i
Es ergibt sich also α = −hv2 , w1 i und somit w̃2 = v2 − hv2 , w1 iw1 6= 0, da {v2 , w1 } linear unabhängig
ist. Es ist also
w̃2
w2 =
kw̃2 k
der gesuchte Vektor.
a) Vollenden Sie den Beweis.
b) Wenden Sie das Schmidt’sche Orthonormalisierungsverfahren auf den Unterraum
 
 
 
1
2
2






1
6 , a3 = 9
,
a
=
Span{a1 , a2 , a3 } ⊂ R4 mit a1 = 
2
5
4
0
8
4
2
bezüglich des Standard-Skalarprodukts an.
Aufgabe 10.4
Gegeben sind die Vektoren


3
a =  −2  ,
1


2
b =  2 ,
−2


1
c =  c2 
c3
und


3
x =  −18  .
−3
a) Bestimmen Sie c2 , c3 ∈ R so, dass a, b, c ein orthogonales System bilden.
b) Berechnen Sie mit Hilfe des Skalarprodukts die Koeffizienten α, β, γ der Linearkombination
x = αa + βb + γc.
Hinweis: Betrachten Sie in b) die Skalarprodukte hx, ai, hx, bi und hx, ci .
Aufgabe 10.5
Gegeben seien die Vektoren


1
a= 2 
3


−2
und b =  3  .
1
a) Bestimmen Sie den Winkel α ∈ [0, π] zwischen den beiden Vektoren.
b) Bestimmen Sie einen zu a orthogonalen Vektor c, so dass a und c dieselbe Ebene wie a und b
aufspannen.
c) Ergänzen Sie {a, c } zu einer orthogonalen Basis {a, c, d} des R3 .
Literaturverzeichnis
[1] Beyer, Gottwald, Günther und Wünsch. Grundkurs Analysis vol.1
Teubner Verlag, Leipzig, 1972.
[2] Brieskorn, E.. Lineare Algebra und analytische Geometrie. Vieweg Verlag, 1983.
[3] Brill, M. Mathematik für Informatiker. Hanser-Verlag, 2001.
[4] Fischer, G. Lineare Algebra. Vieweg Verlag, 2002.
[5] Hartmann, P. Mathematik für Informatiker. Vieweg Verlag, 2002.
[6] Burg, K., Haf, H. Höhere Mathematik für Ingenieure, vol. I und II.
Teubner Verlag, 2001, 2002.
[7] Mayberg, K., Vachenauer, P. Höhere Mathematik I. Springer-Verlag, 2001.
[8] Pareigis, B. Lineare Algebra für Informatiker. Springer-Verlag, 2000.
[9] Tarski, A. Der Wahrheitsbegriff in den formalisierten Sprachen Studia philosophika
vol. 1 (1936), pp. 261-405, polnisches Original 1933.
145