Musterbeispiele zur Prozentrechnung
Werbung
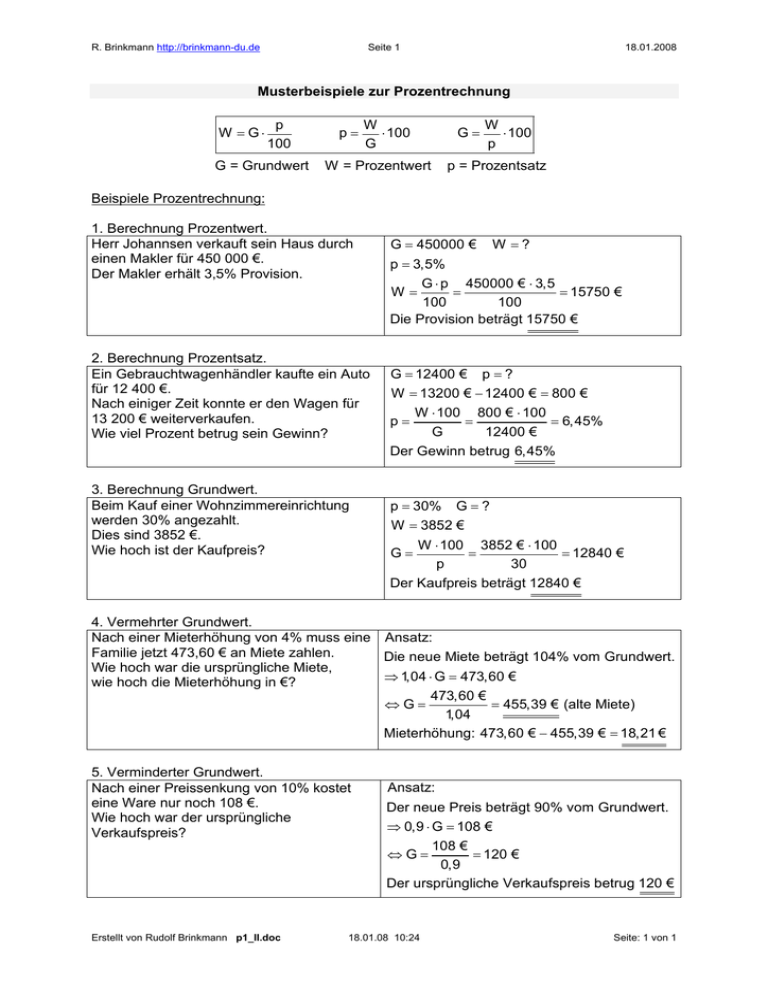
R. Brinkmann http://brinkmann-du.de Seite 1 18.01.2008 Musterbeispiele zur Prozentrechnung W = G⋅ p 100 G = Grundwert p= W ⋅ 100 G W = Prozentwert G= W ⋅ 100 p p = Prozentsatz Beispiele Prozentrechnung: 1. Berechnung Prozentwert. Herr Johannsen verkauft sein Haus durch einen Makler für 450 000 €. Der Makler erhält 3,5% Provision. 2. Berechnung Prozentsatz. Ein Gebrauchtwagenhändler kaufte ein Auto für 12 400 €. Nach einiger Zeit konnte er den Wagen für 13 200 € weiterverkaufen. Wie viel Prozent betrug sein Gewinn? 3. Berechnung Grundwert. Beim Kauf einer Wohnzimmereinrichtung werden 30% angezahlt. Dies sind 3852 €. Wie hoch ist der Kaufpreis? G = 450000 € W =? p = 3,5% G ⋅ p 450000 € ⋅ 3,5 W= = = 15750 € 100 100 Die Provision beträgt 15750 € G = 12400 € p = ? W = 13200 € − 12400 € = 800 € W ⋅ 100 800 € ⋅ 100 p= = = 6,45% G 12400 € Der Gewinn betrug 6,45% p = 30% G=? W = 3852 € W ⋅ 100 3852 € ⋅ 100 = = 12840 € p 30 Der Kaufpreis beträgt 12840 € G= 4. Vermehrter Grundwert. Nach einer Mieterhöhung von 4% muss eine Ansatz: Familie jetzt 473,60 € an Miete zahlen. Die neue Miete beträgt 104% vom Grundwert. Wie hoch war die ursprüngliche Miete, ⇒ 1,04 ⋅ G = 473,60 € wie hoch die Mieterhöhung in €? 473,60 € ⇔G= = 455,39 € (alte Miete) 1,04 Mieterhöhung: 473,60 € − 455,39 € = 18,21 € 5. Verminderter Grundwert. Nach einer Preissenkung von 10% kostet eine Ware nur noch 108 €. Wie hoch war der ursprüngliche Verkaufspreis? Ansatz: Der neue Preis beträgt 90% vom Grundwert. ⇒ 0,9 ⋅ G = 108 € 108 € = 120 € 0,9 Der ursprüngliche Verkaufspreis betrug 120 € ⇔G= Erstellt von Rudolf Brinkmann p1_II.doc 18.01.08 10:24 Seite: 1 von 1 R. Brinkmann http://brinkmann-du.de Arbeitsblatt I Seite 2 18.01.2008 Prozentrechnung 1. In einer Klasse sind 17 Jungen und 8 Mädchen. Wie viel Prozent Jungen bzw. Mädchen sind in der Klasse? 2. Der Listenpreis eines Autos beträgt 23925 €. Der Kunde bekommt den Wagen für 21054 €. Um wie viel Prozent liegt dieser Preis unter dem Listenpreis? 3. Der Kauf eines Autos verteuert sich um 1920,45 €, da die Bezahlung in Raten erfolgt. Wie hoch war der ursprüngliche Preis des Autos, wenn die Verteuerung 10,5% beträgt? 4. Ein Auto verbraucht auf 400 km 47 Liter Benzin, ein anderes Auto verbraucht 65,8 Liter auf 700 km. Um wie viel Prozent ist der Verbrauch eines der beiden Autos niedriger als der des anderen? 5. Der Preis eines Autos erhöht sich durch Teilzahlung von 38950 € auf 42650 €. Wie viel Prozent beträgt der Aufschlag? 6. In einem Kaufhaus werden nach einer Preiserhöhung um 5 % vier Winterreifen zusammen für 327,60 € angeboten. Wie teuer waren die Reifen vorher? 7. Eine Anwaltsgehilfin zahlt monatlich 22% Lohnsteuer, das sind 435,60 €. Wie hoch ist ihr Bruttolohn? 8. Ein Maurer bekommt einen Stundenlohn von 11,76 €, da er im Akkord arbeitet. Um wie viel Prozent liegt er damit über dem Normallohn von 11,20 €. 9. Eine Fachverkäuferin bekommt nach Abzug von 32,8% Abgaben 1428 € Nettogehalt ausgezahlt. Wie hoch ist das Bruttogehalt? 10. Der Stundenlohn eines Industriemechanikers von 11,20 € soll um 2,5% erhöht werden. Wie hoch ist der neue Stundenlohn? 11. Ein Architekt berechnet einem Bauherren als Honorar 8,5% der Baukosten. Wie hoch ist sein Honorar bei einem Einfamilienhaus mit Baukosten in Höhe von 290300 € ? 12. Ein Reihenhaus sollte für 244750 € erstellt werden. Die Kosten stiegen während der Bauzeit auf 259435 €. Wie viel % betrug die Preissteigerung ? 13. Das Wohnzimmer eines Einfamilienhauses soll mit Fliesen ausgelegt werden. Die Wohnzimmerfläche beträgt 36,50 m2. Wie viel m2 Fliesen müssen geliefert werden, wenn mit 6% Verschnitt zu rechnen ist ? 14. Eine Baugrube mit einem festen Bodenvolumen von 400 m3 soll ausgehoben werden. Wie viele LKWs mit 12 m3 Ladung sind bei einer Auflockerung des Bodens von 14% zum Abtransport erforderlich ? 15. Ein Baumarkt gewährt den Mitgliedern von Siedlergemeinschaften auf alle Einkäufe 6% Preisnachlass. Wie viel müsste ein Mitglied für einen Rasenmäher zahlen, der normal 164,50 € kostet. 16. Eine Kundin kauft in einem Sportgeschäft einen Heimtrainer zum Preis von 399,50 €. Als Mitglied eines Sportvereins bekommt sie Ermäßigung und zahlt nur 367,54 €. Wie viel % betrug der Preisnachlass? 17. Ein Gärtner kauft einen Rasentraktor und erhält einen Rabatt. Wie viel Prozent Rabatt bekommt er, wenn er statt 1342,50 € nur 1261,95 € bezahlt ? 18. Für eine Kettensäge zahlt ein Hobbygärtner nach Abzug von 3% Rabatt 184,30 €.. Wie hoch war der ursprüngliche Verkaufspreis ? 19. Der Grundpreis eines Wagens beträgt 27500 €. Die Sonderausstattung erhöht den Preis um 1000 €. Wegen Barzahlung erhält der Käufer 12% Rabatt. Wie viel Prozent vom Grundpreis sind tatsächlich gezahlt worden ? Erstellt von Rudolf Brinkmann p1_II.doc 18.01.08 10:24 Seite: 2 von 2 R. Brinkmann http://brinkmann-du.de Seite 3 18.01.2008 Lösungen: Arbeitsblatt I Prozentrechnung Ergebnisse: E1: Der Anteil der Jungen beträgt 68%, der der Mädchen 32%. E2: Der Kaufpreis liegt 12% unter dem Listenpreis. E3: Der ursprüngliche Preis des Autos betrug 18290 €. E4: Der Verbrauch von Auto II liegt um 20% unter dem von Auto I. E5: Der Aufschlag bei Teilzahlung beträgt etwa 9,5%. E6: Vor der Preiserhöhung kosteten die Reifen 312 €. E7: Der Bruttolohn der Anwaltsgehilfin beträgt 1980 €. E8: Der Akkordlohn liegt 5% über dem Normallohn. E9: Das Bruttogehalt der Fachverkäuferin beträgt 2125 €. E10: Der neue Stundenlohn des Industriemechanikers beträgt 11,48 €. E11: Das Honorar des Architekten beträgt 24675,50 €. E12: Die Preissteigerung betrug 6%. E13: Es müssen mindestens 38,69 m2 Fliesen geliefert werden. E14: Zum Abtransport der Erde sind 38 LKW’s erforderlich. E15: Ein Mitglied der Siedlergemeinschaft muss für den Rasenmäher 154,63 € bezahlen. E16: Der Preisnachlass betrug 8%. E17: Der Gärtner bekommt 6% Rabatt. E18: Der ursprüngliche Preis der Kettensäge betrug 190 €. E19: Tatsächlich wurden 91,2% vom Grundpreis gezahlt. Erstellt von Rudolf Brinkmann p1_II.doc 18.01.08 10:24 Seite: 3 von 3 R. Brinkmann http://brinkmann-du.de Seite 4 18.01.2008 Ausführliche Lösungen: A1: 17 Jungen + 8 Mädchen = 25 Schüler 100% p= Gesucht wird der Prozentsatz: W ⋅ 100% G 17 ⋅ 100% = 68% 25 8 Mädchen: G = 25 W =8 p= ⋅ 100% = 32% 25 Der Anteil der Jungen beträgt 68%, der der Mädchen 32%. Jungen: G = 25 W = 17 p= A2: Listenpreis: 23925 € Kaufpreis: 21054 € W Gesucht wird der Prozentsatz: p= ⋅ 100% G G = 23925 € W = 23925 € − 21054 € = 2871€ 2871€ p= ⋅ 100% = 12% 23925 € Der Kaufpreis liegt 12% unter dem Listenpreis. E3: 10,5% vom Grundwert sind 1920,45 € W ⋅ 100% p Prozentwert W = 1920, 45 € Gesucht wird der Grundwert: Prozentsatz p = 10,5% G= 1920, 45 € ⋅ 100% = 18290 € 10,5% Der ursprüngliche Preis des Autos betrug 18290 €. G= E4: Verbrauch auf 100 km: Auto I: 47 Liter = 11,75 4 100 km Auto II: 65,8 Liter = 9, 4 7 100 km Auto I hat den höchsten Verbrauch ⇒ G = 11,75 W = 11,75 − 9, 4 = 2,35 W 2,35 ⋅ 100% = ⋅100% = 20% G 11,75 Der Verbrauch von Auto II liegt um 20% unter dem von Auto I. Gesucht ist der Prozentsatz: p= E5: G = 38 950 € W = 42 650 € − 38 950 € = 3 700 € W 3 700 € Gesucht ist der Prozentsatz: p= ⋅ 100% = ⋅ 100% ≈ 9,5% G 38 950 € Der Aufschlag bei Teilzahlung beträgt etwa 9,5%. Erstellt von Rudolf Brinkmann p1_II.doc 18.01.08 10:24 Seite: 4 von 4 R. Brinkmann http://brinkmann-du.de Seite 5 18.01.2008 E6: Vermehrter Grundwert. Der neue Preis betägt 105% vom Grundwert. 327,60 € ⇒ 1,05 ⋅ G = 327,60 € ⇔ G = = 312 € 1,05 Vor der Preiserhöhung kosteten die Reifen 312 €. E7: Prozentsatz p = 22% Prozentwert W = 435,60 € W 435,60 € Gesucht wird der Grundwert G= ⋅ 100% = ⋅ 100% = 1980 € p 22% Der Bruttolohn der Anwaltsgehilfin beträgt 1980 €. E8: Grundwert G = 11,20 € Prozentwert W = 11,76 € − 11,20 € = 0,56 € W 0,56 € Gesucht wird der Prozentsatz p= ⋅ 100% = ⋅ 100% = 5% G 11,20 € Der Akkordlohn liegt 5% über dem Normallohn. E9: Prozentsatz p = 32,8% Gesucht wird der verminderte Grundwert. Das Nettogehalt beträgt 67,2% vom Grundwert. 1428 € ⇒ 0,672 ⋅ G = 1428 € ⇔ G = = 2125 € 0,672 Das Bruttogehalt der Fachverkäuferin beträgt 2125 €. Prozentsatz p = 2,5% E10: Grundwert G = 11,20 € Gesucht ist der Prozentwert G 11,20 € W= ⋅p = ⋅ 2,5% = 0,28 € (Lohnerhöhung) 100% 100% Neuer Lohn : 11,20 € + 0,28 € = 14, 48 € Der neue Stundenlohn des Industriemechanikers beträgt 11,48 €. Grundwert G = 290 300 € E11: Prozentsatz p = 8,5% Gesucht wird der Prozentwert G 290 300 € ⋅p = ⋅ 8,5% = 24 675,50 € W= 100% 100% Das Honorar des Architekten beträgt 24675,50 €. Erstellt von Rudolf Brinkmann p1_II.doc 18.01.08 10:24 Seite: 5 von 5 R. Brinkmann http://brinkmann-du.de Seite 6 18.01.2008 E12: Grundwert G = 244 750 € Prozentwert p = 259 435 € − 244 750 € = 14 685 € W 14 685 € Gesucht wird der Prozentsatz p= ⋅ 100% = ⋅ 100% = 6% G 244 750 € Die Preissteigerung betrug 6%. E13: Grundwert G = 36,25 m2 Prozentsatz p = 6% Gesucht wird der Prozentwert G 36,25 m2 ⋅p = ⋅ 6% = 2,19 m2 (Verschnitt) W= 100% 100% Gesamtbedarf: 36,25 m2 + 2,19 m2 = 38,69 m2 Es müssen mindestens 38,69 m2 Fliesen geliefert werden. E14: Grundwert G = 400 m3 Prozentsatz p = 14% Gesucht wird der Prozentwert G 400 m3 ⋅p = ⋅ 14% = 56 m3 (Volumenvergrößerung durch Auflockerung) 100% 100% Abzutransportieren sind 400 m3 + 56 m3 = 456 m3 . W= 456 m3 = 38LKW ' s m3 12 LKW Zum Abtransport der Erde sind 38 LKW’s erforderlich. Ein LKW fasst 12 m3 Erde. ⇒ Anzahl der LKW's = Prozentsatz p = 6% E15: Grundwert G = 164,50 € Gesucht wird der Prozentwert G 164,50 € ⋅p = ⋅ 6% = 9,87 € (Preisnachlass) W= 100% 100% Endpreis = 164,50 € − 9,87 € = 154,63 € Ein Mitglied der Siedlergemeinschaft muss für den Rasenmäher 154,63 € bezahlen. E16: Grundwert G = 399,50 € Prozentwert W = 399,50 € − 367,54 € = 31,96 € W 31,96 € Gesucht wird der Prozentsatz p= ⋅ 100% = ⋅ 100% = 8% G 399,50 € Der Preisnachlass betrug 8%. Erstellt von Rudolf Brinkmann p1_II.doc 18.01.08 10:24 Seite: 6 von 6 R. Brinkmann http://brinkmann-du.de Seite 7 18.01.2008 E17: Grundwert G = 1342,50 € Prozentwert W = 1342,50 € − 1261,95 € = 88,55 € W 88,55 € Gesucht wird der Prozentsatz p= ⋅ 100% = ⋅ 100% = 6% G 1342,50 € Der Gärtner bekommt 6% Rabatt. E18: Verminderter Grundwert. Der neue Preis beträgt 97% vom Grundwert. 184,30 € ⇒ 0,97 ⋅ G = 184,30 € ⇔ G = = 190 € 0,97 Der ursprüngliche Preis der Kettensäge betrug 190 €. E19: Grundpreis: 27 500 € Sonderausstattung: +1 000 € Rabatt: G 28 500 € W= ⋅p = ⋅ 12% = 3 420 € 100% 100% 28 500 € Prozentsatz: 12% Rabatt: −3 420 € W ⋅ 100% p= zu zahlen sind: 25 080 € G 2 420 € Mit W = 27 500 € − 25 080 € = 2 420 € ⇒ p = ⋅ 100% = 8,8% 27 500 € Tatsächlich zu zahlen: 100% − 8,8% = 91,2% Tatsächlich wurden 91,2% vom Grundpreis gezahlt. Erstellt von Rudolf Brinkmann p1_II.doc 18.01.08 10:24 Seite: 7 von 7 R. Brinkmann http://brinkmann-du.de Seite 8 18.01.2008 Musterbeispiele zur Zinsrechnung Zinsformeln: Z=K⋅ p 100 K = Kapital z= Z ⋅ 100 K Z = Zinsen K= Z ⋅ 100 p z = Zinssatz Zinsen nach Monaten berechnet: Z=K⋅ z ⋅m 100 ⋅ 12 m = Zeit in Monaten Zinsen nach Tagen berechnet Z=K⋅ z ⋅t 100 ⋅ 360 t = Zeit in Tagen Ein Jahr hat 360 Zinstage, Ein Monat hat 30 Zinstage. Beispiele Zinsrechnung: 1. Berechnung der Jahreszinsen. Wie viel € Zinsen bringen in 1 Jahr bei 5% 850 € ? z = 5% Z=? K = 850 € K ⋅ z 850 € ⋅ 5 Z= = = 42,50 € 100 100 Die Zinsen betragen 42,50 € 2. Berechnung der Zinsen. Wie viel € Zinsen bringen in 7 Monaten bei 4,3% 1200 € ? z = 4,3% K = 1200 € Z=? m=7 K ⋅ z ⋅ m 1200 € ⋅ 4,3 ⋅ 7 Z= = = 30,10 € 100 ⋅ 12 100 ⋅ 12 Die Zinsen betragen 30,10 € 3. Berechnung der Zinsen. Wie viel € Zinsen bringen in 300 Tagen bei 5,1% 950 € ? z = 5,1% K = 950 € Z=? t = 300 K⋅z⋅t 950 € ⋅ 5,1⋅ 300 Z= = = 40,38 € 100 ⋅ 360 100 ⋅ 360 Die Zinsen betragen 40,38 € Erstellt von Rudolf Brinkmann p1_II.doc 18.01.08 10:24 Seite: 8 von 8 R. Brinkmann http://brinkmann-du.de Seite 9 18.01.2008 4. Berechnung des Kapitals. z = 4% K=? Herr Clausen möchte bei einer Bank Geld anlegen. Z = 2400 € Die Bank bietet 4% Zinsen jährlich. Z ⋅ 100 2400 € ⋅ 100 Wie viel muss Herr Clausen anlegen, K= = = 60000 € z 4 wenn er im Jahr 2 400 € Zinsen erhalten will? Die Anlage beträgt 60000 € 5. Berechnung des Zinssatzes. Herr Hansen muss für einen Kredit in Höhe von 18 000 € Zinsen in Höhe von 792 € zahlen. Welchen Zinssatz berechnet die Bank? K = 18000 € z=? Z = 792 € Z ⋅ 100 792 € ⋅ 100 z= = = 4,4% K 18000 Der Zinssatz beträgt 4,4% 6. Berechnung der Zinstage. Ein Kapital von 19 200 € war zu K = 19200 € t=? 4,5% ausgeliehen. z = 4,5% Es brachte 249,60 € Zinsen. Z = 249,60 € Berechne, wie lange das K⋅z⋅t Z ⋅ 100 ⋅ 360 249,60 € ⋅ 100 ⋅ 360 Kapital ausgeliehen war. Z= ⇒t= = = 104 100 ⋅ 360 K⋅z 19200 € ⋅ 4,5 Das Kapital war 104 Tage angelegt. 7. Berechnung des Kapitals. Frau Blank nimmt für 13,5% bei der Zockerbank am 10.1.03 einen Kredit auf. Am 15.6.03 zahlt sie den Kredit zurück. Die Bank berechnet ihr 581,25 € Zinsen. Wie hoch war der Kredit? Berechnung der Laufzeit: vom 10.1 bis 10.6 sind es vom 10.6. bis 15.6. sind es vom 10.1. bis 15.6 sind es z = 13,5%% 5 ⋅ 30 = 150 Tage 5 Tage 155 Tage K=? Z = 581,25 € t = 155 K⋅z⋅t 100 ⋅ 360 Z ⋅ 100 ⋅ 360 581,25 € ⋅ 100 ⋅ 360 ⇒K = = = 10000 € z⋅t 13,5 ⋅ 155 Die Kredithöhe betrug 10000 € Z= Erstellt von Rudolf Brinkmann p1_II.doc 18.01.08 10:24 Seite: 9 von 9 R. Brinkmann http://brinkmann-du.de Seite 10 18.01.2008 Arbeitsblatt zur Prozent und Zinsrechnung 1. Ein Kapital von 22500 € wird zu einem Zinssatz von 7,5% angelegt. Wie hoch ist der Zins nach 9 Monaten und 10 Tagen? 2. Das Haus der Familie Müller ist mit einer Hypothek belastet. Familie Müller zahlt bei einem Zinssatz von 8,5 % monatlich 637,50 €. Wie hoch ist die Hypothek? 3. Ein Sparer erhält für sein Kapital von 42500 € bei einem Zinssatz von 6,5% 552,50 € ausgezahlt. Wie lange war das Kapital angelegt? 4. Für ein Darlehn von 33000 € mussten bei einem Zinssatz von 8% insgesamt 9240 € an Zinsen gezahlt werden. Nach welcher Zeit wurde das Darlehn abgelöst? 5. Herr Schmidt kauft ein Auto zum Preis von 13750 € und lässt diese Summe vom Autohändler finanzieren. In einem Jahr hat Herr Schmidt 15331,25 € gezahlt. Wie hoch war der Zinssatz? 6. Ein Handwerker kauft Werkzeuge für 2300 € ein. Er erhält einen Rabatt von 6% und, da er bar zahlt, noch 2% Skonto. Welchen Preis muss er zahlen? 7. In einem Baumarkt werden zwei Artikel zu Einzelpreisen von 65 € und 47,50 € angeboten. Beide Artikel zusammen bekommt man für 102 €. Wie hoch sind die Rabatte, wenn für den ersten Artikel der Rabatt 2,5 – mal so hoch ist, wie der Rabatt für den zweiten? 8. Ein Schüler findet eine Brieftasche mit 1125 € Inhalt. Der Verlierer zahlt den gesetzlichen Finderlohn von 5% für die ersten 500 € und 3% für den Rest. Wie hoch ist der Finderlohn? 9. Wie viel Prozent Preisnachlass gewährt ein Fliesenleger seinem Auftraggeber, wenn er statt 13700 € nur 12604 € berechnet? 10. Herr Boller plant in seinem Garten einen Teich anzulegen. Das Volumen des Teiches würde 15,6 m3 betragen. Wie viel Boden muss Herr Boller per Container abfahren lassen, wenn mit einer Auflockerung von 15% zu rechnen ist? 11. In einem Kaufhaus mit einer Fotoabteilung werden Poster der Größe 20 x 30 cm vom Negativ im Sonderangebot für 0,57 € angeboten. Normal kosten solche Vergrößerungen 0,95 €. Wie viel Prozent beträgt die Ermäßigung? 12. Herr Steger hat ein Kapital auf 5 Jahre zu 6% festgelegt. Wie hoch war das Kapital, wenn Herr Steger nach 5 Jahren 45500 € ausgezahlt wurden? 13. Ein Unternehmer muss für eine Materiallieferung 8229 € bezahlen, da die Preise um 5,5% angehoben wurden. Wie viel hätte er vor dieser Verteuerung bezahlen müssen? 14. Um ein Zimmer mit Holz zu verkleiden, sind 50 m2 Holzpaneele vorhanden. Die zu verkleidende Fläche beträgt 46,8 m2. Wie viel m2 Paneele müssen noch nachgeliefert werden, wenn mit 18% Verschnitt zu rechnen ist? 15. 500 g Erdbeeren werden auf dem Wochenmarkt für 1,75 € angeboten. Beim Kauf von 1,5 kg zahlt der Kunde nur 4,50 €. Wie viel Prozent beträgt die Ersparnis? 16. Sonnenschirme, Durchmesser 2,70 m, aus Aluminiumrohr mit einer wetterfesten Polyesterbespannung werden in einem Baumarkt von 87,50 € auf 70 € herabgesetzt. Wie viel Prozent beträgt der Preisnachlass? 17. Zum Bau eines Einfamilienhauses benötigt Familie Koch eine Hypothek von 150000 €. Die Zinsen für die ersten 5 Jahre sind auf 6% pro Jahr festgelegt. Außerdem muss Familie Koch 1% Tilgung pro Jahr zahlen. Wie hoch sind die monatlichen Kosten der Familie Koch? 18. Familie Stein zahlt für eine Eigentumswohnung 840 € pro Monat. Der Zinssatz für das Darlehn, das Familie Stein benötigte, beträgt 6,5%, die jährliche Tilgung 1%. Wie hoch ist das Darlehn, das Familie Stein benötigte? Erstellt von Rudolf Brinkmann p1_II.doc 18.01.08 10:24 Seite: 10 von 10 R. Brinkmann http://brinkmann-du.de Seite 11 18.01.2008 Lösungen: Arbeitsblatt I Zins- und Prozentrechnung Ergebnisse: E1: Nach 9 Monaten und 10 Tagen belaufen sich die anfallenden Zinsen auf 1312,50 €. E2: Die Hypothek beträgt 90000 €. E3: Das Kapital war 2 Monate und 12 Tage angelegt. E4: Das Darlehn wurde nach 42 Monaten (3,5 Jahren) abgelöst. E5: Der Zinssatz betrug 11,5%. E6: Der Handwerker muss 2118,76 € zahlen. E7: Auf Artikel I ist ein Rabatt von 12,5% und auf Artikel II von 5%. E8: Der Finderlohn beläuft sich auf 43,75 €. E9: Der Fliesenleger gewährt seinem Auftraggeber einen Preisnachlass von 8%. E10: Insgesamt müssen 17,94 m3 Boden abgefahren werden. E11: Die Ermäßigung beträgt 40%. E12: Vor 5 Jahren betrug das angelegte Kapital 35000 €. E13: Vor der Verteuerung hätte der Unternehmer 7800 € zahlen müssen. E14: Es müssen ca. 5,3 m2 Paneele nachgeliefert werden. E15: Die Ersparnis beim Kauf von 1,5 kg Erdbeeren beträgt etwa 14,3%. E16: Der Preisnachlass beträgt 20%. E17: Familie Koch hat in den ersten 5 Jahren monatlich 875 € zu zahlen. E18: Die Höhe des Darlehns betrug 134400 €. Erstellt von Rudolf Brinkmann p1_II.doc 18.01.08 10:24 Seite: 11 von 11 R. Brinkmann http://brinkmann-du.de Seite 12 18.01.2008 Ausführliche Lösungen: E1: Kapital K = 22 500 € Zinssatz p = 7,5% Laufzeit 9 Monate und 10 Tage = 9 ⋅ 30 Tage + 10 Tage = 280 Tage. Gesucht sind die in dieser Zeit anfallenden Zinsen: p 7,5% Z =K⋅ ⋅ t = 22 500 € ⋅ ⋅ 280 Tage = 1312,50 € 100% ⋅ 360 Tage 100% ⋅ 360 Tage Nach 9 Monaten und 10 Tagen belaufen sich die anfallenden Zinsen auf 1312,50 €. E2: Zinssatz p = 8,5% Monatliche Zahlung 637,50 € ⇒ jährliche Zahlung Z = 12 ⋅ 637,50 € = 7650 €. Gesucht ist das Kapital (Hypothek). Z 7650 € ⋅ 100% = ⋅ 100% = 90 000 € p 8,5% Die Hypothek beträgt 90000 €. K= Zinssatz p = 6,5% Zinsen Z = 552,50 € E3: Kapital K = 42 500 € Gesucht ist die Zeit, für die das Geld angelegt wurde. p Z Ansatz: Z = K ⋅ ⋅t ⇔ t = ⋅ 100% ⋅ 360 Tage 100% ⋅ 360 Tage K ⋅p 552,50 € t= ⋅ 100% ⋅ 360 Tage = 72 Tage 2 Monate und 12 Tage 42 500 € ⋅ 6,5% Das Kapital war 2 Monate und 12 Tage angelegt. Zinssatz p = 8% Zinsen Z = 9240 € E4: Kapital K = 33 000 € Gesucht ist die Laufzeit. p Z Ansatz: Z = K ⋅ ⋅m ⇔ m = ⋅ 100% ⋅ 12Monate 100% ⋅ 12Monate K ⋅p 9240 € m= ⋅ 100% ⋅ 12Monate = 42Monate oder 3,5 Jahre. 33 000 € ⋅ 8% Das Darlehn wurde nach 42 Monaten (3,5 Jahren) abgelöst. E5: Kapital K = 13 750 € Zinsen Z = 15 331,25 € − 13 750 € = 1581,25 € Z 1581,25 € ⋅ 100% = 11,5% Gesucht ist der Zinssatz p = ⋅ 100% = K 13 750 € Der Zinssatz betrug 11,5%. Erstellt von Rudolf Brinkmann p1_II.doc 18.01.08 10:24 Seite: 12 von 12 R. Brinkmann http://brinkmann-du.de E6: Bruttopreis: 6% Rabatt: Seite 13 18.01.2008 Rabatt : G⋅p 2300 € ⋅ 6% = = 138 € W= 100% 100% 2162,00 € Skonto : −43,24 € 2% Skonto: G⋅p 2162 € ⋅ 2% W= = = 43,24 € Rechnungsbetrag: 2118,76 € 100% 100% Der Handwerker muss 2118,76 € zahlen. 2300,00 € −138,00 € Einzelpreis 65,00 € (Grundwert I = G I ) E7: Artikel I: Einzelpreis 47,50 € (Grundwert II = G II ) Artikel II: Preis ohne Rabatt: Artikel I und Artikel II 112,50 € −102,00 € 10,50 € (Prozentwert I + Prozentwert II = W I + W II ) Gesamtrabatt Es gilt p I = 2,5 ⋅ p II (1) und mit WI = GI ⋅ pI und W I + W II = 10,50 € ( 2 ) W II = G II ⋅ p II gelangt man zu folgendem Ansatz: 100% 100% G I ⋅ p I G II ⋅ p II 65 ⋅ p I 47,50 ⋅ p II + = + = 10,50 € W I + W II = 100% 100% 100% 100% mit (1) gilt: (Rechnung ohne Einheiten) 65 ⋅ 2,5 ⋅ p II 47,50 ⋅ p II 162,5 ⋅ p II + 47,50 ⋅ p II 210 ⋅ p II + = = = 2,1⋅ p II = 10,50 100 100 100 100 10,50 ⇔ p II = = 5 ⇒ p II = 5% 2,1 mit (1) gilt: p I = 2,5 ⋅ p II = 2,5 ⋅ 5% = 12,5% Auf Artikel I ist ein Rabatt von 12,5% und auf Artikel II von 5%. E8: Der Gesamtbetrag von 1125 € wird aufgeteilt in 500 € zu 5% und 1125 € − 500 € = 625 € zu 3% Finderlohn = 500 € ⋅ 0,05 + 625 € ⋅ 0,03 = 43,75 € Der Finderlohn beläuft sich auf 43,75 €. E9: Grundwert G = 13 700 € Prozentwert W = 13 700 € − 12 604 € = 1096 € W 1096 € p= ⋅ 100% = ⋅ 100% = 8% G 13 700 € Der Fliesenleger gewährt seinem Auftraggeber einen Preisnachlass von 8%. Erstellt von Rudolf Brinkmann p1_II.doc 18.01.08 10:24 Seite: 13 von 13 R. Brinkmann http://brinkmann-du.de Seite 14 E10: Grundwert G = 15,6 m3 18.01.2008 Prozentsatz p = 15% G⋅p 15,6 m ⋅ 15% = = 2,34 m3 100% 100% Insgesamt: 15,6 m3 + 2,34 m3 = 17,94 m3 W= 3 Insgesamt müssen 17,94 m3 Boden abgefahren werden. E11: Grundwert G = 0,95 € Prozentwert W = 0,95 € − 0,57 € = 0,38 € W 0,38 € p= ⋅ 100% = ⋅ 100% = 40% G 0,95 € Die Ermäßigung beträgt 40%. E12: Laufzeit 5 Jahre, Zinssatz p = 6% pro Jahr, das sind in 5 Jahren 5 ⋅ 6% = 30% (ohne Zinseszins). Nach 5 Jahren wird ausgezahlt: 45 500 € = 35 000 € K + 0,3K = 45 500 € ⇔ 1,3K = 45 500 € ⇔ K = 1,3 Vor 5 Jahren betrug das angelegte Kapital 35000 €. E13: Preisanstieg um 5,5% auf 8229 € bedeutet vermehrter Grundwert. 8229 € 1,055 ⋅ G = 8229 € ⇔ G = = 7800 € 1,055 Vor der Verteuerung hätte der Unternehmer 7800 € zahlen müssen. E14: Grundwert G = 46,8 m2 Prozentsatz p = 18% G⋅p 46,8 m2 ⋅ 18% = = 8, 424 m2 (Verschnitt) 100% 100% Insgesamt erforderlich 46,8 m2 + 8, 424 m2 = 55,224 m2 W= Vorhanden sind 50 m2 Differenz 55,224 m2 − 50 m2 = 5,224 m2 ≈ 5,3 m2 Es müssen ca. 5,3 m2 Paneele nachgeliefert werden. E15: 3 ⋅ 500 g Erdbeeren kosten 3 ⋅ 1,75 € = 5,25 € (Grundwert G) 1,5 kg Erdbeeren kosten 4,50 € Ersparnis = 5,25 € − 4,50 € = 0,75 € (Prozentwert W) W 0,75 € Ersparnis in % p= ⋅ 100% = ⋅ 100% ≈ 14,3% G 5,25 € Die Ersparnis beim Kauf von 1,5 kg Erdbeeren beträgt etwa 14,3%. Erstellt von Rudolf Brinkmann p1_II.doc 18.01.08 10:24 Seite: 14 von 14 R. Brinkmann http://brinkmann-du.de Seite 15 18.01.2008 E16: Preisnachlass von 87,50 € auf 70 € Grundwert G = 87,50 € Prozentwert W = 87,50 € − 70 € = 17,50 € W 17,50 € Prozentsatz p= ⋅ 100% = ⋅ 100% = 20% G 87,50 € Der Preisnachlass beträgt 20%. E17: Hypothek 150000 € (Kapital K) in den ersten 5 Jahren gilt: Zinssatz pZ = 6% Tilgung pT = 1% Annahme: Zinssatz und Tilgung beziehen sich auf K = 150 000 € Jährlich sind zu zahlen: K ⋅ p Z K ⋅ pT K 150 000 € ⋅ 7% = 10 500 € + = Z= ( p Z + pT ) = 100% 100% 100% 100% 10 500 € € Das sind im Monat = 875 12Monate Monat Familie Koch hat in den ersten 5 Jahren monatlich 875 € zu zahlen. E18: Monatliche Zahlung 840 € das sind 12 ⋅ 840 € = 10 800 € pro Jahr. Zinssatz und Tilgung belaufen sich auf 7,5%. Z 10 800 € K = ⋅ 100% = ⋅ 100% = 134 400 € p 7,5% Die Höhe des Darlehns betrug 134400 €. Erstellt von Rudolf Brinkmann p1_II.doc 18.01.08 10:24 Seite: 15 von 15