3.2 Repräsentation Graphen

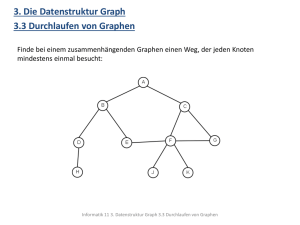
3. Die Datenstruktur Graph
3.2 Repräsentation von Graphen
Für die Darstellung eines Graphen eignet sich die sog.
Adjazenzmatrix .
Dabei handelt es sich um eine Tabelle, in der die Zeilen- und
Spaltenüberschriften die Knotenbezeichner sind.
In eine Zelle wird eine 1 eingetragen, wenn es zwischen den
zugehörigen Knoten eine Kante gibt.
Informatik 11 3. Datenstruktur Graph 3.2 Repräsentation von Graphen
3.2 Repräsentation von Graphen
Beispiel 1:
Graph
Adjazenzmatrix
v1
v1
v2
1
v3
1
v4
1
v5
v2
v3
v4
1
1
1
v5
v6
1
1
1
1
1
v6
1
In eine Zelle wird eine 1 eingetragen, wenn es zwischen den zugehörigen Knoten
eine Kante gibt. Die Adjazenzmatrix ist symmetrisch zur Hauptdiagonale.
Informatik 11 3. Datenstruktur Graph 3.2 Repräsentation von Graphen
3.2 Repräsentation von Graphen
Beispiel 2:
Graph
Adjazenzmatrix
v1
v1
v2
v3
v4
1
1
1
v5
v6
v2
v3
v4
v5
1
1
1
1
v6
1
Bei einem gerichteten Graphen muss die Adjazenzmatrix nicht mehr
symmetrisch zur Hauptdiagonale sein.
Informatik 11 3. Datenstruktur Graph 3.2 Repräsentation von Graphen
3.2 Repräsentation von Graphen
Beispiel 3:
Graph
Adjazenzmatrix
v1
v1
v2
v3
v4
10
20
10
20
10
v2
10
v3
20
20
v4
10
10
v5
v5
v6
10
30
10
v6
Bei einem gewichteten Graphen trägt man die Kantenwerte ein.
Informatik 11 3. Datenstruktur Graph 3.2 Repräsentation von Graphen
40
30
40
3.2 Repräsentation von Graphen
Implementierung einer Matrix in Java:
Beispiel: (keine Adjazenzmatrix!)
1
2
3
4
5
6
mat[0] = Feld mit 3
Elementen
mat[1] = Feld mit 3
Elementen
int[][] mat;
public Matrix(){
mat = new int [zeilen] [spalten];
Informatik 11 3. Datenstruktur Graph 3.2 Repräsentation von Graphen
3.2 Repräsentation Graphen
Implementierung einer Matrix in Java:
1
2
3
4
5
6
public class Matrix{
int zeilen = 2;
int spalten = 3;
int[][] mat;
public Matrix(){
mat = new int [zeilen] [spalten];
mat[0][0] = 1;
mat[0][1] = 2;
mat[0][2] = 3;
mat[1][0] = 4;
mat[1][1] = 5;
mat[1][2] = 6;
}
}
Informatik 11 3. Datenstruktur Graph 3.2 Repräsentation von Graphen
3.2 Repräsentation Graphen
Ausgabe der Matrix mit
verschachtelten Schleifen:
1
2
3
4
5
6
public void ausgabe(){
for(int i = 0; i< zeilen; i++){
for(int j = 0; i<spalten; j++){
System.out.print(
"mat[" + i + "] [" + j + "] = " + mat[i][j]+"
}
System.out.println();
}
Informatik 11 3. Datenstruktur Graph 3.2 Repräsentation von Graphen
");
3.2 Repräsentation von Graphen
Modellieren
eines Graphen:
Informatik 11 3. Datenstruktur Graph 3.2 Repräsentation von Graphen
3.2 Repräsentation von Graphen
Verwalten von Knoten und Kanten:
A
B
C
D
A
0
5
8
3
B
5
0
-1
5
C
8
-1
0
-1
D
3
5
-1
0
Knotenfeld:
knoten[0]
Bezeichner "A"
Knotennummer 0;
knoten[1]
Bezeichner "B"
Knotennummer 1;
Matrix:
0 für die
Elemente der
Hauptdiagonale;
-1 steht für eine
nicht vorhandene
Kante, diese
Zelle bleibt bei
der Ausgabe leer.
Informatik 11 3. Datenstruktur Graph 3.2 Repräsentation von Graphen
3.2 Repräsentation von Graphen
Einfügen eines neuen Knotens :
A
B
C
D
E
A
0
5
8
3
-1
B
5
0
-1
5
-1
C
8
-1
0
-1
-1
D
3
5
-1
0
-1
E
-1
-1
-1
-1
0
Knotenfeld
ergänzen;
vorausgesetzt,
der Knoten ist
noch nicht
vorhanden und die
maximale Anzahl
ist nicht
überschritten
Matrix:
0 und -1 in der
neuen Spalte und
der neuen Zeile
ergänzen.
Informatik 11 3. Datenstruktur Graph 3.2 Repräsentation von Graphen
3.2 Repräsentation von Graphen
Einfügen einer neuen Kante :
A
B
C
D
E
A
0
5
8
3
-1
B
5
0
-1
5
9
C
8
-1
0
-1
-1
D
3
5
-1
0
-1
E
-1
9
-1
-1
0
Matrix:
Gewichtung
eintragen
Informatik 11 3. Datenstruktur Graph 3.2 Repräsentation von Graphen