1 Theoretische Grundlagen

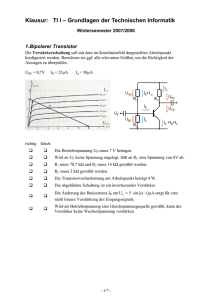
1
1 Theoretische Grundlagen
1.1 Einleitung
Verstarker werden in der Elektronik in vielfaltiger Weise eingesetzt. Durch die moderne
integrierte Schaltungstechnik steht ein breites Spektrum an Verstarkerbausteinen zur Verfugung, bei denen sich der Anwender in Gegensatz zu fruheren Verstarkern, die mit diskreten Bauelementen aufgebaut waren, nicht um den detaillierten inneren Aufbau zu kummern
braucht. Diese sehr universell einsetzbaren Verstarker werden allgemein als Operationsverstarker bezeichnet, wobei diese Bezeichnung historisch bedingt ist. Sie ist dadurch entstanden, da man fur die fruher verwendeten Analogrechner zur Durchfuhrung von mathematischen Operationen (vor allem zur Addition, Subtraktion und Integration) hochverstarkende Verstarkereinheiten benotigte, die fur Gleich- und Wechselspannungen geeignet waren.
Der prinzipielle Aufbau dieser Verstarker als Dierenzverstarker ist bei den modernen
Verstarkerbausteinen beibehalten worden. Im folgenden werden die fur den Praktikumsversuch notwendigen theoretischen Grundlagen der Operationsverstarker vorgestellt.
1.2 Grundsatzlicher Aufbau des Operationsverstarkers
1.2.1 Schaltsymbol, Gehause
Der Operationsverstarker wird in Schaltungen allgemein durch ein Dreieck dargestellt, dessen Spitze in Richtung des Signalusses (von den Eingangen zum Ausgang) weist. Dabei
sind die Eingange mit 00+00 (P-Eingang) und 00 00 (N-Eingang) bezeichnet. Legt man an
den P-Eingang ein Signal, so ist das Ausgangssignal gleichphasig zum Eingangssignal; deshalb bezeichnet man diesen Eingang als nichtinvertierenden Eingang. Ein am N-Eingang
angelegtes Signal tritt am Ausgang gegenphasig zum Eingangssignal auf; man nennt den
N-Eingang deshalb invertierender Eingang. Zusatzlich zu den Signalanschlussen gibt es
mindestens die Anschlusse fur die Versorgungsspannungen, die bei sehr vielen Operationsverstarkertypen 15 V betragen. Abhangig vom speziellen Typ gibt es noch Anschlusse
fur die Osetkompensation und die Frequenzgangkorrektur. Diese Einzelheiten mu der
Anwender aus den Herstellerangaben entnehmen. In Prinzipschaltbildern werden haug
zur Vereinfachung nur die Signalanschlusse benutzt.
Durch die integrierte Schaltungstechnik (IC = Integrated Circuit) sind alle Elemente des
Operationsverstarkers in einem Gehause untergebracht. Die am haugsten verwendeten
Gehausetypen dieser IC-Bausteine sind das zylindrische Transistorgehause (TO-Version)
und das Dual-In-Line-Package (DIP-Version).
2
Theoretische Grundlagen
1.2.2 Innerer Aufbau
Obgleich fur den Einsatz des Operationsverstarkers nur seine Eigenschaften als Bauelement
bekannt sein mussen, ist zum Verstandnis dieser Eigenschaften die Kenntnis uber seinen
prinzipiellen inneren Aufbau nutzlich.
Ein Operationsverstarker ist in der Regel ein dreistuger Verstarker, der sich aus Eingangs, Koppel- und Ausgangsstufe zusammensetzt. Die im folgenden benutzten neuen Begrie
werden in den weiteren Abschnitten erklart.
Die Eingangsstufe von Operationsverstarkern wird grundsatzlich als Dierenzverstarker
symmetrisch aus paarweise moglichst gleichen Transistoren aufgebaut. Dadurch werden die
insbesondere bei bipolaren Transistoren unvermeidbaren Temperaturabhangigkeiten (Temperaturdrift) und Nichtlinearitaten weitgehend kompensiert. Weiterhin wird durch den Differenzverstarker eine hohe Gleichtaktunterdruckung und eine hohe Dierenzverstarkung
erreicht. Hier erfolgen i. a. auch Manahmen zur Osetkompensation.
Die auf die Eingangsstufe folgende Koppelstufe dient der weiteren Verstarkung des Ausgangssignales der Eingangsstufe. In dieser Stufe wird erforderlichenfalls die Frequenzgangkorrektur durchgefuhrt.
Als dritte Stufe folgt eine niederohmige Ausgangsstufe. Sie wird durch eine Gegentaktendstufe gebildet, die eine ausreichende Leistungsverstarkung bietet. Das Ausgangssignal
dieser Stufe ist bei symmetrischer Spannungsversorgung zu Null symmetrisch.
Im Anhang ist fur Interessierte die innere Schaltung eines gebrauchlichen Operationsverstarkers (A741) mit der Beschreibung der einzelnen Stufen angegeben.
3
Theoretische Grundlagen
2 Eigenschaften von Operationsverstarkern
Die realen Werte der Eigenschaften eines Operationsverstarkers, seine Kenngroen, werden auf Datenblattern angegeben. Im Praktikumsversuch werden die Operationsverstarker
A748 bzw. A741 benutzt, von denen in der Tabelle die wichtigsten Daten aufgefuhrt
sind.
Leerlaufverstarkung v
105
Gleichtaktunterdruckung G
90 dB
Eingangsosetspannung U
1 mV
Osetspannungsdrift
3V/C
Eingangsruhestrom I
80 nA
Grenzfrequenz f (A741)
10 Hz
Transitfrequenz f (A741)
1 MHz
Slewrate S (A741)
0,6 V/s
Dierenzeingangswiderstand r 2 M
Gleichtakteingangswiderstand r 109
Ausgangswiderstand r
75 Max. Ausgangsstrom
20 mA
Linearer Aussteuerungs13 V
bereich bei einer Betriebsspannung von 15 V
o
of f
B
g
T
e
gl
a
Im folgenden Text werden die realen Eigenschaften und ihre Auswirkungen im Zusammenhang mit den einfachsten Verstarkerschaltungen diskutiert. In den aufgefuhrten Gleichungen werden fur die Symbole fur Spannungen und Strome stets Grobuchstaben verwendet,
wobei impliziert ist, da es sich dabei in der Regel um A nderungen der entsprechenden
Groen handelt. So ist eine Verstarkung v = U =U , obgleich es korrekt v = dU =dU
heien mute. Von dieser abgekurzten Schreibweise wird nur in Einzelfallen zur Verdeutlichung abgewichen.
a
e
a
e
2.1 Verstarkung
Unter der Leerlaufverstarkung v (Index o als Abkurzung fur open loop gain) versteht man
die Dierenzverstarkung bei unbelastetem Ausgang und nicht gegengekoppeltem Operationsverstarker bei sehr tiefen Frequenzen:
U
(2.1)
v =
U
Dabei ist U die Dierenzspannung zwischen den beiden Eingangen und U die Ausgangsspannung des Operationsverstarkers. Bei der Berechnung von Schaltungen wird der Kennwert der Leerlaufverstarkung zur Vereinfachung oft als ideal angenommen: v = 1.
o
a
o
d
d
a
o
4
Theoretische Grundlagen
Die Leerlaufverstarkung des unbeschalteten Operationsverstarkers ist fur die meisten Praxisanwendungen viel zu gro. Die Eigenschaften des Operationsverstarkers werden deshalb
durch die auere Beschaltung dem jeweiligen Problem angepat. Fur Verstarkerschaltungen
ist diese auere Beschaltung immer eine Gegenkopplung, die ein Spezialfall der Ruckkopplung ist.
Ruckkopplung allgemein ist die Ruckfuhrung der Ausgangsgroe eines Schaltungsgliedes
auf den Eingang desselben Gliedes - hier also eines Operationsverstarkers. Ist die Ruckkopplung gegenphasig, so weisen das Eingangssignal des Verstarkers und das Ruckkopplungssignal unterschiedliche Polaritat oder unterschiedliche Tendenz auf. Man spricht dann
von einer Gegenkopplung. Sie wirkt verstarkungsmindernd, weil die Ruckfuhrung auf den
invertierenden Eingang (gegenphasig) vorgenommen wird. Durch die Ruckfuhrung auf den
invertierenden Eingang kann die Verstarkung je nach Beschaltung stark verringert werden;
man erreicht aber gleichzeitig eine wirksame Stabilisierung der Verstarkerschaltung. Damit
lassen sich praxisgerechte Verstarkungen erzielen.
2.1.1 Grundschaltungen
Die beiden einfachsten Gegenkopplungsschaltungen fuhren zum nichtinvertierenden und
invertierenden Verstarker.
Nichtinvertierender Verstarker:
Abbildung 2.1 zeigt den Schaltplan eines nichtinvertierenden Verstarkers:
Ud
R2
Ue = U+
Ua
R1
U-
Abbildung 2.1: Nichtinvertierender Verstarker
Nun soll die Betriebsverstarkung v = U =U dieser Schaltung berechnet werden. Dabei
sind U+ und U die an den beiden Eingangen des Operationsverstarkers anliegenden Eingangsspannungen bezogen auf Masse. Die Dierenz dieser Eingangsspannungen liegt als
Dierenzspannung U am Operationsverstarker an und wird um den Verstarkungsfaktor
b
d
a
e
5
Theoretische Grundlagen
v
o
verstarkt:
vU
U+
=
=
U
=
v U
=
a
U
a
a
U
e
o
U
d
e
= v (U+ U )
; U = R R+1 R
o
1
R1
R 1 + R2
R1
U
+
U
v
R1 + R2
o
e
U
2
U
daraus folgt:
a
bzw.
a
a
o
Daraus erhalt man die Gleichung fur die Betriebsverstarkung:
1 = 1 + R1
U
=
(2.2)
U
v
v
R1 + R2
Mit v ! 1 (dies gilt fur den idealen Operationsverstarker) folgt als Betriebsverstarkung
der nichtinvertierenden Operationsverstarkerschaltung:
e
a
b
o
o
v
b
= RR2 + 1
(2.3)
1
Fuhrt man den Kopplungsfaktor k = R1=(R1 + R2 ) in die Gleichung (2.2) ein, so erhalt
man mit der Abkurzung v = kv
v
(2.4)
v =
1+v
wobei v Schleifenverstarkung genannt wird. Fur v 1 folgt v v =v
s
o
o
b
s
s
s
s
o
b
Invertierender Verstarker:
I2
I1
R1
R2
I3
Ud
Ue
Ua
Abbildung 2.2: Invertierender Verstarker
Abbildung 2.2 zeigt das Schaltbild eines invertierenden Verstarkers. Hier soll ebenfalls der
Verstarkungsfaktor berechnet werden:
U = v U = v (U+ U )
dabei ist
U+ = 0
; U =U U
a
o
d
o
e
R1
6
Theoretische Grundlagen
Da der Eingangswiderstand des Operationsverstarkers sehr gro ist, kann I3 = 0 gesetzt
werden, und damit gilt I1 = I2; d. h. R1 und R2 wirken als Spannungsteiler. Man erhalt
U = U +U +U
R1
U =
(U U ) somit ist
R +R
R1
e
R1
U
=
U
=
a
U
v
a
o
+ R R+1 R
1
2
a
R2
1
v
2
U
o
U
e
e
a
+ R R+1 R (U
1
2
R1
1
e
a
R1 + R2
e
U
a
)
bzw.
Man erhalt somit fur das Verhaltnis von Eingangs- zu Ausgangsspannung:
v R1
1
+
= v1 = v1 R1 R+1 R2
1 R +R
o
U
U
e
a
bzw. vereinfacht
b
1
1 = 1 R1 + 1 + v
v
v R
b
o
(2.5)
o
o
2
2
R1 R1 1
=
1
+
R2
R2
v
o
1
v
(2.6)
o
Da die Leerlaufverstarkung eines Operationsverstarkers sehr gro ist, d.h. v ! 1 , al t
sich der erhaltene Ausdruck zu
R2
(2.7)
v =
R1
vereinfachen. Fur die Betriebsverstarkung der invertierenden Verstarkerschaltung erhalt
man also im Idealfall ebenfalls eine sehr einfache Gleichung. Setzt man in Gleichung (2.5)
den Kopplungsfaktor k ein, so erhalt man
o
b
v
= 1 +v v (1
o
b
s
k)
(2.8)
2.2 Gleichtaktunterdruckung
Gibt man zwei Signale auf die Eingange eines Operationsverstarkers, so soll im Idealfall
nur deren Dierenz verstarkt werden - der in beiden Signalen enthaltene Gleichtaktanteil
hingegen soll unterdruckt werden. Fur den realen Operationsverstarker deniert man eine
Gleichtaktverstarkung v , die den Zusammenhang von Gleichtakteingangsspannung U
und Ausgangsspannung U gibt; dabei ist v immer sehr viel kleiner als v .
gl
gl
a
gl
v
gl
o
= UU
a
gl
(2.9)
7
Theoretische Grundlagen
Man deniert die Gleichtaktunterdruckung G (auch als CMRR = Common Mode Rejection
Ratio bezeichnet) als:
v
G=
(2.10)
v
In Datenblattern wird die Gleichtaktunterdruckung ublicherweise in dB1 angegeben.
Beim nichtinvertierenden Verstarker ist U+ ungefahr gleich U , so da er eine sehr groe
Gleichtaktaussteuerung erfahrt. Bei ihm wird sich also eine endliche Gleichtaktunterdruckung
auswirken:
U =v U +v U
Da U U , kann U U gesetzt werden. Mit U = U kU erhalt man:
U = v U kv U + v U
1
U (1 + kv ) = U (v + v ) = U v 1 +
G
Somit folgt dann:
U
1 = 1 + v 1 + 1 (2.11)
=
U
v
v
G
Falls G sehr gro ist, erhalt man fur die Betriebsverstarkung das bekannte Ergebnis der
Gleichung (2.4).
o
gl
a
d
gl
gl
o
d
gl
e
d
a
a
gl
o
o
e
e
o
o
a
gl
e
e
a
gl
e
e
o
s
a
b
o
2.3 Eingangsosetspannung
Schaltet man die beiden Eingange eines Operationsverstarkers kurz, so erwartet man, da
fur die Ausgangsspannung gilt: U = 0 V. Wegen unvermeidbarer Unsymmetrien in dem
inneren Aufbau des Operationsverstarkers, ist dies jedoch nicht unbedingt der Fall. Man
mu dann an einen Eingang noch eine kleine Gleichspannung legen, um U = 0 V zu
erhalten. Diese Gleichspannung, am P-Eingang angelegt, wird Osetspannung genannt.
Die Osetspannung ist zusatzlich temperaturabhangig. Viele Operationsverstarker haben
einen Anschlu, um die Osetspannung kompensieren zu konnen.
a
a
2.4 Eingangsruhestrome (input bias current)
Eine weitere Kenngroe von Operationsverstarkern ist der Eingangsruhestrom, welcher
die Signal-Eingangsstrome des Operationsverstarkers uberlagert. U bersichtlicherweise gibt
man den Mittelwert der beiden Eingangsruhestrome an:
1
I = (I + + I )
(2.12)
2
B
1 dB
B
B
(Dezibel) ist ein logarithmisches Ma und ist als der Logarithmus eines Leistungsverhaltnisses
deniert: x dB = 10 log(N1 =N0 ). Wenn N1 und N0 durch Spannungen U1 und U0 an gleich groen Widerstanden gemessen werden, so gilt auch x dB = 20 log(U1 =U0 )
8
Theoretische Grundlagen
Wie bei der Osetspannung tritt auch hier eine Temperaturabhangigkeit auf. Die beiden
Einzelstrome weichen voneinander ab. Man deniert ihre Dierenz als Osetstrom.
2.5 Frequenz- und Phasengang
Operationsverstarker sind mehrstuge Verstarker. Die Kollektorwiderstande der einzelnen
Stufen bilden mit den Eingangskapazitaten der folgenden Stufen RC-Glieder, die als Tiefpa wirken. Dies fuhrt zu einem Frequenzgang fur den Betrag und die Phase der Leerlaufverstarkung des Verstarkers. Zur Verdeutlichung soll zunachst die U bertragungsfunktion
eines einfachen RC-Tiefpasses (Abbildung 2.3) berechnet werden.
R
C
Ue
Ua
Abbildung 2.3: RC-Tiefpa
log|H( ω)|
ωg
log ω
0
-3dB
idealisierter
Frequenzgang
ϕ
0
0
log ω
0
45
0
90
Abbildung 2.4: Bodediagramm des RC-Tiefpasses
9
Theoretische Grundlagen
Die U bertragungsfunktion H (!) ( ! = 2 f, f = Frequenz2 ) beschreibt ganz allgemein
das Verhalten eines Systems im Frequenzbereich. Sie lat sich aus dem Verhaltnis von
Ausgangs- zu Eingangsspannung bei einer Frequenz ! berechnen. Bei Systemen, die aus
linearen Bauelementen R, L und C gebildet werden, kann dieses Verhaltnis aus den komplexen Widerstanden ermittelt werden.
Bei dem RC-Tiefpa bilden R und C einen Spannungsteiler, so da sich die U bertragungsfunktion sofort aus dem Spannungsteilerverhaltnis ergibt als:
1
(2.13)
H (! ) =
1 + i !!
g
= 1 =RC nennt man die Grenzfrequenz. Aus (2.13) folgt fur den Betrag und die Phase
von H (!):
jH (!)j = s 1 ! 2
(2.14)
1+ !
!
g
g
!
!
tan ' =
g
(2.15)
Tragt man den Betrag von H (!) doppeltlogarithmisch uber der Frequenz und den Phasenwinkel linear/logarithmisch auf, erhalt man ein sogenanntes Bodediagramm, Abbildung
2.4. Je nach Anwendung werden Betrag und Phase uber der Frequenz f oder der Kreisfrequenz ! aufgetragen.
Aus der Rechnung
ersieht man, da bei der Grenzfrequenz die Ausgangsspannung um den
p
Faktor 1= 2 =: 3 dB abgefallen ist. Fur ! ! fallt jH (!)j 1=!, d. h. pro Oktave ergibt
sich ein Abfall von 6 dB bzw. pro Dekade ein Abfall von 20 dB.
Ein Operationsverstarker besteht normalerweise aus zumindest drei Stufen, so da das eben
beschriebene Tiefpaverhalten auf den Fall von drei hintereinandergeschalteten Verstarkerstufen zu ubertragen ist. Man erhalt somit das Bodediagramm der Abbildung 2.5, wobei
die Frequenz, bei der die Leerlaufverstarkung den Wert 1 erreicht, als Transitfrequenz bezeichnet wird. Aus dem Bodediagramm folgt insbesondere, da die Phasendrehung Werte
uber 180 annehmen kann, was zu Instabilitaten fuhren kann, wie weiter unten gezeigt
wird.
Wie das Bodediagramm eines real existierenden Operationsverstarkers tatsachlich verlauft,
hangt vom inneren Aufbau ab, durch den die Lage der einzelnen Grenzfrequenzen festgelegt wird. In sehr vielen Fallen liegt die 3. Grenzfrequenz oberhalb der Transitfrequenz. Bei
den sogen. universell korrigierten Operationsverstarkern (s. unten) liegt sogar die 2. Grenzfrequenz weit oberhalb der Transitfrequenz, so da sich der Frequenzgang eines einfachen
RC-Tiefpasses ergibt.
g
2 Der
Begri "Frequenz" wird im folgenden sowohl fur f als auch fur ! benutzt.
10
Theoretische Grundlagen
Wird ein Operationsverstarker als gegengekoppelter Verstarker eingesetzt, so verkleinert
sich die Betriebsverstarkung. Gleichzeitig erhoht sich jedoch die Grenzfrequenz der Schaltung. Dies wird anhand der Abbildung 2.6 deutlich, die den Fall eines Operationsverstarkers
mit der 2. Grenzfrequenz oberhalb der Transitfrequenz zeigt.
Die Grenzfrequenz wird auch als Bandbreite B bezeichnet und gibt an, bis zu welcher
Frequenz die Schaltung als Verstarker ohne groen Verstarkungsverlust eingesetzt werden
kann.
Mit den Werten aus Abbildung 2.6 kann man folgende wichtige Aussage uber das sogen.
Verstarkungs-Bandbreite-Produkt ableiten:
log v log v = 1 bzw. log v = log f 0 = log B 0
log f 0 log f
v
f
B
Damit ergibt sich, da das Verstarkungs-Bandbreite-Produkt konstant ist:
B v = B 0 v = const
(2.16)
Bei einer Herabsetzung der Betriebsverstarkung um den Faktor der Schleifenverstarkung
v erhoht sich dafur also die Bandbreite um den gleichen Faktor.
b
o
o
g
g
g
b
g
o
o
o
b
s
logv 0
6 dB/Oktave
12 dB/Oktave
18 dB/Oktave
ωT
log ω
0
ϕ
0
0
ωg1
ωg2
ωg3
log ω
0
- 90
- 180 0
Abbildung 2.5: Bodediagramm des Operationsverstarkers
11
Theoretische Grundlagen
logv
v0
vs
vb
vs
fT
0
fg
log ω
f’g
Abbildung 2.6: Erhohung der Bandbreite durch Gegenkopplung
2.6 Slewrate S
Die Slewrate S ist ein Ma fur die schnellste uberhaupt mogliche A nderungsgeschwindigkeit der Ausgangsspannung des Operationsverstarkers. Diese Begrenzung der A nderungsgeschwindigkeit ergibt sich dadurch, da der Ausgangsstrom I1 der Eingangsstufe, durch den
die Eingangskapazitat C der nachfolgenden Koppelstufe aufgeladen werden mu, einen
maximalen Wert I1 nicht uberschreiten kann. S ist also gegeben durch:
I1
dU
=
(2.17)
S=
dt
C
k
max
a
max
k
Solange dieser Wert nicht uberschritten wird, wird das Zeitverhalten durch den Frequenzgang des Operationsverstarkers bestimmt. Liegen jedoch schnellere Spannungsanderungen
vor, so kann die Gegenkopplungsspannung nicht schnell genug aufgebaut werden, und es
entstehen Signalverzerrungen.
Ein Sinussignal der Form U = U0 sin !t hat im Nulldurchgang die maximale Steigung
d
U
= !U0
dt
Soll die Steigung die Slewrate nicht uberschreiten, so mu gelten:
S !U0 = 2 fU0
Die Frequenz f , bei der ein Sinussignal mit der maximal moglichen Amplitude U0 gerade
noch unverzerrt ubertragen werden kann, wird mit Grosignalbandbreite f bezeichnet:
S
(2.18)
f =
2U
a
amax
G
G
G
0
2.7 Eingangswiderstand
Bei einem realen Operationsverstarker wirken durch die innere Beschaltung am Verstarkereingang der Dierenzeingangswiderstand r und der Gleichtakteingangswiderstand r (s.
Abbildung 2.7).
d
gl
12
Theoretische Grundlagen
rgl
ra
rd
rgl
Abbildung 2.7: Widerstande des realen Operationsverstarkers
Fur ein Gleichtaktsignal am Eingang wirkt die Parallelschaltung des r am P-Eingang und
des r am N-Eingang, so da sich ein Gesamtgleichtaktwiderstand von insgesamt (1=2)r
ergibt. Fur das Gegentaktsignal ist nur der zwischen den Eingangen liegende Widerstand
r zu berucksichtigen.
Beim invertierenden Verstarker liegen r und r parallel vom N-Eingang zur Masse. Sie
konnen jedoch in der Regel unberucksichtigt bleiben, da der Eingangswiderstand des invertierenden Verstarkers durch R1 gegeben ist. Dieser Eingangswiderstand ergibt sich aus der
U berlegung, da der N-Eingang wegen der sehr kleinen Dierenzspannung U (U = U =v )
zwischen dem N- und dem P-Eingang virtuell auf Masse liegt.
Fur den nichtinvertierenden Verstarker bestimmt r den Eingangswiderstand des Verstarkers.
U. U. mu man den Widerstand r als Parallelschaltung zu r berucksichtigen. Dazu die
folgende U berlegung:
An r liegt die Spannung U =v U =(v v ) = U =v . Durch r iet also der Strom
U =(v r ). Der Dierenzeingangswiderstand erscheint also vom Eingang her gesehen um
den Faktor der Schleifenverstarkung hochtransformiert. Hieraus kann mit den aktuellen
Werten fur r und r abschatzen, ob r zu berucksichtigen ist.
gl
gl
gl
d
gl
d
d
d
a
o
gl
d
d
e
s
a
gl
o
a
s
b
e
s
d
d
d
gl
d
2.8 Ausgangswiderstand
Der Ausgangswiderstand r0 des gegengekoppelten Operationsverstarkers ist in der ausfuhrlichen Schreibweise deniert als:
a
r0
a
= dU
dI
a
a
;
bei U = const
e
(2.19)
In welcher Weise sich der Ausgangswiderstand des gegengekoppelten Operationsverstarkers
ergibt, zeigt die folgende U berlegung:
13
Theoretische Grundlagen
Wird der Ausgang belastet, so andert sich U um dU =
Ausgang eine Ausgangsspannungsanderung von
d
dU
a
= v dU + r dI =
o
d
a
kdU
d
a
v kdU
o
a
a
. Daraus ergibt sich am
+ r dI
a
a
Dabei entspricht r dI dem zusatzlichen Spannungsabfall am Ausgangswiderstand r . Somit folgt:
r
r
(2.20)
r0 =
1 + kv v
a
a
a
a
a
a
o
s
Der Ausgangswiderstand wird also durch die Gegenkopplung sehr stark reduziert. Man mu
jedoch berucksichtigen, da v ab der 1. Grenzfrequenz kleiner wird. r0 steigt demnach mit
wachsender Frequenz an.
s
a
2.9 Stabilitatsbetrachtung bei Operationsverstarkern
Eine wichtige Konsequenz aus der Frequenzabhangigkeit des Operationsverstarkers ist die
Gefahr der Instabilitat bei Ruckkopplungsanordnungen. Die negative Phasenverschiebung
des Ausgangssignal kann bei hohen Frequenzen auf 180 ansteigen. Diese Phasenverschiebung von 180 ergibt zusammen mit der Gegenkopplung auf den invertierenden Eingang
des Operationsverstarkers eine Mitkopplung. Der Verstarker wird dann instabil und kann
selbsterregte Schwingungen ausfuhren.
2.9.1 Stabilitatsbedingungen
Die Grenzbedingungen fur die Instabilitat ergeben sich unmittelbar aus den Gleichungen
(2.4) und (2.8), wenn der Nenner gleich 0 wird und somit v ! 1 . Dies ist der Fall wenn
kv = v = 1 ist. Somit ist die Stabilitatsgrenze bei jv j = 1 mit '(v ) = 180 gegeben.
Die Operationsverstarkerschaltung ist also instabil falls bei
'(v ) 180 die Schleifenverstarkung jv j 1 ist.
Da die Schleifenverstarkung unterhalb der Grenzfrequenz stets groer als 1 ist, mu die
interne Phasenverschiebung weniger als der kritische Wert von 180 betragen. Fur die
weiteren U berlegungen wird der Begri der Phasenreserve (phase margin) ' = '(v )+180
eingefuhrt. Fur ein stabiles Verhalten arbeitet man mit einer Phasenreserve zwischen 45
und 90. Die Abbildung 2.8 zeigt, da mit zunehmender Gegenkopplung - also abnehmender
Verstarkung - die Bandbreite des Verstarkers zwar groer wird. Gleichzeitig verringert
sich aber die Phasenreserve. Je kleiner die Phasenreserve ist, desto groer ist die Neigung
des Operationsverstarkers zur Instabilitat, was zu den Resonanzuberhohungen fuhrt. Es
wird daher i.a. erforderlich sein, geeignete Manahmen zur Erzielung einer ausreichenden
Stabilitat vorzusehen (s. unten).
b
o
s
s
s
s
s
r
s
14
Theoretische Grundlagen
log|v|
100dB
vo
80dB
60dB
40dB
90
0
60
0
45
0
20 0
20dB
10
0
0dB
f
10
100
1k
10k
100k
1M
Hz
Abbildung 2.8: Verstarkungskurven bei verschiedener Phasenreserve
2.9.2 Sprungantwort bei geringer Phasenreserve
Falls ein Operationsverstarker eine nicht genugend groe Phasenreserve besitzt, zeigt das
Ausgangssignal beim Anlegen einer Rechteckspannung ein unerwunschtes Einschwingverhalten, wie als Beispiel in der Abbildung 2.9 gezeigt ist.
Abbildung 2.9: Sprungantwort bei geringer Phasenreserve
2.9.3 Frequenzgangkorrektur
Operationsverstarkertypen, die bei der gewunschten Betriebsverstarkung keine ausreichende Phasenreserve bieten, mussen in ihrem Frequenzverlauf korrigiert werden. Diese erforderlichen Manahmen bezeichnet man als Frequenzgangkorrektur (oder auch Frequenzgangkompensation). Ein Beispiel dazu zeigt die Abbildung 2.10. Grundsatzlich mu durch
15
Theoretische Grundlagen
log|v|
logf
f’g1
f g1
Abbildung 2.10: Frequenzgangkorrektur
geeignete Schaltungsmanahmen die 1. Grenzfrequenz zu tieferen Frequenzen verschoben
werden. Die hochste Anforderung ist dann gegeben, wenn eine Verstarkerschaltung bis zur
Verstarkung v = 1 stabil sein soll. Wird in diesem Fall auch noch eine Phasenreserve von
90 verlangt, so mu der Frequenzgang von v bis zur Transitfrequenz der Frequenzgang
eines RC-Tiefpasses sein. Man spricht dann von einer universellen Frequenzgangkorrektur.
Von den Halbleiterherstellern werden Operationsverstarker angeboten (z.B. A741), die eine solche universelle Frequenzgangkorrektur bereits eingebaut haben. Dieser Frequenzgang
wird durch eine vergroerte Eingangskapazitat der Koppelstufe erreicht.
Andere Operationsverstarker haben Extraanschlusse fur eine individuelle Einstellung der
Frequenzgangkorrektur. Der A748 besitzt diese Moglichkeit durch Zuschalten eines externen Kondensators. Dadurch ist eine bessere Anpassung der Frequenzkurve an die verlangten Verstarkungseigenschaften gewahrleistet.
b
o
2.9.4 Betrieb bei kapazitiver Belastung
Wird der Ausgang eines Operationsverstarkers kapazitiv belastet, wie in Abbildung 2.11 gezeigt, so bildet der Kondensator C mit dem Ausgangswiderstand des Operationsverstarkers
einen Tiefpa, der zu der internen Phasendrehung des Operationsverstarkers eine zusatzliche Phasendrehung addiert. Dadurch verringert sich die Phasenreserve, so da sich die
Stabilitatsgrenze zu hoheren Verstarkungen verschiebt. Als Gegenmanahme kann ein Kondensator C parallel zum Widerstand R2 geschaltet werden, der mit dem Widerstand R1
einen Hochpa bildet. Ein RC-Hochpa erzeugt im Gegensatz zum RC-Tiefpa eine positive ("vorauseilende") Phasenverschiebung, mit der die Wirkung des Lastkondensators C
L
C
L
16
Anwendungen
I2
I1
R1
I3
R2
CC
RC
Ud
Ue
CL
Ua
Abbildung 2.11: Kompensation bei kapazitiver Belastung
kompensiert werden kann. Man bezeichnet diese Kompensation als "Lead-Kompensation".
Diese Kompensation kann noch durch einen in Abbildung 2.11 eingezeichneten Widerstand
R von typischerweise 10 bis 100 verstarkt werden.
C
3 Anwendungen von Operationsverstarkern
3.1 Spannungsfolger
Der Spannungsfolger stellt einen Spezialfall des nichtinvertierenden Verstarkers dar. Aus
Gleichung (2.4) folgt mit R2 = 0 und R1 ! 1 , dav = 1 (im Idealfall) ist. Der Nutb
Ue
Ua
Abbildung 3.1: Spannungsfolger
zen dieser Schaltung liegt in einem sehr hohen Eingangswiderstand und einem kleinen
Ausgangswiderstand. Der Spannungsfolger eignet sich also hervorragend fur Anpassungen
zwischen hochohmigen Signalquellen und niederohmigen Lastwiderstanden. Da der Operationsverstarker maximal gegengekoppelt ist, mu auf eine gute Frequenzgangkorrektur
geachtet werden.
17
Anwendungen
3.2 Addierer
R1
R4
R2
R3
U1 U2 U3
Ua
Abbildung 3.2: Addierer
Die Addition von analogen Signalen lat sich leicht mit der in Abbildung 3.2 gezeigten
Schaltung durchfuhren. Wendet man die Knotenregel auf den invertierenden Eingang an,
erhalt man im Idealfall (r ! 1 ; v ! 1 ):
I1 + I2 + I3 + I4 = 0
Somit ergibt sich die Ausgangsspannung zu:
U 1 U 2 U 3
(3.1)
+R +R
U = R4
R
e
o
e
e
a
1
e
2
3
3.3 Dierenzverstarker
R1
R1 /a
Ue1
Ua
R2 /b
Ue2
R2
Abbildung 3.3: Dierenzverstarker
Der Operationsverstarker eignet sich auf Grund seiner Dierenzeingangsstufe sehr gut zur
Dierenzbildung von Spannungen. Wichtig ist dabei die moglichst groe Gleichtaktunterdruckung, weil die Spannungsdierenz oft in Anwesenheit groer Gleichtaktsignale gemessen werden mu. Abbildung 3.3 zeigt die einfachste Schaltung zur Dierenzbildung. Zur
18
Anwendungen
Berechnung der Ausgangsspannung werden der P- und N-Eingang dieser linearen Schaltung
getrennt betrachtet:
1. U 2 = 0:
Die Schaltung ist dann ein invertierender Verstarker mit U = aU 1 .
2. U 1 = 0:
Die Schaltung ist jetzt ein nichtinvertierender Verstarker mit einem Eingangsspannungsteiler. Somit ist
b
R2
U2
U = (1 + a)U+ ; U+ =
U
=
2
R2
+
b
1
R2 +
b
Nimmt man die Ergebnisse von 1. und 2. zusammen so erhalt man:
1 + a
U =
1 + b bU2 aU1
Falls a = b, erhalt man das gewunschte Ergebnis:
U = a(U2 U1 )
(3.2)
Nachteilig an dieser Schaltung ist jedoch, da a und b sehr genau gleich sein mussen. Ist
das nicht der Fall, so entsteht eine Verschlechterung der Gleichtaktunterdruckung, wie im
folgenden gezeigt wird:
U 1 und U 2 werden in einen Gleichspannungs- und Dierenzspannungsanteil zerlegt:
1U ; U = U + 1U
U1=U
2
2
2
Dann ergibt sich die Ausgangsspannung als:
1 + a bU + 1 + a b U aU + 1 aU
U =
1+b
1+b2
2
(1 + a)b a(1 + b) U + (1 + a)b + a(1 + b) U U
U =
1+b
1+b
2
Der Faktor vor U ist die Gleichtaktverstarkung v und der Faktor vor U die Dierenzverstarkung v . Die Gleichtaktunterdruckung G wird also zu:
v
1 (1 + a)b + (1 + b)a
G=
=
v
2 (1 + a)b (1 + b)a
Fur kleine Abweichungen von a = a0 1=2a0 und b = a0 + 1 =2a0 kann diese Gleichung
vereinfacht werden:
a0
G (1 + a0 ) 0
a
Die Teilerfaktoren a und b mussen also sehr genau abgeglichen werden, damit diese zusatzliche Gleichtaktunterdruckung gegenuber der durch den Operationsverstarker gegebenen,
vernachlassigt werden kann.
Die einfache Schaltung nach Abbildung 3.3 hat noch weitere Nachteile:
e
a
e
e
e
e
a
a
a
e
e
e
a
d
gl
gl
e
d
gl
gl
d
d
d
a
gl
gl
gl
gl
d
d
gl
d
19
Anwendungen
1. Sie besitzt relativ niedrige und verschiedene Eingangswiderstande.
2. Der Innenwiderstand der Signalquelle ist bei a und b zu berucksichtigen.
3. Eine A nderung der Verstarkung erfordert ein synchrones Verstellen von a und b.
Deshalb wird bei hoheren Anforderungen die nun folgende Schaltung als Vorstufe eingesetzt. Die gesamte Schaltung wird dann als Instrumentenverstarker bezeichnet.
3.4 Instrumentenverstarker
R1
R3
Ue1
Ua 1
R1 /a
R4
R2 /b
Ua 2
R5
Ue2
Ua
R2
Abbildung 3.4: Instrumentenverstarker
Da im Idealfall die Spannung zwischen P- und M-Eingang der beiden Operationsverstarker
der Vorstufe null ist, liegt die Dierenz der Eingangsspannungen am Widerstand R4 . Der
Strom I durch die drei Widerstande ist somit:
U
U2
I= 1
R4
Jeder einzelne Operationsverstarker stellt einen Spannungsfolger dar, so da folgt:
R
U 1 = U 1 + R3 I = U 1 + 3 (U 1 U 2 )
R
e
a
U2
a
=
U2
e
e
e
4
R5
(U
R4 1
R5 I = U 2
e
U2
a
e
e
e
e
U 2)
e
= R3 + RR4 + R5 (U 1 U 2 )
4
U 2 ) ist die Betriebsverstarkung dieser Vorstufe.
R + R4 + R5
v = 3
R
U1
Der Faktor vor (U 1
e
e
a
e
e
b
4
(3.3)
20
Anwendungen
Auerdem ist
= 21 (U 1 + U 2 ) = 21 (U 1 + U 2) + R32R R5 (U 1 U 2 )
4
U
= v U +v U
Hieraus folgt: v = 1 und v = 0, wenn R3 = R5 . Insgesamt erhoht also die Schaltung
die Gesamtdierenzverstarkung um den Faktor v , der Betriebsverstarkung der Vorstufe,
wahrend die Gleichtaktverstarkung nicht vergroert wird. Damit verbessert sich auch die
Gesamtgleichtaktunterdruckung um den Faktor v . Auerdem bietet die Schaltung hochohmige Eingange, und die Verstarkung kann leicht durch R4 verandert werden.
U
agl
agl
gl
gl
a
a
gl
dgl
e
e
e
e
d
dgl
b
b
3.5 Integrator
Eine besonders wichtige Anwendung des Operationsverstarkers in der Analogtechnik ist
der Integrator. Er bildet allgemein einen Ausdruck der Form
U
a
=A
Z
U (t)dt
(3.4)
e
Abbildung 3.5 zeigt die Schaltung eines Integrators, dessen Ausgangsspannung sich wie
folgt berechnet:
Man wendet die Knotenregel auf den Summationspunkt am invertierenden Eingang des
Operationsverstarkers an und erhalt im Idealfall (r = 1):
I +I =0
Fur den Strom, der durch den Kondensator iet, gilt allgemein:
e
R
I
C
C
= C dU
dt
a
IC
R
C
IR
Ue
Ua
Abbildung 3.5: Integrator
21
Anwendungen
Durch Einsetzen folgt:
+ C dU
=0
dt
und man erhalt fur die Ausgangsspannung den Ausdruck:
1 Z U dt + U (t = 0)
U =
U
R
a
e
a
RC
e
(3.5)
a
Somit kann mit dieser Schaltung die Eingangsspannung auntegriert werden. Ist die Eingangsspannung eine sinusformige Wechselspannung U = U0 sin !t, so wird die Ausgangsspannung
Z
1
U
U0 sin !tdt = 0 cos !t
(3.6)
U =
RC
!RC
e
a
Die Amplitude der Ausgangsspannung ist also umgekehrt proportional zu !. Tragt man
das Verhaltnis von Ausgangs- und Eingangsspannung in Abhangigkeit zur Frequenz doppellogarithmisch auf, so ergibt sich eine Gerade, die mit 20 dB/Dekade fallt.
Man deniert: Eine Schaltung ist als Integrator in dem Frequenzbereich verwendbar, in
dem die Frequenzgangkurve mit 20 dB/Dekade fallt und die Phasenverschiebung 90
betragt.
log|v|
idealer Integrator
vo
idealisierter Frequenzgang des
Operationsverstärkers
1/RC
1
voRC
fT
logf
fg
realer Integrator
Abbildung 3.6: Frequenzgang des idealen und realen Integrators
22
Anwendungen
Die errechnete Gleichung gilt fur einen idealen Integrator. Die Eigenschaften des realen
Operationsverstarkers schranken den Arbeitsbereich des Integrators z.T. erheblich ein. Abbildung 3.6 zeigt den Frequenzgang eines realen Integrators. Bei tiefen Frequenzen knickt
der Integratorfrequenzgang infolge der endlichen Verstarkung des Operationsverstarkers
in die Horizontale ab. Bei hohen Frequenzen wird der Abfall des Frequenzganges ab der
Stelle f auf 40 dB/Dekade erhoht. Bei Berucksichtigung des realen Verlaufes der Leerlaufverstarkung mu man sich noch ausreichend weit von den beiden Knickstellen entfernt
halten, um Integrationsfehler klein zu halten.
In der Praxis schaltet man einen Widerstand R2 parallel zum Kondensator C und verhindert so die Auadung des Kondensators durch Eingangsruhestrom und Osetspannung.
Die Schaltung dient zur Integration von Wechelspannungen, deren Frequenz oberhalb der
durch R2 und C gegebenen Frequenz liegen. Es ist dann ausreichend, den idealisierten Integratorfrequenzgang erst bei dieser Frequenz einsetzen zu lassen. Unterhalb dieser Frequenz
kann der Frequenzgang konstant sein. Unter Berucksichtigung der realen Verhaltnisse wird
man den U bergang von dem Integratorfrequenzgang zum konstanten Frequenzgang etwa
eine Dekade niedriger als die kleinste Frequenz der zu integrierenden Wechselspannung
legen.
T
3.6 Dierentiator
Einen Dierentiator erhalt man, wenn man beim Integrator
Eingangsstrom I ladt den Kondensator C auf, wobei
R
und C vertauscht. Der
e
I
e
= C dU
dt
e
ist. Dieser Strom iet uber R zum Ausgang (Idealfall: r = 1), so da I =
Die Ausgangsspannung ist daher
dU
U = RC
dt
e
e
e
a
Ia
C
R
Ie
Ue
Ua
Abbildung 3.7: Dierentiator
I
a
=
U =R.
a
(3.7)
23
Anwendungen
Bei sinusformiger Eingangsspannung U = U0 sin !t ist
U = RC!U0 cos !t
(3.8)
Der zu einem idealen Dierentiator gehorende Frequenzgang zeigt somit einen zur Frequenz
proportionalen Anstieg mit 20 dB pro Dekade und eine Phasenverschiebung von +90. Hohe
Frequenzen werden also mehr verstarkt als tiefe. Darin liegt jedoch ein erheblicher Nachteil
von Dierentiatorschaltungen. Das stets vorhandene Rauschen, das eine groe Bandbreite
besitzt, und andere hochfrequente Storungen werden gegenuber dem eigentlichen Signal
stark herausgehoben. Um dies zu vermeiden, legt man in der Praxis einen Widerstand R0
in Reihe mit dem Kondensator C . Damit wird die maximale Verstarkung auf den Wert
R=R0 beschrankt. Gleichzeitig wird eine Stabilisierung der Schaltung erreicht. Abbildung
3.8 zeigt den Frequenzgang dieser Schaltung.
e
a
log|v|
vo
idealer Differentiator
R
R’
idealisierter Frequenzgang des
Operationsverstärkers
realer Differentiator
!
RC
fT
logf
fg
Abbildung 3.8: Frequenzgang des idealen und realen Dierentiators
3.7 Aktive Filter
Ein aktives Filter enthalt zusatzlich zu mindestens einem Bauelement mit frequenzabhangigen Impedanz einen Verstarker als aktiven Teil. Dabei lat sich der integrierte Operationsverstarker sehr vorteilhaft als aktives Bauelement einsetzen. Als Bauelemente mit frequenzabhangiger Impedanz passen hierzu Kondensatoren, die man mit ohmschen Widerstanden
zusammenwirken lat. Schaltungen, die aus Kondensatoren und ohmschen Widerstanden
aufgebaut sind, nennt man RC-Netzwerke. Im folgenden beschaftigen wir uns mit aktiven
Filtern, die aus RC-Netzwerken und Operationsverstarkern bestehen.
24
Anwendungen
Die Filtergrundtypen sind Tief-, Hoch- und Bandpasse sowie Bandsperren.
Als Grenzfrequenz eines Filters wird diejenige Frequenz bezeichnet, bei der das Verhaltnis
von Ausgangs- zur Eingangsspannung um 3 dB vom fur den Durchlabereich geltenden
Wert abgesunken ist.
Man unterscheidet bei Hoch-, Tief- und Bandpassen sowie bei Bandsperren Filter erster,
zweiter, dritter,.... Ordnung. Damit kennzeichnet man die Frequenzgang-Flankensteilheit
oberhalb (Tiefpa) bzw. unterhalb (Hochpa) der Grenzfrequenz. Bei einem Tiefpa n-ter
Ordnung fallt der Frequenzgang nach der Grenzfrequenz mit n 20 dB/Dekade ab. Bei
einem Hochpa steigt er mit entsprechendem Wert vor der Grenzfrequenz an.
Fur die Entwicklung von Filtern gibt es Standardverfahren, bei denen auf bestimmte Eigenschaften optimierte U bertragungsfunktionen, benutzt werden. Am Beispiel des Tiefpasses
soll ein solches Verfahren kurz skizziert werden.
Fur einen einfachen RC-Tiefpa ist die U bertragungsfunktion durch
1
A(! ) =
1 + i!RC
gegeben. In der Filtertheorie wird anstelle von i! die Variable s = + i! benutzt, und
die U bertragungsfunktion wird im Bildbereich der Laplace-Transformation beschrieben.
Auerdem wird die Variable s normiert: S = s=! mit ! = 1 =RC. Somit erhalt man
1
A(S ) =
(3.9)
1+S
Benotigt man steilere Frequenzabfalle oberhalb der Grenzfrequenz, so kann man n Tiefpasse
in Reihe schalten, woraus sich eine U bertragungsfunktion der Form
1
A(S ) =
(3.10)
(1 + k1 S )(1 + k2S ) (1 + k S )
ergibt. Durch Ausmultiplizieren des Nenners gewinnt man dann die allgemeine U bertragungsfunktion eines Tiefpasses n-ter Ordnung:
A0
A(S ) =
(3.11)
1 + c1 S + c2S 2 + + c S
Das Nennerpolynom wird wie folgt in Faktoren zerlegt:
A0
A0
=
(3.12)
A(S ) =
Q
2
2
(1 + a S + b S )(1 + a S + b S ) (1 + a S + b S 2)
g
g
n
n
1
1
2
2
n
i
i
Zur Erzielung bestimmter Eigenschaften der U bertragungsfunktion haben sich fur das Nennerpolynom einige bekannte Polynome als gunstig herausgestellt. Dies sind:
Butterworth-Polynome: Sie ergeben einen moglichst lange horizontal verlaufenden
Frequenzgang, der erst kurz vor der Grenzfrequenz scharf abknickt. Fur das zeitliche Verhalten ergibt sich hieraus allerdings fur die Sprungantwort ein erhebliches
U berschwingen, das mit zunehmender Ordnung groer wird.
25
Anwendungen
Tschebysche-Polynome: Diese Polynome ergeben ein noch scharferes Abknicken der
U bertragungsfunktion bei der Grenzfrequenz als die Butterworth-Polynome. Dafur
zeigt sich im Durchlabereich eine Welligkeit mit konstanter Amplitude. Je groer
man die Welligkeit zulat, umso scharfer ist der Abfall bei der Grenzfrequenz. Das
U berschwingen der Sprungantwort ist starker als bei den Butterworth-Polynomen
und steigt mit zunehmender Welligkeit der U bertragungsfunktion.
Bessel-Polynome: Bei ihnen erzielt man eine optimale Sprungantwort. Dafur mu
jedoch ein nicht so scharfer Abfall der U bertragungsfunktion bei der Grenzfrequenz
in Kauf genommen werden.
Fur diese Filtercharakteristiken sind die notwendigen Koezienten a und b in der folgenden Tabelle bis zur 4. Ordnung aufgefuhrt:
Ordnung
Filter-Nr. a
b
Butterworth
1
1
1.0000 0.0000
2
1
1.4142 1.0000
3
1
1.0000 0.0000
2
1.0000 1.0000
4
1
1.8478 1.0000
2
0.7654 1.0000
Tschebysche
1
1
1.0000 0.0000
2
1
1.0650 1.9305
3
1
3.3496 0.0000
2
0.3559 1.1923
4
1
2.1853 5.5339
2
0.1964 1.2009
Bessel
1
1
1.0000 0.0000
2
1
1.3617 0.6180
3
1
0.7560 0.0000
2
0.9996 0.4772
4
1
1.3397 0.4889
2
0.7743 0.3890
i
i
i
i
3.7.1 Tiefpa-Hochpa-Transformation
Von einem Tiefpa zum entsprechenden Hochpa kommt man, indem man die Frequenzgangkurve an der Grenzfrequenz spiegelt. Die zu Gleichung (3.12) fur Hochpasse entspre-
26
Anwendungen
chende erhalt man, wenn 1=S fur S gesetzt wird, was der Spiegelung in der logarithmischen
Darstellung des Frequenzganges gleichkommt. Somit lautet die analoge U bertragungsfunktion fur Hochpasse:
A1
(3.13)
A(S ) = Q b a
1 + S + S2
Entsprechend lassen sich aus dem Tiefpa auch der dazugehorige Bandpa und die entsprechende Bandsperre errechnen. Die dazugehorenden Transformationen sind jedoch komplizierter.
i
i
3.7.2 Realisierung von Tiefpaltern 1.Ordnung
Fur einen Tiefpa erster Ordnung erhalten wir aus Gleichung (3.12) folgende U bertragungsfunktion:
A0
A(S ) =
(3.14)
1 + a1 S
Sie lat sich mit einem einfachen RC-Glied realisieren. Da jedoch bei Belastung des RCGliedes seine Eigenschaften sich andern, schaltet man einen Operationsverstarker nach,
dessen Verstarkungsfaktor durch die Widerstande der Ruckkopplung frei gewahlt werden
kann. Man erhalt somit die Schaltung in Abbildung 3.9 fur einen aktiven Tiefpa erster
Ordnung:
R1
R2
Ue
C
Ua
R3
Abbildung 3.9: Tiefpalter 1. Ordnung
3.7.3 Realisierung von Tiefpaltern 2. Ordnung
Tiefpalter 2. Ordnung haben die U bertragungsfunktion
A(S ) =
A0
1 + a1 S + b1 S 2
Diesen Filtertyp kann man durch mitgekoppelte Operationsverstarker realisieren.
(3.15)
27
Anwendungen
C2
R1
R2
R3
C1
Ue
Ua
R4
Abbildung 3.10: Tiefpa 2. Ordnung
Abbildung 3.10 zeigt eine Schaltung fur einen Tiefpa zweiter Ordnung: Dabei stellt der
Spannungsteiler R3, R4 uber die hierdurch erfolgte Gegenkopplung die innere Verstarkung
k = 1 + R3 =R4 des Operationsverstarkers ein. Die Mitkopplung erfolgt uber den Kondensator C2.
Unter den moglichen Realisierungen solcher Schaltungen sollen hier nur zwei Spezialfalle
betrachtet werden.
Spezialfall 1:
Die innere Verstarkung k wird 1 gesetzt. Der Operationsverstarker arbeitet dann als Spannungsfolger. Ohne explizite Herleitung erhalt man fur die U bertragungsfunktion:
1
A(S ) =
(3.16)
1 + ! C1 (R1 + R2 )S + !2R1R2 C1C2S 2
Gibt man C1 und C2 vor, so ergibt sich durch Koezientenvergleich mit der Gleichung
(3.15):
q
a1 C2 a21 C22 4b1 C1 C2
(3.17)
A0 = 1
; R1 2 =
4f C1C2
Damit sich reelle Werte ergeben mu die Bedingung
C2 4b1
(3.18)
g
g
;
g
C1
a21
erfullt sein. Die gunstigste Dimensionierung liegt dann vor, wenn das Verhaltnis C2 =C1
nicht viel groer gewahlt wird, als die Bedingung vorschreibt.
Spezialfall 2:
 bertragungsfunktion hat dann (ohne Herleitung)
R1 = R2 = R und C1 = C2 = C . Die U
die Form:
k
A(S ) =
(3.19)
1 + ! RC (3 k)S + ( ! RC )2 S 2
g
g
28
Anwendungen
Durch Koezientenvergleich mit Gleichung (3.15) erhalt man:
p
a
b1
RC =
;
k = A0 = 3 p 1
2f
b1
Daraus ist zu ersehen, da die innere Verstarkung nicht von der Grenzfrequenz abhangt
sondern vielmehr von den Koezienten a1 und b1 . Die Groe k bestimmt damit den Filtertyp. Setzt man die in der Tabelle fur die Filtercharakteristiken angegebenen Koezienten
der Filter zweiter Ordnung ein, so erhalt man fur k die Werte:
Butterworthlter: k = 1 :586
Tschebyschelter: k = 2 :234
Bessellter: k = 1 :268
g
3.7.4 Realisierung von Tiefpassen hoherer Ordnung
Um Filter mit scharferer Filtercharakteristik zu erhalten, schaltet man Filter erster und
zweiter Ordnung in Reihe. In der obigen Tabelle sind fur solche Filter (dritter und vierter
Ordnung) die Filterkoezienten der Teillter (Filter-Nr.) angegeben. Auf die weiteren
Einzelheiten wird jedoch hier nicht eingegangen.
3.8 Nichtlineare Anwendungen von Operationsverstarkern
In den beiden vorangegangenen Abschnitten wurden lineare Schaltungen mit Operationsverstarkern beschrieben. Dabei hatten A nderungen der Eingangsgroen stets linear proportionale Ausgangsgroenanderungen. Bei nichtlinearen Schaltungen ist dies nicht mehr
der Fall.
3.8.1 Einweggleichrichter
Als eine der am haugsten verwendeten nichtlinearen Schaltungen ist die Anwendung des
Operationsverstarkers als Gleichrichter zu nennen. Dabei haben Gleichrichterschaltungen
mit Operationsverstarkern die Eigenschaften einer idealen Diode: In Sperrichtung ist die
Ausgangsspannung des Gleichrichters gleich null und in Durchlarichtung direkt proportional zur Eingangsspannung.
In Abbildung 3.11 ist eine Einweggleichrichterschaltung angefuhrt.
Durchlabereich:
Bei einem positiven Eingangssignal erscheint am Verstarkerausgang eine invertierte, also
negative Spannung. Die Diode D1 wird leitend und die Schaltung arbeitet wie ein invertierender Verstarker mit Betriebsverstarkung v = R2 =R1. (Diode D2 sperrt!)
b
29
Anwendungen
R2
D2
R1
D1
Ue
Ua
Abbildung 3.11: Einweggleichrichter
Sperrbereich:
Ist das Eingangssignal negativ, so wird die Ausgangsspannung des Operationsverstarkers
positiv und somit sperrt die Diode D1. Es iet nur noch der Diodenstrom, der am Widerstand R2 einen zu vernachlassigenden Spannungsabfall erzeugt. Somit ist das Eingangssignal vollig gesperrt.
Im Sperrbereich geht die Ausgangsspannung des Operationsverstarkers in die Sattigung,
weil die Ruckfuhrungsschleife durch die gesperrte Diode D1 geonet ist (wie unbeschaltete
Anordnung). Durch diese U bersteuerung entstehen unsaubere Nulldurchgange, die durch
die bei der U bersteuerung entstehende Erholzeit verursacht werden. Eine Begrenzung der
Dierenzverstarkung mit einer weiteren Diode D2 im Ruckkopplungsweg, die nur leitet,
falls die Ausgangsspannung des Operationsverstarkers positiv ist, schaltet diesen Eekt
aus.
3.8.2 Zweiweggleichrichter
Diese Schaltung wird verwendet, um eine Betragsbildung des Eingangssignales vorzunehmen. Wie aus Abbildung 3.12 zu ersehen ist, setzt sich eine Zweiweggleichrichterschaltung
aus einem Einweggleichrichter und einem Addierer zusammen. Legt man am Eingang des
Gleichrichters ein Sinussignal an, so soll die erste Halbwelle verdoppelt werden - d.h. der
Gleichrichter ist so zu beschalten, da er in Durchlarichtung als invertierender Verstarker
mit Faktor zwei wirkt. Die zweite Halbwelle wird gesperrt. Jetzt wird das Ausgangssignal
des Gleichrichters mit dem ursprunglichen Sinussignal addiert. Man wahlt hier einen invertierenden Verstarker mit Verstarkungsfaktor eins. Durch die Addition erhalt man nun
gleichhohe Halbwellen gleicher Polaritat.
Setzt man zusatzlich einen Kondensator parallel zum Widerstand des Ruckkopplungszweiges des Addierers, so lat sich eine Mittelwertsbildung durchfuhren.
30
Versuchsdurchfuhrung
2R
R
D2
C
R
R
D1
R
Ue
U a1
Ua 2
Abbildung 3.12: Zweiweggleichrichter
4 Versuchsdurchfu
 hrung
Durch den Einsatz von modernen elektronischen Geraten sind fur die Aufnahme der verschiedenen Mekurven keine punktweisen Einzelmessungen erforderlich. Alle Versuchsergebnisse konnen als Schreiberkurven aufgezeichnet werden. Lassen Sie sich vom Assistenten
Funktion und Bedienung der Megerate erklaren.
4.1 Versuchsanordnung
Fur die Durchfuhrung der Messungen stehen die folgenden Gerate zur Verfugung:
Speicheroszillograf
Funktionsgenerator
Versuchsschaltung
Gleichrichter
und
Logarithmierer
Schreiber
Phasenmesser
Abbildung 4.1: Versuchsanordnung
1. Der Funktionsgenerator liefert die benotigten Eingangssignale fur die zu untersuchenden Operationsverstarkerschaltungen. Weiterhin bietet er die "log-sweep"-Funktion,
mit der bei den Frequenzkurvenaufzeichnungen eine logarithmische Frequenzachse
moglich ist.
2. Mit dem Zweistrahlspeicheroszilloskop konnen die Ein- und Ausgangssignale der
verschiedenen Operationsverstarkerschaltungen untersucht und festgehalten werden.
Versuchsdurchfuhrung
31
Das Oszilloskop kann in der ublichen Weise periodische, analoge Signale darstellen
und zusatzlich beliebige Signale digitalisieren und speichern. Von dieser Moglichkeit
wird bei der Aufzeichnung der verschiedenen Ausgangssignale aus den Versuchsschaltungen auf dem Schreiber Gebrauch gemacht.
3. Das Ausgangssignal des Operationsverstarkers wird bei den Frequenzganguntersuchungen auf den Eingang eines Gleichrichters und anschlieend zum Logarithmierer
gefuhrt. Zusammen mit der "log-sweep"- Funktion des Funktionsgenerators lat sich
damit die doppeltlogarithmische Darstellung der Frequenzgange (Bode-Diagramm)
realisieren.
Da der Gleichrichter eine zeitliche Mittelwertsbildung durchfuhrt, darf der Frequenzdurchlauf nicht zu schnell erfolgen. Fur einen Durchlauf sollten mindestens 60 s
gewahlt werden, da sonst die aufgezeichnete Kurve fehlerhaft ist.
4. Zur Messung der Abhangigkeit der Phasenverschiebung von der Frequenz wird ein
Phasenmesser eingesetzt.
5. Die Versuchsergebnisse werden von einem XY-Schreiber aufgezeichnet, der sowohl
vom Funktionsgenerator als vom Oszilloskop im Digitalbetrieb gesteuert werden
kann. Fur den Wechsel zwischen der Aufzeichnung vom gespeicherten Oszillografenbild und den Frequenzkurven mit dem Funktionsgenerator ist ein Umschalteinschub
vorhanden. Auf diesem Umschalteinschub benden sich 2 Potentiometer, mit denen
im Bedarfsfall die Empndlichkeit des XY-Schreibers zwischen den festen Empndlichkeitsstufen variiert werden kann. Am Schreiber ist deshalb immer die Stellung
CAL zu belassen.
4.2 Operationsverstarkerschaltungen
Die einzelnen Operationsverstarkerschaltungen werden auf vorgegebenen Steckbrettern
aufgebaut. Die entsprechenden elektronischen Bauteile liegen als Steckteile bereit.
4.2.1 Das Zentralsteckbrett
Das Zentralsteckbrett wird fur den Aufbau der meisten Teilversuche benotigt. Auf ihm
bendet sich ein A748-Operationsverstarker, mit dem man die beiden Grundschaltungen,
sowie die Untersuchungen der Kenngroen und die Aufnahme der Frequenz- und Phasengange durchfuhren kann. Auerdem werden einige Anwendungsbeispiele wie Integrator,
Dierentiator, Dierenz verstarker und einfache Filterschaltungen realisiert. Das Zentralsteckbrett ist so allgemein aufgebaut, da alle vorgesehenen Schaltungen mit ihm realisiert
werden konnen.
Die Spannungsversorgung der Operationsverstarker wird uber das Zentralsteckbrett erreicht. Das Steckbrett hat einen Anschlu fur +15 V / 0 V / -15 V. Mit einem Schalter
32
Versuchsdurchfuhrung
kann diese Versorgungspannung direkt am Zentralsteckbrett ein- und ausgeschaltet werden.
Mit dem Potentiometer links neben dem Schalter kann die Osetspannung des Operationsverstarkers kompensiert werden. Auerdem sind zwei Buchsen zur Frequenzgangkompensation (Frequenzgangkorrektur) vorgesehen.
4.2.2 Die Hilfssteckbretter
Fur Schaltungen mit mehreren Operationsverstarkern stehen Hilfssteckbretter bereit, die
seitlich an das Zentralsteckbrett angekoppelt werden. Dies geschieht mit Hilfe von seitlichen
Steckverbindungen, die gleichzeitig die Spannungsversorgung der Operationsverstarker auf
den Hilfssteckbrettern gewahrleisten. Im ganzen gibt es drei verschiedene Hilfssteckbretter,
die fur drei unterschiedliche Anwendungsbeispiele verwendet werden:
1. Das erste Hilfssteckbrett wird fur die Instrumentenverstarkerschaltung verwendet.
Dabei dient es als Vorstufe zu der Dierenzverstarkerschaltung. Das Hilfssteckbrett
wird von links an das Zentralsteckbrett gesteckt, wobei das Zentralsteckbrett als
Dierenzverstarker geschaltet wird.
2. Mit dem zweiten Hilfssteckbrett konnen Filterschaltungen 2. Ordnung aufgebaut werden.
3. Fur die Zweiweggleichrichterschaltung wird eine Vorstufe benotigt. Auf dem Hilfsteckbrett Gleichrichter wird die Einweggleichrichterschaltung aufgebaut. Das anschlieende Zentralsteckbrett dient als Addierer.
Versuchsdurchfuhrung
33
5 Versuchsanleitung
5.1 Hinweise fur die Benutzung der Megerate
1. Am XY-Schreiber mu fur beide Achsen immer die Einstellung CAL gewahlt werden.
Damit kann am Schreiber die Empndlichkeit nur mit den Drehschaltern in groben
Stufen verandert werden. Fur eine eventuelle Feinstellung mussen die Potentiometer
am Umschaltereinschub in den Stellung VAR der CAL/VAR-Umschalter benutzt
werden.
2. Fur die Aufzeichnung der Frequenzgangkurven sind fur beide Achsen am Schreiber
0,2 V/cm einzustellen. Bei den Phasengangmessungen mu die Y-Empndlichkeit
auf 1 V/cm gesetzt werden.
Alle Kurven sollen auf ein lin/log-Papier mit 4 Dekaden geschrieben werden, wobei die Empndlichkeitseinstellung der X-Achse des XY-Schreibers zweckmaigerweise so gewahlt wird, da der durchlaufene Frequenzbereich mit der entsprechenden
Dekadenanzahl zusammenfallt. Diese Einstellung wird fur die X-Achse durch das
Potentiometer am Umschalteinschub erreicht. An der Frontseite des XY-Schreibers
bendet sich neben dem Eingangskabel ein Schalter fur das Ausschalten der automatischen Schreiberstiftsteuerung, wodurch leicht ein Probedurchlauf einer Frequenzkurve durchgefuhrt und die richtige Empndlichkeitseinstellung der X-Achse
vorgenommen werden kann.
3. Bei den Frequenzgangkurven wird das Ausgangssignal der Versuchsschaltung uber
den logarithmischen Verstarker auf den XY-Schreiber gefuhrt.
Hierbei ist zu beachten, da die Signalamplitude des Funktionsgenerators so eingestellt wird, da fur das maximal auftretende Ausgangssignal aus der Schaltung das
Ausgangssignal des logarithmischen Verstarkers -0,05 bis -0,1 V betragt. Der logarithmische Verstarker liefert bei fallendem Eingangssignal ein steigendes Ausgangssignal
mit negativem Vorzeichen. Der Nullpunkt des XY-Schreibers ist deshalb nach links
oben zu verlegen.
Der logarithmische Verstarkers gibt pro Dekade eine Spannungsanderung von 2 V
ab. Durch die Wahl 0,2 V/cm fur die Y-Achse entsprechen 10 cm einem Signalanderungsfaktor von 10. Der VAR/CAL-Schalter fur die Y-Achse am Umschaltereinschub
mu auf CAL gestellt werden.
4. Bei der Aufzeichnung vom gespeicherten Oszillografenbild mu fur die richtige Einstellung der Empndlichkeit des Schreibers fur beide Achsen 0,05 V/cm gewahlt und
der CAL/VAR-Schalter am Umschalteinschub auf CAL gestellt werden.
5. Mit Ausnahme der Messungen in den Abschnitten 5.2, 5.3, 5.5.4 und 5.5.5 mu
das Ausgangssignal des Funktionsgenerators uber einen 20 dB-Abschwacher auf die
Schaltungen gegeben werden. Dadurch wird vermieden, da der Funktionsgenerator
34
Versuchsdurchfuhrung
in seinem unteren Amplitudenbereich arbeitet. Der genaue Abschwachungsfaktor =
10,53. Der Abschwacher mu dazu mit einem 50 -Widerstand abgeschlossen werden.
6. Alle Spannungsangaben fur die Ausgangsspannung des Funktionsgenerators sind immer Volt-Spitze-Spitze und konnen direkt am Funktionsgenerator eingestellt werden.
7. Zu beachten: Das Verbindungskabel vom Ausgang der aufgebauten Operationsverstarkerschaltungen zu dem jeweiligen Megerat stellt eine kapazitive Belastung von etwa 100
pF/m Kabellange. Diese Belastung wirkt sich auf den Frequenzgang des Operationsverstarkers aus, s. dazu 5.4.7. Benutzen Sie deshalb immer das gleiche Mekabel.
5.2 Grundschaltungen
5.2.1 Nichtinvertierender und invertierender Verstarker
Diese ersten Messungen sollen im wesentlichen dazu dienen, den Umgang mit den verschiedenen Geraten zu erlernen. Hier sollten Sie den Assistenten um seine Hilfe bitten. Nutzen
Sie vor allem die Moglichkeiten des Speicheroszillografen.
Kondensator fur die Frequenzgangkorrektur: C = 3,3 pF
Widerstandswerte: R1 = 1 k
, R2 = 10 k
.
Sinus mit f 1 kHz.
Stellen Sie die Amplitude am Funktionsgenerator so ein, da die Verstarkerschaltung nur
maig (einige Volt) ausgesteuert wird.
Fuhren Sie diese Messungen sowohl fur den invertierenden als auch fur den nichtinvertierenden Verstarker durch.
Der tatsachliche Verstarkungsgrad ist zu messen (Cursor- und Calculator-Funktion des
Speicheroszilloskops benutzen!) und mit dem Wert, der sich aus R1 und R2 ergibt, zu vergleichen. Die Widerstande haben eine Genauigkeit von 0,5%. Die Megenauigkeit des
Oszillografen betragt 3%.
Ein- und Ausgangssignal sind auf dem Speicheroszilloskop zu speichern und mit dem XYSchreiber festzuhalten, so da deren Phasenlage verglichen werden kann.
Die dargestellten Signale im Digitalbetrieb zeigen im Unterschied zu den "glatten" Kurven
im Analogbetrieb ein uberlagertes Storsignal, das durch die begrenzte Auosung von 8
bit (256 Amplitudenstufen) bei der Analog-Digital-Wandlung entsteht und als "Quantisierungsrauschen" bezeichnet wird. Fur die U bertragung auf den XY-Schreiber sollten Sie
die Moglichkeit der Mittelwertsbildung (Menu PROCESS-AVERAGE) zur Kurvenglattung
ausnutzen.
k
5.3 Aussteuerungsbereich, Osetspannung, Slewrate
Bei diesen Messungen mu das Ausgangssignal des Funktionsgenerators ohne den oben
genannten Abschwacher auf den Eingang der Schaltung gegeben werden.
35
Versuchsdurchfuhrung
5.3.1 Linearer Aussteuerungsbereich
Beobachten Sie mit dem invertierenden Verstarker mit v = 10 die maximale Aussteuerung
und messen Sie die maximale Ausgangsamplitude.
b
5.3.2 Oseteinstellung
Im Zentralsteckbrett ist oben ein Potentiometer eingebaut, mit dessen Hilfe fur die folgenden Versuche die Osetspannung des Operationsverstarkers eingestellt wird. Mit dem
Potentiometer mu die Osetspannung so abgeglichen werden, da das Ausgangssignal
symmetrisch zur Nullinie liegt. Am besten wahlen Sie dazu eine Ausgangsamplitude unter
1 V und eine dazu passende Oszillografenempndlichkeit.
5.3.3 Slewrate
Mit Hilfe des Speicheroszillografen kann die Slewrate (maximale A nderungsgeschwindigkeit des Ausgangssignals des Operationsverstarkers) in Abhangigkeit vom Kondensator C
fur die Frequenzgangkompensation bestimmt werden. Dazu wird bei dem invertierenden
Verstarker ein Rechtecksignal im Frequenzbereich von 1 bis 10 kHz und groer Amplitude
als Eingangssignal benutzt.
Fur den Kondensator C sind die Werte 0, 1, 3,3, 10 und 33 pF einzusetzen. Nutzen Sie
dazu die Messung im Digitalbetrieb mit Hilfe der Cursor aus.
Eine der Messungen soll auf den XY-Schreiber aufgezeichnet werden.
Auswertung:
Aus der Auftragung 1=S = f (C ) (s. Gleichung (2.17)) konnen der maximale Auadestrom
des Kompensationskondensators und der intern vorhandene Koppelkondensator ermittelt
werden (s. Schaltung der 741).
k
k
k
5.3.4 Grenzfrequenz des maximalen, unverzerrten Ausgangssignales
Fur einen invertierenden Verstarker mit v = 10 wird mit einem Sinussignal bei niedriger
Frequenz ( 1 kHz) der Verstarker maximal ausgesteuert. Die Frequenz wird dann solange
erhoht bis das Ausgangssignal am Oszillografen verzerrt auftritt. Diese Messung ist fur 2
verschiedene Werte (3,3 und 33 pF) fur den Kondensator C durchzufuhren.
Auswertung:
Der zugehorige Frequenzwert wird mit dem theoretischen Wert verglichen (f = S=(2U0 )).
Die Messung ist nicht sehr genau, da die Beurteilung der Signalverzerrung subjektiv ist.
b
k
G
36
Versuchsdurchfuhrung
5.4 Frequenz- und Phasengange
Der Frequenz- und Phasengang sind wichtige Eigenschaften des Operationsverstarkers. Es
sollen im folgenden die Abhangigkeit des Frequenz- und Phasengangs von verschiedenen
Parametern erarbeitet werden.
Bei diesen Messungen kommt es sehr auf die gute Ausnutzung von Funktionsgenerator und
XY-Schreiber an. Deshalb wird nun das Ausgangssignal des Funktionsgenerators um 20 dB
gedampft.
5.4.1 Frequenzgang bei unterschiedlicher Beschaltung
Schaltung (auf Zentralsteckbrett): Invertierender Verstarker mit R1 = 1 k
und verschiedenen Widerstandswerten fur R2:
1) R2 = 100 k
,
2) R2 = 33 k
,
3) R2 = 10 k
,
4) R2 = 3,3 k
,
Kondensator C = 10 pF.
Aufnahme der Frequenzkurven im Frequenzbereich f = 1 kHz - 1 MHz auf ein gemeinsames
Blatt.
Auswertung:
Mit Hilfe der aufgenommenen Frequenzgange ist zu uberprufen, ob das Verstarkungsbandbreiteprodukt konstant ist.
k
5.4.2 Frequenzgang bei unterschiedl. Verstarkung, ohne externe Frequenzgangkorrektur
Schaltung: Invertierender Verstarker auf dem Zentralsteckbrett.
Widerstandswerte: R1 = 1 k
,
R2 :
1) R2 = 100 k
,
2) R2 = 33 k
,
3) R2 = 10 k
,
4) R2 = 4,8 k
.
Frequenzbereich: f = 1 kHz - 1,5 MHz.
Auswertung:
Erklarung des Unterschiedes in den Frequenzkurven.
37
Versuchsdurchfuhrung
5.4.3 Frequenzgang bei unterschiedl. Aussteuerung, ohne externe Frequenzgangkorrektur
Schaltung: Invertierender Verstarker auf dem Zentralsteckbrett.
Widerstandswerte: R1 = 1 k
, R2 = 4,8 k
,
Frequenzbereich: 1 kHz - 1,8 MHz,
Ausgangsspannung am Funktionsgenerator:
1) 0,6 V,
2) 1,2 V,
3) 2,4 V,
4) 4,8 V.
Die einzelnen Kurven sind durch die Verschiebung des Y-Nullpunktes ubereinanderzuschreiben.
Auswertung:
Erklarung der Ursache fur die Abhangigkeit von der Aussteuerung. Hierzu wird auf die
Grenzfrequenz des maximalen, unverzerrten Ausgangssignales verwiesen.
5.4.4 Frequenzgang bei unterschiedlicher Frequenzgangkorrektur
Schaltung: Invertierender Verstarker auf dem Zentralsteckbrett.
Frequenzbereich: 1 kHz - 1,5 MHz,
Ausgangsspannung am Funktionsgenerator 2,0 V,
Widerstandswerte: R1 = 1 k
, R2 = 10 k
,
C -Werte:
1) 0 pF,
2) 1 pF,
3) 3,3 pF,
4) 10 pF.
Auswertung:
Erklarung der verschiedenen Frequenzkurven. Welcher C -Wert liefert einen optimalen Frequenzgang?
k
k
5.4.5 Phasengang bei unterschiedlicher Beschaltung
Die Messung des Phasenganges erfolgt mit dem Phasenmesser. Dazu ist auf den oberen
Eingang das direkte Signal aus dem Funktionsgenerator und auf den unteren Eingang das
Ausgangssignal der Verstarkerschaltung zu geben. Das Ausgangssignal des Phasenmesser
wird mit dem Y-Eingang am Umschalteinschub verbunden.
Der Phasenmesser mu vor der Messung in folgender Weise abgeglichen werden:
Neben den Eingangsbuchsen benden sich Lemo-Buchsen als Testausgange. Sie liefern
2 Rechtecksignale, die beide auf dem Oszillografen darzustellen sind. Durch die beiden
38
Versuchsdurchfuhrung
Einstellknopfe sind die Rechtecke zunachst bei der unteren Frequenz des durchzufahrenden
Frequenzbereiches moglichst genau symmetrisch (postive und negative Halbschwingung
gleiche Breite) zu machen. Dann wird der gleiche Einstellvorgang bei der oberen Frequenz
wiederholt. Diese Einstellung ist bei jeder Messung durchzufuhren.
Durch die interne Schaltung des Phasenmessers ist das Vorzeichen der Phase nicht eindeutig. Daher kann z.B. bei dem Phasenverlauf eines invertierenden Verstarkers bei der einen
Messung die Phase von 180 in Richtung 360 laufen und in einer anderen Messung in
Richtung 0.
Der Phasenmesser liefert bei 0 0 V und bei 360 14,6 V. Die Y-Empndlichkeit des Schreibers ist dann zweckmaigerweise auf 1 V/cm (CAL) einzustellen.
Schaltung: Invertierender Verstarker auf Zentralsteckbrett.
Widerstandswerte: R1 = 1 k
, R2 = 10 k
,
Frequenzbereich: f = 2 kHz - 1 MHz,
1. Messung mit C = 10 pF,
2. Messung mit C = 0 pF.
Auswertung:
Vergleichen Sie diese Messung mit den Frequenzgangen der entsprechenden Schaltungen
oben und interpretieren Sie den Verlauf der Phase.
k
k
5.4.6 Sprungantwort
Dazu wird ein Rechtecksignal bei verschiedenen Kondensatoren fur die Frequenzgangkorrektur auf die Schaltung gegeben und das Ausgangssignal zusammen mit dem Eingangssignal auf dem Digitalspeicheroszillografen dargestellt und auf dem XY-Schreiber aufgezeichnet.
Schaltung: Invertierender Verstarker auf dem Zentralsteckbrett.
Widerstandwerte: R1 = 1 k
, R2 = 10 k
,
Ausgangsspannung am Funktionsgenerator 2,0 V,
Frequenz 60 kHz,
C -Werte:
1) 0 pF,
2) 1 pF,
3) 3,3 pF,
4) 10 pF.
Auswertung:
Vergleich der Sprungantworten mit den entsprechenden Frequenzkurven.
k
Versuchsdurchfuhrung
39
5.4.7 Lastkapazitat
Schaltung: Invertierender Verstarker auf dem Zentralsteckbrett.
Widerstandswerte: R1 = 1 k
, R2 = 10 k
,
C = 3,3 pF.
Lastkapazitat: 47 nF.
Jede Messung einmal mit und einmal ohne Lastkapazitat auf gleichem Blatt
Ausgangsspannung am Funktionsgenerator 1,0 V.
1. Messung mit einem Rechtecksignal fur die Bestimmung der Sprungantwort,
Frequenz 6 kHz,
2. Messung des Frequenzganges im Bereich 1 kHz - 1 MHz.
Auswertung:
Erklarung fur den Einu der Lastkapazitat.
k
5.5 Anwendungen
5.5.1 Wechselspannungsintegrator
Schaltung auf dem Zentralsteckbrett.
Messung der Sprungantwort und des Frequenzganges.
Widerstandswerte: R1 = 1 k
, R2 = 100 k
,
C = 3,3 pF,
Kondensatorwert: C = 1 nF,
Ausgangsspannung am Funktionsgenerator 1,0 V.
Sprungantwort bei f 2 kHz und 20 kHz auf gleichem Blatt
und gleicher Oszillografeneinstellung
Betrachten Sie das Ausgangssignal bei Variation der Frequenz und schatzen Sie ungefahr
ab, ab welcher Frequenz das Rechteck "richtig" integriert wird.
Frequenzgang im Bereich 100 Hz - 1 MHz,
Ausgangsspannung am Funktionsgenerator 0,6 V.
Messung mit und ohne Kondensator auf gleichem Blatt
Auswertung:
In welchem Frequenzbereich ist diese Schaltung als Integrator einsetzbar?
k
5.5.2 Dierentiator
Schaltung auf dem Zentralsteckbrett.
Widerstandswerte: R1 = 470 (in Reihe mit C), R2 = 10 k
,
C = 33 pF,
Kondensatorwert: C = 47 nF.
1. Messung: Frequenzgang im Bereich 100 Hz - 1 MHz,
Ausgangsspannung am Funktionsgenerator 1,0 V.
k
40
Versuchsdurchfuhrung
Messung mit und ohne Kondensator auf gleichem Blatt.
2. Messung: Mit einem Dreieckssignal als Eingang wird das Ausgangssignal beobachtet.
Aufnahme der Signalformen bei 2 verschiedenen Frequenzen:
1) f 200 Hz. Hierbei ist die Ausgangsspannung am Funktionsgenerator
genugend gro zu wahlen.
2) f 5 kHz.
Betrachten Sie das Ausgangssignal bei Variation der Frequenz und schatzen Sie ungefahr
ab, ab welcher Frequenz das Dreieck "richtig" dierenziert wird.
Auswertung:
In welchem Frequenzbereich ist diese Schaltung als Dierentiator einsetzbar?
5.5.3 Dierenzverstarker und Instrumentenverstarker
Bei diesen Messungen wird zunachst der einfache Dierenzverstarker untersucht. Fur den
Aufbau wird auf die Abbildung 3.3 verwiesen.
Widerstandswerte: R1 = 270 k
, R1/a = R2 /b = 10 k
,
R2 = 225 k
- 325 k
variabel,
Sinussignal mit f 5 kHz.
Zu messen sind die Dierenzverstarkung und die Gleichtaktverstarkung. Dazu mu zuvor
a = b gemacht werden. Zur Messung des schwachen und daher verrauschten Gleichtaktsignales am Verstarkerausgang lat sich sehr gut die Mittelwertsbildung im Digitalbetrieb
des Oszillografen heranziehen.
Aufbau entsprechend der Abbildung 3.4 des gesamten Instrumentenverstarkers mit R3 =
R5 = 2,1 k
. Der veranderbare Widerstand R4 hat einen maximalen Wert von 10,25 k
.
Bestimmen Sie hier bei 2 verschiedenen Verstarkungen der Vorstufe ebenfalls die Dierenzverstarkung und die Gleichtaktverstarkung.
Auswertung:
Berechnung der Gleichtaktunterdruckung fur die verschiedenen Falle in dB.
5.5.4 Aktive Filter
Bei den folgenden Filterschaltungen sind fur alle der Frequenzgang und die Sprungantwort aufzunehmen. Plotten Sie die Frequenzkurven auf ein gemeinsames Blatt ebenso
die Sprungantworten, die Sie durch unterschiedliche Y-Position am Oszillografen trennen
konnen. Bei allen Schaltungen sind die gewunschte Grenzfrequenz und die notwendigen
Kondensatoren angegeben. Die zugehorigen Widerstande sind auszurechnen und aus den
vorhandenen Widerstanden die jeweils am nachsten liegenden Werte einzubauen.
Frequenzbereich: f: 100 Hz - 100 kHz,
Sinussignal mit 2,0 V ohne Abschwacher.
41
Versuchsdurchfuhrung
Tiefpa 1. Ordnung
Verstarkungsfaktor: v = 1,
Grenzfrequenz: f = 10 kHz,
Kondensatorwert: C = 2,2 nF.
Der Widerstandswert ist zu errechnen.
Tiefpa 2. Ordnung: Schaltung auf dem Hilfsbrett fur Filterschaltungen.
Verstarkungsfaktor: v = 1,
Grenzfrequenz: f = 10 kHz,
Kondensatorwerte:
Butterworth-Filter: C1 = 2,2 nF, C2 = 4,8 nF.
Tschebysche-Filter: C1 = 270 pF, C2 = 2,2 nF.
Bessel-Filter: C1 =2,2 nF, C2 = 3,3 nF.
Die notigen Widerstandswerte sind zu berrechnen.
g
g
5.5.5 Ein- und Zweiweggleichrichter
Benutzen Sie hierzu das Hilfssteckbrett fur die Gleichrichterschaltung zusammen mit dem
Zentralsteckbrett. Das Eingangssignal ist fur alle Messungen ein Sinussignal. Benutzen Sie
fur die Einweggleichrichtung R1 = 1 k
und R2 = 2,1 k
und fur die 3 Widerstande der
Summationsstufe der Doppelweggleichrichtung 10 k
.
Signalamplitude am Funktionsgenerator = 2,0 V, kein Abschwacher,
Frequenz = 2 kHz.
Aufnahme und Plotten der Signalformen:
1) Einweggleichrichter ohne Diode D2 im Ruckkopplungsweg,
2) Einweggleichrichter mit Diode D2 im Ruckkopplungsweg,
3) Ausgangssignal des Summierers ohne Kondensator.
Registrierung der Ausgangsgleichspannung (C = 2,2 F) auf dem XY-Schreiber im Frequenzbereich 1 kHz - 1 MHz. Lassen Sie dazu auch als Referenz die Nullinie zeichnen.
Erklaren Sie den Verlauf dieser Kurve. Dazu sollten Sie sich das Signal der Einweg- und der
Doppelweggleichrichtung (ohne C) uber einen groeren Frequenz- und Amplitudenbereich
anschauen.
42
Versuchsdurchfuhrung
5.6 Anhang, Aufbau des Operationsverstarkers 741
Die innere Schaltung des 741 zeigt 3 Stromspiegel als Konstantstromquellen, die aus den
Transistorpaaren T8 /T9 , T10 /T11 und T12 /T13 gebildet werden. Der Referenzstrom wird
durch den Widerstand R5 und die Transistoren T10 und T13 festgelegt. Neben den Stromspiegeln zeigt die Schaltung den vielfach benutzten dreistugen Aufbau: Eingangsstufe,
Zwischenstufe und Endstufe.
Eingangsstufe:
Sie benutzt als Eingangstransistoren die beiden npn-Transistoren T1 und T2 , die als Emitterfolger geschaltet sind. Das Kollektorpotential wird durch den Stromspiegel T8 konstantgehalten. Als Arbeitswiderstande dienen die beiden pnp-Transistoren T3 und T4 , die als
Basisschaltung betrieben werden, was daraus zu ersehen ist, da die beiden Basisanschlusse
mit dem Stromspiegel T12 konstantes Potential haben. Die Verwendung der beiden Emitterfolger ergibt einen hohen Eingangswiderstand des 741. Da der Emitterfolger eine Spannungsverstarkung von 1 besitzt, liegt die Eingangsspannung quasi an den beiden Transistoren T3 und T4 , die den Dierenzverstarker bilden. Die Emitter von T3 und T4 sind uber
T1 und T2 zusammen auf den Stromspiegel T8 gelegt, wie es fur einen Dierenzverstarker
erforderlich ist. Die Arbeitwiderstande fur T3 und T4 sind die Transistoren T6 und T7 mit
den Widerstanden R1 und R3. T6 und T7 sind stromgegengekoppelte Emitterschaltungen,
deren konstanter Basis-Strom durch T5 und R2 geliefert wird. Stromgegengekoppelte Emitterschaltungen haben einen hohen Ausgangswiderstand (einige M
), so da sich eine hohe
Dierenzverstarkung ergibt. Der extern gezeichnete Widerstand R dient der Kompensation
der Osetspannung.
Zwischenstufe:
Von T7 wird die verstarkte Eingangsdierenzspannung auf die aus den Transistoren T15
und T16 (Darlingtonschaltung mit hoher Stromverstarkung b) gebildete Emitterschaltung
gegeben. Der Arbeitswiderstand dieser Stufe ist der Stromspiegel T11 , wodurch nochmals
eine hohe Spannungsverstarkung erreicht wird. R9 ergibt eine leichte Stromgegenkopplung
zur Stabilisierung der Verstarkung.
Endstufe:
Die Endstufe ist ein typischer Komplementar-Gegentakt-Leistungsverstarker aus den Transistoren T18 und T20 . Den hierfur notwendigen Ruhestrom bzw. die notige Vorspannung (die
Basis-Emitter-Spannung mu etwas uber 0,6 V liegen) stellt der Transistor T14 mit R6 und
R7 ein. R10 und R11 sind Gegenkopplungswiderstande. T17 und T19 verhindern eine U berlastung der Ausgangstransistoren bei Kurzschlu. Frequenzgangkompensation: Der 741 ist
ein universell frequenzgangkompensierter Operationsverstarker. Dieser Frequenzgang wird
durch den Kondensator C zwischen dem Ausgang und dem Eingang der Zwischenstufe realisiert. C bewirkt eine frequenzabhangige Spannungsgegenkopplung (Miller-Eekt). Daher
erscheint C um den Faktor der Verstarkung vergroert als Eingangskapazitat, die zusammen mit dem Ausgangswiderstand der Eingangsstufe einen RC-Tiefpa bildet.