Wechselstromkreise - Freie Universität Berlin
Werbung

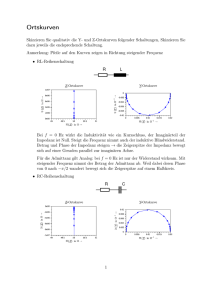
Wechselstromkreise Christopher Bronner, Frank Essenberger Freie Universität Berlin 29. September 2006 Inhaltsverzeichnis 1 Physikalische Grundlagen 1 2 Aufgaben 5 3 Messprotokoll 3.1 Geräte . . . 3.2 Aufgabe 1 . 3.3 Aufgabe 2 . 3.4 Aufgabe 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 5 5 6 7 9 4 Auswertung 10 4.1 Aufgabe 1 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 10 4.2 Aufgabe 2 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 4.3 Aufgabe 3 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 14 5 Diskussion 1 14 Physikalische Grundlagen Gleichspannung. Die Beziehung zwischen der Spannung die an einem Bauelement abfällt und dem Strom, der durch es hindurch fließt, sieht in den drei hier betrachteten Fällen von Widerstand, Kondensator (Kapazität) und Spule (Induktivität) aus wie folgt: • Widerstand: UR = −RIR • Kapazität: IC = −C U˙C • Induktivität: UL = −LI˙L Wechselspannung. In einem Wechselstromkreis haben Spannung und Strom die Form 1 (1) (2) U (t) = U0 cos(ωt) I(t) = I0 cos(ωt + ϕ) wobei die Frequenz gleich, die Phase jedoch konstant um ϕ verschoben ist. Man nennt hier U0 und I0 die Amplituden von Spannung und Stromstärke. Man kann Wechselspannungen aber auch als Realteil einer komplexen Exponentialfunktion vom Betrag der Amplitude interpretieren. U (t) = Re(U0 eiωt ) =: Re(Ũ (t)) ˜ I(t) = Re(I0 eiωt ) =: Re(I(t)) (3) (4) Das Äquivalent zum Ohmschen Widerstand im Gleichstromkreis ist die Impedanz im Wechselstromkreis. Sie ist definiert als das Verhältnis der Amplituden von Spannung und Stromstärke über bzw. durch ein Bauteil. U0 (5) I0 Die Impedanz hängt eng mit dem komplexen Widerstandoperator Z eines Bauteils zusammen. Ausserdem ist die Phasendifferenz zwischen Spannung und Strom für ein Bauteil charakteristisch. X := Bauteil Widerstand R Kapazität C Induktivität L Impedanz X XR = R 1 XC = ωC XL = ωL Widerstandsoperator Z ZR = R 1 ZC = iωC ZL = iωL Phase ϕ π − π2 + π2 Tabelle 1: Bauteile Am Widerstand sind Strom und Spannung im Prinzip in Phase, haben jedoch entgegengesetztes Vorzeichen, da die Spannung am Widerstand einen Spannungsabfall darstellt. An der Kapazität “eilt der Strom der Spannung vorraus”, an der Induktivität dagegen ist es umgekehrt: “Der Strom hinkt der Spannung hinterher”. Wechselstromnetzwerke lassen sich mathematisch ähnlich Gleichstromnetzwerke behandeln. Dabei rechnet man mit den Impedanzen im Prinzip so, als wären sie Widerstände. Der Unterschied besteht darin, dass die imaginäre Eigenschaft bei Spule und Kondensator auftauchen muss. Mann rechnet daher erst mit den komplexen Widerstandsoperatoren wie mit Ohmschen Widerständen und erhält im Allgemeinen eine komplexe Größe. Deren Betrag ist die Impedanz der Gesamtschaltung. XReihe 1 XP arallel ¯X ¯ ¯ ¯ = ¯ Zi ¯ ¯X ¯ ¯ 1 ¯¯ = ¯¯ Zi ¯ 2 (6) (7) Die Beziehung für die Phasendifferenz ϕ zwischen Strom und Spannung in einem Wechselstromnetzwerk errechnet sich für Reihen- und Parallelschaltungen wie folgt. ϕReihe ϕP arallel P Im Zi P Re Zi P 1 Im P Z1i = arctan Re Zi = (8) arctan (9) Leistung. Die Leistung ergibt sich wie im Gleichstromnetzwerk aus dem Zusammenhang (10) P (t) = U (t)I(t) Leistung, Spannung und Stromstärke sind Funktionen der Zeit mit der selben Periodizität (Frequenz ω). Ist ist also sinnvoll, über eine Periode T = 2π ω zu mitteln. (Dabei benutzt man Gln. 3, 4.) 1 < P >:= T ZT P (t)dt = 1 U0 I0 cos ϕ 2 0 s Mit der Definition für die Effektivwerte Uef f := 1 T RT (11) U 2 (t)dt (Ief f analog) 0 und deren Anwendung auf unsere Wechselspannungen und Ströme, also Uef f = √1 U0 (Ief f analog), erhält man sehr einfach die mittlere Leistung 2 < P >= Uef f Ief f cos ϕ (12) Es fällt auf, dass im Falle von Kapazität und Spule, wo cos ϕ = 0 ist, im Mittel keine Leistung aus der Spannugnsquelle entzogen wird. Allerdings gilt das nur für ideale Kondensatoren und Spulen. In der Realität verbrauchen Spulen und Kondensatoren auch Leistung. Ein Maß für die verbrauchte Leistung ist der Verlustfaktor. d= 1 tan ϕ (13) Um der Realität in dieser Hinsicht gerecht zu werden, ersetzt man Induktivitäten und Kapazitäten durch Ersatzschaltungen. Diese können entweder als Reihen- oder als Parallelschaltung auftreten. Es ist XReihe 1 XP arallel p R2 + (ωLr )2 s r 1 1 = + Rp2 (ωL)2 = 3 (14) (15) Für die Phasenverschiebungen gilt ϕReihe ϕP arallel ωLr Rr Rp = arctan − ωLp = arctan − (16) (17) Spannungsteiler. Wegen ihrer unterschiedlichen Frequenzabhängigkeit eignen sich die folgenden drei Schaltungen als Filter für Frequenzbereiche. Kreis R-C R-L R-C-L Filtertyp Hochpass Tiefpass Bandpass Tabelle 2: Frequenzweiche Wheatstonesche Brücke. Diese Schaltung erlaubt die Bestimmung unbekannter Impedanzen aus einer anderen bekannten Impedanz bei bekannter Frequenz. Abbildung 1: Wheatstonesche Brückenschaltung Der Zeiger, in dem ein Voltmeter verbaut ist, wird über einen Widerstand geschoben, bis die Spannung verschwindet. Dann sind die Teilspannungen über den beiden linken und den beiden rechten Ästen gerade gleich und bei gleichem Strom (in den jeweiligen Ästen) ergibt sich das Verhältnis 4 RA X0 RB (18) R1 R0 − R0 R2 (19) XX = RX = 2 Aufgaben 1. Aufbau eines R-C-Kreises. Einstellung der charakteristischen Frequenz mit UR = UC . Messung der Generator- und der Teilspannungen und Bestimmung der Phasenverschiebung. Unabhängige Messung von R und C mit einem Multimeter und Vergleich der Beobachtungen am R-C-Kreis mit den theoretischen Erwartungen. 2. Messung des Frequenzganges UR /UG (Verbraucherspannung zu Generatorspannung) an einer Tonfrequenzweiche (Drei-Wege-Weiche mit R-LTiefpass, R-C-L-Bandpass und R-C-Hochpass) und Vergleich mit dem theoretischen Verlauf durch unabhängige Messung der Werte der Widerstände, Kapazitäten und Induktivitäten mit Digital-Multimetern. 3. Messung der Induktivität und des Verlustwiderstandes einer der beiden Spulen auf Aufgabe 2 mit einer Wechselstrombrücke und Vergleich mit der unabhängigen Messung (Digitalmultimeter) von L und dem Gleichstromwiderstand R der Spule. 3 Messprotokoll Tutor: Theis Datum: 29. September 2006 Beginn: 14.45, Ende: 18.00 3.1 Geräte • Steckbrett mit Reitern, div. Widerständen, div. Kondensatoren, div. Spulen (beschrieben im jeweiligen Aufgabenteil) • Multimeter Metra Hit 12S für Widerstandsmessung. ∆R → 0, 5% + 3dgs. • Multimeter Voltcraft 3860M für Spannungs- und Strommessung. ∆UAC → 2, 5% + 5dgs., ∆IAC → 2, 5% + 3dgs. • Multimeter Escort ELC 131D zur Messung von Kapazität und Induktivität. 100µF-100nF:∆C → 0, 7% + 5dgs. 10nF und 1000µF: ∆C → 1% + 5dgs. 1H-100H: ∆L → 0, 7% + 5dgs. 5 100mH und 1000H: ∆L → 1% + 5dgs. 10mH: ∆L → 2% + 5dgs. • Oszilloskop Hameg 203-4 : 3% Fehler + Ablesefehler (±0,1 Skt.) • Frequenzgenerator 3.2 Aufgabe 1 Wir haben auf dem Steckbrett einen R-C-Kreis an eine sinusförmige Spannungsquelle angeschlossen und die Spannungen über Widerstand und Kondensator sowohl mit jeweils einem Multimeter gemessen als auch zur Bestimmung der Phasenverschiebung an das Oszilloskop angeschlossen. Abbildung 2: RC-Kreis Wir haben zunächst Widerstand und Kapazität mit einem Multimeter direkt gemessen: R = 989 Ω, C = 0, 980 µF Danach haben wir die Frequenz des Funktionsgenerators variiert, bis die Spannungen über Widerstand und Kondensator gleich waren. UC = UR = 2, 437 V . Der Punkt zwischen Widerstand und Kondensator war geerdet (durch den Anschluss am Oszilloskop), was aber nichts ausmachte, da die Spannungen ja auf beiden Seiten gleich war und das Potential somit sowieso Null. Die Übernahmefrequenz betrug ν = 163 Hz. Die Spannung am Generator haben wir zu U0 = 3, 451 V direkt gemessen. Die beiden Kurven auf dem Oszilloskop haben wir so zunächst kalibriert, dass die Nulllinie (abgeklemmter Anschluss) auf der Nulllinie der Skala lag. Dann haben wir die Nulldurchgänge einer vollen Periode für beide abgelesen. Beide betrugen 6 cm. Die Phasenverschiebung zwischen UC links und UR rechts betrug 1,5 cm. Dabei war die Skala auf 1 ms cm eingestellt. 6 3.3 Aufgabe 2 Hier haben wir jetzt die Frequenzweiche aufgesteckt. Abbildung 3: Frequenzweiche Auch hier haben wir zuerst alle Bauteile direkt gemessen. R1 = 8, 33 Ω, R2 = 8, 44 Ω, R3 = 8, 36 Ω C1 = 44, 94 µF , C2 = 3, 320 µF L1 = 4, 766 mH, L2 = 495, 4 µH Dann haben wir die Frequenz in (mit Hinblick auf die logarithmische Auswertung) sinnvollen Schritten verändert und die Spannungen am Generator U0 und über den Verbraucherwiderständen U1 , U2 und U3 gemessen. 7 U1 /mV 198,0 196,0 191,1 185,2 155,9 109,0 82,1 65,7 54,9 33,6 21,0 13,6 9,6 7,3 5,6 4,9 4,0 3,0 42,8 36,1 31,7 28,5 24,0 22,0 20,1 U2 /mV 43,0 50,9 65,3 78,4 126,2 169,5 185,6 193,3 197,6 203,7 172,7 121,3 87,8 67,6 50,3 43,1 36,4 31,0 201,9 203,7 203,2 200,3 187,6 178,6 167,9 U3 /mV 2,8 3,4 4,5 5,5 9,8 16,7 23,3 30,2 37,9 82,5 174,7 212,7 221,7 223,8 224,1 223,9 223,3 222,6 54,0 71,9 92,6 113,7 151,3 156,8 180,3 U0 /mV 308,1 306,1 302,4 298,1 277,4 243,9 226,8 221,3 221,5 252,0 290,0 284,0 271,0 260,7 274,7 241,9 236,7 232,4 230,1 243,9 258,1 269,5 284,0 287,7 289,5 ν/kHz 0,050 0,060 0,080 0,100 0,199 0,400 0,600 0,801 1,008 2,008 4,01 6,02 8,00 10,00 12,95 14,86 17,36 20,22 1,402 1,793 2,209 2,620 3,404 3,790 4,19 Tabelle 3: Uind über ν Wie aus der Tabelle ersichtlich haben wir erst eine grobe Messreihe durchgeführt und anschliessend in dem Bereich, in dem große Änderungen der Spannungen auftraten, zur späteren besseren Auswertung noch ein paar Messwerte aufgenommen.So sah die Frequenzweiche in Labor aus: 8 Abbildung 4: Frequenzweiche im Labor 3.4 Aufgabe 3 In dieser Aufgabe haben wir eine Brückenschaltung zur Bestimmung einer Induktivität gesteckt. Abbildung 5: Wheatstonesche Brückenschaltung Der Widerstand R0 zur Anpassung der Phase wurde durch einen regelbaren 9 Widerstand realisiert. Zuerst haben wir wieder die Referenzspule L0 , R0 und die unbekannte Spule LX , RX vermessen. L0 = 1, 494 mH, R0 = 7, 32 Ω LX = 4, 767 mH, RX = 5, 84 Ω Um RA , RB und R0 zu bestimmen, drehten wir immer den einen Drehwiderstand zu einem relativen Minimum und dann den anderen und so immer wieder im Wechsel hin und her, bis das absolute Minimum gefunden wurde. Dabei begannen wir die Messung des Querstroms mit groben Spannungen, dann feinen Spannungen, dann groben Stromstärken und feinen Stromstärken bis wir schließlich ein Minimum von Iquer = 0, 1 µA erreichten. Die Frequenz bei diesem Versuch betrug ν = 513 Hz. Nachdem das Minimum gefunden war, haben wir die Widerstände, die zur Berechnung nötig sind, gemessen. RA = 0, 768 kΩ, RB = 241, 9 Ω, R0 = 18, 02 Ω 4 Auswertung 4.1 Aufgabe 1 Der theoretische Wert ergibt sich aus der Gleichheit von UR = UC . Ersetzt man beide nach U = XI, wobei X die Impedanz ist, erhält man nach Kürzen mit I: = XC (20) 1 R = (21) ωC 1 ν = (22) 2πRC Danach ergibt sich mit den gemessenen Werten von R und C der theoretische Wert der Übernahmefrequenz XR ν = (164 ± 3) Hz (23) Der tatsächlich gemessene Wert beträgt ν = 163 Hz (24) Das Multimeter, das wir zur Messung der Frequenz verwendet haben (wir haben uns natürlich nicht auf die Angabe auf dem Funktionsgenerator verlassen!) hat leider keine Fehlerangabe bzgl. der Frequenz und deshalb müssen wir diesen Wert als exakt annehmen. Trotzdem stimmen die beiden Werte sehr gut überein (zumal der abgelesene Wert sogar noch zwischen 163 Hz und 164 Hz geschwankt hat). Zur Bestimmung der Phasendifferenz haben wir die Periodendauer und den Zeitunterschied zwischen den beiden Signalen bestimmt: T = (6, 0 ± 0, 3) ms, ∆t = (1, 5 ± 0, 2) ms. Nun kann man die Phasendifferenz bestimmen. Das Minuszeichen fügen wir ein, da das zweite Signal (UR ) dem ersten (UC ) zeitlich hinterherhinkt. 10 2π∆t = −(1, 57 ± 0, 22) T Dies entspricht voll und ganz der Erwartung. ϕ = ω∆t = ϕ=− 4.2 (25) π ≈ −1, 57 2 Aufgabe 2 Betrachtet man einen der drei Pässe der Frequenzweiche, dann ergibt sich zum einen die Gleichung für die Generatorspannung U0 und zum anderen eine Gleichung für die Spannung über dem jeweiligen Verbraucher. U0 Ui (26) (27) = Xi Ii = Ri Ii Dabei ist Xi die Impedanz des iten Passes. Wenn wir nun die Stromstärke eliminieren, erhalten wir einen Zusammenhang für das Verhältnis der Spannung über dem Verbraucher zu der Generatorspannung. Ui Ri = U0 Xi (28) Mit den Regeln für das Rechnen mit komplexen Widerstandsoperatoren und Impedanzen ergeben sich die drei Impedanzen zu q X1 = X2 = s R12 + (2πνL1 )2 µ R22 + 2πνL2 − s X3 = µ R32 + 1 2πνC2 (29) 1 2πνC1 ¶2 (30) ¶2 (31) Setzt man nun die drei Impedanzen für die einzelnen Pässe in die Gl. 28 Ui ein, erhält man drei Funktionen U (ν), die zusammen mit den entsprechenden 0 gemessenen Werten in den folgenden Grafiken dargestellt sind. 11 1 Abbildung 6: Tiefpass also ln[ U U0 ] über ln[ν] 2 Abbildung 7: Bandpass also ln[ U U0 ] über ln[ν] 3 Abbildung 8: Hochpass also ln[ U U0 ] über ln[ν] 12 Abbildung 9: Alle drei Pässe zusammen 13 Die Ergebnisse entsprechen in sehr zufriedenstellender Weise den theoretischen Vorraussagen. 4.3 Aufgabe 3 Für die unbekannten Größen in der Wheatstoneschen Brückenschaltung gelten folgende Beziehungen zu den gemessenen Parametern. LX = RX = RA L0 RB RA R0 − R 0 RB (32) (33) Die entsprechenden Fehler lauten δLX ∆RX q 2 + δR2 + δL2 δRA 0 B s 2 2 R R 2 + δR2 + δR2 ) = ∆R02 + A2 0 (δRA 0 B RB = (34) (35) Damit erhält man als Wert aus der Messung der Brückenschaltung: LX = (4, 7 ± 0, 2) mH RX = (5, 2 ± 0, 4) Ω Die direkt mit einem Multimeter gemessenen Werte lauten: LX = (4, 8 ± 0, 1) mH RX = (5, 84 ± 0, 06) Ω Die Ergebnisse für die Induktivität stimmen sehr gut überein, die für den Gleichstromwiderstand der Spule sind zumindest verträglich. 5 Diskussion Als maßgebliche Fehlerquelle kann bei allen durchgeführten Experimenten der hohe Gerätefehler der diversen Multimeter und der des Oszilloskops gesehen werden. Wir glauben jedoch auch hier, dass diese nicht die tatsächlichen Messungenauigkeiten dieser Geräte widerspiegeln, da die Ergebnisse an sich sehr gut waren. Nichtsdestotrotz müssen sie natürlich voll berücksichtigt werden. Leider stand für die Frequenzmessung mit dem Multimeter auch diesmal wieder keine Fehlerangabe zur Verfügung, wobei diese Messung wohl recht präzise ist und der Fehler wohl ohnehin nicht besonders ins Gewicht fallen dürfte. 14 Des Weiteren vermuten wir, dass in unseren doch recht umfangreichen Schaltungen mit vielen Kabeln und Reitern die Widerstände dieser Bauteile schon ins Gewicht fallen könnten, was auch eine Überschlagsrechnung in Aufgabe 1 zeigt: Die beiden p gleichen Spannungen von UC und UR müssten mit der Beziehung U0 = UC2 + UR2 die Generatorspannung ergeben, jedoch ergibt sich danach U0 = 3, 446 V , was zum tatsächlich gemessenen Wert U0 = 3, 451 V einen Spannungverlust in der Schaltung von etwa 5 mV nahelegt. Da die erste Schaltung gerade im Vergleich mit der der Frequenzweiche noch relativ einfach ist, kann dieser Effekt wohl schon ins Gewicht fallen. Bei Aufgabe zwei hätten wir wohl in unseren theoretischen Überlegungen die Verlustwiderstände der Spulen mit einer Ersatzschaltung berücksichtigen müssen, was wir erst nach der Messung feststellten und dann wegen der nicht gemessenen Widerstände von L1 und L2 nicht durchführen konnten. Möglicherweise erklärt das auch die Abweichung von der erwarteten Kurve gerade bei niedrigen Frequenzen im Tiefpass. In der praktischen Durchführung ist noch zu beklagen, dass die zur Verfügung stehenden Kabel teilweise zu dünne Stecker hatten und daher manchmal "Wackelkontakte" auftraten. Auch die Unzuverlässigkeit des einen Funktionsgenerators bei niedrigen Frequenzen war ärgerlich, jedoch nicht weiter tragisch, da wir einfach den Generator wechselten und sowieso die Frequenzen mit einem Multimeter überprüften. Abschließend kann der Versuch im Hinblick auf die gemessenen Werte und ihre hohe Konsistenz mit der Theorie aber als (sehr) erfolgreich bezeichnet werden. 15