Kapitel 7 Anwendungen der Kernphysik - Hera-B

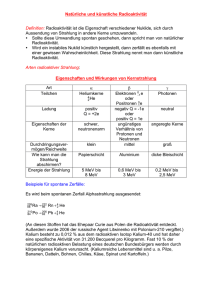
Kapitel 7
Anwendungen der Kernphysik
Seit dem 2. Weltkrieg ist die Kernspaltung nicht mehr aus unserer Gesellschaft wegzudenken. Über Gefahren und Nutzen ist und wird immer noch sehr kontrovers
diskutiert. In diesem Kapitel sollen die notwendigen physikalischen Grundkenntisse
vermittelt werden, um Kernreaktionen zu verstehen und um deren Gefahrenpotential abzuschätzen. Wir werden uns dabei auf die beiden wichtigsten Phänomene
beschränken, die für die Energiegewinung von Bedeutung sind:
• Kernspaltung: induzierte Kernspaltung, Kernkraftwerke
• Kernfusion
Auch auf den Missbrauch der Kernenergien für kriegerische Zwecke soll eingegangen
werden.
7.1
7.1.1
Kernspaltung
Der Spaltprozess
Um den Kernspaltungsprozess zu erklären, macht man einen ähnlichen Ansatz wie
beim α–Zerfall (sieh Kap. 6.4.1), bei dem die beiden Kernfragmente den gemeinsamen Coulomb–Wall durchtunneln müßen, um sich voneinander zu trennen. Aus der
Massenformel von Gl. 5.1 kann man ableiten, wann eine Kernspaltung energetisch
möglich ist. Für den symmetrischen Fall der Spaltung in zwei Kerne mit halber
Masse erhält man:
2
1
Z Z
A 2
Z A 1
0 < m(Z, A) − 2m( , ) = aS A 3 − 2( ) 3 + aC Z 2 · A− 3 − 2( )2 ( )− 3
2 2
2
2
2
2
2
− 31
3
= −0.26 · aS · A + 0.37 · aC · Z · A
(7.1)
2
⇒ Z /A > 17.3
(⇒ A & 90)
(7.2)
Die tatsächliche spontane Spaltung hängt von weiteren Faktoren ab, wie etwa der
Tunnelwahrscheinlichkeit. Ab einer Grenze von Z 2 /A > 47 spalten sich die Nuklide instantant, oberhalb von Z = 92 gibt es keine stabilen Nuklide. Die instantane
7.1 Kernspaltung
103
Abbildung 7.1: Der Spaltprozess von Kernen: Energieverhältnisse nach dem Tröpfchenmodell sowie ein Modell der Spaltung nach einer Deformation.
Spaltung solle einer Energie der Spaltprodukte oberhalb des Coulombwalles entsprechen, was sich aber aus Gl. 7.1 nicht ergibt. Der tatsächliche Spaltprozess läuft
dynamischer und komplexer ab, als mit Gl. 7.1 beschrieben werden kann.
In Abb. 7.1 ist der Prozess dargestellt: Der Kern deformiert sich zunächst, so
dass die Oberflächenenergie zunimmt und dadurch die Coulombenergie abnimmt1 .
Ab einer bestimmten Deformation ist es für den Kern günstiger, in zwei Teile zu
zerfallen. Die Spaltprodukte sind im Allgemeinen instabil, da N/Z mit A anwächst,
was bedeutet, dass Kerne mit A/2 einen Neutronen–Überschuss haben, den sie durch
β–Zerfälle oder n–Emission (Spaltneutronen) wieder abbauen. Durch den Einfang
solcher Neutronen kann eine weitere Kernspaltung induziert werden, dies führt dann
zu einer sogenannten Kettenreaktion.
7.1.2
Induzierte Kernspaltung
Wie oben erwähnt, kann Kernspaltung durch Neutronen induziert weden. Das bekannteste und am meisten in der Energiegewinnung verwendete Beispiel ist die Spaltung von 235 U:
n +235 U → K1 + K2 + ν · n
(7.3)
wobei ν die Anzahl der freiwerdenden Neutronen bezeichnet. Der mittlere Energiegewinn dieser Reaktion ist:
∆E ≈ 200 MeV/Spaltung
1
relativ zu dem statischen Wert der Massenformel
104
Anwendungen der Kernphysik
A
Gehalt
[%]
235
0.7
238
99.3
Spaltschwelle
[MeV]
5.8
6.3
∆EB (U + n) notwendige
[MeV]
n–Energie
6.4
therm.
4.8
≥ 1.5 MeV
σ(n, f )
[b]
582
≤ 1
Tabelle 7.1: Natürliches Uranvorkommen.
was mit der Energiebilanz von ca. 10 eV bei der Verbrennung von Kohlenstoff zu
vergleichen ist. Etwa 160 MeV des Energiegewinnes gehen in die kinetische Energie
der Spaltprodukte, der Rest wird in Form von Strahlung (n, γ, e, νe ) frei. Wenn bei
der Spaltung mehr als ein Neutron frei wird (ν > 1), so kann die oben erwähnte
Kettenreaktion einsetzen. Für 235 U gilt ν(235 U) = 2.43. Allerdings gibt es zwei
Probleme:
• Das Isotop
den.
235
U ist nur in sehr geringen Mengen im natürlichen Uran vorhan-
• Die Neutronen müssen für einen effektiven Einfang thermisch sein, bei der
Emission haben sie allerdings eine Energie im Bereich von MeV.
Die Verhältnisse für natürliches Uran sind in Tabelle 7.1 dargestellt, demnach ist
das häufigste Isotop 238 U nicht geeignet, da die Spaltschwelle über dem Energiezuwachs durch Neutroneneinfang liegt. Die Verteilung der Energien der bei der Spaltung emittierten Neutronen ist in Abb. 7.2 dargestellt. Von thermischen Energien
(dh. Zimmertemperatur) spricht man allerdings erst bei En = kT ≈ 25 meV. Da
der Wirkungsquerschnitt für die Spaltung erst dort groß wird, müssen die Neutronen abgebremst (moderiert) werden. Dabei gibt es beim Abbremsen allerdings
Abbildung 7.2: Energieverteilung der bei der Spaltung emmitierter Neutronen.
einen kritischen Bereich oberhalb der thermischen Energien. Wie in Abbildung 7.3
dargestellt ist, wird dort der Wirkungsquerschnitt für (n, γ)–Reaktionen sehr groß,
wodurch in diesem Bereich an Stelle von Kernspaltungen γ–Übergänge durch den
7.1 Kernspaltung
105
Abbildung 7.3: Wirkungsquerschnitte für n–Uran Reaktionen als Funktion der Neutronenergie En .
Moderator
H2 O
D2 O
Graphit
σabs [b] lbrems [cm
0.664
5.3
0.001
11.2
0.0045 19.1
Tabelle 7.2: Gängige Moderatoren.
n–Einfang angeregt werden können. Deshalb werden separate Moderatoren eingesetzt, um die Neutronen durch elastische Streuungen abzubremsen. Moderatoren
müssen einerseits einen kleinen Wirkungsquerschnitt σabs für den n–Einfang haben
sowie über kleine Bremslängen lbrems verfügen. Ideal sind Materialien mit leichten
Kernen, die nahe an der Neutronenmasse sind.
Die gängigsten Moderatoren sind in Tabelle 7.2 dargestellt. Der Vorteil von Wasser ist, dass es gleichzeitig als Kühlmittel gilt (bei Druck– und Siedewasserreaktoren), die Kettenreaktion sinkt bei Verlust des Kühlmittels, das Isotop 235 U muss
allerdings angereichert werden. Hingegen kann mit Graphit und schwerem Wasser
die Kettenreaktion auch in natürlichem Uran aufrecht aufrecht erhalten werden.
7.1.3
Kernspaltungsreaktoren
Die wichtigste Größe, um die Kettenreaktion in einem Reaktor zu kontrolieren, ist
die Neutronenbilanz. In einem Schritt i seien Ni thermische Neutronen vorhanden,
106
Anwendungen der Kernphysik
Abbildung 7.4: Schematische Darstellung verschiedener Reaktortypen (Druckwasserreaktor und Siedewasserreaktor.
die sich im nächsten Schritt um den Faktor kef f vermehren:
Ni+1 = kef f · Ni
(7.4)
Die Kettenreaktion verläuft nur dann stationär (dh. stabil), falls kef f = 1, wobei der
effektive Vermehrungsfaktor mittels kef f = k∞ · pgeom mit dem Vermehrungsfaktor
p∞ für unendlich große Reaktoren über einen Geometriefaktor zusammenhängt. Der
Vermehrungsfaktor k∞ wird in weitere Faktoren zerlegt:
k∞ = η · · p · f
(7.5)
wobei die folgenden Definitionen gelten:
η Vermehrungsfaktor für thermische Neutronen (Zahl der erzeugten schnellen
Neutronen pro thermischem Neutron), η ≈ 1.3 . . . 2.1
7.1 Kernspaltung
107
Wahrscheinlichkeit für Spaltung durch schnelle Neutronen
p Wahrscheinlichkeit für Entkommen der (n, γ)–Resonanzen
f Wahrscheinlichkeit für Entkommen der Absorption im thermischen Bereich
Um den Reaktor nun kontrolliert zu betreiben, muß die Neutronendichte zeitlich
stabil gehalten werden, also kef f ≈ 1 gehalten werden (Reaktorregelung). Für die
zeitliche Änderung der Neutronendichte gilt:
(k − 1) · ρ
dρ
=
dt
t0
⇒
ρ = ρ0 · et/τ
(7.6)
und daraus folgt für die Zeitkonstante des Neutronenanstieges:
τ=
t0
k−1
(7.7)
Die typischen Zeiten für die Abbremsung und den Einfang der Neutronen sind im
Bereich von etwa 1 ms, dies ist zu kurz für mechanische Regelungssysteme. Die kann
umgangen werden, wenn man ausnützt, dass etwa 1 % der Neutronen verzögert zum
Spaltprozess erzeugt werden:
235
U + n →
148
La +
87
Br
↓
87
Kr
+ n
β − (55.6 s)
→ 86 Kr + n
(7.8)
Die Regelung erfolgt dann duch Einführung von Materialien, die Neutronen gut absorbieren, wie etwa B– oder Cd–Stäbe (σth (B) = 770 b, σth (Cd) = 2450 b). Was
verlangt wird, ist ein passiver Schutz, was bedeutet, dass sich bei jeder unkontrollierten Veränderung im Reaktor der Vermehrungsfaktor erniedrigen muss ( dk
< 0). Bei
dt
Leichtwasserreaktoren ergibt sich dann die Ereigniskette Überhitzen → Blasenbildung → weniger thermische Neutronen im Falle einer Störung. Bei anderen
Reaktortypen (Graphitreaktoren, wie etwa Tschernobyl) sind die Funktionen des
Moderators (Graphit) und die des Kühlmittels (Wasser) nicht voneinander getrennt.
In Abb. 7.4 sind die beiden gängigsten Reaktortypen dargestellt: ein Druckwasserreaktor (Biblis) und ein graphitmoderierter Siedewasserreaktor (Tschernobyl).
7.1.4
Brutreaktionen
Das Anreichern von Uran ist technisch und energetisch sehr aufwendig. In einem
Brutreaktor wird ein Teil der Neutronen aus 235 U zur Erzeugung von 239 Pu verwendet, es wird also gleichzeitig spaltbares Material produziert. Diese Reaktion ist in
Abb. 7.5 dargestellt. Die Reaktionskette beginnt mit der Spaltung von 239 Pu mit
schnellen Neutronen. Ein Teil der Spaltneutronen wird vom 238 U, das nur schnelle
Neutronen absorbiert, eingefangen, woraus nach einigen Zerfällen wieder ein 239 Pu
entsteht. Als Kühlmittel darf demnach kein moderierendes Material wie Wasser
verwendet werden, es werden flüssige Metalle wie Natrium eingesetzt. Dies führt
108
Anwendungen der Kernphysik
zu einer sehr hohen Energiedichte und macht den Reaktor technologisch sehr viel
aufwendiger. Ferner ist Plutonium durch schnelle Neutronen spaltbar (mit einer Lebendsdauer von 35000 Jahren!!) und damit ein kernwaffenfähiges und hochgiftiges
Material.
Abbildung 7.5: Spalt–Brutkette des Schnellen Brüters.
7.1.5
Spaltprodukte und nukleare Entsorgung
Eines der größten Probleme der industriellen Nutzung der Kernenergie ist das Anfallen von hochradioaktivem Abfall, wie abgebrannte Brennelemente, dem Reaktorkern
sowie die aktivierten Behältermaterialien. Die Radioaktivität kommt von den Spaltprodukten, die in der Regel einen Neutronenüberschuss haben. Dieser wird durch
β–Zerfälle, seltener auch durch Neutron–Emission ausgeglichen. Die Anregungsserien klingen durch γ–Strahlung ab. Der größte Teil der Aktivität ist nach einigen
Monaten abgeklungen (Abb. 7.6), wobei dann die extrem langlebigen Aktiniden
(Spaltprodukte wie U, Pu oder Np) übrigbleiben, und den hochproblematischen nuklearen Müll verursachen, der z.B. in geologisch sicheren Salzstöcken endgelagert
werden muss. Während der ersten schnellen Abklingphase werden die abgebrannten
Brennelemente in einem Wasserbecken im Reaktorbereich gelagert, die abgegebene Wärmeleistung beträgt anfangs ca. 10 MW pro Tonne Brennstoff. Dies klingt
innerhalb eines Jahres um einen Faktor 10 ab, nach 10 Jahren auf 1 kW. Wiederaufbereitung ist technisch sehr aufwendig und verursacht hohe Strahlungsbelastungen.
Da abgebrannte Brennstäbe auch einen Teil (ca. 1%) an gebrütetem Plutonium
enthalten, fällt bei der Wiederaufarbeitung auch kernwaffenfähiges Material an.
7.2
Kernfusion
Wie wir bereits in Abb. 4.8 gesehen haben, hat die Bindungsenergie pro Nukleon ihr
Maximum bei A ≈ 60. Deshalb ist es für leichtere Kerne energetisch günstiger durch
Kernfusion zu schwereren Kernen zu verschmelzen. Dabei muß allerdings zuerst die
Coulombabstoßung überwunden werden, wofür eine Energie von mehr als 1 keV
notwendig ist. Umgerechnet auf die notwendige Temperatur erhält man:
k · T = 1 keV
⇒
T = 11.6 · 106 K
(7.9)
7.2 Kernfusion
109
Abbildung 7.6: Abklingen von Wärmeleitung und Radioaktivität bei abgebrannten
Brennelementen.
Das sind Temperaturen die typischerweise im Innern von Sternen auftreten, und
sind entsprechend auf der Erde technisch nur sehr schwer realisierbar. Nahezu alle
Energie, die auf der Erde zur Verfügung steht, ist auf die Energieerzeugung in der
Sonne, und damit auf Kernfusion, zurückzuführen.
7.2.1
Sonnenernergie
Wenn im Universum Wasserstoffgas kontrahiert und der Gasball eine hinreichend
große Masse erreicht, so entstehen im Innern hohe Temperaturen und Drücke, so dass
Fusionsprozesse ablaufen können. Im Innern der Sonne herrscht eine Temperatur von
T = 15.5 · 106 K, eine Dichte von ρ = 105 kg/m3 sowie ein Druck von p = 2 · 1015 Pa,
somit ist Kernfusion möglich. Sie läuft im wesentlichen durch Verschmelzung von
Wasserstoff zu Helium über zwei Reaktionstypen ab. Die Reaktionsbilanz lautet
dabei:
4p → 4 He + 2e+ + 2ν + 26.73 MeV
(7.10)
Pro Heliumkern wird also eine Energie von 27 MeV frei, die beiden entstehenden
Neutrinos tragen davon im Mittel je ca. 1% weg. Die Sonne verliert durch Energieabstrahlung pro Sekunde eine Masse von ca. 4 · 106 t. Es gibt im wesentlichen zwei
Zyklen, die kurz erläutert werden sollen:
Der pp–Zyklus
Unter dem in der Sonne und entsprechenden Sternen extremen Druckbedingungen
bilden die Protonen und Elektronen ein Plasma. Die Protonen können zu Deuterium
wie folgt verschmelzen:
p + p → 2 H + e+ + νe + 0.42 MeV
(7.11)
110
Anwendungen der Kernphysik
Da dies ein Prozess der schwachen Wechselwirkung ist (wie der β–Zerfall,
Kap. 6.4.2), ist der Wirkungsquerschnitt sehr klein und jedes Proton reagiert im
Mittel nach 1010 Jahren, was die Langzeitstabilität der Sonne garantiert. Im folgenden Schritt wird das Heliumisotop 3 He gebildet:
2
H+p →
3
2 He
+ γ + 5.49 MeV
(7.12)
Anschließend gibt es drei unterschiedliche Prozesse, wie das Endprodukt 4 He entstehen kann:
pp–I
3
3
4
2 He +2 He →2 He + 2p + 12.86 MeV
pp–II
3
4
2 He +2 He
7
−
4 Be + e
7
3 Li + p
→
→
→
7
4 Be + γ + 1.59 MeV
7
3 Li + νe + 0.86 MeV
4
4
2 He +2 He + 17.35 MeV
pp–III
3
4
2 He +2 He
7
4 Be + p
−
8
5B + e
∗
8
4 Be
→
→
→
→
7
4 Be + γ + 1.59 MeV
8
5 B + γ + 0.14 MeV
∗
8
−
4 Be + e + νe + 14.03
4
4
2 He +2 He + 3.03 MeV
MeV
Der CNO–Zyklus
Im pp–III Zyklus kann mit kleiner Wahrscheinlichkeit der angeregte 84 Be∗ –Kern einen
weiteren 42 He–Kern einfangen und in ein 12 C übergehen. Mit dem Kohlenstoffkern
setzt dann der CNO–Zyklus ein:
12
6 C
+p
13
7 N
13
6 C+p
14
7 N+p
15
8 O
15
7 N+p
→
→
→
→
→
→
13
7 N + γ + 1.94 MeV
13
+
6 C + e + νe + 1.20 MeV
14
7 N + γ + 7.55 MeV
15
8 O + γ + 7.29 MeV
15
+
7 N + e + νe + 1.74 MeV
12
4
6 C +2 He + 4.96 MeV
Der Kohlenstoff 12 C dient in dieser Reaktionsreihe als Katalysator. Zur Überwindung
des Coulombwalles sind in dieser Reaktion höhere Energien notwendig, weshalb der
Prozess nur mit etwa 3% zur Energieerzeugung in der Sonne beiträgt, er kann allerdings bei heißeren Sternen dominant werden. Der stabilste Zustand wird bei A ≈ 60
(Eisen) erreicht. Die schwereren Elemente können bei schwereren Sternen (ca. 20
Sonnenmassen) mit höheren Temperaturen gebildet werden, dort wird Silizium zu
7.2 Kernfusion
111
Eisen verschmolzen. Ist der Brennstoff eines Sternes nach einigen Milliarden Jahren verbraucht, so stirbt der Stern in einer Supernova–Explosion2 . Dabei entstehen
Elemente oberhalb des Stabilitätsmaximums.
7.2.2
Technische Nutzung der Kernfusion
Für die technische Nutzung der Kernfusion kommt natürlicher Wasserstoff als Brennstoff nicht in Frage. Die erste Reaktionsstufe (Gl. 7.11) ist auf Grund der schwachen
Wechselwirkung zu langsam. Geeigneter sind Deuterium 21 H oder Tritium 31 H, die
folgende Fusionsreaktionen ermöglichen:
2
1H
2
1H
2
1H
+21 H
+21 H
+31 H
2
3
1 H +4 He
→
→
→
→
3
1 H + p + 4.0 MeV
3
2 He + n + 3.3 MeV
4
2 He + n + 17.6 MeV
4
2 He + p + 18.3 MeV
Den größten Wirkungsquerschnitt bei günstigstem Energiegewinn hat die
Deuterium–Tritium Reaktion. Deuterium kommt im Meereswasser mit einer Häufigkeit von 0.2% vor und ist stabil. Tritium kann aus der folgenden Reaktion (α–Zerfall
von Litium nach Neutronanregung) gewonnen werden:
6
Li + n →
7
Li + n →
3
H +4 He
3
H +4 He + n
und hat eine Halbwertszeit von τ1/2 = 12.3 Jahren. Kontrollierte Fusion findet bis
heute auf der Erde nur für Sekundenbruchteile ohne einen Energienettogewinn ausschließlich in Forschungsreaktoren statt. Den offensichtlichen Vorteilen, wie die sehr
hohe Energieausbeute, praktisch unbegrenzter Brennstoffvorrat und wenig Radiokativität, stehen erhebliche technische Schwierigkeiten entgegen.
Für die Deuterium–Tritium Reaktion ist eine Temperatur von mindestens
4 · 107 K notwendig. Bei diesen Temperaturen sind die 3 H und 2 H Atome vollständig
ionisiert und bilden ein Plasma. Um ein kontrolliertes stationäres Brennen zu erreichen, muß das Plasma genügend lange bei hinreichend großem Druck und Dichte
eingeschlossen sein. Dabei dient das Produkt aus Teilchendichte und Einschlusszeit
als Kriterium: n · τ > 1014 s · cm−3 (Lawson–Kriterium).
Es gibt verschieden technische Ansätze, um den Einschluss zu realisieren:
• Einschluss in einer magnetischen Flasche (Tokomak–Prinzip, toroidale magnetische Kammer)
• Laserfusion: 2 H–3 H Kügelchen werden mit sehr kurzen, hochintensiven Laserpulsen komprimiert
• Beschleunigerbeschuss: analog zum Laserprinzip, nur werden anstelle von Photonen Ionen benutzt
2
Zu einer Supernova kommt es, wenn der Strahlungsdruck des “ausgebrannten” Sternes der
Gravitation nicht mehr standhalten kann und kollabiert.
112
Anwendungen der Kernphysik
• µ–katalysierte Fusion: negative Myonen, die im Kern eingefangen werden, senken das Coulombpotential ab
Wir wollen uns das Tokomak–Prinzip abschließend noch etwas näher betrachen.
In Abbildung 7.7 ist das Tokomak–Prinzip der Kernfusion mit magnetischem Ein-
Abbildung 7.7: Das Tokamak–Prinzip: Anordung von Torus, Plasma und Transformator sowie das resultierende Magnetfeld.
schluss dargestellt. Das Plasma befindet sich in einem von Feldspulen umwickelten
Torus und wird von einem starken toroidalen Magnetfeld auf einer Kreisbahn bewegt. Dieser Strom erzeugt ein zweites Magnetfeld, das den Plasmastrom zusammenhält. Das Toroidalfeld zusammen mit dem zirkularen Feld des Plasmastromes
ergibt die in Abb. 7.7 gezeigte verschraubte Struktur. Die Aufheizung erfolgt dann
durch den starken Plasmastrom (Ohm’scher Widerstand) und/oder duch Einschießen externer Strahlung (z.b. von hochenergetischen Atomen). In Abbildung 7.8 sind
die verschiedenen notwendigen Komponenten für eine kontrollierte Fusion dargestellt. Es ist äusert schwierig, die erforderlichen Plasmadichten bei hohen Tempera-
Abbildung 7.8: Komponenten des Fusionsreaktors nach dem Tokomak–Prinzip.
turen für hinreichend lange Einschlußzeiten zu realisieren. Bisher ist das europäische
Projekt JET (Joint European Torus) in Culham (England) den Anforderungen an
selbstständiges thermonukleares Brennen am nächsten gekommen.