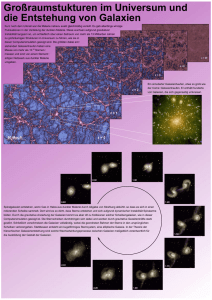
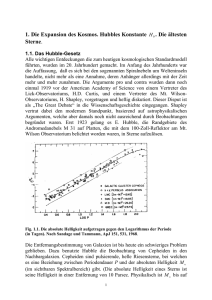
13 mit Anhang - Uni Regensburg/Physik

7. Die Nukleosynthese der leichten Elemente.
7.1. Der heiße Strahlungskosmos.
Wie bereits im vorigen Kapitel erwähnt, waren G. Gamow und sein Mitarbeiter Alpher (1945)
die Ersten, die aus den kosmologischen Modellen Konsequenzen für einen heißen Anfang
zogen. Es ging um die Frage, ob nicht Protonen und Neutronen, während der Abkühlung der
heißen Phase der kosmischen Entwicklung zu Atomkernen kondensierten. Das trifft in der Tat
zu, aber wie sich etwas später herausstellen sollte, nur für die leichten Elemente (bis zu 7Li ),
da keine stabilen Kerne der Massen 5 und 8 existieren. So müssten z.B. für die Erzeugung von
12
C-Kernen drei 4He-Kerne aufeinander treffen. Für solche Dreierstöße ist aber die BaryonenDichte während der Entstehungsphase viel zu klein. Schwere Kerne können deshalb nur in
den dichten heißen Zentren massereicher Sterne erbrütet werden, wie Fred Hoyle 1946 zeigte.
Sein Kollege und Mitarbeiter Alfred Fowler, der 1983 mit dem Nobelpreis geehrt wurde, hat
Hoyles Leistung und Priorität in seiner Autobiographie ausdrücklich anerkannt.
Gamow, der keine Gelegenheit für einen guten Witz ausließ, hatte sich über den Erfolg des jüngeren Hoyle mit
einer Umdichtung der Genesis (Moses 1) verbreitet: Gott schuf die Elemente. Gott vergaß aber die Massen 5 und
8 aufzurufen, so konnten keine schweren Elemente gebildet werden. Gott war enttäuscht und wollte den Kosmos
wieder zusammenfallen und neu beginnen lassen. Aber Er besann sich auf eine höchst ungewöhnliche Art,
seinen Fehler zu korrigieren: Gott sprach: „Es werde Hoyle!“ Und es ward Hoyle. Und Gott sah ihn…..und
sprach zu ihm, er solle schwere Elemente machen, so wie es ihm gefällt. Und Hoyle entschied sich, schwere
Elemente in Sternen zu machen und sie durch Supernova-Explosionen auszustreuen.
Auf der anderen Seite kann die Häufigkeit von 4Helium, das 24% der Masse baryonischer
Materie ausmacht, nicht allein in Sternen entstanden sein. Dieser Anteil macht nämlich nur
wenige Prozent aus. Eine Erklärung der Häufigkeit von Helium macht darum den heißen
Anfang des Kosmos geradezu notwendig. Die Energie des heißen Plasmas sollte kleiner als
1 MeV gewesen sein, da die Bindungsenergie des Deuterons, eines wichtigen Zwischenglieds
der Big-Bang-Nukleosynthese bei 2 MeV liegt. Die Temperatur des kosmischen Plasmas
sollte deshalb unter 1010 K gefallen sein (1MeV = 1,160 ⋅1010 K). Wie groß war aber die
Dichte und welche Zeit verging seit dem Anfang des Kosmos?
Weil die Energiedichte des Strahlungsfelds sich wie ε r ∝ T 4 ∝ a −4 verhält, gilt
a0 T
=
a T0
(2.34)
Mit T0 = 2,725 ± 0,002 K aus den CMB-Messungen und a 0 = 1 wird der Skalenfaktor bei
einer Temperatur von T = 10 K nur noch a10 = 2,7 ⋅ 10
ist bei dieser Temperatur dann
10
ρB =
ρ c,0
a103
h2Ω B =
−10
betragen. Die Baryonendichte
1,88 ⋅ 10 −26
⋅ 0.50 ⋅ 0,04 = 18,5 ⋅ kg ⋅ m −3
2,023 ⋅ 10 − 29
(7.1)
aT 4
bestimmt mit
c2
(wobei hier nur die Freiheitsgrade der Photonen berücksichtigt
Die Gesamtdichte ist jedoch durch die Dichte der Strahlung ρ γ =
ρ γ (1010 K ) = 84,8 ⋅ 10 7 kg ⋅ m −3
wurden). Um die Zeit abzuschätzen, wann 1010 K erreicht wurden, gehen wir von Gl. (2.8)
und (2.30) aus und setzen die Strahlungsdichte ρ γ direkt ein.. Wir finden
76
a (t ) = 2 ⋅ Ω r 2
1
2
1
⎛ 32πGρ r ⎞ 2
⋅ H0 ⋅t = ⎜
⎟ t
3
⎠
⎝
(2.30)
oder
⎛ 32πGaT04
a(t ) = ⎜⎜
2
⎝ 3c
1
1
⎞ 4 12
⎟⎟ t = (1,8 ⋅ 10 −10 ) t 2
⎠
Wir rechnen aus dem Skalenparameter die Temperatur aus
⎛a
T = T0 ⎜ 0
⎜a
⎝
1
−
2
⎞
−1
⎟ = 2,725 ⋅ t
= 1.51 ⋅ 1010 ⋅ t 2 K
10
−
⎟
1,8 ⋅ 10
⎠
(7.2)
Damit erhalten wir T = 1,5 ⋅ 1010 nach t = 1,0 s oder T = 1,0 ⋅ 1010 nach 2,25 s. Werden die
Neutrinos mit berücksichtigt (s. G. Börner: The Early Universe. 4th Ed. 2003) , erhält man
T = 1010 K nach 3,16 s.
Wir entnehmen daraus, dass bis zur Abkühlung auf 109 K weitere 225 s = 3,75 Minuten
vergehen. Die Kernprozesse, um welche es sich hier handelt, spielen sich deshalb in den
ersten 3 Minuten des Kosmos ab. „Die ersten 3 Minuten“, das ist der (deutsche) Titel eines
populären Buchs über die Big-Bang-Nukleosynthese geschrieben von dem Nobelpreisträger
Steve. Weinberg.
7.2. Die Kernprozesse
77
Fig. 7.1. Netzwerk der Kerne der leichten Elemente. In der Abszisse ist die Zahl der Neutronen,
in der Ordinaten die Zahl der Protonen aufgetragen.
Bei Temperaturen T > 1010 K und Zeiten kürzer als eine Sekunde sorgen die Reaktionen
p + e − ↔ n + v und n + e + ↔ p + v
(7.4)
für thermisches Gleichgewicht, wobei das Neutron zu Proton Verhältnis durch
den Boltzmann-Faktor
n
Q
= exp−
p
kT
(7.6)
bestimmt ist. Hier ist Q die Differenz der Ruhenergien (1MeV = 1,160 ⋅1010 K).
Q = (mn − m p ) c 2 = 1,2934 MeV
(7.7)
n/p nähert sich eins, wenn T > 1,5⋅1010 K und die Zeit t < 1 s wird. Bei Temperaturen T <
1010 K verschiebt sich das Gleichgewicht zu Ungunsten der Neutronen; denn die Neutronen
haben eine etwas größere Masse und zerfallen mittels der schwachen Wechselwirkung in die
Endprodukte
n → p + e− + v
(7.8)
Die Lebensdauer der Neutronen wurde im Labor sehr genau zu
881,5 ± 1,5 s
(7.9)
bestimmt. Gäbe es keine weiteren Kernreaktionen, dann würde der Kosmos
nur aus Wasserstoff bestehen. Aber die Lebensdauer der Neutronen τ n reicht aus, um eine
andere Reaktion ins Spiel zu bringen
p+n↔d +γ
(7.10)
Die Neutronen überleben in Deuteronen, deren Bindungsenergie beträgt
Δ D = 2,23 MeV
(7.11)
Zunächst verzögern noch Photonen mit Energien E > Δ D die Bildung von Deuteronen (s.
Rückreaktion Gl. 7.10). Die wirksame Photonendichte nγ für die Rückreaktion (7.10) verhält
sich wie folgt
nγ ∝ η −1 ⋅ exp−
ΔD
kT
(7.12)
wobei η = 6,1⋅10 −10 (WMAP) das Verhältnis Baryonen zu Photonen bedeutet (s. Gl. 6.13).
Eben weil mehr als 109 Photonen auf ein Nukleon kommen, liegen die Bildungstemperaturen
allgemein etwa einen Faktor 30 niedriger als eine Abschätzung allein aus den
Bindungsenergien ergibt. Wenn die Temperatur auf 109 K sinkt, überflügelt die Bildungsrate
die Photodissoziationsrate. Deuteronen bilden sich und können zu He4 weiter reagieren.
78
d + n → H
H
3
+ γ
+ p → He
4
+ γ
d + p → He
3
+ γ
3
He
3
+ n → He
4
(7.12)
+ γ
Diese Reaktionen enden alle bei He4, das eine große Bindungsenergie von
Δ He = 28,30 MeV
besitzt. Noch rascher als die Reaktionen 7.12 mit elektromagnetischer Wechselwirkung
verlaufen die folgenden Prozesse der starken Wechselwirkung
d + d → He 3 + n
d + d → H3 + p
H 3 + n → He 4 + n
(7.13)
He 3 + d → He 4 + p
Nach einigen hundert Sekunden und Temperaturen von etwas unter 109 K sind praktisch alle
Neutronen in He4-Kernen gebunden.
Fig. 7.2. Die Anteile der verschiedenen Isotope und ihre Änderung mit Zeit und Temperatur.
Das Häufigkeitsmaximum des Deuteriums liegt bei etwa 109 K. Danach wird es in den
Reaktionen 7.12 und 7.13 im Wesentlichen zu Helium abgebaut.
79
Wie groß ist am Ende der Anteil des Heliums an der baryonischen Gesamtmasse? Die
Temperatur, bei welcher die Neutronen „ausfrieren“, beträgt etwa 1010 K oder 0,9 MeV. Mit
diesem Wert ergibt Gl. 7.6
n
= 0,223
p
(7.14)
Aus Fig. 7.2. ist ersichtlich, daß die Bildung von He4 erst einen Sättigungswert erreicht, wenn
Neutronen bereits wieder zerfallen, wodurch der Wert von n/p
auf etwa n/p ≈1/7= 0,143 absinkt. Der Anteil Y von Helium an der Gesamtmasse wird dann
Y=
2n p
≅ 0,25
1+ n p
(7.15)
Alle schwereren Isotope bis Li7 kommen in sehr geringer Häufigkeit vor. Damit ist die
Synthese leichter Elemente abgeschlossen. Um C12 zu bilden, sind Dreierstöße notwendig.
Dazu aber ist die Baryonendichte des kosmischen Plasmas viel zu gering. Das Erbrüten von
Kohlenstoff 12 kommt erst in den entarteten Zentren massereicher Sterne in Gang, worauf
zuerst Fred Hoyle hingewiesen hat.
80
Fig. 7.3. Die berechneten Häufigkeiten der leichten Elemente in Abhängigkeit der
Baryonendichte. Die gemessenen Werte liegen etwa im Bereich der grauen Vertikalen
Das erstaunliche Ergebnis: Vorausgesetzt es hat einen heißen Beginn der kosmischen
Entwicklung gegeben, dann finden wir die Isotope der leichten Elemente mit Häufigkeiten,
die sich über einen Bereich von 10 Größenordnungen erstrecken. Um die Häufigkeiten zu
berechnen, ist nur die Kenntnis der Reaktionsraten der Kernprozesse notwendig, mit
Parametern die größtenteils aus Labormessungen bekannt sind. Eine weitere Voraussetzung
ist die Kenntnis des Verhältnisses von Baryonen- zu Photonenzahl und schließlich Zahl der
Neutrinos, die bei allen schwachen Wechselwirkungen eine Rolle spielen. Um die
2
gemessenen Häufigkeiten zu erhalten, sollte ΩB im Bereich 0,009 < Ω B h < 0,025 liegen
und die Zahl der Neutrinos 3 sein.
7.3. Ergebnisse der Beobachtungen
Beginnen wir mit den Messungen der Heliumhäufigkeit. Allerdings muß eingeräumt werden,
dass nach Fig. 7.3 andere Parameter, wie z.B. die Baryonendichte kaum von der Häufigkeit
des ursprünglich gebildeten (primordialen) Heliums abhängen. He4 wird in sogenannten HIIGebieten (Wolken ionisierten Wasserstoffs mit Hα-Emission) beobachtet. Man sucht
Fig. 7.4. Massenanteil von He4 , Y , aus der kosmischen Nukleosynthese (primordiales Helium).
Mit der Zunahme schwerer Elemente im interstellaren Gas nimmt auch die He4-Häufigkeit zu.
Nach B.D. Fields, K.A. Olive, Astrophys. J. 506, 177 (1998)
dabei besonders nach Gebieten, in welchen noch wenig Sternentwicklung stattgefunden hat,
um zu vermeiden, daß Helium aus der Kernfusion der Sternen das Ergebnis beeinflußt. Solche
Gebiete befinden sich z.B. in sogenannten „kompakten blauen Zwerggalaxien“, die als relativ
junge Gebilde des Kosmos angesehen werden. Tatsächlich erkennt man aus Fig. 7.4 eine
positive Korrelation mit der Zunahme schwerer Elemente (hier angegeben durch den
Massenateil von Sauerstoff bzw. Stickstoff). Diese Zunahme wird verursacht durch Abstoßen
81
von Hüllen im Riesenstadium der Sterne sowie durch Supernova-Explosionen, durch welche
die Produkte der Kernreaktionen aus dem Inneren der Sterne in das interstellar Gas gelangen.
Es ist also sinnvoll, die Helium-Häufigkeit Y (s. Fig. 7.4) gegen den Anteil schwerer
Elemente, Z, aufzutragen und dann gegen Z = 0 zu extrapolieren. Das Ergebnis für
„primordiales“ Helium ist
Yp = 0,238 ± 0,002 ± 0,005 ,
wobei die erste Fehlerangabe statistischer, die zweite sytematischer Natur ist. Die Ergebnisse
anderer Bestimmungen (M. Peimbert , A. Peimbert, M.T. Ruiz, Astrophys. J. 541, 688 (2000)
und A. Peimbert, M. Peimbert, V. Luridiana, Astrophys. J. 565, 668 (2002) bewegen sich in
der gleichen Fehlerbreite.
Zur Bestimmung der Konzentration von Li6 und Li7 eignen sich metallarme, heiße Sterne der
Population II in unserer Galaxis. Bei geringem Anteil schwerer
Elemente Z beobachtet man keinen Einfluß auf die Li-Häufigkeit. Erst bei relativ großem Z
(hier als Fe/H aufgetragen) steigt die Li-Häufigkeit an, was auf
Fig. 7.5. Die Häufigkeit der Lithium-Isotope aufgetragen gegen die Häufigkeit von Eisen. Nach
S.G. Ryan et al., Astrophys. J. 530, L57 (2000); S.G. Ryan, J.E. Norris, T.C. Beers, Astrophys. J.
523, 654 (1999).
Kernreaktionen durch kosmische Strahlung zurückgeführt werden kann. Wenn in Sternen der
Pop. II Lithium durch Konvektion in die heißen zentralen Zonen gelangen würde, ginge ein
signifikanter Teil durch Fusionsreaktionen verloren. Wie groß dieser Anteil ist, bleibt
unbekannt. Allerdings spricht die geringe Streuung der Daten in Fig. 7.5 bei kleinen
Konzentrationen schwererer Elemente eher gegen solche Prozesse. Damit erhält man
[Li / H ]p = (1,23 ± 0,06 +−00,,6832+0,56 ) ⋅ 10 −10
82
die letzten Fehlerangeaben (kleingedruckt) beziehen sich auf den schon erwähnten Abbau von
Li durch Konvektion in den Sternen der Pop II.
Die Anwesenheit von Deuterium wurde in hoch aufgelösten Spektren von Quasaren mit
großer Rotverschiebung entdeckt. Die Absorption von Deuterium in primordialen Gaswolken
ist gegenüber der Lyα-Absorption um 2,7 Promille langwellig verschoben. Nimmt man nun
an, dass es sonst keine astrophysikalischen Quellen von Deuterium gibt (dagegen kann
Deuterium durchaus abgebaut werden), dann ergeben die Messungen eine untere Grenze des
Deuteriumgehalts (s. dazu Fig. 7.6). Die Streuung der Ergebnisse ist ziemlich groß und zwar
sowohl bei QSO-Beobachtungen als auch bei
× 10 5
Fig. 7.6. Links beobachtete Häufigkeit von Deuterium und im interstellaren Medium. Rechts
He3-Häufigkeit in galaktischen H II-Regionen. Die Skala der Ordinaten ist ebenfalls mit 105 zu
multiplizieren. Nach B.D. Fields et al., Astrophys. J. 563, 653 (2002) und D.S. Balser et al.
Nature 415, 54 (2002)
Ergebnissen aus dem Interstellaren Medium, was möglicherweise auf Prozesse, welche
Deuterium abbauen, hinweist. Deshalb lässt sich die Häufigkeit von Deuterium nur in relativ
weiten Grenzen angeben
1,3 ⋅ 10 −5 < [D / H ] p < 9,7 ⋅ 10 −5
Für He3 gibt es nur Beobachtungen im Sonnensystem und H II Wolken in unserer Galaxie,
aus welchen sich eine Obergrenze angeben lässt
[He
3
/H
] < (1,9 ± 0,6) ⋅ 10
p
83
−5
Fig. 7.7. 3He-Häufigkeit im Abstand vom galaktischen Zentrum zur besseren Übersicht noch
einmal aus Fig.7.6. rechts heraus gezeichnet (nach Einstein Online).
Wie Fig. 7.7. zeigt, hängt 3He-Häufigkeit kaum von der Lage in der Galaxie ab. Stattdessen
würde man vermuten, dass der Einfluss stellarer Nukleosynthese umso größer ist, je näher die
entsprechende Region zum galaktischen Zentrum liegt. Dass davon kaum etwas zu sehen ist,
zeigt in diesem Fall, dass unser Verständnis der stellaren Nukleosynthese von 3He noch
Einiges zu wünschen übrig lässt.
Wenn man den Werten für Deuterium Vertrauen schenkt, liegt die relative Baryonendichte im
Bereich von
0.0095 ≤ Ω B h 2 ≤ 0,023
Die neuesten Daten des WMAP-Satelliten ergeben Ω B h = 0,0224 ± 0,0009 und für das
Verhältnis Baryonen/Photonen
2
η = 6,1⋅10 −10 ± 0,3
Die folgenden beiden Figuren dienen zum Vergleich von Theorie und Beobachtung. Im
Wesentlichen sind die Ergebnisse von Fig. 7.3. heraus vergrößert worden.
84
Fig. 7.8. zeigt den breiten Bereich der Häufigkeiten, in welchem 4He beobachtet wurde und die
dazu die berechnete Kurve. Die gelbe Vertikale gibt das von WMAP bestimmte η an.
7.9. Gemessene Häufigkeiten von D, 3He und 7Li im Vergleich zu Berechnungen (durchgezogene
Linien) nach Vangioni, Intitute d’Astrophysique de Paris.
7.4. Zusammenfassung
Die leichten Elemente Deuterium, Helium und Lithium sind in den ersten 3 Minuten des
Kosmos bei Temperaturen zwischen 1010 und 109 Kelvin entstanden. Die kosmologische
Nukleosynthese bleibt bei 7Li stehen; denn es gibt keine stabilen Elemente mit den
Massenzahlen 5 oder 8. Die Synthese von 12C schließlich läuft über Stöße von 3 α-Teilchen
ab, was viel höhere Dichten erfordern würde.
85
Die 4He-Häufigkeit liegt bei 0,24 (Massenanteilen), die von Deuterium zwischen 10-4 und 105,
von 3He bei 1 - 2·10-5 und 7Li bei 1 - 2·10-10. 4He ist nur wenig abhängig vom Baryon-zuPhoton-Verhältnis η. Eine größere Empfindlichkeit zeigen D und 3He. Außer bei 7Li, mit
einer Abweichung Faktor 2, stimmen berechnete und gemessene Werte gut überein, was über
10 Größenordnungen der Häufigkeiten doch ein großer Erfolg ist.
7.5. Literatur
H. Reeves: On the Origin of the light elements (Z < 6). Rev. Mod. Phys. 66, 193 (1994)
D.N. Schramm and M. Turner: Big bang nucleosynthesis enters the precision era. Rev. Mod.
Phys. 70, 303 (1998)
S. Sarkar, Measuring the baryon content of the universe: BBN vs CMB
astro-ph/0205116
K. Hagiwara et al. : Big Bang Nucleosynthesis. Phys. Rev. D66, 010001-1 (2002)
G. Steigman : Primordial Nucleosynthesis. astro-ph/0308511
B.D. Fields, K.A. Olive, Astrophys. J. 506, 177 (1998)
D.S. Balser et al. Nature 415, 54 (2002)
B.D. Fields et al., Astrophys. J. 563, 653 (2002)
S.G. Ryan et al., Astrophys. J. 530, L57 (2000)
S.G. Ryan, J.E. Norris, T.C. Beers, Astrophys. J. 523, 654 (1999).
C. Charbonnel, F. Primas: The Lithium Content of the Galactic Halo Stars
http://arxiv.org/abs/astro-ph/0505247
The Big Bang Nucleosynthesesis Homepage
http://www.physics.ohio-state.edu/~phillips/bang/bang.html
Einstein
online:
Big
Bang
online.info/en/spotlights/BBN_obs/index/html
Nucleosynthesis.
http://www.einstein-
7.5. Aufgaben.
7.5.1 Berechne, wie groß die mittlere kinetische Energie bzw. die Temperatur im Moment
der ersten Sekunde nach dem „Big Bang“ war. Benutze dazu nur die Temperatur der
Hintergrundstrahlung von T0 = 2,725 K und vernachlässige andere Effekte außer der
Strahlung (s. Gl. 2.8 und 2.20).
7.5.2 Wie groß war das Neutron zu Proton-Verhältnis nach der ersten Sekunde?
86
7.5.3 Bestimme die freie Weglänge des Lichts zur Zeit der Rekombination bei z = 1089 mit
dem Ionisationsgrad x = 0,1 und der optischen Tiefe τ = 0,09. Achtung: Du brauchst
dazu ρb = ρch2Ωb(z + 1)3 und den Thomson-Streuquerschnitt für Elektronen
σ e = 6,65 ⋅ 10 − 29 m 2 .
87
8. Schwierigkeiten des Standardmodells und das inflationäre
Paradigma.
8.1. Die Probleme des Standardmodells
Das Standardmodell der Kosmologie, in der englischen Literatur auch „Standard Big Bang“
(SBB) oder „lambda cold dark matter model“ ( ΛCDM ) genannt, geht von sehr wenigen
Voraussetzungen aus. Es sind 3 Säulen, auf welchen das Modell ruht: 1. Das kosmologische
Prinzip, d.h. es gilt Isotropie und Homogenität des Kosmos. 2. Gültigkeit der allgemeinen
Relativitätstheorie, ausgedrückt durch die Einsteinschen Gleichungen (oder entsprechend die
Friedmann-Gleichungen). 3. Die Materie verhält sich wie eine ideale Flüssigkeit.
Das unter diesen Voraussetzungen gebildete Modell ist außerordentlich einfach. Es beschreibt
die Entwicklung des Kosmos durch einen einzigen Parameter a(t). Die Materiedichte verhält
sich dabei wie a-3, die Energiedichte der Strahlung wie a-4 und eine etwaige Raumkrümmung
wie a-2. Die Temperatur der Strahlung nimmt mit der Vergangenheit wie T ∝ 1 / a zu. Wenn
Strahlungs- und Materiedichte sowie Raumkrümmung zum heutigen Zeitpunkt bekannt sind,
lässt sich der Zustand der kosmischen Entwicklung für jeden früheren Zeitpunkt angeben.
Dieses klassische Modell wird durch 3 fundamentale Beobachtungsergebnisse gestützt, die es
qualitativ und quantitativ erklärt: nämlich 1) durch die Hubble-Expansion, 2) die
Mikrowellen-Hintergrundstrahlung und 3) durch die Häufigkeit der leichten Elemente. Damit
kann die Entwicklung des Kosmos von der ersten Sekunde bis heute, d.h. nach 4,4⋅1017
Sekunden, über 17 Größenordnungen in der Zeit korrekt beschrieben werden.
Allerdings gibt es im Rahmen des Modells auch eine Reihe nicht beantwortbarer Fragen, die
wir hier aufzählen und auf welche wir in den folgenden Abschnitten näher eingehen wollen.
1. Das Horizont-Problem: Nach dem Standardmodell müsste der beobachtbare Kosmos
heute aus vielen Bereichen bestehen, die kausal nicht miteinander verbunden sind.
Stattdessen ist er homogen und isotrop in allen seinen Teilen.
2. Das „Flatness-Problem“: Warum folgt der Kosmos dem unwahrscheinlichsten Fall κ = 0 ,
also warum ist die Geometrie euklidisch?
3. Der sehr heiße Anfang des Kosmos sollte auch zur Entstehung massiver exotischer
Teilchen beigetragen haben, die aber bisher nicht beobachtet wurden.
4. Es gibt keinen kausalen Prozess, der die „Keime“ der Anisotropien erklären kann, welche
notwendig sind, um die Anisotropien der Hintergrundstrahlung und die heutigen
Strukturen des Kosmos zu verstehen.
5. Das Standardmodell hat bei t = 0 eine nicht behebbare Singularität. Offensichtlich versagt
die Allgemeine Relativitätstheorie als klassische Theorie bei sehr frühen Zeiten
(Planckzeit).
6. Auf ein Baryon kommen mehr als 109 Photonen. Warum gibt es keine Antimaterie im
Kosmos?
7. Woraus besteht die dunkle Materie?
8. Woher kommt die dunkle Energie ( Λ ≠ 0 )?
8.2. Das Horizontproblem
Das Horizont-Problem des Standardmodells ergibt sich wie folgt. Wenn wir die Zeit
rückwärts laufen lassen bis in die Epoche des von Strahlung dominierten Kosmos, dann
88
schrumpft der Teilchenhorizont mit d H = 2ct rascher als der Skalenparameter a (t ) ∝ t 2 (s.
Gl. 3.35 und Fig. 8.1). Am Ende zerfällt der frühe Kosmos in Bereiche, die nicht mehr kausal
miteinander verbunden sein können, weil die Zeit, die seit dem „Urknall“ vergangen ist, zu
kurz war, um alle Gebiete, die wir heute beobachten, durch Wechselwirkungen, welche sich
höchstens mit Lichtgeschwindigkeit ausbreiten können, zu verbinden (s. dazu Fig. 8.2). Aus
Betrachtungen der Entropie kann man abschätzen, dass die Zahl der nicht
zusammenhängenden Bereiche in der Größenordnung 103 liegt. Damit bleibt die hohe
Isotropie und Homogenität des CMB ungeklärt.
1
Zeit / tH
Skalenparameter
Fig. 8.1. Zur Veranschaulichung des Horizont-Problems: Die Expansion des Horizonts verläuft
mit Lichtgeschwindigkeit (grün) und ist langsamer als die Expansion des Skalenparameters (rot)
Fig. 8.2. Die Konsequenz von Fig. 8.1.: Wir beobachten heute (d.h. bei A) kosmische
Mikrowellenstrahlung (CMB), die aus ganz verschiedenen Regionen des Kosmos kommt, ohne
dass sich Unterschiede (bis auf Anisotropien <10-4) feststellen lassen. Nach der Figur war die
Zeit, die seit dem Beginn vergangen ist, zu kurz zum Austausch von Lichtsignalen zwischen B
und C.
89
8.3. Das Problem der „Flachheit“.
Wenn Ω dicht bei 1 liegt, dann können wir die Friedmanngleichung (s. Gl. 5.2 und 5.14) dazu
benutzen, das Verhalten des Ausdrucks Ω − 1 als Funktion der Zeit zu beschreiben. Ω − 1
ist proportional zum Krümmungsterm
κc 2
H (Ω − 1) = − 2
R
2
0
(8.1)
Wir können Ω durch die Energiedichte ε ausdrücken
Ω=
8πG
ε
3c 2 H 02
(8.2)
Division durch H 0 und Ω ergibt
2
Ω −1
κ 3c 4
=− 2
Ω
R 8πGε
(8.3)
−4
Nehmen wir noch die Abhängigkeit vom Skalenparameter R ∝ a und ε ∝ a , dann wird
2
2
Ω −1
= C ⋅ a2
Ω
(8.4)
2
und nimmt proportional zu a ab, wenn wir die Zeit zurück laufen lassen. Heute
ist etwa
Ω − 1 / Ω 0 ≅ ±0,01 ,
Man kann leicht ausrechnen, welches enorme „Finetuning“ in frühen Zeiten des Kosmos
notwendig wäre, um die heutige Euklidizität zu garantieren. Die Anfangsbedingungen
müssten unvorstellbar genau eingestellt sein, damit daraus die geringen gegenwärtigen
Abweichung vom euklidischen Raum ( κ = 0, Ω = 1 ) resultieren, eine sehr unbefriedigende
Situation (s. dazu Aufg. 8.10.1).
8.4. Entropie und Strahlung
Wir hatten mit Gl. 6.16 festgestellt, dass die Entropiedichte proportional zur Photonendichte
ist. Nach der Abkopplung des Strahlungsfelds bleibt die Zahl der Zahl der Photonen konstant
und nach (6.11) gleich nγ = 4,2 ⋅ 10 8 ⋅V . Damit bleibt auch die Entropie im Wesentlichen
konstant. Die Entropiedichte der Photonen ist nach Gl. 6.16
sγ = 1,5 ⋅ 10 9 k B
Schätzt man das gegenwärtige Volumen mit dem Radius des Horizonts zu V ≈ 10 m ab, so
erhält man für die gesamte Entropie der Strahlung
78
90
3
S γ ≈ 1087 k B
Die Neutrinos ergeben etwa den gleichen Betrag. Für die Abschätzung wurde der Faktor vor
der Zehnerpotenz weggelassen. An der Konstanz der Entropie ändert die Strahlung der
astronomischen Objekte nur wenig. Das bedeutet aber, dass der größte Teil der Entropie
schon bei Beginn des Kosmos (beim Urknall) entstanden sein muss.
Ein anderes Problem ergibt sich aus dem Verhältnis der Baryonenzahl zur Zahl der Photonen
η = 6,1⋅10 −10 . Es bedeutet, dass auf ein Baryon 1,6 ⋅10 9 Photonen kommen. Geht man davon
aus, dass bei genügend hoher Temperatur Gleichgewicht zwischen Materie und Antimaterie
herrschte, dann muss sich beim Abkühlen das Gleichgewicht um η zugunsten der Materie
verschoben haben. Das bedeutet, es hat eine winzige Symmetriebrechung gegeben, der wir
Fig. 8.3. Verlauf der Wechselwirkungsparameter für elektromagnetische WW (α1), schwache
(α2) und starke WW (α3) bei hohen Energien (obere Skala in Einheiten der Planckenergie). Die
drei Wechselwirkungen konvergieren bei ca. 1016 GeV. Ein Schnitt mit der Gravitation (αG) ist
nur in supersymmetrischen Theorien möglich und ist hier weggelassen.
das Überleben der Materie und damit unsere Existenz verdanken. Diese Überlegung hat zuerst
Andrej Sacharow angestellt. Ob die Symmetriebrechung bereits in den bekannten
Wechselwirkungen enthalten ist (z.B. in der schwachen Wechselwirkung) oder ob sie durch
eine Abweichung vom thermischen Gleichgewicht bei der Expansion und Abkühlung auftrat,
ist bis heute nicht geklärt.
8.5. Eine inflationäre Expansion würde viele Rätsel lösen.
Die Idee der kosmischen Inflation stammt ursprünglich von Alan Guth, der Ende der siebziger
Jahre als „Postdoctorial Fellow“ an der Cornell Universität arbeitete. Er beschäftigte sich als
theoretischer Physiker damals mit den „Grand Unified Theories“ (GUTs). Die drei
Wechselwirkungen, welche in der Teilchenphysik eine Rolle spielen, sind die
elektromagnetische Wechselwirkung mit der
Symmetriegruppe U(1), die schwache
91
Wechselwirkung mit der Symmetriegruppe SU(2) und die starke Wechselwirkung,
Symmetriegruppe SU(3). Sie unterscheiden sich nicht nur in ihrer Stärke und in ihren
Reichweiten, sondern eben auch in der Symmetrie ihrer inneren Freiheitsgrade, wie z.B. Spin,
Isospin, Flavor, etc. Diese Symmetrien werden Eichsymmetrien genannt. Man suchte nun
nach einer umfassenden Symmetriegruppe, U(1) × SU(2) × SU(3). Eine höhere Symmetrie
müsste bei Teilchenenergien auftreten, bei welchen die Extrapolation der gemessenen
Wechselwirkungsparameter zu einem Wert hin konvergiert (s. Fig. 8.2). Bei diesen Energien,
wie sie möglicherweise unmittelbar nach dem Urknall herrschten, gab es dann nur noch eine
umfassende Wechselwirkung („grand unification“). Die uns bekannten Wechselwirkungen
wären beim Abkühlen durch Brechung der Eichsymmetrien „auskondensiert“. Dazu muss
man sagen, dass heute eine experimentelle Absicherung nur bis zu einigen 100 GeV existiert,
also weit links in der Skala von Fig. 8.3. Der dann folgende Bereich bis zu 1016 GeV heißt im
Jargon der Hochenergiephysiker die „Wüste“, eben wegen der fehlenden Experimente, aber
auch weil man nichts grundsätzlich Neues erwartet. Man ist weitgehend überzeugt davon,
dass in diesem Bereich eigentlich keine neue Physik zu erwarten ist, d.h. eichinvariante
Quantenfeldtheorien sollten bei allen Energien richtig sein, bei welchen die Wechselwirkung
mit der Gravitation noch keine Rolle spielt (E < 1018 GeV). Darüber hinaus allerdings
erwartet man eine neue Physik, welche wahrscheinlich eine Quantentheorie der Gravitation
erfordert. Eben wegen der fehlenden experimentellen Absicherung haben die Modelle, um die
es hier geht, einen wesentlich größeren spekulativen Anteil, als die Physik des
Standardmodells, die bis einschließlich Kap. 7 behandelt wurde.
In den Theorien, welche Alan Guth untersuchte, waren Symmetriebrechungen mit
Phasenumwandlungen verbunden (Beispiel einer bekannten Phasenumwandlung ist der
Übergang flüssig - gasförmig). Beim Abkühlen entsteht eine „Tieftemperaturphase“, welche
den Raum in Domänen aufteilt. An den Bereichsgrenzen ändert sich der Ordnungsparameter
ziemlich abrupt. Nach den „grand unified theories“ (GUTs) sind die Felder dort stark gestört.
A. Guth untersuchte null-dimensionale Störungen, sogenannte magnetische Monopole, die als
massive Teilchen auftreten sollten. Da aber (bis jetzt) offensichtlich keine magnetischen
Monopole beobachtet werden, muss es einen Mechanismus geben, der ihr Auftreten sehr
unwahrscheinlich macht. Das könnte eine Phase exponentieller Expansion a(t ) ∝ exp αt
gewesen sein, welche die Konzentration der magnetischen Monopole so stark verdünnte, dass
sie praktisch unbeobachtbar wurden. Hierzu wäre es notwendig, dass Ω Λ ≈ 1 , d.h. die
„dunkle Energie“ der bei weitem dominierende Beitrag ist. Aus Gl. 5.11 wird dann
2
κ
⎛ a& ⎞
2
2
⎜ ⎟ = H 0 ΩΛ − 2 2 ≈ H 0 ΩΛ
a R0
⎝a⎠
(8.5)
a(t ) wird so stark anwachsen, dass der Krümmungsterm rechts bald vernachlässigt werden
kann. Die Lösung, die de Sitter schon angegeben hat, lässt sich bei nur wenig veränderlicher
Funktion H(t) schreiben
t2
a
(8.6)
a (t ) = a1 exp ∫ H (t ) ⋅ dt ≈ 1 exp H (t 2 − t1 )
H
t1
mit
H2 =
8πG
εΛ
3c 2
(8.7)
(s. dazu Gl. 5.8). Wenn man davon ausgeht, dass die Entropie am Anfang sehr klein und von
kB
gewesen
ist,
dann
muss
die
Zunahme
des
der
Größenordnung
92
Volumens V f Vi ≈ 10 gewesen sein, und damit sollte die Zunahme des Skalenparameters
87
wenigstens a f ai ≈ 10
29
= e 66, 7
betragen.
Fig. 8.4. Beginn: positive Krümmung mit endlischem Krümmungsradius. Bei exponentieller
Expansion nimmt der Krümmungsradius rasch zu. Am Ende ist der Krümmungsradius über
alle Maßen gewachsen, so dass ein euklidischer Raum entstanden ist.
Bei geeigneten Annahmen von ε Λ schafft ein solcher Ansatz eine genügend starke
„Verdünnung“ der Reliktmonopole und löst das Horizontproblem, weil sich der Raum
rascher ausbreitet, als Lichtsignale, so dass der heute dem Beobachter zugängliche Raum
kausal zusammenhängend ist. Schließlich geht die Raumkrümmung in Gl. 8.3 und 8.5 gegen
Null. Der Raum wird euklidisch, ohne dass spezielle Anfangsbedingungen erforderlich sind
(s. Fig. 8.3). Der Beginn der Inflation kann aus E1 < 1016 GeV abgeschätzt werden, was auf
eine Zeit t1 > 10-38 s führt. Der heute beobachtbare Kosmos war zu dieser Zeit so klein, dass
ervon Quantenfluktuationen des Materiefelds beherrscht wurde. Sie könnten die Ursache für
die „Keime“ der An isotropie sein. Damit könnte eine inflationäre (oder beschleunigte)
Expansion die ersten 4 Punkte unserer Aufzählung am Anfang des Kapitels mühelos erklären.
Woher aber sollte im frühen Kosmos ein zeitweise konstantes (oder höchstens schwach
veränderliches) ε Λ kommen?
8.6. Skalares Feld und Symmetriebrechung.
Ein Urfeld, welches die Inflation in Gang gesetzt hat, genannt Inflaton-Feld, sollte
unabhängig vom Skalenfaktor a (t ) sein wie die dunkle Energie. Dazu gibt es sehr viele
Modelle. Am einfachsten geht man von einem skalaren Feld aus. Auch das Higgs-Feld der
Teilchenphysik, dessen Wechselwirkung mit den Teilchenfeldern die Teilchenmassen
erzeugen soll, ist ein skalares Feld. Es könnte auch bei Vereinigung der 3 Wechselwirkungen
bei 1016 GeV eine Rolle gespielt haben. Skalare Felder haben den Vorteil besonders einfach
zu sein. Wir setzen c = 1 und schreiben die Lagrange-Dichte des skalaren Feldes zunächst im
Minkowski-Raum wie folgt
1
L = ημν ∂ μ φ∂ ν φ − V (φ )
2
93
(8.8)
mit ημν = (1 -1 -1 -1). Der Variationsansatz
δ ∫ L dVdt = 0
(8.9)
führt auf die Euler-Lagrange-Gleichung
d ⎛ ∂L ⎞⎟
∂L
=0
− μ ⎜⎜
∂φ dx ⎝ ∂ (∂ μ φ) ⎟⎠
woraus man
φ&& − Δφ +
(8.10)
∂V
=0
∂φ
(8.11)
erhält. Für das Potential V kann man verschiedene Ansätze machen. Der einfachste Ansatz ist
m2 2
V (φ ) =
φ
(8.12)
2
Man erhält so aus Gl. 8.11 die Klein-Gordon-Gleichung
φ&& − Δφ + m 2φ = 0
(8.13)
oder in Fourier transformierter Form
r
( E 2 − p 2 − m′ 2 ) φ = 0
(8.13a)
Das Teilchen (Inflaton), welches durch das skalare Feld beschrieben wird, hat die Masse m
und es gilt aus (8.13a) weiterhin der relativistische Energiesatz
r
E 2 − p 2 = m′ 2
r
wobei p 2 = p12 + p 22 + p32 bedeutet und m′ 2 = m 2 h 2 . Fordert man Homogenität, wird Δφ = 0 .
Will man Phasenumwandlungen beschreiben, sollte das Potential auch Potenzen höherer
Ordnung in φ enthalten (i. a. 4. Ordnung). Ein Beispiel ist das so genannte Higgs-Potential
V (φ ) = −
(
1
m 2 − λφ 2
2λ
)
2
(8.14)
mit m < 0 und λ < 0 . Das Potential (s. Fig. 8.5) hat bei φ = 0 ein Maximum
2
V (φ = 0) = −
m4
2λ
(8.15)
und 2 Minima bei
φ± = ±
m2
(8.16)
λ
mit
94
V (φ ± ) = 0
(8.17)
Das Potential ist spiegelsymmetrisch. Wird dagegen durch eine Störung ein bestimmtes
Minimum ausgewählt worden (z.B. φ + = υ + ς ), ist die Symmetrie gebrochen.
Fig. 8.5. Verlauf des Potentials von Gl. 8.18
Wir sehen nun, wie ein ε Λ zustande kommen könnte. Wenn das Materiefeld ein Potential wie
in Fig. 8.5 besitzt, dann kann es vor einem Phasenübergang einen metastabilen Zustand bei
φ = 0 einnehmen. Damit gäbe es ein zeitweise konstantes ε Λ . Nur muss ε Λ auch wieder
schnell genug abklingen, denn die inflationäre Expansion soll nur kurze Zeit andauern („the
graceful exit problem“).
Für ein skalares Feld im frühen Kosmos müssen wir Gl. 8.8 allerdings statt in MinkowskiMetrik ημν = (1,-1-1-1) in der Robertson-Walker-Metrik mit den entsprechenden gμν
1
aufschreiben. Wir schreiben die Lagrange-Dichte mit V (φ ) = m 2φ 2 wie folgt
2
1 μν
L = [ g ∂ μ φ ∂ν φ − V (φ )]
(8.18)
2
mit der Euler-Lagrange-Gleichung
∂μ
(
)
− g ⋅ g μν ∂ν φ + − g
∂V
=0
∂φ
(8.19)
Hier ist g = Det g μν . Nach Einsetzen von g μν und Differenzieren erhält man
als Bewegungsgleichung des Feldes eine modifizierte Klein-Gordon-Gleichung (s. dazu 3.
Aufgabe am Schluss des Kapitels)
∂V
a 3φ&& + 3a 2 a&φ& − a∇ 2φ + a 3
=0
∂φ
oder
a&
a
φ&& + 3 φ& − a − 2 ∇ 2φ +
∂V
=0
∂φ
95
(8.20)
wobei wir das Glied mit ∇ weglassen werden als Folge der Homogenität und wegen des
Anwachsens von a 2 im Nenner. Setzt man jetzt z.B. das Potential Gl. 8.12 ein, so erhält man
die Gleichung einer gedämpften Schwingung
2
φ&& + 3Hφ& + m 2φ = 0
(8.21)
Die Schwingung des Feldes wird durch die Expansion des Raumes gedämpft. Wir sehen, dass
in der Robertson-Walker-Metrik das skalare Feld von selbst an den expandierenden Raum
koppelt. Man spricht von minimaler Kopplung, die nur über die Metrik abläuft. Wenn die
Dämpfung durch H groß genug ist, bewegt sich das System im aperiodischen Grenzfall, was
im Jargon der inflationären Kosmologie eben als „slow roll down“ bezeichnet wird. Die
zweite Ableitung kann dann vernachlässigt werden. Das skalare Feld ist genügend „langsam
veränderlich“. Danach bleibt nach Wiedereinsetzen von m φ =
2
übrig
∂V
3Hφ& = −
∂φ
∂V
∂φ
folgende Gleichung
(8.22)
Um an die Gleichungen 8.5 – 8.7 anschließen zu können, benötigen wir noch einen Ausdruck,
der anstelle der klassischen Dichte steht. Mit dem Energie-Impulstensor Tμν ist es möglich,
die entsprechenden Ausdrücke zu finden. Die Feldtheorie bietet zur Berechnung von Tμν aus
der Lagrangedichte des Feldes ein Standardverfahren an
⎡1
⎤
Tμν = ∂ μ φ ∂ν φ − g μν ⎢ g αβ ∂ α φ ∂ β φ + V (φ )⎥
⎣2
⎦
(8.23)
Bei Vernachlässigung der Gradientenglieder (Homogenität) und mit c =1 erhält man hieraus
1
p = φ& 2 − V (φ )
2
(8.24)
und
1
2
ε = φ& 2 + V (φ )
Mit der „slow roll condition“
wieder
(8.25)
1 &2
φ << V (φ ) erhält man außerdem aus Gl. 8.24 und 8.25
2c 2
p = −ε
(5.7)
Wir suchen zunächst den Zusammenhang von Skalenparameter a und Feld φ . Dazu
schreiben wir die Friedmann-Gleichung auf, wobei wir annehmen wollen, dass sich die
Energiedichte des skalaren Feldes wie der Λ-Term verhält und der Krümmungsterm sowie
etwaige Volumen abhängige Felder während der inflationären Epoche schnell genug
verschwinden (s. 2.8 und 2.9)
H2 =
⎞
⎞
8πG ⎛ φ& 2
1 ⎛ φ& 2
⎜
⎟
⎜
⎟⎟
V
V
+
=
+
2 ⎜
2
⎟ 3M ⎜ 2
3c ⎝ 2
⎠
⎠
P ⎝
96
(8.26)
Hier ist M P =
MP
hc
=
0,4341 ⋅ 10 -8 kg die reduzierte Planckmasse.
8πG
8π
Bezeichnung
Plancklänge
Definition
Planckzeit
Planckmasse
Größe
lP =
hG
c3
1.616 252(81) × 10−35 m
tP =
hG
c5
5.391 24(27) × 10−44 s
hc
G
2.176 44(11) × 10−8 kg
MP =
Tab. 8.1. Die Planckgrößen
Mit der „slow roll condition“ erhalten wir außerdem aus (8.26)
H2 ≈
8πG
1 ⎛ m2 2 ⎞
⎜
(
)
=
φ
φ ⎟⎟
V
3c 2
3M P2 ⎜⎝ 2
⎠
(8.26a)
und
1
1
⎛ 8πG ⎞ 2
H ≈ ⎜ 2 ⎟ V (φ ) 2 =
⎝ 3c ⎠
mφ&
6M P
Aus Gl. 8.26a ergibt sich durch Differenzieren nach der Zeit
1
2 HH& = −
m 2φφ&
2
3M P
Danach dividieren wir durch 3Hφ& = −m 2φ (s. Gl. 8.22)
∂H
1 &
=−
φ
∂φ
2M P2
(8.26b)
(8.27)
(8.28)
integrieren über φ und schreiben links die Hubblefunktion aus
∂
1
ln a = −
φφ&
2
∂t
2M P
(8.29)
Nach Integration über die Zeit erhalten wir schließlich
a (t ) = ai exp
1
[φ02 − φ 2 (t )]
2M P2
97
(8.30)
wobei wir für V (φ) das einfache quadratische Potential der Gl. 8.12. Es ist das Potential von
& eliminieren
Andrej Lindes „chaotischer Inflation“. Aus Gl. 8.22 und 8.26b lässt sich φ
φ& = −
2
mM P
3
(8.31)
was integriert nach der Zeit
2
mM P ⋅ t
3
φ = φ0 −
(8.32)
ergibt. Nach Andrej Linde startet das Feld bei etwa φ 0 ≈ 10 (in Planck-Einheiten). Dann
6
sollte m ≈ 3 ⋅ 10 sein, damit die Fluktuationen der CMB die richtige Größe bekommen. Die
inflationäre Expansion klingt ab, wenn der Exponent von Gl. 8.30 kleiner als eins wird also
11
−43
etwa nach t ≤ 4 ⋅ 10 t P (mit der Planckzeit t P = 0,538 ⋅ 10 s ) d.h. die Inflation endet
−6
nach etwa 2 ⋅ 10
−32
s.
Vergleich von Gl. 8.30 und 8.26a liefert den Zusammenhang
a(t ) = ai exp H Δt
(8.33)
Nach jeweils einer Hubble-Zeit Δt = H −1 vergrößern sich die Längenmaße um den Faktor e =
2,718. Die Zahl der e-Entfaltungen während der inflationären Periode ist
N = ln
af
ai
tf
φf
ti
φii
H
= ∫ H (t )dt = ∫ dφ ≈
&
φ
φi
1 V
8π φi2
dφ = 2
M P2 φ∫f V ′
MP 4
(8.34)
Der letzte Ausdruck rechts ergibt sich aus der Division von Gl. 8.26a durch 8.22. Der Wert
von N hängt wesentlich von der Wahl des Potentials V ab. Mit dem quadratischen Potential
2
12
Gl. 8.12 wird N = 8π φ 0 4 ≈ 2π ⋅ 10 . In anderen Modellen wird N mit mindestens 60
angesetzt, um das Horizontproblem zu lösen.
Zur Geschichte des inflationären Paradigmas ist Folgendes anzumerken. Alan Guth, von dem
die Idee ursprünglich stammte, untersuchte zunächst Phasenübergänge 1. Ordnung mit einem
Potential wie in Fig. 8.4. Die Bereiche, die Inflation zeigen, verhalten sich ähnlich wie
Gasblasen in einer siedenden Flüssigkeit. Aber die Blasen können kollidieren und
expandieren überhaupt zu stark. Um das zu vermeiden, ist eine Feinabstimmung notwendig,
welche das Modell gerade beseitigen wollte. 1982 wurde von Steinhardt und Albrecht ein
Modell mit einem Phasenübergang 2. Ordnung vorgeschlagen. Fig. 8.6 zeigt das Potential.
Wenn die Temperatur unter eine kritische Temperatur Tc sinkt, kann das skalare Feld in das
neue Minimum abrollen (neue Inflation). Das heute bevorzugte Modell hat den Namen
„chaotische Inflation“ erhalten und stammt von Andrej Linde. Es enthält keine
Phasenumwandlung. In diesem Modell werden nur minimale Annahmen gemacht,
insbesondere versucht Linde ohne explizite Anfangsbedingungen auszukommen. Nach Linde
muss die Amplitude des Feldes zu Beginn der Inflation etwa 106 Planck-Einheiten sein
−6
(s.oben), was sehr hoch erscheint, aber die Masse wird mit m ≈ 10 M P angesetzt, so dass
die Energiedichte nicht größer als 1 Planckeinheit beträgt.
98
8.6. Die Freie Energie eines Phasenübergangs 2. Ordnung enthält ein effektives
Potential, das von der Temperatur abhängig ist.
Bei der Expansion erfolgt Abkühlung. Beim Übergang in das Minimum, bzw. in das wahre
Vakuum, wird potentielle Energie in Feld-Energie umgesetzt. Das Feld bleibt in einem hoch
angeregten Zustand zurück und erzeugt Teilchen. Dabei entsteht eine Abkühlung. Die
Wechselwirkungen der Teilchen, die möglicherweise in andere zerfallen, erzeugen eine
kinetische Energiedichte (d.h. Wiederaufheizung), der eine negative potentielle Energiedichte
aus der Gravitation entgegensteht. Bei euklidischer Geometrie kompensieren sich beide
gerade.
Zusammenfassend können wir feststellen: Die inflationäre Expansion behebt viele der oben
&& > 0 , die
genannten Schwierigkeiten. Sie verlangt eine Epoche beschleunigter Expansion, a
von der potentielle Feldenergie angetrieben wird. Weiterhin müssen die „Bedingungen des
langsamen Abrollens“ erfüllt sein. Das bedeutet
a&& &
= H + H2 >0
a
(8.31)
Die spezielle Gestalt des Potentials V (φ ) und die der Feldfunktion φ sind dabei von
geringerer Bedeutung. Das drückt sich im Attraktor-Verhalten von H (t ) aus und bedeutet
Folgendes: Wenn es beim Abrollen des skalaren Feldes eine inflationäre Lösung gibt, dann
nähern sich alle linearen Störungen dieser Lösung an und zwar mindestens exponentiell (s.
dazu A.R. Liddle & D.H. Lyth: Cosmological Inflation and Large Structure, Cambridge
University Press 2000). Nach erfolgtem Abrollen endet die Inflation und geht in die
Expansion des Standardmodells über. Diese Prozesse wurden für das quadratische Potential
näher untersucht. Es besteht die Hoffnung, dass sich in Zukunft, wenn die Ergebnisse des
europäischen
Planck-Satelliten
vorliegen
und
bei
besserer
Kenntnis
des
Fluktuationsspektrums viele Modelle für V (φ ) ausschließen lassen. Das beobachtete
Fluktuationsspektrum des CMB unterstützt bis jetzt eher möglichst einfache Modelle.
8.7. Quantenfluktuationen.
Man erinnere sich, dass der Ereignishorizont der geometrische Ort alles Punkte ist, von
welchen ein Lichtsignal den Beobachter nicht mehr in endlicher Zeit erreicht. Bei
exponentieller Expansion ist der Abstand zum Ereignishorizont (in mitbewegten Koordinaten
99
s. Gl. 3.37) endlich und während der Inflation bei schwach veränderlichem H (t ) fast
stationär
∞
rEH = ∫
t
∞
c
c dt
(t → 0)
= c exp ∫ − H (t )dt ≈
H (t )
a (t )
t
(8.32)
Der Ereignishorizont bildet eine absolute Begrenzung für die Moden k S = 2π λ S des Felds,
d.h. λ max ≈
c
. Die Unschärfebeziehung besagt in diesem Fall
H
Δp = h Δk = h ⋅ 2π
Es
ist
deshalb
sinnvoll,
nach
H
c
(8.33)
Fluktuationen
ΔE = δφ = h Δt = h ⋅ H
in
der
Hintergrundstrahlung zu suchen, die als Quantenfluktuationen beginnen, nach Überqueren des
Horizonts stehen geblieben sind und später zu klassischen Störungen anwuchsen. Ihre
räumliche Ausdehnung bekommt durch die Inflation makroskopische Größenordnungen. Sie
bilden die Keime für die Entstehung von Anisotropien in der CMB und für inhomogene
Massenverteilungen und später gebildete Strukturen wie Galaxiencluster.
8.8. Zusammenfassung
Eine Reihe von Problemen können nicht im Rahmen des Standardmodells gelöst werden. Sie
können aber durch Annahme einer sehr frühen inflationären Epoche, während dessen
a&&(t ) > 0 , befriedigend erklärt werden. Dazu gehören 1) das Horizontproblem, 2) das
Flachheitsproblem, das Entropieproblem. 3) Das Fehlen exotischer Teilchen. 4) Die
Anisotropien der Hintergrundstrahlung. Die inflationäre, exponentielle Expansion um einen
Faktor größer als exp(60) wird durch die Energie eines „Urfelds“ (auch Inflaton-Feld
genannt) ausgelöst. Die Energie hält sich während der inflationären Epoche auf einem nahezu
konstanten Wert, muss danach aber genügend schnell wieder abklingen. Zu 6): zwischen
Materie und Antimaterie muss es eine geringfügige Asymmetrie gegeben haben (ca. 1:109),
die durch Inflation nicht zu erklären ist. Das Modell gibt auch auf 5) , 6), 7) und 8) keine
Antwort. Die Keime für die Strukturbildung werden durch Quantenfluktuationen des InflatonFeldes gebildet, die durch die Inflation zu makroskopischer Größe aufgebläht werden. Die
Singularität bei t = 0 kann nur im Rahmen der Quantengravitation behoben werden, die in
inflationären Modellen meist nicht diskutiert wird. Das bedeutet, dass man außerhalb der
Planckgrößen bleibt.
8.9. Literatur
E.W. Kolb, The inflationary decade. Phys. Rept. 227 (1993) 2
Andrei Linde: Elementarteilchen und inflationärer Kosmos. Spektrum. Akademischer Verl.
1993
Gary Scott Watson: An Exposition on Inflationary Cosmology .
astro-ph/0005003. http://nedwww.jpac.caltech.edu/level5/Watson
100
Andrew R. Liddle, David Lyth: Cosmological Inflation and Large-Scale Structure. Cambridge
Univ. Press 2000
Gerhard Börner; The Early Universe. 3rd Edition. Springerverl. 2003
Robert H. Brandenberger, Principles, Progress and Problems in Inflationary Cosmology.
ArXiv: astro-ph/0208103
Andrei Linde, Inflation and String Cosmology. http://xxx.uni-augsburg.de/abs/hepth/0503195
8.10. Übungen
1) Die relative Abweichung vom euklidischen Raum kann durch eine Umformung des
Krümmungsterms wie folgt beschrieben werden (s. 8.4)
Ω −1
= C ⋅ a2
Ω
Nimm an dass in der Gegenwart die Abweichung kleiner als 2% ist: Ω − 1 / Ω 0 < 0,02 .
Wie präzise müsste das „fine tuning“ 1 Sekunde nach dem Urknall sein?
2) Zeige, dass die Gleichung (in Minkowski-Metrik)
∂V
m 2φ 2
= 0 mit V (φ ) =
φ&& − Δφ +
∂φ
2
den relativistischen Energiesatz erfüllt (Klein-Gordon-Gl.).
3) Wir untersuchen die Euler-Lagrange-Gleichung des skalaren Feldes in der RobertsonWalker-Metrik
∂V
1
∂ μ − g ⋅ g μν ∂ν φ +
=0
∂φ
−g
(
)
Zeige, dass daraus folgende Gleichung wird (c = 1)
a&
a
φ&& − a − 2 ∇ 2φ + 3 φ& +
∂V
=0
∂φ
Was versteht man unter der „slow roll down“- Näherung? Hilfe: Es ist leichter, wenn du statt
der Kugelkoordinaten karthesische verwendest und die Ableitung für den euklidischen Fall
damit durchziehst. Verwende also mit (κ = 0)
ds 2 = dt 2 − a 2
dx 2 + dy 2 + dz 2
1+
κ
4
:
(x + y + z )
2
101
2
2
9. Fluktuationen der Mikrowellenstrahlung (CMB)
9.1. Das Fluktuationsspektrum, eine Fundgrube für Kosmologen.
Die Anisotropien der Mikrowellenstrahlung (CMB), wie sie vom COBE-Satelliten in der
−4
Größe von ΔT / T < 10 gemessen wurden, zeigt die untere Fig. 6.3. Diese Resultate wurden
von der Fachwelt zunächst mit Skepsis aufgenommen. Das COBE-Team machte aber die
Daten allgemein zugänglich, ebenso wie die Methoden der Datenauswertung. So wich die
Skepsis bald großer Begeisterung, denn sowohl die Existenz als auch die Größenordnung der
Fluktuationen passten sehr gut in das Bild eines inflationären Kosmos. Die Fluktuationen im
Plasma des frühen Kosmos sind keine Schwankungen um Mittelwerte der GleichgewichtsThermodynamik. Diese wären viel zu klein. Stattdessen stammen die Anisotropien von
Quantenfluktuationen, die am Beginn der inflationären Phase winzig klein waren und zu
Störungen der Metrik führten, die während der Inflation zu makroskopischer Größe
aufgebläht wurden (s. Gl. 8.33). Sie blieben nach dem Überqueren des Horizonts während der
inflationären Epoche (in mitbewegten Koordinaten) stehen. Die Störungen der Metrik führten
ihrerseits nach dem Ende der Inflation zu Dichte- bzw. Temperatur-Inhomogenitäten im
Plasma. Nach der Entkopplung von der Materie enthält das Strahlungsfeld diese Störungen
auch heute noch in gleicher Struktur.
Bei den Messungen werden die Temperaturen punktweise über einen Ausschnitt des Himmels
oder, wenn möglich, über den ganzen Himmel verteilt registriert und auf diese Weise
Zweipunkt-Korrelationsfunktionen gebildet. In den Projekten nach COBE wurden
Abweichungen vom Mittelwert der Temperatur mit einer Genauigkeit von
Θ = ΔT / T ≈ 10 −6 gemessenen. Die Anisotropien liegen im Bereich von 50 µK. Ihre Größe
und Verteilung wird einer Zerlegung nach Kugelflächenfunktionen unterworfen. Die
Messwerte einer Temperaturdifferenz mit den Koordinaten ϑ, ϕ werden in einen
transformierten Wert umgeformt
ΔT
(ϑ , ϕ ) = Θ(ϑ , ϕ ) = ∑ alT,mYl ,m (ϑ , ϕ )
T
l ,m
und die Rücktransformation
alT,m = ∫∫ Θ(ϑ,ϕ ) ⋅ Ylm (ϑ,ϕ )sin ϑ ⋅ dϑ ⋅ dϕ
(9.1)
(9.2)
ϑϕ
Hier sind die Ylm die Kugelflächenfunktionen. Zusätzlich wird noch eine Fensterfunktion
berücksichtigt, welche die Strahlauflösung beschreibt, die wir hier zur besseren
Übersichtlichkeit weggelassen haben. Zum Vergleich mit Modellen dient das
Leistungsspektrum. Dazu bildet man die Korrelationsfunktion (unter der Voraussetzung, dass
der Raum isotrop ist)
ΔT
ΔT
(nˆ1 )
(nˆ 2 )
T
T
= C (θ ) =
21
1
4π
∑C
2
l
Pl (cos θ )
(9.3)
l
Hier bedeuten nˆ1 , nˆ 2 Einheitsvektoren, welche die Himmelsrichtung definieren und welche
den Winkelabstand θ haben: nˆ1 ⋅nˆ 2 = cos θ . Ausserdem ist Pl (cos θ ) das LegendrePolynom der l-ten Ordnung. Die eckigen Klammern bedeuten eine Mittelung über alle
102
Produkte zu gleichem Winkel θ . Die Entwicklungskoeffizienten C l lassen sich aus der
Korrelationsfunktion mit den transformierten Temperatur-Fluktuationen Θ l ,m gewinnen
alT,m alT′,m′ = C l δ ll ′δ mm′
TT
(9.4)
Die eckige Klammer bedeutet Summation und Mittelbildung. Der Zusammenhang von
Temperatur-Temperatur-Korrelationsfunktion und Leistungsspektrum ist wie folgt
(ΔT ) 2 l (l + 1) T T
=
Cl
2π
T2
(9.5)
hängt nur noch von l ab (s. fig. 9.1).
Fig. 9.1. Das Leistungsspektrum C lT T der Temperatur-Temperatur-Korrelationen aus
7-jährigen Messungen des WMAP-Satelliten. Die durchgezogene Kurve ist ein „Bestfit“
auf der Basis des ΛCDM-Modells. Die kosmologischen Parameter sind die folgenden:
Ω b h 2 = 0,02270, Ω M h 2 = 0,1107, Ω Λ h 2 = 0,738, τ = 0,086, n S = 0,969, Δ2R = 2,38 ⋅ 10 −9 ,
ASZ = 0,52
103
Die Winkelausdehnung δϑ der Gebiete mit einer Abweichung vom Mittelwert der
Temperatur läßt sich aus δϑ ≈ 180° / l abschätzen. Modell-Rechnungen zeigen, dass die C lT T ,
die das Leistungsspektrum oder „Fluktuationsspektrum“ bilden, stark von den Parametern der
kosmologischen Modelle abhängen, weshalb außergewöhnliche Anstrengungen unternommen
wurden, das Spektrum mit möglichst geringen Fehlern zu vermessen.
9.2. Die Experimente und ihre Ergebnisse
Die Bedeutung, welche die CMB-Messungen in der Kosmologie haben, kann nicht hoch
genug eingeschätzt werden. Sie wird auch an der großen Zahl von Mess-Programmen
deutlich, welche bereits gelaufen sind oder sich im Stadium der Planung befinden. WMAP
liefert gegenwärtig besten Daten zur Bestimmung kosmologischer Parameter Messungen,
welche den gesamten Himmel überdecken, können nur mit Satellitensonden durchgeführt
werden. Die Ergebnisse des COBE-Satelliten wurden bereits im Kap. 7 erläutert. Daran
schloss sich das WMAP-Projekt an. Der WMAP-Satellit (Wilkinson Microwave Anisotropy
Probe) wurde 2001 gestartet. Nach Eichung und Test der Instrumente hat er kontinuierlich
Daten geliefert. Erst kürzlich konnten die Ergebnisse von 7 Jahren Daten-Aufnahme und –
Analyse vorgestellt werden. Auch der 2010 gestartete PLANCK-Satellit der europäischen
Raumfahrtorganisation (ESO) liefert längst Daten. Um die höhere Auflösung gegenüber
WMAP wirklich auszunutzen, sind umfangreiche Untersuchungen der Mikrowellen- und
Infrarotstrahlung von galaktischen und extragalaktischen Quellen notwendig. Entsprechende
Ergebnisse wurden publiziert, ebenso wie Messungen des Sunyaev-Zeldovich-Effekts, mit
welchen bisher unbekannte Galaxien-Cluster nachgewiesen werden konnten.
Daneben laufen Beobachtungen mit Teleskopen, die im Mikrowellen- und Millimeterbereich
Daten liefern (ACBAR, APEX, BICEP, BIMA, CBI, DASI, SZ-Cluster, South Pole
Telescope). Bekannt geworden sind insbesondere die Ergebnisse von Ballon-Experimenten.
Das waren Beobachtungen mit Sonden, welche jeweils von einem Stratosphären-Ballon
getragen wurden. Diese Programme sind um Größenordnungen billiger als
Satellitenprogramme, erfassen aber immer nur einen Ausschnitt des Himmels und können
wegen der begrenzten Flugzeit des Ballons nur eine begrenzte Datenmenge registrieren. Die
interessantesten Ergebnisse kamen von den Ballonexperimenten MAXIMA und
BOOMERANG. Wegen des begrenzten Gesichtsfelds beschränkte man sich darauf, einen
Ausschnitt des Himmels zu untersuchen.
BOOMERANG war ein Experiment, bei welchem die Flughöhe 38 km betrug. Der Ballon
wurde 1200 km vom Südpol entfernt im antarktischen Sommer gestartet. Die Flugroute
nutzte dabei das zirkumpolaren Windsystem der Antarktis,
104
Fig. 9.2. Das BOOMERANG-Experiment: Starten des Ballon-Aufstiegs in der Antarkis. Im
Hintergrund der Mt. Eurebus.
so daß man 7 – 20 Tage Beobachtungszeit unter optimalen Verhältnissen gewann. Die
Messungen wurden mit 16 Bolometern in 4 Frequenzfenstern vorgenommen: 90, 150, 240
und 400 Ghz. Die beiden ersten Frequenzen sind so gewählt, daß der galaktische Vordergrund
weitgehend vermieden wird, während die zwei letztgenanten Frequenzen gerade diesen
Vordergrund empfangen. Das Ziel des Projekts war die genaue Vermessung des so genannten
akustischen „Peaks“, der danach bei l = 203 ± 6 liegt. Im Winkelmaß ausgedrückt haben die
entsprechenden Gebiete am Himmel eine Ausdehnung von ϑ = l / 360 ≈ 0,6° . Sie sollten sich
am heutigen Teilchenhorizont befinden, dessen mitbewegter Abstand sich wie folgt
abschätzen läßt
dt
da
3.38
rH (t 0 ) / c = ∫ = ∫ 2
=
= 15,26 Gpc
(9.4)
a
a H (a ) H 0
Berücksichtigt wurden hier in H (a ) Masse Ω M = 0,27 und dunkle Energie Ω Λ = 0,73 mit h
= 0,71. Würde nur der Beitrag der Massendichte berücksichtigt, erhält man 3,85 / H 0 .
Dichtefluktuationen nehmen an akustischen Schwingungen des Plasmas teil, dass aus
baryonischer ionisierter Materie, dunkler Materie und vor allem aus Photonen besteht.
Den akustischen Peak fanden wir bei ϑ = 0,6° .
(für eine genaue Abschätzung s. Fig. 9.3)
Demnach ist die heutige Ausdehnung des
entsprechenden Gebiets
rAH (t 0 ) = rH (t 0 ) ⋅ sin ϑ ≈ 15,26 ⋅ 0,01047 = 159Mpc
(9.5)
Zur Zeit der Rekombination war die Größe des
Gebiets um 1 /( z + 1) kleiner, also
rAH (t rec ) = 159 / 1090 = 147 kpc
(9.7)
Fig. 9.3. Zur Lage des akustischen Peaks. Nach
D.J. Eisenstein and Ch. Bennett, Physics
Today April 2008 p. 46
oder
rAH (t 0 ) = rH (t rec ) ⋅ ( z + 1) ⋅ sin ϑ
105
(9.7a)
Das lässt sich mit dem Winkelabstand DA schreiben
D A = rH (t rec ) ⋅ sin θ
(9.7b)
Wir berechnen jetzt die Schallgeschwindigkeit im heißen, von Photonen dominierten Plasma
und berücksichtigen dabei, dass die Dichte ihr Photonen 3-mal so groß ist wie ihr Druck
1
(9.8)
pγ = ε γ
3
Deshalb gilt für die Schallgeschwindigkeit
cS =
pγ
εγ / c
2
=
c
(9.9)
3
Diese Schallwellen haben nur die Zeit t rec zur Verfügung, sich auszubreiten. Damit schaffen
sie eine maximale Strecke
c
3
⋅ t rec = λ / 2 = rAH / 2
(9.10)
Das ergibt λ = rAH = 144 kpc . Der wichtige Punkt ist hier, dass euklidische Geometrie
vorausgesetzt wurde. Genau das haben die Ballon-Experimente mit hinreichender
Genauigkeit zeigen können. Wir können nach Kap. 3 nachvollziehen, dass bei der
Berechnung des Horizont-Abstands bei positiver Krümmung nach (3.12) für rH ein kleinerer
Wert und bei negativer Krümmung nach (3.16) ein größerer Wert entsteht
rH (κ = +1) =
DH
ΩK
1
sin( Ω K
∫a
0
106
2
da
)
E (a )
(9.11)
Fig. 9.4. Veranschaulichung des Zusammenhangs
Winkelausdehnung des akustischen Peaks.
mit
von
Raumkrümmung
E (a) = Ω M a −3 + Ω Λ + Ω K a −2
und
(9.12)
bei negativer Krümmung tritt (2.11) ein sinh anstelle von sin. Bei der Lösung führt
eine Reihenentwicklung näherungsweise zum Ziel (s. Gl. 3.22). Mit ξ =
1
ΩK
∫a
0
2
da
E (a )
1
1
erhalten wir sin ξ ≈ ξ − ξ 3 + ... und sinh ξ ≈ ξ + ξ 3 + ... .Ist außerdem Ω K << Ω M
6
6
1
da
1
so kann man ∫ 2
≈
rH (κ = 0) setzen. Die Krümmung erscheint dann im 2. Glied
D
(
)
a
E
a
H
0
der Entwicklung.
Das Ergebnis der BOOMERANG- Mission (Fig. 9.4) spricht für einen euklidischen Raum
κ = 0 . Die Fälle κ = ±1 sind in Fig. 9.4 auf der linken und rechten Seite simuliert. Die
Krümmung ( Ω K ) als Abweichung von der kritischen Dichte von Ω − Ω 0 geht ein mit
Ω K = − H 0−2 ⋅
DH2
c 2κ
=
−
κ
R2
R2
(9.13).
Der Einfluß der Massendichte lässt sich im Spektrum genähert durch
l Peak ≈ 220 / Ω M
107
(9.14)
oder durch sin ϑ ∝ Ω M darstellen. Näherungsweise gilt ϑ ≈ 1,2° ⋅ Ω M Wenn κ > 0 ist
(geschlossener Raum), wird Ω K negativ (s. Gl. 5.2) und es würde rAH und damit der Winkel
ϑ größer werden. Für κ < 0 (offener Raum) würde ein kleinerer Wert rAH erwartet als im
Fall κ = 0 . Das BOOMERANG-Experiment hat mit einer Genauigkeit von ca. 5% (ebenso
das Projekt MAXIMA mit etwas geringerer Genauigkeit) den Nachweis erbracht, dass Ω = 1
und der Raum euklidisch ist, noch ehe entsprechende Daten von der WMAP-Sonde vorlagen.
Der Grundschwingung l Peak = l1 folgen höhere Harmonische
l m = ml1 mit l = 1, 2,..
(9.15)
Näheres dazu siehe unten bei (9.20) und (9.22).
9.3. Die WMAP-Sonde
Das spannendste Experiment war und ist zweifellos WMAP. Der 830 kg schwere Satellit
wurde im Sommer 2001 gestartet und reiste 3 Monate bis er den äußeren Langrange-Punkt L2
im Sonne-Erde System in 1,5 ⋅106 km erreichte, den er seither in Pendelbewegungen
(Lissajous-Figuren) umkreist. Der Satellit liefert seit Beginn des Jahres 2003 die ersten
Ergebnisse. Das System detektiert in 5 Frequenzkanälen von 23, 33, 41, 61 und 94 GHz mit
Winkelauflösungen von 0,93 bis < 0,23°. Das Radiometer des Empfängers misst
Temperaturdifferenzen und die Polarisation der Strahlung. Die beiden Primärspiegel von 1,4
× 1,6 m sind als duales optisches Gregory-System angeordnet, welche Strahlung von zwei
Fig. 9.5. WMAP : Die Instrumente s. Beschriftung und Text
108
Fig. 9.6. WMAP: Der Empfänger, ausgerüstet als duale Mikrowellen-Meßbrücke ist in der Lage,
Differenzen der Mikrowellenleistung sowie Polarisation der Strahlung zu messen. Die Kühlung
auf ca. 90 K wird durch passive Abstrahlung erreicht.
Punkten aufnehmen kann. Diese liegen 140° auseinander liegen und werden 10 getrennten
Differential-Empfängern zugeleitet. Die fokale Ebene umfasst ein Gesichtsfeld von 3,5 × 3,5
°. Die Lebensdauer des Satelliten wird mit mindestens 27 Monaten angegeben. Die ersten
Ergebnisse, dargestellt in Fig. 9.8 sind frappierend. Im Vergleich zu COBE fällt die enorm
gesteigerte Auflösung ins Auge. Lange Messzeiten und eine hohe Zahl von Messpunkten
schaffen eine bisher unerreichte Genauigkeit der Messdaten.
109
Fig. 9.7. Anisotropie der CMB gemessen mit COBE (oben und WMAP (unten)
Das zeigt sich insbesondere im Fluktuationsspektrum in Fig. 9.1. Die Begrenzung des
Gesichtsfelds auf 3,5 × 3,5 ° führt in der Auftragung gegen die Multipolordnung l zu einer
galoppierenden Vergrößerung der Fehler jenseits von l = 700 .
9.4. Interpretation der Spektren
Es sind eine Reihe von Programmen verfügbar, mit welchen die Spektren der CMBFluktuationen simuliert werden können. Neben den verschiedenen Beiträgen zu Ω , geht H0,
die CBM-Temperatur T0, der skalare spektrale Index n, die optische Tiefe bei der letzten
Lichtstreuung, die Rotverschiebung z bei Beginn der Reionisierung in die Rechnung ein.
Andere Parameter wie die Neutrinozahl oder Ω Λ müssen eingegeben werden. Damit können
nicht nur anderweitig gemessene Parameter auf ihre Verträglichkeit überprüft, sondern auch
Details untersucht werden wie die Reionisation, die mit der Entstehung erster Sterne bei ca.
z ≤ 20 (was etwa 200 ⋅ 10 6 Jahren entspricht) zusammen fällt. Wir werden am Schluß des
Kapitels die von dem WMAP-Team bestimmten kosmologischen Parameter in einer Tabelle
angeben und uns jetzt einigen mehr qualitativen Diskussionen über das Zustandekommen des
Spektrums widmen.
110
Fig. 9.7 Die nacheinander folgenden kleinen Graphiken zeigen die Ausbreitung der Akustischen
Welle als Dichtestörung von Dunkler Materie, Baryonen, Photonen und Neutrinos ausgehend
von einer zentralen Störung s. (a). Die Photonen und Baryonen wandern gemeinsam bis (d). Bei
(e) haben sie sich vollständig getrennt. Die Neutrinos laufen bereits bei (c) voraus, währen die
dunkle Materie nur langsam voran kommt und erst bei (f) ein zweites Maximum bildet. Nach
Rechnungen der Autoren in D.J. Eisenstein and Ch. Bennett, Physics Today April 2008 p. 46.
Zum Verständnis der akustischen Schwingungen betrachtet man das Plasma aus Baryonen,
Elektronen und Photonen als relativistische Flüssigkeit. Das Plasma wird durch starke
elektromagnetische Wechselwirkung im thermischen Gleichgewicht gehalten. Die Kopplung
der Photonen an die Materie ist durch Streuprozesse vermittelt, wobei wir unterscheiden
können zwischen Streuung von Photonen an Elektronen (s. Kap. 6), an Atomen (RayleighStreuung) und Absorptionen durch Wasserstoffatome, die aber bei abnehmender Temperatur
111
immer seltener werden. Das Plasma ist vor der Entkopplung undurchsichtig. Die freie
Weglänge der Photonen lph wächst an bis zur völligen Entkopplung, wobei sie ziemlich
schnell die Größenordnung der Horizontlänge erreicht
l ph = σ ne ≈ H (t* )
(9.16)
Die Teilchendichte der Elektronen lässt sich aus dem Ionisationsgrad x (s. Gl. 6.21) und der
Baryonendichte bestimmen
n e = x Ω 0 b a −3
(9.17)
Fig. 9.8 Oben ist der Ionisationsgrad unten die Sichtbarkeitsfunktion eines Photons
aufgetragen gegen die Temperatur und gegen die konforme Zeit aufgetragen, die in der
Figur τ genannt wird, sie entspricht dem Koordinatenabstand r im Text. Die
Sichtbarkeitsfunktion, welche die Wahrscheinlichkeit angibt, dass ein Photon zum
letzten Mal gestreut wird (Thomson-Streuung an freien Elektronen), ist aufgetragen
gegen die heute beobachtete Horizontskala. Nach M. Zaldarriaga: An Introduction to
CMB Anisotropy. Lecture Notes.
Fig. 9.8 zeigt das Abklingen des Ionisationsgrads x (s. Gl. 6.21) mit der Zeit. Die akustischen
Schwingungen entstehen aus einem Wechselspiel von Kompression durch Gravitation und
rücktreibendem Strahlungsdruck. Wenn die Photonen aus dem Gravitationspotential wieder
entweichen, hat eine Temperaturerniedrigung stattgefunden (Sachs-Wolfe-Effekt). Da die
Umkehrpunkte Extrema der Geschwindigkeit der Plasmas-Schwingung sind, hat die
Geschwindigkeit eine Phasenverschiebung von 90° zur Temperaturschwingung. Die
Geschwindigkeit verursacht eine Dopplerverschiebung in Richtung zum Beobachter. Würde
man den Effekt der Baryonen vernachlässigen, dann hätten die Doppler-Oszillationen die
gleiche Amplitude wie die Temperatur-Oszillationen, sie wären nur um 90° zueinander
phasenverschoben. Die Erhöhung der Baryonendichte erhöht auch die effektive Masse des
Plasmas. Bei Berücksichtigung der Baryonen (baryon loading) steht für die
Schallgeschwindigkeit
112
c S2 = c 2 / 3(1 + Q) mit Q = 3ρ b / 4 ρ γ ,
(9.18)
die akustischen Wellen breiten sich langsamer aus. Die Baryonen verstärken auch die
Amplitude der Temperaturschwingungen und die Höhe der Kompressions-Peaks. Damit fällt
gleichzeitig die Amplitude der Geschwindigkeiten. Zusätzlich müssen Dämpfungsprozesse
der Schwingungen in Betracht gezogen werden. Hier ist in erster Linie an einen
Energietransport durch Strahlung zu denken, was Streuprozesse der Photonen besorgen,
welche dadurch eine begrenzte freie Weglänge bekommen (s. Gl. 9.12 u. 9.13). Sie haben den
Namen Silk-Dämpfung erhalten und spielen besonders auf kleinen Längenskalen eine Rolle
Δϑ ≤ 5' , was zu l ≥ 2500 führt.
Wie werden die Schwingungen angetrieben? Wie oben schon behauptet, werden sie von
Fluktuationen angetrieben, welche aus der Inflation stammen. Diese sind selbstähnlich, weil
die Inflation eine exponentielle Expansion und a& / a skalenunabhängig ist. Das zeigt sich im
Leistungsspektrum der Temperaturvarianz
Δ2T
P (k )
l (l + 1)
Cl ≡ 2 ≈ k 3 T 2 ∝ k n −1
T
2π
2π k
(9.19)
Sie sind nicht mehr von k abhängig, d.h. es sollte n = 1 sein. Der beste Wert für den
spektralen Index n ist heute n = 0,964 ± 0,014 Die Fluktuationen der Geometrie sind
eingefroren, weil die Störungen jetzt außerhalb des Horizonts liegen. Sie lassen sich als
Störung von Raummetrik
δ g kl = 2a 2 Φ δ kl k , l = 1,2,3
(9.20)
und Zeitmetrik
δ g tt = 2Ψ
(9.21)
verstehen. Wenn wir Ψ = δ t / t setzen, und für den Skalenparameter den allgemeinen
Ausdruck
a ∝ t 2 /[ 3(1+ w )]
(9.15)
wählen mit der Zustandsgleichung
p = wρ
(9.16)
dann erhalten wir für die Temperaturfluktuation
ΔT
δa
2
=−
=−
⋅Ψ
T
a
3[1 + w]
(9.17)
In der Strahlungsdominierten Epoche wird die Temperaturfluktuation mit w = 1 / 3 zu
ΔT / T = −Ψ / 2 , dagegen in der Materie dominierten Epoche wird ΔT / T = −2Ψ / 3 . Man
sieht daraus, dass die anfängliche Temperaturfluktuation untrennbar mit den anfänglichen
Störungen des Gravitationspotentials verbunden ist.
Wir verzichten hier aus Platz- und Zeitgründen auf die explizite Angabe der
Oszillatorgleichungen, was einen Einstieg in die relativistische Hydrodynamik erfordern
113
würde. Stattdessen geben wir nur die Frequenz ω der Moden an, die als stehende Wellen der
Wellenzahl k beobachtet werden
ω2 =
c2
k2
3(1 + Q)
(9.18)
Hier ist Q das Impulsdichteverhältnis von Baryonen zu Photonen
Q = ( pb + ρb ) /( pr + ρ r ) =
4 ρb
≈ 26.6 Ωb h 2 ( z / 103 ) −1
3 ργ
(9.19)
Wenn die Baryonendichte gegen Null geht, nähert sich das Quadrat der
2
2
Schallgeschwindigkeit im Photonen-Plasma c s = c / 3 an und wird bei Rekombination mit
c
Q ≈ 0,65 , und c S =
≈ 0,45c . Die Ausdehnung des akustischen Horizonts sollte
3(1 + Q )
gleich einer halben Wellenlänge der Grundschwingung sein, also λ = 2 rAH (t 0 ) . Dann wird
der k-Vektor der Grundschwingung ( m = 1) und Oberschwingungen ( m > 1)
k m = mπ / rAH (t 0 )
(9.20)
Die Ordnungszahl (der Kugelfunktion) l n ist ungefähr proportional zu k n
und
l m ∝ k m ∝ m l1
(9.22)
l1 ≈ π / ϑ
(9.23)
Ob überhaupt akustische Peaks mit Oberschwingungen beobachtet werden können, hängt von
der Kohärenz der Schwingungen ab. Sie ist keineswegs selbstverständlich, sondern eine
Konsequenz der Inflation, welche die Schwingungen, die über den Horizont ausgedehnt
werden, phasengleich starten lässt.
Ungeradzahlige Peaks markieren Gebiete größerer Dichte, die geradzahligen Peaks Gebiete
geringerer Dichte. Die Höhendifferenz der Peaks (abzüglich des Untergrunds) beträgt
(1 + 2Q) 2 − 1 . Da Q ≈ 3ρ b / 4 ρ γ das Baryon zu Photon Verhältnis enthält, kann das CMBSpektrum helfen, die Baryonenkonzentration zu bestimmen.
Nach der beobachteten Abfolge der akustischen Peaks würde man l1 ≈ 300 erwarte.
Stattdessen liegt l1 bei 220. Ein Grund ist u.a. die Expansionsrate ändert sich durch das
Auftreten der dunklen Energie. Dadurch erscheint der erste Peak zu niedrigeren Multipolen
bzw. die Oberschwingungen zu höheren Multipolen verschoben. Die Empfindlichkeit der
akustischen Skala, die in Fig. 9.9 dargestellt ist, wird nach Hu und Dodelson noch einmal
numerisch angegeben
114
Δ Ωb h 2
Δ Ωmh2
Δ Ω tot
Δ ΩΛ
Δl
+ 0,17
− 0,11wΛ + 0,07
− 0,24
≈ −1,1
Ωb h 2
Ωmh2
ΩΛ
l
Ω tot
(2.24)
Fig. 9.9. zeigt, wie die Modell-Spektren von der Baryonendichte Ωb, der Materiedichte
Ωm, der Dichte der dunklen Energie ΩΛ (hier Ωe genannt)und Zustandsgleichungh der
dunklen Energie wΛ (hier we genannt) abhängen. Die Rechnungen gingen von einem
euklidischen Modell aus mit den Parametern ΩΛ= 0,65, wΛ = -1, Ωbh2 = 0,02, Ωmh2=0,15
und n = 1 nach W. Hu, S. Dodelson, Ann. Rev. Astron. Astrophys. 40 (2002) 171.
Die Modelle hängen auch von der dunklen Energie und der Materie ab, wie die Fig. 9.10
zeigt. Daraus hat sich eine ziemlich genaue Bestimmung dieser Größen ergeben unter der
Vorgabe euklidischer Geometrie. Man erhält mit h = 0,72 , Ω M = 0,26 und Ω Λ = 0,74 .
Die baryonische Materie nimmt davon insgesamt nur den Anteil 0,04 ein.
9.5. Polarisation.
Außer Temperaturdifferenzen wurden von WMAP auch Polarisation der
Mikrowellenstrahlung in verschiedenen Frequenzkanälen gemessen, zuerst vom DAS’IExperiment 2002. Die signifikante polarisierte Strahlung des Vordergrunds stammt sowohl
von galaktischer Synchrotronstrahlung (bes. bei 40 GHz und l < 50) wie auch von thermischer
Strahlung aus interstellarem Staub (bes. bei 94 GHz) in der galaktischen Ebene. Das
115
polarisierte Signal wird mit den Stokes-Parametern Q, U beschrieben. Die beiden
r
r
Einheitsvektoren e1 , e2 geben die Achsen der Polarisation an. I 11 und I 22 sind die
Intensitäten des polarisierten Lichts parallel zu den Achsen und I 12 = E1 (45°) E 2 (45°) die
Intensität in 45° zu den Achsen. Dann ist
Q=
1
( I 11 − I 22 ) ,
4
U=
1
1
I 12 und die Temperatur T = ( I 11 + I 22 )
2
4
(2.25)
Man kann aus Q und U einen komplexen Messwert formen und ihn nach
Kugelflächenfunktionen entwickeln
r
r
(Q + iU )(n ) = ∑ a l ,m ⋅ Yl ,m (n )
(2.26)
r
der sich bei Rotationen wie ein Spinor mit j = 2 verhält, d.h. [expm 2iψ ] ⋅ (Q + iU )(n ) . Die Eund B-Moden können nun mit Hilfe der al ,m entwickelt werden
r
r
r
r
E (n ) = ∑ alE,mYl ,m (n ) und B(n ) = ∑ alB,mYl ,m (n )
l ,m
mit
(2.26)
l ,m
1
1
alE,m = − (al ,m + a ∗ l ,m ) und alB,m = − (al ,m − a ∗ l ,m )
2
2i
(2.27)
Mit (2.26) ist das Feld der linearen Polarisation vollständig spezifiziert. Die Polarisation aus
der galaktischen Ebene kontaminiert die gesuchten Effekte im CMB. Bei den Messungen mit
WMAP liefert der Kanal von 61 GHz in hohen galaktischen Breiten Daten, die am wenigsten
von der Vordergrund-Polarisation kontaminiert sind.
Fig. 9.10. Lage der E-Polarisation von WMAP bei 61 GHz gemessen.
116
Fig. 9.11. E- und B-Polarisation in der Umgebung einer kreisförmigen Störung niedrigerer
Temperatur (links) und höhere Temperatur (rechts). Also rotationsfreies Feld oben,
divergenzfreies Feld unten.
Fig. 9.12.a) Strahlung aus einem kälteren b) Die Tensor-Symmetrie lässt sich durch die
(links) und einem heißeren Gebiet (oben Kugelflächenfunktion Y2, 0 (ϑ , ϕ ) darstellen.
Mitte) wird an Elektronen gestreut. Die
Stralungsquelle hat Tensor-Symmetrie.
Man hat neben dem Spektrum der Temperatur- oder TT-Korrelation (Gl. 9.4) auch das EEund das TE Korrelationsspektrum gemessen. Das EE-Spektrum wird interpretiert als
Thomsonstreuung der Strahlung von einem lokalen Quadrupol an Elektronen (im
Wesentlichen zur Zeit der Rekombination) auf dem Weg zum Detektor (s. 9.12).
Die optische Tiefe liegt dabei nach 7 Jahren WMAP-Daten bei 0,085. Der skalare spektrale
Index wird mit n S = 0,96 angegeben. Die Streuung ist eine tensorielle Eigenschaft, die durch
unterschiedliche Intensitäten der Strahlung aus 2 Richtungen zustande kommt. Die EPolarisation besitzt keine Chiralität (sie hat gerade Parität und ist symmetrisch gegenüber
Links- und Rechtshändigkeit). Das bedeutet, dass das Feld der E-Moden rotationsfrei ist.
Anders das Feld der B-Moden. Es enthält „Wirbel“, ist aber divergenzfrei (s. Fig. 9.13). Das
B-Feld geht auf die Inflation und die Aktivität der Gravitationswellen sowie auf „Lensing“
117
zurück. Leider ist derAnteil der B-Moden sehr klein und bisher nicht sicher nachgewiesen.
Die relativen Stärken der TT-, EE-, TE- und BB-Spektren zeigt Fig. 9.13. Die Korrelationen
TB und EB verschwinden aus Gründen der Symmetrie.
Sachs-Wolfe
Silk
Damping
Acoustic
Oscillations
Gravitational
Lensing
Reionisation
Gravitational
Waves
Fig. 9.13. (letzte Seite unten) Die Skizze zeigt die Korrelationsfunktionen TT, TE, EE, und BB
auf einer logarithmische μK -Skala. Die Prozesse, welche Peaklagen und Zwischenbereiche
bestimmen, sind seitlich angegeben. Das BB-Spektrum erscheint mehrere Größenordnungen
schwächer. Es würde eine Aussage über die Dynamik des Inflatons ermöglichen.
9.6. Zusammenfassung
Die Fluktuationen der Hintergrundstrahlung können heute mit Prozent-Genauigkeit gemessen
werden. Das geschieht mit Satelliten, mit Ballon-Sonden und terrestrischen Teleskopen für
die Millimeterwellenstrahlung. Die Analyse des Leistungsspektrums ermöglicht eine große
Zahl von kosmologischen Parametern mit hinreichender Genauigkeit zu bestimmen. Das
Spektrum bestätigt das einfachste Modell der Inflation, es zeigt eine euklidische Geometrie an
und ermöglicht, die Zusammensetzung der Energiedichte qualitativ und quantitativ zu
bestimmen. Darüber hinaus bestätigt es das ΛCDM-Modell. Die Effekte der E-Polarisation
sind noch eine Größenordnung kleiner als Temperaturfluktuation. Die angefügten Tabellen
stellen die kosmologischen Parameter zusammen, wie sie nach den Daten von WMAP nach 3
und 7 Jahren Messung bestimmt wurden.
9.6. Kosmologische Parameter aus den WMAP-Daten
118
119
Tab. 3. Kosmologische Parameter nach 5 Jahren WMAP-Datenaufnahme
Aus G. Hinshaw et al. Five Year Wilkinson Microwave Ansiotropy Probe (WMAP)
Observations: Data Processing, Sky Maps, and Basic Results APJ Suppl. 148, 135
120
Tab. 4. Kosmologische Parameter nach 7 Jahren WMAP-Datenaufnahme nach
E. Komatsu et al. Seven Year Wilkinson Microwave Ansiotropy Probe (WMAP)
Observations: Cosmological Interpretations. APJ Suppl. XXXX
9.7. Literatur
M. Zaldarriaga: An Introduction to CMB Anisotropy. Lecture Notes.
A.R. Liddle, D.H. Lyth : Cosmological Inflation and Large-Scale Structure. Cambridge Univ.
Press 2000
W. Hu, N. Sugiyama, & J. Silk. The Physics of Microwave Background Anisotropies. Nature
37 (1997) astro-ph/9604166
G. Hinshaw et al., First Year WMAP Observations: The Angular Power Spectrum. APJ 148
(2003) 63
A. Kogut et al., WMAP first Year Observations: TE Polarisation. APJ 148
(2003) 161
L. Page et al., First Year WMAP Observations: Interpretation of the TT
TE Angular Power Spectrum Peaks, APJ 148 (2003) 23
G. Hinshaw et al. Five Year Wilkinson Microwave Ansiotropy Probe (WMAP) Observations: Data
Processing, Sky Maps, and Basic Results APJ Suppl. 148, 135
121
E. Komatsu et al. Seven Year Wilkinson Microwave Ansiotropy Probe (WMAP)
Observations: Cosmological Interpretations. APJ Suppl. XXXX
http://xxx.uni-augsburg.de/abs/astro-ph0603449
http://map.gsfc.nasa.gov/m_mm/ob_techres.html
http://www.hep.upenn.edu/~max/cbm/experiments/html
http://cosmo.nyu.edu/matiasz/CBMFAST/parameters.html
9.8. Aufgaben
1) Die Rekombination hat nicht nur Einfluss auf die Lichtstreuung, sondern sie
verursacht auch einen Zusammenbruch der Schallgeschwindigkeit um viele
Zehnerpotenzen. Wir wollen nachweisen.
Für T > Trec ist cS = c / 3
Bei T = Trec setzt Baryonloading ein. Dann wird cS = c / 3(1 + Q )
pb / c 2 + ρ b 4 ρ b
Was wir mit Q =
≈
ausrechnen wollen.
pγ / c 2 + ρ γ 3 ρ γ
Wenn schließlich die Rekombination passiert und das Gas neutral ist,
dann ist bei T ≤ Trec die Schallgeschwindigkeit eines idealen Gases erreicht, welches
aus 75% atomaren Wasserstoff und 25 % Helium besteht. Die adiabatische
p
Wir erinnern uns dazu an die ideale
Schallgeschwindigkeit ist c S = γ
ρ
Gasgleichung p =
ρ
M
RT . M ist die mittlere Molmasse des Gases und γ =
CP
CV
2) Nach Gl. (2.13) und (2.14) Verschiebt eine vorhandene Raumkrümmung den ersten
akustischen Peak. Gib eine quantitative Abschätzung des Effekts an.
3) Wenn Du in Gl. (9.10) die Lichtgeschwindigkeit an Stelle der Schallgeschwindigkeit
einsetzt, bekommst du aus der Lage des ersten akustischen Peaks die Größe des
Horizonts zur Zeit der Rekombination. Das war die Größe eines kausal zusammen
hängenden Bereichs zu dieser Zeit. Wie viele solcher Bereiche passen heute in den
vollen Raumwinkel?
Du erinnerst Dich, dass das die Frage war, die uns beim „Horizontproblem“
begegnete. Anleitung: Schätze die Fläche eines solchen Bereichs auf der Einheitskugel
ab und dividiere die volle Fläche der Einheitskugel (also 4π ) durch diese Fläche.
122
10. Was war am Anfang?
10.1. Inflationsmodelle und Beobachtungen
Wir hatten in Kap. 8 am Beispiel eines einfachen Models der „chaotischen Inflation“
gesehen, wie die inflationäre Phase beschrieben werden kann. Dazu wurde ein skalares Feld
φ angenommen, dass sich am Anfang in einem Zustand hoher potentieller Energie befindet.
Das Potential wird meist in Potenzen von φ angegeben. Wir haben „slow roll“-Bedingungen
vorausgesetzt, die sich verallgemeinert durch die beiden slow-roll Parameter
⎛V ′ ⎞
⎜ ⎟
⎝V ⎠
M P2
εˆ(φ ) =
16π
M P2 ⎛ V ′′ ⎞
und η =
⎜ ⎟
8π ⎝ V ⎠
2
(10.1)
ausdrücken lassen. Es stellt sich nun die Frage, ob sich aus den kosmologischen Parametern
Schlüsse auf das Inflations-Potential ziehen lassen. Wird nur ein einziges, skalares Feld
angenommenund stammen die „curvature perturbations“ von den Vakuumfluktuationen des
φ -Felds dann läßt sich das Leistungsspektrum der skalaren Fluktuationen wie folgt
⎛ hc ⎞
ausdrücken (mit M P = ⎜ ⎟
⎝G⎠
⎛H
PS (k ) = ⎜⎜
⎝ φ&
1
2
= 2,18 ⋅ 10 −8 kg )
2
⎞ ⎛H ⎞
⎟⎟ ⎜
⎟
⎠ ⎝ 2π ⎠
2
=
k = aH
1
V
24π M εˆ
2
4
P
(10.2)
k = aH
Entsprechendes gilt für die Tensorflutuationen
8
PT (k ) = 2
MP
⎛H ⎞
⎜
⎟
⎝ 2π ⎠
2
=
k = aH
2
V
3π M P4
(10.3)
2
k = aH
Dabei wurde angenommen H ≈ konst. und d ln k ≈ d ln a . Man kann in diesem einfachen
Fall direkt auf das Potential schließen.
Eine andere Möglichkeit auf das Potential zu schließen. bieten die spektralen Indizes n und r.
PS (k ) wird dargestellt
nS −1
⎛ k ⎞
(10.4)
PS (k ) = AS (k 0 ) ⋅ ⎜⎜ ⎟⎟
⎝ k0 ⎠
Der Zusammenhang mit der gemessenen Fluktuationsamplitude skalarer Moden ist
Δ2R = k 3 / 2π 2 ⋅ AS
. Für den Fall, dass sich n mit k ändert, führt man einen
k = k0
„running index“ α S ein
αS =
dn
d ln k
(10.5)
den wir in (10.4) nicht berücksichtigt haben. Von Nutzen ist auch das Tensor-SkalarVerhältnis
123
PT
PS
Schreibt man das Potential in einer normierten Form
υ (φ ) =
r=
(10.6)
V (φ )
V (φ ) CMB
(10.7)
wobei im Nenner der Wert des Potentials am Ende der Inflation steht, so wird
r = 8υ ′ 2
und
(10.8)
[
n S − 1 = 2υ ′′ − 3υ ′ 2
]
(10.9)
Auf diese Weise lässt sich eine Taylor-Reihe bestimmen
V (φ ) = V (φ∗ ) + V ′(φ∗ )(φ − φ∗ ) + V ′′(φ∗ )(φ − φ∗ ) + .....
(10.10)
Allerdings ist die Unsicherheit von n S − 1 ziemlich groß (ca. 30%). Von r lässt sich nur eine
obere Grenze angeben.
Auf die Bedeutung der B-Polarisation für den Nachweis der Tensor-Fluktuationen war schon
im vorigen Kapitel hingewiesen worden. Hier darf man auf Ergebnisse zukünftiger
Präzisionsmessungen gespannt sein. Von diesen Entwicklungen wird es auch abhängen, ob
man in der Lage sein wird, Modelle mit mehreren Feldern oder mit Abweichungen von
Gaußscher Statistik an beobachteten Daten zu testen. Gaußsche Statistik (Gaussianity) bezieht
sich hier auf die Störungen am Anfang, die als Wellen ganz verschiedener Wellenzahl und
willkürlicher Amplitude auftreten und deren Verteilungsfunktion eine Gauß-Kurve darstellt..
10.1. Die Planck-Aera.
Das Modell der Inflation benötigt keine speziellen Anfangsbedingungen, ja es scheint nur die
Fluktuationen des Inflatonfelds (φ + δφ ) aus der Schlussphase der Inflation zu erhalten und
„Erinnerungen“ an frühere Epochen auszulöschen. Die Frage nach dem, was davor war,
erscheint demnach vielleicht überflüssig, so lange man sich mit einer phänomenologischen
Beschreibung, wie oben dargestellt, begnügt. Sie ist aber keineswegs sinnlos, wie sich schon
aus der Frage nach der Singularität am Anfang zeigt. Die Herausforderung bei der
Behandlung einer prä-inflationären Epoche hängt zum einen an unserer Unkenntnis der frühen
Materiefelder, andererseits sind wichtige Fragen, nach dem Ursprung der Inflation
unbeantwortet. Die Notwendigkeit, in der chaotischen Inflation (Fall des starken Felds) das
skalare Feld bei einem Vielfachen der Planckenergie beginnen zu lassen, provoziert sofort die
Frage, ob wir hier nicht eine Quantisierung der Raumzeit berücksichtigen müssten. Die
Dimensionen, bei welchen eine Quanten-Gravitation ins Spiel kommt, heißen PlanckEinheiten.
Als es Max Planck um 1900 klar geworden war, dass er mit „h“ eine neue Naturkonstante
gefunden hatte, versuchte er, aus h, c und G natürliche Einheiten der Länge, der Zeit und der
Energie zu bilden. Allerdings lagen und liegen diese Einheiten so weit außerhalb der damals
124
wie heute messbaren und vorstellbaren Welt, dass sie zunächst wieder in Vergessenheit
gerieten. Heute spricht man bei folgenden Größen von Planck-Einheiten (s. a. Tab. 8.1):
1
Plancklänge
⎛ Gh ⎞
lP = ⎜ 3 ⎟
⎝c ⎠
Plankzeit
⎛ Gh ⎞ 2
t P = ⎜ 5 ⎟ = 5,38 ⋅ 10 − 44 s
⎝c ⎠
Planckmasse
⎛ hc ⎞
MP = ⎜ ⎟
⎝G⎠
2
= 1,61 ⋅ 10 −35 cm
(10.11)
1
1
2
= 2,18 ⋅ 10 −8 kg
Planckenergie E P = M P c 2 = 1,22 ⋅ 1019 GeV .
(10.12)
(10.13)
(10.14)
Neben diesen fundamentalen Größen sind eine Reihe von abgeleiteten Größen in Gebrauch:
Plancktemperatur TP =
Planckdichte ρ P =
M P c2
= 1,41 ⋅ 10 32 K
kB
(10.15)
MP
= 5,2 ⋅ 10 93 g ⋅ cm −3 = 5,2 ⋅ 10 96 kg ⋅ m −3
l P3
(10.16)
Planck selbst hat die Deutung dieser Größen nicht weiter verfolgt, Man geht jedoch heute
davon aus, dass die Planck-Einheiten den Bereich der Quantengravitation bezeichnen. Man
stellt sich vor, dass im Bereich von 10-33 cm und 10-43 s Quantenfluktuationen der Metrik so
stark sind, dass Angaben über die klassische Raumzeit nicht mehr gemacht werden können.
Das Standardmodell der Kosmologie basiert auf einer klassischen Kontinuumstheorie, der
−1
ART. Der Reziprokwert des Skalenparameters a weist am Anfang (t = 0) ebenso wie die
−3
Dichte ρ ∝ a eine Singularität auf, welche sich im Rahmen der ART nicht beseitigen lässt,
wie von S.W. Hawking und R. Penrose 1970 und S.W. Hawking und G.F.R. Ellis 1973
gezeigt wurde. Wenn also der Skalenparameter verschwindet, d.h. a (t ) → 0 , divergiert
Materiedichte ρ(0) → ∞ und kinetische Energiedichte T (0) → ∞ . Inzwischen gibt es
Ansätze zu einer Quantengravitation insbesondere in der String Theorie und in der „Loop
Quantum Theory“.
10.3. Wege zur Quantengravitation: Stringtheorie.
Den Weg zu einer umfassenden Theorie der Materie, welche die Quantengravitation
einschließt, wird von Vertretern der Stringtheorie (oder umfassender M-Theorie genannt)
eingeschlagen. Diese Theorie sieht sich heute als eine „Grand Unified Theory“. Stringtheorie
(oder M-Theorie) arbeitet in (10 + 1) Dimensionen. Ihre Elementaranregungen sind nicht
punktförmig wie in der Standardtheorie der Elementarteilchen, sondern linienförmig oder
haben auch höhere Dimension (D-branes). Die Stringtheorie schließt Supersymmetrie und
Gravitation ein. In einem kurzen Review-Artikel von Tom Banks von 1999 wird gezeigt, wie
Eichfelder die Supersymmetrie (bei welcher Bosonen und Fermionen immer als Paare mit
gleicher Masse auftreten) brechen können und dabei auch Inflatonfelder entstehen. Aber eine
125
konsistente Baryonsynthese fehlt noch. Drei Jahre später stellen Paul J. Steinhardt und Neil
Turok (2002) ein Modell auf der Grundlage der M-Theorie vor, das die Autoren
„ekpyrotisches“ Modell nennen und dass einen zyklischen Kosmos beschreibt, der
weitgehend die Parameter des Standardmodells annimmt. In dem Modell von Steinhardt und
Turok werden 6 Dimensionen kompaktifiziert. Es bleiben eine Zeitdimension und 4
Raumdimensionen übrig, die von der Gravitation beherrscht werden. Der 4d-Raum ist
begrenzt durch zwei 3d-Hyperflächen oder „D-Branes“. Die Materie unserer sichtbaren Welt
bewegt sich auf einem dieser „Branes“. Die Materie der anderen (unsichtbaren) „Brane“
wechselwirkt mit der sichtbaren Welt nur über die Gravitation und wirkt als dunkle Materie.
Auch in diesem Modell kommt ein skalares Feld vor. Es bestimmt den Abstand zwischen den
Branes. Das Potential V(ϕ) beschreibt die Kraft zwischen den Branes, die sie zur Kollision
und zum Auseinanderdriften bringt. Die Beobachtungen können gegenwärtig nicht zwischen
beiden Modellen, dem der klassischen Inflation mit einem einmaligen Anfang und dem
zyklischen Braneworld-Model, unterscheiden. Nach dem zyklischen Model treten nur
Dichtefluktationen aber keine Gravitationswellen auf, während nach der klassischen Inflation
beides auftreten sollte. Allerdings gibt es in dem ekpyrotischen Modell auch eine Reihe neuer
Schwierigkeiten, die nicht ausreichend behoben wurden. Für eine experimentelle Prüfung
müssten insbesondere die B-Moden gemessen werden. Bisher sind noch keine Anzeichen für
Gravitationswellen gefunden worden (s.o. die sehr kleine BB-Polarisation des CMB), aber die
gegenwärtig erreichte Empfindlichkeit reicht bei weiten noch nicht zu einer definitiven
Unterscheidung aus. Die Autoren betonen, dass zu ihrem Modell keine zusätzlichen
Annahmen nötig seien.
Es gibt aber auch eine Reihe von Schwierigkeiten, die sich auftun, wenn versucht wird
wohlbekannte Konstruktionen, wie z.B. die deSitter-Kosmologie mit Hilfe der Stringtheorie
(meist Typ IIB) zu verifizieren. Universen mit negativer kosmologischer Konstanten oder
negativer Energie erscheinen unproblematisch. Dagegen bereiten Modelle mit positiver
kosmologischer Konstanten und Inflationsmodelle erhebliche Probleme.
Die verschiedenen Stringtheorien werden heute eher als verschiedene Fälle einer MasterTheorie, der M-Theorie angesehen. Der Raum der Lösungen heißt Supermoduli-Raum (L.
Susskind 2003). Um die vielen Lösungen zu erreichen, müssen gewisse dynamische Moduli
variiert werden, wobei die Moduli, welche als Parameter die Form der Kompaktifizierung
beherrschen, mehr als Felder anzusehen sind. Ob im Supermoduli-Raum oder außerhalb,
Stringtheorie kann mit einer ungeheuer großen Zahl von metastabilen Vakua aufwarten, man
spricht von 10 500 . Die Vorstellung, der sich auch namhafte Kosmologen angeschlossen haben,
besteht darin, anzunehmen, dass in dieser großen Zahl auch ein Vakuum sein sollte, aus dem
unser (sehr spezieller) Kosmos mit seinen fundamentalen Kräften und seiner sehr schwachen
kosmologischen Konstanten hervorgegangen ist. Es sind auch Welten denkbar, in welchen
völlig andere Größen verwirklicht und andere fundamentale Wechselwirkungen gegeben sind.
In gewissem Sinne kann man die „landscapes“ als multi-dimensionale Verallgemeinerungen
von Potentialen ansehen, wie sie an eindimensionalen Beispielen in Kap. 8 skizziert wurden.
Der Zustand des frühen Kosmos landet damit durch einen zufälligen Prozess in einem
Minimum der Hyperfläche und definiert so seine fundamentalen Parameter. Da sich diese
Hypothese aber prinzipiell nicht falsifizieren lässt, gilt sie bei Kritikern als
unwissenschaftlich. Letzten Endes handelt es sich bei den „String-landcapes“ um eine
Konkretisierung des anthropischen Prinzips, das ebenfalls versucht, den vielen speziellen
Merkwürdigkeiten unseres Kosmos den mythologischen Charakter zu nehmen, indem es
feststellt, dass die Welt so ist wie sie ist, weil es uns (als intelligente Beobachter) gibt. Die
Evolution erscheint damit als eine Folge von Zufällen. Nur rückblickend können wir
behaupten, dass wir in einer (nur etwas) anderen Welt nicht aufgetreten wären. Die Idee eines
anthropischen Universums wurde zuerst 1973 von Brandon Carter formuliert (Carter hat sich
126
als Erforscher der Physik rotierender schwarzer Löcher einen Namen gemacht). Wir brechen
die Diskussion hier ab, nicht ohne zu bemerken, dass sich auch das anthropische Prinzips
(AP) nicht falsifizieren lässt, ja dass es die Form eines Zirkelschlusses annimmt. Wir kommen
in Kap 10. 7. noch einmal ausführlicher darauf zurück.
10.4. Wege zur Quantengravitation. „Loop Quantum Gravity“.
„Loop Quantum Gravity“ (LQG) ist eine kanonische Quantisierung der hamiltonschen
Formulierung der ART in (3+1) Dimensionen. Sie ist nicht die erste und einzige. Allen (3+1)dimensionalen Theorien ist gemeinsam, dass der Raum als ein 3-dim. Schnitt der 4dRaumzeit erscheint, nach Arnowitt, Deser und Miesner ADM-Aufspaltung genannt. Damit
geht zwar die kovariante Symmetrie der Ausdrücke verloren. Man gewinnt aber die
Möglichkeit, kanonisch konjugierte Variable zu definieren, welche die Vertauschungsregeln
erfüllen. Der Hamiltonoperator beziehungsweise der komplizierte Ausdruck, der an seine
Stelle tritt, wird Hamiltonsche Bedingung (Hamiltonian constraint) genannt. Man gewinnt
schließlich eine Gleichung, die Wheeler-DeWitt-Gl., die formal der Schrödinger Gleichung
ähnlich sieht. In den einfachsten Fällen, in welchen die Wheeler-DeWitt-Gl. sich lösen lässt,
beschreibt sie den Beginn des Universums als Tunneleffekt. Diese Theorie wurde 1986 von
Abhay Ashtekar durch Einführung neuer kanonischer Variablen abgeändert, so dass eine
renormierbare Quantenfeldtheorie entsteht, die auf eine etwas vereinfachte Hamiltonsche
Bedingung führt und die Wheeler-DeWitt-Gl. löst. Die kanonisch konjugierten AshtekarVariablen sind einerseits Konnektionen, also Größen des Paralleltransports und andererseits
ein Vektorfeld, das sich als Dreibein beschreiben lässt (Vector Triade). Sie verhalten sich
r
v
ähnlich wie die Vektorfelder E und A der Elektrodynamik. Das E-Dreibein hängt z. B. mit
den räumlichen Komponenten des metrischen Tensors wie folgt zusammen
Eia Eib = g ab g
a, b = 1, 2, 3
(10.17)
Da sich diese Größen aber noch nicht ohne weiteres quantisieren lassen, bildet man aus dem
r
Fluss des Vektorfelds A durch eine Fläche einen Strom. Außerdem wird eine Holonomie,
d.h. ein Loopintegral über die Konnektionen gebildet (ähnlich definiert wie in Gl. A.5.9).
Dazu kommen Randbedingungen, wie die Hamiltonsche Randbedingung (Hamiltonian
constraint) und die Bedingung der Invarianz gegenüber Diffeomorphismus, d.h.
Unabhängigkeit von irgendeiner
Hintergrundmetrik. Die Details sind mathematisch
kompliziert und müssen in der Originalliteratur nachgelesen werden. Es können Flächen- und
Volumenoperatoren gebildet werden. Eigenzustände sind Darstellungen der Gruppe SU 2.
Deswegen treten in den Eigenwerten halbzahlige Quantenzahlen j = 12 , 1 , 32 , 2.... wie beim
2
3
atomaren Drehimpuls auf. Die elementaren Einheiten haben die Größenordnung l P und l P .
Wir geben hier als Beispiel die Eigenwerte des Volumenoperators an
V j = ( γl P2 ) 3 2
1
j ( j + 12 )( j + 1)
27
(10.18)
γ ist der Barbero-Immirzi-Parameter ( γ ≅ 0,247 ), der sich nicht von selbst aus der Theorie
ergibt. In älteren Versuchen der kanonischen Quantisierung der Gravitation z.B. in der
Wheeler-DeWitt-Gleichung treten nur Operatoren mit kontinuierlichen Eigenwertspektren
auf, d.h. es gibt keine diskreten Eigenwerte wie in der LQG. Die Eigenzustände der LQG127
Operatoren sind Spinnetzwerke. Die Verbindungslinien der Knotenpunkte sind Vielfache von
j, daher der Name „Spinnetzwerke“. Ihre geometrische Bedeutung kann dual interpretiert
werden. Knoten, in welchen die Spins enden, sind nulldimensionale Elemente und
entsprechen einem (3 - 0)-dimensionalen Volumenelement. Linien sind eindimensionale
Gebilde und entsprechen einem (3 - 1)-dimensionalen Flächenelement. Auf diese Weise kann
man das Spinnetzwerk interpretieren und sich einen Raum aus elementaren Raum- und
Flächen- Elementen denken , der wie mit einem Baukasten aufgebaut ist.
Fig. 10.1 Schema eines Spin-Netzwerks (hier in der Fläche dargestellt). Es besteht aus Knoten
und gerichteten Strecken (s. Pfeile), die mit einer Zahl j bezeichnet sind (Bild aus Einstein-online
des AEI, Potsdam).
Fig. 10.2. Symbolische Darstellung der Dualität: Dem Punkt in der Mitte des Würfels entspricht
das Volumen, einer Linie ist die darauf senkrecht stehende Fläche zugeordnet (Bild aus
Einstein-online des AEI, Potsdam).
Kosmologische Anwendungen der LQG wurden in den letzten Jahren von Martin Bojowald
entwickelt. Aus dem Hamiltonoperator erhält man eine Differenzengleichung für die
Volumina. Diese Gleichung ist eine exakte Lösung und auch für kleine Volumina korrekt. Sie
128
steht anstelle der Friedmanngleichung. Für große Volumina geht sie in eine effektive
Friedmanngleichung über.
−3
−3 j ,l
Was wird aus der Singularität von ρ ∝ a ? Es gelingt, Eigenwerte des Operators ( aˆ ) μ
auszurechnen. Für den komplizierten Ausdruck lässt sich eine Näherung für j angeben
⎛ a2 ⎞
− 3 j ,l
−3
ˆ
(a ) μ (a ) = a pl ⎜⎜ 2 ⎟⎟
⎝ a max ⎠
3
2−2l
(10.19)
wobei
2
a max
= γ j l P2 / 3
(10.20)
a2
>> 1 wird die Funktion pl → 1,
a P2
(10.21)
Für große Argumente
für kleine Argumente
⎛ a ⎞
a2
⎟⎟
<< 1 wird pl ≈ 3(l + 1) −1 ⎜⎜
2
a
aP
⎝ max ⎠
2 −1
(10.22)
a2
Der Übergang zwischen beiden Gebieten liegt bei 2 ≈ 1 wie Fig. 10.3 zeigt.
aP
Fig. 10.3. Links ist die effektive Dichte (horizontal) gegen den Skalenparameter (vertikal)
aufgetragen. Die Dichte hat ein Maximum und geht bei a → 0 gegen Null, während die
klassische Dichte divergiert.
Rechts ist der Skalenparameter (senkrecht) gegen die Zeit (waagerecht) aufgetragen (aus
Martin Bojowald, The Early Universe in Loop Quantum Cosmology. http://arxiv.org/abs/grqc/0503020)
Um Bojowalds effektive Friedmanngleichung mit der klassischen Friedmanngleichung
vergleichen zu können, schreiben wir diese zunächst
(s. Gl. 5.2) etwas um
129
κ
a& 2
8πG
+ c2 2 2 = 2 ε
2
a
a R0
3c
in dem wir κ R0 = k
Wir erhalten so
2
2
(5.2)
und c = 1 setzen, außerdem multiplizieren wir beide Seiten mit a .
3
3(a& 2 + k 2 ) a = 8πGεa 3
(10.23)
Bojowald behandelt die Fälle k = 0, 1. Für den Fall k = 0 setzt er für die Energiedichte
(entsprechend der Einsteingleichung mit einem homogenen skalaren Materiefeld)
1
2
ε = d (a) eff pφ2 + a 3V (φ )
(10.24)
wobei pφ der Impuls des Feldes und d ( a ) eff der effektive Wert der Dichte ist.
Für a = 0 geht die Feldenergie gegen Null abhängig von der speziellen Gestalt von V (φ) .
Anstelle der klassischen Klein-Gordon-Gleichung 8.20 tritt folgender Ausdruck einer
effektiven Gleichung
&φ& = φ& a& d lg d (a ) eff − a 3 d (a ) V ′(φ)
eff
da
(10.25)
&& ergibt
Eine effektive Gleichung für a
⎛ 1 d ln(a 3 d (a ) eff ) ⎞
a&&
8πG −3
−1 & 2
⎟ − V (φ)]
=−
(10.26)
[a d (a ) eff φ ⎜⎜1 − a
⎟
a
da
3
2
⎝
⎠
&
Der klassische Dämpfungsterm a&φ in Gl. 10.11 führt in der Inflation zum langsamen
Abrollen. In der effektiven Klein-Gordon-Gleichung kann er wegen der logarithmischen
Ableitung von a das Vorzeichen umkehren. Der Verlauf von a(t) zeigt eine frühe und eine
&& > 0 ), die jeweils bei einem Wendepunkt in a(t) beendet werden
späte inflationäre Epoche ( a
&& = 0 ). Man sieht also, dass durch LQG das Problem des „graceful exits“ aus der Inflation
(a
gar nicht auftritt. Auch das Materiefeld zeigt ein vernünftiges Verhalten: φ(t ) ist Null bei a =
0, wächst zunächst mit a(t) an, fällt aber nach längerer Zeit ab und schwingt schließlich um
einen Nullpunkt (s. Fig. 10.4 rechts unten).
Die Zeit t = 0 erscheint nicht besonders ausgezeichnet. Nur die Zeitrichtung muss vorgegeben
sein, die Zeitskala lässt sich auch zu negativen Werten erweitern. Dadurch lässt sich
untersuchen, was aus der klassischen Singularität werden kann. Die Ausdrücke Gl. 10.9 –
10.12 lassen auch einen Zusammensturz auf ein minimales Volumen (big crunch) mit
&& > 0 wird, was allerdings klassisch
Wiederanstieg zu. Dazu ist nur nötig, dass a& = 0, a
ausgeschlossen ist.
130
Fig. 10.4. zeigt den Verlauf von Skalenparameter und Feldfunktion mit der Zeit, links nach
&& > 0 (inflationäre
relativ kurzen Zeiten, rechts nach langen Zeiten. Es gibt zwei Epochen mit a
&& = 0 ). Der dargestellte
Epochen). Die Inflation geht zu Ende, wo a(t) einen Wendepunkt hat ( a
Verlauf ist mehr qualitativ zu betrachten (aus Martin Bojowald, The Early ‚Universe in Loop
Quantum Cosmology. http://arxiv.org/abs/gr-qc/0503020)
.
Abschließend ist zu sagen, dass LQG, die mit dem eher bescheidenen Anspruch auftritt, sich
auf die Quantisierung der Gravitation zu beschränken, beachtliche Erfolge vorweisen kann.
Sie kann die Singularität bei a(t) = 0 beseitigen, es treten inflationäre Phasen in a(t) auf, ohne
dass spezielle Annahmen über das Potential des Materiefelds V (φ) gemacht werden müssen.
Die inflationäre Phase schließt von selbst ab, es gibt kein „graceful exit“-Problem. Schließlich
nimmt das skalare Materiefeld einen vernünftigen Verlauf an, ohne dass besondere
Annahmen gemacht werden müssen. Dennoch bleiben Fragen offen. Das Materiefeld ist ein
klassisches Feld. Wie daraus die uns bekannten Felder, werden bleibt weiterhin offen. Die
Frage nach der dunklen Energie könnte vielleicht mit Hilfe der LQG einer Lösung näher
gebracht werden. Dennoch ist auch diese Frage noch völlig offen. Das Problem der
Anfangsbedingungen vereinfacht sich, dennoch bleibt reichlich Spielraum (z.B. in der
Annahme von j), verschiedene Möglichkeiten auszuprobieren.
10.4. Immerwährende Inflation („Eternal Inflation“)
Wir kehren wieder zu den Modellen zurück, welche Effekte der Quantengravitation nicht
berücksichtigen. Man kann diese Effekte ausblenden, wenn man sich weit genug von den
Planckgrößen entfernt hält. Linde sieht jedoch kein prinzipielles Problem darin, die
Energiedichte des skalaren Feldes gleich einer Planckeinheit zu setzen. Die typischen
Anfangsbedingungen wären dann nach Linde in Planckeinheiten (die Energiedichte hat die
4
Dimension M P = 1 )
1 &2 1
φ + (∇φ) 2 + V (φ) ≈ 1
2
2
131
(10.27)
Fig. 10.5. Verhalten der potentiellen Energiedichte des skalaren Feldes V (φ) nach A. Linde.
Inflation eines betrachteten Raumbereichs setzt ein, wenn sich eine besonders große Fluktuation
von V (φ) ereignet. Dabei sind 3 Bereiche zu unterscheiden
A:
mM P3 < V (φ) < M P4
Quantenfluktuationen
Quantenfluktuationen des skalaren Feldes
der
Raumzeit
sind
klein
aber
φ können groß sein
m M < V (φ) < mM Fluktuationen des skalaren Feldes φ sind klein. Die
B:
Feldamplitude kriecht oder rollt langsam gegen Null
C: das skalare Feld φ oszilliert und erzeugt dabei Paare von Elementarteilchen mit großer
kinetischer Energie. Das Universum wird heiß.
2
2
P
3
P
und
1 &2 1
φ ≈ (∇φ) 2 ≈ V (φ) ≈ O(1)
2
2
(10.28)
Inflation setzt ein, wenn in einer betrachteten Domäne die potentielle Energiedichte größer ist
als die kinetische und die Gradientenenergie, d.h. es ist
1 &2 1
φ + (∇φ) 2 < V (φ)
2
2
(10.29)
Fig. 10.5. zeigt anschaulich, unter welchen Bedingungen Inflation bei V (φ) ≤ M P entstehen
kann.
4
Wir betrachten jetzt den Prozess sich wiederholender Inflationen. Das Feld sei anfangs in der
betrachteten Domäne nahezu konstant und homogen, besitzt aber irgendwelche beliebigen
Werte in den Nachbardomänen. In der betrachteten Domäne wächst das Volumen V während
−1
der Zeit Δt = H um
132
δV = (e Δt ⋅H ) = e 3 ≈ 20
3
(10.30)
Im Vergleich zum Anfangsvolumen sind es 20 Domänen oder 20 Miniuniversen („Pocket
Universes“), wobei jedes einen Radius cH hat. Man beachte, dass die inflationäre Expansion
schneller als Lichtgeschwindigkeit verläuft. Da aber Signale und kausale Prozesse nur mit
Lichtgeschwindigkeit ablaufen können, ist jedes Miniuniversum kausal von seinen Nachbarn
getrennt und kann von diesen nicht beeinflusst werden. Die Fluktuationen des Feldes führen
dazu, dass in einem Bruchteil der Miniuniversen wieder Inflation einsetzt. Im folgenden
−1
Zeitintervall Δt = H hat sich das Volumen gegenüber dem Beginn um einen Faktor 100
vergrößert. Jedes Miniuniversum hat wieder einen etwa konstanten Wert des Feldes φ , das
sich aber wegen der Fluktuationen um einen Betrag δφi vom dem der Nachbarn unterscheidet.
In einem Bruchteil der Miniuniversen mag φ durch eine entsprechend große Fluktuation δφ
groß genug geworden sein, auf dass es wieder zu einer Inflation kommt. Man kann diese
Iteration weiter fortführen und kommt so zu dem Schluß, dass in diesem Modell Inflation
endlos ist („eternal inflation“), dass sie möglicherweise keinen Anfang und sicher kein Ende
hat und in jedem Zeitintervall eine fraktale Struktur von Miniuniversen hinterlässt. Man
möchte annehmen, dass sich in diesen Prozessen ein stationärer Zustand heraus bildet. Aber
dazu müsste es eine Obergrenze für die Feldamplitude geben, was wieder eine Behandlung im
Rahmen der Quantengravitation notwendig machen würde. In bisherigen Behandlungen des
Problems konnte nicht gezeigt werden, dass „Eternal Inflation“ ohne Anfang ist. Auf jeden
Fall aber werden die Anfangsbedingungen, so wie die Wahrscheinlichkeit einer anfänglichen
Inflation, irrelevant.
Fig. 10.6. Die Entstehung von Pocket-Universen bei immerwährender Inflation. Nach A. Linde:
Elementarteilchen und inflationärer Kosmos. Spektrum Akad. Verl. 1993. Es ist wichtig, noch
einmal hervorzuheben, dass Lindes Model nur in anfänglich sehr kleinen Bereichen von der
Größe der Plancklänge Homogenität voraussetzt. Inflation plus Expansion im Standardmodel
haben bis zur Gegenwart aus einem winzigen Bereich ein gewaltiges Universum gemacht, von
dem unser sichtbarer Kosmos mit einer Ausdehnung von einigen 1010 Lichtjahren nur ein
kleiner Teil ist. Es ist danach möglich, dass ständig andere, uns unzugängliche und kausal
unabhängige Bereiche, in welchen eine genügend große Fluktuation von V (φ) entstand, selbst
wieder zu einer inflationären Expansion ansetzen. In diesem Bild (chaotic inflation) erkennt
man keinen Anfang aber auch kein Ende dieser Entwicklung.
133
Eine gewisse Rolle spielen auch Modelle mit mehr als einem Feld. Solche Versuche haben
eine Berechtigung, wenn eine konsistente theoretische Beschreibung angestrebt wird. Aber je
komplexer die Modelle werden, umso schwieriger wird es, sie an den Beobachtungen zu
testen. Denn je mehr Parameter zur Anpassung an empirische Daten nötig werden, um so
geringer ist der Wert, dem man einem Model beimisst. Die experimentellen Daten
insbesondere von WMAP scheinen eher die einfachsten Modelle zu unterstützen.
10.5. Unser spezieller Kosmos und das anthropische Prinzip.
Wenn der inflationäre Prozeß mit einer Symmetriebrechung verbunden ist, wie es in der
„neuen Inflation“ gefordert wird, dann wird sich das Inflatonfeld von einem Punkt hoher
Symmetrie des Potentials, wo es eine Zeit lang verharrt, in ein neues Minimum mit
gebrochener Symmetrie bewegen. Im Allgemeinen wird dieses Potential sehr kompliziert sein
und Punkte hoher Symmetrie so wie mehrere Minima mit niedriger Symmetrie enthalten.
Allgemeine Theorien wie etwa die Stringtheorie lassen viele mögliche Lösungen zu. Nimmt
man diese Ergebnisse ernst, dann folgt daraus, dass die kosmische Entwicklung am Anfang
keineswegs eindeutig war, dass es viele mögliche Universen geben könnte und dass unser
Universum mit den Wechselwirkungen der „vier Kräfte“ eine durchaus spezielle Kombination
ist. Gedankenexperimente, in welchen man versuchte die Stärke der Wechselwirkungen zu
ändern, um herauszufinden, wie die kosmische Evolution mit anderen Parametern verlaufen
wäre, haben gezeigt, dass wir in einer ziemlich einzigartigen Welt leben. Aber warum ist sie
so wie sie ist? Im „schwachen anthropischen Prinzip“ sagt man, die Welt ist so wie sie ist,
weil wir da sind, d.h. kosmische Evolution verlief so, dass intelligentes Leben möglich wurde.
Das anthropische Prinzip in seiner starken Form, behauptet, dass der Kosmos so gestaltet sein
muss, dass intelligente Beobachter möglich sind. Der Gläubige wird darin das Walten eines
göttlichen Willens sehen, der die Welt so geschaffen hat, um dem Menschen, der Krone der
Schöpfung, ein Habitat zu geben. Vom Standpunkt der Naturwissenschaft ist dagegen nichts
einzuwenden. Naturwissenschaft und Religion bewegen sich auf verschiedenen Ebenen. Der
Naturwissenschaftler stellt keine Sinnfragen. Stattdessen wird er zunächst einmal in dieser
Einzigartigkeit einen Auswahleffekt sehen: Der Kosmos ist so wie er ist, weil wir da sind.
Eine Welt mit abweichenden Naturkonstanten hätte kein Leben und damit auch keinen
Menschen hervorgebracht. Das schwache anthropisches Prinzip ist eigentlich trivial oder ein
Zirkelschluß. Die starke Form könnte zusammen mit der Vielwelten-Interpretation der
Quantentheorie von Bedeutung sein. Die kosmische Evolution kann als ein historischer
Prozeß angesehen werden, in welchen der Mensch eingebunden ist und aus dem er sich nicht
befreien kann. Für die Wissenschaft bleibt zu bedenken: Um das Universum zu verstehen
muss die Möglichkeit des organischen Lebens, ja sogar des höher organisierten Lebens mit
gedacht werden.
10.6. Wie geht es nach der Inflation weiter?
Nach dem Ende der inflationären Epoche bleibt das Inflatonfeld in einem hoch angeregten
Zustand zurück. Man kann nun in die Lagrangedichte Gl. 8.23 noch weitere Felder einbauen,
welche mit dem Inflatonfeld wechselwirken, seine Energie abbauen und auf diese Weise
Teilchenpaare erzeugen. Je nach dem Ansatz kann die Teilchenerzeugung langsam (bei
134
Fermionen) oder explosionsartig (bei Bosonen) erfolgen. Die kinetische Energie der Teilchen
sorgt für eine hohe Temperatur. Neben der großen Vereinigung verlegt man auch die
Brechung der Supersymmetrie (Fermionen und Bosonen treten paarweise auf) zu sehr hohen
Energien. Die Supersymmetrie kann vielleicht das Problem der dunklen Energie lösen helfen,
weil sich in diesen Theorien Vakuumenergien kompensieren lassen. Da aber bisher keine
supersymmetrischen Partner gefunden wurden, muß man annehmen, daß sie schon im frühen
Kosmos in leichtere Teilchen zerfallen sind. Die Frage, ob sich die dunkle Materie durch ein
supersymmetrisches Teilchen erklären läßt, ist noch offen.
Bei der Zuordnung von Temperatur und Zeit ist auf die Freiheitsgrade der Teilchen zu achten.
Die Gl. 6.3
ε r = u = a BT 4
gilt für Photonen die zwei Freiheitsgrade (Polarisationen) besitzen. Man kann die Formel
verallgemeinern, indem man alle relativistischen Teilchen mit der effektiven Zahl der
Freiheitsgrade berücksichtigt
εr =
1
g ∗ a BT 4
2
(10.31)
wobei
4
⎛ Tj
7
⎛ Ti ⎞
g ∗ = ∑ g i ⎜ ⎟ + ⋅ ∑ g j ⎜⎜
8 Fermionen ⎝ T
Bosonene ⎝ T ⎠
⎞
⎟⎟
⎠
4
(10.32)
Es ist berücksichtigt worden, dass Fermionen und Bosonen verschiedene Temperaturen haben
können. Tatsächlich steigt g∗ oberhalb 100 MeV kräftig an.
Fig. 10.4. die Evolution der Freiheitsgrade relativistischer Teilchen in der SU(3)×SU(2)
×U(1)-Theorie. Nach E.W. Kolb & M.S. Turner: The Early Universe. Addison-Wesley
Pub. Comp. 1990
135
Bei kleinen Energien sind neben den Photonen auch Elektronen-Postronen-Paare und vor
allem Neutrinos berücksichtigt worden. Wenn kBT < 1 MeV ist, ist g∗ = 3,36. Dabei ist
1
⎛4⎞ 3
Tν = ⎜ ⎟ Tγ . Die Energiedichte der CMB ist bei T0 = 2,7325 K
⎝ 11 ⎠
u (T0 ) = (4,19 ⋅10 −13 ± 0,01) erg ⋅ cm −3 = (4,19 ⋅10 −14 ± 0,01) Joule ⋅ m −3 . Daraus
ergibt sich für Temperaturen T > 1010 K
⎛T ⎞
1
u (T ) = g ∗u (T0 )⎜⎜ ⎟⎟
2
⎝ T0 ⎠
4
(10.33)
Es ist außerdem
4
g ∗ ⎛ T ⎞ ⎛ a0 ⎞ ⎛ t 0 ⎞
⎜ ⎟ =⎜ ⎟ =⎜ ⎟
2 ⎜⎝ T0 ⎟⎠ ⎝ a ⎠ ⎝ t ⎠
4
2
(10.34)
und
⎛ 2⎞
t = ⎜⎜ ⎟⎟
⎝ g∗ ⎠
1
2
2
⎛T ⎞
⋅ ⎜ 0 ⎟ ⋅ t0
⎝T ⎠
(10.35)
Ohne Berücksichtigung von g ∗ ergeben sich t = 2,3 s für T = 1010 K (s. Gl. 7.3), mit
Berücksichtigung von g ∗ ist t = 1,02 s. In ähnlicher Weise kann man die Hubblefunktion
a& / a für den frühen Kosmos bestimmen
⎛g ⎞
H (t ) = H 0 Ω r ⎜ ∗ ⎟
⎝ 2 ⎠
1
2
1
2
2
⎛T ⎞
⎛g ⎞
⎜⎜ ⎟⎟ = 1,61⋅10 −21 ⎜ ∗ ⎟
⎝ 2 ⎠
⎝ T0 ⎠
1
2
2
⎛ T ⎞ −1
⎜⎜ ⎟⎟ s
⎝ T0 ⎠
(10.36)
Hier sind folgende Werte eingesetzt worden
H 0 = 3,24 ⋅10 −18 ⋅ h s −1 = 2,30 ⋅10 −18 s −1
1
Ω r = 4,9 ⋅10 −5 und Ω r 2 = 0,70 ⋅10 −3
Der plötzliche Anstieg von g bei 150 MeV liegt in der Nähe der Pionenmassen, mit m(π±) =
140 MeV/c2 und m(π0) = 135 MeV/c2 dem Spin S = 0; das entspricht 3 Freiheitsgraden. Bei
Temperturen T > 150 MeV/kB und den entsprechenden Dichten stellt sich ein Quark-GluonPlasma ein, wobei das „Confinement“ der Quarks aufgebrochen und diese eine
136
1. Generation
u (up)
0,0024
Q = +2/3
Masse vorh.Zeile
GeV
Q = -1/3
d (down)
Masse vorh.Zeile
0,0048
GeV
Spin immer ½
„Farbe“ :
blau, gelb, rot
Tabelle 10.1. Liste der Quarks
Elektronen
Q
Spin
Masse MeV
Neutrinos
1. Generation
e
-1
1/2
0,511
1/2
<2,2
Bosonen
G (Gluon)
s (strange)
0,104
b (bottom)
4,2
0
0
1
μ
-1
1/2
105,7
νμ
0
Spin
Masse eV
3. Generation
t (top)
171,2
2.Generation
νe
Q
2. Generation
c (charmed)
1,37
3. Generation
τ
-1
1/2
1777
0
1/2
<0,17
Bosonen
γ
1
ντ
W, Z
0
0
W ± 1 Z= 0
GeV
80,4 90,2
<15,5
Tabelle 10.2. Liste der Leptonen
„asymptotische Freiheit“ annehmen. Die Zahl der Freiheitsgrade ändert sich drastisch. Die
Quarks haben 3 Flavors, 3 Farben und 2 Spins, dazu kommt noch einmal die gleiche Zahl bei
den Antiquarks. Schließlich gibt es 8 Gluon-Arten mit 2 verschiedenen Helizitäten, macht
alles zusammen 52 Freiheitsgrade. Dieses Bild ist zunächst ein Ergebnis der Theorie. Es wird
inzwischen mehr und mehr durch Schwerionenexperimente bestätigt, welche erste Anzeichen
für das Auftreten des Quark-Gluonen-Plasmas zeigen. Bei T < 150 MeV/c2 sind die Quarks
gebunden, so liegen z.B. in den Pionen Quark-Antiquark-Paare vor, mit Massen m(π±) =
139,6 MeV/c2 und m(π0) = 136 MeV/c2 und Zusammensetzung
π + = ud
π− = u d
π0 =
1
dd − uu
2
(10.37)
Dabei sind setzen sich die Zustände noch aus Summen über die Farben bzw. Antifarben
zusammen, die in der starken Wechselwirkung das Gegenstück zu den Ladungen in der
elektromagnetischen Theorie bilden. In den Nukleonen, Proton und Neutron, liegen jeweils 3
Quarks gebunden vor
p = uud
n = udd
(10.38)
Das entsprechende gilt für die Antinukleonen. Die Pionen zerfallen nach dem Schema
π − → μ − + νμ , π − → e − + ν e und π 0 = γ + γ
137
(10.39)
wobei der zweite Prozeß nur mit einer Wahrscheinlichkeit 1/8000 neben dem ersten auftritt.
Die Myonen sind Leptonen und zerfallen in Elektronen und Neutrinos
μ + = e + + ν e + νμ und μ − = e − + ν e + ν μ
(10.40)
Baryonen und Antibaryonen können in verschiedenen Prozessen miteinander reagieren, die
hier nicht weiter verfolgt werden sollen. Wichtig ist für die Kosmologie, daß diese Reaktionen
auf Grund einer Symmetrie-Brechung zwischen Materie und Antimaterie am Ende nur
Materie, Neutrinos, Elektronen und Photonen übrig lassen.
Tab. 10.2. Epochen der kosmischen Entwicklung nach K. Grotz und H.V. Klapdor: Die
schwache Wechselwirkung in Kern-, Teilchen- und Astrophysik. Teubner Verl. 1989
10.6. Zusammenfassung.
Mit den Anfangsbedingungen des Universums wird die „Planck-Epoche“ diskutiert. Neben
einem knappen Überblick über die Versuche einer Quantisierung der Gravitation, wobei es
bisher nur die Loop Quantum Gravity geschafft hat, eine konsistente Quantenkosmologie zu
entwickeln, wird zu Vergleich noch einmal der Ansatz der chaotischen Inflation von A. Linde
gegenüber gestellt, der ausdrücklich auf eine nähere Untersuchung der Planck-Epoche
verzichtet. Die Folgerungen, wie „Eternal Inflation“ wereen ebenso diskutiert wie der Beginn
unseres Universums als Zufallsprozess. Nachdem am Ende de Inflation Teilchen entstanden
sind, geht mit fortschreitender Expansion und Abkühlung die Entwicklung hin zu den uns
heute bekannten Teilchen. Dabei ist die effektive Zahl der Freiheitsgrade als Funktion der
Temperatur zu beachten.
10.7. Literatur
D. Baumann et al. :CMB Polarization mission concept study. Arxiv: 0811.3919
138
Robert H. Brandenberger : Inflationary Cosmology. Progress and Problems.
hep-ph/9910410
A. Ashtekar: Quantum Mechanics of Geometry. gr-qc/9901023
B. Rovelli : Loop Quantum Gravity. Living Reviews on Relativity. (1997)
http://wwww.livingreviews.org/Articles
T. Thiemann : Introduction to Modern Canonical General Relativity. gr-qc/0110034
Robert H. Brandenberger : Principles, Progress and Problems in Inflationary
Cosmology. Astro-ph/0208103
A. H. Guth: Inflation and eternal inflation. Phys. Rep. 333/334 (2000) 555
A. Linde: Inflationary Cosmology. Phys. Rep. 333/334 (2000) 575
A. Guth: The Inflationary Universe. Addison Wesley Publ. Comp. 1997.
M. Gasperini: Birth of the universe in string cosmology. http://arxiv.org/abs/gr-qc/9706037
J. Khouri, P.J. Steinhardt, D. Waldram : Inflationary solutions in the brane world.. Phys. Rev.
D 63 (2001) 103505
P.J. Steinhardt and N. Turok: A cyclic model of the universe. Science 296. 24 May 2002, p.
1436
L. Smolin, "Did the universe evolve?," Classical and Quantum Gravity 9, 173–191 (1992).
L. Smolin, The Life of the Cosmos (Oxford, 1997)
L. Susskind, "The anthropic landscape of string theory", arXiv:hep-th/0302219.
L. Susskind, The cosmic landscape: string theory and the illusion of intelligent design (Little,
Brown, 2005). M. J. Rees, Just six numbers: the deep forces that shape the universe (Basic
Books, 2001). R. Bousso and J. Polchinski, "The string theory landscape", Sci. Am. 291, 60–
69 (2004).
M. Bojowald : Isotropic Loop Quantum Cosmology. http://arxiv.org/abs/gr-qc/0202077
M. Bojowald and K. Vandersloot: Loop Quantum Cosmology, Boundary Proposals, and
Inflation. http://arxiv.org/abs/gr-qc/gr-qc/0303072
Martin Bojowald, The Early ‚Universe in Loop Quantum Cosmology. http://arxiv.org/abs/grqc/0503020
Kristina Giesel: Loop-Quantengravitation. Die Quanten der Schwerkraft. Sterne u. Weltraum.
Juli 2011, S.30
139
J.C. Baez: An Introduction to Spin Foam Models of BF Theory and Quantum Gravity.
http://arxiv.org/abs/gr-qc/9905087
W.H. Kinney et al. WMAPping inflationary physics. hep-ph/0305130
J. Rosen : The anthropic principle. Am J. Physics April 1985 & May 1988
B. Kanitscheider : Das Anthropische Prinzip- ein neues Erklärungsschema der Physik?
Physikalische Blätter 45 Nr. 12 (1989) 9
J.D. Barrow, F.J. Tipler : The anthropic cosmological principle. Oxford Univ. Press 1986
10.8. Aufgaben
1) Wir wollen polarisierte Mikrowellen-Intensitäten aus gemessenen Stokes Parametern
Q und U umrechnen. Eine Temperaturmessung ergab die Intensität I 0 . Weitere Werte
sind Q = 0,080 I 0 und U = 0,705 I 0 . Wie groß sind die Beträge von E1 , E 2 und
E(45°)?
2) Benutze die slow-roll Parameter Gl. (10.1) und zeige, am Beispiel der „chaotischen
Inflation“ mit starkem skalaren Feld, dass sie erfüllt sind. Siehe dazu Kap. 8 Gl. (8.21)
- (8.32).
3) In welchen Eigenschaften findest Du „cosmic coincidences“, die mit einem
„anthropischen Universum einen Sinn bekommen?
140
11. Bildung von Strukturen.
Fig. 11.1 2dF-Programm. Die inhomogenen Verteilung von mehr als 63000 Galaxien und deren
Rotverschiebung wurde in einem scheibenförmigen Sektor gemessen. Das Ganze besteht aus
zwei 4°-Ausschnitte aus einer Gesamtmenge von 210 000 Galaxien.
11.1. Dichtekonstrast im linearen hydrodynamischen Modell
Die Verteilung der leuchtenden Materie im heutigen Kosmos ist sehr ungleichmäßig. Neben
Sternen gibt es Sternassoziationen, Sternhaufen, Galaxien. Diese wieder bilden
Galaxienhaufen (s. Fig. 11.1), die wieder in Superhaufen zusammenhängen und durch riesige
Hohlräume voneinander getrennt sind. Es ist die Frage, die uns in diesem Kapitel beschäftigen
wird, wie denn aus den Fluktuationen der Hintergrundstrahlung (s. z.B. Fig. 9.4 und 9.7),
−5
deren relative Amplitude δT = ΔT / T ≈ 10
nur eine winzige Abweichung von der
Homogenität darstellt, die heutigen Strukturen und ihre Hierarchien entstanden sind. Wir
interessieren und dabei für den Dichtekontrast
r
r ρ( x ) − ρ
δ( x ) =
ρ
(11.1)
Er hängt mit der Temperaturfluktuation (CMB) wie folgt zusammen
r
r
ΔT ( x )
δ( x ) = 3 ⋅
T
141
(11.1a)
Anstelle der Dichtestörung im x-Raum wird häufig deren Fourier-Transformierte benutzt
()
r 1
r
r
δ k = ∫ δ( x )exp ikx ⋅ d 3 x
V
(11.2)
wobei V das Volumen bedeutet. Fig. 11.2 zeigt eine eindrucksvolle Darstellung der heutigen
Kenntnis von δ(r ) und den entsprechenden Beobachtungsmethoden.
()
Fig. 11.2. Dichtefluktuationen δ r , zusammengestellt vom Team des „Sloan Digital Sky
Survey“ (SDSS). Die Beobachtungen beziehen sich auf CMB, die Häufigkeit von GalaxienCluster (gut im Röntgengebiet durch die Strahlung des heißen intergalaktischen Gases zu
beobachten), die Auswertungen von SDSS, die Häufigkeit von Gravitationslinseneffekten und
der intergalaktische neutrale Wasserstoff, beobachtet als Lyman-Alpha-Wald. Nach Max
Tegmark’s Cosmological Library. http:/www.hep.upenn.edu/~max/2df1.html
Die Entfernungsskala in Fig. 11.2 kann auch als Zeitskala interpretiert werden. Bei etwa 109
Lj ist der Dichtekontrast bereits auf Prozente abgeklungen. Es sind mitbewegte Abstände, also
Entfernungen bezogen auf den heutigen Kosmos, wobei die Grenze durch den
Teilchenhorizont rH = 3.38 DH ≈ 15,26 ⋅ 10 9 pc gegeben ist. Neben dem Dichtekontrast wird
häufig auch die Streuung angegeben
δ( x ) = σ 2 = konst.
2
(11.3)
Im k-Raum erhält man das Leistungsspektrum
δ (k )
2
= (2π ) 3 P (k ) ⋅ δ (k − k ′)
142
(11.4)
was mit σ auf folgende Weise zusammenhängt
2
σ2 =
4π
P(k )k 2 dk
3 ∫
(2π )
(11.5)
Die Größen in eckigen Klammern sind Mittelbildungen über das Ensemble. Die
Auswertungen von Daten der Himmelsdurchmusterungen zeigen, dass das sich das Spektrum
P(k) für r > 100 Mpc oder k < 10-2 Mpc-1 nicht mehr bestimmen lässt. Über größere
Abstände herrscht praktisch Homogenität (s. a. Fig. 11.10).
r
Um die zeitliche Entwicklung kleiner Störungen δ( x, t ) ≡ δ zu untersuchen, werden in
Newtonscher Näherung die hydrodynamischen Gleichungen und die Poisson-Gleichung des
Gravitationspotentials herangezogen. Daraus lässt sich eine Wellengleichung ableiten, welche
in einem stationären Medium die Form annimmt
1 &&
δ − ∇ 2δ = 4πGρ
c S2
(11.6)
wobei ρ ≡ ρ die mittlere Dichte ist. Gl. 11.6 unterscheidet sich von der Wellengleichung in
der Elektrodynamik durch das Glied auf der rechten Seite, dass die Selbstgravitation der
Materie beschreibt. Setzt man die Wellenlösung ein
[(
)]
rr
δ ∝ exp i k x − ωt ,
(11.7)
so erhält man als Fourier-Transformierte von Gl. 11.6 eine Dispersionsbeziehung
ω2 = k 2 cS2 − 4πG ρ = cS2 (k 2 − k J2 )
(11.8)
mit der so genannten Jeans-Wellenzahl
⎛ 4πG ρ ⎞
k J = ⎜⎜ 2 ⎟⎟
⎝ cS ⎠
1
2
(11.9)
wobei m die mittlere Masse der Gasatome, M und R Masse und Radius der Materie bedeuten.
Wellenausbreitung ist nur möglich, wenn k > k J ist. Für k < k J ist ω < 0 . Es gibt keine
laufende Welle mehr, stattdessen zwei Lösungen, eine exponentiell wachsende und eine
exponentiell abklingende. Aus (11.09) lässt sich eine charakteristische Masse, die JeansMasse ableiten
2
4π ⎛ π
M J = ⎜⎜
3 ⎝ kJ
3
⎞
⎟⎟ ρ oder
⎠
1/ 2
3/ 2
⎛k T ⎞
⋅ ⎜⎜ B ⎟⎟ ⋅ ( ρ ) −1 / 2
(11.10)
⎝Gm ⎠
Der Begriff Jeans-Masse, Jeans-Wellenzal oder Jeans-Radius taucht hier neu auf. Diese
Größen spielen als Kriterien eine Rolle, ab wann eine sphärische Gaswolke instabil gegenüber
Gravitation wird und z.B. zu Sternen kondensieren kann. Dazu muss
E kin ≤ E grav
⎛6⎞
MJ = ⎜ ⎟
⎝π ⎠
143
oder
3M
3GM 2
kT ≤
2m
5R
(11.11)
Das Gleichheitszeichen steht für den kritischen Fall, den der britische Physiker James Jeans
(1877 – 1946) am Anfang des 20. Jahrhunderts zuerst untersucht hat.
Die Situation ändert sich, wenn man die kosmische Expansion berücksichtigt. Dazu setzt man
r
r
r
x=
a(t )
(11.12)
und erhält unter Vernachlässigung von Druckkräften
c S2 k 2
3
&
&
&
δ + 2 Hδ + 2 δ − ΩH 2δ = 0
2
R
(11.13)
wobei wir unter Benutzung der Friedmann-Gleichung
8πG ρ = 3H 2 Ω
(11.14)
gesetzt haben. Raum-und Zeitvariable lassen sich trennen. Für ein Universum mit Ω = Ω 0 = 1
( R → ∞) gibt es zwei Lösungen
r
r
δ( x , t ) = D± (t ) ⋅ δ( x )
(11.15)
mit
D+ (t ) = A ⋅ t
2
3
∝ a(t ) und D− (t ) = B ⋅ t −1
(11.16)
Die Expansion scheint das Anwachsen (und Abklingen) der Störung zu behindern, denn
anstelle eines exponentiellen Wachstums (oder Abklingens) mit Gl. 11.7 und 11.8 ergibt sich
ein moderates Potenzgesetz.
Wir können das Verhalten der Jeans-Masse für Baryonen untersuchen, wenn wir
k J = k J′ / a schreiben. Es ist nach Gl. 11.10 M J ∝ ρ . In der strahlungsdominierten Epoche
−3
ist ρ ∝ T . Andererseits ist k J ∝ T (Gl. 11.6). Also wird mit Gl. 11.7 M J ∝ T . In Fig.
11.3 ist der Übergang von der strahlungsdominierten zur materiedominierten Epoche abrupt
4
2
eingezeichnet. Dabei fällt die Schallgeschwindigkeit von c S = c / 3 = 1,7 ⋅ 10
8
m/s auf
c 2 S = 5 / 3 ⋅ k B T / μm P und c S = 4,7 ⋅ 10 3 m/s ab, was zu einem Absinken der
Jeansmasse um viele Zehnerpotenzen führt ( mP Protonenmasse, μ mittlere Massenzahl pro
Teilchen).
144
Fig. 11.3. Jeans-Masse der Baryonen MB-J und die Baryonen-Masse innerhalb des Horizonts MBMS ist die Silkmasse, s. dazu den Text. Als baryonische Dichte wurde
HOR.
Ω B h 2 = 0,047 angenommen.
Nach E.W. Kolb, M.S. Turner : The Early Universe. Addison
Wesley 1990.
Sie liegt vor der Rekombination zwischen 1014 und 1018 Sonnenmassen, wobei die untere
Grenze etwa der Größe von Galaxienhaufen entspricht. Unmittelbar nach der Rekombination
( z ≈ 1090 ) liegt sie jedoch bei ca. 106 Sonnenmassen, das ist etwa die Größe eines
Kugelsternhaufens. Auch Dämpfungseffekte können in der strahlungsdominierten Epoche
eine Rolle spielen. Sie wurden von J. Silk zuerst behandelt und in Fig. 11.3 als „Silkmasse“,
MS, eingetragen. Es muss aber festgestellt werden, dass diese Abschätzungen die Entstehung
von Galaxien nicht erklären kann. Außerdem kann man leicht zeigen, dass die Entwicklung
des Dichtekontrastes mit baryonischer Materie allein völlig unzureichend ist. Wir gehen zur
r
−5
Zeit der Rekombination von einem Dichtekontrast δ( x , t rec ) ≈ 5 ⋅ 10 aus. Nach Gl. 11.15
würde der Wert dann in der Gegenwart auf
r
r
δ( x , t 0 ) ≈ δ( x , t rec ) ⋅ ( z rec + 1) ≈ 10 −2
r
(11.17)
anwachsen. Notwendig wäre aber δ( x , t 0 ) ≈ 1 , damit der Gravitationskollaps einer Gaswolke
einsetzt. Wenn wir für den Beginn der Galaxienbildung z = 10 einsetzten, wird das Ergebnis
um noch eine Größenordnung kleiner. Man sieht hier schon, dass während der Expansion
nach dem Standardmodell die Baryonen allein den Kontrast nicht genügend verstärken
können. Dunkle Materie muss hinzukommen. Diese breitet sich offensichtlich stoßfrei und
ohne Dissipation der Energie aus. Baryonische Materie dagegen kann kinetische Energie nur
durch Abstrahlung verlieren. In einer Wolke aus dunkler und baryonischer Materie wird sich
die baryonische unter Verlust von kinetischer Energie und Drehimpuls in das Innere der
Wolke bewegen. Dort kann daher leicht ein ausreichenden Dichtekontrast entstehen. Die
dunkle Materie bildet dagegen einen nahezu stationären Potentialtopf, in welchem die
baryonische Materie einer Galaxie eingeschlossen ist.
Man kann auch für eine dunkle, stoßfreie fermionische Materie eine maximale Jeansmasse
ableiten. Doch diese ist abhängig von der Masse der Teilchen der dunklen Energie. Diese ist
145
noch völlig unbekannt, weshalb mit diesen Überlegungen wenig gewonnen ist (s. z.B. G.
Börner: The Early Universe. 4th Edition Ch. 10.2.2.).
In Fig. 11.4 ist ein jüngst publiziertes Beispiel zu sehen, wo sich im Innern einer großen
Wolke dunkler Materie viele Galaxien befinden. Man geht davon aus, dass die Galaxien oder
Protogalaxien alle ihr Halo aus dunkler Materie mitbringen und dass im Laufe der Zeit
weitere Vereinigungen zu größeren Strukturen ganz wesentlich von den Halos der dunklen
Materie bestimmt werden. Während heftiger Sternbildung kommt es häufig zu SupernovaExplosionen, bei welchen große Mengen heißer Gase (d.h. H, He und geringe Mengen
schwerer Elemente) in den intergalaktischen Raum ausgeschleudert werden.
Fig. 11.4. Ein Bild-Komposit von „Abell 520“. Die Galaxien des Cluster sind als diffuse weiße
Flecken zu sehen. Die rot dargestellte Wolke aus intergalaktischen Materie (IGM), welche im
Lichte der emittierten Röntgenstrahlung (Chandra) zu sehen ist, hat die fast 10fache Masse der
leuchtenden baryonischen Materie. Schließlich stellt die blaue Wolke die Verteilung der dunklen
Materie dar, die indirekt durch „Scannen“ mittels des Gravitationslinseneffektes bestimmt
wurde. Ihre Masse überwiegt die der gesamten baryonischen Materie um etwa einen Faktor 7.
Quelle der Aufnahme X-ray: NASA/CXC/CfA/ M. Markkevitsch et al. Lensing: NASA/STScI,
ESO WFI, Magellan/U. Arizona/D.Clowe et al. Optical: NASA/STScI, Magellan/U.
Arizona/D.Clowe et al. 2006
11.2. Die weitere Entwicklung des Dichtekontrasts. Das sphärische
Kollapsmodell.
In der von Materie dominierten Epoche wächst δ( x ) rasch an, so dass einer linearen
Behandlung, wie wir sie bisher dargestellt haben, nicht mehr vertraut werden kann.
Stattdessen werden wir ein sphärisches Kollaps-Modell (s. dazu A.R. Liddle, D.H. Lyth :
Cosmological Inflation and Large-Scale Structure, Chap. 11. Cambridge Univ. Press 2000)
146
benutzen. Dazu betten wir in das Universum mit kritischer Dichte, ( Ω = 1) , ein sphärisches
Volumen ein mit einer „Überdichte“ Ω = 1 + δ > 1.
Fig. 11.5. Entwicklung des Skalenfaktors. Untere Kurve für
Ω0 = 1 + δ
exakt gerechnet.
Mittlere Kurve für Ω 0 = 1 + δ in linearer Näherung. Obere Kurve für Ω 0 = 1 (kritische
Massendichte des Hintergrunds). Nach A.R. Liddle, D.H. Lyth : Cosmological Inflation and
Large-Scale Structure. Cambridge Univ. Press 2000.
Das Gebiet außerhalb entwickelt sich wie ein Universum mit kritischer Dichte. Dagegen
gelten jetzt für das kollabierende Gebiet Ω > 1 die beiden Gleichungen 2.21
a(t ) 1 Ω
(1 − cos θ)
=
a(t 0 ) 2 Ω − 1
H 0t =
1
Ω
(θ − sin θ )
2 (Ω − 1)3 2
(11.18)
(11.19)
Die Funktion Gl. 11.18 erreicht ein Maximum bei θ = π , daher können wir Gl. 11.18 und
11.19 in a max und t max ausdrücken (was in Fig. 11.5 untere Kurve als „non-linear“
dargestellt ist)
a(t ) 1
t
1
= (1 − cos θ ) und
= (θ − sin θ )
amax 2
t max π
(11.20)
Um Gl. 11.20 auch im linearen Bereich zu untersuchen, entwickeln wir bis zur zweiten
Ordnung
a(t ) θ 2 θ 4
t
1 ⎛ θ3 θ5 ⎞
⎟
≅
−
und
≅ ⎜ −
4 48
amax
t max π ⎜⎝ 6 120 ⎟⎠
147
(11.21)
Setzen wir t in a(t) ein, so erhalten wir in „linearer“ Näherung
alin (t ) 1 ⎛
t ⎞
⎟
≅ ⎜⎜ 6π
amax
4 ⎝ t max ⎟⎠
2
3
2
⎡
⎛
⎞ 3⎤
1
t
⎟⎟ ⎥
⋅ ⎢1 − ⎜⎜ 6π
⎢ 20 ⎝ t max ⎠ ⎥
⎦
⎣
(11.22)
Diese Funktion wird in Fig. 11.4 durch die mittlere Kurve (linear) dargestellt. In Gl. 11.17
beschreibt der erste Faktor auf der rechten Seite den kritischen Fall Ω = 1 und entspricht
damit Gl. 2.20. Wir nehmen an, dass der Skalenfaktor des Hintergrunds dem kritischen Fall,
also der euklidischen Geometrie im Materie dominierten Universum entspricht, siehe obere
Kurve „background“ in Fig. 11.4. Wir können jetzt den Dichtekonstrast für verschiedene
Entwicklungsstadien ausrechnen. Wie verhält sich z.B. der lineare Dichtekonstrast
3
ρ lin
aback
= 3
1 + δ lin =
ρback
alin
(11.23)
Der letzte Ausdruck auf der rechten Seite von Gl. 11.23 läßt sich aus Gl. 11.22 gewinnen,
indem wir zunächst beachten dass der erste Faktor auf der rechten Seite von Gl. 11.17 die
Entwicklung des Hintergrundes beschreibt und zur 3. Potenz im Zähler und im Nenner von
11.18 auftritt, d.h. er kann herausgekürzt werden. Es bleibt die eckige Klammer aus dem
Nenner stehen mit dem folgenden Ergebnis
2
⎡
⎞ 3⎤
⎛
1
t
⎢1 −
⎟ ⎥
⋅ ⎜ 6π
⎢ 20 ⎜⎝ t max ⎟⎠ ⎥
⎣
⎦
und
−3
⎡
3 ⎛
t
≈ ⎢1 +
⋅ ⎜⎜ 6π
⎢ 20 ⎝ t max
⎣
3⎛
t ⎞
⎟
δ lin = ⎜⎜ 6π
20 ⎝ t max ⎟⎠
2
⎞
⎟⎟
⎠
2
3
⎤
⎥ ≈ 1 + δ lin ,
⎥
⎦
3
(11.24)
Dieser Ausdruck wird am Umkehrpunkt, bei t = t max
δ lin (t max ) =
2
3
(6π) 3 = 1,06
20
(11.25)
Der Dichtekontrast ist also praktisch „1“, wenn bei der nichtlinearen Lösung der
Umkehrpunkt zum Kollaps erreicht ist. Das ist auch die Grenze der Anwendbarkeit der
linearen Näherung. Am Endpunkt des Kollaps, bei t = 2t max
ist der Dichtekonstrast in der linearen Theorie
δ lin (2t max ) =
2
3
(12π ) 3 = 1,686
20
(11.26)
Interessanter ist es, jetzt 1 + δ(tmax) in der nichtlinearen Theorie auszurechnen
3
Der Nenner ergibt nach Gl. 11.22 „eins“, so dass nur aback im Zähler etwas beiträgt
3
aback
(6π )
1 + δ(t max ) = 3 = 3 = 5,55
amax
4
2
148
(11.27)
Damit wird der Dichtekonstrast über 4-mal so groß wie in der linearen Theorie. Es ist nicht
realistisch jetzt den Fall t = 2t max zu untersuchen, denn die Dichte divergiert. Wir können
uns aber vorstellen, dass zu Beginn eine Masse M der Ausdehnung R im wesentlichen
potentielle Energie besitzt
E ges ≈ U = −α
GM 2
R
(11.28)
Hier ist α ein Faktor von der Größenordnung „1“ der häufig 3/5 gesetzt wird. Der Kollaps
heizt die Materie auf, ihre thermische (oder kinetische ) Energie verhindert zunächst den
weiteren Kollaps. Man spricht von Virialisierung, wenn sich stabile, zeitlich konstante
Mittelwerte der potentiellen Energie U und der kinetischen Energie T eingestellt haben. Dann
ist
1
1
T =− U
und
E ges = U
(11.29)
2
2
Wenn die Gesamtenergie ungefähr konstant geblieben ist, wird nach (11.23)
RVir ≈
R
2
(11.30)
Damit wäre die Virialisierung abgeschlossen. Wir wollen hier nicht berücksichtigen, dass die
kollabierende Wolke im Infraroten Strahlungsenergie abgibt. Stattdessen berücksichtigen wir
die Virialisierung indem wir a und aback bei t = 1,82 tmax berechnen, wenn a/amax auf ½
gefallen ist. Das Ergebnis ist
⎛ a(1,82 ) ⎞
1 + δ(vir ) = ⎜
⎟ = 157
0
,
5
⎝
⎠
3
(11.31)
Der Wert für den Dichtekonstrast bei abgeschlossener „Virialisierung“ (wenn ein stationärer
Zustand erreicht ist), den man aus numerischer Simulation gewinnt, liegt bei 178. Bei
Annahme eines Universums mit Ω M und Ω Λ = 1 − Ω M erhält man näherungsweise
1 + δ(vir ) ≅ 157 ⋅ Ω −M0, 6 .
149
(11.32)
11.3. Katalogisierungen von Galaxien und Galaxienhaufen
Fig. 11.6. Einbringen von Glasfasersträngen in die Brennebene des 2,5m Teleskops des „Sloan
Digital Sky Survey„ (Kitts Peak Observatory).
Fig. 11.7. Ein 2,5° Ausschnitt mit 24 915 Galaxien aus der SDSS-Durchmusterung. Der äußere
Kreis entspricht z = 0,2. Aus V.J. Martinez & E. Saar : Statistics in Cosmology. SPIE
Proceedings Vol. 4847, 2002, Astronomical Data Analysis. J.L. Stark and F. Murtagh, eds.
150
Die empirische Untersuchung des Dichtekontrasts bezieht sich auf umfangreiche Kataloge
von Galaxien, deren Position und Rotverschiebung. Moderne Multi-Glasfaser-Techniken
ermöglichen es gegenwärtig, 70 – 2000 Rotverschiebungen von Galaxien pro Nacht
spektroskopisch zu vermessen, während es vor Einführung dieser Technik nur 5 – 10 waren.
Die Grenz-Größenklasse im blauen Spektralbereich stieg von 14 auf 19,5, ein Fortschritt der
nicht nur größeren Teleskopen sondern vor allem auch dem Einsatz von CCD-Platten, den
elektronischen Fotoplatten (s. Fig. 11.5), zu verdanken ist. Zwei zur Zeit laufende große
Projekte sind das 2dF (2 degree field) und der SDSS (Sloan Digital Sky Survey). Die SDSSDurchmusterung ist z.Zt. die umfangreichste. Sie wird in 5 Wellenlängenbereichen mit einer
Mosaik-CCD-Kamera durchgeführt. Die Photometrie erreicht dabei Objekte bis 23. Größe,
die Analyse der Rotverschiebung reicht bis zur Größe 17,7. Diese Untersuchungen sind nicht
nur für die Massenverteilung von großem Interesse, sondern auch für das Verständnis der
Entwicklung morphologischer Merkmale. Jede Galaxie wird durch 3 Angaben charakterisiert:
Position ( α, δ, r = comoving distance), n (r ) = radiale Selektionsfunktion, n (rˆ ) =
r
Winkelselektionsfunktion mit rˆ = r / r . Der gesamte untersuchte Raumwinkel beträgt 2499
Quadratgrad. Das zweite Großprojekt ist der „Anglo-Australian 2dF Galaxy Redshift Survey“
(Mt. Stromlo Observatory). Im Jahr 2001 wurden die ersten 105 Galaxien des Südhimmels mit
Rotverschiebungen publiziert (M. Colless et al. : MNRAS 328, 1039, 2001). Die Objekte sind
heller als Größe 19,5. Das untersuchte Gebiet umfasst 2000 Quadratgrad und erreicht z = 0,2 (
ca. 600 h-1 Mpc). Man rechnet bei Beendigung des Projekts mit 250 000 Galaxien, deren
Position und Rotverschiebung vermessen wurden.
Fig.11.8. Fornax Cluster im Röntgenlicht, gemessen von Chandra bei 1 keV.
Credit: NASA /CXC/Columbia U./C.Scharf et al. 2004
Die Verteilung der Galaxiencluster kann am besten an Hand ihrer Röntgenbremsstrahlung
untersucht werden, wobei die Energie bei 1 – 10 keV liegt. Diese Methode hat sich auch als
der beste Weg erwiesen, große, homogene Cluster zu identifizieren. und wurde im Projekt
REFLEX (ROSAT-ESO Flux Limited X-ray) bis zum Jahre 2002 auf 452 Cluster angewandt.
Durch Messung des Röntgenspektrums kann man aus der Temperatur des heißen (und sehr
dünnen) Plasmas direkt die Masse bestimmen. Man geht dabei vom Virialsatz aus
151
3
1 GμmP M vir 1
= μmP σ 2υ
k BT =
2
2
r
2
(11.31)
wobei mP die Protonenmasse, μ die mittlere Massenzahl der Teilchen (μ ≅ 0,6),
σ 2υ = 3 υ r die Geschwindigkeits-Dispersion der Galaxien in radialer Richtung und Mvir
2
die Virialmasse des Clusters bedeuten.
Fig. 11.9. Räumliche Verteilung der „X-ray Cluster“ des REFLEX Survey. Jeder Punkt
stellt einen Galaxienhaufen mit hunderten bis tausenden Galaxien dar. Kettenartige
Strukturen sind zu erkennen. Nach s. Borgani, L. Guzzo : Nature 410, 169, (2001).
Die Intensität der Röntgenstrahlung verhält sich zur Dichte n des Plasmas und der Temperatur
T wie
I X ∝ n 2T
1
2
(11.32)
Da die optische Intensität nur mit dem Quadrat von n geht, folgt, dass IX für diesen Zweck
einen wesentlich besseren Kontrast erwarten lässt als optische Untersuchungen. Unter
Zugrundelegung eines Dichteprofils kann man den Massenanteil des Plasmas bestimmen. Die
ermittelte Clustermasse umfaßt die Gesamtmasse, d.h. dunkle Materie und baryonische
Masse. Dabei ist der Anteil des heißen intergalaktischen Plasmas an der Gesamtmasse gleich
f gas = 0,113 , dabei aber um etwa einen Faktor 6 größer als die optisch leuchtende Masse der
Galaxien (s. S.W. Allen et al. astro-ph/0205007).
Schließlich sei noch der „IRAS Point Source Catalogue (PSC) Redshift Survey“ erwähnt, der
24 500 Galaxien enthält, bei 60 µm über 84% des Himmels abdeckt und alle Punktquellen mit
einem Fluß ≥ 1,2 Jansky einschließt. Von IRAS PSC sind Leistungsspektren P(k) publiziert
152
worden (s. W. Sutherland et al. astro-ph/9901189), auf die wir später noch zurückkommen
werden.
11.4. Leistungsspektren der Massenverteilung
Fig. 11.10. Links (unten): Leistungsspektren P(k ) von je 147 000 2dF-Galaxien und
105 SDSS-Galaxien, (oben) P(k ) von REFLEX-Cluster. Rechts: ZweipunktKorrelationsfunktionen ξ(r ) von 2dF- , SDSS- und Las Campanas-Galaxien
Wir wollen hier zunächst noch die Zweipunkt-Korrelationsfunktion definieren. Dazu sei die
r
r
Dichte an jeweils zwei verschiedenen Punkten gegeben durch x und y . Es wird nun das
r
r
Produkt ρ ( x ) ρ ( y ) gebildet und über das Ensemble gemittelt (Eckige Klammer)
r
r
r
r
r r
ρ ( x ) ρ ( y ) = ρ 2 [1 + δ ( x )][1 + δ ( y )] = ρ 2 [1 + ξ ( x , y )]
wobei
r r
r
(11.33)
r r
bedeutet. Auf kleinen Skalen x − y = r < 12 Mpc lässt sich
r
ξ ( x , y ) = δ ( x )δ ( y )
ξ durch ein Potenzgesetz darstellen
⎛r ⎞
ξ (r ) = ⎜ 0 ⎟
⎝r⎠
1,8
(11.34)
mit r0 / h = 5 Mpc . Aus der Korrelationsfunktion lässt sich das Spektrum P(k) ausrechnen
ξ (r ) =
1
(2π )
2
∫ dk k
2
P(k )
sin(kr )
kr
(11.35)
Alternativ bietet auch Gl. (11.4) eine Möglichkeit. Für einen Vergleich mit Modellen wird das
r
Spektrum P(k ) dem Dichtekontrast δ( x ) (Gl. 11.2 und Fig. 11.2) vorgezogen. Man kann
das Leistungsspektrum durch ein Potenzgesetz annähern
153
P(k ) = A ⋅ k n
Im Strahlungsuniversum (z > 3000) und im Bereich sehr großer Raumdimensionen (kleiner kWerte) nähert sich n ≈ 1 (aus Fluktuation des CMB). Man spricht vom Harrison-ZeldovichSpektrum. Für kleine Raumdimensionen (große k-Werte) wird n ≈ −1,8 . Den
entsprechenden Übergangsbereich liefert bei den berechneten Kurven nur das „Cold Dark
Matter“(CDM-)Modell. In Fig. 11.12 ist das Leistungsspektrum von IRAS-Galaxien
aufgetragen. Sie überdecken einen größeren Raumbereich. Hier ist die Andeutung eines
Maximums zu sehen. Bei der Normierung der P(k ) -Kurven muss beachtet werden, dass die
leuchtende Materie der Galaxien nur einen Bruchteil von etwa 0,005 der Gesamtmasse
ausmacht. Man definiert deshalb zur Normierung einen Bias-Faktor
b2 =
PGal (k )
PM (k )
(11.36)
Viele Messungen von Massen und Massendichten sind von sicheren Bestimmungen der
Entfernung abhängig. Es wäre deshalb hilfreich, wenn es neben Standardkerzen auch ein
kosmisches Standard-Metermass gäbe. Tatsächlich wurde etwas Entsprechendes gefunden.
Untersucht man nämlich das Spektrum der Dichtekorrelationen gewonnen aus Daten des
Sloan Digital Sky Atlas (SDSS), so findet man Oszillationen, die wohl auf akustische
Oszillationen zurückgehen zur Zeit der Rekombination. Da dieser Effekt überall im für uns
beobachtbaren Kosmos auftreten sollte, hätten die Astronomen damit eine universellen
Massstab.
a) Korrelationsfunktion ξ (s) für
„Luminescent Red Galaxies“ des SDSS.
Der „fit“ wurde innerhaln des ΛCDMModells mit 3 verschiedenen
Massendichten Ω M h 2 = 0,12; 0,13 und
0,14 von oben nach unten ausgeführt.. Die
durchgezogene Linie ohne akustisches
Maximum benutzte Ω M h 2 = 0,105
b) Auftragung von ξ ( s ) s 2 mit den gleichen
Massendichten wie in a). Eone zu große Massendichte
Verschlechtert beträchtlich die Anpassung an den Peak
Bei kleinen Abständen (30 Mpc). Nach
D. Eisenstein et al:The Astrophysical Journal 12/31/2004
Fig.11.11. “Baryon Acoustic Oscillations” im Dichtespektrum des SDSS
154
Fig. 11.12. Transferfunktion für ein „Cold Dark Matter“ (CDM) Model für die
Parameter Γ = 0,5; 0,4; 0,3; 0,2. Die heutigen Konkordanz–Werte ergeben Γ = 0,17 .
Nach J.M. Bardeen et al. ApJ 304, 15 (1986).
Geht man von einer Störung δ(k , t rec ) zur Zeit der Rekombination trec aus, dann wird eine
Transferfunktion im Rahmen der linearen Theorie angesetzt, welche die Entwicklung der
Störung zu einer späteren Zeit beschreibt
δ (k , t ) = Τ(k , t ) ⋅ δ (k , t rec )
(11.37)
Fig. 11.11 gibt ein Beispiel. Die Transferfunktion gilt für die gegenwärtige Beobachtung und
ist für ein „Cold Dark Matter“ (CDM) Model berechnet. Die Abhängigkeit von der
Wellenzahl wird qualitativ richtig dargestellt. Bei kleinen Wellenzahlen, d.h. großen Skalen
nimmt T (k ) den Wert eins an, weil das ursprüngliche Leistungsspektrum durch CDMTeilchen nicht gestört wird; d.h. das Leistungsspektrum, wie es in der Rekombination-Phase
vorliegt, ist k-unabhängig, wie von der Inflation gefordert (Gl. 10.6 und 10.7). Die
Transferfunktion in Fig. 11.9 wird als Funktion T (q ) einer normierten Wellenzahl q
angegeben.
155
Fig. 11.13. Das Leistungsspektrum P(k ) der IRAS-Galaxien (1,2 Jy) im Vergleich zu
anderen Durchmusterungen. Gestrichelt ist das Ergebnis einer linearen CDM-Theorie
für Γ = 0,2 und 0,5 sowie σ8 = 0,8 eingetragen.
Bei der Berechnung von P(k ) aus den Meßdaten muß berücksichtigt werden, dass im
Gegensatz zur mathematischen Form der Fouriertransformation, welche die Integration über
einen unendlichen Raum erfordern, die Beobachtung immer nur ein endliches Raumelement
überdeckt. Deshalb müssen Fensterfunktionen im k-Raum angesetzt werden, deren Effekt
sorgfältig getestet werden muß.
11.5. N-Teilchen-Simulationen
Erst in den letzten Jahren sind P(k ) -Auftragungen, die aus Beobachtungen gewonnen
wurden, genau genug, um daran theoretische Modell zu testen. Das „Hot Dark Matter Model“
(HDM) hat dabei nur noch historische Bedeutung. Eine wichtige und testbare Vorhersage des
Modells, war eine Entwicklung von großen zu kleinen Strukturen (top down model), welche
von den Beobachtungen nicht gestützt wird. Das HDM wurde in den 80er Jahren von dem
„Cold Dark Matter Model“ (CDM) abgelöst, das eine Entwicklung von kleinen zu großen
Strukturen vorhersagt, was sehr viel besser mit den Beobachtungen übereinstimmt. Aus dem
CDM entwickelte sich ein „Standard Cold Dark Matter Model“ (SCDM) mit den Parametern
Ω 0 = 1 , h = 0,5 (Hubble Konstante in Einheiten von 100 km/s⋅Mpc), n = 1 (HarrisonZeldowich-Spektrum) und b = 1,5 – 2,5. Das SCDM konnte ausgeschlossen werden, da es die
gemessenen Spektren nur unzureichend wiedergibt. So wird die Haufenbildung von Galaxien
über größere Skalen beobachtet, als aus dem SCDM hervorgeht. Eine Alternative ist das Open
Cold Dark Matter Model OCDM mit Ω 0 < 1.
156
Fig. 11.14. Simulationsergebnisse zu den unten im Text beschriebene Modellen.
Es vergrößert den Horizont zur Zeit der Gleichheit von Materie und Strahlung, wodurch
vermehrte Haufenbildung auf großen Skalen auftritt. In einem anderen Modell wird, unter
Beibehaltung von Ω 0 = 1 , Ω M = 0,2 gesetzt, so dass Ω Λ = 1 − Ω M wird. Dieses Modell
wird „Λ Cold Dark Matter Model“ (ΛCDM) genannt, wobei der größte Einfluß auf P(k ) von
Ω M kommt, während Ω Λ kaum beiträgt. Wenn stattdessen der Anteil relativistischer
157
(heißer) Materie erhöht wird, schafft man einen ähnlichen Effekt. Dieses Modell wird τCDM
gernannt. Unter dem Eindruck der Ergebnisse des WMAP-Projekts spricht man in jüngster
Zeit vom „Concordance Model“ mit Parametern wie Ω M = 0,3 , h = 0,7 .
Fig. 11.15. Ergebnisse der „Milleniums-Simulation, einer der größten bisher
durchgeführten N-Teilchen Simulationsrechnung mit mehr als 1010 Teilchen
Dargestellt ist die Entwicklung der Materieverteilung (dunkle Materie) in der
Gegenwart 13,7 Gigajahre nach dem Big Bang. Das untere Bild zeigt das gleich
Ergebnis wie oben aber mit mehr als 10-facher linearer Vergrößerung (nach Volker
Springel, MPI f. Astrophysik Garching).
Es muss noch einmal betont werden, dass die Strukturen, welche sich bei den Simulationen
ergeben, aus dunkler Materie bestehen. Diese bilden Bereiche eines niedrigeren
Gravitationspotentials, in welchen sich baryonische Materie sammelt. Offen ist noch die
Frage, ob in Ω M nicht auch noch heiße dunkle Materie verborgen ist, z.B. „schwere“
158
Neutrinos (μ- und τ-Neutrinos). Es ist möglich, dass diese Frage in den nächsten Jahren
durch Präzisionsmessungen der Hintergrundstrahlung mit dem PLANCK-Satelliten der ESA
gelöst werden kann. Die Modellrechnungen werden einerseits mit N-Teilchen-Simulationen
durchgeführt, andererseits mit semianalytischen Methoden. Die umfangreichsten
N-Teilchen-Simulationen werden z. Zt. vom Virgo-Team vorangetrieben, an welchem auch
das MPI f. Astrophysik in Garching beteiligt ist. Das Model LCDM geht von den Werten
Ω M = 0,3 , Ω L = 0,7 , h = 0,7 und σ8 = 0,9 aus. σ8 ist die Streuung in einem Würfel der
Kantenlänge r = 8/h Mpc. Die jüngste Auswertung von WMAP- und SNIa-Daten ergibt den
+0 , 036
Wert σ8 = 0,772 −0 , 048 . Der in den zitierten Modellen simulierte Würfel hat eine Länge von
3000/h Mpc mit 109 Massenelementen. Die Simulation beginnt bei z = 35. Fig. 11.13 zeigt
das Ergebnis einer der umfangreichsten Modellrechnungen mit den Parametern des
Konkordanzmodells.
Zu den semianalytischen Modellen muß auf die Literatur verwiesen werden. Hinweise finden
sich L. Guzzo : Large-Scale Structure from Galaxy to Cluster Surveys. Review in
DARK2002, 4th Heidelberg Conf. On Dark Matter in Astro- and Particle Physics. H.-V.
Klapdor-Kleingrothaus & R. Viollier eds. Springer 2002. H.J. Mo, S. Mao, S.D.M. White:
The formation of galactic disks. MNRS 295 (1998) 319
11.6.
Weitere Meßmethoden zur Massenverteilung
Machen wir uns noch einmal klar : Nur 4% der Masse des Univesums ist baryonische Masse.
96% sind Materie- bzw. Energieformen, die uns noch völlig unbekannt sind. Diese
Feststellung ist so ungeheuerlich, daß von Seiten der Beobachtung alles getan werden muß,
das Ergebnis Ω B = 0,04 , Ω M = 0,3 , Ω Λ = 0,7 abzusichern. Das kann vor allem durch
möglichst viele verschiedene, völlig unabhängige Meßverfahren geschehen. Wir wollen hier
einige neue Verfahren kurz erwähnen, deren Anwendung sich noch in den Anfängen befindet,
deren Bedeutung in Zukunft aber sehr wahrscheinlich zunehmen wird.
11.6.1.Der Sunyaev-Zeldovich-Effekt (SZE) beschreibt inverse Comptonstreuung von
Photonen des CMB an heißen Elektronen des intergalaktischen Plasmas in
Galaxienhaufen. Damit kann die Massenverteilung der Cluster untersucht werden. Solche
Untersuchungen wurden bei 150, 210 und 275 GHz mit einem Bolometer-Array am ViperTeleskop gemacht, das am Südpol aufgestellt ist. Die 3 Frequenzkanäle gestatten es, die
spektrale Verschiebung des CMB-Spektrums zu höheren Frequenzen zu detektieren. Mit
der hier zitierten Messung wurden u.a. zwei Cluster untersucht, welche im REFLEXKatalog die größte Röntgen-Helligkeit besitzen: Abell S 1063 (z = 0,347) und 1E 0657-67
(z = 0,299). Fig. 11.12 zeigt die Ergebnisse von 1E 0657-67. Die Effekte erfordern eine
hohe Empfindlichkeit der Messung, die z.Zt. knapp erreicht wird. Der SZE führt zu einer
völlig unabhängigen Bestimmung von Cluster-Morphologien und Massen.
11.6.2.Gravitationslinsen-Effekte hängen i.a. von der dunklen Energie und im Detail von
der Massenverteilung großer Galaxien ab, die für entfernte Galaxien und Quasare als
Linsen wirken. Man unterscheidet normale Linseneffekte, d.h. Ablenkungen im Bereich
von Bogensekunden, und Weitwinkelaufspaltungen ( Δθ ≥ 4" ), wobei diese sehr
empfindlich auf Dichteverteilungen ansprechen. Auf der Grundlage der bisher
beobachteten Systeme lassen sich die verschiedenen Effekte noch nicht trennen.
159
Fig. 11.16. Farbcodierte Bilder der CMB-Temperaturen des Galaxienhaufens 1E065767. Die darüberliegenden weißen Konturen sind ROSAT-Messungen. Der
Strahldurchmesser des ACBAR –Mikrowellen-Teleskops beträgt 4,5 Bogenminuten. Die
Farbcodierung umfaßt den Temperatur-Bereich von –200 bis +200 µK. Nach P. Gomez
et al. astro-ph/0311263.
Das sollte aber mit einer größeren Ansammlung von Beobachtungsmaterial möglich
sein. Gravitationslinsen bieten eine interessante unabhängige Methode, die dunkle
Energie zu untersuchen,
deren Größe bis jetzt im Wesentlichen aus SN Ia-Beobachtungen und in jüngster Zeit
aus den von WMAP mit großer Genauigkeit gemessenen Fluktuations-Spektrum des
CMB bestimmt wurde.
11.6.3. Neben der Hubble-Fluchtgeschwindigkeit besitzen alle Galaxien auch
noch Eigenbewegungen. Ihre Geschwindigkeit oder genauer deren
radiale Komponente wird als störender Effekt immer mitgemessen, wenn
Rotverschiebungen bestimmt werden. Die Eigenbewegungen (auch
Pekuliarbewegungen genannt), zeigen Beschleunigungen in
Gravitationsfeldern an. Damit enthalten sie wichtige Informationen über
Ω M im allgemeinen und über die Massenverteilung in Galaxienhaufen
im Speziellen. Zur Bestimmung der Pekuliarbewegungen werden die
Daten aus Galaxienkataloge, welche die Rotverschiebungen enthalten,
160
zu grunde gelegt.
11.5.4. Kreuzkorrelationen von Intensitäten der CMB und der Intensität der
Röntgen-Hintergrundstrahlung führen dazu, inelastische Streuungen der CMBPhotonen an dem Gravitationspotential großräumiger Materieverteilungen zu
detektieren. Dieser sogenannte Sachs-Wolfe-Effekt entsteht erst nach der
Rekombination, wenn sich bereits erste Dichtekontraste gebildet haben. Fig. 11.13
zeigt die Ergebnisse. Eine ähnliche Kreuzkorrelation wurde vom gleichen Team
zwischen CMB-Fluktuation und der Verteilung der Radiogalaxien gefunden.
Fig. 11.17. Kreuzkorrelaltion zwischen der Intensität des Röntgenhintergrunds
und der CMB-Intensität. Aus St. Boughn, R. Crittenden, Nature 427 (2004) 45.
11.7.
Zusammenfassung.
Die Physik der kosmischen Strukturbildung muss erklären, wie die
Dichtefluktuationen δ ≈ 10 −5 bis zur ersten Sternbildung auf δ ≥ 1 anwuchsen, was
ohne Hinzunahme der dunklen Materie nicht möglich ist. Im so genannten linearen
Bereich wächst der Dichtekontrast etwa wie a (t ) ∝ t 2 / 3 . Hat sich eine dichtere Wolke
gebildet, kann man auf weitere Verdichtungen die Lösungen der FriedmannGleichungen für Ω > 1 anwenden. Man erhält vor der Virialisierung eine Zunahme des
Dichtekontrasts δ = 5,5 , welche dunkle und baryonische Materie betrifft. Nach der
Virialisierung ist der Radius der Wolke um die Hälfte geschrumpft, der
Dichtekonstrast hat um den Faktor 28 zugenommen. Der baryonische Anteil der
Wolke hat sich aufgeheizt. Eine weitere Verdichtung ist nur möglich, wenn
(kinetische) Energie durch Strahlung abgegeben wird, wozu nur der baryonische Teil
der Materie in der Lage ist. Verschiedene Modelle (hot dark matter, cold dark matter
und Λ-cold dark matter) wurden durch N-Teilchensimulationen darauf überprüft, wie
sie die Evolution der Strukturen beschreiben. Vergleiche mit den gemessenen
Dichtespektren wurden angestellt. Nur das frühe Universum zeigt Selbstähnlichkeit:
P(a) ∝ k γ mit γ = 1 . Die spätere Entwicklung wird eher durch einen Exponenten
γ = −1.8 beschrieben. Nur ein kleiner Teil der baryonischen Materie befindet sich in
Sternen. Der größere Teil wird als stark verdünntes heißes Gas zwischen den Galaxien
161
durch seine Röntgenstrahlung gefunden. Der Sunyaev-Zeldovich-Effekt wird ebenfalls
zum Aufspüren von Galaxien-Clustern verwendet. Er beruhrt auf einer
Frequenzverschiebung der Hintergrundstrahlung durch Streuung an heißen Elektronen.
Literatur
A.R. Liddle, D.H. Lyth: Cosmological Inflation and Large-Scale Structure, Chap. 11.
Cambridge Univ. Press 2000
P. Schneider: Extragalactic Astronomy and Cosmology. Springer Verl. 2006
L. Guzzo : Large-Scale Structure from Galaxy to Cluster Surveys. Review in
DARK2002,
4th Heidelberg Conf. On Dark Matter in Astro- and Particle Physics.
E.W. Kolb, M.S. Turner : The Early Universe. Addison Wesley 1990.
G. Börner: The Early Universe. Facst and Fiction. Springer Verl. 2004
11.8. Aufgaben
1. Die Dichte einer sphärischen Molekülwolke beträgt 10 Teilchen pro cm3 bei einer
Temperatur von 40 K. Wie groß in in diesem Fall die Jeans-Masse MJ und die JeansLänge lJ?
2. Berechne mit den obigen Werten die Schallgeschwindigkeit und und die Zeit tS,
welche der Schall benötigt, um die Jeanslänge zu durchlaufen. Wenn Du 1) nicht
gelöst hast, verwende lJ = 6,5 pc. Schätze die freie Fallzeit ab für einen Kollaps einer
1
sphärischen Masse mit Radius lJ. (in diesem Fall ist t 2ff ≈
). Zeige, dass für die
Gρ
Jeans-Instabilität näherungsweise gilt t S ≈ t ff .
3. Die Kollabierende Wolke soll vor dem Kollaps eine Temperatur von 40 K und eine
Gesamtenergie
GM 2
E ges = − E pot = −α
R
gehabt haben die kinetische Energie konnte hier noch vernachlässigt werden).
Nach dem Kollaps hat sich ein „Virial“ gebildet, ein neuer stationärer Zustand, für
welchen der Virialsatz gilt
1
1
E ges = E kin + E pot = − E pot und E kin = − E pot
2
2
2
1
α GM
mit
E ges = − E pot = −
und α = 3 / 5
2
2 R/2
Der Radius hat sich durch die Virialisierung halbiert. Es ist mittlere kinetische Energie
entstanden. Schätze die mittlere kinetische Energie 3 / 2 ⋅ k B T pro Teilchen ab
(10 cm-3). Um wie viel ist die Temperatur angestiegen?
162
12. Erste Sterne. Reionisation. Galaxien.
12.1. Erste Sterne.
Zur Zeit der Rekombination bei z = 1089 und einer Temperatur von 2970 K lag das
Intenitätsmaximum der Strahlung bei etwa 1 µm. Es verschob sich im Laufe der Zeit weiter
zu längeren Wellen und erreichte nach 180 Mill. Jahren bei z = 20 etwa 55 µm und eine
Strahlungstemperatur von 56 K. Bei dieser Rotverschiebung sollten nach den Ergebnissen von
WMAP die ersten Sterne aufgetreten sein. Es ist die Zeit der Reionisation, verursacht durch
die ersten, extrem leuchtkräftigen Sterne. Ein Beobachter hätte bis dahin eine große
Dunkelheit wahrgenommen. Im sichtbaren Bereich gab es so gut wie keine Strahlung. Man
spricht vom dunklen Zeitalter, das mit der Epoche der Reionisation endet.
Inzwischen haben sich aber, wie wir in Kap. 11 gesehen haben, aus sehr kleinen
Dichteschwankungen Bereiche größerer Dichte entwickeln können. Beim Dichtekontrast von
δ ≈ 4,5 bildeten sich kollabierende Wolken dunkler Materie (s. Gl. 11.22). Die baryonische
Materie allein würde dazu nicht ausreichen; denn nach Gl. 11.15 ist δ ∝ a , d.h. δ kann von z
= 1089 bis z = 20 nur um einen Faktor 55 wachsen. Wie groß waren die kollabierenden
Wolken? Die ersten Objekte müssen baryonische Massen von ca. 106 Sonnenmassen gehabt
haben, welche sich innerhalb von Wolken dunkler Materie ansammelten. Die Abkühlungszeit
tcool bei der Bildung baryonischer Massen muss kürzer gewesen sein als die Hubblezeit. Nach
4
der „Virialisierung“ war ihre Temperatur durch Abstrahlung auf ca. T ≈ 10 K gesunken.
Weitere Abkühlung ist nur möglich, wenn sich molekularer Wasserstoff bilden kann, wozu
eine ganze Kaskade komplizierter chemischer Prozesse in dem Gas der Urmaterie aus
atomarem Wasserstoff und Helium (unter Einbeziehung ihrer Ionisationsstufen) ablaufen
muss. Da das H2-Molekül Schwingungs- und Rotationsfreiheitsgrade besitzt, die eine
Abstrahlung im Infraroten ermöglichen, können die Wolken weiter abkühlen. Solange die
Abkühlung effizient ist, d.h. die Abkühlungzeit tcool im Verhältnis zur Zeit des freien Falls tff
kurz ist, werden die Wolken kollabieren und weiter fragmentieren, d.h. kleinere Klumpen
bilden. Die Fragmentierung kommt zum Stillstand, wenn tcool = tff geworden ist. Die
Abkühlung hängt vom Quadrat der Dichte und sehr stark von der „Metallizität“, d.h. vom
Massenanteil Z schwerer Elemente ab (schwerer als 4He). In der Sonne erreicht Z einige
Prozent. In der Urmaterie ist Z < 10-4⋅ZSonne und damit ist die Abkühlung ziemlich ineffizient.
Wolken mit so geringer Metallizität wurden lange nicht gefunden. Erst kürzlich wurde in
einer Arbeit von Fumagalli et al. unter den Lyα-Absorbern ein Objekt mit z = 3,3 beschrieben,
dass keine messbaren schweren Elemente (C, O, N etc.) enthält. Die Dichte entspricht etwa 90
Protonen /m3. Die Fragmentierung endet bei baryonischen Wolken von etwa 103
Sonnenmassen, die sich in Potentialmulden aus dunkler Materie befinden. Man muss deshalb
davon ausgehen, dass die ersten Sterne tatsächlich Massen von 103 Sonnenmassen erreichten
mit extrem kurzen Lebensdauern. 3-dimensionale Simulationen zeigen, dass diese Gebilde
durchaus stabil sein können. Diese Eigenschaft steht im Gegensatz zu der massereicher Sterne
mit normaler Metallizität, d.h. Z > 10-4 ⋅ZSonne, welche durch starken Sternenwind schnell
Masse verlieren. Die Fragmentierung von Wolken der Urmaterie mit Z < 10-4⋅ZSonne verläuft
anders. Sie endet schon bei großen Massen und läßt damit superschwere Sterne zu. Aus der
kollabierenden Urmaterie bildet sich schließlich ein protostellares Zentrum mit einer Hülle,
aus welcher weitere Materie auf das Zentrum fällt.
163
Fig. 12.1. Die Masse der ersten Sterne am Ende ihrer Entwicklung aufgetragen gegen ihre
anfängliche Masse. Sterne oberhalb 260 Sonnenmassen kollabieren zu schwarzen Löchern, ohne
dass Masse ausgeschleudert wird. Das Entsprechende passiert auch mit Sternen im
Massenbereich 40 – 140 Sonnenmassen. Sterne zwischen 140 – 260 Sonnenmassen dagegen
werden bei der Supernovaexplosion völlig zerissen, ohne das ein Neutronenstern oder ein
schwarzes Loch gebildet wird. Die Explosionsenergien sind etwa 100mal größer als bei normalen
„Core-Collaps SNe“. Dabei werden ca. 50 Sonnenmassen Nickel ausgeschleudert. Damit
wiederum kann eine nächste Generation von 500 Mill. Sternen mit Sonnenmassen mit einer
Metallitität von Z = 10-4 ausgestattet werden. Die durchgezogenen Gerade bezeichnet die Masse
ohne Massenverslust. Die darunter liegende Kurve berücksichtigt Massenverluste. Aus A.
Heger, S.E. Woosley, I. Baraffe and T. Abel: Evolution and Explosion of Very Massiv
Primordial Stars (2002), to appear in Proc. Lighthouses in the Univers, „ESO Astrophysics
Symposia“, Springer Verl.
In massereichen Sternen mit normaler Metallizität verläuft die Fusion von Wasserstoff im
Wesentlichen über den CNO-Prozess. Dazu sind jedoch schwere Elemente als Katalysatoren
notwendig, welche in den ersten Sternen nicht vorhanden sind. Der CNO-Prozess ist deshalb
nicht möglich, und das Brennen verläuft nach dem ineffizienteren p-p-Prozess. Im Zentrum,
164
des Sterns ist Dichte und Temperatur nach der Erschöpfung des Wasserstoffs bald so hoch,
daß der 3 α -Prozeß mit Bildung von Kohlenstoff einsetzt. Bei Temperaturen T > 109 K, wenn
hv ≥ 2me c 2 wird, werden aus Photonen (in der Nähe von Kernen) Elektron-Positron-Paare
gebildet. Dieser Prozess entzieht dem Photonengas Energie. Der adiabatische Exponent,
definiert als γ ad = c p / cυ oder
1 ⎛ d ln ρ ⎞
≡⎜
⎟
γ ad ⎝ d ln P ⎠ ad
(12.1)
Fig. 12.2. Produktionsfaktoren der Elemente relativ zur solaren Häufigkeit
Gestrichelte Linie mit offenen Dreiecken von Sternen mit 12 – 40 Sonnenmassen. Die durch
gezogene Linie berücksichtigt auch Sterne der Massen 140 – 260 Sonnenmassen. Im
Massenbereich 100 – 140 MO werden die äußeren Hüllen abgestoßen, wobei kaum schwere
Elemente nach außen gelangen. Im Bereich 40 – 100 MO fällt der He-Core völlig in das
entstehende schwarze Loch, sodaß schwere Elemente nicht nach außen gelangen. Es ist dabei
angenommen worden, daß die Häufigkeit der Sternmassen (Initial Mass Function = IMF) wie
IMF ∝ M −1,5
verläuft. Aus A. Heeger and S.E. Woosley: The Beginning of Stellar
Nucleosynthesis (2002), to appear in Proceedings of the 11th Workshop on Nuclear Astrophysics,
Ringberg Castle, eds. E. Müller and W. Hillebrandt, MPA Proceedings Garching.
nimmt ab. Für einatomige Gase ist γ ad = 5 / 3 , für ein Photonengas wird γ ad = 1, was zur
Instabilität führt. Die Grenze zur Instabilität liegt bei γ ad = 4 / 3 ; sie wird erreicht, wenn die
Entwicklung des Sterns in die sogenannten Paar- Instabilität läuft. Dann kollabiert der Stern
in einer Paar-Supernova-(SN)-Explosion. Dabei werden praktisch keine schweren Elemente
jenseits von Zn (Z = 30) gebildet. Die Kerne mit ungerader Neutronen- und ungerader
165
Protonenzahl treten mit ein bis zwei Zehnerpotenzen geringerer Ausbeute auf. Die höchste
Ausbeute erreicht Si.
Was folgt daraus für die Beobachtung? Die großen Massen der ersten Sterne (Sterne der
Population III) bescherten ihnen nur eine Lebensdauer von wenigen hunderttausend Jahren
6
(bei 40 Sonnenmassen dauert die Zeit des Wasserstoff-Brennens etwa 2 ⋅ 10 Jahre bei 100
Sonnenmassen nur noch 0,25 ⋅10 6 Jahre). Ihre nuklearen Aschen enthielten genügend
schwere Elemente für die nächsten Sterngenerationen (Sterne der Population II). In den
Sternatmosphären dieser sehr alten „low metallicity stars“ sollten sich die in Fig. 12.2.
dargestellten Abweichungen von der üblichen Elementhäufigkeit wieder finden. Ein Beispiel
bildet der kürzlich entdeckte extrem metallarme Stern HD 0107- 5240 im galaktischen Halo.
Er ist ca. 10 kpc entfernt und seine Metallizität im Verhältnis zum solaren Wert beträgt
0,5 ⋅ 10 −5 .
Die Beobachtung von „Pair Supernova“-Prozessen könnte im Prinzip möglich sein wegen der
gegenüber normalen „Core-Collaps-SNe um etwa 2 Zehnerpotenzen größeren
Energieausstoßes (Hypernovae). Dabei ist zu bedenken, dass die Prozesse bei einer
Rotverschiebung von etwa z = 20 auftreten müßten. Das bedeutet, dass das Licht aus dem
Zerfall radioaktiver Nukleide im mittleren Infraroten zu erwarten ist und daß die Zeitskala des
Zerfalls um einen Faktor 20 gedehnt ist. Man ordnet die kosmischen Gammablitze (Gamma
Ray Bursts = GRBs), die mit einer Dauer von über 2 Sekunden bis Minuten auftreten, den
Core-Collaps von Sternen über 25 Sonnenmassen zu. In diesen Fällen führt der Core-Collaps
massiver Sterne zur Entstehung stellarer schwarzer Löcher. In dem Häufigkeits-Diagramm
der GRBs in Fig. 12.3 werden die Prozesse unter dem rechten Maximum HypernovaProzessen zugeordnet. Eine Koinzidenz von GRB und einer optisch leuchtenden SN konnte in
vielen Fällen bis zu z ≅ 4 nach gewiesen werden. Deshalb ist es durchaus möglich, daß man in
Zukunft GRBs mit sehr großem z empfangen kann und zusätzlich vielleicht ein Nachleuchten
im IR beobachtet.
Fig. 12.3. Die Häufigkeiten von GRBs geordnet nach der Pulslänge. Die Verteilung unter dem
rechten Maximum wird Core-Collaps-Prozessen massereicher Sterne zugeordnet.
166
Fig. 12.4. Künstlerische Darstellung einer Hypernova, das Ende eines Sterns mit M > 25 MO. Im
Innern der Plasmakugel ist ein schwarzes Loch entstanden. Entlang der Rotationsachse hat sich
ein Jet ausgebildet. Er besteht im Wesentlichen aus einem Plasma von Elektron-PositronPaaren. Wenn der Jet auf die abgestoßenen Materiehüllen der Prae-SN trifft, wird jeweils eine
Schockwelle energiereicher γ − Strahlung erzeugt.
12.2. Galaxienentstehung
Galaxienbildung, dieser so wichtige Prozeß der Strukturbildung, erweist sich als ungeheuer
komplex und ist in vielen Details noch nicht verstanden. Galaxien mit extremer
Rotverschiebung ( z ≥ 8 ) sind wegen ihrer geringen Helligkeit, ihrer starken Rotverschiebung
und unregelmäßigen Gestalt äußerst schwierig zu beobachten. Wie oben schon erwähnt
leuchteten die ersten Sterne in fragmentierten Wolken (bei z = 20) bereits 180 Mill. Jahre
nach dem Beginn unseres Universum auf. Man kann davon ausgehen, daß sie sich in den
Fragmenten der abgekühlten, langsam rotierenden Gaswolken von anfänglich ca. 100 kpc
Ausdehnung bildeten bei einer mittleren Massendichte von ρ ≅ 200ρ c ( ρ c ist die kritische
Massendichte), was etwa 500 Protonen/m3 entspricht. Die baryonischen Gaswolken sind
eingebettet in Halos aus dunkler Materie, so daß auch die Protogalaxie wiederum von einem
Halo aus dunkler Materie umgeben ist, welches die Kondensation der Wolken ermöglichte
und wesentlich zu ihrer gravitativen Bindung beitrug. Der gesamte Entstehungsprozeß einer
stabilen galaktischen Struktur dürfte bis etwa 109 Jahre gedauert haben. Es gibt aber Hinweise
darauf, dass auch wenige 100·106 Jahre nach dem Urknall bereits voll ausgebildete Galaxien
vorhanden waren, d.h. dass es eine heftige Sternbildung in dieser Epoche gegeben haben
muss. Wir kommen weiter unten noch einmal auf die Rolle der Halos aus dunkler Materie
zurück.
Wie schon weiter oben beschrieben, lebten die ersten Sterne nur kurz und endeten nach
gewaltigen Explosionen als schwarze Löcher. Sie verstreuten dabei große Mengen schwerer
Elemente, die zum Teil als Staub (Russ und Silikate) im Submillimeter-Wellenlängen-Gebiet
sichtbar werden. Für diese Beobachtungen wird in der Atacama-Wüste in 5000 m Höhe ein
System von 66 12m-Teleskopen aufgestellt. Während diese erdgebundenen Teleskope die
wenigen atmosphärischen Fenster ausnutzen müssen, kann das Satellitenteleskop Herschel
mit 3,5 m Öffnung die Bereiche 157–212 µm und 240–625 µm voll erfassen.
167
Die nach SN-Explosionen entstandenen schwarzen Löcher sammeln sich im Zentrum junger
Galaxien an und vereinigten sich wahrscheinlich dort zu einem supermassiven schwarzen
Loch. Im innersten Bereich der Scheibe entsteht dann eine Akkretionsscheibe, aus welcher
ständig Materie in das zentrale schwarze Loch fließt. Dabei kann bis zu etwa 40% der
aufgeschluckten Masse in Energie umgewandelt werden. Ein Quasar hat sich gebildet mit
einer gewaltigen Ausstrahlung, welche die Eddington-Leuchtkraft erreicht. In diesem Fall
wird der Strahlungsdruck gleich dem Gravitationsdruck
⎛M
LEdd ≅ 3,2 ⋅ 10 4 ⎜⎜ BH
⎝ MO
⎞
⎛M
⎟⎟ LO = 1,2 ⋅ 10 38 ⎜⎜ BH
⎠
⎝ MO
⎞
⎟⎟ erg/s
⎠
(12.2)
und begrenzt gleichzeitig die Akkretionsrate. Die Eddingtonleuchtkraft hängt nur noch von
der Masse des schwarzen Lochs M BH ab. Die Leuchtkraft ist in Gl. 12.2 in Einheiten der
Sonnenleuchtkraft LO sowie in erg/s wie in der Astrophysik üblich angegeben (107 erg/s = 1
Watt). Die Beobachtungen haben ergeben, dass M BH proportional der Masse des zentralen
ellipsoidischen Teils der Galaxie M E ist
M BH = 10 −3 M E ,
(12.3)
was die Modelle einer Koevolution von Galaxien und zentralen schwarzen Löchern stützt.
Während der Aktivität werden auch große Mengen ionisierter Materie in den
intergalaktischen Raum geschleudert. Die Phase der Quasar-Aktivität nimmt dann ab, wenn
die Akkretion von Materie in der Umgebung des schwarzen Lochs nachläßt. Man sagt auch :
„das schwarze Loch hungert aus“. Das führt dazu, dass es im frühen Universum bei z > 1 viel
mehr Quasare gegeben hat (und mehr Sternbildung) als in späteren Zeiten.
Im allgemeinen hatten Galaxien nach ihrer Entstehung noch nicht ihre endgültigen Form
angenommen. Es gab viele unregelmäßige Gebilde, die viel kleiner waren als heutige große
Galaxien. Benachbarte Galaxien übten Gezeitenkräfte auf einander aus und vereinigten sich
zu größeren Gebilden. Um die Morphologie der Galaxien zu verstehen ist deshalb auch die
Kenntnis ihrer Umgebung wichtig. Das Universum war zur Zeit der Reionisation um einen
Faktor 103 bis 104 dichter heute. Die Halos aus dunkler Materie, welche die Galaxien
umgeben, spielten bei der Galaxienentstehung eine ganz wichtige Rolle. Die noch
unbekannten Teilchen der dunklen Materie wechselwirken nur durch die Gravitation
miteinander. Deshalb lässt sich die Entstehung der Halos sehr gut mit N-Teilchen
Simulationen untersuchen, woraus sich analytisch ein universelles Profil für ein CDM-Halo in
folgender Form angeben lässt. Es ist für r > rS
ρ(r ) =
4ρ S
(r / rS )(1 + r / rS )2
(12.4)
Hier ist rs der (Skalen-)Radius des Halos und ρ S die Dichte an dieser Stelle. Für die Masse
war bereits eine Näherungsformel angegeben worden (s. Gl. 11.35). Ein weiteres wichtiges
Ergebnis der Simulationen ist der Verlauf der Halobildung, welche mit einer schnellen
Kollapsphase beginnt, in welcher das Gravitationspotential des Halos entsteht. Daran schließt
sich eine zweite Phase mit einer langsamen Akkretion von Materie, welche in den zentralen
Bereich des Halos sinkt, ohne einen wesentlichen Einfluß auf das Potential zu nehmen. Eine
wichtige Größe für die Massenverteilung ist der Konzentrationsparameter c
168
c ≡ rH / rS
(12.5)
Während rH die Ausdehnung des Halos angibt, beschreibt rS die Größe des zentralen Bereichs,
in welchem sich in der Phase langsamer Akkretion die Galaxie bildet. Während sich aus den
Simulationen c = 11 ergibt, legen die Beobachtungen c ≈ 4 nahe. Die Masse der galaktischen
Scheibe ist ein Bruchteil der Halomasse. Man wird zunächst annehmen, daß dieser Bruch
M d / M H eine Konstante ist, etwa von der Größe Ω b / Ω M ≅ 0,17. Die abgeschätzte Masse
in Galaxien ist aber viel kleiner, was bedeuten kann, daß die fehlende baryonische Materie in
Form von neutralem oder ionisiertem Gas vorliegt, in welchem keine oder noch keine Sterne
gebildet wurden. Diese Vorstellung wird durch die Ergebnisse von WMAP bestätigt, die eine
frühe Reionisation der Gaswolken nahelegen. Für die Abhängigkeit der Scheibenmasse von
der Rotverschiebung gilt deshalb Gl. 11.35, was wir auch
M d ∝ H 0 / H (z )
(12.6)
schreiben können, d.h. bei z = 2 ist z.B. die Masse der galaktischen Scheibe M d nur noch ein
Drittel der Masse, welche unter sonst gleichen Bedingungen bei einer heutigen Entstehung
auftreten würde.
Es muß auch erwähnt werden, daß Simulationen, welche eine Mischung aus dunkler Materie
und baryonischem Gas berücksichtigen, bei entsprechende Vorgabe des Drehimpulses zwar
scheibenförmige Spiralstrukturen ergeben, daß aber der Durchmesser der Scheibe kleiner ist
als beobachtet. Aus den Simulationen entnimmt man, dass gasförmige Scheiben instabil
werden, wenn
εc =
υ max
< 0,9
GM d / Rd
(12.7)
wird, wobei Rd der Radius der galaktischen Scheibe ist. Für stellare Scheiben gilt ε c < 1,1 .
12.3. Gaswolken und Gasausflüsse.
Gibt es eine Möglichkeit, Gaswolken, die zu Protogalaxien werden können, vor der
Entstehung von Sternen zu beobachten? Ja durchaus, wenn man in Quasarspektren die
scharfen Absorptionslinien in der langwelligen Flanke der Lyα-Emission untersucht. Jede
Linie gehört zu einer bestimmten Rotverschiebung zi (Lyα-Forest), welche in die mitbewegte
Koordinate ri umgerechnet werden kann. Auf diese Weise ergibt sich das Bild, hintereinander
liegender Wolken, getrennt durch Hohlräume oder durch Bereiche voll ionisierter Plasmen.
Fig.12.5. Das Licht des Quasars passiert auf dem Weg zum Beobachter verschiedene Wolken,
die zu 75% aus neutralen Wasserstoff bestehen. Lyman-Alpha-Licht wird bei λ =1216⋅(zi+1)
169
absorbiert und bringt dabei den atomaren Wasserstoff aus dem Grundzustand n = 1 in den
angeregten Zustand n = 2.
Die Häufigkeit der Wolken nimmt mit fallendem z ab. Wenn in einer Wolke Sterne entstehen,
wird offensichtlich nur ein kleiner Teil der baryonischen Masse für den Aufbau von Sternen
verbraucht.
Fig. 12.6. Bild einer Computer Simulation von Lyα-Wolken bei z = 3. Die Kantenlänge des
Volumens beträgt 20⋅106 Lj (oder ca. 7 Mpc).
Durch SN-Explosionen wird ebenfalls heiße, vollständig ionisierte Materie in das interstellare
und das intergalaktische Medium geschleudert. Aber auch durch die extrem starke UVStrahlung der ersten Sterne wird neutraler Wasserstoff reionisiert. Eine plötzlich einsetzende
Sternentstehung (star burst), entweder in jungen Galaxien oder in wechselwirkenden
Systemen, setzt eine Menge Gas frei, das meist als heißes Plasma in den intergalaktischen
Raum hinaus geschleudert wird. Abschätzungen aus Beobachtungen ergeben eine
Massenverlustrate, welche bis zu 5 mal so groß ist wie die Sternentstehungsrate. Solche
Massenverluste machen das Potential im Zentrum flacher, was dazu führt, daß sich das Halo
der dunklen Materie ausdehnt.
Unsere eigene Galaxie hat eine K-Helligkeit (spektrales Fenster im nahen Infraroten bei 2,2
µm) von –24,02 was einer Leuchtkraft von 8,3⋅1010 LO entspricht. Nimmt man an, daß das
Verhältnis von leuchtender Masse zur Masse der Scheibe Md gleich eins ist, kommt man auf
8,3⋅1010 MO. Das Massenverhältnis von leuchtendem zentralen Ellipsoid ( engl. „bulge“) ME
zur Scheibe ist M E / M d ≈ 1 / 5 . Daraus ergibt sich ein Verhältnis leuchtenden Masse zur
baryonischen Gesamtmasse von etwa 3,4 %. Aus den kosmologischen Parametern Ωb/ΩM
würde sich 16 % ergeben. Andererseits ist die Masse der leuchtenden Materie nur 1/6 der
Masse des heißen intergalaktischen Plasmas. Ob die oben erwähnten Prozesse allein schon
ausreichen, um die großen Mengen heißer Materie in den Galaxienhaufenzu erklären, bleibt
noch zu prüfen.
170
12.4. Galaxien bei großen Rotverschiebungen und die Kartierung der Dunklen Materie.
In den letzten Jahren wurde das Hubble-Teleskop wie auch terrestrische Großteleskope dazu
benutzt, Galaxien bei z > 6 aufzufinden. Dazu wird meist ein Ausschließungsverfahren
benutzt, bei welchen durch geeignete Filter im nahen Infraroten die Lyman-Kante aufgesucht
wird (Lyman-break Galaxies). Aus der Polarisation der kosmischen Hintergrundstrahlung hat
man Anhaltspunkte dafür, dass Reionisation durch Sternbildung bereits sehr früh, etwa 200
Mill. Jahre nach dem Beginn (15 < z < 20) eingesetzt hat. Die Schwierigkeit für ein sicheres
Auffinden liegt vor allem in dem geringen Signal zu Rauschverhältnis, das bei terrestrischen
Teleskopen durch Sauerstoff-Emission der Erdatmosphäre im roten Spektralbereich weiter
verschlechtert wird, ein Problem, das bei dem „Hubble Space Telescope“ (HST) und bei dem
Satelliten gestützten Infrarotteleskop „Spitzer“ nicht auftritt. „Spitzer“ hat eine Öffnung von
85 cm und kann Objekte bei Wellenlängen von 3,6 – 160 µm beobachten. Gegenwärtig ist
Herschel mit 3,5 m Öffnung für das FIR im Orbit. In einer Gemeinschaftsarbeit von
Wissenschaftlern der ESO und amerikanischen Kollegen wurden die bekannten GalaxienCluster Abell 1835 und AC 114 als Gravitationslinsen benutzt, um das Licht weit dahinter
liegender Galaxien zu fokussieren und damit zu verstärken. Die Aufnahmen wurden mit dem
HST in den Bereichen des nahen Infraroten SZ (1,06 µm), J (1,25 µm), H (1,65 µm) und K
(2,2 µm) gemacht. Es wurden schließlich 13 Objekte ausgesucht, welche alle Kriterien
passierten, insbesondere auch das Verhalten des Farbindices in der Auftragung J – H gegen H
– K.. Als Rotverschiebungen werden Werte von z = 7,38 bis 8,54 angegeben. Im gleichen
Projekt wurden die Effekte der Gravitationslinsen dazu benutzt, eine Kartierung der Dunklen
Materie zu erstellen. Um eine 3d-Kartierung zu erhalten, wurde die Massenbelegung von
Flächen konstanter Rotverschiebung rekonstruiert. Meist fallen, wie erwartet, die
Dichtemaxima der Dunklen Materie mit entsprechenden leuchtender Materie zusammen.
Allerdings ist das nicht immer der Fall, wobei aber die Autoren einräumen, dass die
Ergebnisse noch als vorläufig zu betrachten sind. Weitere spektrale Untersuchungen mit den
Very Large Telescopes (VLT) der ESO sollen folgen. Ähnliche Suchprojekte liefen unter der
Bezeichnung „Hubble Ultra Deep Field“ (UDF).
12.5. Morphologische Entwicklungen.
Wie schon oben erwähnt, zeigen Simulationsrechnungen, dass auf eine schnelle KollapsPhase eine langsame Akkretionsphase folgt. Man wird die Entstehung des ellipsoidförmigen
zentralen Bereichs („bulge“) einer Scheibengalaxie in die schnelle Kollapsphase verlegen,
während die Entstehung der galaktischen Scheibe eher der langsamen und lang anhaltenden
Akkretionsphase zu zuordnen ist. Auch die Vereinigung von 2 Galaxien wurde in
Simulationen modelliert. Dabei zeigte sich, dass sich zuerst die Halos der dunklen Materie
vereinigen, während die Galaxien ihre orbitalen Energien durch dynamische Reibung
verlieren und dabei in das Zentrum des Halos sinken, um sich zu vereinigen. Die Morphologie
der Spiral/Scheibengalaxien scheint, glaubt man den Simulationen, ebenfalls stark von der
Verteilung der dunklen Halomaterie abzuhängen. Wenn die Galaxie ein ausgedehntes Halo
aus dunkler Materie besitzt, dann wird sein Einfluss auf die Morphologie der Galaxie eher
gering sein, so dass sich ausgeprägte Spiralstrukturen ausbilden können.
Edwin Hubble, der Klassiker der Galaxienbeobachtung, hat in den 30er Jahren eine
morphologische Klassifikation vorgeschlagen, die im Wesentlichen noch heute in Gebrauch
171
ist. Über 90% der Galaxien des lokalen Superhaufens passen in dieses Schema (s. Fig. 12.7).
Es gibt allerdings eine große Zahl von Zwerggalaxien in der lokalen Gruppe, die zu Hubbles
Zeiten noch nicht bekannt waren
Fig. 12.7. Hubbles morphologische Klassifikation der Galaxien in schematischer
Darstellung, bekannt als „Stimmgabeldiagramm“.
und deren Zahl die der „normalen“ Galaxien bei weitem übersteigt. Auch den bekannten
Kugelhaufen M 13 im Herkules klassifiziert man heute als Zwerggalaxie. Allerdings trägt die
Masse der Zwerge nur wenig zur Masse aller Galaxien bei.
Wenn man nach einer Entwicklung galaktischer Morphologien sucht, muss man ähnliche
Strukturen bei verschiedenem z miteinander vergleichen und wenn möglich, durch
Auszählung feststellen, ob bestimmte Formen bei gewissen Rotverschiebungen z besonders
häufig vorkommen. Wenn sich bei großem z die optische Auflösung verschlechtert,
erscheinen einerseits die Strukturen der Galaxien verwaschener, andererseits verschiebt sich
das Spektrum vom UV ins sichtbare, vom sichtbaren in das infrarote Spektralgebiet, was
bedeuten kann, dass identische Galaxientypen ein verschiedenes Aussehen bekommen. Dabei
können Veränderungen in der Struktur vorgetäuscht werden. Es ist deshalb ratsam, Galaxien
bei z > 0,8 in Spektralgebieten bei Laborwellenlängen von λ > 1µm aufzunehmen (d.h.
Filterbereiche J, K und L). Ergebnisse kritischer Auswertung für z ≤ 1,3, was Galaxien bis zu
Größenordnungen 25 oder 26 einschließt, sind im Überblick in Fig. 12.8 zu sehen. Man
beobachtet bei den Spiralgalaxien mit steigendem z einen graduellen Verlust von Struktur und
Organisation. Balkenspiralen werden bei z > 0,5 selten, die Fragmentierung nimmt zu.
Letzteres ist auch bei den Unregelmäßigen rechts auffällig, wobei allerdings anzumerken ist,
dass diese am wenigsten verstanden sind. Die elliptischen Galaxien, die zu den ältesten
galaktischen Strukturen gerechnet werden, (zu sehen links in Fig. 12.8) behalten ihre Struktur
unverändert bei. Allerdings nimmt mit z die Intensität im Blauen besonders im Zentrum zu,
was auf vermehrte Sternbildung in frühen Zeiten hinweist. 30% aller Objekte die in Hubble
Deep Field Aufnahmen bei großem z erfasst werden, besitzen eine außergewöhnliche Gestalt
(„peculiar“) bzw. befinden sich in einem Vereinigungsprozeß, der stets mit starker
Sternbildung einhergeht (star burst). Man beachte dabei, daß der Abstand zwischen den
Galaxien bei z =1 auf die Hälfte, bei z = 3 auf ein Drittel abgenommen hat. Neben den
Elliptischen (Typ E) zeigen auch die Spiralen Sab wenig Änderung im Bereich 0 < z < 1 .
172
Dagegen nimmt der Anteil der Sb-Spiralen um einen Faktor 2 ab, der Anteil an Irregulären
(Ir) und der Vereinigungen bis z = 0,95 um etwa 30% zu. Untersuchungen bei z > 1 müssen
im Infraroten vorgenommen werden, wobei zu bemerken ist, dass Galaxien, welche im
Sichtbaren als irregular (Ir) eingestuft werden, auch im IR irregulär bleiben. Meist sind sie
Komponenten eines Vereinigungsprozesses. Im Großen und Ganzen scheint sich die „bottomup“ Entwicklung des „Cold Dark Matter“-Modells zu bestätigen.
In jüngster Zeit wurden Projekte begonnen, in welchen die Morphologie von Galaxien als
Funktion ihrer lokalen Umgebung untersucht wird. Ein Projekt, das unter der Bezeichnung
COSMOS läuft und jeweils eine Fläche von 2 mal 2 Winkelgrad registriert, benutzt dazu das
HST. Eine andere Untersuchung läuft an einem von ESOs VLT. Es wurden dazu mit VIMOS
(Visible Imager and Multi-Object Spectrograph) 6500 Galaxien in veschiedenen Umgebungen
und Entwicklungsphasen untersucht. Im Ergebnis findet man einen starken Einfluss der
Umgebung auf die Morphologie der Galaxien. So wird die Sternbildung in Galaxien, die
Mitglieder eines Haufens sind, schneller unterdrückt als wenn sie isoliert vorkommen. Auch
erschöpfen leuchtkräftige Galaxien ihr Material zur Sternbildung eher als schwächere
Exemplare.Die leuchtkräftigsten Galaxien bilden schon nach 2·109 Jahren (z = 4,0) keine
Sterne mehr, während Galaxien mittlerer Leuchtkraft mit der Sternbildung weitere 11·109
Jahre fortfahren. Nach diesen Untersuchungen scheint der Anteil der Vereinigungen (Merger)
an der Sternbildung eher moderat zu sein.
Zum Schluss sei noch einmal darauf hingewiesen, dass das hier skizzierte Gebiet sich in einer
raschen Entwicklung befindet. Die Ergebnisse sind erst in Umrissen verfügbar, z.T. noch
unverstanden, manchmal auch widersprüchlich, besonders wenn es sich um den Vergleich
von Simulationen mit Beobachtungen handelt. Die Situation bessert sich rasch. Einerseits
gelingt es, die kosmologischen Parameter immer genauer zu bestimmen. Andererseits rückt
auch die Beobachtung mit verbesserten Methoden zu immer größeren Rotverschiebungen z
vor.
12.5. Zusammenfassung.
Baryonische Materie reichert sich in Wolken dunkler Materie an, die sich im Laufe der
Expansionzu größeren Einheiten vereinigten. Aus der Polarisation der Hintergrundstrahlung
kann man schließen, dass die ersten Sterne zwischen 15 < z < 20 aufleuchteten. Mit ihnen
setzte eine teilweise Reionisation des baryonischen Gases ein. Neutrale Gaswolken, welche
noch keine Sterne gebildet haben, können in den Spektren von Quasaren als so genannter
Lyman-α-Wald nachgewiesen werden. Nur in seltenen Fällen bestehen sie noch aus
primordialer Materie. Meist haben sie bereits geringe Mengen schwerer Elemente
aufgenommen. Die Generation der ersten Sterne (Population III) konnte bisher nicht direkt
beobachtet werden. Modellrechnungen legen nahe, dass sie Massen von einigen hundert
Sonnenmassen und damit eine relativ kurze Lebensdauer besaßen. Sie trugen zur
Anreicherung des baryonischen Gases mit schwereren Elementen bei. In Durchmusterungen
begrenzter Himmelbereiche konnten nach extrem langen Belichtungszeiten Galaxien bis etwa
z = 8 nachgewiesen werden. Die die Strahlung von Galaxien mit heftiger Sternbildung (100
Sonnenmassen/Jahr) durch absorbierend Staubschichten verdeckt werden, sind weitere
Beobachtungen vor allem im fernen IR erfolgreich (ALMA-Projekt und Herschel-Teleskop)
Was die Mophologie betrifft, so nimmt die Zahl der regelmäßig aufgebauten Galaxien,
welche sich nach dem Hubbleschen Diagramm klassifizieren lassen, mit zunehmender
173
Fig. 12.8. Galaxien aufgenommen mit dem HST bei verschiedenen Rotverschiebungen z. Links
elliptische Galaxien, Mitte Spiralen, rechts die Kolumne der Unregelmäßigen. Die Bilder
wurden aus Filteraufnahmen im Blauen, Gelben und nahen Infraroten gewonnen.
Rotverschiebung z nimmt von unten nach oben zu bei etwa gleichem z in der Horizontalen.
Nach H. Ferguson, M. Dickinson, R. Williams, DTRcI and NASA
174
Fig. 12.9. NGC 4676 als Beispiel zweier Galaxien in Vereinigung. Nach N-Körper-Simulationen
vereinigen sich erst die Halos der dunklen Materie. Dabei geht die orbitale Energie durch
Reibung verloren. Die langausgezogenen leuchtenden Scheife zeigen die Ausdehnung der Halos
an. Bild HST NASA.
12.10. Verteilung sichtbarer (baryonischer ) Materie links und Dunkler Materie rechts.
Die Untersuchungen dazu wurden mit dem HAST gemacht unter Verwendung von
Gravitationslinseneffekten.
175
Fig. 12.11. Galaxienvereinigungen (hier „galactic cannibalism“ genannt) im Galaxienhaufen
Abell 3827 im Röntgengebiet beobachtet.
Rotverschiebung z
< 0,3
≈ 0,5
> 0,6
Morphol. Entwicklung
look back time in 109 Jahre
<4
Große Spiralen. Hubbles
Klassif. trifft voll zu
Balkenspiralen selten.
≈ 5,5
Spiralarme nicht entwickelt.
Hubbles „Stimmgabel“Form verschwindet
>6
Bruchteil der
Vereinigungen steigt rapide
30% atypische Formen
Tabelle 13.1. Zusammenfassung der mit zunehmender Rotverschiebung z beobachteten
morphologischen Änderungen der Galaxien. Nach R.G. Abraham und Sidney van den Bergh
s.u.
z 0,5 1,0 1,5 2,0 2,5 3,0 3,5 4,0 5,0 6,0 6,5 7,0
t
7,5
10
15
20
8,3 5,6 4,1 3,2 2,5 2,1 1,7 1,5 1,1 0,9 0,8 0,74 0,67 0,46 0,21 0,17
Tabelle 13.2. Zuordnung von Rotverschiebungen z zur Zeit t, die seit dem Beginn des Kosmos
vergangen ist ( Ω M = 0,3; Ω Λ = 0,7 ; t 0 = 13,7 Gy ). t ist angegeben in Gy (1Gy = 109 Jahre)
Rotverschiebung z ab zugunsten unregelmäßiger Formen. Sternentwicklung nimmt mit
steigendem z zu; dazu tragen Vereinigungen von Galaxien bei. In den meisten grioßen
Galaxien konnten zentrale schwarze Löcher nachgewiesen werden. Solange in unmittelbarer
Nähe des schwarzen Lochs Materie vorhanden ist, wird bei der Akkretion ein Teil davon in
Strahlung verwandelt. Die Galaxie befindet sich dann in der Quasar-Phase Diese Phase ist
beendet, wenn keine Materie im Zentrum mehr vorhanden ist Die Galaxie erscheint dann
ohne ein aktives galaktisches Zentrum (wie z.B. unsere eigene Galaxie oder M31).
176
Offensichtlich wird dabei auch Gas und Staub aus der Galaxie entfernt, so dass auch die
Sternbildung zum Erliegen kommt (z < 1,5).
12.6. Literatur
A. Heger, S.E. Woosley, I. Baraffe and T. Abel: Evolution and Explosion of
Very Massiv Primordial Stars (2002), to appear in Proc. Lighthouses in the Universe, „ESO
Astrophysics Symposia“, Springer Verl.
A. Heeger and S.E. Woosley: The Beginning of Stellar Nucleosynthesis (2002),
to appear in Proceedings of the 11th Workshop on Nuclear Astrophysics, Ringberg Castle, eds.
E. Müller and W. Hillebrandt, MPA Proceedings Garching.
C.L. Fryer, S.E. Woosley, A. Heger: Pair Instability Supernovae, Gravity Waves, and Gamma
Ray Transients. ApJ 541, (2000) 1033, astro-ph/0007176.
S.W. Campbell: Nucleosynthesis in Early Stars, astro-ph/0305009
T.C. Beers: Telling the tale of the first stars. Nature, 422 (2003) 825. astro-ph/0304468
R.G. Abraham and Sidney van den Bergh: The Mophological Evolution of Galaxies, astroph/0109358
A. Bunker et al. : Stellar Population and Galaxy Morphology at High
Redshift, astro-ph/0004348
S. Mao, H.J. Mo and S.D.M. Wight: The evolution of galactic discs. Mon. Not. R.
Astron.Soc. 297, (1998) L71
H.J. Mo and S. Mao: Galaxy formation in pre-processed dark halos, Mon. Not. R. Astron.Soc.
124, (2003) 18
J.R. Primack, Sommerville: Semianalytic Modeling of Galaxy Formation. MNRAS 320
(1999)1087
B. Alcock: The dark halo of the milky way. Science 287 (2000) 74
J.J. Dalcanton, D.N. Spergel and F.J. Summers : The Formation of Disk Galaxies. ApJ 482
(1997) 659
M.R. Corbin, W. Freundling, K.T. Korista : Iron Emission in z ≈ 6 QSOs and its Possible
Implication, in Neutron Stars in Supernova Remnants. ASP Conference Series, Vol 9999,
2002 P.O. Slane and B.M. Gaensler eds.
F.C. von den Bosch X. Yang and H.J. Mo: Linking Early and Late Type Galaxies to their
Dark Maetter Haloes. Mon Not. R. Astron. Soc. (2003) ??
astro-ph/0210495
177
ESO
Press
Release
34/03:
The
Colour
of
http://www.eso.org/outreach/press-rel/pr-2003/pr-34-03/html
the
Young
Universe.
M.J. West et al. Reconstructing galaxy histories from globular clusters. Nature Vol. 427, 1
January 2004, p. 31
M.D. Lehnert and M. Bremer : Luminous Lyman Break Galaxies at z > 5 and the Source of
Reionisation. http://xxx.uni-augsburg.de/abs/astro-ph/0212431
R.J. Bouwens et al. : Rapid evolution of the most luminous galaxies during the first 900
million years. Nature Vol 443 (14. Sept. 2006) p. 189
L. Tresse et al. : The cosmic star formation rate evolution from z = 5 to z = 0 from The
VIMOS VLT Deep Survey. . http://xxx.uni-augsburg.de/abs/astro-ph/0609005
R. Massey et al.: Dark matter maps reveal cosmic scaffolding. Nature Vol 45 (18. Jan. 2007)
p. 286
M. Fumagalli et al. Science 334, 1245 (2011)
A. Amblard: Submillimeter Galaxies…,Nature, Vol. 470, p.24. (2011)
J. Dunlope: Galaxy Connections. Natur vol. 459, p. 43 (2009)
12.7. Aufgaben
Wähle aus den folgenden Vorschlägen die Antwort aus, welche Dir korrekt erscheint und
begründe Deine Wahl in ein par Sätzen.
1) Dunkle Matere (DM) und Baryonische Materie (BM) entwickeln sich getrennt. Man
kann von der Verteilung der einen nicht auf die andere schließen.
2) Die Verteilung von DM und BM entwickelt sich so, dass maximale Dichte von DM
mit der von BM zusammen fällt.
3) Sternbildung ist an der intensiven UV-Strahlung junger Sterne zu erkennen. Das gilt
auch für „high z“ Galaxien, nur ist die UV-Strahlung hier rot-verschoben.
4) Im Gebiet der mm-Wellen und des FIR können Staubmassen und Sternbildung in
unserer Galaxie verfolgt werden. Für die extragalaktische Forschung dagegen haben
sie wenig Anwendung und nur eine geringe Bedeutung.
5) Große Galaxien bilden sich aus vielen Zwerggalaxien.
6) Große Galaxien werden schon bei großem z gebildet. Sie behalten ihre Form in der
weiteren Entwicklung.
7) Schwarze Löcher treten mit ganz unterschiedlichen Massen im Zentrum von Galaxien
auf. Dafür gibt es keine Regeln.
8) Die Masse zentraler schwarzer Löcher steht in einem festen Verhältnis zur Masse des
inneren ellipsoidischen Bereichs einer Galaxie.
178
13. Die Dunkle Materie.
13.1.Astronomische Massenbestimmungen.
Machen wir uns noch einmal klar: Nur 4,4% der Masse des Universums ist baryonische
Masse. 96% bestehen aus Materie- bzw. Energieformen, die uns noch völlig unbekannt sind.
Diese Feststellung ist so überraschend, dass von Seiten der Beobachtung alles getan werden
muss, das Ergebnis Ω B = 0,04 4, Ω M = 0,27 , Ω Λ = 0,73 abzusichern. Das kann vor allem
durch möglichst viele verschiedene, völlig unabhängige Messverfahren geschehen. Wir hatten
bereits in den voran gegangenen Kapiteln gesehen, dass Messungen der Gravitation etwa 7
mal soviel dunkle wie baryonische Materie ergeben. Von der baryonischen Materie selbst
wieder ist nur etwa 1/6 leuchtende Materie im Sichtbaren in Form von Sternen oder Gas. Wir
haben oben schon gesehen, dass ein großer Teil der baryonischen Materie in Form eines
heißen, intergalakischen Plasmas geringer Dichte vorliegt, das vor allem durch SupernovaAusbrüche, aktive galaktische Kerne oder bei Vereinigung von Galaxien in den
intergalaktischen Raum geschleudert wird und nur im Röntgengebiet beobachtet werden kann.
Durch die Abstrahlung kühlt das Plasma langsam ab und braucht dazu Zeiten, die wesentlich
größer als das Weltalter sind. Eine Obergrenze für die baryonische Materie erhält man aus der
Nucleosynthese der leichten Elemente. Es gehen nur ein die Dichte des Strahlungsfelds der
Hintergrundstrahlung, die recht genau bekannt ist, und die Anzahl der Neutrino-Flavors, die
heute allgemein mit 3 angegeben wird (das sind Elektronen-, Myonen- und Tau-Neutrinos).
Daraus ergibt sich die Anzahl der Baryonen pro Photon, aus der man wiederum den
baryonischen Beitrag Ωb = 0,044 erhält.
13.1.1. Viriale Masse.
Die Geschichte der „Dunklen Materie“ beginnt mit der Feststellung von Fritz Zwicky von
1933, dass die Geschwindigkeitsdispersion σ r2 in Galaxienhaufen so groß ist, dass die Masse
der leuchtende Materie allein keinen gebundenen Zustand ergeben würde. Die nach dem
Virialsatz ermittelte Masse ( − 2 E kin = E pot ) wäre dann bis zu 2 Zehnerpotenzen größer als
die leuchtende Masse. Diese Abschätzung kommt wie folgt zustande
2 E kin =
∑ m (υ
i
2
ir
+ υ i2ϑ + υ i2ϕ ) ≅ M 3υ ir2 = 3Mσ r
2
(13.1)
i
weiterhin ist
3 GM 2
5 R
Daraus ergibt sich folgende für die Praxis wichtige Beziehung
E pot = −
σ r2 =
1 GM
5 R
(13.2)
(13.3)
Hier bedeutet mi die Masse einer einzelnen Galaxie, M die Gesamtmasse des Haufens und R
sein Radius. Die Größe σ 2 wird Geschwindigkeits-Dispersion genannt. Neben der HubbleFluchtgeschwindigkeit besitzen alle Galaxien wie schon in Kap. 1 erwähnt, noch
Eigenbewegungen. Ihre Geschwindigkeit, oder genauer deren radiale Komponente, wird als
störender Effekt immer mit gemessen, wenn Rotverschiebungen bestimmt werden. Die
Eigenbewegungen (auch Pekuliarbewegungen genannt), zeigen Beschleunigungen in
179
Gravitationsfeldern an. Damit enthalten sie wichtige Informationen über Ω M im
Allgemeinen und über die Massenverteilung in Galaxienhaufen im Speziellen. Zur
Bestimmung der Pekuliarbewegungen werden die Daten aus Galaxienkatalogen, welche die
Rotverschiebungen enthalten,zu Grunde gelegt. Nehmen wir an, dass Virialisierung
stattgefunden hat, dann ist mit Gl. (13.3) eine Abschätzung der gesamten Masse möglich.
Zwicky untersuchte auf diese Weise den Coma Cluster und kam als erter auf das „missing
mass problem“. Man findet für die Gesamtmasse nach (13.3)
2
⎛
⎞ RC
σr
⎟⎟
M = 1,5 ⋅ 10 M O ⎜⎜
⎝ 1000 km / s ⎠ 1 Mpc
15
(13.4)
Hier bedeutet MO die Sonnenmasse und RG einen mittleren Abstand zwischen den Galaxien
im Cluster. Vergleicht man die Gesamtmasse mit der Leuchtkraft, so erhält man
näherungsweise (Näheres in Peter Schneider: „Extragalactic Astronomy and Cosmology“)
M
M
(13.5)
≈ 300h O
Ltot
LO
(in Sonnen-Einheiten).
13.1.2.Rotationskurven der Spiralgalaxien.
Auf kleinerer Skala d.h.aus Rotationskurven einzelner Galaxien erhält man ein auch eine
Aussage über die Verteilung der DM (s. Fig.13.1).
Fig. 13.1. Rotationskurve der Galaxie NGC 3189. Obere Kurve verbindet Meßpunkte
(Geschwindigkeiten der Sterne als Funktion des Abstands vom Zentrum der Galaxie). Mittlere
Kurve (disk) gibt den erwarteten Verlauf wieder, wenn nur die Masse der Scheibe beitragen
würde. Untere Kurve ist der ermittelte Beitrag des Halos. Aus J. Binney and S. Tremaine ,
Galactic Dynamics. Princeton University Press 1987
Die äußeren Sterne in den Armen der Spiralgalaxien umlaufen die innere Masse Mr der
Galaxie praktisch auf Kreisbahnen, wobei das Quadrat der Geschwindigkeit proportional zum
Gravitationspotential ist,
υ 2 (r ) =
GM r
r
180
(13.6)
wobei M r die innerhalb des Radius r befindliche Masse darstellt. Mit lichtstarken Teleskopen
werden die Geschwindigkeiten von weit außen liegenden Sternen gemessen (s. Fig. 13.1).
Fig. 13.2. Rotationskurven von Spiralgalaxien. G’emessen wurde die scharfe CO-Linie in den
Wolken molekularer Gase innerhaln der äußeren Spiralarme. Credit: Rotation Curves of Spiral
Galaxies, Y.Sofue & V.Rubin 2001, ARAA 39, 137-174. siehe : www.ioa.s.u-tokyo.ac.jp/~sofue/hrot.htm
Aber nicht nur durch Dopplerverschiebungen von Sternspektren lassen sich RotationsGeschwindigkeiten messen. In Wolken kalter molekularer Gase (z.B . H2 und CO bei 10 K)
lassen sich die scharfen CO-Emissionslinien bei 2,6 und 1,3 mm relativ einfach messen. Auf
diese Weise wurden Rotationskurven für eine ganze Reihe von Spiralgalaxien abgeleitet (s.
Fig. 13.2). Man würde nun erwarten, dass die Geschwindigkeit nach außen abnimmt, weil
der Abstand zur inneren Masse immer mehr zunimmt. Das ist aber, wie man sieht, nicht der
Fall. Was man stattdessen findet, ist eine nahezu konstante Geschwindigkeit. Daraus lässt
sich die Dichteverteilung eines Halos aus dunkler, nicht-baryonischer Materie ableiten (s. Fig.
13.1).
13.1.3. Simulationen
Etwas mehr Informationen lassen sich aus Simulationen von N gravitierenden Punktmassen
gewinnen. Danach werden für die Dichteverteilung im Halo verschiedene Funktionen
−α
angegeben, die alle wie ρ ∝ r
( α > 1 ) abklingen. Uneinig ist man sich noch über den
Verlauf der Dichte im zentralen Teil dem „cusp“. Die Simulationen zeigen auch, dass
komplizierte Wechselwirkungen zwischen den entstehenden Strukturen der Spiralgalaxien
und den Halostrukturen auftreten. Auch Drehimpuls wird dabei ausgetauscht. Eine
Abschätzung der Halomasse ist mit folgender einfacher Formel möglich
υ3circ
MH =
10GH ( z )
(13.7)
Hier ist υ circ die vom Radius unabhängige Kreisgeschwindigkeit (in Fig. 13.1 ist υcirc ≅ 150
km/s), H ( z ) ist die Hubblefunktion zur Epoche z
181
[
H ( z ) = H 0 Ω Λ + Ω M (1 + z )
3
]
1
2
(13.8)
Eine analytische Form für die Dichte des Halos aus Dunkler Materie ρ( r ) nach Navarro,
Frank und White wurde bereits in Gl. 12.4 angegeben und ist in Fig. 13.3. graphisch
wiedergegeben.
13.3. Darstellung der Funktion der Dichte eines Halos aus Dunkler Materie durch
ρ (r ) =
4ρ S
(r / rS )(1 + r / rS )2
mit ρ S = 1 und r / rS = x .
Kreuzkorrelationen von Intensitäten der CMB und der Intensität der RöntgenHintergrundstrahlung führen dazu, inelastische Streuungen der CMB-Photonen an den heißen
Elektronen von Galaxien-Huafen zu detektieren (SZ-Effekt). Ausserdem verlieren die CMBPhotonen im Schwerefeld großräumiger Materiekonzentrationen Energie durch den
sogenannten Sachs-Wolfe-Effekt der erst nach der Rekombination entsteht, wenn sich bereits
erste Dichtekontraste gebildet haben.
Die Möglichkeit eines kosmischen Metermasses bieten die „Baryon Acoustic Oszillation“
(BAO). Es sind die Spuren der akustischen Schwingungen, die zur Zeit der Rekombination
den Horizont errichten, seitdem erstarrt sind und sich in den Dichtekorrelationen, die aus den
Daten von SDSS und anderen Katalogen gebildet werden. Fig. 13.4 zeigt die Ergebnisse. Die
Winkelausdehnug Δϑ entspricht der Wellenlänge hängt von z ab. Über die „angular distance
DA schließt man auf H0 und H(z), was wiederum dunkle Energie und Massendichte enthält.
Schließlich konnte WMAP auch den Beitrag leichter Neutrinos, welche gern als „Hot Dark
2
Matter“ beigemischt werden, auf Ω v h < 0,0076 begrenzen. Außerdem wurde die Bildung
der ersten Sterne auf etwa 200 ⋅ 10 Jahre vorverlegt, was auch den Beginn der Reionisation
betrifft, die einen verzögernden Einfluss auf die weitere Bildung (oder Verzögerung) von
Strukturen nimmt.
6
182
Fig. 13.4. Baryon Acoustic Oscillations im Dichte.Korrelationsspektrum der SDSS-Galaxien.
Zum großen Erfolg der Λ CDM-Kosmologie gehört es, dass gezeigt wurde, wie in
hierarchischer Strukturbildung sich große Systeme aus kleinen gebildet haben. Kleine
Galaxien vereinigen sich und formen große Galaxien. Aber die Größe ist begrenzt, denn das
Gas in größeren Strukturen würde zur Abkühlung zu lange brauchen, um noch größere
Galaxien zu bilden. Deshalb treten größere Strukturen nur als Cluster und Supercluster auf.
Diese wieder haben sich aus Galaxien und Galaxienhaufen aufbauen können. Heute wissen
wir, dass es in erster Linie die Halos aus dunkler Materie sind, welchen wir die im Laufe der
Zeit zunehmende Hierarchisierung, d.h. die Vereinigungen zu immer größeren Einheiten
verdanken.
13.2. Gravitationslinsen-Effekte. „Weak Lensing“.
Gravitationslinsen-Effekte zeigen vor allem DM an und im Detail auch die Massenverteilung
großer Galaxienhaufen, die für entferntere Galaxien und Quasare als Linsen wirken. Man
unterscheidet normale Linseneffekte, d.h. Ablenkungen im Bereich von Bogensekunden, und
Daneben kommt den
Weitwinkelaufspaltungen ( Δθ ≥ 4" ), wie z.B. Einsteinringe.
183
schwachen Linseneffekten (Weak Lensing, s. unten) zur Ausmessung ausgedehnter
Strukturen neuerdings eine große Bedeutung zu, vorausgesetzt es lassen sich in einem relativ
großen Feld möglichst viele Galaxien beobachten, was nur mit dem Hubbleteleskop und
terrestrischen Teleskopen ab 3,5 m Öffnung möglich ist.
Wegen der Wichtigkeit des „Weak Lensing“ widmen wir der Methode hier einen eigenen
Abschnitt. Man geht davon aus, dass die Abstände der Galaxien eines Haufens untereinander
klein sind im Vergleich zum Abstand Erde-Galaxienhaufen und dass die ablenkende Masse
(oder Linse) praktisch in einer Ebene senkrecht zur Beobachtungsrichtung liegt. Jede
beobachtete Galaxie des Haufens ist nun um einen Winkel α in der Bildebene gegenüber
einem fiktiven Bild ohne „weak lensing“ verschoben. Ein Lichtstrahls, der im Abstand ξ an
einer Punktmasse M(ξ) vorbei läuft, wird um folgenden Winkel abgelenkt
~ (ξ) = 4GM (ξ) 1
α
c2
ξ
(13.9)
~ , wenn der Abstand ξ = R gleich dem Sonnenradius
Bei der Sonne beträgt die Ablenkung α
Ο
ist, 1,74 Bogensekunden. Wenn ξ sehr klein ist gegenüber dem
Fig. 13.5. Ablenkung des Lichts der Quelle S durch die Linse L. Der Beobachter sieht
bei zwei Teilstrahlen auch zwei Bilder S1 und S2 der Quelle S.
184
Fig. 13.6. Der rechte Teil der Fig. 13.6. ist in der Näherung für dünne Linsen durch
gerade Linien und Dreiecke ersetzt worden. In der Bildebene η liegt die Quelle S bei
dem Winkel β. Durch „Weak Lensing“ (Linsenebene bei ξ) ist sie aber verschoben bei S1
unter dem Winkel θ = β + α zu sehen.
Abstand von Quelle-Beobachter DS und Linse-Beobachter DL, kann man aus Fig. 13.6 für die
Bildebene η entnehmen, dass folgende Linsen-Gleichung näherungsweise gilt (sin-Funktionen
wurden durch die Winkel ersetzt):
~D
θDS = βDS + α
LS
(13.10)
Tatsächlich liegt ξ in Galaxienhaufen bei einigen 100 kpc, der Abstand DS dagegen bei Gpc.
Wir definieren den reduzierten Ablenkungswinkel
~ ⋅ DLS
α=α
DS
(13.11)
und teilen 13.5 durch DS . Wir erhalten so die (2-dimensionale) Linsengleichung
r r r r
β = θ − α(θ)
(13.12)
die wir gleich vektoriel geschrieben haben, denn die Fig. 13.4 kann um die Achse OL um
einen beliebigen Winkel gedreht werden. Den Zusammenhang mit der Masse bekommen wir,
wenn wir 13.4 in 13.6 einsetzen mit ξ = DL ⋅ θ . Wir erhalten
r
DLS 4GM θ
r
α(θ) =
DS D L c 2 θ 2
185
(13.13)
Fig.13.7. Gravitationslinse. Links HST-Aufnahme im nahen IR (NICMOS). Dazu sind auch
Konturen von Radio-‚Intensitäten eingetragen. Rechts noch einmal HAST-Bild (NICMOS)
farbig.
wobei der Ablenkungswinkel so definiert ist, dass er immer zur Punktmasse hin gerichtet ist.
Für den Fall dass Quelle und Linse exakt hintereinander liegen, d.h. β = 0 ist, liegen alle
Bildpunkte auf einem Kreis mit dem Radius θ, dem Einstein-Kreis
θ=
4GM DLS
c 2 D L DS
(13.14)
Für eine Quelle mit der Rotverschiebung zS = 2,0 und einer Linse der Masse von 1012 MО bei
zL = 0,5 erhält man mit H0 = 70 km/s·Mpc
θ = 1,3
M
arc sec
1012 M Ο
186
(13.15)
Fig. 13.8. Die Galaxie im Vordergrund LRG 3-757 (Luminescent Red Galaxy) wirkt als
Gravitationslinse für eine weit im Hintergrund liegende ferne Galaxie, die hier als Einsteinring
mit dem Radius θ E ≈ 1 arcsec auftritt. (NICMOS, HST, NASA)
Ein Einsteinring tritt dann auf, wenn Σ = Σ crit und die kritische Flächendichte über die Fläche
des Rings verschmiert ist. Daraus kann man sofort die Masse der Linse abschätzen
M (θ E ) = π( DL θ E ) 2 Σ crit
(13.16)
r
In der Schreibweise von Gl. 13.8 definiert α ein 2-dimensionales (rotationsfreies)
Vektorfeld, das sich aus einer skalaren Potentialfunktion ψ ableiten lässt. Wegen
r
r θ
∇ θ ln θ = 2
θ
(13.17)
können wir das Potential auch schreiben
ψ=
Es wird dann
r
r r 2
1
′
κ
(
θ
)
ln
θ
− θ′ d θ′
π∫
r
α = ∇ θψ
(13.18)
(13.19)
Um eine Kartierung der Ablenkungen in einem Bild von sehr vielen Galaxien zu erhalten,
r
r
r r
r
geht man von β = θ − α(θ) (Gl.13.7) aus und bildet ∇ θβ
187
∂β i
∂α i
∂ 2ψ
= δ ij −
= δ ij −
= δ ij − ψ ij = A
∂θ j
∂θ j
∂θ i ∂θ j
(13.20)
Die Vergrößerung ergibt sich aus dem Reziproken der Determinanten von A
μ=
1
det A
(13.21)
Die Spur von ψ ij ergibt 2mal die Konvergenz
ψ11 + ψ 22 = 2κ
(13.22)
welche die Form (z.B. Kreisform) erhält. Die Scherungen γ1 und γ2 sind wie folgt definiert
sind
γ 1 = (ψ11 − ψ 22 )
(13.23)
und
γ 2 = ψ 21 = ψ 21
(13.24)
Fig. 13.9. Als Beispiel für eine Abbildung unter der Voraussetzung des „Weak Lensing“ sei eine
kreisförmige Quelle betrachtet. Im Falle von κ > 0 und γ1,2 = 0 erhält man ein vergrößertes,
unverzerrtes Bild. Ist jedoch κ = 0 und γ1,2 > 0 dann ist das Bild eine Ellipse.
188
Fig. 13.10. Der Galaxienhaufen Abell 1689 im Vordergrund führt zu einer Verzerrung der
Bilder der dahinter liegenden (blauen) Galaxien.
Sie ändern die Form und machen z.B. aus einem Kreis eine Ellipse (s. Fig.). Die Auswertung
ist dann möglich, wenn sehr viele Hintergrundgalaxien beobachtet werden. Diese erscheinen
zunächst alle mit einer natürlichen Elliptizität, z.B. dadurch dass bei Spiralgalaxien die
Blickrichtung einen Winkel mit der Scheibenebene bildet oder die Galaxie eine elliptische
Struktur besitzt. Die Richtungen dieser Ellipsen sind statistisch verteilt, weshalb diese
Elliptizität durch Summation über viele Galaxien als Untergrund eliminiert werden kann.
Übrig bleibt die Elliptizität durch gravitative Scherung (Gl. 13.23 und 13.24) verursacht durch
die Masse einer Galaxie oder eines Galaxienhaufens im Vordergrund. Die Orientierung dieser
Elliptizität weist auf die Symmetrie der Vordergrundmasse.
Inzwischen wurde eine Reihe von entsprechenden Aufnahmen ausgewertet, die sehrt schön
die Masse und die Massenverteilung der Dunklen Materie zeigen. Im großen Ganzen stimmt
die Verteilung der sichtbaren Galaxien mit der der Dunklen Materie überein. Bei den
Massenbestimmungen gibt es Unterschiede zu denen, welche aus Röntgen-Emission
gewonnen wurden. Die Unterschiede können behoben werden, wenn die Dynamik der
Clustergase berücksichtigt wird.
189
Fig. 13.11. Computersimulation der Wirkung einer Gravitationslinse, welche eine elliptische
Verzerrung der Galaxien verursacht. Die großen Achsen der Ellipsen sind auf Kreisen um die
Linse angeordnet, welche die Form von Einsteinringen haben (aus Peter Schneider:
„Extragalactic Astronomy and Cosmology“. Springer-Verl. 2006).
Gravitationslinsen bieten somit eine interessante unabhängige Methode, die Verteilung der
Dunklen Materie zu untersuchen. Ihr Anteil an der kosmischen Dichte wurde im
Wesentlichen aus dem Fluktuations-Spektrum des CMB gewonnen, welches aus den
Messungen von WMAP mit großer Genauigkeit vorliegt. Aber auch die Hubble-Konstante
geht über die Abstände in die Gravitationslinsen-Effekte ein.
Auf die Bilder der wechselwirkenden Galaxienhaufen sei an dieser Stelle noch einmal
eingegangen. Nach de Analyse des Bullet-Cluster wurde noch ein zweiter Fall von
wechselwirkenden Cluster gefunden (Abell 520) gefunden. Beiden ist gemeinsam, dass heißes
Gas und Galaxien getrennt wurden. DM und Galaxien scheinen den Kontakt zweier Haufen
weitgehend unbeeinflusst zu überstehen, während das intergalaktische Gas zurückbleibt. Das
heiße Plasma, dessen Röntgenemission seine Ausdehnung anzeigt, ist rot gezeichnet. Die
Verteilung der Gesamtmasse (also im Wesentlichen DM) wurde durch Auswertung des „weak
lensing effects“ bestimmt und blau gezeichnet.
190
Fig. 13.12. Die Kollision von 2 Galaxienhaufen Abell 520 bei z = 0,201 (entspricht 2,4 ·109 Lj.)
wurde mit Hilfe von „Gravitational Shear“ untersucht. Rot ist die Verteilung des heißen Gases
im Cluster dargestellt, so wie sie sich durch die Beobachtung mit dem Röntgensatelliten
Chandra zeigt. Blau ist die Verteilung der dunklen Materie entsprechend der Auswertung der
Bildverzerrung der Hintergrundgalaxien. Das Bild zeigt 5 ‚Massekonzentrationen, die sich
relativ zueinander bewegen. Die Bereiche dunkler Materie und die leuchtender Materie wurden
offensichtlich getrennt. (nach A. Mahdavi Univ. Victoria, NASA, CXC, CFHT)
Fig. 13.13. Wechselwirkende Galaxienhaufen 1 E 0657-558 (Bullet Cluster). Die Galaxien
konzentrieren sich in 2 Subcluster. Das heiße intergalaktische Gas (hier auf Grund seiner
191
Röntgenstrahlung detektiert und rot gekennzeichnet gruppiert sich zwischen die leuchtende
Materie. Galaxien und dunkle Materie (blau angezeigt) haben nach der Kollision ihre Bahn
ungehindert fortgesetzt, während das heiße Plasma aufgehalten durch Stöße sich davon getrennt
hat.
13.3
Die Teilchen der Dunklen Materie.
Wenn die dunkle Materie keine baryonische Materie ist, as ist sie dann? Wie konnten die
WIMP vom frühen Universum bis jetzt überleben? Kann es sein, dass sie mit dem Erhalt einer
(additiven oder multiplikativen) Quantenzahl verbunden sind und ein nicht verschwindendes
chemisches Potential bilden? Aber selbst wenn das nicht der Fall ist, könnten die WIMPs sich
mit ihren Antiteilchen bei höheren Dichten ausgelöscht haben, bis die Rate der Annihilationen
schließlich zu gering wurde, um die Dichte weiter zu reduzieren. Hier ist n die
n σ υ
Teilchendichte, υ die Relativgeschwindigkeit und σ der Annihilationsquerschnitt. Man kann
annehmen, dass bei sehr hohen Temperaturen WIMPs thermisch erzeugt werden. Unterhalb
einer Schwellenenergie ist die Erzeugung unterdrückt. Wenn schließlich die Temperatur
unter die Ruhenergie fällt k B T < m χ c 2 , „frieren die WIMPs aus“ und bleiben als thermische
Relikte im frühen ‚Universum zurück. Für die verbleibende Dichte gilt dann
1/ 2
xf
s 0 ⎛ 45 ⎞
1
2
⎜
⎟
Ωχ h =
2 ⎜
⎟
ρ c / h ⎝ π g * ⎠ M Pl σ υ
(13.25)
Es bedeuten hier s0 die Entropiedichte, ρc kritische Dichte, h der Korrekturfaktor der HubbleKonstanten, g* die effektive Zahl der relativistischen Freiheitsgrade, MPl die Planckmasse,
mχ c 2
≈ 25 charakterisiert die inverse Temperatur des Ausfrierens (Näheres bei D.
xf =
k BT f
Hooper und E.A. Baltz in Ann. Rev. Nucl. Part. Sci. (2008) Vol. 58). St. Weinberg schätzt
mit ähnlichen Überlegungen (Auswertung und Diskussion der Boltzmanngleichung) aus
ΩW h 2 ≈ 0,15 eine Untergrenze für die Masse von m χ c 2 > 10 GeV ab (St. Weinberg:
Cosmology)
Wir diskutieren zunächst, welche Teilchen als Kandidaten für Dunkle Materie infrage
kommen und welche man ausschließen kann.
13.4.1 . Neutrinos
Setzt man für die Neutrinomasse mν < 2,05 eV, so ergibt sich als Obergrenze für den
Massenanteil der Neutrinos Ω ν h ≤ 0,07 für alle 3 Neutrinoarten. Das bedeutet, dass die
Neutrinos einfach nicht zahlreich genug sind, um in der Dunklen Materie eine Rolle zu
spielen. Als ultrarelativistische Teilchen würden Neutrinos sich stoßfrei ausbreiten und dabei
Fluktuationen der Materie unter 40 Mpc auslöschen. Das wiederum würde zu einer „topdown“ Entwicklung kosmischer Strukturen führen, was gerade nicht beobachtet wird.
13.4.2 . Axionen wurden eingeführt, um die CP-Verletzung in der Teilchenphysik zu
beheben. Nach den Grenzen, welche bisherige Beobachtungen setzen, sind Axionen sehr
leichte Teilchen mit Massen ma ≤ 0,01 eV. Gegenwärtig laufen Experimente, Axionen in
der Sonnenstrahlung nachzuweisen. Theoretisch besteht noch die Möglichkeit durch
geeignete Wahl der Parameter, alle Randbedingungen, welche die Dunkle Materie erfordert,
mit Axionen zu erfüllen.
2
192
13.4.3 . Supersymmetrische Kandidaten. Die supersymmetrischen Theorien manifestieren
sich im so genannten Superraum, der neben den Koordinaten der üblichen MinkowskiRaumzeit auch anti-kommutierende Weyl-Spinoren enthält. Die Theorie enthält Operatoren
Q, welche Bosonen in Fermionen und umgekehrt verwandeln können
Q Fermion = Boson und Q Boson = Fermion
(13.26)
Fermionen und Bosonen erscheinen bei ungebrochener Symmetrie im gleichen Multiplett bei
gleicher Energie. Die Energie des Grundzustands ist exakt Null, d.h. es gibt keine
Nullpunktsenergie. Allen Eichfeldern sind fermionische Superpartner zugeordnet, die mit der
Endung „-ino“ (z.B. Gluino), angehängt an den Namen des Eichbosons, bezeichnet werden.
Entsprechend sind allen Fermionen skalare bosonische Partner zugeordnet, dafür steht am
Anfang der Fermionenbezeichnung ein „s-„
(z.B. Squarks oder Sleptonen). Die
Kommutatoren der Operatoren Q zeigen eine Gruppeneigenschaft, der die Supersymmetrie
(SuSy) zugrunde liegt. Bis heute sind keine supersymmetrischen Teilchen beobachtet worden.
Sie könnten bei höheren Energien (E > 250 GeV) liegen. Dann wäre allerdings die strenge
SuSy gebrochen. Wenn die Teilchen der Dunklen Materie, was zu vermuten ist, nicht mehr im
Standardmodell der Elementarteilchen enthalten sind, bietet sich SuSy als nächster Ausweg
an, um neue Teilchenzustände zu schaffen. SuSy liefert allerdings insofern wieder eine
phänomenologische Theorie, als eine große Zahl von freien Parametern eingegeben werden
muss. Da man diese nicht kennt, versucht man die Zahl der freien Parameter durch plausible
Annahmen und Gleichsetzungen weitgehend zu reduzieren. So entsteht dann ein „Minimales
supersymmetrisches Standardmodell“ (MSSM). Im Modell ist eine Symmetrie brechende
Wechselwirkung eingebaut. So werden die Wino- und Higgino-Zustände zu neuen
Masseneigenzuständen gemischt, Charginos genannt. Entsprechend werden auch aus den
Higgsino, den Binos und Winos die Masseneigenzustände der Neutralinos. Die Energie des
Neutralinos ist die niedrigste in der Abfolge der supersymmetrischen Teilchen. Es sollte
demnach stabil sein, könnte sich aber langsam durch Selbst-Annihilation in Strahlung
verwandeln. Dann wäre möglicherweise das Teilchen sein eigenes Antiteilchen (MajoranaTeilchen). Die Stabilität der niedrigsten supersymmetrischen Zustände (lightest
supersymmetric particle = LSP) wird auch durch die so genannte R-Parität beschrieben. Die
R-Parität ist + 1 bei Teilchen des Standardmodells (linke Seite der Tab. 13.1) und -1 bei
supersymmetrischen Teilchen (rechte Seite der Tab. 13.1). Die R-Parität ist bei mehreren
Teilchen ist multiplikativ. Übergänge, bei welchen sich die R-Parität ändert, sind verboten,
was eben besonders für die LSP-Zustände zutrifft. (Näheres dazu bei G. Bertone, Dan Hooper
and J. Silk hep-ph/0404175) Somit wäre das Neutralino ein Kandidat für ein „weakly
interacting massive particle“ (WIMP), dessen Masse zwischen 100 GeV und 1 TeV erwartet
wird.
14.4.4. Extra Dimensionen.
In verschiedenen Theorien (bes. in der Stringtheorie treten zusätzliche Raumdimensionen
auf. Da man z.B. in der Planetenbewegung solche Extradimensionen nicht beobachtet, werden
sie
in der Theorie „kompaktifiziert“. Das kann so geschehen, dass die Extradimension als
Kreisumfang dargestellt 2πR wird, dessen Radius R
man gegen sehr kleine Werte
gehen lässt. Extradimensionen ergeben zusätzliche Energieleitern ( mit m SM der Masse des
supersymmetrischen Teilchens
n2
2
m=
+ mSM
2
R
193
(13.27)
deren Stufen umso größer ausfallen, je kleiner R gewählt wird. Die niedrigsten Stufen
gehören in der Massenskala zu den leichtesten Teilchen, die auch „lightest Kaluza-Klein
particles“ (LKP) genannt werden. Auch hier erwartet man ein neutrales massives Teilchen im
Bereich 100 GeV < Mc2 < 1TeV. Kaluza und Klein haben in den 30er Jahren durch
Einführung einer 5. Dimension (= 4. Raumdimension) gezeigt, dass allgemeine Relativität
und Elektrodynamik in einer vereinheitlichten Feldtheorie zusammengefasst werden können.
Leider ergaben sich daraus keine neuen experimentell nachprüfbaren Zusammenhänge, so
dass die
Entdeckung lange Zeit unbeachtet blieb. Eine Extradimension sollte auch die
Newtonsche Gravitation für kleine Abstände beeinflussen. Allerdings ist bisher trotz
sorgfältiger Messungen bis zu Bruchteilen von Millimetern keine
Abweichung
gefunden worden. Entsprechend verhält es sich mit den Energieleitern, die ebenfalls bei den
bisher erreichbaren Energien nicht nachgewiesen werden konnten. Die Hoffnungen richten
sich jetzt auf den „Large Hadron Collider“ (LHC) bei CERN in Genf, der gegenwärtig läuft.
Was können wir aus den astronomischen Beobachtungen über die WIMPs lernen? Sie sind
dunkel, wechselwirken also nicht mit dem elektromagnetischen Feld. Sie sind neutral. Ihnen
fehlt die Möglichkeit der Abstrahlung, deshalb werden sie ihre kinetische Energie nicht los
und können nicht in die Ebene der Spiralgalaxien relaxieren (ausgedehnte Halos). Die
Dynamik der Strukturbildung zeigt, das die dunkle Materie „kalt“ ist, d.h. sie ist nicht
relativistisch; die kinetische Energie der WIMPs muß viel kleiner sein als ihre Ruhenergie. In
den beiden Beispielen interagierender Cluster, der Bullet Cluster und Abell 520, zeigt sich das
verschiedene Verhalten des heißen Plasmas geladener Teilchen, welche Streuprozesse
erleiden und der WIMPs, die unbeeinflusst ihre Bahn ziehen.
Wie konnten die WIMP vom frühen Universum bis jetzt überleben? Es kann sein, dass sie mit
dem Erhalt einer (additiven oder multiplikativen) Quantenzahl verbunden sind und ein nicht
verschwindendes chemisches Potential bilden. Aber auch wenn das nicht der Fall ist, könnten
sich mit ihren Antiteilchen bei höheren Dichten ausgelöscht haben, bis die Rate der
Annihilationen n σ υ
schließlich zu gering wurde, um die Dichte weiter zu
reduzieren. Hier ist n die Teilchendichte, υ die Relativgeschwindigkeit und σ der
Annihilationsquerschnitt. Man kann annehmen, dass bei sehr hohen Temperaturen WIMPs
thermisch erzeugt werden. Unterhalb einer Schwellenenergie ist die Erzeugung unterdrückt.
Wenn schließlich die Temperatur
unter die Ruhenergie fällt k B T < mW c 2 , „frieren die WIMPs aus“ und bleiben als thermisches
Relikt im frühen ‚Universum zurück. Für die verbleibende Dichte gilt Gl. (13.25) (Näheres
bei D. Hooper und E.A. Baltz in Ann. Rev. Nucl. Part. Sci. (2008) Vol. 58). St. Weinberg
schätzt mit ähnlichen Überlegungen (Auswertung und Diskussion der Boltzmanngleichung)
aus ΩW h 2 ≈ 0,15 eine Untergrenze für die Masse von mW c 2 > 10 GeV ab (St. Weinberg:
Cosmology).
13.5. Direkter Nachweis von WIMPs.
Die Schwierigkeiten, Teilchen der dunklen Materie (WIMPs = weakly interacting massiv
particles), welche mit anderen Elementarteilchen nur gravitativ oder schwach wechselwirken,
im Labor nachzuweisen, sind außerordentlich groß. Dennoch werden große Anstrengungen
dazu unternommen. WIMPs übertragen beim inelastischen Stoß mit Atomkernen Energie.
Eine Methode welche diese Energie bestimmen soll, ist der Aufbau von TieftemperaturKalorimetern. Die Rückstossenergie variiert mit der WIMPs und der Targetmasse
194
ER ≅
2υ 2 mT
(1 + m
T
/ mχ )
2
(13.28)
Die Bedingung für Rückstoss ist besonders günstig, wenn mT = m χ ist. Wenn die Verteilung
der Rückstossenergie gemessen werden kann, ließe sich auch die WIMP-Masse bestimmen.
Die Exposition des Detektors wird als Masse·Zeit [kg ⋅ Tage] angegeben. Sie wächst, wie die
Detektionswahrscheinlichkeit mit der Masse des Detektors. Gegenwärtig arbeiten viele
Arbeitsgruppen bereits mit der zweiten. Generation ihrer Methode und planen die Dritte.
Wir werden im Folgenden die Prinzipien einiger experimenteller Methoden skizzieren.
Die direkten Nachweismethoden müssen berücksichtigen, dass die gesuchten Prozesse selten
sind. Sie müssen deshalb gegen radioaktive Verunreinigungen und kosmische Höhenstrahlen
gut abgeschirmt werden. Um Letzteres zu erreichen, finden die Experimente tief unter der
Erde in verlassenen Bergwerken oder Seitenzweigen von Strassentunnelsystemen statt.
Das DAMA (= Dark Matter) NaJ-Experiment arbeitete im Gran-Sasso-Tunnel, d.h. im
Untergrundlabor des Gran Sasso in Italien unter einer Bedeckung von 1400 m Felsen, mit
100 kg NaJ:Tl als Detektormaterial. Die Thallium dotierte Natriumjodid- Einkristalle waren
auf 9 Exemplare zu je 9,7 kg verteilt. Die Szintillation jedes NaI-Kristalls wird durch jeweils
2 Photomultiplier (PM) kontrolliert. Es gibt keine direkte Diskriminierung von HintergrundEreignissen. Stattdessen wird in der Statistik der Ereignisse nach einer jahreszeitlichen
Modulation der Zählrate gesucht, hervorgerufen durch die Bewegung der Erde um die Sonne,
die sich relativ zu den WIMPs mit 230 km/s bewegt. DAMA wurde 2002 außer Betrieb
gesetzt.
Fig. 13.14 Schema des DAMA 100 kg NaJ:Tl-Experiments
Inzwischen arbeitet DAMA/LIBRA (ca. 250 kg hochreinem NaI:Tl) seit März 2003 und kam
bis 2006 auf 107731 kg·Tage Beobachtungen. DAMA behauptet, eine Modulation gefunden
195
zu haben. Bisher konnten aber diese Ergebnisse von anderen Gruppen (die allerdings mit
anderen Methoden arbeiten) nicht verifiziert werden.
Fig. 13.15. Die jährliche Modulation des DAMA-Signals. Aufgetragen sind
3 Energiebereiche. Das behauptete Signal befindet sich bei 6,3
(DAMA/LIBRA)
σ.
Ein Experiment, das ebenfalls im Gran Sasso Labor stattfindet, trägt den Namen CRESST (=
Cryogenic Rare Events Search with Superconducting Thermometers). Die WIMPs sollen in
einem Saphir- (Al2O3) oder Kalziumwolframat-Kristal (CaWO4) absorbiert werden. Die
übertragene Energie erreicht als Phononen-Impuls den supraleitenden Detektor, der aus je
einem dünnen Wolfram-Film auf den Endflächen des Saphir-Kristalls besteht. Das unter
Reinraumbedingungen laufende Experiment trägt Kupfer- und Bleiabschirmungen. Die
Empfindlichkeit wird durch die Restradioaktivität der Umgebung bestimmt, die trotz
Vorkehrungen nicht ganz zu eliminieren ist.
196
1. Fig.13.16.
Prinzip-Skizze des CRESST- Experiments (Cryogenic Rare Event Search with
Superconducting Thermometers). Die übertragene Energie wird mit Cryodetektoren
(supraleitende Filme geeigneter Sprungtemperatur) im Millikelvin-Bereich gemessen, wo die
Wärmekapazität des Absorbers außerordentlich klein ist. Zusätzlich kann ein
Lumineszenzsignal detektiert werden. CRESST ist eine Kollaboration europäischer
Physiker und wird im Gran Sasso Labor betrieben.
Die Arbeitstemperatur liegt zwischen 20 und 40 mK, je nach Sprungtemperatur des
Supraleiters. Je kleiner die Masse der WIMPs, umso stärker sind die Rückstoß-Spektren zu
niedrigen Energien verschoben (s. Gl. 13.28) Neben Saphir wird auch Calziumwolframat
(CaWO4) als Detektormaterial und Iridium-Gold-Filme als supraleitendes Thermometer
(CRASST II-Experiment) verwendet. Darin wird neben einem Wärmepuls auch ein
Szintillations-Signal erzeugt. Aus dem Verhältnis von Lumineszenz- und Wärme-Puls lassen
sich verschiedene Prozesse, wie z.B. Gammastrahlen und Rückstoßprozesse, unterscheiden.
Bisher wurde CRESST mit
1 kg Detektormasse betrieben. Aber wegen der geringen Wechselwirkung der WIMPs mit
Materie ist die Nachweiswahrscheinlichkeit gering, auch wenn eine große Zahl von WIMPs
den Detektor durchläuft. Andererseits hängt die Nachweiswahrscheinlichkeit von der
Detektormasse ab, weshalb das Experiment zurzeit auf 10 kg aufgerüstet wird.
In einem anderen Experiment mit dem Namen EDELWEISS II (Experiment pour détecter
les WIMPS en Site Souterrain), das im französischen Frejus-Tunnel aufgebaut ist, benutzt
man 10 Germanium-Kristalle von je 400g Masse als Detektoren Es wird bei 17 mK der
Phonon-Wärmepuls sowie Ionisationsstrom aus Elektron-Loch-Paaren. In einer Auftragung
der Ionisationsausbeute gegen Energie des Wärmepulses können die verschiedenen Prozesse
unterschieden und damit gesuchte Ereignisse vom Untergrund getrennt werden. Im
vergangenen Jahr wurden 5 Ereignisse als mögliche Kandidaten ausgefiltert. Der Untergrund
liegt bei 3 Ereignissen. Der detektierbare Massenbereich liegt bei 10 – 100 GeV/c2.
197
Das US-amerikanische CDMS (= Cryogenic Dark Matter Search) benutzt 2 Silizium- (100 g )
und 4 Germanium-Detektoren (250 g). Das Prinzip der Detektion ist damit dem von
EDELWEISS sehr ähnlich. Das zeitliche Verhalten des thermischen Pulses wird hier zur
Unterscheidung von Störsignalen herangezogen. CDMS II wird im aufgelassenen SoudanBergwerk aufgebaut, eine der ältesten und tiefsten Eisenminen in Minnesota. Dort wird
außerdem auch ein 6000 Tonnen Neutrino-Detektor untergebracht. Der messbare
Massenbereich betägt 10 – 100 GeV/c2.
Fig. 13.17. Prinzip des CDMS II-Experiments. Ein WIMP trifft auf ein Ge-Atom in
einem der Ge-Kristalle. Ein Phononpuls wird ausgelöst und mit einer supraleitenden AlSchicht auf der Oberfläche des Ge-Kristalls detektiert. Gleichzeitig werden ElektronLoch-Paare freigesetzt, und dieser elektrische Puls wird ebenfalls gemessen. Das Timing
zwischen beiden Signalen wird ebenfalls gemessen
198
Fig. 13.18. Ionisationsausbeute gegen Verzögerungszeit für Rückstoßenergien von 1 –
100 keV in Germanium. Für diese Messungen wurden radioaktive Referenz-Substanzen
zum Eichen der Apparatur verwendet. Rote Punkte sind Elektronen aus 133Ba,
schwarze Punkte entsprechen Elektronen niedriger Ausbeute und blaue Punkte sind
Neutronen aus 252Cf.
Das ZEPLIN II-Experiment ist in der „Boulby Mine“ in England in einer Tiefe von 2800 m
aufgebaut. Der Detektor besteht aus 30 kg Xenon in flüssiger und gasförmiger Phase (Sdp.
165 K, Dichte 3,52 g/cm3) und wird von mehreren PM kontrolliert. Außerdem befindet sich
an der Oberfläche der Flüssigkeit ein elektrisches Feld. Ein einfallendes Teilchen löst im
flüssigen Xenon einen Szintillations-Impuls aus. Wenn der Stoß des Teilchens zur Ionisation
eines Xe-Atoms führt, werden die freigesetzten Elektronen durch das elektrische Feld
beschleunigt und lösen im Gas einen sekundären Lichtpuls aus. Durch Vergleich des primären
und sekundären Lichtpuls kann die Natur des Teilchens identifiziert werden. Ein Ausbau des
Experiment mit 1 t Xe ist für die Zeit von 2008 bis 2012 vorgesehen und soll noch Teilchen
bei einem Stossquerschnitt von 10-9 picobarn nachweisen können. Ein nuklearer Rückstoß,
wie er bei der Wechselwirkung eines WIMP mit einem Xe-Atom erwartet wird, erzeugt ein
extrem niedriges Ionisationssignal. Das macht die Unterscheidung von anderen
(unelastischen) Teilchenstößen durch einen Faktor 10-3 extrem günstig. Ausserdem sind bei
dem Xe-Experiment keine extrem tiefen Temperaturen nötig. Problematisch ist das
Eliminieren von Verunreinigungen mit 85Kr, ein β-Strahler mit 10,76 Jahren Halbwertszeit.
Das erfordert sorgfältige und kostspielige Reinigungsprozesse.
Das XENON 100 Experiment, das von einer Kooperation US-amerikanischer und
europäischer Institute betrieben wird, ist ebenfalls ein 2-Phasen-Detektor, der mit 100 kg
flüssigem Xenon betrieben wird und bebenfalls im Gran-Sasso-National-Laboratory
untergebracht ist. Über und unter dem Xenonbehälter ist eine Reihe von Photomultipliern
angebracht. Gemessen wird S1, das erste Lumineszenzsignal beim Stoß eines WIMPs mit
einem Xe-Kern und S2, das 2. Lumineszenzsignal von der Ionisationsladung, welche an der
Phasengrenze flüssig/gasförmig auftritt. S1 ist ein Mass für die Rückstossenergie, S2 misst die
199
Ionisation Die Messung ist Orts empfindlich. Der Messbereich wird mit 100GeV/c2 und σ > 6
·10-45 cm2 oder 6 ·10-9 pb angegeben. Xenon 100 ist das Nachfolge–Experiment von Xenon
10, mit welchem Machbarkeit und Aufwand untersucht wurden.
Fig. 13.19. Empfindlichkeiten der verschiedenen WIMP-Nachweismethoden nach Angeben der
Xenon 100-Arbeitsgruppe.
Einige weitere Arbeitsgruppen sollen nur kurz erwähnt werden. CoGeNT arbeite mit 500 g
Ge-Einkristall in der Soudan-Mine / Minnesota ausgelegt für Massen < 10 GeV/c2. LUX
arbeite in der Homestake –Mine/ South Dakota mit 350 Kg flüssigem Xenon ausgelegt für
Massen 10 – 100 GeV/c2. Schließlich XMASS in Kamioka / Japan plant 1000 kg flüssiges
Xenon und einem Massenbereich wie LUX..
13.6. Indirekter Nachweis von WIMPs durch Annihilation.
13.6.1. Hochenergetische Gammastrahlung
Geht man davon aus, dass WIMPs SuSy-Teilchen sind und sich mit einer gewissen, wenn
auch geringen Wahrscheinlichkeit paarweise vernichten können, sollte die
Vernichtungsstrahlung als hochenergetische Gamma- oder Neutrinostrahlung oder als
Antimaterie beobachtbar sein. Die Dichte der dunklen Materie nimmt zum Zentrum der
Galaxie zu und erreicht dort ein Maximum. Eine Aussage über die Höhe des Maximums ist
200
unsicher, weil die empirischen Dichtefunktionen darüber keine Angaben machen können. In
jüngster Zeit wurde TeV-Gammastrahlung aus dem Galaktischen Zentrum mit den
Cherenkov-Teleskopen H.E.S.S. beobachtet. Sie konnte wegen der guten Winkelauflösung
von 5,8 arcmin mit der Position von Sgr A*, der Position des schwarzen Lochs der
Milchstrasse, identifiziert werden. Es ist durchaus möglich, dass die Gammastrahlung durch
den inversen Compton-Effekt entsteht und ihre Energie aus ultrarelativistischen
Teilchenströmen in der Nähe des Lochs bezieht. Dann hätte sie nichts mit WIMPs zu tun. Die
Strahlung zeigt während der Beobachtungszeit keine Variabilität, was bei einer Entstehung
aus der Akkretionsscheibe eines schwarzen Lochs häufig der Fall ist. Es ist deshalb durchaus
möglich, dass die TeV-Strahlung aus der Annihilation von WIMPs stammt. Danach würden
die Teilchen eine Masse von 12 -18 TeV haben, wozu eine DM-Dichte von ca. 1100
−26
3 −1
Sonnenmassen pro pc3 notwendig wäre, was einem Wert < συ > = 3 ⋅ 10 cm s
entspricht. Die stellare Dichte ist in einer Entfernung von 10 pc vom Zentrum etwa doppelt so
hoch.
Mit dem „Fermi Large Area Gamma Telescope“ haben A. Geringer-Sameth und S.M.
Koushiappas 7 Zwerggalaxien in der Nähe unserer Milchstrasse beobachtet (Phys. Rev. Lett.
107, 241303 (2011). Fermi LAG kann Gammastrahlung bei Energien von 20 MeV bis über
300 GeV detektieren und abbilden. Es überdeckt 20% des Nachthimmels und führt einen
vollen Scan des Himmels in 3 Stunden aus. Zwerggalaxien haben ein besonders hohes MasseLeuchtkraft-Verhältnis M / L . Die Autoren subtrahieren den diffusen Untergrund. Für den
Bereich 19 – 240 GeV können die Autoren mit 95% Sicherheit Vernichtungsstrahlung von
WIMPs ausschließen.
Ein konkurrierendes Projekt mit Fermi LAT die „Fermi-LAT Collaboration“ (M. Ackermann
et al. Phys. Rev. Lett. 107, 241302 (2011)), kommt zu einem ähnlichen Ergebnis. Sie
untersuchen 10 Satellitengalaxien der Milchstrasse und geben ebenfalls mit 95% Sicherheit
folgende Grenzen an: für συ = 10 −26 cm 3 / s bei 5 GeV bis συ = 10 −23 cm 3 / s bei 1 TeV.
Damit schliessen sie auch die üblicherweise angenommenen Wert von
συ ≈ 3 ⋅ 10 −26 cm 3 / s für einen reinen s-Wellen-Querschnitt (keine Spinabhängigkeit) aus.
13.6.2. Hochenergetische Neutrinos.
Hochenergetische Neutrinos können durch die Cherenkov-Strahlung ihrer Sekundärteilchen
(Myonen) beobachtet werden. Am Südpol wird das Inlandeis als Detektor benutzt (Ice Cube
Experiment). Dazu werden PM-Ketten mit über 5000 Photomultipliern an Kabeln in das Eis
eingeschmolzen und bis zu 2450 Tiefe versenkt. Wenn die Neutrinos auf einen Atomkern
treffen, emittieren sie Myonen, welche sich durch ihre Tscherenkow-Strahlung nachweisen
lassen. Es werden nur solche Neutrinos registriert, die von Norden kommend die Erde als
Filter passiert haben. Das in der Vergangenheit ausgelaufene Experiment AMANDA
detektierte einen diffusen Untergrund von Neutrinos. Es ließ sich aber keine spezielle Quelle
am Himmel erkennen.
13.6.3. Antimaterie
Das Pamela-Experiment ist ein Satellit mit Teilchendetektoren und einem
Magnetospektrometer, der Leptonen, Baryonen und deren Antiteilchen im Energiebereich von
50 MeV bis mehreren 100 GeV untersuchen kann. PAMELA registriert Teilchen, darunter
auch Positronen und Antiprotonen und ist insbesondere für den Nachweis von Antimaterie
201
ausgerüstet. Eine frühere Auftragung des Positronenstroms aus der Richtung des galaktischen
Zentrums, das von einer besonders hohen Dichte dunkler Materie umgeben sein sollte, ließ
einen Anteil WIMPs-Annihilationsstrahlung zu. Inzwischen konnte diese Option durch neuere
und genauere Messungen aber ausgeschlossen werden.
13.6.4. Beschleunigerexperimente.
Der LHC (Large Hadron Collider) bei CERN arbeitet seit über einem Jahr problemlos. Er
arbeitet mit 2 gegenläufigen Protonenstrahlen, erreicht gegenwärtig (Februar 2012) 7 TeV,
soll aber in naher Zukunft bis auf 14 TeV hoch gefahren werden. An die Experimente
knüpfen sich viele Hoffnungen, so z.B. der Nachweis des Higgs-Bosons, mögliche SuSyTeilchen und natürlich Kandidaten der DM. Ein WIMP könnte aus den Reaktionsprodukten
verschwinden, ohne eine Spur zu hinterlassen, und sich nur als Defizit in der Energiebilanz
zeigen. Da bei Proton-Proton-Kollisionen sehr viele Teilchen beteiligt sind, schließt sich an
die Experimente eine komplizierte und zeitaufwendige Auswertung an. Bei seltenen
Ereignissen müssen Messreihen entsprechend lange laufen, ehe man genügend Gewissheit
gesammelt, um spannende Ergebnisse zu veröffentlichen. Deshgalb müssen sich die
Interessenten wohl noch in Geduld üben.
13.7. Zusammenfassung.
Aus der Dynamik von Galaxien (Rotationskurven) und Galaxien-Haufen lässt sich die
Gesamtmasse dieser Objekte bestimmen. Diese wiederum ist im Wesentlichen durch die DM
bestimmt, deren Anteil sieben Mal so groß ist wie die baryonische Masse. Deren Obergrenze
wiederum ist durch die Häufigkeit der leichten Elemente festgelegt. Zur Untersuchung der
Massenverteilung leistet der Effekt der Gravitationslinsen unschätzbare Dienste. Einsteinringe
findet man allerdings nur in glücklichen Fällen. Häufiger sind schwache, aber mit heutiger
Technik noch gut beobachtbare Verzerrungsfelder verursacht durch weiträumige
Massenkonzentrationen, welche so rekonstruiert werden können. Die bekanntesten Beispiele
(Abell 520 und der Bullet-Cluster) zeigen, dass sich dunkle Materie beim Kontakt von zwei
Clustern unbeeinflusst weiter bewegt, während das heiße baryonische Plasma durch Streuung
abgebremst wird. Die hypothetischen Teilchen (WIMPs) sollten nach den Beobachtungen
neutral sein, relativ große Masse besitzen und deshalb eine nichtrelativistische Dynamik
besitzen. Da sich im Standardmodell der Teilchenphysik kein geeigneter Kandidat findet,
vermutet man WIMPs under den am tiefsten liegenden Zuständen der Supersymmetrie.
Die Versuche des direkten Nachweises der DM-Teilchen finden in Labors, die von der
kosmischen Strahlung abgeschirmt sind, statt. Methoden der Tieftemperatur-Physik können
die Stoßenergie direkt messen. Daneben werden Lumineszenz-Prozesse und der Nachweis
von Ladungsträgern benutzt. Die lumineszierenden Materialien reichen von NaJ:Tl über
CaWO4 bis zu flüssigem Xenon. Die Wahrscheinlichkeit einer Detektion steigt mit der
Detektormasse, weshalb die Anlagen sukzessive vergrößert wurden. Bisher konnten noch
keine Ereignisse nachgewiesen werden, die einer allgemeinen Kritik standhielten.
Indirekte Nachweise untersuchen mögliche Zerfallsprodukte einer WIMP-Annihilation im
Kosmos. Dazu gehören Positronen-Emission (bes. aus dem galaktischen Zentrum),
hochenergetische Neutrinos und γ-Strahlung im GeV-Bereich. Die Ergebnisse dieser
Messunen konnten bisher nur Untergrenzen setzen. WIMPs scheinen eine beträchtliche Masse
(M >> 20 GeV/c2)
202
Zu besitzen und eine niedrigere Zerfallsrate n χ συ als allgemein angenommen. Auch bei
der Auswertung der LHC-Daten ist man bisher noch nicht auf Prozesse gestoßen, welche eine
Erzeugung von WIMPs vermuten lassen.
13.8. Literatur
V. Zacek: Dark Matter. http://arXiv.org/abs/0707.0472vl
Gianfranco Bertone, Dan Hooper and Joseph Silk: Particle Dark Matter: Evidence, Candidates
and Constraints. http://arxiv.org/abs/hep-ph/0404175
Michael E. Peskin: Dark Matter and Particle Physics. http://arXiv.org/abs/07071536
s. auch home page der Projekte zum Nachweis von WIMPs
http://astroteilchenphysik.de/topics/dm.html
Jodi A. Cooley: Status and Perspectives of Dark Matter Searches.
http://arxiv.org/abs/astro-ph/0607621
Dan Hooper and Brenda L. Dingus: Limits on Supersymmetric Dark Matter From EGRET
Observations of the Galactic Center Region.
http://arxiv.org/abs/astro-ph/0210617
B. Schwarzschild. Phys. Today 60(8), 16 (2007)
D. Hooper, Annu. Rev. Nucl. Part. Sci. (2008) Vol. 58
A.Mann, Nature 24 MARCH 2011 | VOL 471, p. 433
203
Anhang.
Der Anhang enthält Ableitungen von Formeln und Vertiefungen spezieller Themen. Er enthält
folgende Topics:
A.1. Helligkeiten Größenklassen und Entfernugen.
A.2. Hubble-Gesetz.
A.3. Das Birkhoff-Theorem.
A.4. Roberson-Walker-Metrik und hypersphärische Geometrie.
A.5. Mehr über Abstände.
A.6. Horizonte
A.7. Konforme Zeit, Friedmann-Gl für κ ≠ 0 .
A.8. Einige Beziehungen aus der Riemannschen Geometrie
A.9. Der Dopplereffekt in der speziellen Relativitätstheorie
A.10. Der Energie-Impuls-Tensor
A.11. Kosmologische Entfernungen
A.12. Fluid-Gl. und erste Friedmann-Gl.
A.1. Helligkeiten, Größenklassen und Entfernungen
Die visuelle Helligkeit mυ eines Sterns ist ein physiologisches Maß. Es geht zurück auf den
griechischen Astronomen Hipparchos (190 – 120 v. Chr.), der die Sterne in 6 Größenklassen
einteilte. Die hellsten Sterne ordnete er in die 1. Größenklasse. Die höheren Ordnungszahlen
bedeuten geringere Helligkeiten. Offensichtlich hängt mυ logarithmisch von der Leuchtkraft L
(Strahlungsleistung in Watt) ab
− mυ = log L + C
(A.1.1)
wird in Größenklassen gemessen und bezieht sich nur auf ein Fenster im sichtbaren
Spektrum. Je schwächer ein Stern erscheint, um so höher ist seine Größenklasse. Integriert
man über das ganze Sternspektrum, so erhält man die bolometrische Helligkeit mbol , die
meist benutzt wird, wenn die Leuchtkraft L aus der Helligkeit bestimmt werden soll. Die
Differenz zwischen mbol und mυ heißt bolometrische Korrektur (BC)
BC = mbol − mυ
(A.1.2)
Aus der Differenz der bolometrischen Helligkeiten läßt sich das Intensitätsverhältnis durch
folgende empirische Formel bestimmen
m2 − m1 = 2 ,5 ⋅ log
I1
I2
(A.1.3)
(Der Index wurde hier der Einfachheit halber weggelassen). Wenn I1 > I2 dann ist m2 - m1
positiv. Befinden sich 2 Sterne in verschiedenen Entfernungen, hat man nach Gl. 1.1
log
I1
L
r
= log 1 − 2 ⋅ log 1
I2
L2
r2
1
(A.1.4)
Sind die Leuchtkräfte gleich aber die Entfernungen verschieden, dann erhält man für die
Differenz der Größenklassen
m1 − m2 = 5 ⋅ log
r1
r2
(A.1.5)
Man denkt sich einen Stern aus der Entfernung r (pc) in eine Entfernung Standardentfernung
von 10 pc gebracht. Seine Helligkeit in dieser Entfernung heißt absolute Helligkeit M . Es ist
dann
⎛ r ⎞
⎟⎟ = 5 ⋅ log r − 5
m − M = 5 ⋅ log⎜⎜
(A.1.6)
10
pc
⎝
⎠
16
wobei r in pc gemessen wird. 1 pc = 3,0857 ⋅ 10 m = 3,2616 Lichtjahre . Der Ausdruck
auf der rechten Seite von Gl. A.1.6 heißt Entfernungsmodul. Wurde die Messung wie häufig
in einem bestimmten Spektralgebiet gemacht, so muß dieses als Index angegeben werden.
Seitdem die elektronische CCD-Platte die Photoplatte ersetzt hat, misst man I direkt, als Zahl
detektierter Lichtquanten
I = j ⋅ hv
(A.1.7)
wobei j die Zahl der Photonen/m2⋅s ist.
A.2. Hubble-Gesetz: aus Isotropie folgt Homogenität.
Die Geschwindigkeit unterliegt einer Dehnung (und eventuell einer Rotation) des Raumes
r
r ˆ r
υ = Σˆ ⋅ r + Ω
⋅r
(A.2.1)
⎛ ∂υi ⎞
ˆ
⎜
⎟ = Σˆ + Ω
⎜ ∂x ⎟
⎝ j⎠
(A.2.2)
Hier ist
der Dehnungstensor der Geschwindigkeit, der sich in einen symmetrischen Teil (Dehnung
und Scherung) und einen antisymmetrischen Teil (Rotation) zerlegen lässt. Die
Beobachtungen geben keinen Hinweis auf eine globale Rotation. Deshalb setzen wir
ˆ =0
Ω
(A.2.3)
Wir denken uns nun den symmetrischen Teil auf Hauptachsen transformiert. Isotropie
bedeutet dann
∂υ1 ∂υ 2 ∂υ 3
=
=
= H0
∂x1 ∂x 2 ∂x 3
2
(A.2.4)
Was für einen Punkt gilt, muss bei einer globalen Eigenschaft für alle Punkte gelten. Also gilt
auch Homogenität. Der umgekehrte Schluss (von Homogenität auf Isotropie) lässt sich
allerdings nicht ziehen.
A.3. Das Birkhoff-Theorem
Der amerikanische Mathematiker Georg David Birkhoff bewies 1923 im Rahmen der
allgemeinen Relativitätstheorie folgendes Theorem:
Für eine sphärisch symmetrische Massenverteilung haben die Einsteinschen Feldgleichungen
eine eindeutige Lösung. Innerhalb eines Hohlraum, der frei von Materie ist und den
Symmetrie-Punkt enthält, erhält man die Minkowski-Metrik, d.h. es gilt
ds 2 = c 2 dt 2 − dx 2 − dy 2 − dz 2 = c 2 dt 2 − dr 2 − r 2 (dθ 2 + sin 2 θdφ 2 )
(A.3.1)
Damit lässt sich die relativistische Verallgemeinerung der Ableitung in Kap. 2, die im
Rahmen der Newtonschen Physik abgeleitet wurde, angeben. In einem Loch, das in einer
sphärischen Materieverteilung zentriert ist, trifft man auf eine „flache Raumzeit“, d.h. der
Raum ist euklidisch. Unter dieser Voraussetzung wird das Ergebnis, das wir in Kap. 2
erhalten haben, als korrekt bestätigt.
A.4. Roberson-Walker-Metrik und hypersphärische Geometrie
Eine nützliche Form der Robertson-Walker-Metrik ist die folgende
[
]
ds 2 = c 2 dt 2 − R 2 dχ 2 + sin 2 χ ⋅ (dθ 2 + sin 2 dφ 2 )
(A.4.1)
In einem Raum mit positiver Krümmung ( κ = +1) , genauer eine 3d-Kugelfläche R3 in einem
4d-Raum gilt
R 2 = x 2 + y 2 + z 2 + w2
(A.4.2)
Wir können folgende hypersphärische Koordinaten einführen
w = R cos χ
z = R sin χ cosθ
(A.4.3)
y = R sin χ sin θ sin φ
x = R sin χ sin θ cos φ
Einen Raum mit negativer Krümmung ( κ = −1) , genauer eine 3d-Hyperboloid-Fläche H3 in
einem 4d-Raum erhalten wir, wenn wir ersetzen
R → iR, w → iw, χ → iχ
(A.4.4)
Dann wird
3
− R 2 = x 2 + y 2 + z 2 − w2
(A.4.5)
Die Polarkoordinaten werden
w = R cosh χ
z = R sinh χ cosθ
etc.
(A.4.6)
und die Metrik
[
]
ds 2 = c 2 dt 2 − R 2 dχ 2 + sinh 2 χ ⋅ (dθ 2 + sin 2 dφ 2 )
(A.4.7)
R3 ist kompakt und hat ein endliches Volumen. Das Volumen von H3
unbeschränkt. Man kann auch Gl. A.4.7 verallgemeinern, indem man schreibt
[
]
ds 2 = c 2 dt 2 − R(t ) dχ 2 + f κ (χ ) ⋅ [dθ 2 + sin 2 θ dφ 2 ]
2
2
mit
⎧sin χ
⎪
f κ (χ ) = ⎨sinh χ
⎪χ
⎩
dagegen ist
(A.4.8)
κ = +1
κ = −1
für
(A.4.9)
κ=0
Wir wollen mit Gl. 3.17 noch eine Anwendung der Metrik geben. Nehmen wir an, der Raum
habe eine positive Krümmung und wir beobachten eine Galaxie, deren Winkelausdehnung
dθ betrage. Ihre wirkliche räumliche Ausdehnung sei dl = ds. Wir halten dabei t, χ und φ
konstant. Mit Hilfe von Gl. A.4.8 läßt sich dann dl aus dθ bestimmen
dθ =
dl
R sin χ
(A.4.10)
Nehmen wir weiter an, der Beobachter befinde sich im Pol der Hypersphäre. Die
Winkelausdehnung erreicht ein Minimum bei χ = π / 2 , d.h. dann wenn die Galaxie sich am
Äquator der Hypersphäre befindet. dθ divergiert bei χ = π und das Bild der Galaxie
überdeckt den ganzen Himmel, wenn sie sich als Antipode am gegenüberliegenden Pol
befindet). Der Raum mit positiver Krümmung verhält sich ähnlich wie eine Sammellinse. Die
Winkelbreite dϑ des Bildes hängt von der Radialkoordinate des Objekts ab hier χ .
Für kleine Winkel χ gilt wieder
f κ2 ≈ χ und R (t ) χ = a (t ) r1
4
(A.4.12)
A.5. Mehr über Abstände
Der Lichtweg entspricht der Zeit, welche das Licht braucht, um zum irdischen Beobachter zu
gelangen. Der Lichtweg lässt sich durch Integration von cdt ausrechnen. Die entsprechende
Zeit heißt auch „light travel time“ oder wenn man von der Gegenwart zurück rechnet auch
„look back time“. Dazu schreiben wir das Differential der Zeit dt etwas um
cdt = c
Mit
da
a&
(A.5.1)
a& = H (t )a = H 0 aE (a)
(A.5.2)
da
aE (a)
(A.5.3)
wird daraus (mit c = 1)
H 0 dt =
Die Integration und Übergang zur Rotverschiebung z mit da a = − dz z ergibt
a
H 0t = ∫
0
∞
da
dz
=∫
aE (a ) 0 ( z + 1) E ( z )
(A.5.4)
Es ist
[
E ( a ) = Ω M , 0 a −3 + Ω Λ + Ω R a − 2
mit
Ω M ,0
]
1
(A.5.5)
2
8πGρ c
− c2
Λc 2
=
, ΩΛ =
, ΩR =
3H 02
3H 02
( H 0 R0 ) 2
(A.5.6)
Den Beitrag der Raumkrümmung können wir auch schreiben
Ω M ,0 + Ω Λ − 1 = Ω R
(A.5.7)
Der Ausdruck oben wird dann
[
E (a) = Ω M ,0 a −3 + Ω Λ + (Ω M , 0 + Ω Λ − 1)a − 2
]
1
(A.5.8)
2
Für κ = 0 und Ω R = 0 lässt sich das Integral über a analytisch angeben
a
H 0t = ∫
0
a
da
da
=∫
−1
aE (a ) 0 Ω M , 0 a + (1 − Ω M , 0 )a 2
[
⎡⎛ 1 − Ω
2
−1
M ,0
−1 ⎢
2
H 0 t = ⋅ (1 − Ω M ,0 ) ⋅ sinh ⎜⎜
⎢⎝ Ω M , 0
3
⎣
⎞
⎟
⎟
⎠
(A.5.9)
]
1
2
⎤
⋅a ⎥
⎥
⎦
3
2
Mit Ω M , 0 = 0,30 erhält man schließlich für die „look-back-time“
5
(A.5.10)
3
−3
H 0 t = 0,797 ⋅ sinh −1 ⎡1,527 ⋅ a 2 ⎤ = 0,797 ⋅ sinh −1 ⎡1,527 ⋅ ( z + 1) 2 ⎤
⎢⎣
⎥⎦
⎢⎣
⎥⎦
(A.5.11)
Wir plotten die Funktion f(z) =
in Einheiten der Hubble-Zeit
1/H0 . Die Ordinate gibt die Zeit an, um von dem Ereignis bei „z“ zum irdischen Beobachter
zu gelangen.
Hubble-Zeit
Fig. 5.1. look-back-time als Funktion von z in Bruchteilen von tH .
Der mitbewegte Abstand (comoving distance) oder Koordinatenabstand r eines Objekts der
Rotverschiebung z entspricht der konformen Zeit. Die Zeitdehnung wird durch a (t ) im
Nenner gerade kompensiert.
t
dt ′
(A.5.12)
DC = r = c ∫
a (t ′)
t0
Diesen Ausdruck formen wir um und benutzen dabei die Beziehungen (z ist Rotverschiebung)
da = −a 2 dz
(A.5.13
und
dt =
da
a H (t )
(A.5.14)
Wir erhalten schließlich
1
0
0
dt
da
dz ′
dz ′
= c∫ 2
= c∫
= DH ∫
a (t )
H ( z ′)
E ( z ′)
t0
a a H (a)
z
z
t
DC = r = c ∫
6
(A.5.15)
c
dz
= 4,228·109 pc oder 13.8 ·109 Lj.
. Der Hubble-Abstand beträgt DH =
2
H0
( z + 1)
Leider lässt sich die Integration von (A.5.15) nur numerisch ausführen. Berechnet man den
mitbewegten Abstand für κ = 0 zum Horizont (a = 1 bis a = 0) und berücksichtigt nur die
Massendichte so erhält man
2 DH
rH =
= 3,85 Gpc
(A.5.16)
ΩM
mit da =
wobei Ω M = 0,27 eingesetzt wurde. Nimmt man auch die dunkle Energie mit also
E (a) = (Ω M a −3 + Ω Λ ) ergibt sich (numerisch)
rH = 3,35 Gpc .
(A.5.17)
Liegt ein transversaler mitbewegter Abstand l vor, so dass gilt
l = rH ⋅ dθ
(A.5.18)
Für κ ≠ 0 geht man von Robertson-Walker-Metrik aus
c 2 dt 2 = a 2 R02 sin 2 (r / R0 ) ⋅ dθ 2
(A.5.19)
Nachdem man die Wurzel gezogen hat, kann man die rechte Seite von (5.19) und die rechte
von (5.18) geleichsetzen.
1
Man erhält dann c ∫
a
da
1
⎡
⎤
= rH (κ = ±1) = R0 ⎢(r / R0 ) m (r / R0 ) 3 ⎥
6
a H (a)
⎣
⎦
2
(A.5.20)
oder
rH (κ = +1) =
DH
ΩK
1
sin( Ω K
∫a
0
2
da
)
E (a )
(A.5.21)
Für negative Krümmung steht anstatt „sin“ dann „sinh“. Wenn die Krümmung klein ist, kann
man für r näherungsweise r = rH (κ = 0) siehe oben setzen.
Als Nächstes wollen wir den Eigenabstand DP (proper distance) definieren, wobei die
Raumpunkte, welche den Abstand DP definieren, gleichzeitig gemessen werden müssen, d.h.
dt = 0 . Wir erhalten aus − ds 2 = R0 a(t ) ⋅ dχ für DP
t2
DP = c ∫ dt = a(t ) ⋅ r = DC ⋅ ( z + 1)
−1
(A.5.22)
t1
In nichteuklidischen Fällen kann χ (z ) wieder durch eine Reihenentwicklung entsprechend Gl.
(5.20) ersetzt werden.
7
D H 0 dz ′
DP = R0 a (t ) ∫ dχ = a (t ) ∫ dr = a (t ) ⋅ DC =
( z + 1) ∫z E ( z ′)
0
0
1
1
(A.5.23)
.
Wir waren bei den Beobachtungen zum Hubble-Gesetz noch auf ein anderes Entfernungsmaß
gestoßen: die scheinbare Helligkeit. Von der Abstrahlung einer Quelle mit der Leuchtkraft L
im Abstand r1 a(t 0 ) messen wir die ankommende Intensität I. Die Leuchtkraft L wird in Watt
gemessen. Mit der Definition des Leuchtkraft-Abstands DL, tun wir so, als ob wir die
Messung in einem statischen euklidischen Raum vornehmen würden
I=
L
4π DL
2
=
L a 2 (t )
4π r12 a02
(A.5.24)
Die Energie der ankommenden Photonen nimmt aber wie a = ( z + 1) −1 mit wachsender
Rotverschiebung ab. Außerdem kommen um 1 / z + 1 weniger Photonen pro Zeiteinheit beim
Beobachter an. Dies zusammen ergibt (A.5.14) und durch Vergleich mit r1 = DC
DL = (1 + z ) DC
(A.5.25)
Die übliche Diskussion des Winkelabstands D A (angular distance) wollen wir hier für ein
Objekt führen, dass sich in konstantem Abstand r1 (dr = 0, dt = 0) bei der Rotverschiebung z
senkrecht zur Sichtlinie befindet und die Ausdehnung ds besitzt (proper distance). Für die
beobachtete Winkelausdehnung dθ gilt dann nach Gl. (A.4.8)
ds 2 = a 2 r12 dθ 2 = D A2 dθ 2
(A.5.26)
und für den Zusammenhang von D A und DC
DA =
DC
z +1
(A.5.27)
Gl. (A.5.26) beschreibt die gleich Situation wie (A.5.18) mit dem Unterschied, dass wir das
transversale Streckenelement bei der Rotverschiebung z betrachten. Dann ist der
Zusammenhang mit dem Winkelelement durch DA gegeben, was man aber leicht aus DC
gewinnt.
Vergleichen wir noch mit Gl. (A.5.25) dann ergibt sich
DL = D A (1 + z ) 2
(A.5.22)
Welches Entfernungsmaß ist am Ende das richtige? Jedes steht für eine bestimmte
Messmethode. So ist der Lichtweg mit DC (1 + z ) verknüpft, die Entfernung aus
Helligkeitsmessungen mit DL , Winkelabstände und Gravitationslinsen-Effekte mit DA .
8
A.6. Horizonte
Selbst wenn unser Kosmos unendlich ausgedehnt wäre (was nur für κ = 0, − 1 zuträfe),
könnten wir nur den Teil beobachten, von welchem uns Lichtsignale erreichen. In diesem
Sinne definiert man den Teilchenhorizont als den geometrischen Ort aller Ereignisse, von
welchem Lichtsignale beim Beobachter gerade noch eintreffen können. Wenn die
Lichtsignale zur Zeit t1 = 0 emittiert wurden und zur Zeit t 2 = t bei r = rH detektiert
werden, dann ist der Weg in mitbewegten Koordinaten
t
a
dt ′
da
= c∫ 2
rH = c ∫
(A.6.1)
a(t ′)
0
0 a H (a)
Im euklidischen Kosmos κ = 0 ist dominiert die Materie mit Ω M a −3 die Expansion, wenn gilt
z eq >> z >> 0 (s. dazu P.Schneider: Extragalactic Astronomy and Cosmology.Springer Verl.
2006 Ch. 4.5) . In diesem Fall ist
H 2 = H 02 Ω M a −3
(A.6.2
und
1
a 2 H = H 0 Ω M2 a
1
(A.6.3)
2
Wir berechnen nach (A.6.1) den (Koordinaten-)Abstand des Horizonts (z.B. bei
Rekombination), dem der Skalenparameter a = ( z + 1) −1 zugeordnet ist
1
rH = c ∫
a
a′
−1
2
da ′
1
H 0 Ω M2
=
2c a
1
1
2
=
1
H 0 Ω M2
a
2c
1
H 0 Ω M2
⎤
⎡
1
⎥
⎢1 −
1
⎢⎣ ( z + 1) 2 ⎥⎦
(A.6.4)
Für den Horizont der Hintergrundstrahlung ergibt sich mit z = 1089
0
rH ≈
2c
1
H 0 Ω ( z + 1)
2
M
1
= 13,7 ⋅ 10 9 ⋅ (3,92 − 0,030) = 53,29 ⋅ 10 9 Lj
2
(A.6.5)
z =1089
Ganz analog lässt sich für den Fall, dass die Strahlung Ω γ a −4 die Expansion dominiert, d.h.
für z >> z eq zeigen, dass gilt
0
rH ≈
c
(A.6.6)
1
H 0 Ω γ 2 ( z + 1)
9
z
Der Teilchenhorizont ist die Fläche, die alle Punkte enthält, von welchen
uns Lichtsignale gerade noch erreichen
t
t0
r
rH
Fig. A.6.1. Ausbreitung eines Signals auf dem Lichtkegel bis zum Horizont, der realistisch mit
Rekombination zusammenfällt.
Um Verwechslungen vorzubeugen, definieren wir noch den Ereignishorizont. Er ist der
geometrische Ort aller Ereignisse, von welchen ein Lichtsignal eine unendliche Zeit benötigt,
um zum Beobachter zu gelangen
10
Der Ereignishorizont enthält alle Ereignisse, von welchen das Licht zu
bis zu uns eine unendlich lange Zeit benötigt
∞
r
rEH = ∫
t
cdt ′
= DC
a(t ′)
EH
Integral divergiert für Materie- und Strahlungskosmos, d.h. alle Signale
erreichen in endlicher Zeit den Beobachter. Für Ω jedoch ist rEH endlich, d.h.
Signale von Ereignissen, welche im Endlichen liegen erreichen uns nicht
mehr.
Λ
Fig. A.6.2. Der Ereignishorizont in der Skizze liegt außerhalb des Lichtkegels des Beobachters.
∞
rEH = ∫
t
cdt ′
a(t ′ )
(A.6.7)
Sowohl für den Strahlungskosmos wie auch für den Materiekosmos divergiert das Integral,
d.h. alle Signale erreichen noch in endlicher Zeit den Beobachter.
Wenn die Dunkle Energie, wie wir später sehen werden, den überwiegenden Anteil zur Dichte
beiträgt, dann gilt
2
⎡ a& ⎤
2
⎢⎣ a ⎥⎦ = H 0 Ω Λ
(A.6.8)
a = a (t 0 ) exp( H 0 Ω1Λ/ 2t )
(A.6.9)
was integriert ergibt
Aus Gl. 3.36 erhält man dann
rH =
D
c
= 1H/ 2
1/ 2
H 0Ω Λ
ΩΛ
(A.6.10)
wobei DH die Hubble-Länge ist ( Ω1Λ/ 2 = 0,904 ).
11
A.7. Konforme Zeit, Friedmann-Gl für κ ≠ 0 .
Die konforme Zeit (conformal time) wird in der Kosmologie häufig benutzt
dη =
dt
a(t )
(A.7.1)
Wie man aus Gl. 3.24 sieht, hängt η mit dem Lichtweg bzw. der mitbewegten Koordinaten
zusammen
t
dt ′
r = c∫
= c ⋅η
(A.7.2)
a(t ′)
0
(3.37)
Im Allgemeinen ist η nur bis auf eine Konstante bestimmt. Mit der Einführung von dη lässt
sich die Robertson-Walker-Metrik für κ = 0 besonders einfach schreiben
[
(
ds 2 = a 2 (t ) ⋅ c 2 dη 2 − dr 2 − r 2 dθ 2 + sin 2 ϑdφ 2
)]
(A.7.3)
wobei wir noch c = 1 gesetzt haben.
Wir werden jetzt die 2. Friedmann-Gl. (2.14) für κ ≠ 0 mit Hilfe der konformen Zeit lösen,
indem wir setzen dt = a(η ) dη . Das ergibt
a′2 +
Wir setzen
κ c2
R02
κ c2
2
0
R
a2 =
8π G
ρ a4
3
(A.7.4)
= k , differenzieren noch einmal nach η und erhalten zunächst
8πG
a ′a ′′
+ 2ka ′ =
4 ρ a 2 a ′ + ρ ′a 3
a
3
Dann ersetzen wir ρ ′ mit Hilfe von (2.19)
[
2
]
(A.7.5)
a′
( ρ c 2 + p)
a
Das Ergebnis ist folgende Dgl.
ρ ′ = −3
a ′′ + ka =
(A.7.6)
4π G
( ρ c 2 − 3 p)a 3
3
(A.7.8)
1) Lösung für ein Strahlungsuniversum ρ = ρ γ mit p =
a ′′ + ka = 0
1
ρ c 2 ergibt
3
(A.7.9)
mit
12
κ c2
mit κ = −1, 0, + 1
R02
Die Lösungen sind
k=
a (η ) = a m sinh η
a (η ) = a mη
a (η ) = a m sin η
(A.7.10)
κ = −1
κ= 0
κ = +1
(A.7.11)
Hier ist a m eine Integrationskonstante; außerdem wurde für alle 3 Lösungen die
Anfangsbedingung a(η = 0) = 0 gewählt. Wir können jetzt die Zeit berechnen
aus
dt = a (η )dη
t = t m ⋅ (cosh η − 1)
!
t = tm η 2
2
t = t m ⋅ (1 − cosη )
(A.7.12)
2) Lösungen für ein Materie (Staub) gefülltes Universum mit p = 0 . Wegen
ρ M ⋅ a 3 = konstant ist die rechte Seite von (2.51) eine Konstante. In diesem Fall sind
die Lösungen
1
a m ⋅ (cosh η − 1)
2
a (η ) = a m ⋅ η 2
a (η ) =
a (η ) =
(A.7.13)
1
a m ⋅ (1 − cosη )
2
Im letzten Ausdruck ist
aM =
Ω M ,0
Ω M ,0 − 1
und
t = t m ⋅ (sinh η − η )
1
t = tm ⋅ η 3
3
t = t m ⋅ (η − sin η )
(A.7.14)
mit
tm =
Ω M ,0
tH
⋅
2 (Ω − 1) 3 2
M ,0
13
A.8. Einige Beziehungen aus der Riemannschen Geometrie.
Die Riemannsche Geometrie befaßt sich mit n-dimensionalen Räumen, in welchen ein
Längenelement gegeben ist durch Gl. 3.1
ds 2 = g αβ dx ε dx β
(A.8.1)
mit nicht verschwindender Determinante
g = Det g αβ
(A.8.2)
Diese Räume heißen Riemannsche Räume oder Riemannsche Mannigfaltigkeiten.
Wir unterscheiden ko- und kontravariante Vektoren und deren Differentiale
dx μ = (cdt ,−dx,−dy,−dz )
(A.8.3)
dx μ = (cdt , dx, dy, dz )
(A.8.4)
bzw.
Zwischen der ko- und der kontravarianten Form des metrischen Tensors besteht die
Beziehung
g μν g νλ = δ μλ
(A.8.5)
Der metrische Tensor hebt und senkt Indizes
A α = g αβ Aβ
(A.8.6)
Aα = g αβ Aβ
(A.8.7)
14
Fig. A.8.1. Paralleltransport eines Vektors auf einer Kugelfläche. In diesem extremen
Beispiel hat sich die Richtung des Vektors nach einem Umlauf im Dreieck um +90°
geändert.
Der parallele Transport eines Vektor auf einer geschlossenen Kurve in krummlinigen
Koordinaten ändert i.a. die Richtung des Vektors im Gegensatz zum parallelen Transport in
karthesischen Koordinaten. Die Änderung eines Vektors nach einem Umlauf durch eine
geschlossene Schleife ist
μ
δA μ = − ∫ Γαβ
A α dx β
(A.8.8)
μ
Die Γαβ heißen Konnektionen oder Christoffel-Symbole.
Anstelle der gewöhnlichen partiellen Differentiation tritt in der Riemannschen Geometrie die
kovariante Differentiation. Man nimmt dabei die Änderung des Vektors an dem benachbarten
μ
μ
μ
α
Punkt A ( x ) → A ( x + δx ) und zieht davon die Parallelverschiebung ab Γαβ A . Im
Gegensatz zur gewöhnlichen Differentiation steht hier der Index der Koordinaten, nach
welcher differenziert wurde, hinter einem Semikolon
∂Aμ
A = ν + Γνλμ Aλ = A,μν + Γνλμ Aλ
∂x
μ
;ν
(A.8.9)
Kurz gesagt berücksichtigt die kovariante Differentiation auch die Änderung des
Bezugssystems in einem krummlinigen Koordinatensystem.
Ko- und kontravariante Form lassen sich wieder durch den metrischen Tensor ineinander
überführen
A;βμ = g αβ Aβ;μ und Aβ;μ = g αβ A;βμ
15
(A.8.10)
Die Konnektionen (Christoffel-Symbole) gewinnt man aus den Komponenten des metrischen
Tensors wie folgt
1
Γνλμ = g μσ (gσν , λ + gσλ ,ν − gνλ ,σ )
(A.8.11)
2
In torsionsfreier Geometrie sind folgende Komponenten gleich
Γνλμ = Γλνμ
(A.8.12)
Aus Gl. A.8.10 und A.8.12 findet man, daß die kovariante Ableitung des metrischen Tensors
verschwindet
g μν;λ = 0 und g ;μν
λ =0
(A.8.13)
Bei der zweifachen kovarianten Ableitung kommt es auf die Reihenfolge des Differenzierens
an. Insbesondere ist
σ
Aμ;ν ;λ − Aμ;λ ;ν = Aσ Rˆ μνλ
(A.8.14)
σ
Hier ist R̂μνλ der Riemannsche Krümmungs-Tensor. Zieht man den oberen Index
nach unten
ρ
Rσμνλ = g σρ Rμνλ
(A.8.15)
so gelten für den Riemann-Tensor folgende Symmetrie-Beziehungen
Rσμνλ = − Rμσνλ = − Rσμλν
(A.8.16)
Rσμνλ = Rνλσμ
(A.8.17)
Permutation der letzten 3 Indizes ergibt die Beziehung
Rσμνλ + Rσνλμ + Rσλμν = 0
(A.8.18)
Die so genannte Bianchi-Beziehung erhält man durch kovariantes Differenzieren
σ
σ
σ
Rμνλ
; ρ + R μρν ;λ + R μλρ ;ν = 0
(A.8.19)
Der Ricci-Tensor Rμν , der in den EG vorkommt, lässt sich aus dem Riemann-Tensor wie
folgt gewinnen
σ
Rμν = g λσ Rλμσν = Rμσν
(A.8.20)
16
Zur Berechnung von Rμν aus den g σλ bedient man sich am besten der Beziehung
λ
λ
σ
σ
λ
Rμν = Γμνλ ,λ − Γμλ
,ν + Γμν Γλσ − Γμλ Γνσ
(A.8.21)
Schließlich erhalten wir den Ricci-Skalar
R = g μν Rμν
(A.8.22)
Zur Diskussion des Einstein-Tensors gehen wir von der Bianchi-Beziehung aus
σ
ˆσ
ˆσ
Rˆ μνλ
;ρ + Rμρν;λ + Rμλρ;ν = 0
und kontrahieren sie über σ und ν (d.h. Multiplikation mit g
Indizes) mit dem Ergebnis
(A.8.23)
σμ
und Summation über gleiche
σ
ˆ
Rˆ μλ;ρ − Rˆ μλρ
;σ − Rμρ;λ = 0
(A.8.24)
Nach einer weiteren Kontraktion über μ und ρ erhalten wir schließlich
1
Rˆ λσ;σ − Rˆ ;λ = 0
2
(A.8.25)
was man abgekürzt schreiben kann
Gλσ;σ = 0
(A.8.26)
Dieser kovariant differenzierte symmetrische Tensor
1
Gβα = Rˆ βα − Rˆ δ βα
2
(A.8.27)
heißt Einstein-Tensor, seine kovariante Ableitung (oder kovariante Divergenz) verschwindet.
Die Ableitung des Ortsvektors nach dem Kurvensegment ds ergibt den Tangentenvektor
ξα =
Die (kovariante) Ableitung
oder auch mit ds = dτ
dx α
ds
(A.8.28)
D
des Tangentenvektors erhält man nach Gl. A.5.10 wie folgt
ds
Dξ μ
d 2x
= ξ μ ; S = 2 + Γλνμ ξ λξ ν
ds
ds
17
(A.8.29)
Hier ist s oder τ sind Parameter auf der Kurve, zu der ξ α die Tangente bildet. (A.829) heißt
Geodätengleichung. Die Geodäte ist der kürzeste Abstand zwischen zwei Punkten , also das
Resultat einer Variation von
δ ∫ ds = 0
oder
δ ∫ ds 2 = 0
(A.8.31)
was hier nicht bewiesen werden soll. Es führt auf die Geodätengleichung
λ
ν
d 2xμ
μ dx dx
+
Γ
=0
λν
ds ds
ds 2
(A.8.30)
Das erste Glied beschreibt die Änderung der Tangente entlang ds, das zweite Glied subtrahiert
davon den Anteil der Parallelverschiebung. Auf einer Geodäten kompensieren sich beide
Teile, d.h. die zweifache kovariante Ableitung verschwindet. . In der ART verlaufen
kräftefreie Bewegungen von Massen immer auf Geodäten, d.h. das Extremalprinzip Gl.
A.8.31 ist immer erfüllt
A.9. Der Dopplereffekt in der speziellen Relativitätstheorie.
Eine Lichtquelle bewege sich mit der Geschwindigkeit υ in positiver x-Richtung. Das
Korodinatensystem der Lichtquelle sei (ct , x, y, z ) , das des Detektors (ct ′, x′, y ′, z ′) . Die
Phase der Lichtwelle
kx − ωt = k ′x′ − ω′t ′
(A.9.1)
ist ein Skalar und ändert sich nicht bei einer Lorentz-Transformation
x = γ ( x′ + βct ) und ct = γ (ct ′ + βx′ )
mit
β=
1
υ
und γ =
c
1 − β2
(A.9.2)
(A.9.3)
Wir setzen Gl. A.7.2 in Gl. A.7.1 auf der rechten Seite ein und erhalten
ω⎞
ω⎞
ω′
⎛
⎛
γ⎜ k − β ⎟ x′ − γ⎜ − kβ + ⎟ct ′ = k ′x′ − ct ′
c⎠
c⎠
c
⎝
⎝
(A.9.4)
Koeffizientenvergleich ergibt
ω′ ⎛ ω
⎞
= γ⎜ − kβ ⎟
c
⎝c
⎠
Im Vakuum ist
18
(A.9.5)
k=
ω
c
(A.9.6)
was wir rechts in Gl. A.7.5 einsetzen. Wir erhalten für die Frequenzen
⎛1 − β ⎞
1− β
ω′
=
=
⎜
⎟
ω
1 − β2 ⎝ 1 + β ⎠
1
2
(A.9.7)
oder für die Wellenlängen
λ′ ⎛ 1 + β ⎞
=⎜
⎟
λ ⎝1 − β ⎠
1
2
(A.9.8)
Für kleine Geschwindigkeiten β << 1 erweitern wir den Bruch mit (1 + β )
und erhalten so
λ′ − λ
≅β
λ
1
2
(A.9.9)
Man beachte aber, dass es sich bei der kosmologischen Rotverschiebung nicht um einen
Dopplereffekt handelt.
A.10. Der Energie-Impuls-Tensor
Der Energie-Impuls-Tensor enthält die Quellen des Gravitationsfelds. In einem Inertialsystem
in der Minkowski-Metrik hat er für eine ideale Flüssigkeit die Form
T μν
⎛ε
⎜
⎜0
=⎜
0
⎜⎜
⎝0
0
0
p
0
0
p
0
0
0⎞
⎟
0⎟
0⎟
⎟
p ⎟⎠
(A.10.1)
Ein Energie-Impuls-Tensor kann für jedes klassische Feld (Flüssigkeiten, Gase,
elektromagnetische Felder) angegeben werden. Wenn sich die Flüssigkeit mit der 4Geschwindigkeit
r
u μ = γ (1,− υ / c )
(A.10.2)
bewegt, lauten die Komponenten
T μν = (ε + p )u μ u ν − pημν
19
(A.10.3)
wobei η μν ≡ (1,−1 − 1 − 1) der metrische Tensor der Minkowski- Metrik bedeutet. In der ART
ist η μν durch g
μν
zu ersetzen. F ür die kontravariante Form gilt
Tμν = (ε + p )uμ u ν − pg μν
Tμν = T λσ g λμ g σν
und
(A.10.4)
Das Inertialsystem in der Kosmologie hat nach Kap. 3 die 4–Geschwindigkeit
u μ = (1,0,0,0)
(A.10.5)
Unter Berücksichtigung der Komponenten des metrischen Tensors
g 00 = 1 ,
g11 = − R 2 / (1 − κr 2 ), g 22 = − r R , g 33 = − sin θ R r
2
2
2
2
2
erhalten wir
T00 = ε , T11 = pR 2 / (1 − κr 2 ) ,
T22 = pr 2 R 2 , T33 = pr 2 sin 2 θ R 2
(A.10.6)
In der Minkowski-Metrik leitet man aus dem Verschwinden der Divergenz von Gl. A.10.3
Erhaltungsdsätze für die Energieströmung her
∂ μν
T = T,vμν = 0
ν
∂x
(A.10.7)
In der ART tritt anstelle von Gl. A.8.7 die kovariante Ableitung
μ
ν
T;vμν = T,vμν + Γνσ
T σν + Γνσ
T μσ = 0
(A.10.8)
Um die ziemlich unübersichtliche Rechnung zu erleichtern, empfielt es sich, die Summen
zunächst nach ν = 0, 1, 2, 3 zu gliedern
T;vμν = T, 0μ 0 + Γ0μσT σ 0 + Γ00σT μσ
+ T,1μ1 + Γ1μσT σ1 + Γ11σT μσ
(A.10.9)
+ T, 2μ 2 + Γ2μσT σ 2 + Γ22σT μσ
+ T,3μ 3 + Γ3μσT σ3 + Γ33σT μσ = 0
Es werden zur Auswertung noch benötigt
Γ110 = c −1 RR& / (1 − κr 2 ) ,
Γ220 = c −1r 2 RR& ,
Γ330 = c −1r 2 sin 2 θ RR& ,
1
Γ01
= c −1 R / R& ,
Γ111 = κr / (1 − κr 2 ) ,
1
Γ22
= −r / (1 − κr 2 ) ,
20
Γ331 = −r (1 − κr 2 )sin 2 θ ,
Γ022 = c −1 R / R& ,
Γ122 = 1 / r ,
Γ332 = − sin θ cos θ ,
Γ033 = c −1 R / R& ,
Γ133 = 1 / r ,
Γ233 = ctgθ
Nach Weglassen der Glieder, welche sich gegenseitig wegheben, erhält man aus Gl. A.8.9
folgendes Resultat (nach Zeilen geordnet)
ε&
+
c
p R& ε R&
+
+
c R cR
p R& ε R&
+
+
c R cR
p R& ε R&
+
+
=0
c R cR
T;vμν =
(A.10.10)
oder
ε& + 3(ε + p )
R&
=0
R
(A.10.11)
Zur Diskussion von Gl. A.10.11. : Wenn p << ε (baryonische Materie) dann wird
R&
ε&
= −3
R
ε
(A.10.12)
ε ∝ R −3
(A.10.13)
oder
d.h. Masse, bzw. Energie bleibt erhalten. Wenn der Druck p nicht verschwindet, ist noch eine
Zustandsgleichung erforderlich. Für Strahlung ist z.B. p =
ε r ∝ R −4
1
ε r und man erhält
3
(A.10.14)
Eine Aussage über den Verlauf von R(t ) , bzw. a (t ) für p ≠ 0 erhält man auf folgende
3
Weise aus Gl. A.8.11: Addition von p& auf beiden Seiten, danach Multiplikation mit R . Das
Resultat kann man wie folgt schreiben
21
ε& R 3 =
Wir überführen
[
]
d 3
R (ε + p )
dt
(A.10.15)
d
d
in
, indem wir durch R& dividieren. Nach Umordnen der Glieder
dt
dR
erhalten wir
d
(εR 3 ) = −3 pR 2
dR
(A.10.16)
−3
Ist p > 0 dann nimmt die Dichte mit zunehmendem R(t) wenigstens wie R ab.
A. 11. Kosmologische Entfernungen (s. Gl. 3.32 , 3.34 und 5.14).
Wir geben hier die gerechneten Kurven für 3 Größen an: die „look-back-time“ ( t − t 0 ) zu z,
den mitbewegten Abstand (comoving distance) r eines Objekts der Rotverschiebung z. Er
beschreibt den Lichtweg und ist der konformalen Zeit proportional
dt ′
= −c ∫ ( z + 1)dt ′
′
(
)
a
t
0
0
t
t
DC = r = c ⋅ τ = c ∫
(A.11.1)
schließlich den Eigenabstand
DP = a(t ) ⋅ r = r ⋅ ( z + 1)
−1
(A.11.2)
a(t ) wird mit Gl. 5.14 berechnet. Alle 3 Größen werden sind in einem Digramm aufgetragen
und in 106 Lichtjahren angegeben (1 pc = 3,2616 Lj). Die Farben bedeuten: rot „look-backtime“, grün mitbewegter Abstand
22
Fig. A.11.1. Rote Kurve : Look-back-time , Güne Kurve : „conformal time“ τ oder
mitbewegter Abstand r . Blaue Kurve : Eigenabstand d . Alle Werte in 106 Lichjahren
gegen Rotverschiebung z (1 pc = 3,6216 Lj).
Fig. A.11.2. Wie oben aber Rotverschiebung bis z = 7 aufgetragen.
Die „look-back-time“ wurde mit folgender Beziehung aus Gl. 5.14 berechnet
23
t = 13,7 ⋅ 0,787 ⋅ Ar sinh(1,64(1 + z )
−3
2
)
(A.11.3)
Die „look-back-time“ wird dann
t l = 13,7 − t
(A.11.4)
A.12. Fluid-Gleichung und erste Friedmann-Gleichung.
Man kann die 1. Friedmann-Gl. auch mit Hilfe der Newtonsfhen Mechanik ableiten, benötigt
dazu aber die Thermodynamik. Wir beginnen mit dem 1. Hauptsatz der Thermodynamik
dU + pdV = TdS
(A.12.1)
Für die Energie pro Volumen im expandierenden Kosmos setzen wir
⎛ 4π 3
⎞ 4π 3 2 &
dU = d ⎜
a ⋅ ρ c2 ⎟ =
a c ⋅ ρ dt + 4πa 2 a& da ⋅ ρ c 2
⎝ 3
⎠ 3
(A.12.2)
und für
pdV = p ⋅ 4πa 2 da
(A.12.3)
Bei adiabatischer Ausdehnung ( dS = 0 ) ist die zeitliche Entwicklung
dE
dV
+p
=0
dt
dt
(A.12.4)
Einsetzen ergibt
a& ⎛
p⎞
⎟=0
a⎝
c2 ⎠
Diese Gleichung beschreibt die Erhaltung von Masse und wird manchmal
auch „Fluid-Gleichung“ genannt (s. A. Liddle).
ρ& + 3 ⎜ ρ +
(A.12.5)
Wir wollen nun Gl. (2.14) nach der Zeit ableiten
2
κ c2
⎛ a& ⎞ 8πG
ρ =− 2 2
⎜ ⎟ −
3
R0 a
⎝a⎠
(A.12.6)
nach der Zeit ableiten
2
κ c 2 a&
a& aa&& − a& 2 8π
&
ρ
=
+
2
a a2
3
R0 a 3
24
(A.12.7)
a&
mit Hilfe von (2.14). Damit landen wir
a
schließlich bei der ersten Friedmann-Gleichung (2.5a)
Wir ersetzen ρ& aus (2.19) und eliminieren
a&&
4π ⎛
3p ⎞
=−
G⎜ ρ + 2 ⎟
a
3 ⎝
c ⎠
(A.12.8)
25