Übungsblatt 5
Werbung
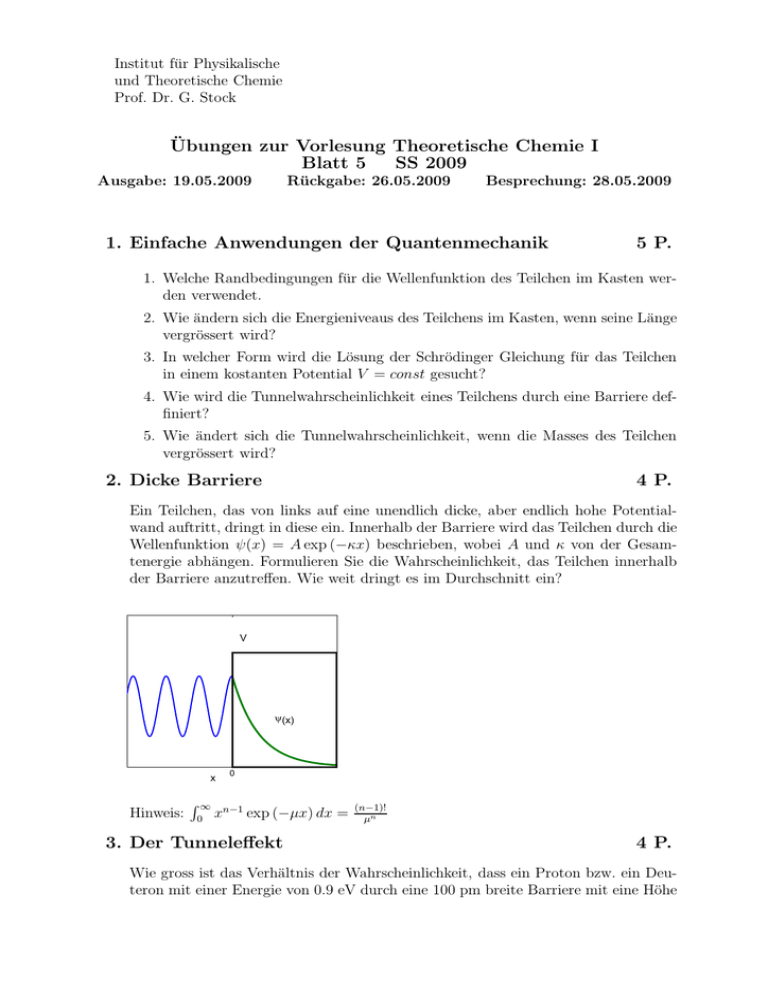
Institut für Physikalische und Theoretische Chemie Prof. Dr. G. Stock Übungen zur Vorlesung Theoretische Chemie I Blatt 5 SS 2009 Ausgabe: 19.05.2009 Rückgabe: 26.05.2009 Besprechung: 28.05.2009 1. Einfache Anwendungen der Quantenmechanik 5 P. 1. Welche Randbedingungen für die Wellenfunktion des Teilchen im Kasten werden verwendet. 2. Wie ändern sich die Energieniveaus des Teilchens im Kasten, wenn seine Länge vergrössert wird? 3. In welcher Form wird die Lösung der Schrödinger Gleichung für das Teilchen in einem kostanten Potential V = const gesucht? 4. Wie wird die Tunnelwahrscheinlichkeit eines Teilchens durch eine Barriere deffiniert? 5. Wie ändert sich die Tunnelwahrscheinlichkeit, wenn die Masses des Teilchen vergrössert wird? 2. Dicke Barriere 4 P. Ein Teilchen, das von links auf eine unendlich dicke, aber endlich hohe Potentialwand auftritt, dringt in diese ein. Innerhalb der Barriere wird das Teilchen durch die Wellenfunktion ψ(x) = A exp (−κx) beschrieben, wobei A und κ von der Gesamtenergie abhängen. Formulieren Sie die Wahrscheinlichkeit, das Teilchen innerhalb der Barriere anzutreffen. Wie weit dringt es im Durchschnitt ein? V ψ(x) x Hinweis: R∞ 0 0 xn−1 exp (−µx) dx = 3. Der Tunneleffekt (n−1)! µn 4 P. Wie gross ist das Verhältnis der Wahrscheinlichkeit, dass ein Proton bzw. ein Deuteron mit einer Energie von 0.9 eV durch eine 100 pm breite Barriere mit eine Höhe von 1.0 eV tunnelt. Wie gross is das Verhältnis der beiden Wahrscheinlichkeiten, wenn die Barriere bei sonst gleichen Bedingungen doppelt so breit ist? 4. Harmonischer Oszillator Ein harmonischer Oszillator mit dem Hamiltonian Ĥ = in dem Quantenzustand 4 P. p̂2 2m + 12 mω 2 x2 , befindet sich 1 mω 1/4 X2 Ψ1 (x) = √ exp − 2X , 2 2 ~π wobei X = p mω x ist. Berechnen Sie die mittlere Gesamtenergie ~ D 2E p̂ des Systems. mittlere kinetische Energie 2m D E Ĥ und die











