1 Einleitung

1 Einleitung
Dieser Teil der Vorlesung beschäftigt sich mit mathematischen Methoden der Signalverarbeitung.
Ein Signal ist dabei eine Funktion t 7−→ x(t), die Information trägt.
Das Argument t ist in diesem Zusammenhang meistens als Zeit zu verstehen, wie z.B.
bei einem Sprachsignal.
Es kann aber auch wie z.B. bei der Bildverarbeitung einen Punkt (t1 , t2 ) aus einem zweidimensionalen Bereich repräsentieren. x(t1 , t2 ) ∈ R3 ist dann etwa der RGB-Farbwert
des entsprechenden Bildpunkts.
Im Rahmen der Signalübertragung von einem Sender zu einem Empfänger ist das empfangene Signal etwas Zufälliges, das dem Empfänger vorher nicht bekannt ist (Sonst
hätte es gar nicht gesendet werden müssen).
Mathematisch modellieren wir einen solchen Zufallsvorgang durch einen Wahrscheinlichkeitsraum (Ω, A, P ), eine Indexmenge T , die die Zeit repräsentiert, und eine Abbildung
t, ω 7−→ X(t, ω), die man wie folgt interpretieren kann:
ω ist die zufällig ausgewählte Information, die zum Empfänger gesendet werden soll.
Jedem solchen Informationselement ist zugeordnet die Funktion
t 7−→ X(t, ω)
die diese Information trägt, also das Signal.
Für die mathematische Behandlung von Signalen ist eine andere Sichtweise zweckmäßiger,
nämlich die Beobachtung der möglichen Signalwerte
ω 7−→ X(t, ω)
zu einem festen Zeitpunkt t. Daraus resultiert die folgende
5
Definition 1.1 Eine durch eine Menge T indizierte Familie X = (X(t), t ∈ T ) von
Zufallsvariablen ω 7−→ X(t, ω) auf einem Wahrscheinlichkeitsraum (Ω, A, P ) heißt ein
stochastischer Prozess.
In dieser Vorlesung ist T immer die Zeitachse, wobei wir
kontinuierliche Zeit: T = (−∞, ∞) oder T = [0, ∞)
und
diskrete Zeitpunkte: T = {0, T, 2T, 3T, . . .} oder T = {kT ; k ∈ Z}
unterscheiden. Im letzteren Fall schreibt man meistens Xk anstelle von X(kT ), d.h.
X = (X0 , X1 , X2 , . . .) bzw. X = (. . . , X−2 , X−1 , X0 , X1 , X2 , . . . ) ist eine Folge von Zufallsvariablen.
Für festes ω heißt die Funktion t 7−→ X(t, ω) eine Realisierung des stochastischen
Prozesses X.
2 Zufallsvariable
Eine kurze Zusammenfassung der Begriffe und Größen, die in Verbindung mit Zufallsvariablen wichtig sind.
(Ω, A, P ) sei ein Wahrscheinlichkeitsraum und B bzw. Bn die σ-Algebra der Borelschen
Mengen von R bzw. des Rn .
2.1 Reelle Zufallsvariable
Zufallsvariable
Eine A-B-messbare Abbildung X : Ω −→ R heißt eine (reelle) Zufallsvariable.
Verteilung einer Zufallsvariablen
Die eindimensionale Verteilung P X auf R, die durch P X (B) = P (X ∈ B) festgelegt ist,
heißt die Verteilung von X.
Verteilungsfunktion einer Zufallsvariablen
Die Verteilungsfunktion
F X (t) = P X (−∞, t] = P (X ≤ t)
der Verteilung P X heißt auch die Verteilungsfunktion von X.
Dichte einer Zufallsvariablen
Ist die Verteilung P X absolutstetig, d.h. gibt es eine Funktion f X (t) mit
Z
Z
X
X
P (B) = P (X ∈ B) = 1B (t)f (t) dt =
f X (t) dt
B
so heißt sie die Dichte der Zufallsvariablen X.
Erwartungswert einer Zufallsvariablen
6
Sofern das Integral existiert, heißt
Z
Z
X
EX = X(ω)P (dω) = t f (t) dt
der Erwartungswert von X.
Rechenregeln: Es gilt immer
E (aX + bY + c) = aEX + bEY + c
und für stochastisch unabhängige Zufallsvariable X, Y ist
E (XY ) = EXEY
2.2 Komplexwertige Zufallsvariable
Da der Querstrich in der Stochastik schon eine festgelegte Bedeutung besitzt, bezeichnen
wir die Konjugierte einer komplexen Zahl z = x + jy mit einem ∗: z ∗ = x − jy.
Bei der Behandlung elektrischer Signale kommt man nicht ohne komplexe Zahlen aus.
Daher:
Definition 2.1 Eine komplexe Zufallsvariable ist eine Abbildung X : Ω −→ C der Form
X(ω) = XRe (ω) + jXIm (ω) mit zwei reellen Zufallsvariablen XRe und XIm .
Die Verteilung einer komplexen Zufallsvariablen wird im folgenden keine große Rolle
spielen. Nur der Vollständigkeit halber:
Verteilung einer komplexen Zufallsvariablen
Die Wahrscheinlichkeit P X (B) ist definiert als die Verteilung P (XRe ,XIm ) (B) des zweidimensionalen Zufallsvektors (XRe , XIm ), wobei die Menge B als Teilmenge des R2 aufgefasst wird.
Der Erwartungwert einer komplexen Zufallsvariablen
Der Erwartungswert von X = XRe + jXIm ist definiert als
EX = EXRe + jEXIm
Die Kovarianz zweier komplexer Zufallsvariabler
Für zwei komplexe Zufallsvariable X und Y heißt
cov(X, Y ) = E(X − EX)(Y − EY )∗
die Kovarianz von X und Y .
Rechenregeln für die Kovarianz
• cov(a1 X1 + a2 X2 , Y ) = a1 cov(X1 , Y ) + a2 cov(X2 , Y )
• cov(X, b1 Y1 + b2 Y2 ) = b∗1 cov(X, Y1 ) + b∗2 cov(X, Y2 )
7
• cov(X, Y ) = E (XY ∗ ) − (EX) (EY )∗
• cov(Y, X) = cov(X, Y )∗
Die Varianz einer komplexen Zufallsvariablen
Die Varianz einer komplexen Zufallsvariablen X ist
var(X) = cov(X, X) = E(X − EX)(X − EX)∗ = E|X − EX|2
Rechenregeln für die Varianz
• var(aX + b) = |a|2 var(X)
• var(X) = E (XX ∗ ) − (EX) (EX)∗ = E|X|2 − |EX|2
Aus
(Y − EY )∗ = YRe − jYIm − (EYRe + jEYIm )∗
= (YRe − EYRe ) − j (YIm − EYIm )
folgt
cov(X, Y ) = (cov(XRe , YRe ) + cov(XIm , YIm ))
+j (cov(XIm , YRe ) − cov(XRe , YIm ))
Da XRe und XIm reelle Zufallsvariable sind, ist cov(XIm , XRe ) = cov(XRe , XIm ) Für
die Varianz von X folgt daher
var(X) = cov(X, X) = cov(XRe , XRe ) + cov(XIm , XIm )
= var(XRe ) + var(XIm )
2.3 Bedingte Verteilungen
X und Y seien Zufallsvariable auf einem Wahrscheinlichkeitsraum (Ω, A, P ).
Besitzt Y eine diskrete Verteilung mit der Wahrscheinlichkeitsfunktion
f Y (y) = P Y {y} = P (Y = y) > 0
für alle y aus einer abzählbaren Menge Y, so existiert für alle Borelschen Mengen B und
alle y die bedingte Wahrscheinlichkeit
P X|Y (B|y) = P (X ∈ B|Y = y) =
P [(X ∈ B) ∩ (Y = y)]
P (Y = y)
und besitzt die folgenden beiden Eigenschaften:
• B 7−→ P X|Y (B|y) ist eine Wahrscheinlichkeitsverteilung.
8
(1)
• Nach der Bayes-Formel ist
P (X ∈ B) =
X
P (X ∈ B|Y = y)P (Y = y)
y∈Y
was man auch in der Form
P X (B) =
Z
P X|Y (B|y) P Y (dy)
(2)
schreiben kann.
Für allgemeine Zufallsvariable Y hat man normalerweise P (Y = y) = 0, so dass eine
bedingte Wahrscheinlichkeit nicht durch die Formel (1) definiert werden kann. Man kann
aber zeigen, dass gilt:
Satz 2.1 Zu Zufallsvariablen X und Y gibt es eine Funktion
B, y 7−→ P X|Y (B|y) =: P (X ∈ B|Y = y)
mit den folgenden Eigenschaften
• B 7−→ P X|Y (B|y) ist eine Wahrscheinlichkeitsverteilung,
• y 7−→ P X|Y (B|y) ist P Y -integrabel,
R
• P X (B) = P X|Y (B|y) P Y (dy)
P X|Y (B|y) ist durch diese Eigenschaften P Y -fast überall eindeutig bestimmt und heißt
die bedingte Verteilung von X unter der Bedingung Y = y oder die bedingte
Verteilung von X bedingt durch Y .
Explizit berechnen lässt sich die bedingte Verteilung natürlich nur in speziellen Fällen.
Neben dem Fall (1) einer diskreten Verteilung von Y kann man sie noch berechnen, wenn
die Verteilung des Zufallsvektors (X, Y ) eine Dichte f (x, y) besitzt.
Sind nämlich fX (x) und fY (y) die Marginaldichten von f , so ist P X|Y (B|y) absolutstetig
mit der Dichte
f (x, y)
f X|Y (x|y) =
(3)
fY (y)
wie man aus
X
Z Z
Z
P (B) =
fX (x) dx =
f (x, y)dy
B
Z Z
f (x, y)
=
dx fY (y) dy
B fY (y)
Z
=
P X|Y (B|y) P Y (dy)
B
ersieht.
9
dx
Beispiel 2.1 Die Dichte
f (x, y) =
2e−(x+y) für 0 < y < x
0
sonst
besitzt die Marginaldichten fX (x) = 2e−x 1 − e−x für x > 0 und fY (y) = 2e−2y für
y > 0.
Daraus folgt nach (3)
2e−(x+y)
f X|Y (x|y) =
= e−(x−y)
2e−2y
für x > y, also eine um y verschobene Exponentialverteilung und
f Y |X (y|x) =
2e−(x+y)
e−y
=
2e−x (1 − e−x )
1 − e−x
für 0 < y < x, d.h. eine auf das Intervall (0, x) beschränkte Exponentialverteilung.
Einen anderen Ansatzpunkt bietet der
Satz 2.2 Sind die Zufallsvariable Y und die Zufallsgröße Z stochastisch unabhängig
und ist G(y, z) eine Funktion von zwei Variablen, so gilt für X = G(Y, Z), dass
P (X ∈ B|Y = y) = P (G(Y, Z) ∈ B|Y = y) = P (G(y, Z) ∈ B)
Mit G(y, z) = y + z gilt also zum Beispiel
P (X ≤ a|Y = y) = P (Y + Z ≤ a|Y = y) = P (y + Z ≤ a) = P (Z ≤ a − y)
2.4 Bedingte Erwartungswerte
Sind X und Y Zufallsvariable und P X|Y (B|y) = P (X ∈ B|Y = y) die bedingte Verteilung von X unter Y = y, so kann man natürlich den Mittelwert dieser Verteilung
bilden.
Definition 2.2 Der Mittelwert
Z
E(X|Y = y) =
xP X|Y (dx|y)
der bedingten Verteilung von X unter Y bzw. die Zufallsvariable E(X|Y ):
Z
ω 7−→ xP X|Y (dx|Y (ω))
heißen der bedingte Erwartungswert von X unter der Bedingung Y .
10
Beispiel 2.2 Für die bedingte Verteilung P X|Y aus Beispiel 2.1 gilt
Z
Z ∞
X|Y
xe−(x−y) dx
E(X|Y = y) =
xf
(x|y) dx =
y
Z ∞
Z ∞
Z ∞
ze−z dz
e−z dz +
(y + z)e−z dz = y
=
0
0
0
= y+1
Aus (2) folgt für den bedingten Erwartungswert die Formel
Z
EX = E(X|Y = y) P Y (dy) = E (E(X|Y ))
(4)
3 Stochastische Prozesse
Sei X = (X(t), t ∈ T ) ein stochastischer Prozess auf einem Wahrscheinlichkeitsraum
(Ω, A, P ).
Um Wahrscheinlichkeiten für das Verhalten eines stochastischen Prozesses in Abhängigkeit
von der Zeit berechnen zu können, muss man im Prinzip die Verteilungen aller Zufallsvektoren
(X(t1 ), X(t2 ), . . . , X(tn ))
für beliebige Zeitpunkte t1 , t2 , . . . , tn kennen. Das ist meist nur unter zusätzlichen Voraussetzungen der Fall, z.B. bei Gauß-Prozessen.
3.1 Gauß-Prozesse
Ein Gauß-Prozess, ist dadurch charakterisiert, dass die (reellen) Zufallsvariablen X(t)
normalverteilt mit Mittelwerten mX (t) = EX(t) und Kovarianzen C(s, t) = cov(X(s), X(t))
sind. Die Verteilung des Zufallsvektors (X(t1 ), X(t2 ), . . . , X(tn )) besitzt dann die Dichte
n
1
1
1
> −1
p
f (x) = √
exp − (x − m) C (x − m)
(5)
2
2π
det(C)
mit m = (mX (t1 ), mX (t2 ), . . . , mX (tn ))> und

C(t1 , t1 ) C(t1 , t2 ) . . . C(t1 , tn )
 C(t2 , t1 ) C(t2 , t2 ) . . . C(t2 , tn )

C=
..
..
..
..

.
.
.
.
C(tn , t1 ) C(tn , t2 ) . . . C(tn , tn )





Dabei stellt sich immer noch die Frage, welche Eigenschaften eine Funktion s, t 7−→
C(s, t) besitzen muss, damit (5) eine Dichte ist.
11
3.2 Der Wiener-Prozess
Ein wichtiger Spezialfall eines Gauss-Prozesses ist der Wiener-Prozess. Dies ist ein stochastischer Prozess (X(t), t > 0) mit X(0) := 0, der dadurch charakterisiert ist, dass
EX(t) = 0 für alle t und für beliebige t0 = 0 < t1 < t2 < . . . < tn die Differenzen
X(ti ) − X(ti−1 ) stochastisch unabhängig und normalverteilt mit Varianzen σ 2 (ti − ti−1 )
sind (Prozess mit unabhängigen Zuwächsen).
Anwendungen: Optionenhandel, Black-Scholes-Formel, Brownsche Bewegung, Rauschen.
Übungsaufgabe: Berechnung der Dichte von (X(t1 ), X(t2 ), X(t3 )).
3.3 Der Poissonprozess
Der Poissonprozess ist ein Modell für Situationen, in denen die Häufigkeit des Eintretens
eines Ereignisses gezählt wird, wobei dieses zu zufälligen Zeitpunkten eintritt. Typische
Beispiele solcher Situationen sind
• Das Auftreffen eines Photons auf einem photoelektrischen Sensor,
• das Eintreffen eines Kunden an einem Bedienungsschalter und
• die historisch erste Untersuchung dieser Art: Das Ereignis Tod durch Hufschlag“
”
bei der preussischen Kavallerie.
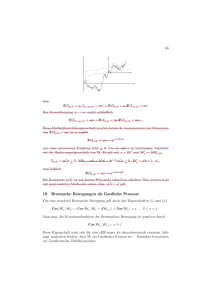
N (t) sei die Häufigkeit des Eintretens des Ereignisses im Zeitintervall (0, t].
N (0) := 0.
6
...
N (t, ω)
-t
Für 0 ≤ s < t sei N (s, t] := N (t) − N (s) die Häufigkeit des Eintretens im Zeitintervall
(s, t]. Dann kann man aus den Axiomen von Chintschin:
• Stationarität: P (N (s + τ, t + τ ] = k) = P (N (s, t] = k) für alle τ > 0 und k ∈ N0 .
• Nachwirkungsfreiheit: Für 0 ≤ s1 < s2 ≤ t1 < t2 sind N (s1 , s2 ] und N (t1 , t2 ]
stochastisch unabhängig.
• Ordinarität:
1
P (N (s, s + t] > 1) = 0
t−→0 t
lim
folgern, dass es ein λ > 0 gibt, so dass
P (N (t) = k) = P (N (s, s + t] = k) = e−λt
12
(λt)k
k!
3.4 Aus dem Poissonprozess abgeleitete Prozesse
0 < S1 < S2 < S3 < . . . seien die Zufallszeitpunkte, zu denen das beim Poissonprozess
N (t) beobachtete Ereignis eintritt.
3.4.1 Schrotrauschen
Wenn ein Photon, das auf einem Sensor auftrifft, einen elektrischen Impuls h(t) auslöst,
ergibt sich durch Überlagerung aller Impulse der stochastische Prozess
X(t) =
∞
X
h(t − Sk )
k=1
Ein derartiger Prozess heißt Schrotrauschen (englisch shot noise process).
3.4.2 Zufallstelegraphensignal
X = (X(t), t ≥ 0) sei ein stochastischer Prozess, der nur die Werte +1 und −1 annimmt,
wobei
1
P (X(0) = +1) = P (X(0) = −1) =
2
und der Prozess X jeweils zu den Eintrittszeitpunkten Sk des Poissonprozesses das Vorzeichen wechselt.
Dieser stochastische Prozess, den Leon-Garcia [1] random telegraph signal nennt, hat
nicht unbedingt praktische Bedeutung, ist aber als Demonstrationsbeispiel füe die mathematischen Konzepte dieser Vorlesung sehr ergiebig.
13
4 Die Momente stochastischer Prozesse
In dieser Vorlesung geht es letztendlich um das Problem, durch geeignete Filterung ein
Signal Y (t) möglichst gut an ein Referenzsignal Z(t) anzupassen, wobei als Abstandsmaß
die mittlere quadratische Abweichung
E|Y (t) − Z(t)|2
benutzt wird. Aus
E|Y (t) − Z(t)|2 = E|Y (t)|2 − EY (t)Z(t)∗ − EY (t)∗ Z(t) + E|Z(t)|2
ist zu ersehen, dass man dazu nur die Momente, Varianzen und Kovarianzen der beteiligten Zufallsvariablen benötigt.
Im folgenden betrachten wir daher stochastische Prozesse X = (X(t), t ∈ T ), bei denen
die Erwartungswerte EX(t) und Varianzen var(X(t)) für alle t existieren.
4.1 Die Mittelwertfunktion
Definition 4.1
mX (t) = EX(t)
heißt Mittelwert oder Mittelwertfunktion des Prozesses.
4.2 Autokorrelation und Autokovarianz
Definition 4.2
RX (s, t) = EX(s)X(t)∗
heißt Autokorrelation oder Autokorrelationsfunktion (AKF) des Prozesses.
Definition 4.3
CX (s, t) = cov(X(s), X(t))
heißt Autokovarianz oder Autokovarianzfunktion (AKV) des Prozesses.
Zusammenhang zwischen AKF und AKV
CX (s, t) = cov(X(s), X(t))
= E (X(s) − mX (s)) (X(t) − mX (t))∗
= EX(s)X(t)∗ − (EX(s)) (EX(t))∗
= RX (s, t) − mX (s)mX (t)∗
14
4.3 Beispiele
4.3.1 Kosinus-Schwingung mit zufälliger Amplitude und konstanter Phase
X(t, ω) = A(ω) cos(2πf t + φ)
wobei die zufällige Amplitude A(ω) im Intervall [0, A0 ] uniform verteilt ist:
1
0 ≤ x ≤ A0
A
A0 für
f (x) =
0
sonst
mX (t) = EX(t) = EA cos(2πf t + φ) =
A0
cos(2πf t + φ)
2
RX (s, t) = EX(s)X(t) = EA2 cos(2πf s + φ) cos(2πf t + φ)
Z A0
1
x2
dx cos(2πf s + φ) cos(2πf t + φ)
=
A0
0
A20
=
cos(2πf s + φ) cos(2πf t + φ)
3
A20
=
(cos(2πf (s − t)) + cos(2πf (s + t) + 2φ))
6
CX (s, t) = cov(X(s), X(t)) = cov(A, A) cos(2πf s + φ) cos(2πf t + φ)
= var(A) cos(2πf s + φ) cos(2πf t + φ)
= EA2 − (EA)2 cos(2πf s + φ) cos(2πf t + φ)
=
=
A20
cos(2πf s + φ) cos(2πf t + φ)
12
A20
(cos(2πf (s − t)) + cos(2πf (s + t) + 2φ))
24
4.3.2 Kosinus-Schwingung mit konstanter Amplitude und uniform verteilter
zufälliger Phase
X(t, ω) = A cos(2πf t + U (ω))
wobei die zufällige Phase U (ω) im Intervall (0, 2π] uniform verteilt ist:
1
0 ≤ x ≤ 2π
U
2π für
f (x) =
0 sonst
Z
A cos(2πf t + x)f U (x) dx
Z 2π
1
= A
cos(2πf t + x) dx = 0
2π
0
mX (t) = EX(t) =
15
Z
RX (s, t) = EX(s)X(t) = A cos(2πf s + x)A cos(2πf t + x)f U (x) dx
Z 2π
1
1
= A2
(cos[2πf (s − t)] + cos[2πf (s + t) + 2x])
dx
2
2π
0
Z 2π
A2 1
=
cos[2πf (s − t)] dx
2 2π 0
A2
=
cos[2πf (s − t)]
2
A2
cos[2πf (s − t)]
2
Beachte: RX (s, t) und CX (s, t) hängen nur von der Zeitdifferenz s − t und nicht von
den absoluten Zeitpunkten ab.
CX (s, t) = RX (s, t) − mX (s)mX (t) = RX (s, t) =
4.3.3 Prozesse mit unabhängigen Zuwächsen
Der Poisson- und der Wiener-Prozess besitzen beide die folgende Eigenschaft:
Definition 4.4 Ein stochastischer Prozess X = (X(t), t ∈ T ) besitzt unabhängige Zuwächse,
wenn für alle Zeitpunkte r < s < t die Differenzen X(s) − X(r) und X(t) − X(s) stochastisch unabhängig sind.
Außerdem gilt bei Poisson- und der Wiener-Prozessen X(0) = 0. Daraus berechnet sich
die Autokovarianzfunktion wie folgt.
Für 0 < s < t sind X(t) − X(s) und X(s) = X(s) − X(0) stochastisch unabhängig.
Daraus folgt
CX (s, t) = cov(X(s), X(t))
= cov(X(s), X(s) + [X(t) − X(s)])
= cov(X(s), X(s)) + cov(X(s), X(t) − X(s))
= var(X(s))
Für 0 ≤ t < s gilt analog
CX (s, t) = cov(X(s), X(t))
= cov(X(t) + [X(s) − X(t)], X(t))
= cov(X(t), X(t)) + cov(X(s) − X(t), X(t))
= var(X(t))
Das kann man zusammenfassen zu
CX (s, t) = var (X(min(s, t)))
16
Beim Poissonprozess ist N (t) Poissonverteilt mit Parameter λt, also mN (t) = EN (t) = λt
und var(N (t)) = λt. Daraus folgt
CN (s, t) = λ min(s, t)
und
RN (s, t) = CN (s, t) + mN (s)mN (t) = λ min(s, t) + λ2 st
Beim Wienerprozess ist mX (t) = 0 und var(X(t)) = σ 2 t, daher
CX (s, t) = RX (s, t) = σ 2 min(s, t)
4.3.4 Das Zufallstelegraphensignal
Für t > 0 ist nach der Formel von der totalen Wahrscheinlichkeit
P (X(t) = 1) = P (X(t) = 1|X(0) = −1)P (X(0) = −1)
+ P (X(t) = 1|X(0) = 1)P (X(0) = 1)
und
P (X(t) = −1) = P (X(t) = −1|X(0) = −1)P (X(0) = −1)
+ P (X(t) = −1|X(0) = 1)P (X(0) = 1)
Nach Konstruktion dieses Prozesses ist
P (X(t) = 1|X(0) = 1) = P (X(t) = 1|X(0) = 1) = P (N (t) ist geradzahlig)
∞
X
(λt)2k −λt
=
e
(2k)!
k=0
1 λt
= e−λt
e + e−λt
2
1
=
1 + e−2λt
2
und
P (X(t) = −1|X(0) = 1) = P (X(t) = 1|X(0) = −1) = P (N (t) ist ungerade)
∞
X
(λt)2k+1 −λt
=
e
(2k + 1)!
k=0
1 λt
= e−λt
e − e−λt
2
1
=
1 − e−2λt
2
Eingesetzt in die obigen Gleichungen ergibt das
1 1
1
1
P (X(t) = 1) =
1 + e−2λt
+
1 − e−2λt
2
2 2
2
17
und
P (X(t) = −1) = 1 − P (X(t) = 1) =
1
2
Für die Mittelwertfunktion ist daher
mX (t) = EX(t) = 1P (X(t) = 1) + (−1)P (X(t) = −1) = 0
und für die Autokovarianzfunktion gilt deshalb
CX (s, t) = RX (s, t) = E (X(s)X(t))
= 1P (X(s) = X(t)) + (−1)P (X(s) 6= X(t))
1
1
=
1 + e−2λ|t−s| −
1 − e−2λ|t−s|
2
2
−2λ|t−s|
= e
Denn es ist X(s) = X(t) bzw. X(s) 6= X(t) genau dann, wenn der Poissonprozess
zwischen den Zeitpunkten s und t eine gerade bzw. ungerade Anzahl von Sprüngen
durchführt.
4.4 Eigenschaften von AKF und AKV
AKF und AKV sind positiv semidefinit
m X
m
X
ai a∗k RX (ti , tk )
=
m X
m
X
i=1 k=1
m
X
i=1 k=1
= E
ai a∗k EX(ti )X(tk )∗
!
ai X(ti )
i=1
n
X
!∗
ak X(tk )
k=1
2
m
X
= E
ai X(ti )
i=1
≥ 0
Analog
m X
m
X
ai a∗k CX (ti , tk )
= var
i=1 k=1
m
X
!
ai X(ti )
≥0
i=1
AKF und AKV sind symmetrisch
RX (t, s) = EX(t)X(s)∗ = (EX(s)X(t)∗ )∗ = RX (s, t)∗
CX (t, s) = RX (t, s) − mX (t)mX (s)∗
= RX (s, t)∗ − (mX (s)mX (t)∗ )∗
= CX (s, t)∗
18
4.5 Kreuzkorrelation und Kreuzkovarianz
X = (X(t), t ∈ T ) und Y = (Y (t), t ∈ T ) seien stochastische Prozesse.
Definition 4.5
RXY (s, t) = EX(s)Y (t)∗
heißt Kreuzkorrelation oder Kreuzkorrelationsfunktion (KKF) von X und Y .
Definition 4.6 X und Y heißen orthogonal, wenn RXY (s, t) = 0 für alle s und t.
Definition 4.7
CXY (s, t) = cov (X(s), Y (t))
heißt Kreuzkovarianz oder Kreuzkovarianzfunktion (KKV) von X und Y .
Definition 4.8 X und Y heißen unkorreliert, wenn CXY (s, t) = 0 für alle s und t.
Beispiel
X1 (t, ω) = A1 cos(2πf1 t + U1 (ω)) und X2 (t, ω) = A2 cos(2πf2 t + U2 (ω)) seien Kosinusschwingungen mit unabhängigen zufälligen Phasen.
Wegen mX1 (t) = mX2 (t) = 0 ist
CXY (s, t) = RXY (s, t) = EX1 (s)X2 (t)
= E cos(2πf1 s + U1 ) cos(2πf2 t + U2 )
Da U1 und U2 stochastisch unabhängig sind, sind es auch X1 (s) und X2 (t), so dass
CXY (s, t) = EX1 (s)X2 (t) = EX1 (s)EX2 (t) = mX1 (s)mX2 (t) = 0
5 Stationäre Prozesse
Definition 5.1 Ein stochastischer Prozess X = (X(t)), t ∈ T ) heißt im engeren Sinne oder streng stationär, wenn für alle Zeitpunkte t1 , t2 , . . . , tn und beliebige Zeitdifferenzen τ die Zufallsvektoren (X(t1 ), X(t2 ), . . . , X(tn )) und (X(t1 +τ ), X(t2 +τ ), . . . , X(tn +
τ )) die gleiche Verteilung besitzen.
Definition 5.2 Ein stochastischer Prozess X = (X(t)), t ∈ T ) heißt im weiteren
Sinne oder schwach stationär, wenn für alle Zeitpunkte t, t1 , t2 und beliebige Zeitdifferenzen τ
EX(t) = mx = const
und
RX (t1 + τ, t2 + τ ) = RX (t1 , t2 )
bzw.
CX (t1 + τ, t2 + τ ) = CX (t1 , t2 )
19
Ein streng stationärer Prozess ist insbesondere ein schwach stationärer Prozess. Die
Umkehrung gilt im allgemeinen nicht. Lediglich bei Gauß-Prozessen fallen die beiden
Begriffe zusammen, da die Dichten nur von EX(t) und CX (t1 , t2 ) abhängen.
Konventionen
Im Rahmen dieser Vorlesung werden nur schwach stationäre Prozesse betrachtet. Unter
einem stationären Prozess ist im folgenden also immer ein schwach stationäre Prozess
zu verstehen. Außerdem werden Autokorrelations- und Autokovarianzfunktion verkürzt
als Funktionen einer Variablen geschrieben. Mit τ = −t isr
RX (s, t) = RX (s − t, 0) =: RX (s − t)
CX (s, t) = CX (s − t, 0) =: CX (s − t)
Ein stationärer Prozess zeichnet sich also dadurch aus, dass die Mittelwertfunktion zeitlich konstant ist und die Autokorrelations- und Autokovarianzfunktion nur von der Zeitdifferenz s − t abhängen.
Beispiele
Für die Kosinus-Schwingung mit zufälliger Phase und das Zufallstelegraphensignal aus
dem Abschnitt 4.3 sind Beispiele für stationäre Prozesse. stationären Prozess.
Ein Beispiel für einen zeitdiskreten stationären Prozess ist die Folge der Zufallsvariablen
Yn =
1
(Xn + Xn−1 )
2
für n = 1, 2, . . ., wenn X0 , X1 , X2 , . . . stochastisch unabhängige N (0, σ 2 )-verteilte Zufallsvariable sind. Denn es ist mY (n) = EYn = 0 und
CY (k, n) = RY (k, n) = E(Yk Yn )
1
=
E [(Xk + Xk−1 )(Xn + Xn−1 )]
4
1
=
[E(Xk Xn ) + E(Xk Xn−1 ) + E(Xk−1 Xn ) + E(Xk−1 Xn−1 )]
4

 21 σ 2 falls k = n
1 2
σ
falls |k − n| = 1
=
 4
0
sonst
hängt nur von der Differenz k − n ab.
5.1 Eigenschaften der AKF
Über die positive Semidefinitheit und die Symmetrie hinaus gilt bei stationären Prozessen
für alle t
E|X(t)|2 = EX(t)X(t)∗ = RX (t − t) = RX (0)
RX (0) heißt deshalb auch die mittlere Leistung des Prozesses.
Die Symmetrieeigenschaft lässt sich hier so formulieren:
RX (−t) = EX(−t)X(0)∗ = EX(0)X(t)∗ = (EX(t)X(0)∗ )∗ = RX (t)∗
20
Satz 5.1 Bei einem stationären Prozess gilt für alle t
|RX (t)| ≤ RX (0)
Beweis: Für beliebige komplexe Zahlen c und Zeitpunkte s und t ist stets
0 ≤ E|cX(s + t) − X(s)|2
= |c|2 E|X(s + t)|2 − 2Re (cEX(s + t)X(s)∗ ) + E|X(s)|2
= |c|2 RX (0) − 2Re (cRX (t)) + RX (0)
= (1 + |c|2 )RX (0) − 2Re (cRX (t))
Ist
RX (t) = |RX (t)| exp(jφ)
die Polarform und setzt man c := exp(−jφ), so folgt
0 ≤ 2RX (0) − 2Re (exp(−jφ)|RX (t)| exp(jφ)) = 2 (RX (0) − |RX (t)|)
und daraus wiederum die Behauptung.
5.2 Zyklostationäre Prozesse
Definition 5.3 Ein stochastischer Prozess X = (X(t)) heißt (im weiteren Sinne) zyklostationär, wenn es eine Konstante T > 0 gibt, so dass für alle t und alle ganzzahligen
Vielfachen mT von T gilt
mX (t + mT ) = mX (t)
und
CX (s + mT, t + mT ) = CX (s, t)
5.2.1 Puls-Amplituden-modulierte Signale
Ein Beispiel für einen zyklostationären Prozess ist das Binärdatensignal
X(t) =
∞
X
Ak p(t − kT )
k=−∞
mit dem Rechteckimpuls
p(t) =
1 für 0 ≤ t < T
0 sonst
und einer Folge
. . . A−2 , A−1 , A0 , A1 , A2 , . . .
von stochastisch unabhängigen Zufallsvariablen Ak , die nur die Werte +1 und −1, jeweils
mit Wahrscheinlichkeit 1/2 annehmen. D.h. im Zeitintervall [nT, (n + 1)T ) wird ein Puls
An p(s) mit der Amplitude An gesendet.
21
Es ist
"
mX (t) = E
∞
X
#
Ak p(t − kT ) =
k=−∞
∞
X
E(Ak )p(t − kT ) = 0 ,
k=−∞
daher CX (s, t) = RX (s, t) und
CX (s, t) = cov(X(s), X(t)) = cov
∞
X
Ak p(s − kT ),
=
=
∞
X
∞
X
!
Am p(t − mT )
m=−∞
k=−∞
=
∞
X
cov(Ak , Am )p(s − kT )p(t − mT )
k=−∞ m=−∞
∞
X
cov(Am , Am )p(s − mT )p(t − mT )
m=−∞
∞
X
E(Am Am )p(s − mT )p(t − mT ) =
m=−∞
22
1 falls mT ≤ s, t < (m + 1)T
0 sonst
Satz 5.2 X = (X(t), t ∈ T ) sei zyklostationär mit Periode T und die Zufallsvariable
U uniform verteilt im Intervall [0, T ] und stochastisch unabhängig von X. Dann ist der
stochastische Prozess Y mit
Y (t) = X(t + U )
stationär.
Beweis: Zum Beweis benötigen wir ein Resultat aus den Übungen: Ist die Funktion
f (t) periodisch mit Periode T und auf [0, t] integrierbar, so ist für jede reelle Zahl s die
Funktion t 7−→ f (s + t) auf [0, T ] integrierbar und es gilt
Z
T
Z
T
f (t) dt
f (s + t) dt =
(6)
0
0
(1) Es ist Y (t) = X(t + U ) = G(U, X), so dass nach Satz 2.2, Formel (4) und schließlich
(6) gilt
Z
Z
U
EY (t) =
E (Y (t)|U = u) P (du) = E (X(t + U )|U = u) f U (u) du
Z
=
E (X(t + u)) f U (u) du
Z
Z
1 T
1 T
=
mX (t + u) du =
mX (u) du
T 0
T 0
= mY
(2) Auf die gleiche Weise erhält man
Z
∗
E (Y (s)Y (s + t) ) =
E (X(s + U )X(s + t + U )∗ |U = u) f U (u) du
Z
1 T
=
E (X(t + u)X(s + t + u)∗ ) du
T 0
Z
Z
1 T
1 T
=
RX (t + u, s + t + u) du =
RX (u, t + u) du
T 0
T 0
= RY (t)
23