F Vektorrechnung F1 Ortsvektoren und Vektorketten a) Mittelpunkt b

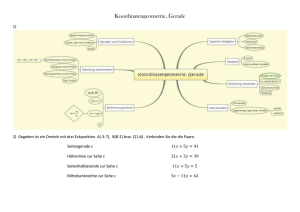
Übersicht Analytische Geometrie
(Die Aufstellung erhebt keinen Anspruch auf Vollständigkeit!)
F Vektorrechnung
Ortsvektoren und Vektorketten
a) Mittelpunkt
b) Schwerpunkt
F1
c) Sonstige (Ergänze zum Parallelogramm; restliche Punkte Quaderermitteln; Teile Strecke im bestimmten Verhältnis d) Zeichnung erstellen
F2 Skalarprodukt a) zur Bestimmung von orthogonalen Vektoren b) sonst
F3 Längen von Vektoren berechnen
F4 a) Linearkombination b) lineare (Un-)abhängigkeit
F5 Besonderes Dreieck/Viereck nachweisen
G Geraden und Ebenen im Raum
a) PF von Geraden aufstellen
G1
b) Punktprobe Gerade c) Punktprobe Strecke
Lagebeziehung von Geraden: a) Schnitt b) windschief c) echt parallel
G2
d) identisch
a) PF von Ebenen ermitteln sowie überprüfen
G3
b) Punktprobe c) Bilden drei° Punkte eine Ebene?
a) NF/KF/HNF für Ebenen ermitteln b) Spurgeraden und Spurpunkte
G4
c) Zeichnung
G5 Lage Gerade und Ebene a) Schnittpunkt b) echt parallel c) g in E
Ebenen auf ihre gegenseitige Lage untersuchen
G6
a) Schnittgerade b) echt parallel c) identisch d) 3 Ebenen e) Besondere Lage
G7 Punkt an einer Ebene spiegeln
G8 Die Hesse‘sche Normalenform aufstellen.
Winkel und Abstände, Volumina im Raum
Winkel zwischen
H1
a) zwei Vektoren b) zwei Geraden c) Ebene–Gerade d) Ebene–Ebene
Flächeninhalt / Volumen
H2
a) Dreieck b) Viereck c) Volumen einer Pyramide d) Volumen Quader o. Ä.
H3 Abstand Punkt–Ebene a) Ursprung – Ebene b) Punkt – Ebene
H4 Abstand Punkt – Gerade
H5 Abstand a) Gerade – Gerade b) Ebene – Ebene
H6 Vektorprodukt zweier Vektoren berechnen und seine Bedeutung angeben.
Mithilfe des Vektorprodukts Normalenvektoren bestimmen.
Übergreifende Aufgaben
Erste Übungen zur Vektorrechnung F1
Aufklärungsflugzeug G2 G2 F3 H4 G5 F3 F1
Multiple–Choice–Test zu Vektoren und Geraden
Drachenprisma F1d F3 G2 F1c H2 F1c F1a F3
Berechnungen am Tetraeder F1, F3, F5, H4
Abitur 2012 HT4 Projektion von Dreiecken
Winkel–, Schnitt– und Abstandsaufgaben
1
F1 Verschiebungen durch Vektoren sowie Punkte im Raum durch Ortsvektoren und
Vektorketten beschreiben und damit realitätsnahe Situationen mathematisch modellieren.
Regeln
Ein Vektor ist Menge aller Pfeile, die parallel, gleich lang
abitourund gleich orientiert sind.
Den Vektor AB kann man als eine Verschiebung interpretieren, die den Punkt A auf den Punkt B abbildet.
Im Quader rechts gehören jeweils 4 Pfeile zum gleichen
Vektor. Z. B. ist AB  EF  HG  DC
H
D
G
C
E
A
F
B
Allgemein ist ein Vektor eine gerichtete Größe, wobei die
Länge des Vektors die Maßzahl der Größe und die Richtung des Vektors die Richtung der Größe
angibt.
Beispiele: gerichtete Kraft, Bewegungsvektor eines Flugzeuges
Zu einem Punkt A nennt man den OA den Ortsvektor von A
In der analytischen Geometrie ermittelt man meistens einen Punkt P, indem man den Ortsvektor
OP mit Hilfe einer Vektorkette ermittelt, z.B. OP OB BC CP .
Unter dem Gegenvektor – a eines Vektors a ersteht man den Vektor, der in Länge und Richtung
mit a übereinstimmt, aber die entgegengesetzte Orientierung hat. Es gilt – AB = BA
Dreiecksregel: AB BC AC ;
Anwendungsbeispiel: OB  DC  CB = OB  CD  BC = OB  BC  CD = OC  CD = OD
2
Addition / Subtraktion zweier Vektoren
Gegeben sind zwei Pfeile, die jeweils einen Vektor /eine
Verschiebung repräsentieren.
a
Grafische Addition
Es wird der Pfeil zum zweiten Vektor gezeichnet,
dessen Fußpunkt an der Spitze des ersten liegt.
(Die Verschiebungen werden hintereinander ausgeführt.) a
b
b
a
Der Summenvektor wird durch den Pfeil repräsentiert,
der vom Fußpunkt des ersten zur Spitze des
zweiten Pfeils führt.
b
b
b
Ein Vektor wird subtrahiert, indem man
den Gegenvektor addiert: a b a ( b)
a
a
b
Typische Anwendungsaufgaben
 Drei Punkte einer Ebene zu einem Parallelogramm ergänzen.
 Restliche Eckpunkte eines Körpers (z. B. Quaders, Prismas) ermitteln.
 Überprüfen, ob ein spezielles Viereck vorliegt (Parallelogramm; Raute; Rechteck; Quadrat;
Drachenviereck, (symmetrisches) Trapez
 Überprüfen, ob ein spezielles Dreieck (rechtwinklig, gleichschenklig; gleichseitig) vorliegt.
 Mittelpunkte, Schwerpunkte bestimmen
Beachte:
1
(OA OB) ,
2
!
(Koordinaten des Mittelpunktes = jeweils der Durchschnitt der Koordinaten.)
Beispiele:
 A(3|4|–2); B(5| –6 | 7)  MAB(4|–1|2,5) )
1
 Für den Schwerpunkt S des Dreiecks ABC: OS
(OA OB OC)
3
(Koordinaten des Mittelpunktes = jeweils der Durchschnitt der Koordinaten der Eckpunkte)
A(3|4|–2); B(5| –6 | 7); C(4|–4|10)  S((3+5+4):3|(4–6–4):3|(–2+7+10):3)  S(4|–2|5)
 Vektorkette beginnt (zunächst) im Ursprung OP O... ...
 Richtung des Vektors beachten
Für den Mittelpunkt M einer Strecke AB gilt: OM
1. Beispiel:
Die nebenstehende Figur zeigt eine quadratische Pyramide,
d. h. das Viereck ABCD ist ein Quadrat.
Drücke die Vektoren AB , BC , DA . CD und SD
durch die Vektoren SA , SB und SC aus.
Lösung
AB = – SA + SB ;
BC = – SB + SC ; DA = – BC = SB – SC ;
CD = – AB = SA – SB ; SD = SC + CD = SC + SA – SB ;
3
Beispiel:
Im Quader rechts sind K und M Mittelpunkte von Kanten,
S der Mittelpunkt der seitlichen Fläche.
a) Drücke durch a, b und c aus:
(i) AK = (ii) OD = (iii) CS =
b) Drücke umgekehrt folgende Vektoren durch Eckpunkte
aus:
(i) b
(ii) c
c
a
(iii) a
c
c) Nun sei für den achsenparallelen Quader F(3|5|–2)
und O(0|0|0). Ermittle die Koordinaten der
Punkte A, B, C, M, S, K.
B
®
a
A
D
®
S
c
M
0,5b
®
b
O
E
G
C
K
d) Überprüfe rechnerisch, ob sich die Geraden g(M,S) und h(B,K) schneiden.
1
2
Lösung: a) AK = b  c
(ii) OD = a  b (iii) CS =
1
1
ab c
2
2
b) (i) b c OG (ii) c a = AC (iii) a c 0,5b OK
c) A(3|0|0), B(0|5|0), C(0|0|–5), M(3|0|–1), S(1,5|5|–1), K(3|2,5|–2)
3. Beispiel:
In der nebenstehenden Figur sind die Seitenmitten eines beliebigen Vierecks verbunden.
a) Drücke die Vektoren MaMb und MdMc durch die
Seitenvektoren a , b , c und d aus.
b) Zeige, dass die Strecken MaMb und MdMc parallel und
gleich lang sind.
d) AD = a b c e) EMCG = c b 21 a
Lösung:
1
1
MaMb = ( a b ); McMd = ( c d );
2
2
Da a b = c d ist, sind die Vektoren gleich, also sind die
Strecken parallel und gleich lang.
4
F
4. Beispiel: (aus Zentralabitur)
Gegeben sind A(13 | −5 | 3), B (11 | 3 | 1), C (5 | 3 | 7)
und S1 (13 | 1 | 9)
Bestimmen Sie die Koordinaten der Eckpunkte P6
und P8 des abgebildeten Würfels, falls die Eckpunkte des Oktaeders auf den Mittelpunkten der Seitenflächen liegen.
Lösung: OP6  OS1  S1P6  OS1  AB  P6(11|9|7)
OP8  OS1  S1P8  OS1  AB P8(15|–7|11)
5
F2 Das Skalarprodukt (SP) zweier Vektoren berechnen und damit entscheiden, ob die Vektoren zueinander orthogonal sind.
Regeln
Rechnerische Ermittlung des SP:
a d
b
e
ad
be
cf
c f
Grafische Ermittlung: Länge des einen Vektors multipliziert mit der (orientierten) Länge
der senkrechten Projektion des anderen auf
den einen.
a b
a b
b
a ba (falls   90°) bzw.
v2
ba
a ba (falls   90°)
a
Spezialfall: Bei kollinearen Vektoren ist das SP gleich dem (negativen) Produkt ihrer Längen,
falls sie gleich (entgegengesetzt) orientiert sind.
Skalarprodukt = 0  Vektoren stehen senkrecht aufeinander.
Bei Formulierungen wie senkrecht oder orthogonal sollte man immer an diesen Satz denken.
Typische Anwendungsaufgaben
 Zeige, dass das Viereck ein Rechteck ist / ein Drachenviereck ist.
(Beim Drachenviereck stehen die Diagonalen senkrecht aufeinander (und die eine halbiert
die andere).)
 Zeige, dass eine Strecke (z.B. in einer Pyramide) eine Höhe ist.
(Die Strecke steht senkrecht auf zwei nicht kollinearen Richtungsvektoren)
 Zeige, dass die Gerade parallel zur Ebene verläuft.
(NV und RV müssen senkrecht aufeinander stehen.)
Beachte:
Das Skalarprodukt ergibt (im Unterschied zum Vektorprodukt) immer eine Zahl, nie einen Vektor.
1. Beispiel: Welcher Term ist ein Vektor, welcher eine Zahl, welcher ist nicht definiert?
  
d)  a  b  c
a) a  b  c  d
  
e) a   b  c   d
b) a  b  c  d
c)
 a  b   c   d

f) a  b  c

Lösung: a) = Zahl·Zahl = Zahl;
b) = Zahl·Vektor=Vektor
c) = (Vektor·Vektor)·Vektor = Zahl · Vektor = Vektor
d) = Vektor – Zahl (nicht definiert)
e) = Vektor·((Zahl·Vektor)·Vektor)= Vektor·(Vektor·Vektor)= Vektor·Zahl = Vektor
f) = Vektor·Vektor=Zahl
6
2. Beispiel:
Ermittle das ungefähre Skalarprodukt der Vektoren (ohne ein KOS einzuzeichnen).
Lösungen (von oben nach unten):
a  b  9,9·4,5 = 44,55; a  b  –9,7·3,2 = –35,89; a  b 4·9,9 = 39,6; a  b  –4,5·7,4 = –33,3
3. Beispiel:(„Skalarprodukt = 0  Vektoren senkrecht“ ausnutzen.)
a) Gegeben sind: A( 80 |400 | 2), B( 100 | 400 | 2 ), C( 100 |1200 | 6 ) und D( 80 | 1200 | 6 )
Untersuche, ob ABCD ein besonderes Viereck ist.
b) Untersuche, ob ABCDS mit A, B, C, D wie oben und S(90|795|1004) eine gerade
Pyramide bilden.
Lösung:
20
a) DC
0 = AB  ABCD ist ein Parallelogramm.
0
20
Zusätzlich gilt: AB AD
0
0
0
800 =0  ABCD ist ein Rechteck.
4
Zusätzlich gilt: AC  BD  0  ABCD ist kein Quadrat.
0
b) MAC(90|800|4) SMAC
5
; SMAC
AB  SMAC
1000
ABCDS ist eine gerade Pyramide.
7
AD  SMAC
EABD
F3: Längen von Strecken im Raum und den Betrag von Vektoren berechnen.
Regeln
Die Länge/der Betrag eines Vektors berechnet sich mit
a
a
3
2
a= b
a 2 b2 im IR .
a2 b2 c 2 im IR bzw. a =
b
c
Tipp: Das Vorzeichen der Komponenten spielt keine Rolle, da jeweils quadriert wird.
Deshalb gibt man besser nur nichtnegative Zahlen in den TR eingeben.
15
Beispiel: 13
152 132 122 , statt ( 15)2 132 ( 12)2 ;
12
Falsch ist die Eingabe
152
132
122
Typische Anwendungsaufgaben
 Untersuche, ob ein Quadrat (ein regelmäßiges Sechseck, eine Raute, ein Trapez,
ein Rechteck, ein Drachenviereck, …) vorliegt.
 Zeige, dass das Dreieck gleichschenklig/gleichseitig ist.
 Einen Vektor n normieren (auf die Länge 1 bei gleicher Richtung bringen): n0 =
n
n
 Zu einem Vektor a einen Vektor b mit gleicher Richtung, aber der Länge k finden. b = k
a
a
 Geschwindigkeit v bei einer Fluggeraden x  p  t  u bestimmen: v = u
LE
ZE
1. Beispiel:
Gegeben sind die Punkte A(–5|2|4), B(3|8|7), C(8|–5|6) .
a) Überprüfe, ob das Dreieck ABC gleichschenklig ist, d.h. gleich lange Seiten hat.
b) Bestimme D so, dass ABCD ein Parallelogramm ist.
c) Untersuche, ob der Mittelpunkt MAC gleich dem Mittelpunkt MBD ist.
d) Bestimme den Schwerpunkt S des Dreiecks ABC.
e) E teilt BC von B aus im Verhältnis 3:1. Ermittle E.
f) Damit drei Punkte ein echtes Dreieck bilden dürfen sie nicht auf einer Geraden liegen.
Beschreibe ein Verfahren, wie man mit Hilfe der Vektorrechnung rechnerisch überprüfen kann,
ob drei Punkte E, F und G auf einer Geraden liegen.
Lösung:
8
13
5
6
64 36 9
109 ; AC
7
222 BC
13
195
a) AB
3
2
1
Alle Seiten sind verschieden lang.
5
5
0
b) OD
11 ; D(0|–11|3)
OA
BC =
2
13
4
1
3
8
1,5
c) OMAC
1,5
1,5 ; OMBD
1,5 Die beiden Mittelpunkte sind gleich,
5
5
d.h. die Diagonalen halbieren sich. Damit ist das Viereck ein Parallelogramm.
2
5 17
1
d) OS
(OA OB OB) = 5 / 3 S(2|3 | 3 )
3
17 / 3
e) OE
OB
3
BC
4
3
8
7
3
4
5
13
1
6,75
1,75 ; E(6,75|–1,75|6,25)
6,25
B
3
E 1 C
f) Die Vektoren EF und FG müssen in die gleiche Richtung zeigen, d. h. es muss EF
für eine Zahl k gelten (die Vektoren müssen kollinear sein).
k FG
2.Beispiel:
Wir betrachten den geradlinigen Horizontalflug eines Sportflugzeuges. Von einem Tower (Koordinatenursprung) aus wird die Flugbewegung beobachtet.
Zum Zeitpunkt t = 0 (Sekunden) befindet sich das Flugzeug am Punkt P 0 (–7000| –3000| 4000),
10 Sekunden später in P10(–6200|–2400|4000) (Angaben in m).
a) Stelle eine Geradengleichung x(t) für die Bewegung des Flugzeuges auf, wobei t die Sekunden seit dem Punkt P0 angibt.
b) Ermittle die Geschwindigkeit v des Flugzeuges in km/h sowie die Entfernung d zum Tower
zum Zeitpunkt t=0.
c) An welcher Position P befand sich das Flugzeug 10 Minuten vor t=0?
d) Nach 20 Minuten wird der Pilot aufgefordert, auf eine Flughöhe von 3000 m Höhe zu wechseln. Er behält seine Horizontalgeschwindigkeit bei (d. h. x– und y–Koordinate des Bewegungsvektors bleiben unverändert) und sinkt zusätzlich um 5 m/s .
Ermittle die Sinkfluggerade y(t) , die Koordinaten der Punkte B zu Beginn und E zu Ende des
Sinkfluges sowie die Dauer des Sinkfluges.
7000
80
1
Lösung: a) x(t) 0P0
P0P10
3000 t 60 ; t in Minuten
10
4000
0
602 m/s = 100 m/s = 360 km/h. d(O, P0) = 72 32 42 km  8,60 km
7000
80
55000
c) 10 min = 600 s; x( 600)
3000 600 60
39000 ; P(–55000|–39000|4000)
b) v =
802
4000
0
4000
89000
80
d) 20 min = 1200 s; OB = x(1200)  B(89000|69000|4000); y(t) = 69000
t 60
4000
5
Der Sinkflug dauert 1000:5 s = 200 s.
Ende des Sinkfluges: OE = y(200)  E(105000|81000|3000)
9
4. Beispiel:
Für jedes t 0 sind die Punkte A(1|0|0), B(5|6|0) und S(t|3|2t); gegeben.
Berechne t so, dass die Seiten AS und BS gleich lang sind.
Lösung:
2
2
AS  BS  (t  1)2  9  4t 2  (t  5)2  9  4t 2  (t–1) =(t–5) (da beide Radikanden positiv
2
2
sind)  t –2t+1=t –10t+25  8t=24  t=3
5. Beispiel:
A( 80 |400 | 2), B( 100 | 400 | 2 ), C( 100 |1200 | 6 ) und D( 80 | 1200 | 6 )
Untersuche, ob ABCD ein besonderes Viereck ist.
Lösung:
20
DC
20
0 = AB  ABCD ist ein Parallelogramm. AB AD
0
0
0
Rechteck. AB
0
800 =0  ABCD ist ein
4
400  AD  640004  ABCD ist kein Quadrat.
6. Beispiel:
53
Gegeben sind zwei Flugbahnen h : y(t)
410
43,75
t
2
100
30 g : x(t)
2550
4
228,75
0,1
t
22
1,5
t in min seit 12.00 Uhr, x(t),y(t) in m.
a) Berechne die Positionen P und Q, in denen sich die beiden Flugzeuge um 12.50 Uhr
befinden.
b) Berechne außerdem den Abstand der beiden Flugzeuge zu diesem Zeitpunkt.
Lösung:
a) P(95|–1450|153,75) Q(153|–1910|243,75)
b) PQ
582
460 2
90 2  472,30 [m]
10
F5 Überprüfen, ob ein besonderes Viereck (Parallelogramm, Rechteck, Raute, Quadrat, (symmetrisches) Trapez, Drachenviereck) vorliegt.
Vierecke werden über Längen, Orthogonalität oder Parallelität definiert.
(Siehe Formelsammlung S. 24)
Diese Eigenschaften lassen sich mit Hilfe der entsprechenden Vektoren (Länge von Seitenvektoren;
Skalarprodukt gleich null; Kollinearität) nachweisen:
Ein Viereck ABCD ist genau dann ein(e) …
… Parallelogramm, falls AB  DC oder AD  BC ist (Nachweis einer Gleichung genügt!)
… Rechteck, wenn es ein Parallelogramm ist und zusätzlich gleich lange Diagonalen besitzt.
… [Alternative: Rechteck, wenn es ein Parallelogramm ist und einen rechten Winkel besitzt.]
… Trapez, falls zwei Seitenvektoren kollinear sind.
… Raute, wenn es ein Parallelogramm ist und zwei aneinander liegende Seitenvektoren gleich lang
sind.
… [Alternative: Raute, wenn es ein Parallelogramm ist und die Diagonalen senkrecht aufeinander
stehen.]
… Quadrat, wenn es eine Raute ist und einen rechten Winkel besitzt.
… [Alternative: Quadrat, wenn es eine Raute ist und die Diagonalen gleich lang sind.]
… Drachenviereck, wenn jeweils zwei nebeneinanderliegende Seiten gleich lang sind.
Beispiele siehe F2 3. Beispiel und 5. Beispiel
11
G1 Parameterdarstellungen für Geraden aus zwei gegebenen Punkten ermitteln sowie überprüfen,
ob ein Punkt auf einer gegebenen Gerade liegt (Punktprobe) und die Ergebnisse im Sachzusammenhang interpretieren.
Regeln
Parameterform einer Geraden durch A und B: g(A,B): x OA r AB , r  IR.
Punktprobe: ein Punkt C liegt auf g, wenn OC OA r AB erfüllt ist, d.h. wenn es einen Wert
für den Parameter gibt, so dass alle drei Koordinatengleichungen erfüllt sind.
Spezialfall: liegt ein Punkt auf einer Strecke?
Ein Punkt C liegt auf AB, wenn OC OA r AB für 0 r 1 erfüllt ist.
7
1. Beispiel: Liegt der Punkt M(2|4|2) auf der Geraden x
2
2
7
Lösung: 2
2
4
t
4
r
4 ?
2
2
4
4  t= 1,25  t= 0,5 [ t =2] M liegt nicht auf g.
2
2
12
G2 Geraden auf ihre gegenseitige Lage untersuchen und möglicherweise vorhandene
Schnittpunkte bestimmen.
Regeln
Mögliche Lagen von Geraden zueinander: echt parallel, identisch, schneidend oder windschief
Vorgehen, um die Lage von g : x a r b und h : x c r d zueinander zu untersuchen:
Sind die RV kollinear (das kann man i. A. ohne Rechnung sehen), so sind die Geraden parallel.
Die zusätzliche Punktprobe c a r b zeigt dann, ob sie echt parallel oder identisch sind.
Sind die RV nicht kollinear, so versucht man den Schnittpunkt zu ermitteln:
hat das LGS aus 3 Gleichungen und 2 Unbekannten eine Lösung, so schneiden die Geraden
sich, ansonsten verlaufen sie windschief.
Beachte: 3. Gleichung muss kontrolliert werden.
Typische Anwendungsaufgaben
 Fluggeraden ermitteln
 Untersuchen, ob sich die Bahnen kreuzen
 Untersuchen, ob es (trotzdem nicht) zu einem Zusammenstoß kommt.
 Untersuchen, ob sich Diagonalen/Strecken in einem Körper schneiden.
Unnötige Arbeit: Obwohl nur Parallelität nachgewiesen werden soll, wird auch noch untersucht, ob
sogar Identität vorliegt.
Beachte:
Bei der Untersuchung von zwei Geraden müssen ggf. die Parameter unterschiedlich benannt
werden.
1.Beispiel:
Untersuche die Lagebeziehung zwischen g und h und berechne ggf. den Schnittpunkt S.
100
0,1
53
2
2550 t 22
h : y(r)
410 r
30 g : x(t)
43,75
4
228,75
1,5
Lösung:
RV sind nicht kollinear (2=(–20)·(–0,1); 4 (-20)·(–1,5))
g  h: –0,1t–2r= – 47  22t+30r=2140  –1,5t–4r=–185  t=70  r=20  2140=2140
Die Geraden schneiden sich im Punkt S(93|–1010|123,75).
13
2.Beispiel:
Gegeben sind die Flugbahnen zweier Flugzeuge
100
0,1
53
g : x(t)
2550 t 22 ; h : y(t)
410
t
2
30 ; t in min; x(t) und y(t) in km, gleiche Zeit-
228,75
1,5
43,75
4
rechnung
a) Zeige, dass die Flugbahnen sich kreuzen.
b) Begründe, ob es zu einem Zusammenstoß beider Flugzeuge kommt.
Lösung:
a) Einen Parameter umbenennen, z. B. x(r) !
LGS aus den ersten beiden Gleichungen (TR):r=70  t=20
3. Gleichung 123,75=123,75  S(93|–1010|123,75)
b) Das erste Flugzeug erreicht den Schnittpunkt nach 70 Minuten, das zweite nach 20.
Es besteht keine Kollisionsgefahr.
3. Beispiel:
Untersuche die Lagebeziehung von g, h und k
3
0,5
1
1
g: x
2 r
2 ; h: x 1 s 4 ; k: x
5
1
1
2
3
3
2
1,5
r
6
3
Lösung:
u1, u2 und u3 seien die Richtungsvektoren der drei Geraden g, h und k.
Man sieht, dass u2
2 u1 , u3 3 u1 ist.  die RV sind kollinear und damit sind die
Geraden g, h und k parallel.
Gilt g=h?
3
1
1
3
2
1 r 4  r=–2  r= –4  g und h sind echt parallel.
5
1
Gilt g=k?
3
2
2
2
1,5
3
5
3
Gilt h=k?
1
2
1
1
3
3
2
5
6  r=3  r= 6  g und k sind echt parallel.
r
3
1,5
r
2
1
6  r=–3  r=3  h und k sind echt parallel.
3
14
G3: Parameterdarstellungen für Ebenen aus drei gegebenen Punkten ermitteln sowie
überprüfen, ob ein Punkt auf einer gegebenen Ebene liegt (Punktprobe) und die
Ergebnisse im Sachzusammenhang interpretieren.
Regeln
Drei Punkte A, B, C, die nicht auf einer Geraden liegen (d. h. AB und AC sind nicht kollinear), legen eine Ebene E fest.
E: x OA r AB s AC , r, s  IR. (Parameterform der Ebene)
Es gibt somit unendliche viele verschiedene Parameterdarstellungen für eine Ebene, da man beliebig andere Punkte der Ebene wählen kann.
Der SV wird häufig auch mit x0 , die RV mit u und v bezeichnet, also E: x x0 r u s v
Um herauszufinden, ob ein Punkt in einer bestimmten Ebene liegt, führt man eine Punktprobe
durch: man untersucht, ob der Ortsvektor des Punktes die Ebenengleichung erfüllt.
Sonderfälle
Wenn man den Definitionsbereich für die Parameter auf Intervalle einschränkt,
erhält man Halbebenen oder Parallelogramme (siehe Zeichnung)
E: OA
u
v ; ,   IR.
Rechte Halbebene E: OA
u
v ;  0,   IR
Untere Halbebene E: OA
u
v ;   IR,  0
Parallelogramm P1: OA
u
v ; 1,5 2; 34
Parallelogramm P2: OA
u
v ; 0 1; 12
u
v ; +  1  , 0
Dreieck QRS: DQRS: OQ
P1
P1
P2
P2
S
S
Q
Q
R
R
Beispiel für eine Punktprobe
4
Gegeben ist die Ebene: E: x
2
1
4
r
2
2
2
1 und der Punkt P (10|–3|10). Liegt P auf E?
s
5
Lösung:
Man setzt den Ortsvektor des Punktes mit der Ebene gleich und erhält ein Gleichungssystem mit
3 Gleichungen und 2 Unbekannten. Wenn dieses eindeutig lösbar ist (man also Werte für r und s
erhält und diese durch Probe bestätigt werden) so liegt der Punkt auf der Ebene, sonst nicht.
(I) 10 = 4+ 4r – 2s
 6 = 4r – 2s
(II) –3 = 2 – 2r – 1s
 –5= –2r –1s
(III) 10 = 1– 2r + 5 s
 9 = –2r+5s
15
Man kann jetzt zum Beispiel die zweite und dritte Gleichung addieren, um das r zu eliminieren.
Hierbei erhält man 4s = 4  s = 1
Durch Einsetzen in die erste Gleichung erhält man dann 8 = 4r  r = 2
Probe mit der zweiten Gleichung geht auf: –5 = –4 –1 Das Gleichungssystem ist lösbar.
Der Punkt P liegt also auf der Ebene.
Alternative Lösung mit GTR und linsolve()
Beachte:
3. Gleichung muss bei Lösung ohne GTR überprüft werden
Nur die Richtungsvektoren darf man verkürzen, nicht den Stützvektor
Umständliches Vorgehen
Richtungsvektoren werden nicht verkürzt, obwohl es weniger Arbeit ist.
Allerdings: bei Fluggeraden wird mit Änderung des RV auch die Zeiteinheit geändert!
Typische Anwendungsaufgaben
 Seiten– und Schnittflächen von Körpern
 Schattengebilde
1. Beispiel:
A( 80 |400 | 2), B( 100 | 400 | 2 ), C( 100 |1200 | 6 ) und D( 80 | 1200 | 6 )
Stelle eine Parameterform der Ebene E durch A, B und C auf und zeige, dass D in
der Ebene E liegt.
Lösung:
4 Punkte A,B,C,D liegen in einer Ebene, wenn (z. B. ) D in der von A, B und C aufgespannten
Ebene liegt.
(Vergleiche: 3 Punkte A,B,C liegen auf einer Geraden, wenn (z. B. ) C auf der Geraden
durch A und B liegt.)
80
20
20
80
E: OA r AB s AC
400 r 0
s 800 = 1200  s= 1  r =–1  2+4=6  D  E.
2
0
4
6
2. Beispiel:
Gegeben sind A(80 |400 | 2), B( 100 | 400 | 2 ), D( 80 | 1200 | 6 ) und L(85 | 750 | 3,75)
Liegt L im Parallelogramm ABCD?
Lösung:
80
20
0
85
7
E: OA r ' AB s' AD
400 r 0
s 800 = 750  r = 0,25  s = 16  2+1,75=3,75 (w)
2
0
4
3,75
Da beide Parameter zwischen 0 und 1 liegen, liegt L innerhalb des Parallelogramms.
16
G4 Normalenform / Koordinatenform einer Ebene ermitteln
Regeln
Eine Ebene ist durch einen Punkt und zwei nicht kollineare RV festgelegt (siehe G3)
Kennt man zu einer Ebene einen Normalenvektor (NV) n , also einen Vektor, der senkrecht
zur Ebene verläuft, sowie einen Punkt P der Ebene, so liegt irgendein Punkt X genau dann
auf der Ebene, wenn der Vektor PX senkrecht zum NV verläuft, wenn also gilt:
n  PX  0  n  OX  OP  0  n  OX  n  OP = n  x  n  OP =c


Alle Punkte der Ebene – und nur diese – bilden mit dem NV also das gleiche SP.
 n1 
 x1 


Schreibt man n   n2  und x   x 2  , so erhält man
x 
n 
 3
 3
die Koordinatenform: n1·x1 + n2·x2 + n3·x3 = c oder n1·x + n2·y + n3·z = c.
Beispiel:
 2
Gesucht ist eine Gleichung der Ebene, die durch den NV n =  3  und den
 5 
 
Punkt P(2|4|–8) festgelegt ist.
 2
Lösung: n  OP = 56; E:  3  · x =56 (Normalenform)  2x + 3y –5z = 56 (Koordinatenform)
 5 
 
Vorteile der Normalenform/Koordinatenform
Punktprobe wird zur Kopfrechenaufgabe (bei der PF musste ein LGS mit 3x2 LGS gelöst werden). Beispiel:
R(1|2|19) liegt nicht auf E, da die Koordinaten die Ebenengleichung nicht erfüllen:
2·1+3·2+10·5 = 56 (f)
Achsenabschnitte kann man im Kopf angeben: setze zwei Koordinaten 0 und berechne die dritte:
2
y=z=0  Sx(28|0|0); x=z=0  Sy(0| 18 |0) x=y=0  Sz(0|0|–11,2)
3
Die Lagebeziehung Gerade – Ebene und Ebene – Ebene zu bestimmen, geht sehr einfach.
 G5, G6
17
Wie wandelt man die 3 Ebenformen (PF, NF, KF) jeweils in die anderen um?
a) Von der Parameterform E: x  OA  r  u  s  v in die Normalenform:
Man ermittelt einen Normalenvektor als Kreuzprodukt der beiden Richtungsvektoren
n u x v ; Es gilt nun E: n x n OA = c  n1·x + n2·y + n3z = c.
 12 
 3   3  4


     
Beispiel: E: x
2 r
2 s 1 ; 2 x 1 =  16   ( 4)  4  ;  4    2   22
 8 
 2   2   1
1
2
5
2
5


     
[Kontrolle: der NV steht senkrecht auf beiden RV, da das SP jeweils 0 ergibt.)
3
E:  4   x  22  3x + 4y +2z = 22
 2
 
[Kontrolle: bilde die Punkte für r=s=0 (4|2|1), r=1; s=0 (8|0|–1) und r=0; s=1 (2|1|6)
und mache im Kopf die Punktprobe.]
b) Von der Normalenform ind die Koordnatenform und umgekehrt:
Die Koeffizienten von x, y und z bilden den Normalenvektor.
4
4
2
4
2
c) Von der Normalenform in die Parameterform:
man ermittelt drei Punkte A, B und C, z. B. die Achsenabschnitte: E : x
OA
r AB
s AC
a) Gegeben sind drei Punkte A, B, C:
Zunächst ermittelt man eine Parameterform (PF) der Ebene, z. B. E: x OA r AB s AC
Nun ermittelt man einen Normalenvektor als Kreuzprodukt der beiden Richtungsvektoren
n AB x AC ; Es gilt nun E: n x n OA = c  n1·x + n2·y + n3z = c.
b) Gegeben sind eine Gerade und ein Punkt P, der nicht auf der Geraden g: x
EP,g: x OA t u r AP
OA
c) Gegeben sind zwei sich schneidende Geraden g: x OA t u und h: x OB
EP,g: x OA t u r v (Man kann auch OS oder OB als SV nehmen:)
d) Gegeben sind zwei echt parallele Geraden g: x
Eg,h: p0
u
(p0
p0
u und h: x
q0
t u liegt.
t v
u
q0 )
e) Ebene verläuft senkrecht zu einer Gerade sowie durch P.
Man nimmt den RV der Geraden als NV und OP als SV.
f) Ebene verläuft senkrecht zu einer Ebene E sowie durch P
Man nimmt einen Vektor, der senkrecht zum NV von E verläuft, als NV und OP als SV.
Weiter wie in a).
Beachte:
Drei Punkte, die auf einer Geraden liegen, bilden keine Ebene.
(Den Fehler bemerkt man i. a. dann, wenn der mit Vektorprodukt gebildete NV gleich dem Nullvektor ist.)
Umständliches Vorgehen:
18
 RV werden vor der Weiterrechnung nicht „verkürzt“ (siehe in G4-2 die Gerade gxy).
(Ausnahme Fluggeraden, wenn dadurch die Zeiteinheit geändert wird.)
 Man erkennt nicht, dass ein NV gegeben ist und nimmt den langwierigen Weg über a)
 Koordinatenebenen und deren Parallelen werden nach a) ermittelt anstatt sie ohne Rechnung anzugeben, z.B.: die xy-Ebene hat die Gleichung z=0.
Typische Anwendungsaufgaben
 Seiten– und Schnittflächen von Körpern
 Begrenzungsebenen bei Flughäfen
Gegeben sind die Punkte B(3 | 3 | 7), C (−3 | 3 | 7) und S(0 | 0 |13)
(1) Berechne eine Gleichung der Ebene E durch B, C und S in Normalenform.
[Zur Kontrolle: E: 2x2 + x3 − 13 = 0 ]
(2) Die Ebene E enthält den Punkt C (−3 | 3 | 7) und ist orthogonal zur Geraden
durch A (3 | −3 | 7) und S(0 | 0 |13). Ermittle eine Gleichung der Ebene E.
[Zur Kontrolle: E: − x1 + x2 + 2x3 = 20]
19
Ebenen anhand ihrer Spurgeraden im Koordinatensystem darstellen.
Regeln
Zum Zeichnen einer Gerade ermittelt man die Achsenabschnitte, indem man jeweils zwei Koordinaten gleich null
setzt und diese Punkte verbindet.
Die Schnittgeraden einer Ebene mit den Koordinatenebenen
heißen Spurgeraden.
Es sind die Geraden durch die Achsenabschnitte, falls diese
existieren.
Spezialfall: Besondere lage von Ebenen
Wenn es einen/zwei Achsenabschnitt(e) nicht gibt, so verläuft die Ebene parallel zu dieser/diesen
Achse(n):
2x+z=4 verläuft parallel zu y-Achse.
y=4 verläuft parallel zur x- und z-Achse, also parallel zur xy-Ebene.
Typische Anwendungsaufgaben
Seiten– und Schnittflächen von Körpern (häufig spezielle Ebenen)
Beachte:
Eine Normalenform einer Geraden im IR3 gibt es nicht, Normalenformen im IR3 sind
3
immer Ebenen! y=3x+4 im IR ist eine Ebene, die parallel zur z–Achse verläuft.
Umständliches Vorgehen:
 RV werden vor der Weiterrechnung nicht „eingekürzt“ (siehe die Gerade gxy. in G4-2)
(Ausnahme Fluggeraden, wenn dadurch die Zeiteinheit geändert wird.)
 man erkennt nicht, dass ein NV schon gegeben ist und nimmt den langwierigen Weg über a)
 Koordinatenebenen und deren Parallelen werden nach a) ermittelt anstatt sie ohne Rechnung anzugeben, z.B.: die xy-Ebene hat die Gleichung z=0.
Beispiel:
Ermittle zur Ebene E: 3x+4y+2z=24 die Achsenabschnitte sowie die Spur dieser Ebene
in der xy–Ebene.
Lösung:
y=z=0 x=8  Sx(8|0|0); entsprechend: Sy(0|6|0) Sz(0|0|8)
8
8
8
1
Ermittlung der Spurgeraden g13 bzw. gxz: gxz : x
0
0
20
r
0
0
8
0
t
0
1
G5 Schnittprobleme zwischen Geraden und Ebenen in Sachzusammenhängen (z.B.
bei Schattenwürfen) untersuchen.
Regeln
Mögliche Lagebeziehungen:
 Gerade liegt in der Ebene
 Gerade verläuft echt parallel zur Ebene
 Gerade schneidet die Ebene
Das Vorgehen hängt davon ab, in welcher Form die Ebene gegeben ist.
Ebene ist in KF oder NF gegeben
Ob Parallelität vorliegt, kann man sofort sehen und sollte deshalb als Erstes untersucht werden:
Gerade und Ebene verlaufen parallel, wenn der RV senkrecht auf dem NV steht.
Eine Punktprobe entscheidet in diesem Fall, ob echte Parallelität vorliegt oder die Gerade in der
Ebene verläuft.
Steht der RV nicht senkrecht auf dem NV, so gibt es einen Schnittpunkt. Diesen ermittelt man,
indem man die Gerade als einen Vektor schreibt, die x/y/z–Koordinate in die Ebenengleichung
einsetzt und die lineare Gleichung mit einer Variablen löst.
Ebene ist in PF gegeben
Hier sollte man entscheiden, ob es sich nicht lohnt, die PF in eine NF umzuwandeln.
Falls es sich nicht lohnt:
Man versucht den Schnittpunkt zu ermitteln (LGS mit 3 Gleichungen und
3 Unbekannten  TR)
Falls es keinen Schnittpunkt gibt, entscheidet eine Punktprobe über die Art der Parallelität.
Typische Anwendungsaufgaben
 Geraden als Umrisse von Schatten
 Eckpunkte des Schattenumrisses sind Schnittpunkte der Geraden.
 Lotgeraden / Höhengeraden
1. Beispiel:
1
Zeige, dass jede Ebene der Schar Er : r x
2r
4 , r  IR, die Gerade durch R(0 | 2 | 4) und
1
S(4 | 2 | 0) enthält.
0
2. Beispiel: Eine von einem Punkt M (0 | 7 | 15 ) ausgehende Gerade, die in Richtung
2,5
5
zeigt, durchstößt die Ebene EBCS mit B(3 | 3 | 7), C (−3 | 3 | 7) und S(0 | 0 |13) im Punkt M*.
*
Ermittle die Koordinaten des Punktes M .
3. Beispiel
3
Untersuche, wie die Gerade k: x
3
1
t
1 , t  IR, zur xy-Ebene verläuft.
13
0
Lösung: k verläuft wegen z=13 (echt) parallel in einem Abstand von 13 LE zur xy-Ebene.
21
4. Beispiel
Durch Ea: 2x1 + x2 + 2x3 + 9⋅ (2a − 5) = 0, a  IR , sei eine Schar von Ebenen Ea gegeben;
h sei die Gerade, die durch die Punkte S1 (13 | 1 | 9) und S2 (5 | −3 | 1) verläuft.
Zeigen Sie, dass jede Ebene Ea der Schar orthogonal zur Geraden h verläuft.
Bestimmen Sie den Schnittpunkt Pa der Ebene Ea mit der Geraden h.
[Zur Kontrolle: Pa(13− 4a | 1− 2a | 9− 4a)]
22
G6 Ebenen auf ihre gegenseitige Lage untersuchen und möglicherweise vorhandene
Schnittgeraden bestimmen.
Mögliche Lagebeziehungen von zwei Ebenen
 Es gibt eine gemeinsame Schnittgerade
 Die Ebenen verlaufen echt parallel
 Die Ebenen sind identisch
Anschauungshilfe: wenn man das Tafelwerk aufklappt, ergeben sich zwei Ebenen,
der Buchrücken verläuft auf der Schnittgeraden.
Ermittlung der Lagebeziehung
Sind die Ebenen in KF oder NF gegeben, so sind sie parallel, wenn die NV kollinear sind.
Sind die Ebenengleichungen sogar äquivalent, so sind die Ebenen identisch.
Sind die NV nicht kollinear, gibt es eine Schnittgerade.
Verlaufen die NV der Ebenen senkrecht zueinander, schneiden sich auch die Ebenen senkrecht.
Geraden und Ebenen im Raum; Flussdiagramm für die Lagebeziehung:
Sind die
NV kollinear?
?
JA
JA
Ebenen sind
identisch
Ebenen–
gleichungen
äquivalent?
NEIN
NEIN
Ebenen
schneiden sich
in einer
Schnittgeraden.
Ebenen sind
echt parallel
Beispiel:
Untersuche die folgenden Ebenen auf besondere Lagebeziehung
(identisch, parallel, senkrecht schneidend).
E1: 2x –3y +6z = –14
E2: –3x + 2y = 12
E3: 2x – y + 2z = 0
E4: 2(x+1)–3(y+4) = –24– 6z E5: –5x +3y – 12z = 13
E6: 3x –1,5y +3z = –18
E7: 10x – 15y + 30z = 70
E8: z = –2
E9:
4y –3z = 10
Lösung:
Löst man bei E4 die Klammern auf und fast zusammen, so erhält man E 4: 2x –3y +6z = –14
Damit gilt E1 = E4; E7 = 2x – 3y +6z = 14 ist zu E1 bzw. E4 echt parallel.
E3 und E6 sind echt parallel, da (nur) die NV kollinear sind.
Das SP der NV ergibt bei E2 und E8 null, so dass sich diese Ebenen senkrecht schneiden.
23
Berechnung der Schnittgerade von zwei Ebenen (Beispiel)
Beispiel: Gegeben sind die Ebenen E1: 6x1+2x2–2x3 = –3 und E2: –3x1+4x2–5x3 = –6
6
Die NV
2 und
2
3
4 sind nicht kollinear, also schneiden sich die Ebenen.
5
Ermittlung der Schnittgerade gs: Lösung des LGS mit 2 Gleichungen und 3 Unbekannten:
1. Schritt Aus den beiden Ebenengleichungen mit je 3 Unbekannten eine Gleichung mit
2 Unbekannten ermitteln. (I)+2·(II): 10x2–12x3 = –15
2. Schritt Man drückt zwei Unbekannte jeweils durch die dritte aus:
3 6
1
x2= –2 +5 x3 ; Einsetzen in E1: x1= –15 x3
1
3 6
3. Schritt Lösungsmenge: IL = ( 
x3 |   x3 | x3 ) | x3  IR}
15
2 5
1 x
1
0
0
1
15 3
15
Schnittgerade: gs: x
3
2
6
5
3
2
x3
0
x3
x3
6
5
1
3
2
=
t 18
0
15
Lagebeziehungen zwischen drei Ebenen
Methode 1:
Man schneidet die ersten beiden Ebenen und dann das Schnittgebilde mit der 3. Ebene.
Methode 2
Man löst das LGS mit 3 Gleichungen und drei Unbekannten.
Beachte:
Das Lösen eines LGS mit 3 Gleichungen und 3 Unbekannten kann man als Schnitt dreier
Ebenen. (Daher kann ein solches LGS auch nicht genau zwei Lösungen haben.)
Typische Aufgaben
 Schnitt zweier Flächen
 Schnittgeraden einer Fläche mit der xy-, xz- und yz-Ebene
 Ebenenscharen
Unnötige Arbeit
Wenn eine der beiden gegebenen Ebenen nur zwei Variablen enthält, braucht man nicht eine
Gleichung mit 2 Variablen herzuleiten.
0
4x+2y+z=6  2x–z=4  z=2x–4  y= –3x+2  IL={(x|–3x+5|2x–4); gs: x
5
4
24
1
t
3
2
G7 Die Koordinaten eines gespiegelten Punktes bestimmen.
Regeln
Wird ein Punkt P wird an einem Punkt Z gespiegelt, so gilt OP'  OP  2  PZ .
Zur Kontrolle: Z muss der Mittelpunkt der Strecke PP‘ sein.
Bei Spiegelung an Koordinatenebenen wechselt nur eine Koordinate ihr Vorzeichen:
Beispiel: P(2|–3|5)  (Spiegelung an der xy–Ebene) P’(2|–3|–5)
Bei Spiegelung an Koordinatenachsen wechseln zwei Koordinaten ihr Vorzeichen:
Beispiel: P(2|–3|5)  (Spiegelung an der y–Achse) P’(–2|–3|–5)
Allgemein gilt: Ist F der Lotfußpunkt des Lotes von P auf eine Gerade g / eine Ebene E,
so ist OP' OP 2 PF OF PF der Ortsvektor des Bildpunktes.
Die eigentliche Arbeit besteht i. A. darin, den Lotfußpunkt zu bestimmen.
Abstände
Abstand eines Punktes zu einer Ebene
Wenn E: n  x  c die KF einer Ebene ist und P ein Punkt, so gilt d(P,E)
n OP
c
.
n
Abstand einer Gerade zu einer Ebene
Das funktioniert natürlich nur, wenn die Gerade echt parallel zur Ebene ist (also vorher prüfen!).
Dann nimmt man irgendeinen Punkt der Geraden als Punkt P, berechnet den Abstand dieses
Punktes zur Ebene.
Abstand einer Ebene E1 zu einer anderen Ebene E2
Auch hier funktioniert das nur, wenn die Ebenen echt parallel zueinander sind. Man berechnet zu
irgendeinen Punkt der einen Ebene den Abstand zur anderen Ebene.
Welchen Abstand haben die Ebenen E: 2x+y+2z = 9 und F: –4x–2y–4z = 24
Lösung: P(0|9|0) liegt auf E.
d(P,F) =
| 18  24 |
 7 LE
6
Welche Ebenen G haben zu E: 2x+y+2z = 9 den Abstand 5 LE?
F: 2x+y+2z = c; d(P, F) =
9c
9c
 5
6
6
=±5c=
 2
 2
 2
1 
1 
1 
Lösung: E:  1   x  3 (HNF); die Ebenen F:  1   x  8 und G:  1   x  2
3 
3 
3 
 2
 2
 2
haben den gewünschten Abstand.
 2
1 
Alternative: P(0|9|0)  E; OP   1   5 =
3 
 2
 10 / 3 
 2
 10 / 3 
1 




 32 / 3  ; OP  3  1   5 =  22 / 3  ergibt die Ortsvektoren
 2
 10 / 3 
 10 / 3 
 




25
 2

zweier Punkte der gesuchten Ebenen. Mit diesen Punkten und dem NV (z.B.)  1  kann man die
 2
 
Ebenengleichungen aufstellen.
Beachte:
 Man muss auf beiden Seiten durch die Länge des Normalenvektors dividieren.
 Die rechte Seite der HNF darf nicht negativ sein.
 Bei der Abstandsformel müssen Beträge gesetzt werden (oder man begründet durch die Lage des Punktes, dass das Ergebnis nichtnegativ sein muss.
 Vor der Abstandsberechnung von Gerade-Ebene oder Ebene-Ebene überprüfen, ob die beiden auch parallel sind (sonst erhält man als Abstand 0).
Aufgabe
Ermittle eine Normalenform der Ebene E durch P(4 | 0 | 2), Q(2 | 0 | 4) und R(0 | 2 | 4) sowie den
Abstand der Ebene zum Ursprung.
6
Lösung: d(E,O)=
 3,46 LE
3
2 6 1 1 2 ( 2) 5
4
Beispiel: E: 2x1 – x2 + 2x3 = 5; P(6|1|–2)  d(P,E)
LE .
3
3
26
H1 Winkel zwischen zwei Vektoren, Schnittwinkel zwischen zwei Geraden, zwischen zwei
Ebenen sowie zwischen einer Gerade und einer Ebene berechnen.
Formeln zur Winkelberechnung (siehe auch Tafelwerk)
Winkel  zwischen zwei Vektoren a und b : cos  
a b
ab
Achtung: Fußpunkt an Fußpunkt, oder Spitze an Spitze; für a  b <0 ist  > 90°.
Schnittwinkel  zweier Geraden mit RV a und b : cos  
a b
ab
Schnittwinkel ist festgelegt als der kleinere der beiden Winkel der Geradenkreuzung.
Schnittwinkel  zweier Ebenen mit NV n1 und n2 : cos  
Schnittwinkel  zwischen Gerade und Ebene sin  
n1  n2
n1  n2
nv
nv
Der Schnittwinkel zwischen Ebene und Gerade ergänzt den Schnittwinkel zwischen Gerade und NV
zu 90°. Der Sinus berechnet automatisch den richtigen Winkel.
Beachte:
 Bei Gerade–Ebene sin  verwenden.
 Keine Beträge bei Winkel zwischen Vektoren (da hier der Winkel über 90° sein kann), sonst
immer Beträge setzen.
 Taschenrechner muss auf DEG stehen
Umständliches Vorgehen:
Statt mit den Winkelformeln kann oft elementargeometrisch schneller gelöst werden:
Innenwinkelsummensätze bei Dreieck, Viereck, n-Eck; Basiswinkelsatz; Winkel im gleichseitigen
Dreieck; Satz des Thales; Berechnung mit Winkelfunktionen; …
Typische Anwendungsaufgaben
 Winkel, den Dachflächen bilden, berechnen.
 Winkel in einem Dreieck, Viereck berechnen.
 Einfallwinkel von Sonnenstrahlen berechnen.
Beispiel
Gegeben sind die Punkte A(1|0|0), B(5|6|0), C(0|–6|0)
Bestimme im Dreieck ABC den Innenwinkel  am Eckpunkt A .
 1
 4
AC  AB
40
 
 
AC  6  ; AB  6  ; cos  

 0,91    155,77 ;
AC  AB  37  52
0
0
 
 
27
Beachte: Bei der Inhaltsberechnung eines Dreiecks ist es oft günstiger einen Innenwinkel zu berechnen und dann die Formel
1
A = 2 b·c·sin  (halbes Produkt zweier Seitenlängen mal Sinus des eingeschlossenen Winkels)
1
zu benutzen (statt die Höhe über Abstand Punkt Gerade zu ermitteln und die Formel A = 2 g·h zu
benutzen.
Am effizientesten geht es allerdings meistens mit AABC = 0,5 · AB x AC
28
H2 Den Flächeninhalt eines Dreiecks und das Volumen von Pyramiden und Prismen
(auch nach elementaren Methoden) bestimmen.
Regeln
Es gibt mehrere Formeln zur Berechnung des Flächeninhalts eines Dreiecks.
Je nach Gegebenheiten sollte man sich die günstigere aussuchen.
Falls keine Besonderheiten vorliegen, wird (IV) der schnellste Weg sein.
1
(I) A = 2 g·h (halbes Produkt aus einer Grundseite und zugehöriger Höhe)
1
(II) A = 2 a·b·sin  (halbes Produkt zweier Seitenlängen mal dem Sinus
des eingeschlossenen Winkels)
(III) A =
1
 a x b (zum Kreuzprodukt siehe H6)
2
Beachte: Es gibt drei verschiedene Grundseiten und drei zugehörige Höhen.
Eine Grundseite muss nicht unten liegen.
Bei rechtwinkligen Dreiecken nimmt man eine Kathete als Grundseite, die andere Kathete ist
dann die zugehörige Höhe.
Beispiel
Gegeben sind die Punkte A(1|0|0), B(5|6|0), C(0|6|0) und S(3|3|6) .
Bestimme im Dreieck ABC den Innenwinkel  am Eckpunkt A sowie den Flächeninhalt des Dreiecks ABC.
Lösung:
 1
 4
AC  AB
32
 
 
AC  6  ; AB  6  ; cos  

 0,73    43,15 ;

37

52
AC

AB
0
0
 
 
 0 
1
1 
1
A= 2 · AB AC sin  15,00 [FE] oder A =  AC x AB =   0  = 15 [FE]
2 
2

 30 
Volumen einer (schiefen) Pyramide mit Spitze S.
1
Es gilt V =  G  h
3
Die Grundfläche G rechnet man mit den entsprechenden Formeln für Dreieck oder Quadrat aus.
Ist die Grundfläche ein unregelmäßiges Viereck, unterteilt man es ggf. in zwei Dreiecke.
Zur Berechnung der Höhe gibt es (mindestens) zwei Verfahren (siehe H3):
1. Man berechnet den Schnittpunkt F der Lotgeraden durch S mit der Ebene. h = SF .
2. Da h = d(S,E) gilt, kann man h mit der Formel d 
n  OS  c
n
29
berechnen (E: n  x  c )
Beispiel: Berechne das Volumen der Pyramide ABCS mit
A(3|6|–1), B(–2|–2|13), C(6|–2|5), S(–6|12|1)
Lösung:
3
8
 5 
3
 5   3   64 
 
 










EABC: x   6  r   8   s   8  ; Normalenvektor:  8  x  8    72  = 8   9 
 1
8
 14 
 6
 14   6   64 
 
 
     
 
 
 64   
1     1
1
G =  AB x AC =   72     642  722  642  3344 ;
2    2
2
 64   
Berechnung der Höhe:
1. Möglichkeit: E: 8x + 9y + 8z = 70; h = d(S,E) =
8  ( 6)  9  12  8  1  70
=
2
209
8 9 8
 6 
8
 5 3 8 9 
 
 


2. Möglichkeit: l: x   12   t   9  ; l  E: TR:  8 8 9 6  )  t  0,01 
 1
8
 14 6 8 2 
 
 


S(–5,92|12,09|1,08) FS =
Volumen in beiden Fällen: V =
2
0,082  0,092  0,082  0,14;
1
 1344  0,14 2,70 FE
3
30
2
2
 0,14
H3 Den Abstand eines Punktes P von einer Ebene E berechnen.
1. Möglichkeit siehe G8
2. Möglichkeit: schneide die Lotgerade OP
n mit der Ebene und berechne den
Abstand des Lotfußpunktes F von P : d(P,E)= PF .
Typische Anwendungsaufgaben
Höhe einer Pyramide bestimmen
1.Beispiel
Die Ebene E enthält den Punkt C (−3 | 3 | 7) und ist orthogonal zur Geraden durch A (3 | −3 | 7)
und S(0 | 0 |13).
(1) Ermittle eine Gleichung der Ebene E. [Zur Kontrolle: E: − x1 + x2 + 2x3 = 20]
(2) Berechne den Abstand des Punktes B(3 | 3 | 7) von der Ebene E.
(3) Begründe die Lage von Ursprung, Punkt B und Ebene E zueinander.
2.Beispiel
Berechnen Sie die Dicke des abgebildeten Oktaeders als Abstand des Punktes C (5 | 3 | 7) von
der Ebene durch A(13 | −5 | 3), B (11 | 3 | 1) und S1 (13 | 1 | 9)
31
H4 Den Abstand eines Punktes R von einer Geraden g berechnen.
1. Man setzt den Lotfußpunkt F variabel an (Gerade als einen Vektor schreiben), bildet den
variablen Vektor PF und ermittelt den Parameter mit Hilfe der Bedingung,
dass PF senkrecht auf dem RV der Geraden stehen muss.
2. Man setzt den Lotfußpunkt F variabel an (Gerade als einen Vektor schreiben), bildet den variablen Vektor PF und berechnet seine Länge in Abhängigkeit vom Parameter. Zu dieser Abstandsfunktion berechnet man mit Mitteln der Differentialrechnung das Minimum. Da die Abstandsfunktion die Wurzel aus einer quadratischen Funktion ist, genügt es die Parabel unter der
Wurzel zu minimieren.
Typische Anwendungsaufgaben
Höhe in einem Dreieck, Parallelogramm berechnen
Abstand einer Kirchturmspitze / Flugballons / … von einer Flugbahn
Länge von senkrecht verlaufenden Stützstäben
1. Beispiel
100
Bestimme den Abstand der Flugbahn g : x(t)
2550
0,1
t
22
228,75
1,5
vom Tower in T( 0 | 0 | 8 ) sowie den Punkt F der Flugbahn, an dem der Pilot dem Tower am
nächsten kommt
Lösung: (Methode 1)
100 0,1t
TF
2550 22t ; TF
220,75 1,5t
0,1
22 =0  –10+0,01t–56100+484t–331,125+2,25t =0
1,5
 486,26t= 56441,125  t 116,07; Einsetzen in TF ergibt d  100 [LE].
100
2550
OF
0,1
116,07
228,75
22
 F(88,39|3,54|54,65)
1,5

Lösung: (Methode 2)
100 0,1t
TF
2550 22t =
220,75 1,5t
(100  0,1t) 2  (22t  2550) 2  (220,75  1,5) 2
d2(t) = 486,26t2 – 112882,25t + 6561230,562; d2‘(t)= 972t – 11288,2t = 0  t  116,07
OF  g(116,07)  F(88,39|3,54| 54,65); dmin  d(116,07) = 100,41
2. Beispiel
Zum Dreieck ABC mit A(4|2|–1); B(10|.8|9); C(4|0|1) soll die Länge der Höhe auf BC berechnet
werden.
Lösung: Die Länge der Höhe ist gleich dem Abstand von A zur Geraden g(B,C).
32
 6t 
 4
 6
g: x(t)   0   t   8  ; d(t) = x(t)  OA   8t  2   36t 2  64t 2  32t  4  64t 2  32t  4
 8t  2 
 1
8


 
 
8
= 164t 2  64t  8 ; d2‘(t) = 328t+64=0  t = –
 0,20
41
(Absolutes Minimum, da d2 eine nach oben geöffnete Parabel ist.)
 1,17 
 4
 6
8
8  


d(– )  1,33 [LE]; OF   0    8   F(2,83|1,56|–0,56) Kontrolle: AF   0,44   1,33
41
 0,44 
 1  41  8 


 
 
33
H5a Den Abstand zweier Geraden g und h berechnen.
1. Fall: Geraden verlaufen echt parallel.
Dann ist der gesuchte Abstand gleich dem Abstand irgendeines Punktes der einen Gerade von
der anderen und kann, wie in H4 beschrieben, berechnet werden.
2. Fall: Geraden schneiden sich oder sind identisch. Dann ist der Abstand gleich null.
3. Fall: die Geraden verlaufen windschief.
Der Abstand ist festgelegt als die Länge derjenigen Verbindungsstrecke GH (G auf g und H auf
h), die senkrecht zu beiden Geraden verläuft. (Diese Verbindung ist die kürzeste Verbindungsstrecke.)
1. Methode: Formelsammlung Seite 46 d
q0
p0 n0
q0 und p0 sind die SV der Geraden und n0 ein Vektor der Läge 1, der senkrecht auf
beiden RV steht ( Kreuzprodukt bilden und normieren).
2. Methode
Man setzt den Verbindungsvektor GH variabel an (beide Geraden als einen Vektor
schreiben), und ermittelt die beiden Parameter mit Hilfe der Bedingung, dass
GH senkrecht auf beiden RV der Geraden stehen muss
( 2 Gleichungen mit 2 Unbekannten).
Beachte:
Methode 1 liefert im Gegensatz zu Methode 2 nicht die Lotfußpunkte
Typische Anwendungsaufgaben
Abstand zweier Flugbahnen
1. Beispiel
Gegeben sind zwei Flugbahnen
100
0,1
53
g : x(t)
410
2550
t
228,75
22
h : y(t)
1,5
2
t
43,75
^ 00.00 Uhr
30 ; t in min; t=0 =
4
a) Zeige, dass die Flugbahnen sich kreuzen.
Begründe, ob es zu einem Zusammenstoß beider Flugzeuge kommt.
b) Ermittle, zu welchem Zeitpunkt die beiden Flugzeuge ihren kleinsten Abstand haben.
a) Parameter von h wird in r umbenannt.
g  h: –0,1t–2r= – 47  22t+30r=2140  –1,5t–4r=–185  t=70  r=20  2140=2140
Die Flugbahnen schneiden sich im Punkt S(93|–1010|123,75).
Da die Flugzeuge den Schnittpunkt im Abstand von 50 Sekunden durchfliegen, kommt es zu keiner Kollision.
b) d(t) =
2,1t
47
52t
2140 =
5,5t
185
2738,66t 2
224792,4t
5477,32t–224792,4=0  t41,04 (Min., da n. o. geöffnete Parabel);
34
2
4616034 ; es genügt d zu minimieren:
2. Beispiel:
Gegeben sind A(1|0|0), B(5|6|0), C(0|6|0) und S(3|3|6);
Berechne den Abstand g(A,B) von h(C,S) sowie die Lotfußpunkte P und Q.
Lösung
Methode 1:
 1
 4   1  4t 
0
 3   3r 
 
  

 
  

g(A,B) : x  OA  t  AB   0   t   6    6t  h(C,S) : x  OC  r  CS   6   r   3    6  3r 
0
0  0 
0
 6   6r 
 
  

 
  

0
 1
 4   3   36 
 6 
 6
1  












Methode 1 q0   6  ; p0   0  ; n   6  x  3    24  =6·  4  ; n0 
  4  ;
77
 0   6   30 
 5 
 5 
0
0
    

 
 
 
 
 1  6 
30
1    
=
 3,42 [LE]
6


4
d
q0 p0 n0 =
77
77    
 0   5 
Methode 2
Seien G  g und H  h die Endpunkte der kürzesten Verbindung. G(3r|–3r+6|6r), H(4t+1|6t|0)
4t 3r 1
GH
6t 3r 6 ; GH CS 0  GH AB 0  –6t–54r+21=0  52t+6r–32=0
6r
 t0,58  r0,32 GH  3,42 (LE] G(0,96|5,04|1,92) H(3,32|1,5|0)
H5b Den Abstand zweier paralleler Ebenen E und F berechnen.
Da die HNF einer Ebene den Abstand zum Ursprung enthält, kann man daraus den Abstand der
Ebenen ermitteln:
Sind E1: n1  x  d1 und E2: n2  x  d2 die HNF zweier Ebenen E1 und E2, so gilt für den
 d1  d2  d1  d2 ,falls n1  n2
Abstand der Ebenen: d(E1, E2) = 
 d1  d2 , falls n1  n2
Beachte, dass die NV der HNF bei parallelen Ebenen entweder gleich oder Gegenvektoren sind.
Beispiel:
Zu der Ebene E: 2x + y – 2z = 9 
2
1
2
x  y  z  3 haben die Ebenen
3
3
3
2
1
2
2
1
2
x  y  z  8 und
x  y  z  2 den Abstand 5 LE.
3
3
3
3
3
3
35
H6 Das Vektor/Kreuzprodukt berechnen und seine Bedeutung angeben
Wenn man einen Vektor sucht, der zu zwei gegebenen Vektoren a und b senkrecht steht, muss
man ein LGS mit 2 Gleichungen und drei Variablen lösen, bei der es unendliche viele (kollineare)
Lösungen gibt.
Eine allgemeine Lösung erhält man durch eine Regel, bei der die Komponenten der Vektoren in bestimmter Weise verrechnet werden. Diese Berechnung heißt
Kreuzprodukt oder Vektorprodukt und wird mit a x b bezeichnet.
Berechnung
a1
b1
a2b3
a3b2
a2
b2 =
(a1b3
a3b1)
a3
b3
a1b2
a2b1
Jede Komponente von n wird aus den 4 Zahlen gebildet, die den Index der jeweiligen Komponente
nicht enthalten, z.B. wird die 2. Kompnente aus a1, b1, a3 und b3 gebildet.
Dazu folgende Definition:
D=
a b
c d
:= ad–bc nennt man die Determinante der Matrix
Damit ist n1 =
Merkregel
a2 b2
a3 b3
a1
b1
a2
b2
a3
b3
a1
b1
a2
b2
a3
b3
, n2 =
a b
.
a b
c d
c d
(Produkt der Hauptdiagonale minus Produkt der Nebendiagonale)
a1 b1
a b1
und n3 = 1
a 3 b3
a 2 b2
Man schreibt die Vektoren noch einmal
untereinander, streicht die erste und die
letzte Zeile und bildet die drei Determinanten.
Achtung! Hier wird das Vorzeichen in der
2. Komponente nicht geändert.
1. Beispiel Ermittle einen Normalenvektor n zur Ebene die von A(4|2|6), B(9|3|5) und C(3|3|7)
aufgespannt wird.
Lösung: der NV muss senkrecht zu zwei (nicht kollinearen) RV laufen, also z. B.
5
 1  5   1  1 1  (1)  1   2 
 
 
AB   1  ; AC   1  ;  1  x  1    (5  1  (1)  (1))  =  4 
 1
 1   1  1   5  1  1 (1)   6 
 
      
  
36
Beachte:
Das Ergebnis beim Vektorprodukt ist ein Vektor, beim Skalarprodukt eine Zahl.
Für das Kreuzprodukt gilt a x b   (b x a) , d. h. das Kommutativgesetz gilt nicht.
Auch das Assoziativgesetz gilt nicht.
Geometrische Bedeutung: Der Vektor a x b steht senkrecht auf
der von a und b aufgespannten Parallelogrammebene und
seine Länge entspricht dem Flächeninhalt des Parallelogramms.
Damit gilt für den Flächeninhalt eines Parallelogramms, das
von a und b aufgespannt wird: A = a x b .
Weil jedes Dreieck ein halbes Parallelogramm ist, gilt für den Flächeninhalt eines Dreiecks mit
1
Seitenvektoren a und b : A =
axb .
2
Beispiel: Berechne den Flächeninhalt des Dreiecks ABC mit A(8|3|10), B(12|1|6) und C( 9|5|12).
 4   1
 4 
1
1     1 
 1
Lösung:  AB x AC     2  x  2     12    260 = 65  8,06 FE.
2
2     2 
 2
 4   2 
 10 
37
Berechnungen an Flugbahnen
Die Bahnen zweier Flugzeuge werden in einem örtlichen KOS mit der Einheit km bezüglich eines
Flughafens beschrieben. Das erste Flugzeug ist gerade gestartet und befindet sich im Steilflug
0
5,25
auf einer Bahn mit der Gleichung g: x
1
7 ,   IR (I)
0
3
Das zweite Flugzeug bewegt sich auf der Bahn mit der Gleichung h: x
3,3
6
5,4
4,5 ,   IR.
12
0
a) Als das erste Flugzeug eine Höhe von 4,5 km erreicht hat, überfliegt es ein Kraftwerk.
Berechne den Abstand des Kraftwerks vom Startpunkt des ersten Flugzeugs.
b) Berechne auch den Steigwinkel für diese Steigflugphase des Flugzeugs.
c) Nachdem das erste Flugzeug 37 km geflogen ist, taucht es in eine Wolkendecke ein.
Bestimme, in welcher Höhe sich die Wolkendecke befindet.
d) Zeige, dass es zu keiner Kollision dieser beiden Flugzeuge bei ihrer Bewegung auf diesen
Flugbahnen kommen kann.
Bestimme auch den Abstand dieser beiden Flugbahnen voneinander.
e) Auf dem Flughafen befindet sich auch eine Radarstation bei Punkt S (0,3 |1,4 | 0), die noch
Flugzeuge in einer Entfernung von 85 km erfassen kann. Beschreibe, wie man den Überwachungsbereich dieser Radarstation modellieren kann und bestimme die Länge der Flugstrecke
des ersten Flugzeugs im Überwachungsbereich dieser Radarstation.
f) In der Nähe des Flughafens verläuft die Grenze zum Nachbarstaat in guter Näherung geradlinig
und zwar durch die Punkte M(94,5|12|0) und N(22,5| –84| 0).
Bestimme, wie weit der Überwachungsbereich der Radarstation in den Nachbarstaat hineinreicht.
Äußere dich kritisch zu den Annahmen der Modellierung.
Lösung
a) P(7,875|11,5|4,5); Höhe 4,5 km; Abstand von P zum Startpunkt 13,125 km.
b)   18,92°
c) t· u = 37  Höhe von 12 km
d) Schnitt der Geraden g und h hat keine Lösung.
PQ u 0  PQ v 0  d(g,h)=9,57 km
e) d(g,S)=85  t = 9,24, die Flugstrecke beträgt 85,41 km.
f) d(S,g(M,N)) = 69 km  16 km liegen im Nachbarland.
38
Berechnungen an einem Tetraeder
Gegeben sind die Punkte A(9|–4 |–2), B(–3 |8|–2), C(–3|–4|10), P(3|2|4) und Q(–2|–3|–1) .
a) Zeige rechnerisch, dass das Dreieck ABC gleichseitig ist.
b) Berechne den Schwerpunkt S des Dreiecks ABC.
c) Das Dreieck ABC bildet mit dem Punkt D(9| 8 |10) eine dreiseitige Pyramide.
Untersuche, ob die Pyramide ein regelmäßiges Tetraeder ist. (Dreiseitige Pyramide, in der alle
Seitendreiecke gleichseitig sind.)
d) (1) Ermittle die Koordinaten des Eckpunkts W des Würfels.
(2) Ermittle zu allen 4 Kanten des Tetraeders die Mittelpunkte MAB, MBC, MCD und MDA.
(3) Untersuche, welche speziellen Eigenschaften das Viereck MABMBCMCDMDA hat.
(4) Ermittle den Abstand des Punktes T(3|2|4) von der Kante AD.
Lösungen  nächste Seite
39
Lösungen zu „Berechnungen an einem Tetraeder“
a) Alle drei Seiten(vektoren) sind 12 2 LE lang;
b) S(1|0|2) (arithmetisches Mittel der Eckpunktkoordinaten)
c) Die Seitenlängen AD, BD und CD betragen alle
288 = 12· 2 LE.
1
AB  W(–3|8|10) (Achtung! Man kann W aus der Zeichnung ablesen, wenn
2
man nachweist, dass die Kanten des Würfels parallel zu den Achsen verlaufen.)
d) (1) OW  OMCD 
(2) MAB(3|2|–2); MBC(–3|2|4); MCD(3|2|10); MDA(9|2|4);
 6 
 6


(3) MABMBC   0  ; MDAMCD   0   Das Viereck ist ein Parallelogramm.
 6
 6 
 
 
0
 12 
 =
 
MABMCD   0  MBCMDA   0   Diagonalen mit 12 LE gleich lang  Rechteck.
 12 
0
 
 
 6
 
MABMDA   0   6 2 = MABMBC  2 benachbarte Seiten sind gleich lang  Quadrat
 6
 
(4) T(3|2|4) ist der Mittelpunkt der Strecke AW und somit der Mittelpunkt des Würfels.
Daher ist der gesuchte Abstand eine halbe Würfellänge: d(T, AD) = 6 LE.
40
Multiple–Choice–Test zur Vektorrechnung Name:
(Es können mehrere Lösungen richtig sein; falsche Lösungen führen zu Punktabzug!)
1
1. 4 2
3
3x
1
2
1
7
1
7  x
… a) 2
6
2
b)
2
1
1
1
c) 1
1
d)
1
1
e) a)  d) sind
falsch
2
G
F
E
2. Für einen Würfel mit achsenparallelen Kanten der Länge 6 ist P(2|3|5).
(Das Quadrat PADE liegt vorne.) Dann ist a) A(8|3|5) b) B(2|8|5)
c) C(2|3|11) d) D(8|9|5) e) E(6|0|0) f) F(–4|9|11) g) a)–e) s. f. z
2
4
3. Ein Meteorit fliegt auf der Bahn x(t)
3 t
6 (t in min).
y
x
8
0,5
D
C
B
P
A
Er schlägt auf nach a) 8 min b) 0,5 min c) 6 min d) 2 min e) 2,5 min f) a) –e) s. f.
4
4. Die Länge des Vektors 1 ist …. a) 7 b) 7 c) 21 d) 21 e) 19 f) a)–e) sind falsch.
2
5. A(–3|3|5) B( –3|2|7)  AB = … a)
6
0
1
b) 1
2
0
c)
2
1
6
d) 5
2
b) AB
DC c) AD
e) 1,5
12
f) a)–e) s. f.
6
D
6. Ein Viereck ABCD ist ein Parallelogramm, wenn gilt
a) AB = DC
3
C
BC d) AC = BD
e) AB = DC und AD = BC f) a)–e) sind falsch
A
B
7. Ein Flugzeug durchfliegt den Punkt P(30|20|2) und nach 2 Minuten den Punkt Q(15|25|3)
(LE in km). Dann beträgt die Geschwindigkeit (in km/h; ganzzahlig gerundet)
a) 251 b) 475 c) 16 d) 951 e) 180 f) a)–e) sind falsch.
20
8. Der Bewegungsvektor eines Flugzeuges für 10 Minuten ist 30 (LE in km). Dann ist die Ge3
schwindigkeit über Grund (km/h)
a)
1
1309 b) 1300 c) 6· 1300 d) 6·1309 e) 10 1300 f) a)–e) s. f.
9. In einem Parallelogramm ABCD sind A, B und C gegeben. Dann könnte man D berechnen mit:
a) 0D 0C b) 0D 0A BC c) 0D 0A AB BC BA d) 0D 0A AD
e) 0D
0B
BD
10. Den Mittelpunkt M in einem Parallelogramm ABCD erhält man mit:
1
1
1
1
a) 0M
AC b) 0M
BD c) 0M 0A
AC d) 0M 0B
BD e) 0M
2
2
2
2
f) a) –e) sind falsch
41
1
(0C
2
0A)
11. Ein möglicher Ansatz für die Gleichung einer Geraden durch die Punkte P und Q lautet:
1
a) x(t) 0P t PQ
b) x(t) 0Q t PQ
c) x(t) 0P t PQ
2
1
d) x(t) 0P t QP
e) x(t)
f) a) –e) sind falsch
0P t PQ
2
2
4
12. Auf der Geraden x(t)
3
t
6 liegt der Punkt
1
1
a) (6|–3|2) b) (–6|15|1) c) (4|6|–2) d) (–2|9|–2)
e) (2|3|–1)
f) a) –e) sind falsch
Lösungen:
Aufg.
Lsg
1
b)
2
f)
1
3
f)
3
1) 4 2
3x
1
2
1
4
d)
7
5
c)
10
6
7
b)c)e) b)
4
7  3x
5
8  x
6
7
4
8
c)
9
b)c)
10
11
c)d)e) abcd
12
b)e)
2
1
1
2) P(2|3|5)  A(2|9|5), B(–4|9|5), C(–4|3|5), D(2|9|11), E(2|3|11), F(–4|9|11), G(–4|3|11)
 Keine der Antworten ist richtig
3) „Boden“ bedeutet: z–Koordinate muss 0 sein. 8–0,5t=0  t=16  f) ist richtig
12 22
21  d) ist richtig
15
km
km
251
7) PQ
= 30· 251 h  475 km/h
5 ; PQ
2 min
1
8) Bei Geschwindigkeit über Grund zählt die z–Koordinate nicht.
4) d=
42
202 302 km in 10 min = 6· 1300 km in 1 h = 6· 1300 km/h
11) Bei einer Geraden kann man den Stützvektor gegen einen Ortsvektor eines anderen Punktes
der Geraden austauschen (wie in b)) und den Richtungsvektor durch einen kollinearen Vektor ersetzen (wie in c) und d)).
12b) (t=–2) 12e) (t=0)
42
Abiturprüfung 2012
Mathematik,
Leistungskurs
Bei der Kunstausstellung „Licht und Schatten" ist in der Mitte der Ausstellungshalle eine gerade, 1 m hohe
Pyramide mit quadratischer Grundfläche von 1 m Seitenlänge ausgestellt. Die Grundfläche der Pyramide
befindet sich (gehalten von vier Stützen) einen Meter über dem Boden der Halle. Die quaderförmige Halle
selbst ist 5 m hoch und hat eine quadratische Grundfläche von 9 m Seitenlänge.
In einem kartesischen Koordinatensystem mit Ursprung in einer Hallenecke und entlang der Hallenkanten
verlaufenden Koordinatenachsen hat die Grundfläche der Pyramide die Eckpunkte A(5|4|1), B(5|5|1),
C(4|5|1) und D(4|4|1). Die Gegebenheiten sind in der Abbildung dargestellt.
a) (1) Zeigen Sie, dass die Pyramidenspitze die Koordinaten S(4,5|4,5|2) hat.
(2) Berechnen Sie die Seitenlängen des Dreiecks ABS.
(3) Bestimmen Sie das Volumen und den Oberflächeninhalt der Pyramide.
b) Ermitteln Sie, unter welchem Winkel die Seitenfläche ABS der Pyramide gegen ihre Grundfläche
ABCD geneigt ist. [Zur Kontrolle: EABS : 2x + z = 11 ]
c) Die Pyramide wird von einer an der rechten Hallenwand (y = 9) befestigten punktförmigen
Lichtquelle angestrahlt (siehe Abbildung).
(1) Die Lichtquelle befindet sich zuerst in der Position L1(4,5|9|1). Der Pyramidenschatten auf der gegenüberhegenden Hallenwand (y = 0) hat die Form eines Dreiecks.
Ermitteln Sie die Koordinaten der Eckpunkte dieses Schattendreiecks. Zeigen Sie, dass es sich um
ein gleichschenkliges Dreieck handelt, und berechnen Sie seinen Flächeninhalt.
(2) Die Lichtquelle wird nun in die Position L2(5|9|1) gebracht.
Beschreiben Sie ohne weitere Rechnung die Form des neuen Pyramidenschattens im
Vergleich zum Schatten aus c) (1).
Nachts werden die Kunstwerke in der Halle durch Laser-Lichtschranken gesichert.
d) Einer der Laserstrahlen ist auf den Schnittpunkt M der Mittelsenkrechten des Dreiecks ABS gerichtet.
(1) Bestimmen Sie rechnerisch die Koordinaten von M. [Zur Kontrolle: M(4,8|4,5|1,4)]
(2) Der Laserstrahl trifft im Punkt M orthogonal auf die Seitenfläche ABS der Pyramide.
Ermitteln Sie die Koordinaten der Position P der zugehörigen Laser-Lichtquelle an
einer der Hallenwände.
43
Lösungen:
b) (1) Jeweils die „Projektionsgerade“ gA(L,A), gB(L,B) und g(L,C) aufstellen und mit
der x2x3–Ebene, die durch die Bedingung x1 = 0 gegeben ist, schneiden.
 40 
 8   0 
 
   
Beispiel: gB(L,B)  x1=0:  10   t   1    a   t=5  B‘(0|15|20).
 10 
 2  b
 
   
a b
b(2) Zwei Winkel im Dreieck A’B’C‘ mit der Formel cos  
berechnen.
ab
‘  108,4°; ‘  38,2°;   180° –  –   33,4°.
c) (2) OMST ist ein Stützvektor der gesuchten Ebene. Die RV der Ebene müssen senkrecht auf dem
 3 
 
Vektor ST =  3  und nicht kollinear sein. Dazu setzt man eine Koordinate 0, vertauscht die bei 0 
 
 3  0
   
den anderen und ändert noch bei den Vertauschungen ein Vorzeichen:  3  ;  0  ;
 0  3
   
 10 
 4 




Wer es allgemein mag: –3n1 – 3n2=0  n1= –n2; n3 beliebig, also z. B.  4  und  10  .
 1 
 127 




c(3) Auch wenn man sich die dreidimensionale Abbildung schwer vorstellen kann, ergibt sich aus
dem Text, dass R auf der Geraden g(L,R‘) und auf der Ebene liegen muss.
Damit erhält man R als Schnittpunkt von g(L,R‘) und E.
c(4) Strategie: genügend Bedingungen für R finden, die sich in Gleichungen übersetzen lassen, so
dass man ein Gleichungssystem aufstellen kann, das sich lösen lässt.
8
8
Erste Bedingung: R liegt auf g(L,R‘), d. h. R hat die Form (40–40·t,10– t,10– t) (I)
3
3
Weitere Bedingung entweder SR  TR  0 (II) (da das Dreieck rechtwinklig ist).
 14  40t   17  40t 

 

 1  (8 : 3)t  ·  2  (8 : 3)t  = 0 … Man erhält eine quadratische Gleichung mit 2 Lösungen,
 3  (8 : 3)t   3  (8 : 3)t 


 
t =735/1816 v t = 3/8. Nur bei t = 3/8 erhält man einen Punkt der einen Abstand von 3 zu den
anderen Eckpunkten S und T hat.
8
8
Alternative: R(40–40·t,10– t,10– t) (I)  SR  3 (II)  TR  3 (III)
3
3
Einsetzen von (I) in (II) ergibt eine quadratische Lösung mit t=591/1816 v t = 3/8.
Kontrolle von (III) zeigt, dass nur t=3/8 eine Lösung ergibt.
44
Winkel–, Schnitt– und Abstandsaufgaben
Aufgabe 1 Berechne die Innenwinkel des Dreiecks A(1|–2|1)B(–3|1|4)C(5|–2|1)
Aufgabe 2 Berechne jeweils den eingeschlossenen Winkel
2
2
9
a) der Geraden g: x s 6 und h: x
6
t
6
3
2
3
b) der Ebenen E1: 3x1 + 4x2 - 12x3 = 0 und E2 : 2x1 + 14x2 - 5x3 = 9
c) der Geraden g und der Ebene E1 (von Teil a und b)
Aufgabe 3 Berechne den Abstand d(P,E) für E: 2x1 –x2 – 5x3 = 3 und P(–1|2|1)
auf zwei verschiedene Arten.
4
1
Aufgabe 4 Berechne den Abstand d(P,g) für g: x
2 t 1 und P(4|6|2)
1
0
Aufgabe 5 Berechne den Abstand der windschiefen Geraden
8
3
7
3
g: x
r 2 und h : x
8
5
Aufgabe 6
2
2
t 3
10
4
2
a) Bestimme die Punkte auf g : x
2
1
1 , die vom Punkt P(2|–1|3) den Abstand 5 haben.
r
3
2
b) Bestimme die zu E: x1 – 2x2 + 2x3 = 5 parallelen Ebenen, die von E den Abstand 5 haben.
Aufgabe 7 Berechne die beiden Winkelhalbierenden W 1 und W 2 der Ebenen:
E1 : 2x1 + x2 + 2x3 = 0 und E2 : 3x1 + 4x2 = 6
Hilfe: W 1 und W2 bestehen aus allen Punkten, die von E1 und E2 den gleichen Abstand haben.
Übersetze diese Information in eine Gleichung und löse diese Gleichung.
Aufgabe 8 Bestimme, falls möglich, die Schnittgerade der beiden Ebenen.
a) E1 : 2x1+11x2+4x3 = 1; E2 : x1+6x2+x3 = 4 b) E1 : 2x1–2x2+x3 = 0; E2 : –2x1+2x2–x3 = 1
2
3
1
6
4
2
c) E1 : x
2 s 1
t
2 , E2 : x
2
r 5
s 1
1
1
4
2
2
0
Aufgabe 9 Bestimme, falls vorhanden, den Schnittpunkt von
3
3
a) E: 2x1+4x2+3x3=1 und g : x
2
c) g : x
2
1
3
r
1
1
und E : x
1
t
b) E: x1–4x3 = 10 und g : x
1
1
1
6
3
2
0
s 1
2
2
r
0
r 1
0
2
0
5
Aufgabe 10 Berechne die Winkelhalbierenden von g : x
5
5
45
2
r 1 und h : x
2
5
3
5
s 4 .
5
0
Lösungen / Lösungsansätze
Aufgabe 1, 2 Formeln: 1a) cos
a b
a b
b) cos
a b
c) sin
|a| |b|
|a| |b|
|a| |b|
1a) Winkel zwischen den Seitenvektoren („Fußpunkt an Fußpunkt“ oder „Spitze an Spitze“ ) mit der
1
Formel berechnen (Ergebnisse über 90° möglich!). A =  AB  AC · sin 
2
2a) a und b sind RV der Geraden sind. 2b) a und b sind NV der Ebenen sind.
2c) a ist ein RV der Geraden und b ein NV der Ebene ist.
1
| n OP c |
Aufgabe 3a) d(P,E) =
n
b) Schnittpunkt F der Lotgeraden x
Aufgabe 4a) F(4+t|2+t|1); u FP
OP
r n mit E berechnen, d= FP .
0 nach t auflösen, FP berechnen
b) Hilfsebene E: u  x  u  OP ; Schnittpunkt mit g ist Lotfußpunkt F.
Aufgabe 5 F(8+3r|8+2r|5+2r); G(7+3t|2+3t|10+4t);
u FG 0  v FG 0 nach r und t auflösen, FG berechnen
Aufgabe 6a) OP 5 u0 ( u0 ist ein RV mit Länge 1); (Alternative: Q(2–2r|–1+r|3+2r);
PQ
5 nach r auflösen (2 Lösungen!) und in Q einsetzen.)
b) Für die gesuchten Punkte Q und Q’ gilt OQ
OP
5 u0 und OQ'
OP 5 u0 ,
1
wobei u0 der normierte RV ist , also hier u0 = 3 u .
1
1
1
1
Aufgabe 7 d(P,E1)=d(P,E2)  |3 (2x+y+2z)| = |5 ·(3x+4y–6)|  3 (2x+y+2z) =±( 5 (3x+4y–6)
Aufgabe 8a) LGS allgemein lösen z.B. x2=2x3+7  x1= –13x3–38; Lösungsvektor
38 13x3
38
7
7
2x3
x3
0
13
x3
2
1
38
; gs: x
7
0
13
r
2
1
b) Ebenen sind echt parallel, da die NV kollinear, die Gleichungen aber nicht äquivalent
sind.
c) Beide Ebenen in NF umformen und wie in a) vorgehen.
Aufgabe 9a) 3+3t für x1, –1–t für x2 und –1–t für x3 einsetzen, nach t auflösen und
in g einsetzen.
b) E ist echt parallel zur z–Achse, g ist die z–Achse  kein Schnittpunkt
c) 3 Gleichungen mit 3 (!) Unbekannten (Parameter r der Gerade (z.B.) in t umbenennen
und mit TR lösen.
5
 2
3
1   1 


Aufgabe 10  5  ist ein SV,   1    4  RV der beiden Winkelhalbierenden
3   5 
5
 2
0
 
46
Genauere Erläuterung auf http://delphi.zsg-rottenburg.de/la1.html#33l
Lösungen (nur Ergebnisse):
Aufgabe 1   133,31°   18,75°   27,94°
Aufgabe 2 a)   51,44° b)   51,27° c)   11,41°
12
Aufgabe 3 F(–0,2|1,6|–1); d =
 2,19 LE
Aufgabe 4 F(6|4|1) d=3 LE
30
Aufgabe 5 d(g,h) = 7 LE
10 2 19
16 8 1
1
5
Aufgabe 6 a) Q1(– 3 |3 | 3 ) Q2( 3 |–3 |–3 ) b) 3 (x1–2x2+2x3)= 3 ±5 = 20/3 (–10/3)
1
1
Aufgabe 7 |3 (2x+y+2z)| = |5 ·(3x+4y–6)|
1
1
1
1
 3 (2x+y+2z) =5 (3x+4y–6) v 3 (2x+y+2z) = –(5 ·(3x+4y–6))
1
7
2
6 19 17 2 6
 15 x–15 y +3 z= – 5 v 15 x+15 y+3 z=5
 x–7y+10z = –18 v 19x+17y+10z=18
38
13
6
23
Aufgabe 8 a) g2: x
b) echt paralell c) gs: x
7
t
2
5
t 1
0
1
Aufgabe 9 a) S(–3|1|1) b) echt parallel c) S(5|3|0)
4
Aufgabe 10 Schnittpunkt S(5|5|5), OS ist ein SB der Geraden; u02
7
3
1
4 u01
5
0
2
1
1 .
3
2
u01 und u02 spannen eine Raute auf, die Diagonale ist Winkelhalbierende, d.h. u01
u02 sind
Richtungsvektoren der Geraden.
Erläuterungen/Hinweise zu den Aufgaben:
Aufgabe 1, 2 Formeln: 1a) cos
a b
a b
b) cos
a b
c) sin
|a| |b|
|a| |b|
|a| |b|
1a) Winkel zwischen den Seitenvektoren („Fußpunkt an Fußpunkt“ oder „Spitze an Spitze“ ) mit der
1
Formel berechnen (Ergebnisse über 90° möglich!). A =  AB  AC · sin 
2
2a) a und b sind RV der Geraden sind. 2b) a und b sind NV der Ebenen sind.
2c) a ist ein RV der Geraden und b ein NV der Ebene ist.
Aufgabe 3a) Formel Abstand Punkt–Ebene benutzen: d(P,E) =
1
| n OP
c|
n
b) Schnittpunkt F der Lotgeraden x
Aufgabe 4a) F(4+t|2+t|1); u FP
OP
r n mit E berechnen, d= FP .
0 nach t auflösen, FP berechnen
b) Hilfsebene E: u  x  u  OP ; Schnittpunkt mit g ist Lotfußpunkt F.
Aufgabe 5 F(8+3r|8+2r|5+2r); G(7+3t|2+3t|10+4t);
u FG 0  v FG 0 nach r und t auflösen, FG berechnen
Aufgabe 6a) OP 5 u0 ( u0 ist ein RV mit Länge 1); (Alternative: Q(2–2r|–1+r|3+2r);
PQ
5 nach r auflösen (2 Lösungen!) und in Q einsetzen.)
47
b) Für die gesuchten Punkte Q und Q’ gilt OQ
OP
5 u0 und OQ'
OP 5 u0 ,
1
wobei u0 der normierte RV ist , also hier u0 = 3 u .
1
1
1
1
Aufgabe 7 d(P,E1)=d(P,E2)  |3 (2x+y+2z)| = |5 ·(3x+4y–6)|  3 (2x+y+2z) =±( 5 (3x+4y–6)
Aufgabe 8a) LGS allgemein lösen z.B. x2=2x3+7  x1= –13x3–38; Lösungsvektor
38 13x3
38
7
7
2x3
x3
0
13
x3
2
1
38
; gs: x
7
0
13
r
2
1
b) Ebenen sind echt parallel, da die NV kollinear, die Gleichungen aber nicht äquivalent
sind.
c) Beide Ebenen in NF umformen und wie in a) vorgehen.
Aufgabe 9a) 3+3t für x1, –1–t für x2 und –1–t für x3 einsetzen, nach t auflösen und
in g einsetzen.
b) E ist echt parallel zur z–Achse, g ist die z–Achse  kein Schnittpunkt
c) 3 Gleichungen mit 3 (!) Unbekannten (Parameter r der Gerade (z.B.) in t umbenennen
und mit TR lösen.
5
 2
3
1   1 


Aufgabe 10  5  ist ein SV,   1    4  RV der beiden Winkelhalbierenden.
3   5 
5
 2
0
 
48
Abituraufgabe
Aufgabe 3
Bei der Kunstausstellung „Licht und Schatten" ist in der Mitte der
Ausstellungshalle eine
gerade, 1 m hohe Pyramide mit quadratischer Grundfläche von
1 m Seitenlänge ausgestellt. Die Grundfläche
der Pyramide befindet
sich (gehalten von vier
Stützen) einen Meter
über dem Boden der
Halle. Die quaderförmige Halle selbst ist 5 m
hoch und hat eine quadratische Grundfläche
von 9 m Seitenlänge.
 Seite 2
49
Lk M1* Q1
4. Klausur Name:
– Seite 2 –
19.5.2014
In einem kartesischen Koordinatensystem mit Ursprung in einer Hallenecke und entlang der Hallenkanten
verlaufenden Koordinatenachsen hat die Grundfläche der Pyramide die Eckpunkte
A(5|4|1), B(5|5|1), C(4|5|1) und D(4|4|1).
Die Gegebenheiten sind in der Abbildung auf Seite 1dargestellt.
a) (1) Zeige, dass die Pyramidenspitze die Koordinaten S(4,5|4,5|2) hat.
(2) Berechne die Seitenlängen des Dreiecks ABS.
(3) Bestimme das Volumen und den Oberflächeninhalt der Pyramide
(Die Oberfläche umfasst vier Seitenflächen und die Grundfläche).
b) Ermittle, unter welchem Winkel  die Seitenfläche ABS der Pyramide gegen die Grundfläche ABCD
geneigt ist. [Hinweis: der Neigungswinkel  ist gleich dem Winkel, den die Vektoren MAB S und
MABMCD einschließen.]
c) Die Pyramide wird von einer an der rechten Hallenwand befestigten punktförmigen Lichtquelle
angestrahlt (siehe Abbildung).
(1) Die Lichtquelle befindet sich zuerst in der Position L1(4,5|9|1). Der Pyramidenschatten auf der gegenüberliegenden Hallenwand hat die Form eines Dreiecks.
Ermittle die Koordinaten der Eckpunkte dieses Schattendreiecks. Zeige, dass es sich um ein gleichschenkliges Dreieck handelt, und berechne seinen Flächeninhalt.
(2) Die Lichtquelle wird nun in die Position L2(5|9|1) gebracht. Beschreibe ohne weitere Rechnung
die Form des neuen Pyramidenschattens im Vergleich zum Schatten aus c) (1).
Nachts werden die Kunstwerke in der Halle durch Laser-Lichtschranken gesichert, die an einer Hallenwand
befestigt sind.
d) (1) Die Laserstrahlen treffen orthogonal auf die Seitenfläche ABS auf. Ermittle
S
einen Richtungsvektor für die Laserstrahlen.
(2) Einer der Laserstrahlen aus (1) ist genau auf den Schnittpunkt M der
Mittelsenkrechten des Dreiecks ABS gerichtet.
(i) Stelle Geradengleichungen für die Mittelsenkrechten m AB und
mAS
mAS auf und berechne dann den Punkt M.
[Zur Kontrolle: M( 4,8 | 4,5 |1,4 ]
(ii) Ermittle die Koordinaten der Position P der Laser-Lichtquelle,
A
die in M senkrecht auftrifft.
 51 53 15 
e) Eine zweite Laser-Lichtquelle schneidet die Ebene EBCS in T  |
|
 , da
 11 11 11 
2
4
gilt: OT  OB   BC   BS . Begründe, ob der Laserstrahl das Dreieck BCS trifft.
11
11
Viel Erfolg!
50
M
mAB
B
Lösungen
Aufgabe 3 a) (1) (1) Berechne MAC und addiere zur z–Koordinate noch 1.
 0   4,5   0   4,5 
0
 0,5 
 0,5 
 = 
   
 a)(2)
 ;

;


AB   1  AS   0,5  BS   0,5  ;
OS  OMAC   0   4,5    0    4,5 
0
 1  1   1  2 
 1 
 1 
 
  
   





1
1
1
AB =1; AS = BS = 1,5 1,22 [m]. (3) V =  G  h =  1 1  [m2].
3
3
3
1
1
1
a)(3) Eine Dreiecksfläche: A =  1 MABS = · 1,25 0,56 ; O = 1·1 + 4· · 1,25  3,24 [m3];
2
2
2
 0,5 
 1
M S  MADMCD
0,5


b) MABS   0  ; MABMCD   0  ;b) cos  = AB
=
   63,43°
1,25

1
M
S
0
 1 
AB
 


c) Die gesuchten Eckpunkte sind die Schnittpunkte der Lichtgeraden gB(L1,B), gC(L1,C) und gS(L1,S)
mit der x-z–Ebene, bei der y=0 gilt.
 4,5 
 0,5 
 4,5 
 0,5 
 4,5 
 0 










gB(L1,B): x   9   r   4  ; gC(L1,C): x   9   r   4  ; gS(L1,S): x   9   r   4,5  .
 1 
 0 
 1 
 0 
 1 
 1 












Man erhält: 9 –4r = 0  r = 2,25  C‘(3,375 |0|1); 9 –4,5r = 0  r = 2  S‘(4,5 |0|3);
9 –4r = 0  r = 2,25  B‘(5,625 |0|1)
1
B'S'  1,1252  22  C'S'  2,29  gleichschenklig; A =  B' C '  2 = 2,25 m2.
2
Der Schatten ist ebenfalls ein Dreieck, aber da es schräg auf die Wand projiziert wird,
ist es nicht mehr gleichschenklig.
51
3d) (1) Der gesuchte Vektor n muss senkrecht zum dem Dreieck ABS, insbesondere senkrecht zu
 0,5   0   1 
 2






 
AS und AB verlaufen: n = AS x AB = 0,5 x 1 =

    0  = –0,5·  0  ;
 1   0   0,5 
 1

   

 
 5 
 0,5 


3d)(2) mAB: x  OMAB  r  MABS =  4,5   r   0  ; ein RV von mAS muss senkrecht zu AS
 1 
 1 




 0,5   1   0,25 
 1   4,75 
 1










und zu n verlaufen:  0,5  x  0  =  1,25  ; mAS: x  OMAS  s   5  =  4,25   s   5 
 2   1,5 
 1   0,5   0,5 
 2 
  

 
 


 
mAB  mAS: y–Gleichung: 4,5= 4,25+5s  s = 0,05; Einsetzen in mAS: M(4,8|4,5|1,4).
Schnittpunkt der Lotgeraden l durch M mit der Vorderwand (x=9):
 4,8 
 2


l: x   4,5  +r·  0  ; 4,8+2r=9  r = 2,1  P(9|4,5|3,5)
 1,4 
 1


 
e) Für Parameterwerte zwischen 0 und 0,5 für r und s wird das Parallelogramm BMBCMCSMBS auf2
4
gespannt. Da dieses innerhalb des Dreiecks BCS liegt und
bzw.
zwischen 0 und 0,5 lie11
11
gen, liegt der Punkt innerhalb des Dreiecks.
52