Mathematik (MA (BT)) - Staatliche Technikerschule Berlin
Werbung
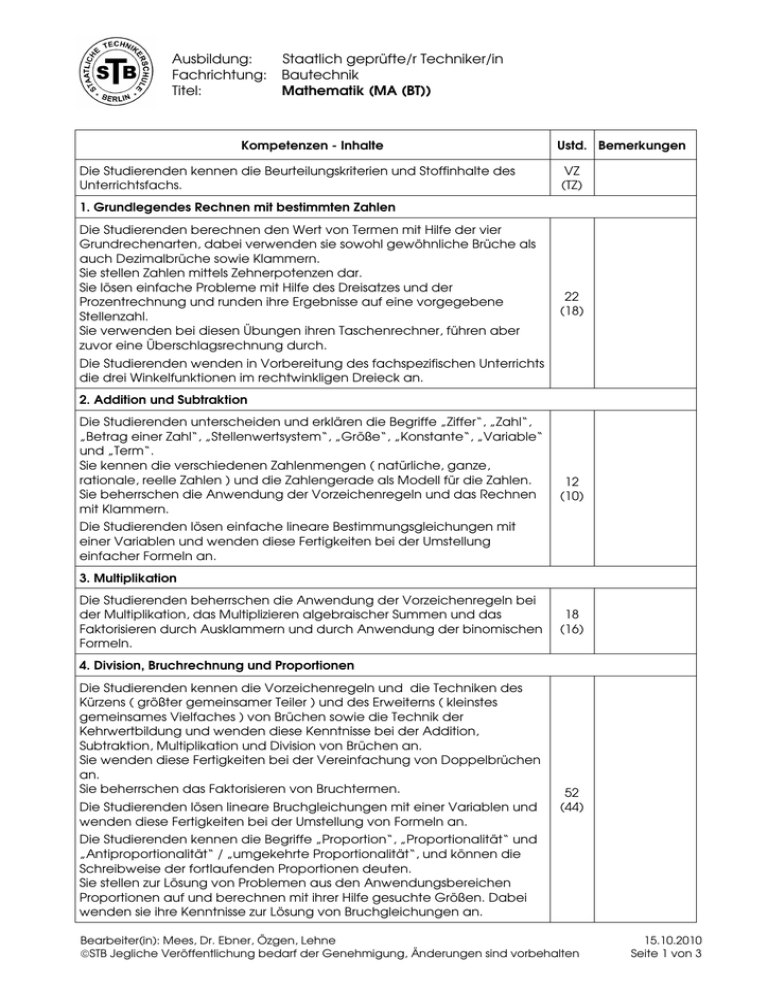
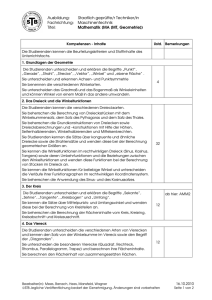
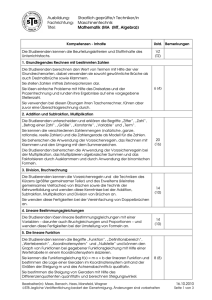
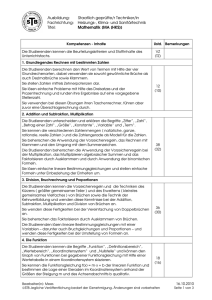
Ausbildung: Fachrichtung: Titel: Staatlich geprüfte/r Techniker/in Bautechnik Mathematik (MA (BT)) Kompetenzen - Inhalte Die Studierenden kennen die Beurteilungskriterien und Stoffinhalte des Unterrichtsfachs. Ustd. Bemerkungen VZ (TZ) 1. Grundlegendes Rechnen mit bestimmten Zahlen Die Studierenden berechnen den Wert von Termen mit Hilfe der vier Grundrechenarten, dabei verwenden sie sowohl gewöhnliche Brüche als auch Dezimalbrüche sowie Klammern. Sie stellen Zahlen mittels Zehnerpotenzen dar. Sie lösen einfache Probleme mit Hilfe des Dreisatzes und der Prozentrechnung und runden ihre Ergebnisse auf eine vorgegebene Stellenzahl. Sie verwenden bei diesen Übungen ihren Taschenrechner, führen aber zuvor eine Überschlagsrechnung durch. 22 (18) Die Studierenden wenden in Vorbereitung des fachspezifischen Unterrichts die drei Winkelfunktionen im rechtwinkligen Dreieck an. 2. Addition und Subtraktion Die Studierenden unterscheiden und erklären die Begriffe „Ziffer“, „Zahl“, „Betrag einer Zahl“, „Stellenwertsystem“, „Größe“, „Konstante“, „Variable“ und „Term“. Sie kennen die verschiedenen Zahlenmengen ( natürliche, ganze, rationale, reelle Zahlen ) und die Zahlengerade als Modell für die Zahlen. Sie beherrschen die Anwendung der Vorzeichenregeln und das Rechnen mit Klammern. 12 (10) Die Studierenden lösen einfache lineare Bestimmungsgleichungen mit einer Variablen und wenden diese Fertigkeiten bei der Umstellung einfacher Formeln an. 3. Multiplikation Die Studierenden beherrschen die Anwendung der Vorzeichenregeln bei der Multiplikation, das Multiplizieren algebraischer Summen und das Faktorisieren durch Ausklammern und durch Anwendung der binomischen Formeln. 18 (16) 4. Division, Bruchrechnung und Proportionen Die Studierenden kennen die Vorzeichenregeln und die Techniken des Kürzens ( größter gemeinsamer Teiler ) und des Erweiterns ( kleinstes gemeinsames Vielfaches ) von Brüchen sowie die Technik der Kehrwertbildung und wenden diese Kenntnisse bei der Addition, Subtraktion, Multiplikation und Division von Brüchen an. Sie wenden diese Fertigkeiten bei der Vereinfachung von Doppelbrüchen an. Sie beherrschen das Faktorisieren von Bruchtermen. Die Studierenden lösen lineare Bruchgleichungen mit einer Variablen und wenden diese Fertigkeiten bei der Umstellung von Formeln an. 52 (44) Die Studierenden kennen die Begriffe „Proportion“, „Proportionalität“ und „Antiproportionalität“ / „umgekehrte Proportionalität“, und können die Schreibweise der fortlaufenden Proportionen deuten. Sie stellen zur Lösung von Problemen aus den Anwendungsbereichen Proportionen auf und berechnen mit ihrer Hilfe gesuchte Größen. Dabei wenden sie ihre Kenntnisse zur Lösung von Bruchgleichungen an. Bearbeiter(in): Mees, Dr. Ebner, Özgen, Lehne STB Jegliche Veröffentlichung bedarf der Genehmigung, Änderungen sind vorbehalten 15.10.2010 Seite 1 von 3 Ausbildung: Fachrichtung: Titel: Staatlich geprüfte/r Techniker/in Bautechnik Mathematik (MA (BT)) 5. Systeme linearer Bestimmungsgleichungen mit 2 Variablen Die Studierenden lösen lineare Gleichungssysteme mit zwei Variablen unter Anwendung der Einsetzungs-, Gleichsetzungs- oder Additionsmethode. Sie wenden diese Technik auf Formelsysteme – speziell mit Gleichungen aus der Bautechnik – an. 18 (16) 6. Quadratische Gleichungen mit einer Variablen (nur reelle Lösungen) Die Studierenden lösen reinquadratische und gemischtquadratische Gleichungen mit Hilfe der p-q-Formel. 14 (12) ab hier: ABH2 7. Die lineare und die quadratische Funktion Die Studierenden kennen die Begriffe „Funktion“, „Definitionsbereich“, „Wertebereich“, „Koordinatensystem“ und „Nullstelle“ und können den Graph von Funktionen bei gegebener Funktionsgleichung mit Hilfe einer Wertetabelle in einem Koordinatensystem skizzieren. Sie kennen die Funktionsgleichung f(x) = m·x + b der linearen Funktion und können die Lage einer Geraden im Koordinatensystem anhand der Größen der Steigung m und des Achsenabschnitts b qualitativ bestimmen. Sie bestimmen die Steigung von Geraden mit Hilfe des Differenzenquotienten quantitativ und berechnen Steigungswinkel. Sie kennen die 2-Punkte-Form der linearen Funktion und wenden diese bei der Bestimmung von Geradengleichungen an (einfache lineare Interpolation ). 12 (12) Die Studierenden kennen die quadratische Funktion y(x) = a x² + bx + c und ihre Sonderfälle sowie ihre graphische Darstellung im Koordinatensystem. Sie wenden ihre Kenntnisse bei der Analyse von Kurven und Diagrammen aus der Bautechnik an. 8. Das Dreieck und die Winkelfunktionen Die Studierenden unterscheiden und erklären die Begriffe „Punkt“, „Gerade“, „Strahl“, „Strecke“ und „Flächeninhalt“ . Sie kennen das Gradmaß und das Bogenmaß als Winkeleinheiten und können Winkel von einem Maß in das andere umwandeln. Die Studierenden kennen die verschiedenen Dreiecksarten. Sie beherrschen die Berechnung von Dreiecksstücken mit dem Winkelsummensatz, dem Satz des Pythagoras und dem Satz des Thales. Sie kennen die Winkelfunktionen im rechtwinkligen Dreieck ( Sinus, Kosinus, Tangens ) sowie deren Umkehrfunktionen und wenden diese Funktionen bei der Berechnung von Stücken im Dreieck an. Sie beherrschen die Anwendung des Sinus- und des Kosinussatzes. 34 (30) Sie Studierenden kennen die Sätze über kongruente und ähnliche Dreiecke sowie die Strahlensätze und wenden diese bei der Berechnung geometrischer Größen an. Sie beherrschen die Grundkonstruktionen von Dreiecken sowie Dreiecksberechnungen und –konstruktionen mit Hilfe der Höhen, Seitenhalbierenden, Winkelhalbierenden und Mittelsenkrechten. Bearbeiter(in): Mees, Dr. Ebner, Özgen, Lehne STB Jegliche Veröffentlichung bedarf der Genehmigung, Änderungen sind vorbehalten 15.10.2010 Seite 2 von 3 Ausbildung: Fachrichtung: Titel: Staatlich geprüfte/r Techniker/in Bautechnik Mathematik (MA (BT)) 9. Der Kreis Die Studierenden unterscheiden und erklären die Begriffe „Sekante“, „Sehne“, „Tangente“, „Kreisbogen“ und „Umfang“. Sie kennen die Sätze über Mittelpunkts- und Umfangswinkel und wenden diese bei der Berechnung von Kreisteilen an. Sie beherrschen die Berechnung der Flächeninhalte vom Kreis, Kreisring, Kreisabschnitt und Kreisausschnitt. ab hier: TBH2 12 (10) 10. Das Viereck Die Studierenden unterscheiden die verschiedenen Arten von Vierecken und kennen des Satz von der Winkelsumme im Viereck sowie den Begriff der „Diagonalen“. Sie unterscheiden die besonderen Vierecke ( Quadrat, Rechteck, Rhombus, Parallelogramm, Trapez ) und berechnen ihre Flächeninhalte. Sie berechnen den Flächeinhalt von zusammengesetzten Flächen. 10 (8) 11. Stereometrie Die Studierenden berechnen den Rauminhalt und die Oberfläche von Würfel, Quader, Prisma, Zylinder, Pyramide, Kegel, Kegelstumpf, Pyramidenstumpf und Kugel. Sie wenden ihre Kenntnisse und Fertigkeiten bei der Berechnung von Rauminhalt und Oberfläche von Dächern, der Länge von Grat- und Kehlsparren, vom First und vom Ortgang sowie bei der Berechnung vom Rauminhalt von Baugruben, Dämmen und Leitungsgräben an. ab hier: ABH3 26 (18) Die Studierenden kennen die Simpson’sche Regel und wenden sie für konkrete Berechnungen an. 12. Potenzrechnung mit ganzzahligen Exponenten Die Studierenden beherrschen das Addieren und Subtrahieren, das Multiplizieren und Dividieren und das Potenzieren von Potenzen durch Anwendung der Potenzgesetze. Sie stellen rationale Zahlen mit Hilfe von Zehnerpotenzen dar und beherrschen den Umgang mit Zehnerpotenzen. 10 (8) 13. Wurzelrechnung (im Bereich der reellen Zahlen) Die Studierenden verstehen Wurzeln als Potenzen mit gebrochenen Exponenten und beherrschen den Umgang mit Wurzeltermen durch Anwendung der Wurzelgesetze. Sie beherrschen die Berechnung bestimmter Terme mit Wurzeln und Potenzen sowie das Umstellen von Formeln mit Wurzeln und Potenzen. 8 (6) 14. Logarithmenrechnung Die Studierenden kennen die Logarithmensysteme für die Basen a = 10 und a = e und beherrschen die Umrechnung zwischen den Logarithmensystemen. Sie wenden die Logarithmengesetze bei der Umformung und Berechnung logarithmischer Ausdrücke an. 4 (4) Verbleibende Stunden (je nach Semestereinteilung, Stundenplan, Feiertage) für Klausuren, punktuelle Vertiefungen, Wiederholungen und zusätzliche Übungen. Ein begleitender Stützkurs wird angeboten. Bearbeiter(in): Mees, Dr. Ebner, Özgen, Lehne STB Jegliche Veröffentlichung bedarf der Genehmigung, Änderungen sind vorbehalten 15.10.2010 Seite 3 von 3