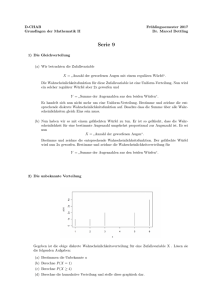
1. Berechne das Volumen der skizzierten Seilrolle. 2. Gegeben ist

Kantonsschule LUZERN
MATURA 1984
MATHEMATIK
Realgymnasium
180 Minuten
Vier vollständige und saubere Lösungen werden mit der Note 6 bewertet.
1. Berechne das Volumen der skizzierten Seilrolle.
2. Gegeben ist die komplexe Funktion f: z a
iz
z +i
, z ∈C -{i}
a) Bestimme die zusammengesetzte Funktion g = f o f und deren Definitionsbereich.
b) Bestimme z so, dass die Punkte A(f(z)), B(g(z)), C(1) in der Gauss’schen Zahlenebene ein positiv
orientiertes, gleichschenklig-rechtwinkliges Dreieck mit dem rechten Winkel in C bilden.
3. Markiere in einem Würfel mit der Kantenlänge a=1 die beiden Eckpunkte einer Körperdiagonalen.
Halbiere dann alle Würfelkanten, die nicht durch einen markierten Eckpunkt gehen, und verbinde
die benachbarten Kantenmitten durch Strecken.
a) Zeichne ein sauberes Schrägbild. (Einheit: 8 Häuschen)
b) Beweise, dass die mit den Kantenmitten erzeugte Figur eben ist.
c) Die erzeugte Figur bildet mit einer markierten Würfelecke eine Pyramide.
Berechne den Winkel zwischen zwei Mantelflächen.
d) Berechne das Volumen der Pyramide.
4. Ein Basketballspiel zwischen zwei Mannschaften A und B steht nach Ablauf der regulären Spielzeit
unentschieden. Jede Mannschaft bestimmt nun für die Freiwurfentscheidung je einen Vertreter.
Der Vertreter der Mannschaft A trifft mit der Wahrscheinlichkeit x und der Vertreter der Mannschaft B
mit der Wahrscheinlichkeit y den Korb. Das Spiel ist entschieden, wenn eine Mannschaft in einem
Durchgang (mit je einem Wurf pro Mannschaft) trifft und die andere Mannschaft nicht trifft.
a) Berechne die Wahrscheinlichkeit, dass das Spiel auch nach dem 1., 2., 3., ... n-ten Durchgang nicht
entschieden ist.
b) Berechne die Wahrscheinlichkeit, dass das Spiel im dem 1., 2., 3., ... n-ten Durchgang von A
gewonnen wird.
c) Berechne die Wahrscheinlichkeit, dass das Spiel im 1., 2., 3., ... n-ten Durchgang entschieden wird.
d) Berechne für x = y = ½ den Erwartungswert für die Anzahl Durchgänge, bis das Spiel entschieden ist.
5. KURZAUFGABEN
Wer 3 der folgenden 4 Aufgaben löst, bekommt die Maximalpunktzahl der Aufgabe.
a) Bestimme alle ganzzahligen Lösungen der Gleichung: x2 + 3y2 = 4
∞
b) Zeige mit vollständiger Induktion:
∫
t n e− t dt = n! (Fakultät)
0
∀n ∈ N o
c) Bestimme die allgemeine Lösung der Differentialgleichung: 2 y’y3 - xex = 0
d) In welchem Punkt des Intervalls I = [0,
5π
2
] ist die Funktion f: x a lim(
2sin x)n definiert?
n→∞
Zeichne für x den Graphen von f (Einheit: ½π A 3 cm), und bestimme alle Punkte von I in denen f nicht
stetig ist.
holzherr
1