6 Uebungen_1_Schularbeit

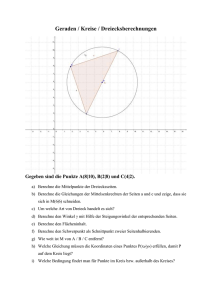
Mathematik
1. Schularbeit Übungsbeispiele
Übungsbeispiele für die 1. Schularbeit
1.
⎛
⎞
⎛
⎞
⎛
⎞
⎛
⎞
Gegeben sind die beiden Geraden a : X = ⎜ −4 ⎟ + s ⋅ ⎜ −7 ⎟ und b : X = ⎜ 0 ⎟ + t ⋅ ⎜ 3 ⎟ sowie zwei
⎝ 48 ⎠
⎝ 24 ⎠
⎝ 20 ⎠
⎝ 4 ⎠
(
)
(
)
Punkte A −15 0 und B 10 0 .
a) Wandle beide Geraden in Normalvektorform um.
b) Berechne den Schnittpunkt C der Geraden a und b.
c) Ermittle eine Normalvektorform der Gerade c durch A und B. Welche besondere Gerade ist das?
d) Berechne den Normalabstand des Punktes A von der Geraden a
2.
e) Die Punkte A, B und C bilden ein Dreieck. Welches besondere Dreieck liegt hier vor?
Gegeben sind folgende vier Geraden:
⎛
⎞
⎛
⎞
a : X = ⎜ 22 ⎟ + r ⋅ ⎜ −7 ⎟
⎝ 0 ⎠
⎝ 17 ⎠
⎛
⎞
⎛
⎞
b : X = ⎜ −7 ⎟ + s ⋅ ⎜ 7 ⎟
⎝ −2 ⎠
⎝ −17 ⎠
⎛
⎞
⎛
⎞
c : X = ⎜ 15 ⎟ + t ⋅ ⎜ −14 ⎟
⎝ 17 ⎠
⎝ 34 ⎠
⎛
⎞
⎛
⎞
d : X = ⎜ 30 ⎟ + u ⋅ ⎜ 17 ⎟
⎝ 72 ⎠
⎝ 1 ⎠
Überprüfe die gegenseitige Lage der folgenden Geraden (s.u.). Falls die Geraden einander schneiden,
berechne den Schnittwinkel. Falls sie disjunkt parallel sind, berechne ihren Abstand. Notwendige
Nebenrechnungen müssen gemacht werden!
a) a und b
b) a und c
c) a und d
3. Zeige, dass die Punkte A(–20|30), B(104|–8) und C(20|72) ein rechtwinkeliges Dreieck bilden und
berechne dessen Flächeninhalt. Bei welchem Punkt ist der rechte Winkel?
4. Gegeben ist das Dreieck A( –4 | 1 ), B( 8 | –1 ) und C( 0 | 6 )
a) Berechne die Längen der Seiten b = AC und c = AB .
b) Berechne mit der Hesse‘schen Normalform die Länge der Höhe hc.
c) Berechne den Winkel α = BAC
d) Ermittle die Fläche des Dreiecks auf zwei Arten: mit der Formel A =
A=
5.
c ⋅ hc
2
und mit der Formel
b ⋅ c ⋅ sin α
2
Gegeben ist das Dreieck A( –1 | 20 ), B( 7 | 4 ) und C( 1 | –20 )


a) Berechne die Länge der Normalprojektion von b auf c .
b) Berechne die Längen von hc und b.
c) Überprüfe die Richtigkeit deiner Ergebnisse durch Einsetzen in den Pythagoräischen Lehrsatz (Skizze!).
6. Berechne Umkreismittelpunkt und Schwerpunkt des Dreiecks A( 0 | 0 ), B( 6 | –12 ) und C( 12 | 12 ).
7. Der Punkt P( 5 | –2 ) wird an der Geraden g: 5x –12y = –120 gespiegelt. Berechne die Koordinaten des
gespiegelten Punkts P‘.
Lösungen
1a) a: 24x + 7y = 240; b: 4x – 3y = –60
(
1b) C 3 24
)
1c) y = 0 ... x-Achse
1d) 24
1e) Zwei Seiten haben die Länge 25, es gibt keinen rechten Winkel ⇒ gleichschenkeliges Dreieck
2a) disjunkt ||, Abstand = 27,58
2b) identisch
2c) schneidend, φ = 70,99°
2
3) A = 3364 E , rechter Winkel bei C
4a) b = 6,40; c = 12,17
4b) hc = 5,59
4c) α = 60,80°
4d) A = 34 E2
5a) 36,67
5b) hc = 16,10; b = 40,05
5c) 36,672 + 16,102 ≈ 40,052
6) U( 13 | –1 ); S( 6 | 0 )
7) P‘( –5 | 22 )