Hinweise - Es sind alle fünf Aufgaben zu lösen. Jede Aufgabe wird

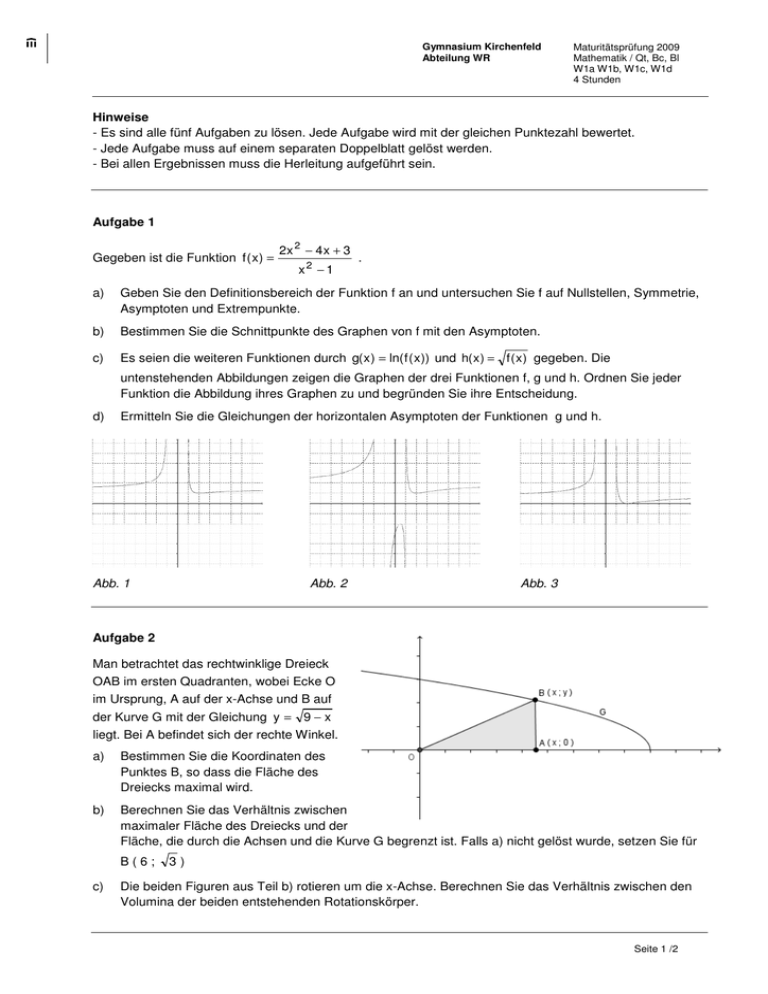
Gymnasium Kirchenfeld
Abteilung WR
Maturitätsprüfung 2009
Mathematik / Qt, Bc, Bl
W1a W1b, W1c, W1d
4 Stunden
Hinweise
- Es sind alle fünf Aufgaben zu lösen. Jede Aufgabe wird mit der gleichen Punktezahl bewertet.
- Jede Aufgabe muss auf einem separaten Doppelblatt gelöst werden.
- Bei allen Ergebnissen muss die Herleitung aufgeführt sein.
Aufgabe 1
Gegeben ist die Funktion f ( x ) =
2x 2 − 4 x + 3
x2 − 1
.
a)
Geben Sie den Definitionsbereich der Funktion f an und untersuchen Sie f auf Nullstellen, Symmetrie,
Asymptoten und Extrempunkte.
b)
Bestimmen Sie die Schnittpunkte des Graphen von f mit den Asymptoten.
c)
Es seien die weiteren Funktionen durch g( x ) = ln( f ( x )) und h( x ) = f ( x ) gegeben. Die
untenstehenden Abbildungen zeigen die Graphen der drei Funktionen f, g und h. Ordnen Sie jeder
Funktion die Abbildung ihres Graphen zu und begründen Sie ihre Entscheidung.
d)
Ermitteln Sie die Gleichungen der horizontalen Asymptoten der Funktionen g und h.
Abb. 1
Abb. 2
Abb. 3
Aufgabe 2
Man betrachtet das rechtwinklige Dreieck
OAB im ersten Quadranten, wobei Ecke O
im Ursprung, A auf der x-Achse und B auf
der Kurve G mit der Gleichung y = 9 − x
liegt. Bei A befindet sich der rechte Winkel.
a)
Bestimmen Sie die Koordinaten des
Punktes B, so dass die Fläche des
Dreiecks maximal wird.
b)
Berechnen Sie das Verhältnis zwischen
maximaler Fläche des Dreiecks und der
Fläche, die durch die Achsen und die Kurve G begrenzt ist. Falls a) nicht gelöst wurde, setzen Sie für
B(6;
c)
3)
Die beiden Figuren aus Teil b) rotieren um die x-Achse. Berechnen Sie das Verhältnis zwischen den
Volumina der beiden entstehenden Rotationskörper.
Seite 1 /2
Maturitätsprüfung 2009
Mathematik / W1abcd
Aufgabe 3
Gegeben sind die drei Punkte A ( 7 / 9 / 16 ), B ( 1 / 6 / 14 ) und C ( –1 / 10 / 14 )
a)
Zeigen Sie, dass das Dreieck ABC rechtwinklig ist (rechter Winkel bei B) und bestimmen Sie den
Flächeninhalt des Dreiecks.
b)
Bestimmen Sie eine Gleichung der Ebene, in der das Dreieck ABC liegt.
c)
Berechnen Sie die Koordinaten eines Punktes D, so dass ABCD ein Rechteck ist.
d)
Über diesem Rechteck als Grundfläche ist eine gerade Pyramide zu errichten, deren Spitze S in der
x-y-Ebene liegt. Bestimmen Sie die Koordinaten der Spitze S und das Volumen der Pyramide.
Aufgabe 4
Frau Fermat erwartet Gäste und will daher im Keller zwei Flaschen Rotwein holen.
Im Keller stehen 3 Kartons die jeweils 6 Flaschen Wein enthalten. Ein Karton enthält 6 Flaschen Weisswein, der zweite Karton 6 Flaschen Rotwein und der dritte Karton ist gemischt, er enthält 2 Flaschen
Weisswein und 4 Flaschen Rotwein. Im Keller ist leider das Licht defekt, so dass nicht erkennbar ist, was
für eine Flasche man in den Händen hat.
a)
Frau Fermat nimmt aus dem gemischten Karton zwei Flaschen. Zeige, dass die Wahrscheinlichkeit,
2
dabei zwei Flaschen Rotwein zu erwischen beträgt.
5
b)
Wie gross wäre die Wahrscheinlichkeit, mindestens 2 Flaschen Rotwein zu erwischen, wenn Frau
Fermat aus dem gemischten Karton sicherheitshalber gleich drei Flaschen gezogen hätte.
c)
Wegen der schlechten Lichtverhältnisse ist leider nicht erkennbar, welchen Weinkarton man vor sich
hat. Frau Fermat wählt zufällig einen der drei Weinkartons und entnimmt ihm zwei Flaschen.
d)
c1)
Wie gross ist die Wahrscheinlichkeit, dass sie zwei Flaschen Rotwein entnommen hat?
c2)
Falls sie wirklich zwei Flaschen Rotwein erwischt hat, wie gross ist dann die Wahrscheinlichkeit,
dass diese aus dem gemischten Karton stammen?
Wie viele Rotwein-Kartons müssten neben dem einen Weisswein-Karton und dem gemischten Karton
im Keller stehen, damit die Wahrscheinlichkeit, beim Ziehen von zwei Flaschen aus einem zufällig
gewählten Karton, zwei Rotweinflaschen zu erwischen, 0,9 beträgt.
Aufgabe 5
Eine Zahlenfolge ist wie folgt gegeben: a1 = 1
a2 = 2 und a n =
a n−1 + 1
für n>2
a n −2
a) Bestimmen Sie die ersten zehn Glieder dieser Folge.
b) Bestimmen Sie die Summe der ersten 2009 Glieder dieser Folge.
c) Eine Folge heisst periodisch mit der Periode p wenn für alle n∈ gilt an+p = an
Zeigen Sie, dass die gegebene Folge immer periodisch ist, unabhängig davon, welche Anfangswerte
a1 und a2 gewählt werden.
Beachte: es gilt (x+1)⋅(y+1) = xy + x + y + 1
d) Es sei a1 = 4. Wie muss a2 gewählt werden, damit die Summe der ersten 5 Glieder der Folge 12
ergibt?
Seite 2 /2