Komplexe Zahlen: Normalform in Polarform - mathe

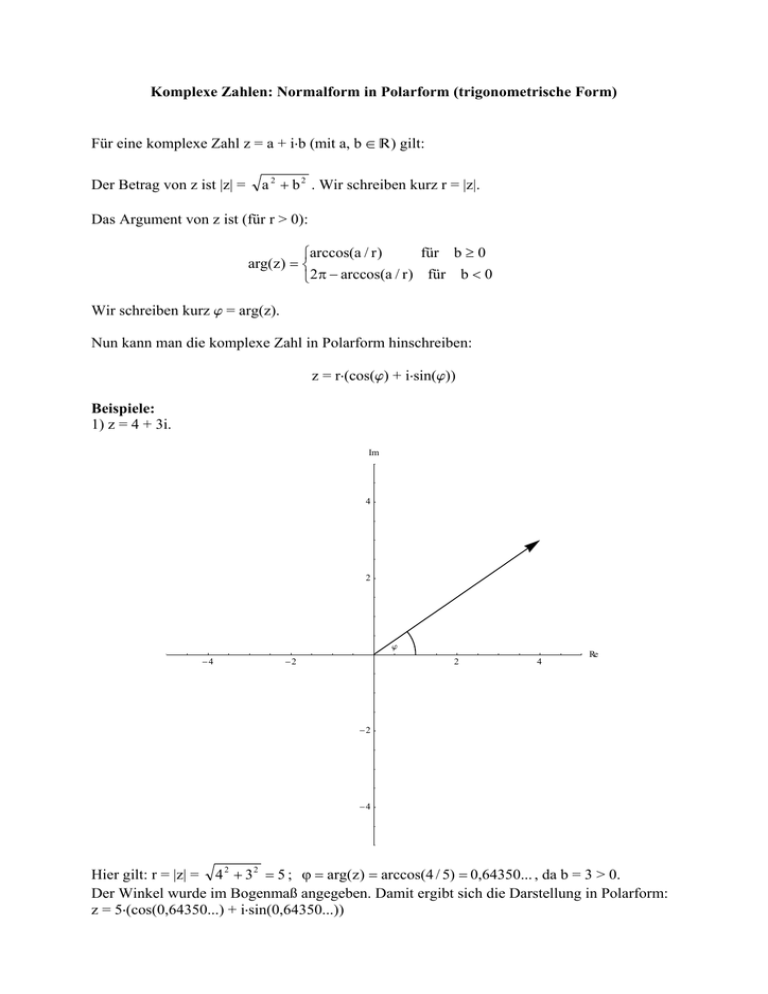
Komplexe Zahlen: Normalform in Polarform (trigonometrische Form)
Für eine komplexe Zahl z = a + iÿb (mit a, b œ Ñ) gilt:
Der Betrag von z ist |z| =
a 2  b 2 . Wir schreiben kurz r = |z|.
Das Argument von z ist (für r > 0):
für b  0
arccos(a / r )
arg(z)  
2  arccos(a / r ) für b  0
Wir schreiben kurz j = arg(z).
Nun kann man die komplexe Zahl in Polarform hinschreiben:
z = rÿ(cos(j) + iÿsin(j))
Beispiele:
1) z = 4 + 3i.
Im
4
2
j
-4
-2
2
4
Re
-2
-4
Hier gilt: r = |z| = 4 2  3 2  5 ;   arg(z)  arccos(4 / 5)  0,64350... , da b = 3 > 0.
Der Winkel wurde im Bogenmaß angegeben. Damit ergibt sich die Darstellung in Polarform:
z = 5ÿ(cos(0,64350...) + iÿsin(0,64350...))
2)
z = -3 - 3i.
Im
4
2
j
-4
-2
2
4
Re
-2
-4
Hier gilt: r = |z| =
(3) 2  (3) 2  18 ;
  arg(z)  2  arccos(3 / 18 )  5 / 4 , da b = -3 < 0.
Der Winkel wurde wieder im Bogenmaß angegeben (Taschenrechner auf RAD stellen).
Damit ergibt sich die Darstellung in Polarform:
z = 18 ÿ(cos(5/4p) + iÿsin(5/4p))
Bemerkungen:
1) z = r  e i ist die Exponentialdarstellung der komplexen Zahl z.
2) Es gilt z = rÿ(cos(j) + iÿsin(j)) = rÿ(cos(j + 2kp) + iÿsin(j + 2kp)) mit k œ Z.
3) Für z = rÿ(cos(j) + iÿsin(j)) gilt zn = rnÿ(cos(nÿj) + iÿsin(nÿj)) mit n œ N.
4) Für z1 = r1ÿ(cos(j1) + iÿsin(j1)) und z2 = r2ÿ(cos(j2) + iÿsin(j2)) gilt
z1ÿz2 = r1ÿ r2ÿ (cos(j1 + j2) + iÿsin(j1 + j2))
und z1/z2 = r1/r2ÿ (cos(j1 - j2) + iÿsin(j1 - j2)) (für r2 > 0).
5) Die zu z = a + iÿb (mit a, b œ Ñ) konjugiert komplexe Zahl ist z = a - iÿb. Dies entspricht
graphisch einer Spiegelung an der reellen Achse (es gilt arg( z ) = 2p - arg(z)). Außerdem ist
a = Re(z) und b = Im(z) (der Realteil und Imaginärteil von z).