Beschreibende Statistik

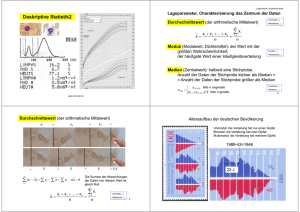
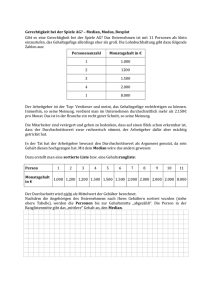
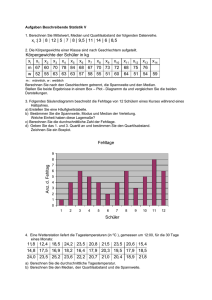
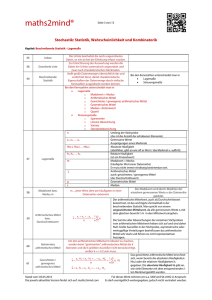
Beschreibende
Statistik
Eine Zusammenfassung
und Beispiele
Uni Klagenfurt/Buch:
Mathematik verstehen 6
Mag. Carmen Kogler
Beschreibende Statistik
Die beschreibende Statistik beschäftigt sich mit der Erhebung, Auswertung und Darstellung von Daten.
In einer statistischen Erhebung wird aus einer bestimmten Grundgesamtheit eine Stichprobe hinsichtlich bestimmter
Variablen(Merkmale) untersucht. Jede Variable kann bestimmte Variablenwerte(Merkmalausprägungen) annehmen.
Beispielweise kann die Variable „Augenfarbe“ die Variablenwerte „blau“, „braun“, „grün“… annehmen.
Man unterscheidet drei Typen von Variablen:
Nominale oder qualitative Variablen: Diese dienen nur zur Unterscheidung von Variablenwerten. Es sind
Merkmalausprägungen, die keine Rechnungen und keine Rangordnung zulassen (Augenfarbe, Geschlecht,
Religionszugehörigkeit, Familienstand,…).
Ordinale Variablen: Diese legen eine Rangordnung der Variablenwerte fest. Man kann mit ihnen zwar nicht rechnen,
aber man kann sie zumindest ordnen(Schulnoten, Güteklassen bei Lebensmitteln, Rangplatz in einer Fußballliga,…).
Metrische Variablen: Diese werden grundsätzlich durch Zahlen dargestellt, wobei es Abstände zwischen den
Variablenwerten gibt. Man kann die Abstände sinnvoll interpretieren und mit ihnen rechnen (Körpergröße,
Einkommen, Kinderzahl,…).
Die erhobenen Daten werden zunächst in einer Urliste angeschrieben. Daraus ermittelt man:
a) Die absoluten Häufigkeit: Sie gibt an, wie oft ein Variablenwert vorkommt
b) Die relative Häufigkeit: Sie erhält man, indem man die absolute Häufigkeit durch die Gesamtzahl dividiert.
Beispiel: Die Augenfarbe von 12 Personen (=Gesamtzahl aller Daten) einer Autofirma wird erhoben:
Urliste: blau, grün, blau, braun, grau, blau, blau, grün, braun, blau, blau, grün
Darstellung der absoluten und relativen Häufigkeiten in einer Tabelle:
Augenfarbe
blau
Absolute Häufigkeit: Hi
6
grün
3
grau
1
braun
2
Relative Häufigkeit: hi
6
= 0,5 = 50%
12
3
= 0,25 = 25%
12
1
≈ 0,08 = 8
%
12
2
≈ 0,17 = 17%
12
Darstellung der Häufigkeiten in drei verschiedenen Abbildungen:
7
6
5
4
3
2
1
0
17%
8%
50%
50%
25%
8% 17%
25%
0%
blau
grün
grau
Stabdiagramm
50%
braun
Kreisdiagramm
Prozentstreifen
100%
Beschreibung der einzelnen Diagrammtypen:
a) Das Stabdiagramm
Beim Stabdiagramm werden die Werte als Längen von Stäben dargestellt. Für die Erstellung eines
Stabdiagramms verwendet man meist die absoluten Häufigkeiten. Ein Vergleich zwischen den Werten ist sehr
gut und schnell möglich.
+
•
•
Vergleich von Größen ist möglich
Sehr übersichtlich
•
Nicht für alle Daten verwendbar
b) Das Kreisdiagramm
Anhand eines Kreisdiagramms lassen sich die Gesamtaufteilung und der Anteil der einzelnen Werte an der
Gesamtheit erkennen. Ein Vergleich zwischen den einzelnen Werten ist schwieriger als beim Stabdiagramm
Die darzustellenden Werte sind als relative Häufigkeiten anzugeben.
(Kreis: 390°=100%)
+
•
Anteile können verglichen werden
•
•
•
Es ist schwer händisch zu erstellen
Anteile sind schwerer zu vergleichen als beim
Stabdiagramm
Nicht für alle Daten verwendbar.
c) Das Streifendiagramm (=Prozentstreifen)
Der Prozentstreifen ist dem Kreisdiagramm sehr ähnlich, allerdings leichter händisch zu zeichnen.
Insbesondere können beim Streifendiagramm auch eher Größenvergleiche zwischen zwei Werten angegeben
werden. Für die Darstellung benötigt man, wie beim Kreisdiagramm, die relativen Häufigkeiten.
+
•
•
•
Die Anteile sind gut vergleichbar
Ein Vergleich ist leichter möglich als beim
Kreisdiagramm
Es ist leicht zu erstellen (händisch)
•
Nicht für alle Daten verwendbar
d) Das Liniendiagramm (=Zeitreihe)
Beim Liniendiagramm werden die zusammengehörigen Werte als Wertepaare aufgefasst und als Punkte in
einem Koordinatensystem eingetragen. Diese Punkte werden dann durch Strecken miteinander verbunden.
An Liniendiagrammen kann man sehr gut erkennen, wie sich ein bestimmter Wert im Verlauf einer gewissen
Zeit verändert (=Zeitreihe). Beispiele dazu sind die Darstellung der Bevölkerungsentwicklung , die Darstellung
der Lebenserwartung im Laufe der Zeit oder die Darstellung für eine Preisentwicklung für ein bestimmtes
Produkt. Beim Liniendiagramm muss man allerdings beachten, dass die gezeichneten Verbindungslinien sich
nicht in jedem Punkt sinnvoll interpretieren lassen.
+
•
Zeitreihenentwicklung
•
•
Nicht für alle Daten verwendbar
Verbindungslinien nicht immer
interpretierbar
Beispiel für ein Liniendiagramm:
Beispiel:
Bei einer Wahl wählen 35% die Partei A, 30% die Partei B, 15% die Partei C, 5% die Partei D, der Rest wählt
ungültig. Die Gesamtzahl der abgegebenen Stimmen beträgt 250000.
a) Gib die absoluten Häufigkeiten der Stimmen an.
Absolute Häufigkeit der Stimmen
Partei A
35% von 250000 =
250000= 87500
250000= 75000
15% von 250000 = 250000= 37500
5% von 250000 = 250000= 12500
15% von 250000 =
250000= 37500
Partei B
30% von 250000 =
Partei C
Partei D
ungültig
b) Fertige ein Kreisdiagramm an:
Relative Häufigkeit der Stimmen
Partei A
= 0,35 = 35%
=
=
=
=
Partei B
Partei C
Partei D
ungültig
0,3 = 30%
0,15 = 15%
0,05 = 5%
0,15 = 15%
Partei A
15%
5%
35%
Partei B
Partei C
15%
Partei D
30%
ungültig
Das Stängel-Blatt-Diagramm
Mit Hilfe eines Stängel-Blatt-Diagramms kann man Daten einer Urliste übersichtlich darstellen. Dabei zerlegt man die
Daten in einen „Stamm“ und in „Blätter“. Als Stamm wählt man, wie im nächsten Beispiel, die Zehnerziffer und als
Blätter die Einerziffer (durch Beistriche getrennt und der Größe nach geordnet)
Beispiel: 25 Schülerinnen und Schüler werden gefragt, wie viele Minuten sie durchschnittlich pro Tag online sind.
Urliste: 12, 45, 21, 13, 24, 39, 10, 7, 56, 42, 37, 75, 19, 23, 38, 26, 22, 20, 39, 16, 39, 39, 18, 61, 30
Stängel-Blatt-Diagramm:
Stamm (Zehnerziffer)
Blätter (Einerziffer)
0
7
1
0,2,3,6,8,9
2
0,1,2,3,4,6
3
0,7,8,9,9,9,9
4
2,5
5
6
6
1
7
5
Man kann die Daten in Intervallen, den so genannten Klassen, die auch unterschiedlich breit sein können,
zusammenfassen:
Zeit (in Minuten)
[0;20[
[20;40[
[40;80[
Absolute Häufigkeit
7
13
5
Bei der Darstellung durch ein Histogramm muss man auf die unterschiedlich breiten Klassen achten.
Die Rechtecke sollen nämlich einen korrekten Eindruck von den absoluten Häufigkeiten liefern:
Beachte: Man ermittelt die Höhe der Rechtecke nach der Formel: Rechteckshöhe =
Histogramm:
!"#!
$%&'!
Statistik und Manipulation:
Bei der graphischen Veranschaulichung statistischer Daten besteht immer die Gefahr, dass der Betrachter in
irgendeiner Weise manipuliert wird. Man muss deshalb solche Grafiken stets sehr kritisch beurteilen.
In den meisten Fällen, vor allem bei Zeitreihen, gibt es keine objektiv „richtigen“ graphischen Darstellungen. Fast jede
Darstellung ist in gewisser Weise subjektiv und manipulativ, und darüber hinaus werden die bewusst und unbewusst
erzielten Effekte auch subjektiv unterschiedlich wahrgenommen. Vielmehr sollte man sich die Frage stellen, ob die
gewählte Darstellung für den intendierten Eindruck brauchbar, angemessen und zweckmäßig ist, oder ob dafür eine
andere Darstellung (oder auch mehrere) besser wäre.
a) Unterschiedliche Skalierungen haben einen Einfluss auf das Aussehen der Darstellung:
Manipulation von Liniendiagrammen:
Die Achseneinheiten sind bei den Graphiken
unterschiedlich gewählt worden.
In der Graphik der Opposition wurde der
Ordinatenursprung verschoben (auf 700000). Der
Zuwachs erscheint somit größer.
In der Graphik der Stadtregierung liegt der
Ordinatenursprung bei 0 und die Skalierungsschritte
sind größer gewählt. Dadurch erscheint der Zuwachs
geringer.
Eine Veränderung der Skalierung der y-Achse
täuscht eine enorme Wachstumszunahme der
Größe der Rekruten vor.
Es entsteht durch die Graphik der Eindruck, dass
sich die Größe der Rekruten in den letzten 100
Jahren verdreifacht hat.
b) Unterbrechung der Stäbe:
Durch die Unterbrechung der Stäbe, der Anordnung der Stäbe und dem Einsatz von Farbe entsteht der
Eindruck, dass Kärnten knapp hinter Tirol und Salzburg liegt und damit sehr hohe Übernachtungszahlen
gegenüber den restlichen Bundesländern hat.
c) Manipulation von Kreisdiagrammen:
Der optische Eindruck von Kreisdiagrammen kann durch die räumliche Darstellung („Torten“) oder der
Perspektive verändert werden.
Auch die Trennung der Kreissektoren (oder eines einzelnen Kreissektors von den anderen), die Anordnung der
Kreisteile oder farbliche Hervorhebungen können den Leser der Graphik täuschen.
3D-Darstellungen
(perspektivische
Darstellungen) verzerren
die realen Werte.
Dies wird noch verstärkt
durch die Auswahl
verschiedener Farben
und durch die Anordnung
der Länder.
Zentralmaße und Quartile
Modus:
Der Modus einer Datenliste ist der am häufigsten vorkommende Wert der untersuchten Variablen.
Dieser Wert ist nicht immer eindeutig bestimmt, da es mehrere häufigste Werte geben kann (d.h. es kann auch zwei
Modi geben)
Median(Zentralwert):
Ordnet man eine Liste von Zahlen der Größe nach, so heißt bei einer ungeraden Anzahl von Zahlen die in der Mitte
stehende Zahl der Median der Liste, bei einer geraden Anzahl von Zahlen bezeichnet man das arithmetische Mittel der
beiden in der Mitte stehenden Zahlen als den Median der Liste.
112234456
1123355567
3+5
2
Median
4
Median
Arithmetisches Mittel (Mittelwert, Durchschnitt):
Unter dem arithmetischen Mittel einer Zahlenliste x1, x2, …… xn versteht man die reelle Zahl:
)* = ) + ) + ⋯ + ),
-
Beispiel: Die durchschnittlichen Temperaturen werden an jedem Augusttag gemessen. Sie sind in der folgenden
Urliste zusammengefasst:
24, 20, 22, 23, 25, 26, 25, 23, 27, 27, 27, 30, 29, 30, 30, 31, 28, 27, 27, 25, 26, 25, 24, 22, 21, 22, 23, 22, 21, 20, 21
Liste ordnen:
20, 20, 21, 21, 21, 22, 22, 22, 22, 23, 23, 23, 24, 24, 25, 25, 25, 25, 26, 26, 27, 27, 27, 27, 27, 28, 29, 30, 30, 30, 31
Median
Modus: 27 ( = der am häufigsten auftretende Wert der Liste)
Arithmetisches Mittel:
./ 0
.1 0⋯0
.2
=
,
00000000000030300000404000000050000
≈
=
)* = Wenn in einer Liste mit den Zahlen x1, x2, …… xn der Wert ai (i=1, 2, 3,…k ≤ -)
mit der absoluten Häufigkeit Hi
beziehungsweise mit der relativen Häufigkeit hi auftritt, dann gilt:
)* = , :><? ;< =<
bzw.
)* = :><? ℎ< =<
24,94
Für das obige Beispiel bedeutet das:
Darstellung der absoluten und relativen Häufigkeiten in einer Tabelle:
Temperaturen: ai
20
Absolute Häufigkeit: Hi
2
21
3
22
4
23
3
24
2
25
4
26
2
27
5
28
1
29
1
30
3
31
1
Relative Häufigkeit: hi
2
≈ 0,06
31
3
≈ 0,097
31
4
≈ 0,129
31
3
≈ 0,097
31
2
≈ 0,06
31
4
≈ 0,129
31
2
≈ 0,06
31
5
≈ 0,161
31
1
≈ 0,032
31
1
≈ 0,032
31
3
≈ 0,097
31
1
≈ 0,032
31
C
B = :HF?C EF GF =
A
D
=
(2 20 + 3 21 + 4 22 + 3 23 + 2 24 + 4 25 + 2 26 + 5 27 + 1 28 + 1 29 + 3 30 + 1 31) = 24,94
beziehungsweise
B = :HF?C JF GF =
A
= 0,06 20 + 0,097 21 + 0,129 22 + 0,097 23 + 0,06 24 + 0,129 25 + 0,06 26 + 0,161 27 + 0,032 28 + 0,032 29 + 0,097 30 + 0,032 31
= 24,94
Berechnung des arithmetischen Mittels bei unterschiedlichen Klassenbreiten:
Häufigkeitsverteilung für Unternehmen und ihre Beschäftigungszahlen:
Beschäftigte
0 bis unter 5000
5000 bis unter 10000
10000 bis unter 20000
20000 bis unter 35000
35000 bis unter 45000
45000 bis unter 50000
)* =
2500+57500+815000+527500+037500+247500
Hi
5
5
8
5
0
2
Klassenbreite : Kb
(in 1000 Beschäftigte)
5
5
10
15
10
5
Höhe =
K<
LM
(in 1000)
1
1
0,8
0,33
0
0,4
= 16100 (Die Zahlen 2500, 7500, 15000, 27500, 37500 und 47500 sind jeweils der Durchschnittswert
der jeweiligen Klassen)
Interpretation des arithmetischen Mittels: Würde jedes Unternehmen die gleiche Anzahl an Mitarbeitern führen,
wäre dies 16100.
Ausreißer:
Betrachtet man die folgende Liste von Daten: 1, 1, 1, 2, 3, 3, 4, 4, 1000, so sieht man, dass die Liste „extreme“
Einzelwerte (=Ausreißer) enthalten kann. (Hier ist es die Zahl 1000)
Wie wirkt sich ein Ausreißer auf die verschiedenen Zentralmaße der Liste aus?
Liste
Arithmetisches Mittel
Modus
00030
1, 1, 1, 2, 3, 3, 4, 4, 1000 )* =
1
=113,22
1, 1, 1, 2, 3, 3, 4, 4
)* =
5
0003
=2,375
5
Median
3
1
2,5
Man sieht:
Das arithmetische Mittel, das aus allen Einzelwerten der Liste berechnet wird, reagiert „empfindlich“ auf Ausreißer.
Modus und Median ändern sich durch Ausreißer dagegen wenig oder auch gar nicht, denn ihr Wert hängt nicht davon
ab, wie groß die „Extremwerte“ im einzelnen sind.
Um Datenmanipulationen zu vermeiden, dürfen „Ausreißer“ nicht ohne Weiteres aus Datenlisten ausgeschlossen
werden. Vielmehr ist zu klären, welche Ursachen die Ausreißer haben könnten.
Argumentieren anhand von Zentralmaßen
Beispiel: In der Klasse 6a wurde eine „Notenstatistik“ für die 1. und 2. Schularbeit im Fach Deutsch angefertigt. Die
Tabelle gibt die jeweilige Anzahl der einzelnen Noten an. Welche der beiden Schularbeiten ist „besser“ ausgefallen?
Argumentiere anhand verschiedener Zentralmaße!
1. Schularbeit
2. Schularbeit
1
4
2
2
5
10
Modus
3
2
Median
3
2,5
Note
3
7
6
4
1
3
5
2
3
Lösung:
1. Schularbeit
2. Schularbeit
Mittelwert
≈ 2,58
≈ 2,79
Aufgrund der verwendeten Zentralmaße kann man hinsichtlich der Frage, welche Schularbeit besser ausgefallen ist, zu
einander entgegengesetzten Antworten kommen. Die persönliche Interessenlage entscheidet letztlich, welche
Antwort man bevorzugt.
Beispiel: Für jede der folgenden Variablen wurde eine Datenliste erhoben. Ist die Berechnung des arithmetischen
Mittels stets sinnvoll? Wenn nicht, welches Zentralmaß wäre sinnvoller?
Arithmetisches Mittel sinnvoll
Anderes Zentralmaß sinnvoll
1)
Temperatur
ja
2)
Lebensalter
ja
3)
Haarfarbe
Modus, da Nominaldaten vorliegen
4)
Alter
ja
5)
Familieneinkommen
ja
6)
Einwohnerzahl
ja
7)
Güteklasse eines Lebensmittels
Median, da Ordinaldaten vorliegen
8)
Rangplatz in der Fußballliga
Median, da Ordinaldaten vorliegen
9)
Zeitdauer
ja
10) Familienstand
Modus, da Nominaldaten vorliegen
11) Kinderzahl
Arithm. Mittel (Kommazahlen sinnlos),
Median, bei hohen Datenzahlen: Modus
12) Gewicht
ja
Quartile:
In einer geordneten Liste liegen vor dem Median gleich viele Zahlen wie nach dem Median. Man bezeichnet den
Median mit q2.
1, 2, 2, 3, 4, 5, 5, 6, 6, 7, 8, 8, 8, 9, 10
Median (q2)
Bildet man für die Zahlen vor q2 wiederum den Median q1 und für die Zahlen nach q2 den Median q3, so erhält man
drei Zahlen q1, q2 und q3, die man als Quartile der geordneten Liste bezeichnet.
1, 2, 2,
3, 4, 5, 5, 6, 6, 7, 8, 8, 8, 9, 10
Median (q2)
q1
q3
Durch die Quartile wird die geordnete Liste in vier gleich große Abschnitte zerlegt.
Es gilt:
Vor q1 liegen ca. 25% aller Daten der geordneten Liste
Vor q2 liegen ca. 50% aller Daten der geordneten Liste
Vor q3 liegen ca. 75% aller Daten der geordneten Liste
Quartilabstand (=Interequartilspannweite): Die Differenz q3 – q1 wird Quartilabstand genannt. Zwischen q1 und q3
liegen ungefähr 50% der Daten der geordneten Liste.
Spannweite: Die Differenz zwischen dem größten Wert (max) und dem kleinsten Wert (min) einer geordneten Liste
heißt Spannweite.
Fünfzahlenzusammenfassung:
Die fünf markanten Werte min, q1, q2, q3 und max einer geordneten Liste können wie folgt, zusammengefasst
werden. Zusätzlich wird noch der Quartilabstand (=Interquartilspannweite) und die Spannweite angegeben.
q2
q1
q3 Quartilabstand
min
max Spannweite
Die graphische Darstellung dieser Werte kann in einem Kastenschaubild (Box-Plot) erfolgen:
Der Bereich von q1 bis q3, in dem sich etwa 50% der Werte befinden, wird als Rechteck wiedergegeben. In diesem
Bereich wird auch der Median q2 eingetragen. Die übrigen Bereiche werden als Strecken gekennzeichnet, sofern die
Werte relativ dicht liegen. Einzelne Punkte werden als Ausreißer gekennzeichnet. Welche Werte als Ausreißer gelten
legt der Anwender aufgrund seiner Kenntnis des untersuchten Sachzusammenhangs fest.
Betrachten wir noch einmal das folgende Beispiel:
25 Schülerinnen und Schüler werden gefragt, wie viele Minuten sie durchschnittlich pro Tag online sind.
Urliste: 12, 45, 21, 13, 24, 39, 10, 7, 56, 42, 37, 75, 19, 23, 38, 26, 22, 20, 39, 16, 39, 39, 18, 61, 30
Stängel-Blatt-Diagramm: Gib die Fünfzahlenzusammenfassung an und zeichne dazu ein Kastenschaubild:
Stamm (Zehnerziffer)
0
1
Blätter (Einerziffer)
7
0,2,3,6,8 | 9
2
0,1,2,3,4,6
3
0,7,8,9,9,9 | 9
4
5
6
7
2,5
6
1
5
Fünfzahlenzusammenfassung:
q1=
05
= 18,5
505
= 39
q2 = 26
q3=
Kastenschaubild: Box – Plot
26
18,5
7
39
75
20,5
68
Beispiele zu Kastenschaubildern (Box – Plots):
1)Die beiden Kastenschaubilder stellen die Studiendauern der Kunst- und Wirtschaftsstudierenden eines Landes dar.
a)
b)
c)
d)
e)
Vervollständige die folgenden Sätze:
_50__% der Kunststudierenden benötigen für ihr Studium 14 bis 17 Semester.
75% aller Wirtschaftsstudierenden benötigen für ihr Studium länger als __10__ Semester.
Im Mittel studieren Kunststudierende um ____4___ Semester länger als Wirtschaftsstudierende.
Studiendauern über __14__ Semester sind bei Wirtschaftsstudierenden extreme Einzelfälle.
Nur _25__% aller Kunststudierenden beenden ihr Studium in höchstens 14 Semestern.
2) Grundwehrdienst
Beim Stellungstermin wurden unter anderem die Körpergrößen von 120 Rekruten festgehalten.
Diese sind hier zusammengefasst in Form eines Diagramms dargestellt:
Aufgabenstellung:
Setzen Sie in den folgenden Aussagen die richtigen Zahlen ein:
Aus dem Diagramm kann man entnehmen, dass
ca. 50% der Rekruten kleiner als …177.. cm sind.
ca. 75% der Rekruten größer als …168.. cm sind.
die Rekruten höchstens ..194.. cm groß sind.
jeder Rekrut mindestens …153… cm groß ist.
von den 120 Rekruten ca. …30… Rekruten mindestens 181 cm groß sind.
von den 120 Rekruten ca. …90… Rekruten größer als 168 cm sind.
ca. …60… Rekruten zwischen 168 cm und 181 cm groß sind.
3) In 33 Wirtschaftsbereichen werden von 66 Beschäftigten die Bruttogehälter (in €) erhoben, wovon jeweils 33
von den Männern und 33 von den Frauen sind. Wie allgemein bekannt, klaffen die Gehälter von Männern und
Frauen auseinander. In der nachfolgenden Abbildung ist die Verteilung der Gehälter getrennt nach Frauen und
Männern in zwei Kastenschaubildern dargestellt.
Bruttoeinkommen von 33 Frauen und 33 Männern (in €)
Interpretiere und vergleiche:
Frauengehälter
Das höchste Gehalt liegt bei ca. 2700€.
Das niedrigste Gehalt liegt bei ca. 650€.
Drei Gehälter sind Ausreißer.
Die meisten Mitarbeiterinnen verdienen zwischen 950€
und 1700€.
50% der Frauen verdienen höchstens 1300€ und 50% der
Frauen verdienen mindestens 1300€.
50% der Frauen verdienen zwischen 1150€ und 1450€.
Die Gehälter der Frauen, die die mittleren 50% darstellen,
sind symmetrisch verteilt. Jedoch ist im „dichten“ Bereich
eine Asymmetrie nach oben vorhanden.
Männergehälter
Das höchste Gehalt liegt bei ca. 3200€.
Das niedrigste Gehalt liegt bei ca.700€.
Sieben Gehälter sind sogenannte Ausreißer.
Die meisten Mitarbeiter verdienen zwischen 1550€ und
2300€.
50% der Männer verdienen höchstens 1800€ und 50%
der Männer verdienen mindestens 1800€.
50% der Männer verdienen zwischen 1650€ und 2200€.
Im „dichten“ Bereich ist eine leichte Asymmetrie nach
oben vorhanden.
Vergleich:
Der Median liegt bei den Männern bei ca. 1800€ und bei den Frauen bei ca. 1300€. Dies bedeutet, dass nur eine
Mitarbeiterin (Gehalt: 2700€) mit ihrem Gehalt in jenen Bereich fällt, in welchem 50% der Männer liegen.
Von dieser einen Mitarbeiterin ausgenommen, verdient keine Frau so viel wie 50% der Männer.
Die Ausreißer nach oben sind ebenfalls bei den Männern höher.
4) Beispiel: Die durchschnittlichen Temperaturen werden an jedem Augusttag gemessen. Sie sind in der
folgenden Urliste zusammengefasst:
24, 20, 22, 23, 25, 26, 25, 23, 27, 27, 27, 30, 29, 30, 30, 31, 28, 27, 27, 25, 26, 25, 24, 22, 21, 22, 23, 22, 21, 20, 21
Erstelle ein Kastenschaubild.
20, 20, 21, 21, 21, 22, 22, 22, 22, 23, 23, 23, 24, 24, 25, 25, 25, 25, 26, 26, 27, 27, 27, 27, 27, 28, 29, 30, 30, 30, 31
q1
Kastenschaubild (Box-Plot)
q2
q3
5)
Urliste aus der Grafik:
1, 1, 1, 2, 2|2, 2, 2, 3, 3
q1=2
q2 =
| 3, 3, 3, 3, 4 | 4, 4, 4, 5, 5
0
=3
Damit kommt nur das zweite Kastenschaubild in der zweiten Reihe in Frage.
(Das Rechteck reicht von 2 bis 4 und der Median q2 liegt bei 3.)
q3=4
6)
Im folgenden Kastenschaubild wird die Verteilung der Netto-Jahreseinkommen der 15 Mitarbeiterinnen eines
Unternehmens veranschaulicht.
a)Formuliere anhand des Kastenschaubilds mindestens drei konkrete Aussagen über die Verteilung der NettoJahreseinkommen der 15 Mitarbeiterinnen.
Das höchste Netto-Jahreseinkommen liegt bei ca. 22000€.
Das niedrigste Netto-Jahreseinkommen liegt bei ca. 4000€. (Ausreißer)
Die meisten Mitarbeiterinnen verdienen zwischen 10000€ und 22000€
50% verdienen höchstens 15000€ und 50% verdienen mindestens 15000€.
50% verdienen zwischen 13000€ und 19000€.
75% verdienen mindestens 13000€.
25% verdienen mindestens 19000€.
b)Das arithmetische Mittel der 15 Netto-Jahreseinkommen beträgt 15200€. Wie hoch ist das arithmetische Mittel,
wenn man den Ausreißer nicht mitrechnet.
)* =
N3
3
= 16000O
Beispiel: Nenne einen Grund, der bei der Angabe von Durchschnittsgehältern (z. B. in einem Betrieb/Unternehmen)
Für die Verwendung des Medians und gegen die Verwendung des arithmetischen Mittels spricht!
Hohe Managergehälter würden das arithmetische Mittel verfälschen. Das arithmetische Mittel ist sehr
ausreißerempfindlich.
Streuungsmaße
Die folgenden Abbildungen zeigen zwei Häufigkeitsverteilungen mit gleichem Mittelwert )* .
Während sich in der linken Abbildung die Daten relativ eng um das arithmetische Mittel gruppieren, weichen sie in der
rechten Abbildung dem Anschein nach durchschnittlich stärker vom arithmetischen Mittel ab.
Man sagt: Die Streuung der Daten um den Mittelwert ist in der rechten Abbildung größer als in der linken Abbildung.
Streuungsmaße:
Mittelwert der Abweichungsquadrate:
(./ N.* )1 0(.1 N.* )1 0⋯PP0(.2 N.* )1 ,
= s² (=Empirische Varianz der Liste)
Dieser Ausdruck ist als Streuungsmaß geeignet, denn jeder Variablenwert trägt umso mehr zur Streuung bei, je
mehr er sich vom Mittelwert )* unterscheidet.
Er hat aber einen Nachteil: Seine Maßeinheit ist das Quadrat der Maßeinheit der untersuchten Variablen. Das
heißt, er misst die Streuung einer Längenvariablen, die in Meter vorliegt, in Quadratmeter. Das ist oft
unerwünscht, deshalb zieht man aus dem ganzen Ausdruck noch die Wurzel und erhält:
Q
(./ N.* )1 0(.1 N.* )1 0⋯PP0(.2 N.* )1 ,
= s (=Empirische Standardabweichung der Liste)
Beispiel: Berechne den Mittelwert und die empirische Standardabweichung der Liste: 3, 1, 2, 5, 4
)* =
00003
=
=3
s=Q
(N)1 0(N)1 0(N)1 0(N)1 0(3N)1 ≈ 1,41
Empirische Standardabweichungen können zum Vergleich von Verteilungen herangezogen werden. Dabei kann nur
entschieden werden, ob eine Verteilung stärker streut als eine andere. Was der konkrete Wert von s für jede einzelne
Verteilung angibt, lässt sich nur ungenau beschreiben. Bei vielen Verteilungen liegt der „Großteil“ der Daten im
Intervall [)* – s, )* + s].
Vereinfachung: Verschiebungssatz für die empirische Varianz
Für die empirische Varianz s² einer Liste x1, x2, ….., xn mit dem Mittelwert )* gilt:
s² =
AC R0
AS R0⋯0AD R
D
B²
A
Somit kann die Standardabweichung für das obige Beispiel auch so berechnet werden:
s² =
TR0CR0SR0UR0VR
–
U
3² = 2 W s = XS ≈ 1,41
Beachte: Sind a1, a2,…,ak die möglichen Werte einer Variablen und treten diese mit den absoluten Häufigkeiten
H1, H2, ….,Hk auf, so gilt:
s=Q
K/ (Y/ N.* )1 0K1 (Y1 N.* )1 0⋯PP0K2 (Y2 N.* )1 ,
,
wobei n = H1 + H2 + …. +Hk
Beispiel: Berechne die empirische Standardabweichung der Liste: 2, 3, 3, 4, 4, 4, 5, 5, 6
ai
2
3
4
5
6
C
B = :HF?C EF GF =
A
D
s=Q
Hi
1
2
3
2
1
003004
=
5
4
K/ (Y/ N.* )1 0K1 (Y1 N.* )1 0⋯PP0K2 (Y2 N.* )1 =
,
S 0S(TNV)S 0T(VNV)S 0S(UNV)S 0C(ZNV)R
Q(SNV)
5
≈ 1,15
Beispiel: Die folgende Tabelle zeigt die Zahl der beim Arbeitsmarkt vorgemerkten Arbeitslosen von 2000 bis 2011:
Jahr
Arbeitslose (in 1000)
2000
194,3
212,3 222,2 239,2 246,7 250,8 252,7 260,3
2001
203,9
2002
232,4
q2
2003
240,1
2004
243,9
q1
q3
2005
252,7
SCS,T0SSS,S0ST\,S0SVZ,]0SU^,_0SUS,]0SZ^,T
2006
239,2
B=
A
= 240,6
]
2007
222,2
2008
212,3
2009
260,3
2010
250,8
2011
246,7
Berechne für die Arbeitslosen für die Jahre 2005-2011 die folgenden Streuungsmaße:
a) Spannweite, b) Interquartilspannweite, c) empirische Varianz, d) empirische Standardabweichung
(48000 Arbeitslose)
a)
Spannweite = xmax – xmin = 260,3 – 212,3 = 48
b)
Interquartilspannweite: q3 – q1 = 252,7 – 222,2 = 30,5 (30500 Arbeitslose)
c)
Empirische Varianz:
s² =
s² =
d)
./ R0
.1 R0⋯0.2 R
- )* ²
,
,R0,R05,R034,R0,R0,R04,R
–
240,6² ≈ 259,59
(259600 Arbeitslose)
Empirische Standardabweichung:
s = [258,59 ≈ 16,112
(16110 Arbeitslose)
Interpretiere die einzelnen Streuungsmaße:
a) Der Unterschied zwischen dem Jahr mit der höchsten und dem Jahr mit der niedrigsten Arbeitslosenanzahl
beträgt 48000 Arbeitslose
b) Die mittleren 50% der Arbeitslosen reichen von 222200 bis 252700 Arbeitslosen, dies bedeutet eine
Spannweite von 30500 Arbeitslosen.
c) s² ist kaum interpretierbar, da die Einheit die Arbeitslosenanzahl² ist.
d) Die mittlere quadratische Abweichung vom Mittelwert beträgt 16110 Arbeitslose.
Beispiel: Bei der Berechnung des arithmetischen Mittels zweier vorgegebener Listen erhält man jeweils den Wert
5. Die Standardabweichung der ersten Liste beträgt 1, die der zweiten Liste 2. Sind folgende Aussagen zutreffend?
Begründe!
a) Beide Listen haben auch den gleichen Median.
Falsch, da aus dem gleichen arithmetischen Mittel nicht folgt, dass die beiden Listen den gleichen Median
haben müssen. (Arithmetisches Mittel und Median sind zwei voneinander unabhängige Werte)
b) Der Modus beider Listen ist ebenso 5.
Falsch, da aus dem gleichen arithmetischen Mittel nicht folgt, dass die beiden Listen den gleichen Modus
haben müssen. (Arithmetisches Mittel und Modus sind zwei voneinander unabhängige Werte)
c) Die Spannweite der zweiten Liste ist größer als die der ersten Liste.
Richtig, denn bei gleichem arithmetischen Mittel bedeutet eine größere Standardabweichung eine größere
Streuung.
d) In der zweiten Liste müssen doppelt so viele Elemente wie in der ersten Liste sein.
Falsch, da Streuungsmaße nichts über die Anzahl der Daten aussagen.
e) Bei einer „gleichmäßigen“ Verteilung der Summe der beobachteten Werte auf die Grundgesamtheit würde
dies bei beiden Listen 5 bedeuten.
Richtig, da das arithmetische Mittel in beiden Listen 5 ist. Und das arithmetische Mittel = Verteilung der
Summe der beobachteten Werte auf die Grundgesamtheit.
f) 50% der Daten liegen unter 5 und 50% der Daten liegen über 5.
Falsch, denn diese Aussage gilt nur für den Median und nicht für das arithmetische Mittel.
Überblick: Welche Aussagen können aus einem Kastenschaubild gefolgert werden:
•
•
•
•
•
•
•
Der Wert des Medians ist ablesbar und zu interpretieren
Die Werte der Quartile können abgelesen und interpretiert werden.
Man kann die Interquartilspannweite bestimmen und interpretieren.
Eine Aussage ist darüber zu treffen, in welchem Bereich die Daten dicht liegen.
Es können die Ausreißer genannt werden.
Man kann das Minimum und das Maximum angeben.
Es ist leicht zu erkennen, ob die Verteilung nahezu symmetrisch ist.