Anwendung - Optimierung eines Batchprozesses mit zwei Substraten

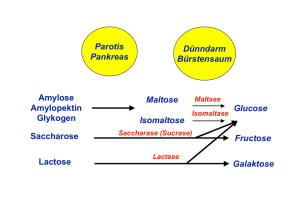
Mirjam Geibel, 12.07.04
Anwendung - Optimierung eines Batchprozesses mit zwei Substraten
Es wird ein Batchprozess optimiert, bei dem den Bakterien zwei Substrate, Glucose
und Lactose, zur Verfügung stehen. Die Bakterien bevorzugen Glucose und erst
wenn diese verbraucht ist, wird der Stoffwechsel auf Lactoseabbau umgestellt.
Hierbei muss das Enzym ß- Galactosidase gebildet werden, welches hier als Produkt
betrachtet wird.Es soll möglichst viel Produkt in kurzer Zeit gebildet werden, daher
lautet die Zielfunktion f =
p
.
t
Als Freiheitsvariablen stehen die zu Anfang des Prozesses zugegebenen Mengen an
Glucose und Lactose zur Verfügung, bzw. deren Verhältnis.
Zuerst werden die Massenbilanzen für die Biomasse x (Bakterien), die Glucose s1,
die Lactose s2 und das Produkt p aufgestellt:
dx
µ... spezifische Wachstumsraten
= ( µ ges − f d ) ⋅ x
dt
fd... spezifische Sterberate
ds 1 − µ 1 ⋅ x
ds 2 − µ 2 ⋅ x
k... Geschwindigkeitskonstanten
=
;
=
dt
Y x / s1
dt
Yx /s2
Yx/s Biomasse/Subtratausbeute
K... Michaeliskonstanten
dp
dt
= (k 1 + k 2 ⋅ µ 2 ) ⋅ x ⋅ s 2
Die Wachstumskoeffizienten µ berechnen sich wie folgt:
µ 1 = µ max 1 ⋅
s1
K s1 + s 1
;
s2
µ 2 = µ max 2 ⋅
K s2
Für die Parameter gilt:
µmax1 =
0.73
µmax2 =
0.29
Ks1
=
0.2
Ks2
=
0.12
Ki
=
0.01
Beschränkungen sind
x≥0
s1≥0
k1
k2
Yx/s1
Yx/s2
fd
s2≥0
;
s 2
+s2 + 1
K i2
=
=
=
=
=
µ ges = µ 1 + µ 2
0.05
0.03
0.4
0.13
0.01
p≥0
Anfangsbedingungen sind
x=0.16
p=0
s1 und s2 sollen optimiert werden.
Da die Differentialgleichungen zu kompliziert sind, um von Hand gelöst zu werden,
wird ein Programm eingesetzt, welches einerseits den Verlauf der Kurven simuliert,
und diese dann auch optimiert