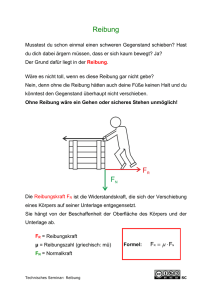
∑ ∑

2.3. Das statische Gleichgewicht: Kräfte  Drehmomente
Greifen mehrere Kräfte F an einem Körper an, so lassen sie sich vektoriell zu einer Gesamtkraft
addieren.
Kräfte, deren vektorielle Summe verschwindet, lassen einen Körper in Ruhe.
Wir betrachten einen in 0 (Koordinatenursprung) drehbar gelagerten Körper:
Wenn der Körper K im Punkt 0 drehbar
gelagert ist, wird die Wirkung der Kraft Fges
umso größer sein, je größer die Kraft selbst ist
und je größer der wirksame Kraftarm r ist.
Definition des Drehmoments M:
Drehmoment  Kraft  wirksamer Kraftarm
M
F
M
rx F
M 
 Nm
 r  F  r  sin 
(5)
Greifen mehrere Drehmomente an K an, dann können sie vektoriell zu einem
Gesamtdrehmomentaddiert werden (Superpositionsprinzip, Kräfteparallelogramm(e)).
Es gilt: Ein Körper befindet sich im statischen Gleichgewicht, wenn die vektorielle Summe aller
angreifenden Kräfte und Drehmomente verschwindet.
Fges   Fi  0
i
(6)
M ges   M i  0
i
Experiment: Hebelgesetz, Drehmomente, Gleichgewichte



stabile
labile
indifferente
Gleichgewichte
V 4 / 1111
V 3 / 2101
V 3 / 2102
V 3 / 2108
V 4 / 0001
Beim stabilen Gleichgewicht bewegt sich der Körper nach kleinen Störungen infolge von
einwirkenden Kräften immer wieder in die Gleichgewichtslage zurück. Er führt dabei Schwingungen
um die ehemalige Ruhelage aus.
Beim labilen Gleichgewicht verlässt der Körper bei einer Störung sofort die (vorher instabile)
Ruhelage und kehrt nicht mehr dorthin zurück.
Beim indifferenten Gleichgewicht wechselt der Körper unter dem Einfluss von Kräften in eine neue
Gleichgewichtslage.
2.4. Dichte und Massenmittelpunkt
Körper unterschiedlicher Stoffe mit gleichen Massen besitzen i.A. unterschiedliche Volumina.
Die Stoffe werden charakterisiert durch die Stoffeigenschaft Dichte.
Definition:
mittlere Dichte 
Dimension:
Masse des Körpers
m

Volumen des Körpers
V
  
(7)
kg
m3
Bei vielen Körpern ist die Dichte an verschiedenen Stellen unterschiedlich:     x, y, z  . Solche
Körper heißen inhomogene Körper. Man muss eine lokale Dichte   r     x, y, z  definieren:
  x, y , z  
dm
dV
(8)
Die Gesamtmasse des Körpers berechnet sich dann nach:
m

Körper
dm     x, y, z  dV     x, y, z  dxdydz
(9)
V
Bei der Beschreibung der Bewegung von Körpern kann man die Verteilung der Masse auf ein
ausgedehntes Volumen oft außeracht lassen und sie sich in einem Punkt konzentriert denken: dem
Massenmittelpunkt MMP (Konzept des Massenpunktes).
Der MMP besitzt darüber hinaus bei vielen mechanischen Problemen eine ausgezeichnete
Bedeutung. Seine Lage (Ortskoordinaten) lässt sich experimentell und (zumindest in einfachen Fällen)
rechnerisch bestimmen.
Wir betrachten zunächst den eindimensionalen Fall:
An einer masselosen Stange sind an den Stellen xi die Masse mi befestigt.
Die Koordinate des Massemittelpunktes ergibt sich als gewichtetes Mittel aller Koordinaten xi
xs 
m3
m1
m2
x1 
x2 
x3
m1  m2  m3
m1  m2  m3
m1  m2  m3
oder allgemein
n
xs  
i 1
mi
m
j 1
(10)
xi
n
j
Beim 3D-Fall gilt analoges für die Koordinaten y und z. Vektoriell zusammengefasst ergibt sich als
Ortsvektor des Massemittelpunktes R
R
m r   m r
M
m
i i
i
(11)
i
j
r   xi , yi , zi 
R   xs , ys , zs 
M   mj
Gesamtmasse
Experimente: Schwerpunktmodelle
V3/1501
V3/1502
V3/1503
Im Falle der kontinuierlichen Masseverteilung wird dieser gedanklich in (kleine) Massenelemente dm
aufgeteilt.
Aus der Summation über einzelne Massepunkte wird dann eine Integration über den gesamten
Köper
R
1
M m0
lim
r
i
mi 
1
rdm
M
(12)
Mit Hilfe der Dichte ergibt sich ein Volumenintegral  dm   dV , wenn   const 
R
1
r  dV
M
(13)
Beispiel zur Bedeutung des Massemittelpunktes:
masselose Stange mit den zwei Massen m1
und m2
Frage: An welchen Stellen xs müsste eine Gegenkraft F an der Stange angreifen, die der gesamten
Gewichtskraft G  G1  G2 das Gegengewicht hält und den Gesamtkörper in der waagerechten Lage
belässt?
Die Gegengewichtsbedingungen (vgl. Gleichung (2.7)) fordern:
-
für die Kräfte:
 F  0 und
i
i
-
für die Drehmomente:
M
i
D.h. für unser Beispiel:
i
0


F   G1  G2 und
G1  xs  x1   G2  x2  xs 
oder
xs 
x1G1  x2G2 x1  m1  g  x2  m2  g m1 x1  m2 x


G1  G2
m1 g  m2 g
m1  m2
Die Koordinaten des Angriffspunktes xs der Kraft F muss also gerade die des Massemittelpunktes
(Schwerpunktes) sein!
Allgemein: Im Gleichgewicht kann die Resultierende paralleler Kräfte im Massemittelpunkt
angreifend gedacht werden bzw. ein im Massemittelpunkt (SP) unterstützender Körper ist in jeder
Lage im statischen Gleichgewicht.
2.5. Reibungskräfte zwischen festen Körpern





Die Reibung ist wichtig für viele Bewegungsabläufe.
Ohne Reibung könnte man nicht laufen, fahren, bremsen.
Reibung bei Bewegung(en) in Flüssigkeiten und Gasen wird als innere Reibung bezeichnet.
Reibung zwischen festen Körpern heißt äußere Reibung.
Die mit der äußeren Reibung verbundenen mikrophysikalischen Vorgänge sind äußerst
kompliziert.
Was geschieht auf nanoskaliger und atomarer Ebene?
 Hier sollen nur phänomenologische Beziehungen betrachtet werden; diese sind oft nur
näherungsweise gültig.
 Die Newton‘schen Axiome 1 und 2 sind Idealisierungen; im täglichen Leben beobachtet man
anderes.
 Nach dem Trägheitsprinzip sollte ein auf waagerechter Ebene rutschender Körper seine
Geschwindigkeit für immer beibehalten. Tatsächlich kommt der Körper aber früher oder später
zur Ruhe. Nach dem Aktionsprinzip sollte eine beliebig kleine Kraft einen Körper in Bewegung
setzen können. Ist jedoch Reibung mit im Spiel, dann vermag eine beliebig kleine Kraft keineswegs
den Körper zu bewegen bzw. zu beschleunigen.
2.5.1. Haftreibung:
Ein Körper haftet auf seiner Unterlage. Es gibt
nie ganz glatte Oberflächen, sondern immer
mikroskopische Verhakungen.
Kräfte, die kleiner sind als die
Haftreibungskraft, lassen den Körper in Ruhe,
siehe dazu die Skizze an der Tafel.
•
Der Körper „antwortet“ in diesem Falle nach dem Gegenwirkungsprinzip mit einer gleich großen
Gegenkraft (actio = reactio).
Experimente:
FHR  FHR  Auflagefläche 
Haftreibung unabhängig von der Größe der Auflagefläche
FHR
 Normalkraft 
Haftreibung ist proportional zur Normalkraft
FHR  H  FN
(14)
 H : Haftreibungskoeffizient
Bis hierher am 03.12.2015, Ende der 8. Vorlesung
##################################################################################
Der Haftreibungskoeffizient  H lässt sich z.B. an einer schiefen Ebene ermitteln:
Winkel, deren Schenkel paarweise
aufeinander  stehen, sind gleich.
Man misst den Neigungswinkel max , bei
dem der Körper gerade zu gleiten beginnt.
Hangabtriebskraft:
FH  FHR  G  sin max
Normalkraft:
FN  G  cos max
Aus FHR  H FN
folgt:
H  tan max
Experimente:
Klotz auf Wagen auf geneigter Ebene
Schüttkegel aus verschiedenen Materialien
 H : spezifisch für bestimmte Stoffpaarungen und Oberflächen
MH
Stahl/Stahl
 0,5 (trocken)
 0,1 (ölschmierig)
Glas/Glas
0,9
Eis/Eis (-10°C)
0,3
2.5.2. Gleitreibung
Nach Überwindung der Haftreibung gleitet der
Körper
mit der Geschwindigkeit v .
Dazu bedarf es der Kraft F , um diese
Geschwindigkeit aufrecht zu erhalten. Die ihr entgegengesetzt gerichtete und betragsmäßig
gleich große, von der Reibung herrührende Kraft heißt: Gleitreibungskraft FGR .
Nährungsweise ist diese geschwindigkeitsunabhängig
FGR  G  FN mit G  H
(15)
Die Richtung von Reibungskräften ist immer entgegengesetzt zur Bewegungsrichtung des Körpers.
2.5.3. Rollreibung


Ohne Haftreibung könnte ein Rad auf seiner Unterlage nicht rollen, sondern nur gleiten.
Die Rollreibung hat ihre Ursache in der Deformation von Rad und Unterlage (an der Kontaktstelle).
Beide sind keine ideal festen starren Körper.
FRR  R  FN



(16)
Mitunter berücksichtigt man, dass die Rollreibung vom Radius des Rades abhängen muss. Bei
gleicher Normalkraft drückt sich ein kleines Rad tiefer in die Unterlage als ein großes.
Die die Bewegung hemmende Reibungskraft muss also für ein kleines Rad größer sein.
Eine relativ gute Annäherung an die praktische Realität gelingt mit einer entsprechend
aufgestellten Beziehung.
l
FRR  FN
r
l: charakteristische Rollreibungslänge
r: Radius des Rades
MR
Autoreibung auf Asphalt
0,025
Stahl auf Stahl
0,003
2.5.4. Seilreibung
Experimente: Seilreibung an der Rolle, siehe auch Tafelbild(er)
l
 5 104 m