temperaturgradienten also

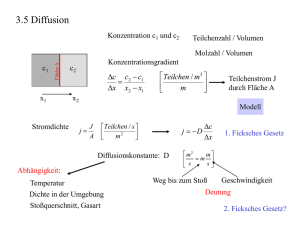
Wärmelehre – Transportphänomene (Wärmeübergänge)
• Wärme - eine Form der Energie (Einheit [Joule])
• Alle Energieformen können in Wärme umgewandelt werden
• Wärmeenergie Zufuhr → Erhöhung der Temperatur
• Wärmeenergie Abfuhr → Temperaturerniedrigung
• Erfahrungstatsache: Wärmetransport geht mit dem Temperaturgradienten,
d.h. vom warmen zum kalten Körper (zwei Systeme haben genau die gleiche
Temperatur, wenn sie sich im thermischen Gleichgewicht befinden → kein
Wärmeübergang )
• Temperatur bei Wärmezufuhr wird durch die spez. Wärme cP beschrieben:
zugeführte Wärmemenge
Masse
ΔQ
cP =
m ⋅ ΔT
⎡ J ⎤
⎢ kg ⋅ K ⎥
⎣
⎦
Temperaturerhöhung
wie aber wird die Wärme transportiert ?!
?
Wärmetransport durch Strahlung
(Wärmestrahlung – auch ohne Medium)
Wärmestrahlung beobachtet man
auch beim Glühen von heißen
Materialien (Flamme, glühende
Körper).
Zu jeder Temperatur gibt es eine
Verteilung der elektromagnetischen
Strahlung auf die verschiedenen
Wellenlängen (für unser Auge Farben),
was durch das Plancksche
Strahlungsgesetz (1900) beschrieben
wird.
Aus der Position des Maximums einer
solchen Verteilung kann man leicht
auf die Temperatur des Körpers
schließen. Unsere Sonne strahlt
maximal im Grünen (Wellenlänge etwa
500nm), woraus sich die
Oberflächentemperatur der Sonne zu
5800 K berechnen läßt.
Emittanz E und Absorptionsvermögen A sind Funktionen der Temp. und Beschaffenheit des
Körpers (hell, dunkel, glatt, rauh). Experimentell wurde festgestellt, daß für jede Wellenlänge
E/A = konstant (Kirchhoffsches Gesetz)
Schwarzer Körper: A = 1, d.h. die auffallende Strahlung wird zur Gänze in Wärme umgewandelt.
Ende des 19. Jahrhunderts war das Interesse an der
Wärmestrahlung sehr groß und man versuchte mit Hilfe der
damals recht jungen Physik der Wärme - der Thermodynamik
oder statistischen Physik - diese Strahlung zu erklären.
J. Stefan und L. Boltzmann gelang es, die Abhängigkeit der
gesamten Strahlungenergie von der Temperatur
vorherzusagen:
[
E ges = A ⋅ σ ⋅ T 4 , σ = 5.67 ⋅10 −8 Wm −2 K −4
]
Wird ein Körper wärmer, so strahlt er
überproportional viel Wärme ab.
Seine Emittanz hängt nur von seiner Temperatur ab.
Für nicht schwarze Körper: A<1.
Achtung - Grünes Buch S. 272: A – Fläche (!!!)
E
Strahlungsbilanz – Lebewesen
[
E ges = A ⋅ S ⋅ σ ⋅ T 4 , σ = 5.67 ⋅10 −8 Wm −2 K −4
Ein Mensch (nackt mit A ≅ 0.9) hat eine Oberfläche von S=2m2 und eine
Hauttemperatur von 32°C. Was passiert in einer Umgebung von 20°C
(T=283K) ? ( Für den Fall von A=1 → Schwarzer Körper).
Nach Stefan - Boltzmann gibt es eine Austrahlungsleistung von EE=981 W
und eine Strahlungsleistung zum Körper von EA=727W.
Es muss also die Leistung von rund (981-727)W=254W nachgeliefert werden
um oben genannte Temperaturdifferenz konstant zu halten !!
Über Zeitperiode von 24 Stunden ergibt diese Leistung eine Energie von:
Q = 254W ⋅ (24 ⋅ 3600) s = 21946kJ (!!!)
Wärmeabgabe kann durch eine Schutzschicht (Kleidung), oder Hauttemperatursenkung verringert werden.
Thermogramm
einer Hand
]
Plancksches Strahlungsgesetz
Max Planck (1858 – 1947),
Nobelpreis 1918.
1878
E ⋅ dλ =
c2
λ
5
1
h⋅
e
c ⋅h
λ ⋅k ⋅T
dλ
−1
1901
Wärmeleitung
Gibt es innerhalb eines
Körpers einen
Temperaturgradienten,
dann tritt ein
mikroskopischer Vorgang
des Wärmeflusses auf,
welcher auf die
Energieübertragung durch
molekulare
Zusammenstöße
zurückführbar ist.
….. dazu ein „Experiment“ (Dank an
Uni Würzburg)
Ein Übergang der Wärme
vom heißen zum kalten Ort
findet statt – es ist die
Wärmeleitung.
Dieses Phänomen ist kein Materiefluss, hängt aber von der Materie ab, denn
durch diese wird die Wärmeenergie transportiert.
Wärmestrom (pro Zeit fließende Wärmemenge) - ∆Q/ ∆t:
ΔQ
∝ ΔT
Δt
ΔQ
∝A
Δt
ΔQ 1
∝
Δt
l
Φ
ΔQ
ΔT
Φ=
= λ ⋅ A⋅
Δt
l
1 ⎤ ⎡ W ⎤
⎡J
≡⎢
λ⎢ ⋅
⎥
⎣ s m ⋅ K ⎦ ⎣ m ⋅ K ⎥⎦
λ … Wärmeleitfähigkeit, Wärmeleitzahl
Metalle, Luft, Wasser – die
Wärmeleitfähigkeiten sind
unterschiedlich, und relativ
einfach zu erklären (Anzahl
und Art der Moleküle).
Was wirklich interessant
erscheint ist
Wärmeleitfähigkeit bei
Polarbären – sie sind de facto
mit Infrarotmethoden nicht
photographierbar (!)
Haut
0.500
Fett
0.16
Federn
0.025
Fell (Kaninchen)
0.025
Daniel W. Koon, "Is Polar Bear Hair Fiber Optic?", Applied
Optics, Vol 37, page 3198 (1998).
Physikalische Vorgänge im Fell des Polarbären
•Es gibt mindestens 2 Vorgänge:
–(a) Reflexion des einfallenden Lichtes
–(b) Konversion (Lumineszenz) in Wärme
–Die Haare dienen hier als Lichtleiter
Stationärer Wärmestrom in geometrisch
einfachen Körpern
Φ=
ΔQ
ΔT
= λ ⋅ A⋅
Δt
l
Diese Beziehung gilt für ein von parallelen Flächen
begrenztes Stück Materie. Querschnitt A = konst.
Für andere geometrische Formen muss Φ berechnet werden. Es ergeben
sich folgende Zusammenhänge:
Φ Hohlzyl .
ΔQ
ΔT
=
= λ ⋅ A⋅
r2
Δt
r2 ⋅ ln( )
r1
Φ Hohlkugel
ΔT
ΔQ
=
= λ ⋅ A⋅
r
Δt
r2 ⋅ ( 2 − 1)
r1
A ist hier die Außenfläche, r1 und r2
die Innen- und Außenradien
Kleines Beispiel:
Wärmefluss durch 1 cm2 Oberfläche von einer Fettschicht (λ=0.16 W/m.K)
mit 1cm Dicke bei ∆T=10°C:
a. Ebene Fläche; b. Zylinder - r1=2cm; Zylinder – r1=29cm
Φ Hohlzyl . =
ΔT
ΔQ
= λ ⋅ A⋅
; ΔT = T1 − T2
r
Δt
r2 ⋅ ln( 2 )
r1
a. Φ = 0.016 W ; b. Φ = 0.013 W ; c. Φ = 0.016 W
Es zeigt sich dass die Formulierung für ebene Flächen in erster Näherung
auch für andere Körperformen recht gut funktioniert. Allerdings werden für
Berechnungen der Wärmeflüsse bei Menschen und Tieren meistens die
Formulierungen für Zylinder verwendet – sie sind etwas genauer.
KONVEKTION
Konvektion wird durch Dichte-, Temperatur- und Konzentrationsunterschiede
innerhalb des Fluids (Gas, Flüssigkeit) oder zwischen dem Fluid und seinen
Grenzflächen hervorgerufen. Jedoch kann auch eine von außen wirkende Kraft,
die das Fluid in Bewegung setzt, zu einer Konvektion führen.
Man unterscheidet daher:
‡freie oder natürliche Konvektion, bei der der Teilchentransport ausschließlich
durch Auswirkungen des Temperaturgradienten, also zum Beispiel durch Auf- bzw.
Abtrieb des Fluids infolge der durch die Temperaturänderung hervorgerufenen
Dichteunterschiede bewirkt wird, und
‡erzwungene Konvektion, bei der der Teilchentransport durch äußere
Einwirkung, zum Beispiel ein Gebläse oder eine Pumpe, hervorgerufen wird.
Freie Konvektion:
Bei Erwärmung dehnen sich Stoffe aus, daher wird ihre Dichte geringer. Innerhalb
einer Flüssigkeit oder eines Gases steigen Bereiche mit geringer Dichte nach
oben, während Bereiche mit höherer Dichte nach unten sinken.
Natürliche Konvektion im Termitenhügel
Erzwungene / freie Konvektion
Das Wasser wird durch die Heizkörper gepumpt (erzwungen). Beim noch
warmen, aber abgeschalteten Heizkörper (freie Konvektion)
Konvektion tritt auf vielfältige Weise auf:
‡Wenn eine Zentralheizung am tiefsten Punkt des Gebäudes installiert wird, kann
sie ohne Umwälzpumpe auskommen, da das warme Wasser durch Konvektion nach
oben in die Heizkörper steigt sich dort abkühlt und wieder nach unten fließt.
‡Luft wird am warmen Erdboden erwärmt und steigt nach oben, ein entscheidender
Faktor für die Entstehung des Wetters
Theoretische Behandlung von Konvektion ist exakt nur in wenigen Sonderfällen
möglich. Auf der Basis von vielen experimentellen Untersuchungen kann jedoch die
Ermittlung von Wärmetransport durch Konvektion mittels diversen Kennzahlen
(dimensionslose Zahlen), welche die Übertragbarkeit von Modelexperimenten auf
reelle Situationen erlauben, ganz gut durchgeführt werden.
Für die Behandlung von Konvektionsvorgängen benötigen wir 3 Kennzahlen:
Reynoldszahl (Re), Nusseltzahl (Nu) und Grashofzahl (Gr):
ρ ⋅v⋅d
Re =
η
Nu =
d
δ
⎡ρ ⎤
Gr = α ⋅ g ⋅ ΔT ⋅ d ⋅ ⎢ ⎥
⎣η ⎦
3
ρ- Dichte; η- Zahigkeit; v- Geschwindigkeit; δ- Äquvalentdicke; α- Ausdehnungskoeffizient, g- Erdbeschleunigung, d- charakt. Länge; ΔT- Temp. Diff.
2
„Zylindermensch“ für Modelrechnungen
⎡ρ ⎤
Gr = α ⋅ g ⋅ ΔT ⋅ d ⋅ ⎢ ⎥
⎣η ⎦
2
3
v
ρ ⋅v⋅d
Re =
η
Nu =
d
δ
Re – sehr nützliche Kennzahl um Strömungszustände zu beschreiben
Nu – beschreibt die Wärmeabgabe durch Konvektion und basiert auf der
Gleichung für Wärmeleitung, jedoch wird die Länge „ l “ durch die Äquivalentdicke
„δ“ ersetzt. Konvektion ist auch zu ΔT und A proportional. „δ“ ist somit eine
Schichte die ein Stoff haben müsste um durch die Wärmeleitung genau soviel
Energie zu verlieren, wie viel durch die Konvektion abgegeben wird. Diese
Äquivalentdicke ist auf die charakteristische Länge „d“ eines Gegenstandes
bezogen. Nu ist bei erzwungener Konvektion lediglich von Re abhängig:
Nu = 0.32 + 0.51 Re 0.52
für 0.1 ≤ Re ≤ 10 4
Nu = 0.24 Re 0.6
für 10 4 ≤ Re ≤ 5 ⋅10 4
Nu = 0.024 Re 0.81
für 5 ⋅10 4 ≤ Re ≤ 4 ⋅105
Gleichungen basieren auf Experimenten
und gelten für Zylinder mit Anströmung
normal zur Zylinderachse (d ist also
Zylinderdurchmesser)
Gr ist eine Kennzahl maßgebend für die freie Konvektion. Für einen Zylinder
mit vertikaler Achse gibt es einen Zusammenhang zwischen Gr und Nu.
Nu = 0.58Gr 0.25
Nu = 0.11Gr 0.33
für 10 4 ≤ Gr ≤ 109
für 109 ≤ Gr ≤ 1012
2
⎡ρ ⎤
Gr = α ⋅ g ⋅ ΔT ⋅ d 3 ⋅ ⎢ ⎥
⎣η ⎦
Bei Gr ist die charakt. Länge „d“ die
Höhe des Zylinders. Gr gilt auch für
andere geom. Formen
Ein Beispiel damit wir ein „Gefühl“ für diese Formeln bekommen:
Bestimmen wir die konvektive Wärmeabgabe eines Menschen mit 1.5m2 Hautfläche.
Hauttemp.= 32°C. Umgebungstemp. = 20°C. Betrachten wir 2 Fälle: ruhende Luft und Wind
mit 10m/s. Der Körper wird durch einen Zylinder mit Höhe h=1.6m. Zylinderradius ergibt sich
aus 2πrh = 1.5m2. r = 0.15m.
‡Fall A – ruhende Luft → freie Konvektion → Gr mit ΔT = 12°C. Gr = 9 x109.
Daraus können wir auch die Nu und folglich δ bestimmen. Nu = 0.11Gr = 212.
δ= 1.6 m / 212 = 0.00755 m. Jetzt können wir den Wärmefluss für Konvektion berechnen:
(ΔQ / ΔT) = 57.2 (J/s)= 57.2 W.
‡Fall B – Wind. Wie groß ist die Re ?
ρ ⋅ v ⋅ d 1.3kgm −3 ⋅10ms −1 ⋅ 0.3m
5
Re =
=
=
2
.
1
⋅
10
1.84 ⋅105 Pa ⋅ s
η
Weil Nu = 0.24Re0.81 so bekommen wir für δ = 0.00061m.
Der Wärmefluss für die erzwungene Konvektion ist somit 713 W.
Nach Stefan-Boltzmann Gesetz wird in dieser Situation auch eine Wärmeabgabe aufgrund
der Strahlung abgegeben und beträgt für unseren „zylindrischen Menschen“ 110 W.
freie Konvektion → 167.2 W
erzwungene Konvektion → 824 W
in 24 Std → 14.4 MJ
in 24 Std → 71.2 MJ
Die Äquivalentdicke ist ein Maß für Wärmeabgabe durch Konvektion. Bei freier Konvektion ist δ =
7.5mm, d.h die Wärmeabgabe erfolgt wie durch eine 7.5mm Luftschichte, bei erzungener
Konvektion erhalten wir nur 0.61 mm – da ist die Wärmeabgabe viel größer.
Wärmefluss vom Körperinneren zur Umgebungsluft erfolgt durch die Wärmeleitung.
Wärmeabgabe an die Außenluft erfolgt durch Konvektion, Strahlung und Wärmeleitung.
40°C
T2
ΔQ (Leitung)
TII
TI
ΔQ (Strahlung)
ΔQ (Konvektion)
ΔQ (Verdunstung)
ΔQ
0°C
ΔQ
ΔQ
ΔQ
TIII
T1
Körper
Fett
Kleidung
Haut
wegen
Außenluft
ΔQ λ ⋅ A
ΔQ 1
l
=
⋅ ΔT ⇒
⋅ ⋅ ∑ i = ∑ ΔTi
Δt
l
Δt A i λi
i
Der Wärmefluss (ΔQ /dt) durch Körperschichten ist durch die jeweiligen Temperaturdiff. ΔTx
determiniert. Dieser Fluss ist dann gleich der Summe aller „Außenflüsse“.
In der Abbildung ist ein schematischer Querschnitt von der Haut von Säugern
und Vögeln abgebildet. Außerdem sind die Wärmeaustausch-möglichkeiten
aufgeführt. Die Pfeile könnten natürlich grundsätzlich in beide Richtungen
weisen, aber im Normalfall weisen sie nach außen
Abb. nach Cleffmann
[
E ges = A ⋅ S ⋅ σ ⋅ T 4 , σ = 5.67 ⋅10 −8 Wm −2 K −4
A=1, S=1.4m2, TH=34°C (307K),
TU=23°C (296K).
Für diese Situation müssen ca.
96 Ws (J) Wärmeenergie
nachgeliefert müssen um
diese Temperaturdifferenz
konstant zu halten.
]
Wärmetauscher
Wärmeübertragung zwischen verschiedenen Medien (Die Medien
können dabei flüssig oder gasförmig sein)
Dient der Erwärmung und Kühlung
Viele Anwendungen: Technik (Haushalt bis Industrie), Biologie
(z.B. Temperaturregelung im Körper, Temperaturaustausch mit
der Umgebung)
Gleich- und Gegenstromtauscher und die Temperaturverteilung
Gegenstromwärmetauscher
Wärmefluß
dq
dt
A
B
w
∆x
Die abgegebene Wärme dq im Kontrollabschnitt:
Δq = m& ⋅ dt ⋅ c p ⋅ ΔTA
und
Δq = m& ⋅ dt ⋅ c p ⋅ ΔTB
(1)
ΔQ λ ⋅ A ⋅ ΔT λ ⋅ A ⋅ (Tai − Tbo )
=
=
l
l
Δt
( 2)
ΔQ
= m& ⋅ c p ⋅ (Tai − Tao ) = m& ⋅ c p ⋅ (Tbo − Tbi )
Δt
m& =
dm
dt
m& =
dm
dt
Wir können nun Gl. (1) und (2) umformen:
ΔQ l
⋅
= Tai − Tbo
(1a )
Δt λA
ΔQ
l
⋅
= Tbo − Tbi
( 2a )
Δt m& ⋅ c p
Daraus erhalten wir den Ausdruck für die im
Wärmetauscher übertragene Wärmemenge:
ΔQ
=
Δt
Tai − Tbi
1
l
+
m& ⋅ c p λ ⋅ A
Gute Wärmetauscher – übertragene Wärmemenge muss groß sein →
Nenner des Bruches sollen beide klein sein. Wann tritt es ein ?
Guter Wärmetauscher – gute Wärmenutzung → kleine Volumsströme. Was
& ?
bedeutet es für die Größe m
Temperaturregulierung des menschlichen Körpers
Bei niedrigen Aussentemperaturen wird das Blut stark abgekühlt um ∆T
herabzusetzen. Danach muss es wieder aufgewärmt werden. Dies basiert
auf den Gegenstromwärmetauscher-Prinzip.
Natürlich spielt auch die äußere
thermische Schutzhülle eine Rolle
Wärmeregulierung im Arm
5
TC = ⋅ (TF − 32 )
9
Bei hohen Temperaturen wird das Blut durch die Venen gleich unter der Haut
geleitet → Kühlung durch die Abgabe von Wärme (Kreuzstromwärmetauscher)
Bei tiefen Temperaturen wird das Blut durch die tiefen Venen geleitet. Sie
umschlingen die Arterien wodurch eine extrem effiziente Wärmeleitung erreicht
wird.
Die Schaltung für die Leitungswahl liegt im Hypothalamus wo sich Temp.
Sensoren befinden
Wärmeleitung in der Natur
Wenn es Robben an Land zu heiß wird, öffnen sie die
sog. Thermofenster: Teile ihrer Körperoberfläche
erhitzen sich durch stärkere Durchblutung und
geben Wärme an die Umgebung ab.
Dafür, dass Robben auch im kalten Eismeer nicht
frieren müssen, sorgt ihre zentimeterdicke,
isolierende Speckschicht, und ein GegenstromWärmetauscher in der Blutversorgung der Flossen:
Speck wäre hier hinderlich, schließlich müssen die
Flossen beweglich sein.
Die Arterien, die das Blut aus dem Körper in die
Extremitäten leiten, sind von einem Netz von Venen
umringt, so dass das in den Flossen abgekühlte Blut
auf dem Rückweg in den Körperkern noch wertvolle
Wärme «mitnehmen» kann. Wenn der Körper aber
überschüssige
Wärme
produziert,
wird
ein
alternatives Venensystem genutzt, das keinen
Kontakt zu den Arterien hat. So kann das Blut in den
Flossen überschüssige Wärme an die Umgebung
abgeben und so den Körper kühlen.
Björn Mauck et al., Thermal
windows on the trunk of hauledout seals: hot spots for
thermoregulatory evaporation?
In: The Journal of Experimental
Biology, Band 206, Seite 17271738 (2003)
Wärmeleitung der Erde
‡Erdtemperatur ist Schwankungen unterworfen
‡Wärmehaushalt der obersten Schichten hängt
von Oberflächentemperatur ab.
Jährliche Temperaturschwankungen
Tägliche Temperaturschwankungen
Die Berechnung der Schwankungen näherungsweise möglich. Man
bilanziert die Wärmeflüsse in gewissen Volumina der Erde.
Es zeigt sich dass die Erdoberfläche (lokal) eine zeitliche Variation
folgender Form hat:
T (0, t ) = T ⋅ A(0) sin ωt
2π
ωTaglich =
= 7.2 ⋅10 −5 s −1
24h
2π
ω Jährlich =
= 2 ⋅10 −7 s −1
24h
T ( z, t ) = T + A(0) ⋅ e
−
z
D
z
z
⋅ sin(ωt − )
D
λ - Wärmeleitfähigkeit; ω - Kreisfrequenz;
ρ - Dichte; κ - Diffusivität
Temperaturen T(z,t) in der Tiefe z.
D=
2λ
2κ
=
ρ ⋅ cp ⋅ω
ω
Form der Schwankung (sinusartig)
Mittelwert
T ( z , t ) = T + A(0) ⋅ e
−
z
D
z
⋅ sin(ωt − )
D
Amplitude der Schwankung
In der Tiefe z = D hat die Amplitude den Betrag:
D entspricht jener Tiefe in der die Schwankung
auf den 1/e-ten Teil abgenommen hat (d.h. 37%)
Die zeitabhängigkeit der Schwankung:
z/D ist die Phasenverschiebung zwischen der
Schwankung an der Oberfläche und in der Tiefe z
Vergleich zwischen gemessenen und gerechneten
Bodentemperaturen in 4 Tiefen. Messungen
genommen in Hebei Provinz, China (115.57 Ost;
36.87 Nord). Messparameter waren:
Oberflächentemperatur, Dichte, Wassergehalt.
Wu, J. and D. L. Nofziger 1999. Incorporating
temperature effects on pesticide degradation into a
management model. J. Environ. Qual. 28:92-100.
A(0) ⋅ e −1
z
sin(ωt − )
D
NASA News Archive:
Terra Satellite Measures Sea
Surface Temperature with
Unprecedented Detail
February 14, 2002
Sensationelle Aufnahmen der
Temperaturschwankungen der Erde.
Aber was ist die Temperatur und wie
wird Temperatur eigentlich ermittelt ?
→ Wärmelehre