Temperatur
Werbung
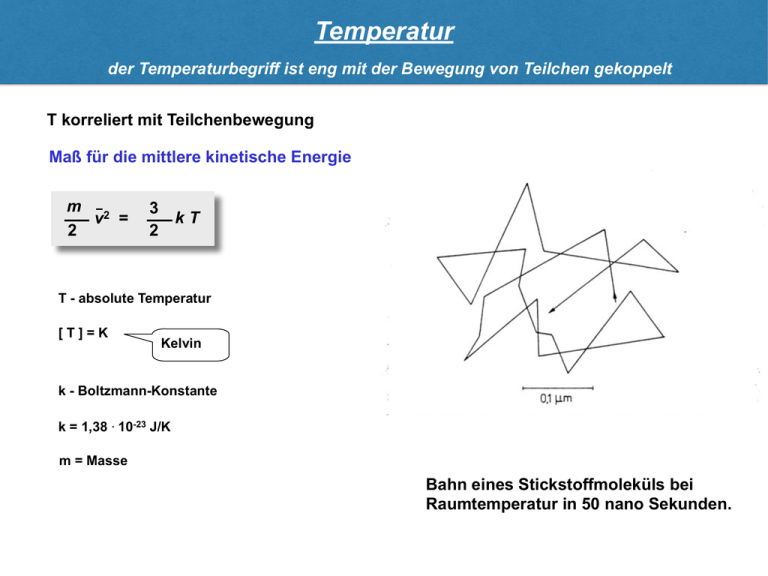
Temperatur der Temperaturbegriff ist eng mit der Bewegung von Teilchen gekoppelt T korreliert mit Teilchenbewegung Maß für die mittlere kinetische Energie m 2 v = 2 3 kT 2 〜 T - absolute Temperatur [T]=K Kelvin k - Boltzmann-Konstante k = 1,38 ⋅ 10-23 J/K m = Masse Bahn eines Stickstoffmoleküls bei Raumtemperatur in 50 nano Sekunden. ! Temperatur der Temperaturbegriff ist eng mit der Bewegung von Teilchen gekoppelt T korreliert mit Teilchenbewegung mittlere kinetische Energie m 2 v = 2 3 kT 2 〜 T - absolute Temperatur [T]=K Kelvin- und Celsiusskala ºC - 273 0 100 Kelvin 273 0 k - Boltzmann-Konstante 373 T = t + 273 K k = 1,38 ⋅ 10-23 J/K m = Masse gleiche Temperaturdifferenzen auf beiden Skalen Formelzeichen für Temperatur in ºC: t bzw. ϑ K Temperatur die Größe und Dichte von Körpern hängt von der Temperatur ab Ausdehnungsthermometer Festkörper und Flüssigkeiten dehnen sich bei Temperaturerhöhung aus lT l0 Δl α - lineare Ausdehnungskoeffizient lT = l0 + Δl lT = l0 (1 + α ΔT) [ α ] = K-1 Dichte von Festkörpern und Flüssigkeiten nimmt bei Temperaturerhöhung ab ρT = ρ0 (1 + γ ΔT) γ - Volumenausdehnungskoeffizient [ γ ] = K-1 γ ≈ 3α Ausnahme: Wasser in der Nähe des Gefrierpunktes stehende Gewässer gefrieren von oben ρmax bei 4 ºC Temperatur auch elektrischen Parameter hängen von der Temperatur ab Widerstandsthermometer RT = R0 (1 + α Δt) α - Temperaturkoeffizient des Widerstandes [ α ] = K-1 Temperatur-abhängige Kontaktspannung an Lötstellen zweier unterschiedlicher Metalle A bei T1 = T2 U1 + U2 = 0 Thermistoren α > 0 Thermoelement Metalle T1 U1 T2 Kontaktstellen Messfühler U2 Eichung ! α < 0 Halbleiter Vorteil: kleiner Messfühler kleine Wärmekapazität Temperatur winziger Objekte kann gemessen werden Wärmemenge und Temperatur durch Zufuhr von Wärme kann ein Körper seine Temperatur erhöhen Wärme ist eine Energieform Wärmezufuhr: Erwärmung des Körpers Phasenumwandlung Verrichten von Arbeit Wärmekapazität ΔQ = m c ΔT Grundgleichung der Kalorik C=mc ΔQ - zugeführte Wärmemenge ΔT - Temperaturänderung m - Masse des Körpers c - spezifische Wärmekapazität [c] = J kg K Beispiel Wasser: J c = 4184 kg K Phasenumwandlung durch Zufuhr oder Abgabe von Wärme kann ein Körper seinen Phasenzustand ändern Temperatur bleibt während der Phasenumwandlung konstant Beispiele: Eis ⎯→ Wasser ⎯→ Wasserdampf Q=rm Q = Wärmemenge für Phasenumwandlung m = Masse r = spezifische Umwandlungswärme Schmelzpunkt Zahlenwerte für r und c Schmelzen (Eis ⎯⎯→ Wasser) 335 ⋅ 103 J/kg T = 273 K Sieden (Wasser ⎯⎯→ Wasserdampf) 2,26 ⋅ 106 J/kg T = 373 K cEis = 2100 J/(kg K) cH2O = 4184 J/(kg K) Siedepunkt Zustandsgleichung idealer Gase Druck, Temperatur und Volumen eines Gases sind miteinander verknüpft Ideales Gas: punktförmige Moleküle (kein Eigenvolumen) keine Wechselwirkungskräfte untereinander Moleküle verhalten sich bei Stößen wie vollelastische Kugeln Zustandsgrößen: beschreiben den Zustand eines Gases Druck p Temperatur T Volumen V pV = nRT Zustandsgleichung n - Stoffmenge des Gases R - Gaskonstante R = 8,314 T – absolute Temperatur (Angabe in Kelvin!) J mol K für eine bestimmte Gasmenge in zwei verschiedenen Zuständen: p1V1 T1 = p2V2 T2 Zustandsänderungen bei bestimmten äußeren Bedingungen können einzelne Zustandsgrößen konstant bleiben pV = nRT isotherm T = const isobar p = const p V = const V~T Gesetz von Boyle-Mariotte Gesetz von Gay-Lussac V p1 Isotherme Beispiel: Zunahme des Druckes bei Erwärmung eines Gases in einem geschlossenem Gefäß p Isobare T2 V = const p~T Beispiel: Ausdehnung eines Gases bei Erwärmung Beispiel: Kompression eines Gases in einem Zylinder durch Kolbendruck p isochor V1 Isochore p2 V2 T1 V T T Gasgemische in einem Gasgemisch verhalten sich die einzelnen Komponenten unabhängig voneinander Beispiel: Luft Sauerstoff, Stickstoff, Wasserdampf, Kohlendioxid, Edelgase RT pi = ni Partialdruck, Druck einer Komponente V Der Druck eines Gasgemisches = Σ der Partialdrücke seiner Komponenten p = p1 + p2 + p3 + ... = Σ pi Gesetz von Dalton pLuft = p N2 + p O2 + p CO2 +p + p Edelgase 101,3 kPa = 79,1 kPa + 21,2 kPa + 0,03 kPa + 0,9 kPa + ... Rest Erster Hauptsatz der Wärmelehre eine Form des Energieerhaltungssatzes unter Berücksichtigung der Wärme a) V = const ΔT Gas V, T, p ↑, Δp ↑ Innere Energie U wird erhöht + ΔQ b) p = const ΔV ↑ ΔW = - p ΔV Volumenarbeit wird verrichtet 1. Hauptsatz der Wärmelehre ΔU = ΔQ + ΔW Die Änderung der inneren Energie eines Systems ist gleich der Summe der zugeführten (bzw. abgegebenen) Wärmemenge und der am System verrichteten (bzw. vom System verrichteten) Arbeit. Zweiter Hauptsatz der Wärmelehre trifft Aussagen über die Richtung von Prozessen und Zustandsänderungen irreversible Prozesse spontan ablaufende Prozesse in nur eine Richtung Umkehrung (ohne Energiezufuhr) nicht möglich Beispiele unelastischer Stoß Lösung eines Salzes in Wasser 2. Hauptsatz der Wärmelehre bei spontan ablaufenden Prozessen nimmt die Entropie des Systems zu Expansion eines Gases Temperaturausgleichvorgänge Entropie als Zustandsgröße dS = δQ T [S]=J/K dS - Änderung der Entropie δQ - zu- oder abgeführte Wärmemenge T - Temperatur, bei der diese Änderung erfolgt Entropie kann auch als Maß für die Anzahl möglicher Mikrozustände eines Makrozustandes definiert werden >> S —> >> Unordnung Entropie = Maß für die Unordnung Entropie und Wahrscheinlichkeit keine Enthalpie Änderung Zeit Diffusion: ! trotzdem freiwillige Reaktion Anzahl möglicher Anordnungen von 8 Teilchen ("Mikrozustände"): 1 8 28 ΔS / Entropie nimmt zu 56 70 Wärmetransportmechanismen man unterscheidet mehrere physikalische Prozesse des Wärmetransports Wärmebilanz in höheren Organismen: konstante Körpertemperatur, in der Regel TK > TUmg d. h. Wärmeerzeugung und -abgabe müssen annähernd gleich sein chemische Reaktionen physikalische Prozesse Wärmeleitung Konvektion Wärmestrahlung Verdunstung Wärmetransportmechanismen man unterscheidet mehrere physikalische Prozesse des Wärmetransports l T1 - T2 A T1 l T2 PQ = - Temperaturgradient ΔQ Δt = λA PQ - Wärmestrom λ - spez. Wärmeleitvermögen T1 - T2 l [ PQ ] = W [ λ ] = W / (m K) Wärme wird infolge von Stoßprozessen zwischen benachbarten Teilchen übertragen Konvektion Wärmetransport erfolgt hierbei durch makroskopische Bewegungen der Stoffe Wärmetransport durch strömende Medien wie Flüssigkeiten und Gase (Wärmeleitung bei Festkörpern) weniger dichte, erhitzte Flüssigkeit steigt auf Gase bzw. Flüssigkeiten werden bewegt: - Pumpen - Druckdifferenzen freie Konvektion erzwungene Konvektion Beispiele: ! - Luftzirkulation in: Räumen (Heizgeräte) Atmosphäre (Klima) - Blutzirkulation Verdunstung dazu wird Energie in Form von Umwandlungswärme benötigt die für die Phasenumwandlung notwendige Wärmemenge wird dem Körper entzogen Wasserdampf H 2O Δm P=r Δt Verdunstung beim Schwitzen: - Wärmetransportmechanismus bei höheren Umgebungstemperaturen - funktioniert nicht bei Wasserdampf gesättigter Luft r - spezifische Verdunstungswärme Δm - verdunstete Wassermenge Δt - Zeit, in der das Wasser verdunstet Wärmestrahlung Energie wird hierbei in Form elektromagnetischer Wellen übertragen zwei thermisch voneinander isolierte Körper Wärmeabgabe bzw. -aufnahme durch elektromagnetische Strahlung sowohl durch Materie als auch durch Vakuum möglich (z. B. Wärmetransport von der Sonne zur Erde) Wärmeabgabe / -strom eines Körpers T1 beide Körper emittieren und absorbieren elektromagnetische Strahlung Stefan-BoltzmannGesetz P = α σ A T4 T2 Wärmeabgabe und -aufnahme A - strahlende Fläche α - Emissionsgrad σ = 5,67 x 10-8 ΔP = α A σ (T4 - Tu4) 0<α<1 W m2 K4 Stefan-Boltzmannideal weiße, Konstante ideal schwarze, stumpfe Oberfläche glänzende Oberfläche Tu - Temp. der Umgebung A - strahlende bzw. absorbierende Fläche sind gleich groß Wärmestrahlung Energie wird hierbei in Form elektromagnetischer Wellen übertragen Intensität Spektralbereich der Wärmestrahlung Emission von Infrarotstrahlung bei ‚normalen Temperaturen‘ Emission von sichtbarem Licht bei deutlich höheren Temperaturen T3 > T2 > T1 glühende Metalle, Glühfaden einer Lampe, Sonnenlicht λmax λ λmax = Wellenlänge mit höchster Strahlenintensität λmax T = const Wien‘sche Verschiebungsgesetz Anwendungen: Thermographie Infrarotkameras Wärmebewegung in Flüssigkeiten und Gasen ändern die Teilchen ständig ihren Ort Alle Teilchen eines Stoffes befinden sich in ständiger Bewegung Flüssigkeiten, Gase: Wechsel in andere Volumenelemente Festkörper: Schwingungen am Ort m 2 v = 2 3 kT 2 3 1 Brownsche Molekularbewegung thermische Bewegung mikroskopisch kleiner Teilchen Kugel mit dem Radius r um ein Teilchen 4 t=0 r 2 nach der Zeit t erreicht das Teilchen die Peripherie der Kugel r2 = 6 D t 1 t 5 5 D= kT 6 πηrT [ D ] = m2/s t ist Mittel aus vielen Experimenten D - Diffusionskonstante Diffusion Diffusionsphänomene resultieren aus der Wärmebewegung der Teilchen Zeit Diffusion - gerichteter Massetransport im Laufe der Zeit resultiert ein vollständiger Konzentrationsausgleich Entropie und Wahrscheinlichkeit keine Enthalpie Änderung Zeit Diffusion: ! trotzdem freiwillige Reaktion Anzahl möglicher Anordnungen von 8 Teilchen ("Mikrozustände"): 1 8 28 ΔS / Entropie nimmt zu 56 70 Diffusionsgesetz es liefert die quantitative Beschreibung für die irreversiblen Diffusionsprozesse c1 A c2 c1 > c 2 Δc Δx J Δx = Dicke Übergangszone J = Δc Konzentrationsgradient Diffusionsstromstärke (Nettostrom durch A) Teilchenstrom von links nach rechts überwiegt Nettomenge der durch A transportierten Teilchen Δn Δt J = - DA Teilchen gelangen in das jeweils andere Kompartement infolge der thermischen Bewegung = c1 - c 2 Δc Δx Diffusionsgesetz 1. Ficksches Gesetz D - Diffusionskonstante / -koeffizient [D] = m2 s–1 Biologische Membranen als Diffusionsbarriere Membranen trennen einzelne Kompartmente (Reaktionsräume) voneinander Δc J = - DA c1 c2 Δx Δx entspricht der Membrandicke d d = 4 nm ... 5 nm d d = 40 Å ... 50 Å beiderseits biologischer Membranen bestehen für viele gelöste Stoffe und Ionen deutliche Konzentrationsunterschiede diese Unterschiede bleiben über lange Zeiträume erhalten (Zu- bzw. Abstrom von Metaboliten, Stoffwechselvorgänge) ⎯⎯→ stationäre Diffusion D Angström 1 Å = 10-10 m Diffusionskonstante für den jeweiligen Stoff in der Membran P= D d J = P A Δc P - Permeabilitätskoeffizient [ P ] = m s-1 Permeabilität durch künstliche Membranen die Diffusion von Stoffen durch Membranen hängt von Eigenschaften dieser Stoffe ab Hydrophobe Moleküle O2, CO2, N2, Benzol H 2O 10-2 P, cm/s 10-4 kleine, ungeladene, polare Moleküle H2O, Harnstoff, Glycerol große, ungeladene, polare Moleküle Glucose, Saccharose Harnstoff, Glycerol Tryptophan Glucose Cl- Ionen H+, Na+, HCO3-, K+, Ca2+, Cl-, Mg2+ K+ Na+ 10-6 10-8 10-10 10-12 10-14 synthetische Lipiddoppelschicht je kleiner ein Molekül ist und je weniger Wasserstoffbrücken es mit Wasser ausbildet, desto schneller diffundiert es durch die Lipiddoppelschicht Transport durch Membranen bestimmte Stoffe benötigen Energie für ihren Transport durch Membranen Passiver Transport entlang Δc Δx keine zusätzliche Energie erforderlich Aktiver Transport entgegen Δc Δx Energiequelle notwendig ATP-ase ATP + H2O ⎯⎯⎯⎯→ ADP + Pi normale Diffusion erleichterte Diffusion spezielle Ionenkanäle spezielle Transportmoleküle Carrier ATP-getriebene Transportmechanismen existieren für H+, Na+ (gekoppelt mit K+), Ca2+, spezielle Transporter eine Substanz wird passiv, eine zweite aktiv transportiert Osmose Membranen sind nur für bestimmte Substanzen permeabel durch eine Trennfläche können nicht alle Komponenten einer Lösung diffundieren kleine Moleküle sind permeabel, große Moleküle nicht semipermeable Membran im Extremfall diffundiert nur das Lösungsmittel, nicht die gelösten Substanzen Pfeffersche Zelle Wilhelm Pfeffer (1845-1920) Zellmembranen sind semipermeabel seit 1887 in Leipzig Pflanzenphysiologe 1877 „Osmotische Untersuchungen“ Pfeffersche Zelle sie dient als Modell für Osmose in Pflanzenzellen Wasser strömt in das kleine Gefäß, Zuckerlösung wird verdünnt Einstellen eines Gleichgewichtes Zuckerlösung h gleiche Wasserströme in beide Richtungen aber: kein Konzentrationsausgleich Lösung im kleinen Gefäß steht unter einem höheren Druck H 2O π = ρgh osmotische Druck semipermeable Membran - durchlässig für H2O - undurchlässig für Zuckermoleküle eine verdünnte Lösung eines Nichtelektrolyten verhält sich wie ein ideales Gas Pfeffersche Zelle er hängt von der Anzahl der dissoziierten Teilchen in Lösung ab π = icRT Formel von van‘t Hoff c - Konzentration des gelösten Stoffes i - Anzahl der Teilchen (Ionen), in die ein Molekül beim Lösen zerfällt Isotone Lösung (Beispiel: Blutzellen) im osmotischen Gleichgewicht mit Zellen des menschlichen Blutes NaCl: 0,9% oder 0,154 mol/l Hypotone Lösung πLösung < πBlut i=1 Glucose, Zuckermoleküle i=2 NaCl, KCl i=3 K2SO4, CaCl2 i=4 FeCl3, K3Fe(CN)6 der osmotische Druck ist eine Funktion der Teilchenzahl Hypertone Lösung πLösung > πBlut Osmose Beispiel: Pflanzenzelle der Protoplast einer Pflanzenzelle ist von einer zusätzlichen, starren Membran (Zellwand aus Zellulose) umgeben kein Platzen in hypotonen Lösungen Zelle ist mehr oder weniger prall gefüllt zusätzliche Druckkomponente in Form eines Stempeldruckes (entspricht der Schweredruckkomponente in der Pfefferschen Zelle) Turgor (Zellwanddruck) wichtig für Stabilität und Steifheit pflanzlicher Gewebe Pflanzen, die Wasser verlieren, werden schlaff und welk