WVV-10 Schuljahr 2012/2013 Lösungen zu Übung 11

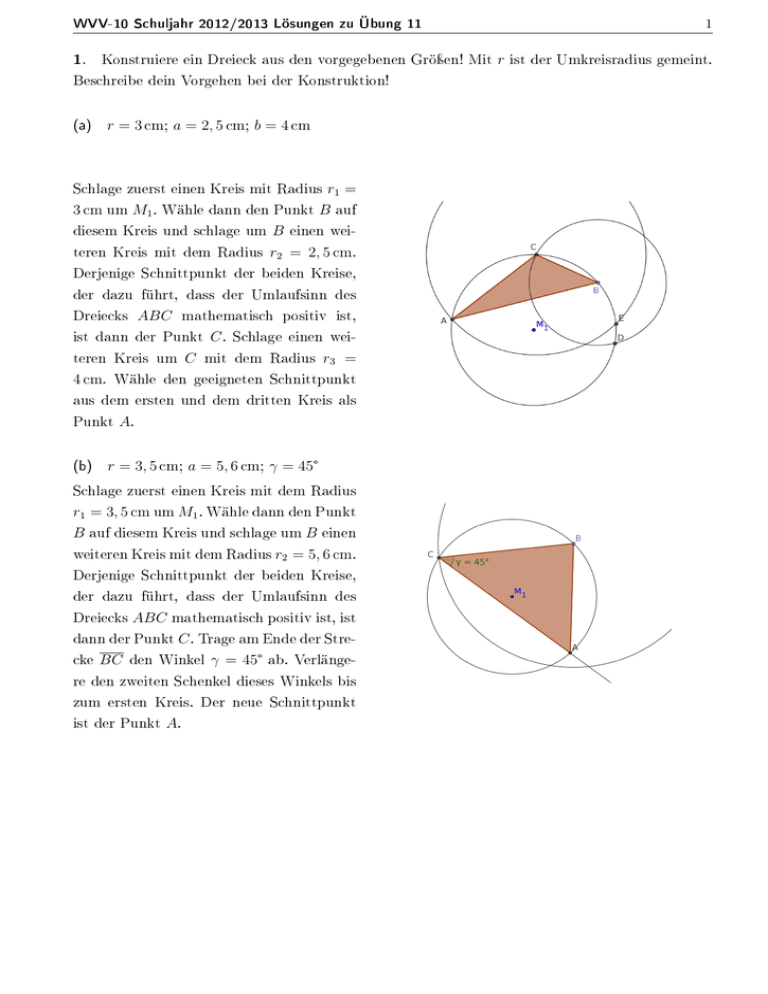
1
WVV-10 Schuljahr 2012/2013 Lösungen zu Übung 11
1.
Konstruiere ein Dreieck aus den vorgegebenen Gröÿen! Mit
Beschreibe dein Vorgehen bei der Konstruktion!
(a)
r = 3 cm; a = 2, 5 cm; b = 4 cm
r1 =
3 cm um M1 . Wähle dann den Punkt B auf
diesem Kreis und schlage um B einen weiteren Kreis mit dem Radius r2 = 2, 5 cm.
Schlage zuerst einen Kreis mit Radius
Derjenige Schnittpunkt der beiden Kreise,
der dazu führt, dass der Umlaufsinn des
ABC
Dreiecks
mathematisch positiv ist,
ist dann der Punkt
teren Kreis um
4 cm.
C
C.
Schlage einen wei-
mit dem Radius
r3 =
Wähle den geeigneten Schnittpunkt
aus dem ersten und dem dritten Kreis als
Punkt
(b)
A.
r = 3, 5 cm; a = 5, 6 cm; γ = 45°
Schlage zuerst einen Kreis mit dem Radius
r1 = 3, 5 cm um M1 . Wähle dann den Punkt
B auf diesem Kreis und schlage um B einen
weiteren Kreis mit dem Radius r2 = 5, 6 cm.
Derjenige Schnittpunkt der beiden Kreise,
der dazu führt, dass der Umlaufsinn des
Dreiecks
ABC
mathematisch positiv ist, ist
C . Trage am Ende der StreWinkel γ = 45° ab. Verlänge-
dann der Punkt
cke
BC
den
re den zweiten Schenkel dieses Winkels bis
zum ersten Kreis. Der neue Schnittpunkt
ist der Punkt
A.
r
ist der Umkreisradius gemeint.
2
WVV-10 Schuljahr 2012/2013 Lösungen zu Übung 11
2.
Zeichne mit Hilfe einer geeigneten Wertetabelle den Graphen der durch
f (x) = 2x
gegebenen Funktion!
Zeichne in das gleiche Koordinatensystem
die Graphen der Funktionen
g , h, i
und
k
−x
g(x) = 2 ,
h(x) = 2x − 1,
i(x) = 0, 5x und
k(x) = 0, 5x−1 !
mit
3.
Bei einem Flugzeug wird die Geschwindigkeit oft als Geschwindigkeit über Grund
vG
angege-
ben.
(a)
Welche andere Geschwindigkeit ist für Flugzeuge wichtig?
Neben der Geschwindigkeit über Grund ist z.B. die wahre Fluggeschwindigkeit, die relativ zur
umgebenden Luftmasse gemessen wird, wichtig.
(b)
Ein Flugzeug iegt mit
unter dem Winkel
α = 10°
vG = 260 km
h
die Landebahn
an. Um wie viele Meter sinkt das Flugzeug
pro Minute?
vs ist
vs = vG · tan (10°) = 260 km
h · tan (10°) ≈
km
1000 m
m
45, 845 h = 45, 845 60 min ≈ 764 min
.
Die Sinkgeschwindigkeit
(c)
In
welcher
horizontalen
Entfernung
200 m beträgt?
≈ 1134 m die horizontale Entfernung, in der das Flugzeug
wird das Flugzeug landen, wenn seine Flughöhe
200 m
Es ist
x
= tan (10°), also x =
200 m
tan(10°)
landet.
(d)
Nach welcher Zeit setzt das Flugzeug unter den Bedingungen von (c) auf dem Boden auf ?
Das Flugzeug setzt nach
t=
1,134 km
260 km
h
≈ 0, 00436 h
auf dem Boden auf. Das sind
15, 7 Sekunden.
3
WVV-10 Schuljahr 2012/2013 Lösungen zu Übung 11
4.
Zeichne in einem gleichseitiges Dreieck (Seitenlänge
(a)
Höhe
beliebig) die Höhenlinie
Stelle eine Formel auf, mit der du die
ha
mit Hilfe der Seitenlänge
nen kannst!
q
ha =
a
a 2
2
a2 −
=
q
3a2
4
a berech-
√
=
3
a
2
(b)
Beweise mit Hilfe der gefundenen Formel die folgenden Gleichungen:
√
√
3
1
cos (30°) = sin (60°) = 12 3; sin
(30
°) = cos (60°) = ; tan (30°) =
; tan (60°)
2
3
√
3
√
a
cos (30°) = sin
(60°) = haa = 2a = 21 3
√
3
√
a
tan (60°) = 2a = 3
2
=
√
3.
ha
ein!