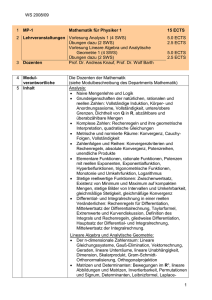
Skript

MA S410 Geometrie und Lineare Algebra
Johanna Schönenberger-Deuel
29. August 2013
Inhaltsverzeichnis
1 Isometrien oder Kongruenzabbildungen
1.1 Einführende Überlegungen . . . . . . . .
1.2 Geradenspiegelung Sg . . . . . . . . . . .
1.3 Isometrien der Ebene . . . . . . . . . . .
1.4 Dreispiegelungssatz . . . . . . . . . . . .
1.5 Die 5 Typen von Isometrien . . . . . . .
1.5.1 Punktspiegelung . . . . . . . . .
1.5.2 Rotation (Drehung) . . . . . . . .
1.5.3 Translation (Parallelverschiebung)
1.5.4 Schubspiegelung (Gleitspiegelung)
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
1
1
3
5
12
15
15
18
20
23
2 Ähnlichkeitsabbildungen
2.1 Dilatationen . . . . . . . . . . . . . . . . . . . .
2.2 Zentrische Streckung . . . . . . . . . . . . . . .
2.3 Harmonische Teilung und Apolloniuskreis . . . .
2.4 Verschiedene Ähnlichkeitsabbildungen . . . . . .
2.4.1 Ähnlichkeitsabbildungen allgemein . . .
2.4.2 Drehstreckungen und Klappstreckungen
2.4.3 Noch zwei Sätze . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
27
28
30
36
40
40
42
44
.
.
.
.
.
.
45
45
50
52
57
58
60
3 Kreisgeometrie
3.1 Kreiswinkelsätze . . . . . .
3.2 Sehnensätze . . . . . . . .
3.3 Satzgruppe des Pythagoras
3.4 Orthogonale Kreise . . . .
3.5 Pol und Polare . . . . . .
3.6 Inversion am Kreis . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
4 Nichteuklidische Geometrien (kurze Einführung)
63
4.1 Euklidische Geometrie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 63
4.2 Modelle nichteuklidischer Geometrien . . . . . . . . . . . . . . . . . . . . . 68
4.2.1 Beispiel einer elliptischen Geometrie . . . . . . . . . . . . . . . . . . 68
i
4.2.2
4.2.3
4.2.4
Kleinsches Modell einer hyperbolischen Geometrie . . . . . . . . . . 69
Poincaré - Modell einer hyperbolischen Geometrie . . . . . . . . . . 71
Künstlerischer Abschluss . . . . . . . . . . . . . . . . . . . . . . . 74
5 Vektorgeometrie
5.1 Einführung . . . . . . . . . . . . . . . . . . . .
5.1.1 Elementare Vektoroperationen . . . . .
5.1.2 Koordinatendarstellung von Vektoren .
5.2 Skalarprodukt zweier Vektoren . . . . . . . . . .
5.2.1 Gesetze des Skalarprodukts . . . . . . .
5.2.2 Berechnung des Skalarprodukts mit Hilfe
5.2.3 Winkel zwischen zwei Vektoren . . . . .
5.3 Parameterdarstellung der Geraden . . . . . . . .
5.4 Parameterdarstellung und Gleichung der Ebene
5.4.1 Parameterdarstellung der Ebene . . . . .
5.4.2 Gleichung der Ebene . . . . . . . . . . .
5.4.3 Abstand eines Punktes von einer Ebene .
5.5 Kugel und Kreis . . . . . . . . . . . . . . . . . .
. .
. .
. .
. .
. .
der
. .
. .
. .
. .
. .
. .
. .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
Koordinaten
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
. . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
77
77
77
80
82
83
84
85
86
88
88
89
90
91
6 Matrizenalgebra
6.1 Matrizen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.2 Rechnen mit Matrizen . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.2.1 Addition von Matrizen und skalare Multiplikation . . . . . . . . .
6.2.2 Multiplikation eines Zeilenvektors mit einem Spaltenvektor: Skalarprodukt . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.2.3 Multiplikation von Matrizen . . . . . . . . . . . . . . . . . . . . .
6.3 Anwendungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.3.1 Beispiel: Gartenbaugeschäft . . . . . . . . . . . . . . . . . . . . .
6.3.2 Stochastische Matrizen . . . . . . . . . . . . . . . . . . . . . . . .
6.3.3 Populationsmatrizen: Bevölkerungsentwicklung . . . . . . . . . . .
6.3.4 Verkehrsfluss . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6.3.5 Inzidenzmatrizen (Graphen als Matrizen) . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
7 Lineare Gleichungssysteme
7.1 Das Gauss’sche Eliminationsverfahren . . . . . . . . . .
7.2 Homogene und inhomogene Gleichungssysteme . . . . .
7.3 Rang einer Matrix, Lösbarkeit von Gleichungssystemen
7.4 Inverse Matrix . . . . . . . . . . . . . . . . . . . . . . .
107
. 107
. 110
. 114
. 116
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
93
. 93
. 96
. 96
97
98
100
100
102
103
104
105
8 Lineare Abbildungen
117
8.1 Lineare Abbildungen im R2 . . . . . . . . . . . . . . . . . . . . . . . . . . 117
8.2 Wichtige Eigenschaften linearer Abbildungen . . . . . . . . . . . . . . . . . 119
8.3 Spezielle lineare Abbildungen . . . . . . . . . . . . . . . . . . . . . . . . . 122
8.3.1 Streckungen . . . . . . . . . . . . . . .
8.3.2 Spiegelungen . . . . . . . . . . . . . .
8.3.3 Rotationsmatrizen in der xy-Ebene . .
8.4 Scherung in x -Richtung in der xy-Ebene . . .
8.5 Zusammensetzung von linearen Abbildungen .
8.6 Rotationsmatrizen im Raum (Computergrafik)
8.7 Kern und Bild einer Abbildung . . . . . . . .
8.8 Fixe Richtungen bei linearen Abbildungen . .
8.9 Eigenwerte und Eigenvektoren . . . . . . . . .
8.10 Spezielle Fälle . . . . . . . . . . . . . . . . . .
8.11 Markov Prozesse (stochastische Matrizen) . .
8.12 Googles PageRank-Algorithmus . . . . . . . .
9 Graphen und Algorithmen
9.1 Einführung . . . . . . . . . .
9.2 Grundbegriffe . . . . . . . . .
9.3 Über Grade von Ecken . . . .
9.4 Bäume . . . . . . . . . . . . .
9.5 Minimal aufspannende Bäume
9.6 Kürzeste Wege in Graphen . .
9.7 Eulersche Graphen . . . . . .
9.8 Hamiltonsche Graphen . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . . . . . . . . . .
. . . . . . . . . . .
. . . . . . . . . . .
. . . . . . . . . . .
(Minimal Spanning
. . . . . . . . . . .
. . . . . . . . . . .
. . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
. . . .
. . . .
. . . .
. . . .
Tree)
. . . .
. . . .
. . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
122
123
124
125
126
127
129
130
131
132
134
136
.
.
.
.
.
.
.
.
139
. 139
. 144
. 147
. 151
. 154
. 157
. 160
. 164
Kapitel 1
Isometrien oder Kongruenzabbildungen
1.1
Einführende Überlegungen
Kongruente Figuren sind deckungsgleiche Figuren.
Eine Figur A wird so bewegt, dass sie mit einer anderen Figur B zur Deckung gebracht
werden kann. Auf diese Weise wird der Kongruenzbegriff auf spezielle geometrische Abbildungen zurückgeführt, die Kongruenzabbildungen oder Isometrien, die man auch Bewegungen nennt.
Eine Isometrie ist somit eine Abbildung, die eine geometrische Figur nur verlagert, ihre
Grösse und Form aber unverändert lässt. Allgemein interessiert man sich für das Verhalten
geometrischer Figuren bei gewissen bijektiven Abbildungen.
Definition 1.1.1.
1. Eine Abbildung φ der Ebene auf sich heisst bijektiv, falls φ umkehrbar ist; d.h. es
gibt nicht nur für jeden Punkt X genau einen Bildpunkt Y sondern umgekehrt gibt
es für jeden Punkt Y genau einen Punkt X, sodass gilt:
1
UZH
MA S410
Geometrie und Lineare Algebra
φ(X) = Y.
2. Die Abbildung, die jedem Bildpunkt Y sein Urbild X zuordnet, heisst zu φ inverse
Abbildung und wird mit φ−1 bezeichnet.
φ−1 (Y ) = X.
.
3. Die Abbildung, die jeden Punkt X auf sich selbst abbildet, nennt man die identische Abbildung oder Identität.
id(X) = X
4. Verknüpfung von Abbildungen
Sind φ1 und φ2 Abbildungen, so nennt man φ2 ◦ φ1 die Verknüpfung (Hintereinanderschachtelung, Produkt) von φ1 und φ2 . (sprich: φ2 nach φ1 , φ2 Ring φ1 ) φ2 ◦ φ1
bildet jeden Punkt X ab auf φ2 [φ1 (X)] = Z
(φ2 ◦ φ1 )(X) = φ2 [φ1 (X)] = φ2 (Y ) = Z
Die Verknüpfung von Abbildungen ist assoziativ.
φ3 ◦ (φ2 ◦ φ1 ) = (φ3 ◦ φ2 ) ◦ φ1
=⇒ Die Verknüpfun von bijektiven Abbildungen ist wieder bijektiv.
5. Eine Isometrie oder Kongruenzabbildung φ der Ebene (oder des Raumes) auf
sich ist eine bijektive, längentreue Abbildung. Das heisst:
Für zwei Punkte A und B und ihre Bildpunkte A0 = φ(A) und B 0 = φ(B) sind die
Strecken AB und A0 B 0 gleich lang:
Bezeichnung: Die Länge der Strecke AB bezeichnen wir mit |AB|.
=⇒ Isometrien sind geradentreue Abbildungen, sie bilden Geraden auf Geraden
ab.
=⇒ Die Verknüpfung von Isometrien ist wieder eine Isometrie.
2
UZH
MA S410
1.2
Geometrie und Lineare Algebra
Geradenspiegelung Sg
Die gesamte Abbildungsgeometrie wird auf den Geradenspiegelungen aufgebaut. Deswegen untersuchen wir zuerst diese Abbildung. Sie ist Ihnen von der Schule her sehr bekannt.
Die wichtigsten Eigenschaften der Geradenspiegelung Sg
1. Zu zwei Punkten P und Q gibt es genau eine Geradenspiegelung, die P auf Q
abbildet. Die Spiegelungsachse ist die Mittelsenkrechte von P Q.
2. Die Geradenspiegelung ist eine involutorische Abbildung, d.h. sie ist zu sich selbst
invers.
Sg ◦ Sg = id
3. Jeder Punkt von g ist Fixpunkt.
Für P ∈ g gilt: Sg (P ) = P
Die Gerade g heisst Fixpunktgerade.
4. Jede zu g senkrechte Gerade ist Fixgerade.
Für P ∈
/ g liegt der Bildpunkt P 0 auf der anderen Seite von g. Die Verbindungsgerade
P P 0 steht senkrecht zu g, ist also Fixgerade.
5. Eine geschlossene Figur und ihr Bild haben entgegengesetzten Umlaufsinn.
3
UZH
MA S410
Geometrie und Lineare Algebra
1. Beispiel
Gegeben sind eine Gerade g und zwei Punkte A und B auf derselben Seite von g. Gesucht
ist der kürzeste Weg vom Punkt A nach B via die Gerade g.
2. Beispiel
Gegeben sind eine Gerade g und zwei Kreise k1 und k2 . Konstruieren Sie Quadrate, die
zwei gegenüberliegende Ecken auf g haben und von denen je eine Ecke auf k1 und k2
liegen.
4
UZH
MA S410
1.3
Geometrie und Lineare Algebra
Isometrien der Ebene
Wir suchen alle Isometrien der Ebene auf sich und wollen die Strukturen dieser Isometrien untersuchen.
Aus ihrem Unterricht in der Sekundarschule oder im Gymnasium kennen Sie die folgenden
Isometrien:
• Geradenspiegelung
• Punktspiegelung
• Rotation (Drehung)
• Translation (Verschiebung)
• Schubspiegelung (vielleicht bekannt!)
Die Frage lautet: Sind das nun wirklich alle Isometrien der Ebene auf sich?
Als erstes suchen wir alle Isometrien, die einen Punkt festlassen, also einen Fixpunkt
besitzen.
Definition 1.3.1. Ein Punkt P heisst Fixpunkt der Abbildung φ , wenn gilt:
φ(P ) = P.
Satz 1.3.2. Isometrien der Ebene mit mindestens einem Fixpunkt
Ist φ eine Isometrie der Ebene und F ein Fixpunkt von φ:
φ(F ) = F.
Dann gilt:
• Entweder ist φ eine Rotation um F um einen Winkel α mit 0 < α < 360◦
• oder φ ist eine Spiegelung an einer Geraden durch F
• oder φ = id.
5
UZH
MA S410
Geometrie und Lineare Algebra
Beweis
Der Beweis ist nur so präzis, wie die Begriffe definiert sind (Ebene, Raum, Geradenspiegelung, Drehung, ...). Wir gehen nicht auf das Axiomensystem ein. (Das Axiomensystem
studieren wir später!)
Voraussetzung: φ ist eine Isometrie mit einem Fixpunkt F : φ(F ) = F .
1. Fall: φ besitzt zwei Fixpunkte F 6= G
φ(F ) = F und φ(G) = G.
Wir zeigen, dass φ dann entweder die Identität oder eine Geradenspiegelung ist.
Alle Punkte Z auf der Geraden g durch die beiden Fixpunkte F, G sind Fixpunkte, da
gilt:
|F Z| = |F φ(Z)| und |GZ| = |Gφ(Z)|, also φ(Z) = Z
Ein Punkt Y ∈
/ g wird mit der Isometrie φ entweder auf sich selbst oder auf den an g
gespiegelten Punkt Y abgebildet.
i) Sei φ(Y ) = Y .
Dann besitzt φ 3 nicht kollineare Fixpunkte F, G, Y . Ein anderer Punkt A ∈
/ g wird
mit der Isometrie φ auch entweder auf sich selbst oder auf den an g gespiegelten
Punkt A abgebildet.
Nehmen wir nun an, dass φ(A) = A0 , dann ist die Längentreue von φ nicht erfüllt:
Somit gilt f§r alle Punkte P : φ(P ) = P und φ= Identität.
ii) Sei φ(Y ) = Y 0 = Sg (Y ).
Dann gilt für alle Punkte P : φ(P ) = Sg (P ) = P 0 und φ = Sg
6
UZH
MA S410
Geometrie und Lineare Algebra
2. Fall: φ hat genau einen Fixpunkt F
Hier zeigen wir, dass φ eine Rotation ist.
Für alle Punkte X 6= F gilt: φ(X) 6= X.
Wir wählen einen Punkt P . Sein Bildpunkt sei P 0 = φ(P ). Da |F P | = |F P 0 | , liegen
die beiden Punkte auf einem Kreis k mit Mittelpunkt F . Wir betrachten die Rotation
um F um den Winkel α = ^(P F P 0 ) und bezeichnen diese mit RF,α . Diese Rotation ist
bestimmt durch den gegebenen Punkt P und sein Bild P .
Zu zeigen bleibt: φ = RF,α .
Die Abbildung ψ = RF,−α ◦ φ besitzt 2 Fixpunkte F und P . Also gilt Fall 1:
Entweder ψ = RF,−α ◦ φ = id und damit φ = RF,α
oder ψ = RF,−α ◦ φ = Sg , also φ = RF,α ◦ Sg . Dies führt zu einem Widerspruch:
Wir wählen den Punkt Q zwischen P und P , so dass ^(P F P 0 ) = α2 . Damit gilt:
φ(Q) = RF,α ◦ Sg (Q) = RF,α (Q0 ) = Q .
Q ist ein weiterer Fixpunkt im Widerspruch zur Annahme.
Also ist φ eine Rotation.
Damit ist der Satz bewiesen. Er gibt einen Überblick über alle Isometrien der Ebene mit
mindestens einem Fixpunkt.
7
UZH
MA S410
Geometrie und Lineare Algebra
Wie erhält man nun alle Isometrien der Ebene, auch z. B. die Translationen? Dazu beweisen wir den folgenden Satz.
Satz 1.3.3. Alle Isometrien der Ebene
Jede Isometrie der Ebene ist eine Verknüpfung einer Translation und einer Isometrie mit
Fixpunkt.
φ ∈ Iso ⇐⇒ φ = T~v ◦ ψ, wobei ψ eine Isometrie mit Fixpunkt
Beweis
i) Schluss von links nach rechts:
φ ∈ Iso
⇒
φ = T~v ◦ ψ, wobei ψ eine Isometrie mit Fixpunkt
Wir wählen einen Punkt P . Sein Bildpunkt sei P 0 = φ(P ). Wir betrachten den Vek−−→
tor ~v = P P 0 . Dieser Vektor definiert eine Translation um ~v : T~v . Diese Translation
ist abhängig vom gewählten Punkt P !
Die Translation in umgekehrter Richtung um −~v wird mit T−~v bezeichnet.
Es sind nun 2 Fälle möglich:
Ist P = P 0 , so ist ~v = ~0. Also ist φ eine Isometrie mit Fixpunkt.
Ist P 6= P 0 , dann betrachten wir die Abbildung ψ = T−~v ◦ φ.
Da ψ(P ) = P , ist ψ eine Rotation oder eine Geradenspiegelung oder die Identität
und φ = T~v ◦ ψ .
ii) umgekehrt: Da T~v und ψ Isometrien sind, ist auch φ = t~v ◦ ψ eine Isometrie.
Damit ist der Satz bewiesen und wir haben im Prinzip alle Isometrien gefunden. Die reine
Translation ist die Verknüpfung der Translation mit der Identität; die Schubspiegelung
die Verknüpfung einer Geradenspiegelung mit einer Translation (später).
Sind 2 Punkte und ihre Bilder bekannt, so beweisen wir nun, dass es genau zwei zugehörige
Isometrien gibt.
Satz 1.3.4.
Sind vier Punkte A, B, A0 , B 0 gegeben mit A 6= B und |AB| = |A0 B 0 | , so gibt es genau
2 Isometrien φ1 und φ2 , die A auf A0 und B auf B 0 abbilden und die sich nur durch eine
Spiegelung an der Geraden g = (A0 B 0 ) unterscheiden.
8
UZH
MA S410
Geometrie und Lineare Algebra
φ1 oder φ2 = Sg ◦ φ1
Beweis
Sind A 6= B, φ(A) = A0 , φ(B) = B 0 , |AB| = |A0 B 0 | und g die Gerade durch A und B,
dann geht der Beweis in zwei Schritten.
i) Es gibt mindestens 2 Isometrien:
a) Sind A = A0 , B = B 0 , dann gibt es 2 Fixpunkte, also gilt:
entweder φ = φ1 = id
oder
φ = φ2 = Sg
b) Sind A = A0 , B 6= B 0 und m = Mittelsenkrechte auf BB 0 , dann gilt:
entweder φ = φ1 = Sm
oder
φ = φ2 = Sg ◦ Sm
c) Sind A 6= A0 , B 6= B 0 und m1 = Mittelsenkrechte auf AA0 und sind B1 =
Sm1 (B), A0 = Sm1 (A) und m2 = Mittelsenkrechte auf B1 B 0 , dann sind 2 Fälle
möglich.
c1 ) Ist B1 = B 0 , dann gilt:
entweder φ = φ1 = Sm1
oder
φ = φ2 = Sg ◦ Sm1
c2 ) Ist B1 6= B 0 , dann gilt:
entweder φ = φ1 = Sm2 ◦ Sm1
oder
φ = φ2 = Sg ◦ Sm2 ◦ Sm1
9
UZH
MA S410
Geometrie und Lineare Algebra
Zwischenresultat:
Jede Isometrie ist mit 1 oder 2 oder 3 Geradenspiegelungen darstellbar.
ii) Es gibt höchstens 2 Isometrien: Ist C ein zu A und B nicht kollinearer Punkt,
so gibt es höchstens 2 Möglichkeiten für den Bildpunkt C 0 : C10 oder C20 .
Also gilt: Mit 3 Punkten und ihren Bildpunkten ist die Isometrie eindeutig
bestimmt.
Satz 1.3.5.
a) Eine Isometrie der Ebene auf sich ist eindeutig festgelegt durch die Bilder dreier
nicht kollinearer Punkte.
b) Eine Isometrie der Ebene auf sich mit drei nicht kollinearen Fixpunkten ist die
Identität.
Satz 1.3.6.
a) Jede Isometrie der Ebene auf sich ist darstellbar als Verknüpfung von höchstens 3
Geradenspiegelungen.
b) Jede Verknüpfung von endlich vielen Geradenspiegelungen ist eine Isometrie.
10
UZH
MA S410
Geometrie und Lineare Algebra
c) Jede Verknüpfung von beliebig vielen Geradenspiegelungen lässt sich darstellen mit
höchstens 3 Geradenspiegelungen.
Bemerkungen
Grundsätzlich unterscheidet sich eine Geradenspiegelung von der Verknüpfung zweier
Spiegelungen schon wegen der Fixpunkteigenschaften.
• Bei der Spiegelung an einer Geraden g sind alle Punkte auf g Fixpunkte, und es
gibt keine weiteren Fixpunkte.
• Bei der Verknüpfung von zwei Spiegelungen muss die Lage der beiden Geraden
beachtet werden!
• Bei der Verknüpfung von Abbildungen ist die Reihenfolge zu beachten!
Wie können die bekannten 5 Isometrien durch Geradenspiegelungen dargestellt werden?
Dazu ist der im nächsten Abschnitt behandelte Satz, der so genannte Dreispiegelungssatz sehr nützlich. Nachher wird es ein Leichtes sein, die bekannten Isometrien durch die
Verknüpfung von höchstens 3 Geradenspiegelungen darzustellen.
11
UZH
MA S410
1.4
Geometrie und Lineare Algebra
Dreispiegelungssatz
Wir wissen nun, dass sich jede Isometrie der Ebene auf sich als Verknüpfung von höchstens
drei Geradenspiegelungen darstellen lässt. Damit können wir einen Überblick über alle
Isometrien der Ebene gewinnen. Die Anzahl und die Lage der Spiegelungsachsen wird
wesentlich sein.
Satz 1.4.1. Dreispiegelungssatz
Die Verknüpfung dreier Geradenspiegelungen, wobei die drei Geraden entweder parallel oder kopunktal (genau einen Schnittpunkt) sind, ist darstellbar durch eine Geradenspiegelung.
Sind die 3 Geraden g, h, k entweder parallel (g||h||k) oder kopunktal (g ∩ h ∩ k = {A}),
dann gibt es eine Gerade m, so dass gilt:
Sk ◦ Sh ◦ Sg = Sm
Für die genaue Lage der Geraden m gilt:
a) Ist g ∩ h ∩ k = {A}, so ist der Winkel zwischen g und h gleich dem Winkel zwischen
m und k.
12
UZH
MA S410
Geometrie und Lineare Algebra
b) Ist g||h||k, dann ist der gerichtete Abstand von g zu h gleich dem gerichteten Abstand von m zu k
Bemerkung 1.4.2. Statt der obigen Gleichung
Sk ◦ Sh ◦ Sg = Sm
kann man auch durch Verknüpfung von links mit Sk (rsp von rechts mit Sg ) die oft
nützlichen äquivalenten Darstellungen erhalten.
Sh ◦ Sg = Sk ◦ Sm
oder
Sk ◦ Sh = Sm ◦ Sg
Jetzt gibt es auf jeder Seite der Gleichung 2 Geradenspiegelungen. Man kann also statt
an h und k auch an g und m spiegeln.
Damit kann man eine Verknüpfung von zwei Geradenspiegelungen ersetzen durch eine
andere Verknüpfung mit den entsprechenden Bedingungen.
Satz 1.4.3.
Eine Verknüpfung von vier Geradenspiegelungen ist stets darstellbar als Verknüpfung
von genau zwei Geradenspiegelungen.
Also ist jede Verknüpfung einer geraden Anzahl Geradenspiegelungen mit Hilfe von
genau zwei Geradenspiegelungen darstellbar.
Bemerkung 1.4.4.
1. Eine Verknüpfung von 3 Geradenspiegelungen kann aber nie durch zwei Geradenspiegelungen dargestellt werden.
13
UZH
MA S410
Geometrie und Lineare Algebra
2. Die Isometrien der Ebene lassen sich in 2 Klassen einteilen:
(a) ungleichsinnige Isometrien: Verknüpfung einer ungeraden Anzahl Geradenspiegelungen (Umwendungen)
(b) gleichsinnige Isometrien: Verknüpfung einer geraden Anzahl Geradenspiegelungen (echte Bewegungen)
3. Lage der Spiegelungsachsen
(a) Bei den gleichsinnigen Isometrien können die beiden Spiegelachsen parallel sein
oder sich schneiden, speziell können sie senkrecht aufeinander stehen.
(b) Die ungleichsinnige Isometrien können als eine oder als 3 Geradenspiegelungen
dargestellt werden.
14
UZH
MA S410
1.5
Geometrie und Lineare Algebra
Die 5 Typen von Isometrien
• Geradenspiegelung: Diese Abbildung haben wir schon untersucht.
• Punktspiegelung: Die beiden Spiegelungsachsen schneiden sich senkrecht.
• Rotation (Drehung): Die beiden Spiegelungsachsen schneiden sich unter einem
beliebigen Winkel.
• Translation (Parallelverschiebung): Die beiden Spiegelungsachsen sind parallel.
• Schubspiegelung (Gleitspiegelung): Verschiebung und Spiegelung erhält man
genau dann, wenn drei Geradenspiegelungen nicht durch eine ersetzt werden können.
Wir werden jetzt die einzelnen Abbildungen in obiger Reihenfolge behandeln. Dies führt zu
relativ einfachen Beweisen und zu wichtigen Sätzen der Elementargeometrie. Der Dreispiegelungssatz, der 3 Geradenspiegelungen durch eine ersetzt, ist ein wichtiges Beweismittel.
Die Lage der Spiegelungsachsen kann dadurch transformiert werden.
1.5.1
Punktspiegelung
Definition 1.5.1.
Eine Abbildung SM der Ebene auf sich heisst Punktspiegelung, wenn sie genau einen
15
UZH
MA S410
Geometrie und Lineare Algebra
Fixpunkt M besitzt und jedem Punkt P den Bildpunkt P 0 so zuordnet, dass die Strecke
|P P 0 | durch M halbiert wird. M heisst das Zentrum der Punktspiegelung.
Satz 1.5.2. Geradenspiegelung und Punktspiegelung
Stehen die beiden Geraden g und h senkrecht aufeinander mit Schnittpunkt M , so
Sh ◦ Sg = SM
Umgekehrt ist jede Punktspiegelung darstellbar als Verknüpfung zweier Geradenspiegelungen an zueinander senkrechten Achsen.
Satz 1.5.3.
In einem Spiegelungsprodukt Sh ◦ Sg sind die beiden Achsen genau dann vertauschbar,
wenn g = h oder g⊥h.
Sh ◦ Sg = Sg ◦ Sh ⇐⇒ g = h oder g⊥h
Die wichtigsten Eigenschaften der Punktspiegelung SM
1. Zu zwei Punkten P und Q gibt es genau eine Punktspiegelung, die P auf Q abbildet.
2. Die Punktspiegelung ist eine involutorische Abbildung, d.h. SM ◦ SM = id.
3. Jede Gerade durch das Zentrum M ist Fixgerade. Eine beliebige Gerade g wird auf
eine zu g parallele Gerade g 0 abgebildet.
4. Die Punktspiegelung als Produkt zweier Geradenspiegelungen ist eine gleichsinnige
Isometrie.
5. Bei einer Punktspiegelung sind eine Gerade und ihr Bild entgegengesetzt orientiert.
16
UZH
MA S410
Geometrie und Lineare Algebra
Aus diesen Eigenschaften lassen sich nun Aussagen über das Parallelogramm folgern.
Definition 1.5.4.
Ein Viereck, dessen Gegenseiten auf paarweise parallelen Geraden liegen, heisst Parallelogramm.
Satz 1.5.5.
Ein Parallelogramm ist punktsymmetrisch in Bezug auf den Diagonalenschnittpunkt M
als Mittelpunkt, d.h. mit der Punktspiegelung SM wird das Parallelogramm auf sich selbst
abgebildet.
Daraus folgen direkt die Eigenschaften herleiten:
1. Die gegenüberliegenden Seiten sind gleich lang.
2. Die Diagonalen halbieren sich.
3. Die gegenüberliegenden Winkel sind gleich gross.
Beispiel 1.5.6. Es sind 3 Punkte M , P und Q gegeben. Konstruieren Sie ein Quadrat
mit dem Mittelpunkt M , von dem 2 gegenüberliegenden Seiten oder deren Verlängerungen
durch P und Q gehen.
17
UZH
MA S410
1.5.2
Geometrie und Lineare Algebra
Rotation (Drehung)
Definition 1.5.7.
Eine Abbildung RM,α der Ebene auf sich heisst Rotation (Drehung), wenn sie einen
Fixpunkt M besitzt und wenn für jeden von M verschiedenen Punkt P und sein Bild P 0
gilt:
|M P | = |M P 0 | ^(P M P 0 ) = α
Spezielfälle:
α = 0◦ , dann ist RM,0◦ = id.
α = 180◦ , dann ist RM,180◦ = SM (Punktspiegelung).
Satz 1.5.8. Rotation und Geradenspiegelung
a) Die Verknüpfung zweier Geradenspiegelungen, deren Achsen g und h sich in einem
Punkt M schneiden, ist eine Drehung um M , deren Drehwinkel gleich dem doppelten
Schnittwinkel der beiden Achsen ist.
Ist g ∩ h = {M } und ^(g, h) = β, dann gilt: Sh ◦ Sg = RM,2β
b) Umgekehrt ist jede Drehung darstellbar als Verknüpfung zweier Geradenspiegelungen, deren Achsen sich im Drehpunkt unter dem halben Drehwinkel als Schnittwinkel
schneiden.
Die wichtigsten Eigenschaften der Rotation RM,α
1. Jede Rotation ist eine Isometrie (geradentreu, längentreu, winkeltreu).
2. Jede Rotation mit Drehwinkel α 6= 0 besitzt genau einen Fixpunkt.
18
UZH
MA S410
Geometrie und Lineare Algebra
3. Eine Rotation mit α 6= 0, 180◦ besitzt keine Fixgeraden.
4. Die zur Rotation RM,α inverse Abbildung ist wieder eine Rotation um M aber
um den Winkel −α.
(RM,α )−1 = RM,−α
Beispiel 1.5.9. Gegeben sind ein Punkt A sowie zwei Geraden b und d. Konstruieren Sie
ein Quadrat ABCD, dessen Ecken B auf b und D auf d liegen.
19
UZH
MA S410
1.5.3
Geometrie und Lineare Algebra
Translation (Parallelverschiebung)
Definition 1.5.10.
Eine Abbildung der Ebene auf sich heisst Translation (Parallelverschiebung) um den
Vektor ~v , wenn für alle Punkte P der Ebene und ihre Bildpunkte P 0 gilt:
−−→0
P P = ~v
Die Translation um ~v wird mit T~v bezeichnet.
Spezielfall: T~0 = id.
Satz 1.5.11.
Zu zwei Punkten A und B gibt es genau eine Translation T~v , die A auf B abbildet, ; sie
−→
ist gegeben durch den Vektor ~v = AB.
Satz 1.5.12. Translation und Geradenspiegelung
a) Die Verknüpfung zweier Geradenspiegelungen an parallelen Geraden g und h ist eine
Translation um den doppelten Abstandsvektor von g und h.
~ h) der Abstandsvektor von g und h, dann gilt: Sh ◦ Sg = T ~
Ist g| |h und d~ = d(g,
2d
b) Umgekehrt ist jede Translation um einen Vektor ~v darstellbar als eine Verknüpfung
zweier Geradenspiegelungen, deren Achsen parallel sind und deren Abstandsvektor
1
~v beträgt.
2
Die wichtigsten Eigenschaften der Translation T~v
1. Jede Translation ist eine Isometrie (geradentreu, längentreu, winkeltreu).
20
UZH
MA S410
Geometrie und Lineare Algebra
2. Eine Translation, die nicht die Identität ist, besitzt keinen Fixpunkt
3. Bei einer Translation werden Geraden auf parallele Geraden abgebildet.
4. Geraden, deren Richtung parallel zum Translationsvektor verlaufen, sind Fixgeraden.
5. Die zur Translation T~v inverse Abbildung ist wieder eine Translation, aber um den
Vektor −~v .
(T~v )−1 = T−~v
Satz 1.5.13.
Eine bijektive Abbildung der Ebene auf sich, die jede Gerade auf eine parallele Gerade
abbildet und die keinen Fixpunkt besitzt, ist eine Translation.
φ : g → g 0 || g ohne Fixpunkt =⇒ φ = Translation
Satz 1.5.14. Translation und Punktspiegelung
a) Die Verknüpfung zweier Punktspiegelungen ist eine Translation.
−−→
SN ◦ SM = T~v , mit ~v = 2M N
b) Jede Translation um einen Vektor ~v ist darstellbar als die Verknüpfung zweier Punktspiegelungen SN ◦ SM , wobei für die Zentren M und N gilt:
−−→ 1
M N = ~v
2
Anwendung: Mittelparallele im Dreieck
−→ 1 −→
P Q = AB
2
−
→ = T−→
SQ ◦ SP = T2−
PQ
AB
21
UZH
MA S410
Geometrie und Lineare Algebra
Satz 1.5.15.
Die Verknüpfung von zwei Translationen ist wieder eine Translation und zwar um den
Summenvektor.
Tw~ ◦ T~v = T~v ◦ Tw~ = T~v+w~
Beispiel 1.5.16.
1. Gegeben sind zwei Kreise k1 und k2 , sowie eine Gerade g. Bestimmen Sie je einen
Punkt A auf k1 und B auf k2 mit Abstand d, sodass die Verbindungsgerade (AB)||g.
2. Bestimmen Sie die Lage der 5 Punkte A, B, C, D, E, wenn folgendes gilt:
SE ◦ SD ◦ SC ◦ SB ◦ SA = SC .
22
UZH
MA S410
1.5.4
Geometrie und Lineare Algebra
Schubspiegelung (Gleitspiegelung)
Definition 1.5.17.
Eine Abbildung der Ebene auf sich heisst Schubspiegelung (Gleitspiegelung) genau
dann, wenn sie aus einer Spiegelung an einer Geraden r und einer Translation um einen
Vektor ~v zusammengesetzt wird, wobei ~v ||r.
Die Gerade r heisst Schubspiegelachse.
Bezeichnung: Sr,~v .
Sr,~v = Sr ◦ T~v = T~v ◦ Sr
Die Schubspiegelung Sr,~v kann dann folgendermassen darstellbar:
Sr,~v = Sr ◦ Sq ◦ Sp , wobei r||~v und p||q⊥r
Spezielfälle:
1. Eine reine Geradenspiegelung ist auch eine Schubspiegelung mit ~v = ~0.
2. Eine Geradenspiegelung nennt man auch uneigentliche Schubspiegelung.
Ist ~v 6= ~0, so spricht man von einer eigentlichen Schubspiegelung.
Damit ist jede ungleichsinnige Isometrie eine Schubspiegelung.
23
UZH
MA S410
Geometrie und Lineare Algebra
Das ist die letzte zu untersuchende Isometrie. Es müssen nur noch die Produkte von drei
Geradenspiegelungen untersucht werden. Schneiden sich die drei Geraden in einem Punkt
oder sind sie alle drei parallel, so kann das Produkt als eine einzige Geradenspiegelung
dargestellt werden. (Dreispiegelungssatz)
Satz 1.5.18.
Ein Produkt aus drei Geradenspiegelungen Sk ◦ Sh ◦ Sg , das nicht durch eine einzige
Geradenspiegelung ersetzt werden kann, ist eine Schubspiegelung Sr,~v .
Die Schubspiegelung ist dann darstellbar als Produkt von drei Geradenspiegelungen, wobei
eine Gerade r zu zwei parallelen Geraden p und q senkrecht steht.
Sk ◦ Sh ◦ Sg = Sr,~v = Sr ◦ Sq ◦ Sp
Zum Beweis untersuchen wir nun das Produkt von drei Spiegelungen an Geraden mit
mehr als einem Schnittpunkt für den Fall, dass g ∩ h = {A} und ^(g, h) = α2 , aber
h ∩ k 6= {A}.
Zuerst transformieren wir das Produkt Sh ◦ Sg mit dem Dreispiegelungssatz zu Sh0 ◦ Sg0 ,
wobei die Gerade h0 durch A senkrecht zu k gewählt wird:
Sk ◦ Sh ◦ Sg = Sk ◦ Sh0 ◦ Sg0
Es ist Sk ◦ Sh0 = SM mit {M } = k ∩ h0 , also
Sk ◦ Sh ◦ Sg = Sk ◦ Sh0 ◦ Sg0 = SM ◦ Sg0
Nochmalige Anwendung des Dreispiegelungssatzes mit h∗ ||g 0 und k ∗ ⊥h∗ ergibt
Sk ◦ Sh ◦ Sg = Sk ◦ Sh0 ◦ Sg0 = SM ◦ Sg0 = Sk∗ ◦ Sh∗ ◦ Sg0
24
UZH
MA S410
Geometrie und Lineare Algebra
~ 0 , h∗ ).
Die Spiegelachse ist also k ∗ und der Translationsvektor ~v = 2d(g
Sk ◦ Sh ◦ Sg = Sk∗ ◦ Sh∗ ◦ Sg0 = Sk∗ ,~v
Die wichtigsten Eigenschaften der Schubspiegelung Sr,~v
1. Jede Schubspiegelung ist eine Isometrie (geradentreu, längentreu, winkeltreu).
2. Eine eigentliche Schubspiegelung besitzt keinen Fixpunkt.
3. Die Schubspiegelachse ist die einzige Fixgerade.
4. Achsenparallele Geraden werden auf gleichorientierte parallele Geraden abgebildet.
5. Zur Achse senkrechte Geraden werden um ~v verschoben und entgegengesetzt orientiert.
6. Bei Sr,~v sind die Spiegelung an r und die Translation um ~v vertauschbar.
7. Liegt der Punkt P nicht auf der Spiegelachse und ist P 0 sein Bild bei der Schubspiegelung, so wird die Strecke P P 0 von der Spiegelachse halbiert.
8. Die zur Schubspiegelung Sr,~v inverse Abbildung ist
(Sr,~v )−1 = Sr,−~v = Sr ◦ T−~v .
Beispiel 1.5.19.
1. Gegeben sind die beiden kongruenten Strecken AB und A0 B 0 . Konstruieren Sie die
Achse g und den Translationsvektor ~v der Schubspiegelung, die A in A0 und B in
B 0 überführt.
2. Was für eine Schubspiegelung ist φ = Sr ◦ Sq ◦ Sp , wenn p, q, r ein gleichseitiges
Dreieck bilden?
3. Bestimmen Sie mit Achsentransformationen die Isometrie φ = Sh,~b ◦ Sg,~a , wenn g||h,
d(g, h) = 4 cm, |~a| = 4 cm, |~b| = 5 cm. Um welche einfache Isometrie handelt es
sich?
25
UZH
MA S410
Geometrie und Lineare Algebra
26
Kapitel 2
Ähnlichkeitsabbildungen
Die Isometrien sind bijektive Abbildungen, die längentreu, geradentreu und winkeltreu
sind. Kongruente Figuren sind deckungsgleiche Figuren (F ∼
= F 0 ).
Verzichtet man auf die Längentreue erhält man die Ähnlichkeitsabbildungen.
Definition 2.0.20. Eine geradentreue und winkeltreue, bijektive Abbildung der Ebene
auf sich heisst eine Ähnlichkeitsabbildung.
Die Bildfigur entsteht durch Vergrösserung des Urbildes (oder Verkleinerung). Jede Strecke wird im gleichen Massstab verändert (z.B. verdoppelt). Die Längenverhältnise zweier
Strecken im Urbild und im Bild sind gleich.
Bezeichnung: zwei ähnliche Figuren A und A0 : A ∼ A0 .
27
UZH
MA S410
2.1
Geometrie und Lineare Algebra
Dilatationen
Fordert man zusätzlich, dass jede Gerade auf eine zu ihr parallele Geraden abgebildet
wird, so spricht man von Dilatation.
Definition 2.1.1.
Eine bijektive Abbildung der Ebene auf sich heisst Dilatation, wenn jede Gerade auf
eine zu ihr parallele Gerade abgebildet wird.
Eigenschaften der Dilatation
1. Die Dilatationen sind winkeltreu, also Ähnlichkeitsabbildungen.
2. Die Translationen sind Dilatationen. Sie sind die einzigen Dilatationen ohne Fixpunkt.
ϕ Translation (6= id) ⇐⇒ ϕ Dilatiation ohne Fixpunkt
3. Bei einer Dilatation mit Fixpunkt ist jede Gerade durch einen Fixpunkt eine Fixgerade.
28
UZH
MA S410
Geometrie und Lineare Algebra
4. Eine von der Identität verschiedene Dilatation hat höchstens einen Fixpunkt.
Eine Dilatation mit genau einem Fixpunkt S heisst zentrische Streckung.
Beweis?
Eine Abbildung ϕ : g → g 0 | | g ist eine Dilatation mit
• ∞ vielen Fixpunkten:
• 0 Fixpunkten:
• 1 Fixpunkt:
ϕ = Identität
ϕ = Tanslation
ϕ = zentrische Streckung
29
UZH
MA S410
2.2
Geometrie und Lineare Algebra
Zentrische Streckung
Definition 2.2.1.
Eine Dilatation mit genau einem Fixpunkt S heisst zentrische Streckung. Der Fixpunkt
S heisst Streckzentrum.
Die zentrischen Streckungen sind ausser der Identität die einzigen Dilatationen mit Fixpunkt.
Eigenschaften der zentrischen Streckung
1. Bei einer zentrischen Streckung mit dem Zentrum S liegen ein beliebiger Punkt P
(6= S) und sein Bild P 0 auf einer Geraden durch den Fixpunkt S.
2. Bei einer zentrischen Streckung wird jede Gerade g, die nicht durch das Zentrum S
geht, auf eine von g verschiedene Parallele abgebildet.
3. Eine zentrische Streckung ist durch ihr Zentrum S und durch einen von S verschiedenen Punkt A und sein Bild A0 eindeutig festgelegt.
Satz 2.2.2.
Bei einer zentrischen Streckung mit Zentrum S gilt für jeden Punkt A und sein Bild A0 :
−−→0
−→
SA = k · SA
wobei k (6= 0) eine feste reelle Zahl ist. k heisst Streckfaktor.
Bezeichnung: zentrische Streckung mit Streckzentrum S und Streckfaktor k: ZS,k
Bemerkung
|k| > 1: Vergrösserung der Entfernung von S
|k| < 1: Verkleinerung der Entfernung von S
k > 0: Urbild und Bild liegen auf derselben Seite von S
k < 0: Urbild und Bild liegen auf entgegengesetzten Seiten von S
30
UZH
MA S410
Geometrie und Lineare Algebra
Beweis von Satz 1: Untersuchung der Längenverhältnisse
1. Für rationale, positive Verhältnisse k:
−→ −−→
Wir wählen einen beliebigen Punkt P , sein Bild sei P 0 . Die Vektoren SP , SP 0 seien
gleichgerichtet und
−−→
−→
m
|SP 0 | = k|SP |, wobei k ∈ Q, k > 0, k = , m, n ∈ N
n
Nun wählen wir den Punkt E, so dass gilt:
−→ −→
nSE = SP
Damit wird
−−→0
−→ m −→
SP = k SP = nSE
n
Liegt der Punkt Q nicht auf der Geraden g durch S und P und ist h die Gerade
durch S und Q, so schneiden die Parallelen zu P Q durch alle Teilpunkte von g auf
31
UZH
MA S410
Geometrie und Lineare Algebra
der Geraden h kongruente Teilstrecken aus.
−→
−→
Der Vektor SE auf g entspricht dem Vektor SF auf h und es gilt:
−→
−→
SQ = nSF
−−→0
−→ m −→
SQ = mSF = SQ
n
Liegt der Punkt R auf der Geraden g, so kann jetzt wie vorher, aber von der Geraden h aus argumentiert werden.
2. für rationale, negative Verhältnisse k:
−→ −−→
Sind die Vektoren SP , SP 0 parallel, aber entgegengesetzt, also k < 0, dann spiegelt
man zuerst A0 an S, ergibt A∗ und folgert wie bei 1.
3. Ist k = 0, also , dann wird jeder Punkt auf S abgebildet. Diese Abbildung ist aber
nicht injektiv!
4. Ist k ∈ R irrational, dann muss die irrationale Zahl durch rationale Zahlen ( z.B.
mit Intervallschachtelungen) approximiert werden.
Beweisende!
Auch die Umkehrung von Satz 1 ist richtig. Damit kann man eine zur Definition der
zentrischen Streckung äquivalente Definition angeben.
Satz 2.2.3.
Eine Abbildung ϕ = ZS,k der Ebene auf sich ist genau dann eine zentrische Streckung mit
Zentrum S und Streckfaktor k, wenn gilt:
Jedem Punkt A wird ein Punkt A0 so zugeordnet, dass A und A0 auf einer Geraden durch
S liegen mit
−−→0
−→
SA = k SA
32
UZH
MA S410
Geometrie und Lineare Algebra
Damit gilt die folgende Verallgemeinerung.
Satz 2.2.4.
Bildet die zentrische Streckung ZS,k A auf A0 und B auf B 0 ab, dann gilt für die Vektoren:
−−
→
−→
A0 B 0 = k AB
Das Bild einer Strecke hat also die |k|- fache Länge der Urbildstrecke.
Bemerkung
k = 1: Die Identität ist ein Spezialfall einer zentrischen Streckung.
k = −1: Die Punktspiegelung ist auch eine spezielle zentrische Streckung.
Die obigen Sätze sind gleichbedeutend mit den Strahlensätzen.
Satz 2.2.5.
1. Strahlensatz
Werden zwei von einem Punkt ausgehende Strahlen (oder deren entgegengesetzte
Strahlen) von parallelen Geraden geschnitten, so verhalten sich die Längen der Abschnitte auf dem einen Strahl wie die Längen der entsprechenden Abschnitte auf
dem anderen Strahl.
|SA0 |
|SB 0 |
=
= |k|
|SA|
|SB|
33
UZH
MA S410
Geometrie und Lineare Algebra
2. Strahlensatz
Werden zwei von einem Punkt ausgehende Strahlen von zwei Parallelen geschnitten, so verhalten sich die Längen der Abschnitte auf den Parallelen wie die der
zugehörigen Scheitelabschnitte auf einem Strahl.
|SA0 |
|A0 B 0 |
=
= |k|
|AB|
|SA|
Weitere Eigenschaften der zentrischen Streckung ZS,k
1. Das Längenverhältnis zweier Bildstrecken ist gleich dem Längenverhältnis ihrer Urbildstrecken.
2. Ein Dreieck und sein Bild haben dieselbe Orientierung.
3. Die Flächeninhalte von Bild und Urbild verhalten sich wie
k2
.
1
4. Die zur zentrischen Streckung ZS,k inverse Abbildung hat dasselbe Streckzentrum
und den Streckfaktor k1 .
(ZS,k )−1 = ZS, 1
k
Die Eigenschaft 3 überlegt man sich zuerst für Dreiecke. Dann betrachtet man Polygone (geschlossene Streckenzüge), die man vollständig mit Dreiecken ausschöpfen kann.
Schliesslich können krummlinig begrenzte Figuren durch Dreiecke beliebig genau approximiert werden.
34
UZH
MA S410
Geometrie und Lineare Algebra
Beispiel 2.2.6. In ein Dreieck ABC soll ein Quadrat P QRS mit P, Q ∈ AB, R ∈ BC, S ∈
AC eingezeichnet werden.
35
UZH
MA S410
2.3
Geometrie und Lineare Algebra
Harmonische Teilung und Apolloniuskreis
Gegeben ist eine Strecke AB (B 6= A) und ein Streckfaktor k (6= 1).
Wo liegt das Streckzentrum S?
Es gilt:
−→
−→
SB = k SA
Definition 2.3.1.
Ist |k2 | = k1 = k (> 0), so wird die Strecke AB durch die Punkte S und T harmonisch
geteilt, wenn gilt
|BT |
|BS|
=
=k
|AS|
|AT |
−→
−→
S ist der innere Teilpunkt, wenn SB = −k SA
−→
−→
T ist der äussere Teilpunkt, wenn T B = k T A
Die Konstruktionsideen werden durch folgende Beispiele klar.
Beispiel 2.3.2. Die Strecke AB soll harmonisch im Verhältnis 2 : 3 geteilt werden.
36
UZH
MA S410
Geometrie und Lineare Algebra
Beispiel 2.3.3. Kennt man die Strecke AB und einen Teilpunkt S, so ist der andere
Teilpunkt T eindeutig bestimmt.
Beispiel 2.3.4. Konstruieren Sie durch den Schnittpunkt S zweier Kreise k1 und k2 eine
Sekante, so dass die beiden auf ihr liegenden Sehnen sich wie 2 : 3 verhalten.
Satz 2.3.5.
Teilen die Punkte S und T die Strecke AB harmonisch im Verhältnis k, so teilen die
Punkte A und B die Strecke ST auch harmonisch, und zwar im Verhältnis
λ=
k+1
.
k−1
(Beweis in den Übungen!)
Zeichnen Sie im Dreieck ABC die Winkelhalbierende des Winkels γ. Diese schneidet die
gegenüberliegende Seite AB = c im Punkt D. In welchem Verhältnis teilt D die Seite c?
37
UZH
MA S410
Geometrie und Lineare Algebra
Satz 2.3.6.
a) In einem Dreieck teilt die Winkelhalbierende eines Innenwinkels die gegenüberliegende Seite im Verhältnis der anliegenden Seiten.
b) Ist das Dreieck nicht gleichschenklig, so teilt auch die Winkelhalbierende des Aussenwinkels die gegenüberliegende Seite im Verhältnis der anliegenden Seiten.
Damit erhalten wir den berühmten Satz des Apollonius.
Satz 2.3.7. Kreis des Apollonius
Die Menge aller Punkte, für die das Abstandsverhältnis zu zwei festen Punkten A und B
den konstanten Wert k annimmt, ist der Kreis mit dem Durchmesser ST , wobei S und T
die Strecke AB harmonisch im Verhältnis k teilen.
38
UZH
MA S410
Geometrie und Lineare Algebra
Beispiel 2.3.8. Konstruieren Sie ein Dreieck aus den Seiten b = 6, c = 3 und der Winkelhalbierenden wα = 3.5.
Satz 2.3.9.
Die Seitenhalbierenden eines Dreiecks schneiden sich in einem Punkt S, der jede Seitenhalbierende innen im Verhältnis 2 : 1 teilt. S heisst der Schwerpunkt des Dreiecks.
Satz 2.3.10.
In einem Dreieck schneiden sich die drei Winkelhalbierenden in einem Punkt.
39
UZH
MA S410
2.4
2.4.1
Geometrie und Lineare Algebra
Verschiedene Ähnlichkeitsabbildungen
Ähnlichkeitsabbildungen allgemein
Satz 2.4.1.
Eine Ähnlichkeitsabbildung ϑ ist durch drei nicht kollineare Punkte und ihre Bildpunkte
eindeutig bestimmt.
a) Zwei Dreiecke sind genau dann ähnlich, wenn zwei Winkel des einen Dreiecks gleich
den entsprechenden Winkeln des anderen Dreiecks sind.
b) Zwei Dreiecke sind genau dann ähnlich, wenn sie in den Verhältnissen der drei
Seitenlängen übereinstimmen.
a0 a
a0
a
= 0 , = 0 , α = α0 , β = β 0 , γ = γ 0
b
b c
c
Satz 2.4.2.
Eine Abbildung ist genau dann eine Ähnlichkeitsabbildung ϑ, wenn sie darstellbar ist als
Verknüpfung einer Isometrie ϕ und einer zentrischen Streckungen ZS,k .
ϑ = Ähnlichkeitsabbildung
⇐⇒
ϑ = ZS,k ◦ ϕ
Beweis
00
⇐=00 :
Ist ϕ eine Isometrie und ZS,k eine zentrische Streckung, so ist die Verknüpfung der beiden
Abbildungen eine Ähnlichkeitsabbildung.
00
=⇒00 :
Ist ϑ eine Ähnlichkeitsabbildung, dann ist sie durch 3 nicht kollineare Punkte und ihre
Bilder eindeutig bestimmt.
ϑ : 4ABC −→ 4A0 B 0 C 0
40
UZH
MA S410
Geometrie und Lineare Algebra
Man kann die Abbildung zum Beispiel zerlegen in eine Translation gefolgt von einer Rotation und einer zentrischen Streckung.
−→
ϑ = ZA0 ,k ◦ RA0 ,µ ◦ T−
AA0
41
UZH
MA S410
2.4.2
Geometrie und Lineare Algebra
Drehstreckungen und Klappstreckungen
Definition 2.4.3. Eine Drehstreckung ist die Verknüpfung einer zentrischen Streckung
und einer Rotation mit demselben Zentrum.
ϑ = RS,α ◦ ZS,k
Es gilt:
ϑ = RS,α ◦ ZS,k = ZS,k ◦ RS,α
Spezielle Drehstreckungen
i) α = 0: zentrische STreckung
ii) k = 1: Rotation
iii) k = 1, α = 0: Identität
Es gilt weiter:
Eine Drehstreckung, die nicht die Identität ist, hat genau einen Fixpunkt.
Bei Drehstreckungen genügt es, positive k zu betrachten, denn
ϑ = RS,α ◦ ZS,k = RS,α+180◦ ◦ ZS,−k
42
UZH
MA S410
Geometrie und Lineare Algebra
Definition 2.4.4. EineKlappstreckung ist die Verknüpfung einer zentrischen Streckung
und einer Geradenspiegelung, deren Achse durch das Streckzentrum geht.
ϑ = Sg ◦ ZS,k
Es gilt:
ϑ = Sg ◦ ZS,k = ZS,k ◦ Sg
Spezielle Klappstreckung:
k = 1: Geradenspiegelung
Es gilt weiter:
Eine Klappstreckung mit |k| =
6 1 hat genau einen Fixpunkt.
Satz 2.4.5.
a) Die Verknüpfung einer gleichsinnigen Isometrie und einer zentrischen Streckung (k 6=
1) ist eine Drehstreckung.
b) Die Verknüpfung einer ungleichsinnigen Isometrie und einer zentrischen Streckung
(k 6= 1) ist eine Klappstreckung.
43
UZH
MA S410
2.4.3
Geometrie und Lineare Algebra
Noch zwei Sätze
Satz 2.4.6.
Die Verknüpfung zweier zentrischer StreckungenZS2 ,k2 ◦ZS1 ,k1 mit verschiedenen Zentren S1 6= S2 und k = k2 · k1 ist:
a) eine zentrische Streckung ZS,k , falls k 6= 1.
Das neue Zentrum S liegt auf der Geraden S1 S2 in folgender Lage
−−→
1 − k2 −−→
S1 S2
S1 S =
1 − k1 k2
b) eine Translation T~v , falls k = 1.
Der Vektor ~v ist parallel zur Geraden S1 S2 und es gilt
−−→
~v = (1 − k2 )S1 S2
Satz 2.4.7.
Gegeben sind eine Translation T~v und eine zentrische Streckung ZS,k (k 6= 1).
Dann ist die Verknüpfung wieder eine zentrische Streckung.
−−→
ZS,k ◦ T~v = ZS ∗ ,k , wobei SS ∗ =
44
k
~v .
1−k
Kapitel 3
Kreisgeometrie
3.1
Kreiswinkelsätze
Definition 3.1.1.
1. Zwei Punkte A und B auf einem Kreis k teilen diesen in zwei zueinander komplementäre Bögen. Die Strecke AB = s heisst Sehne.
2. Ist b ein Kreisbogen mit Endpunkten A und B und liegt der Punkt C auf b, so heisst
der Winkel γ = ^ACB Peripheriewinkel (Umfangswinkel) zum Bogen b.
3. Der Winkel µ = ^AM B Zentriwinkel Mittelpunktswinkel) zum Bogen b.
4. Die Tangente t an den Kreis k in A steht senkrecht auf dem Berührradius r = AM ,
sie bildet mit der Sehne AB den Sehnentangentenwinkel α.
45
UZH
MA S410
Geometrie und Lineare Algebra
Satz 3.1.2.
a) Ein Peripheriewinkel über einem Kreisbogen ist halb so gross wie der zugehörige
Zentriwinkel und gleich gross wie der zugehörige Sehnentangentenwinkel.
b) Alle Peripheriewinkel über demselben Bogen sind gleich gross.
c) Die Peripheriewinkel auf verschiedenen Seiten einer Sehne ergänzen sich auf 180◦ .
Zwei Beweise
1. klassisch
2. mit Geradenspiegelungen
46
UZH
MA S410
Geometrie und Lineare Algebra
Bemerkung 3.1.3.
a) Spezialfall: Thaleskreis
s = Durchmesser, γ = 90◦
b) Sehnenviereck
α + γ = 180◦
β + δ = 180◦
Definition 3.1.4. Der Kreisbogen, auf dem die Scheitelpunkte aller gleich grossen Peripheriewinkel liegen, heisst Ortsbogen (Fasskreisbogen) über der Sehne s.
Grundkonstruktion des Ortsbogenpaares Gegeben ist die Strecke AB der Länge
s = 6 und der Winkel β = 60◦ . Konstruieren Sie das Ortsbogenpaar über AB zum Winkel
β.
47
UZH
MA S410
Geometrie und Lineare Algebra
Es gilt auch die Umkehrung des vorherigen Satzes.
Satz 3.1.5.
Sieht man die Strecke AB von einem Punkt P aus unter dem Winkel γ, dann liegt P auf
dem Ortsbogen-Paar über AB zum Winkel γ.
Beweis
P innerhalb Ortsbogen
P ausserhalb Ortsbogen
Damit gelangt man zu einem neuen geometrischen Ort.
48
UZH
MA S410
Geometrie und Lineare Algebra
Satz 3.1.6.
Der geometrische Ort aller Punkte, von denen aus eine Strecke unter dem Winkel γ
erscheint, ist das Ortsbogen-Paar über der Strecke zum Winkel γ.
Beispiel 3.1.7. Konstruieren Sie ein Dreieck, wenn folgende Grössen bekannt sind.
b = 4cm, hb = 3cm, β = 60◦
49
UZH
MA S410
3.2
Geometrie und Lineare Algebra
Sehnensätze
Satz 3.2.1. Sehnensatz
Haben 2 Sehnen durch einen Punkt P im Inneren eines Kreises die Endpunkte A, A0 und
B, B 0 , so gilt:
|P A| · |P A0 | = |P B| · |P B 0 |
Satz 3.2.2. Sekantensatz
Haben 2 Sekanten durch einen Punkt P ausserhalb eines Kreises die Endpunkte A, A0 und
B, B 0 mit dem Kreis, so gilt:
|P A| · |P A0 | = |P B| · |P B 0 |
50
UZH
MA S410
Geometrie und Lineare Algebra
Satz 3.2.3. Sekanten-Tangentensatz
Von einem Punkt P ausserhalb des Kreises berührt eine Tangente den Kreis im Punkt A
und schneidet eine Sekante den Kreis in den Punkten B, B 0 . Dann gilt:
|P A|2 = |P B| · |P B 0 |
51
UZH
MA S410
3.3
Geometrie und Lineare Algebra
Satzgruppe des Pythagoras
Die meisten Menschen mit einer gewissen Schulbildung kennen den Satz von Pythagoras,
und zwar nur in der Form
a2 + b 2 = c 2 .
Oft wissen sie aber nicht mehr, dass sich die Formel auf ein rechtwinkliges Dreieck bezieht.
Am rechtwinkligen Dreieck benützt man oft die folgenden Bezeichnungen.
• a, b: Katheten
• c: Hypotenuse
• h: Höhe auf Hypotenuse
• p, q: Hypotenusenabschnitte
52
UZH
MA S410
Geometrie und Lineare Algebra
Satz 3.3.1. Kathetensatz des Euklid
Das Quadrat über einer Kathete ist gleich dem Produkt von Hypotenuse und Hypotenusenabschnitt.
Der Kathetensatz kann mit dem Sekantentangensatz bewiesen werden. Es gilt auch die
Umkehrung des Kathetensatzes.
Satz 3.3.2. Umkehrung des Kathensatzes
Gilt für ein Dreieck ABC die Beziehung
|BC|2 = |AB| · |BD|,
wobei D der Höhenfusspunkt der Höhe von C auf AB,
dann ist das Dreieck rechtwinklig bei C.
53
UZH
MA S410
Geometrie und Lineare Algebra
Satz 3.3.3. Höhensatz des Euklid
Das Quadrat über der Höhe ist gleich dem Produkt der beiden Hypotenusenabschnitte.
Der Höhensatz kann mit dem Sehnensatz bewiesen werden. Es gilt auch die Umkehrung
des Höhensatzes.
Satz 3.3.4. Umkehrung des Höhensatzes
Gilt für ein Dreieck ABC die Beziehung
|CD|2 = |AD| · |BD|,
wobei D der Höhenfusspunkt der Höhe von C auf AB,
dann ist das Dreieck rechtwinklig bei C.
Aus dem Kathetensatz kann schliesslich der berühmte Satz von Pythagoras bewiesen
werden. Es gibt natürlich hunderte von Beweisen dieser Sätze!
54
UZH
MA S410
Geometrie und Lineare Algebra
Satz 3.3.5. Satz von Pythagoras
Die Summe der Quadrate über den Katheten ist gleich dem Quadrat über der Hypotenuse.
a2 + b 2 = c 2
Auch hier gilt die Umkehrung.
Satz 3.3.6. Umkehrung des Satzes von Pythagoras
Gilt für ein Dreieck ABC die Beziehung
|BC|2 + |AC|2 = |AB|2
dann ist das Dreieck rechtwinklig bei C.
55
UZH
MA S410
Geometrie und Lineare Algebra
Anwendungen
1. Verwandeln Sie ein gegebenes Rechteck mit den Seitenlängen a und b in ein flächengleiches Quadrat sowohl mit dem Höhensatz wie auch mit dem Kathetensatz.
√
2. Konstruieren Sie 6 auf zwei Arten, indem Sie die Gleichungen 6 = 1·6 und 6 = 2·3
verwenden.
3. Ein Quadrat mit der Seite a = 5cm soll in ein flächengleiches Rechteck mit den
Seitenlängen b, c verwandelt werden, so dass gilt
a) b + c = 11cm
b) b − c = 6cm
4. Ein Parallelogramm mit a = 6cm, ha = 1cm, α = 45◦ soll unter Beibehaltung des
Winkels α in ein flächengleiches Parallelogramm verwandelt werden mit Seitenlänge
a0 .
Die folgende Figur zeigt zwei flächengleiches Parallelogramme.
56
UZH
MA S410
3.4
Geometrie und Lineare Algebra
Orthogonale Kreise
Definition 3.4.1.
Zwei Kreise schneiden sich orthogonal, wenn sich die Tangenten im Schnittpunkt senkrecht schneiden.
Satz 3.4.2. orthogonale Kreise - harmonische Teilung
Zwei Kreise schneiden sich genau dann orthogonal, wenn jeder Durchmesser des einen
Kreises vom anderen Kreis harmonisch geteilt.
57
UZH
MA S410
3.5
Geometrie und Lineare Algebra
Pol und Polare
Wir konstruieren von einem Punkt P ausserhalb eines Kreises k die Tangenten an den
Kreis und verbinden die Beührungspunkte. Diese Verbindungsgerade p untersuchen wir
nun näher.
Für jeden Punkt X ∈ p gilt wegen des Kathetensatzes
|M X| · cos ϕ · |M P | = r2
Definition 3.5.1.
Die durch (3.1) definierte Gerade p heisst die Polare des Kreises k zum Pol P .
Die Gleichung (3.1) gilt auch im Grenzfall P ∈ p.
58
(3.1)
UZH
MA S410
Geometrie und Lineare Algebra
Liegt der Punkt P innerhalb des Kreises k, so liegt die Polare p ausserhalb.
Satz 3.5.2.
Sei p die Polare des Kreises k zum Pol P .
(i) Für Q ∈ p gilt: Die Polare q zum Pol Q geht durch P .
(ii) Für q 3 P gilt: Der Pol Q zur Polaren q liegt auf p.
59
UZH
MA S410
3.6
Geometrie und Lineare Algebra
Inversion am Kreis
Gegeben ist ein Kreis mit Mittelpunkt M und Radius r.
Definition 3.6.1.
Die Abbildung ϕ sei folgendermassen definiert:
ϕ : P → P 0 (P 6= M ), so dass P 0 auf der Halbgeraden von M nach P liegt :
P 0 ∈ g + = (M P )+
|M P | · |M P 0 | = r2
ϕ heisst Spiegelung am Kreis k oder Inversion am Kreis k.
Bei der Inversion am Kreis k werden alle Punkte innerhalb von k (ausser dem Punkt M )
auf Punkte ausserhalb von k abgebildet und umgekehrt.
Satz 3.6.2. Eigenschaften der Inversion am Kreis
1. ϕ ist bijektiv.
2. Fixpunkte von ϕ sind genau die Punkte der Kreislinie k.
3. Jede Gerade durch M (ohne M ) wird auf sich abgebildet.
60
UZH
MA S410
Geometrie und Lineare Algebra
4. Jede Gerade, die nicht durch M geht, wird auf einen Kreis durch M (ohne M )
abgebildet und umgekehrt.
5. Jeder Kreis, der nicht durch M geht, wird auf einen Kreis abgebildet, der auch nicht
durch M geht.
6. Ein Kreis ist genau dann ein Fixkreis, wenn er den Inversionskreis rechtwinklig
schneidet.
Bemerkung 3.6.3.
Die Inversion am Kreis ist ein Beispiel einer Abbildung, die nicht geradentreu ist.
Beispiel 3.6.4. schwierig!
Gegeben sind 2 Kreisek1 , k2 und ein Punkt P . Konstruieren sie einen Kreis k durch P ,
der die beiden Kreise k1 und k2 berührt.
Eine Anwendung
Wie fängt ein Mathematiker einen Löwen in der Wüste? - Er stellt sich in einen kreisrunden
Käfig und muss nur aufpassen, dass sich der Löwe ausserhalb des Käfigs befindet. Mit einer
Inversion am Kreis ist der Löwe im Käfig gefangen und unser Mathematiker ist frei.
Was passiert, wenn sich unser Mathematiker anfangs genau in die Mitte gestellt hat? - Er
landet im Jenseits.
61
UZH
MA S410
Geometrie und Lineare Algebra
62
Kapitel 4
Nichteuklidische Geometrien (kurze
Einführung)
4.1
Euklidische Geometrie
Die Geometrie ist die älteste, systematisierte mathematische Disziplin. Geometrie bedeutet Erdmessung. Ursprünglich waren geometrische Figuren Äcker, Wiesen, Felder. Zunächst ist die Geometrie die Lehre vom Messen und Berechnen von Längen, Winkeln,
Flächen und Volumina. Schon die Babylonier, die Ägypter und die Griechen haben sich
mit geometrischen Sachverhalten der menschlichen Umwelt auseinandergesetzt.
63
UZH
MA S410
Geometrie und Lineare Algebra
Aber erst Thales von Milet (ca. 625 - ca. 547 v. Chr.)
erfand, was wir heute Wissenschaft nennen. So waren
seine geometrischen Figuren rein abstrakte Gebilde. Er
untersuchte das Sammelsurium geometrischer Rezepte,
Daumenregeln und empirischer Formeln, die aus Babylon und Ägypten überliefert wurden. Er merkte, dass
einige Regeln aus anderen hergeleitet werden konnten
und wollte die Geometrie als rein geistige Aktivität sehen.
Pythagoras von Samos (ca. 582 - 500 v. Chr.) hörte von Thales wissenschaftlichen Ideen. Vor allem dessen Geometrie begeisterte ihn. Er studierte in Ägypten.
Später gründete er in Kroton, einer griechischen Stadt
in Süditalien, die Schule der Pythagoräer, eine halb religiöse, halb politische Gemeinschaft, wo man sich mathematischen und philosophischen Fragestellungen widmete. In dieser so genannten Bruderschaft waren aber
Frauen und Männer völlig gleichberechtigt. So wurden
Frauen wichtige Personen in der Weiterentwicklung von
Mathematik und Naturwissenschaften.
Euklid (etwa 340 - 270v. Chr.) lebte in Athen und wurde später ans Museion in Alexandria berufen. Alexander der Grosse hatte diese neue Stadt am Nil gegründet.
Alexandria wurde das aktive Zentrum der Wissenschaften und Mathematik. Euklid hat das bis dahin bekannte
Material gesammelt und systematisch aufbereitet.
In seinen Elemente der Mathematik (insgesamt 13 Bücher) führt er eine axiomatische
Begründung der Geometrie ein. Die Schulbücher beruhen auch heute noch mindestens
indirekt auf den Elementen.
Euklid versucht zunächst, die Grundbegriffe wie ”Punkt”, ”Gerade” und ”Ebene” explizit
zu definieren (Ein Punkt ist, was keine Teile hat), führt dann Grundrelationen ”inzident”, ”zwischen” und ”kongruent” ein und formuliert in den Axiomen (Grundaussagen)
die einfachsten Eigenschaften. Damit kann er neue Begriffe explizit definieren und Sätze
beweisen, indem er sich nur auf sein Axiomensystem stützt.
64
UZH
MA S410
Geometrie und Lineare Algebra
Zwei Anektoten über Euklid
Ein junger Student fragt Euklid: Was habe ich davon, wenn ich all diese Dinge lerne?
Euklid ruft seinen Diener und sagt zu diesem: Gib dem Mann eine Münze, denn er muss
einen Gewinn ziehen aus dem, was er lernt.
König Ptolemaios fragt Euklid: Gibt es in der Geometrie einen kürzeren Weg als die
Elemente?"
Darauf Euklid antwortet: Es gibt keinen K önigsweg zur Geometrie.
Die Elemente sind das älteste, uns überlieferte Beispiel eines axiomatischen Systems. Sie
etablierten sich als Standardwerk zur Einführung in die Geometrie und wurden mehrmals
abgeschrieben und immer wieder etwas verändert.
Theon von Alexandria (2. Hälfte des 4. Jh. n. Chr.) lehrte auch am Museion. Er war
einer der wichtigsten Herausgeber der Elemente. 700 Jahre nach Euklid revidierte er das
Original mit klaren Formulierungen, schob einige Zwischenschritte in den Beweisen der
Sätze ein und fand neue Sätze.
Theon unterrichtete selbst seine Tochter Hypatia (370 - 415). Er wollte ihr die bestmögliche Ausbildung geben, obwohl zu dieser Zeit die Frauen wie Sklaven behandelt wurden.
Sie sollte ein ”vollkommener Mensch” werden.
Hypatia studierte bei ihrem Vater, dann aber auch in
Athen und Italien. Zurück in Alexandria durfte sie offiziell Mathematik und Philosophie lehren. Ihre Schriften
sind Erklärungen und Ergänzungen zu den Büchern von
Euklid und Diophant, sowie zu den Lehren von Platon
und Aristoteles. Studenten aus aller Welt besuchten ihre
Vorlesungen, auch Juden und Christen.
In dieser Zeit gewannen die Christen im römischen Grossreich immer mehr an Bedeutung. Für sie war Mathematik und Philosophie nur eine Irrlehre. 412 wurde Cyrillus, ein
fanatischer Christ, Patriarch von Alexandria. Er verlangte von den Gelehrten, dass sie
den christlichen Glauben annahmen, denn er wollte die Stadt vom Heidentum reinigen.
Hypatia weigerte sich, ihre Lehren und ihre Ideale aufzugeben. So fiel sie einem grausigen
Mordkomplott zum Opfer. Dieser brutale Mord setzte der Verbreitung von Platons Lehre
im ganzen römischen Reich ein jähes Ende.
Hypatia wurde zum Symbol für das Ende der antiken Wissenschaft, denn der Westen
leistete für die nächsten tausend Jahre keine wesentlich neuen Erkenntnisse weder in Mathematik noch in Physik noch in Astronomie. Dafür interessierte man sich für Astrologie
und Mystizismus. Europa trat ins finstere Mittelalter ein, während dem die griechische
65
UZH
MA S410
Geometrie und Lineare Algebra
Wissenschaft in Byzanz überlebte und in der arabischen Welt zu neuer Blüte gelangte.
Seit 1482 sind mehrere griechische Fassungen der Elemente wieder aufgetaucht, die alle
auf Theon und Hypatia zurückgehen.
Euklids Elemente bestehen aus 13 Büchern. Sie haben kein Vorwort, keine Einleitung.
Es werden keine Ziele formuliert, keine Motivation, kein Kommentar. Das Werk beginnt
abrupt mit 23 ”Definitionen”.
Definition 4.1.1. Ein Punkt ist, was keine Teile hat.
Abbildung 4.1: Wo ist der Punkt?
Wie gross ist ein Punkt?
Euklids Elemente unterscheiden sich von den heutigen axiomatischen Theorien wesentlich.
Euklid definiert auch die Grundbegriffe: ”Punkte”, ”Geraden”, ”Ebenen”.
Heute verzichtet man meist auf solch exakte Definitionen der Grundbegriffe. Seit David Hilbert(1862-1943)
werden in Axiomensystemen die Grundbegriffe nicht näher definiert, sondern man postuliert Eigenschaften gewisser Relationen zwischen den Grundbegriffen.
Euklids Modell hat sich über mehr als 2000 Jahre bewährt in Naturwissenschaft, Technik und Kultur. Es wurde auch für andere Wissenschaften zum Vorbild wissenschaftlicher
Darstellung von Theorien. Die sogenannte Euklidische Geometrie kann als die abstrakte Beschreibung unserer ebenen und räumlichen Erfahrung aufgefasst werden.
66
UZH
MA S410
Geometrie und Lineare Algebra
Der Anstoss zur weiteren Entwicklung der Geometrie hat das Parallelenaxiom gegeben,
das besagt, dass es zu jeder Geraden durch jeden Punkt genau eine Parallele gibt. Man
hat lange geglaubt, dass dieses Axiom aus den ersten vier hergeleitet werden kann. Erst
als man Ende des 18. Jahrhunderts die Unabhängigkeit des Parallelenaxioms nachweisen
konnte, war der Weg frei zu anderen Geometrien, den sogenannten Nichteuklidischen
Geometrien.
Als erster erkannte Carl Friedrich Gauss (1777 1855), dass eine in sich widerspruchsfreie Geometrie entsteht, wenn man annimmt, dass zu einer Geraden durch
einen nicht auf ihr gelegenen Punkt mehrere Parallelen
gezogen werden können.
Das war die ”Geburt” der Nichteuklidischen Geometrie.
Aus Furcht vor dem Geschrei engstirniger Philosophen
hat Gauss seine Überlegungen nicht veröffentlicht.
Gauss, dann aber auch Janos Bolyai (1802 - 1860) und Nicolai Lobatschewsky
(1793 - 1856) begründeten mit diesen neuen Gedanken die erste nichteuklidische Geometrie.
Felix Klein (1849 - 1924) kreierte für eine Geometrie
mit unendlich vielen Parallelen den Namen hyperbolische
Geometrie. (hyperbole heisst griechisch der Überschuss:
in der neuen Geometrie gibt es einen Überschuss an parallelen zu einer Gerade durch einen Punkt!).
Eine Geometrie ohne Parallelen heisst elliptisch und die
Euklidische Geometrie parabolisch.
Bei Euklid ist die Kongruenz von Figuren wichtig, also eine eher statische Betrachtung der Objekte. Felix
Klein hat ein dynamisches Vorgehen eingef§hrt und darum den Abbildungsbegriff betont. Diese Abbildungsgeometrie geht auf Felix Klein zurück.
Der Raumbegriff in der Mathematik und Physik unterliegt gerade heute vielfältigen Verallgemeinerungen. Es ist notwendig, dass man diesen Begriff nicht nur im Sinne Euklids
versteht. Im Gegenteil gibt es viele Räume, die man geometrisch untersuchen kann.
67
UZH
MA S410
4.2
4.2.1
Geometrie und Lineare Algebra
Modelle nichteuklidischer Geometrien
Beispiel einer elliptischen Geometrie
Definieren wir auf der Kugeloberfläche die Grundbegriffe folgendernassen:
Definition 4.2.1.
• PUNKT: Paar diametral entgegengesetzter Punkte
• GERADE: Grosskreis auf der Kugel
Damit bestimmen 2 PUNKTE genau eine GERADE und 2 GERADEN genau einen
PUNKT.
Zu einer gegebenen Gerade gibt es durch einen PUNKT ausserhalb der GERADEN keine
Parallele!
Zum Beispiel gibt es zur GERADEN g durch die PUNKTE A und B keine parallelen
GERADEN durch P .
Dies ist ein Beispiel einer Geometrie ohne Parallelen.
68
UZH
MA S410
4.2.2
Geometrie und Lineare Algebra
Kleinsches Modell einer hyperbolischen Geometrie
Das Kleinsche Modell einer hyperbolischen Geometrie heisst auch Bierdeckelgeometrie.
Definition 4.2.2.
• Unter einer Ebene versteht man das Innere eines Kreises.
• Eine Gerade ist jede durch den Rand des Kreises begrenzte Strecke.
• Ein Punkt ist ein euklidischer Punkt im Kreisinnern.
Dann ist jede Gerade, die nicht durch das Innere des Winkels AP B geht, eine
Parallele zu g durch P .
• Die Bewegungen sind Spiegelungen, die durch Polarenspiegelungen definiert sind.
(gewöhnliche Geradenspiegelung, falls g durch den Kreismittelpunkt geht.)
Die Spiegelung ist involutorisch, d.h. Sg ◦ Sg = id.
Zur Geraden g gibt es unendlich viele parallele Geraden durch den Punkt P .
69
UZH
MA S410
Geometrie und Lineare Algebra
Die folgende Skizze zeigt die Konstruktion der Spiegelung des Punktes P an der Geraden
g als Polarenspiegelung, wobei G der Pol zur Polaren g ist.
Bemerkung 4.2.3.
Eine elliptische Geometrie ist auf einer Fläche mit positiver Krümmung lokalisiert (z.B.
Kugeloberfläche).
Einsteins allgemeine Relativitätstheorie (1916) gilt in einer elliptischen Geometrie. Die
Geometrie des Universums ist elliptisch, da dem Weltraum wegen der Verteilung der
Massen im Gravitationsfeld eine positive Krümmung zugeschrieben wird. Nach Einstein
ist der Krümmungsradius mindestens 1.5 · 107 Lichtjahre.
Die euklidische Geometrie als parabolische Geometrie hat die Krümmung null.
Eine hyperbolische Geometrie ist auf einer Fläche mit negativer Krümmung lokalisiert
(z.B. auf einer Pseudosphäre).
70
UZH
MA S410
4.2.3
Geometrie und Lineare Algebra
Poincaré - Modell einer hyperbolischen Geometrie
Henri Poincaré (1854 - 1912) war ein berühmter französischer Mathematiker, Physiker und Philosoph, der wesentliche Beiträge zur Himmelsmechanik, Thermodynamik,
Elektrizitätslehre und Optik veröffentlichte.
Henri Poincaré und Felix Klein haben beide die wesentlichen Theorien, die im 19. und
anfangs 20. Jahrhundert entstanden, zu einem krönenden Abschluss gebracht und sich in
ihren späten Jahren mit allgemeinen Fragen beschäftigt, Poincaré mit philosophischen,
Klein mit ädagogischen.
Im Poincaré-Modell einer hyperbolische Geometrie ist die Ebene eine sehr grosse Kreisfläche oder eine Halbebene.
Ebene
Inneres C eines sehr
grossen Kreises k
Halbebene Σ, durch euklidische
Gerade s begrenzt
Punkt
Euklidischer Punkt
Euklidischer Punkt
Gerade
Kreisdurchmesser
zu s orthogonale Halbgeraden
Kreisteile, die k orthogonal
schneiden
auf s orthogonale Halbkreise
Spiegelung
an g
gewöhnliche Geradenspiegelung, gewöhnliche Geradenspiegelung,
wenn g Kreisdurchmesser
wenn g zu s orthogonale Halbgerade
Inversion am Kreis,
wenn g Kreisteil
Inversion am Kreis,
wenn g Halbkreis
71
UZH
MA S410
Geometrie und Lineare Algebra
Dieses Modell kann auch in Form einer Geschichte erzählt werden. Dadurch kann man
technische Schwierigkeiten vertuschen und erhält trotzdem eine Idee einer nichteuklidischer Geometrie.
Die folgende Geschichte stammt aus dem Buch von R. Trudeau: Die geometrische Revolution, Birkhäuser Verlag, Basel, Boston, Berlin 1998.
72
UZH
MA S410
Geometrie und Lineare Algebra
73
UZH
MA S410
4.2.4
Geometrie und Lineare Algebra
Künstlerischer Abschluss
Das Poincaré-Modell einer hyperbolischen Geometrie ist im Buch von H.S.M. Coxeter
(1907 - 2003) illustriert. M. C. Escher (1898 - 1972), der bekannte niederländische Künstler, hat darin neue Möglichkeiten für seine Annäherungen an die Unendlichkeit gefunden.
Abbildung 4.2: Coxeter: Poincaré-Modell
Abbildung 4.3: Escher: Kreislimit I, 1959
74
UZH
MA S410
Geometrie und Lineare Algebra
Zum Abschluss noch etwas Poetisches von Christian Morgenstern (1871 - 1914)
Die zwei Parallelen
Es gingen zwei Parallelen
ins Endlose hinaus,
zwei kerzengerade Seelen
und aus solidem Haus.
Sie wollten sich nicht scheiden
bis an ihr seliges Grab;
das war nun einmal der beiden
geheimer Stolz und Stab.
Doch als sie zehn Lichtjahre
gewandert neben sich hin,
da ward’s dem einsamen Paare
nicht irdisch mehr zu Sinn.
War’n sie noch Parallelen?
Sie wussten’s selber nicht,
sie flossen wie zwei Seelen
zusammen durch ewiges Licht.
Das ewige Licht durchdrang sie,
da wurden sie eins in ihm;
die Ewigkeit verschlang sie,
als zwei Seraphim.
75
UZH
MA S410
Geometrie und Lineare Algebra
76
Kapitel 5
Vektorgeometrie
5.1
Einführung
Definition 5.1.1. Beide Definitionen sind äquivalent.
1. Unter einem Vektor versteht man die ganze Äquivalenzklasse aller kongruenter und
−−→
gleichgerichteter ”Pfeile” P P 0 . Ein Vektor ist also nicht auf einen festen Anfangspunkt bezogen, sondern kann beliebig im Raum parallel verschoben werden.
2. Zwei Vektoren sind gleich, wenn sie dieselbe Richtung und dieselbe Länge haben.
−−→
~v = P P 0 , (P Anfangspunkt, P 0 Endpunkt)
|~v | = Betrag von ~v = Länge von ~v
5.1.1
Elementare Vektoroperationen
Multiplikation eines Vektors ~v mit einer reellen Zahl λ:
λ > 0 : ~v , λ~v
λ < 0 : ~v , λ~v
λ = 0 : ~v = ~0
gleiche Richtung
entgegengesetzte Richtung
Nullvektor
77
λ~v
UZH
MA S410
Geometrie und Lineare Algebra
Addition und Subtraktion von Vektoren
Definition 5.1.2.
Die Summe ~s = ~a + ~b zweier Vektoren ~a und ~b ist der Vektor ~s, der vom Anfangspunkt
von ~a zum Endpunkt von ~b führt, wobei ~b beim Endpunkt von ~a angesetzt wird.
Kommutativgesetz: ~a + ~b = ~b + ~a
Assoziativgesetz: (~a + ~b) + ~c = ~a + (~b + ~c)
Nullvektor:
~0 neutrales Element bezüglich +. ~a + ~0 = ~a für alle ~a.
Kehrwert zu ~a:
Subtraktion:
−~a = (−1)~a inverses Element zu ~a bezüglich +. ~a + (−~a) = ~0
~a − ~b = ~a + (−~b)
Bemerkung 5.1.3.
Der Raum mit dieser Operation + und der skalaren Multiplikation heisst der dreidimensionale Vektorraum (R3 , +).
Beispiel 5.1.4.
Berechnen Sie ~a aus: 31 (2~a − ~b + ~c) = 2~b + 12 (~a + 2~b − 3~c).
78
UZH
MA S410
Geometrie und Lineare Algebra
Lineare Abhängigkeit und Unabhängigkeit von Vektoren
Definition 5.1.5.
Zwei Vektoren ~a und ~b heissen linear abhängig, wenn sie parallel zu einer Geraden liegen
(gleiche oder entgegengesetzte Richtung). Andernfalls sind sie linear unabhängig.
~a und ~b linear abhängig
Satz 5.1.6.
~a und ~b linear unabhängig
~a und ~b linear unabhängig
⇔
x~a + y~b = ~0 nur für x = y = 0.
Beispiel 5.1.7.
−−→
−−→
Gegeben ist ein Dreieck ABC. Punkt D liegt auf BC, sodass BD = 21 BC und Punkt E
−→
−→
auf AC, sodass AE = 13 AC. Der Punkt F sei der Schnittpunkt der Strecken AD und BE.
−−→
−−→
−→
−−→
Weiter seien DF = xDA und EF = y EB. Berechnen Sie die Bruchteile x und y.
Definition 5.1.8.
1. Drei Vektoren im Raum ~a, ~b, ~c heissen
linear abhängig, wenn sie parallel zu
einer Ebene liegen.
Es gilt ~c = α~a + β~b, d.h. ein Vektor ist als Linearkombination der beiden anderen
darstellbar.
Somit ist der Nullvektor darstellbar als Linearkombination der anderen drei Vektoren, wobei mindestens ein Streckfaktor ungleich 0 ist.
~0 = α~a + β~b + (−1)~c.
79
UZH
MA S410
Geometrie und Lineare Algebra
2. Drei Vektoren sind linear unabhängig, wenn sie einen Raum aufspannen.
Satz 5.1.9.
~a, ~b, ~c sind linear unabhängig
5.1.2
⇔
x~a + y~b + z~c = ~0 nur für x = y = z = 0.
Koordinatendarstellung von Vektoren
Es seien ~e1 , ~e2 , ~e3 die Einheitsvektoren in x-, y-, z-Richtung. Jeder Vektor ~v ist als Summe
der drei Einheitsvektoren darstellbar, daraus ergibt sich die
Koordinatendarstellung:


vx
~v = vx~e1 + vy~e2 + vz~e3 =  vy 
vz
Der Betrag von ~v , |~v |, berechet sich aus dem räumlichen Satz von Pythagoras:
q
|~v | = vx2 + vy2 + vz2 .
Die Addition zweier Vektoren ~a, ~b wird aufgrund der nachfolgenden Herleitung komponentenweise ausgeführt:




ax
bx
~a =  ay  , ~b =  by 
az
bz

 

ax
bx
~a + ~b =  ay  +  by  = ax~e1 + ay~e2 + az~e3 + bx~e1 + by~e2 + bz~e3 =
az
bz


ax + b x
= (ax + bx )~e1 + (ay + by )~e2 + (az + bz )~e3 =  ay + by 
az + b z
80
UZH
MA S410
Geometrie und Lineare Algebra
Ebenso die Multiplikation mit einem Skalar:

 

ax
λax
λ~a = λ  ay  =  λay 
az
λaz
−→
Der Ortsvektor OP eines Punktes P = (px , py , pz ) ist wie folgt definiert:


px
−→ 
py  .
OP =
pz
Durch das Koordinatensystem wird also jedem Punkt P des Raumes umkehrbar eindeutig
ein Zahlentripel (px , py , pz ) zugeordnet.
Abbildung 5.1: Ortsvektor von P
Vektor vom Punkt A zum Punkt B:


b x − ax
−→ −−→ −→ 
b y − ay 
AB = OB − OA =
b z − az
p
−→
|AB| = (bx − ax )2 + (by − ay )2 + (bz − az )2
Beispiel 5.1.10.
Berechnen Sie den Mittelpunkt einer Strecke AB aus den Koordinaten der Punkte A und
B.
81
UZH
MA S410
5.2
Geometrie und Lineare Algebra
Skalarprodukt zweier Vektoren
Definition 5.2.1.
Das Skalarprodukt zweier Vektoren ~a und ~b ist die reelle Zahl
~a · ~b = |~a| · |~b| cos ω
wobei ω = Zwischenwinkel der beiden Vektoren ~a und ~b ist. Somit ordnet das Skalarprodukt zwei Vektoren eine reelle Zahl zu.
~ba = Orthogonalprojektion von ~b auf ~a. Es gilt
|~ba | = |~b| cos ω
~a · ~b
und ~ba =
~a.
|~a|2
Somit ist das Skalarprodukt interpretierbar als
~a · ~b = |~ba | · |~a|.
Bemerkung 5.2.2.
In der Physik ist die Arbeit das Skalarprodukt aus Kraft und Verschiebung.
Der nächste Satz gibt ein Kriterium dafür, dass zwei Vektoren aufeinander senkrecht stehen.
Satz 5.2.3.
Ist ~a 6= ~0 und ~b 6= ~0 , so gilt:
~a · ~b = 0
⇔
82
~a⊥~b.
UZH
MA S410
5.2.1
Geometrie und Lineare Algebra
Gesetze des Skalarprodukts
~a · ~b = ~b · ~a
1. Kommutativgesetz:
2. Assoziativgesetz: ~a · (~b · ~c) = (~a · ~b) · ~c
Warum ist dieses Gesetz falsch?
3. Distributivgesetz:
~a · (~b + ~c) = ~a · ~b + ~a · ~c
Beweis?
4. Betrag eines Vektors:
~a · ~a = |~a|2
5. α, β ∈ R : (α~a) · (β~b) = αβ~a · ~b
83
UZH
MA S410
5.2.2
Geometrie und Lineare Algebra
Berechnung des Skalarprodukts mit Hilfe der Koordinaten
Satz 5.2.4.




ax
bx
Es seien ~a =  ay  und ~b =  by  zwei beliebige Vektoren.
az
bz
Dann berechnet sich das Skalarprodukt folgendermassen

 

ax
bx
~a · ~b =  ay  ·  by  = ax bx + ay by + az bz
az
bz
Beweis. Um diesen Satz zu beweisen zu können, erinnern wir uns an den Cosinussatz.
→
−
→
−
→
−
−
−
−
Cosinussatz: |→
a − b |2 = |→
a |2 + | b |2 − 2|→
a || b | cos ω
oder aus den Gesetzen:
Sind ~a = ax~e1 +ay~e2 +az~e3 und ~b = bx~e1 +by~e2 +bz~e3 , so erhält man durch Ausmultiplizieren
wegen der Orthogonalität der Einheitsvektoren (~ei · ~ej = 0 für i 6= j und ~ei · ~ei = 1):
~a · ~b = (ax~e1 + ay~e2 + az~e3 ) · (bx~e1 + by~e2 + bz~e3 ) = ax · bx + ay · by + az · bz
84
UZH
MA S410
5.2.3
Geometrie und Lineare Algebra
Winkel zwischen zwei Vektoren
cos ω =
~a · ~b
|~a||~b|
⇒
ω = arccos(
~a · ~b
)
|~a||~b|
Beispiel 5.2.5.


 


−1
4
−2
~v =  y  steht senkrecht auf ~a =  3  und ~b =  6 .
z
1
3
Berechnen Sie y und z.
Beispiel 5.2.6.
Das Dreieck ABC ist gegeben durch A(-2,2,0), B (-1,0,2), C (-5,2,-3).
Berechnen Sie den Winkel α.
Beispiel 5.2.7.


1
Zerlegen Sie den Vektor ~v =  7  in eine Summe von zwei Vektoren, von denen der
11


1
eine parallel und der andere senkrecht zu ~a =  −3  ist.
−2
85
UZH
MA S410
5.3
Geometrie und Lineare Algebra
Parameterdarstellung der Geraden
Eine Gerade im Raum ist festgelegt durch einen Punkt und eine Richtung. Graphisch
lässt sich das wie folgt darstellen:
Daraus ergibt sich die Parameterdarstellung (PD) einer Gerade g.
−−→ −→
g : OX = OA + t~g , wobei t ∈ R
Durchläuft der Parameter t die reellen Zahlen, so durchläuft der Punkt X die Gerade g.
  



x
ax
gx
g :  y  =  ay  + t  gy  , t ∈ R
z
az
gz
Beispiel 5.3.1.
Gegeben sind die Punkte A(10, 3, -12) und B (15, 2, -9).
a) Bestimmen Sie die Parameterdarstellung der Geraden g durch A und B.
b) Liegen die Punkte P (4, 5, -18) und Q(5, 4, -12) auf g?
c) Bestimmen Sie die Spurpunkte (Schnittpunkte von g mit den Koordinatenebenen
S1, S2, S3 von g.
86
UZH
MA S410
Geometrie und Lineare Algebra
Gegenseitige Lage zweier Geraden g und h
Gegeben sind zwei Geraden g und h.
−−→ −→
g : OX = OA + t~g
−−→ −−→
h : OX = OB + s~h
Es gibt 4 Möglichkeiten für die gegenseitige Lage.
- zusammenfallend sein, ~g || ~h und A ∈ h,
- parallel sein, ~g || ~h und A ∈
/h
- sich schneiden, g ∩ h = {S},
- windschief sein, ~g nicht parallel ~h und kein Schnittpunkt
zusammenfallend
parallel
sich schneidend
windschief
Beispiel 5.3.2.
Bestimmen Sie die gegenseitige Lage der beiden Geraden g und h.
  

  

x
1 − 2t
x
−1 + s
g :  y  =  1 + t ,
h :  y  =  7 + 2s 
z
−2 + t
z
−s
Beispiel 5.3.3.
Bestimmen Sie die gegenseitige Lage der beiden Geraden g und
   


  
x
9
2
x







y
5
1
y =
g:
=
+t
,
h:
z
0
−2
z
87
h.



6
1
3  + t 0 
1
−3
UZH
MA S410
5.4
5.4.1
Geometrie und Lineare Algebra
Parameterdarstellung und Gleichung der Ebene
Parameterdarstellung der Ebene
Eine Ebene ist festgelegt durch einen Punkt und zwei Richtungen. Graphisch lässt sich
das wie folgt darstellen:
−−→ −→
E : OX = OA + s~u + t~v , wobei s, t ∈ R
Durchlaufen die Parameter s und t die reellen Zahlen, so durchläuft der Punkt X die
EbeneE.
  





x
ax
ux
vx
E :  y  =  ay  + s  uy  + t  vy 
z
az
uz
vz
Beispiel 5.4.1.
Bestimmen Sie die Parameterdarstellung der Ebene E durch die Punkte A(3, 0, 6), B(6, −6, −4),
C(−2, −4, 4).
In welchen Punkten schneidet E die Koordinatenachsen?
Beispiel 5.4.2.
Finden Sie eine Parameterdarstellung der Ebene F, die parallel zur yz -Ebene liegt und
durch den Punkt A(1, 2, 3) geht.
88
UZH
MA S410
5.4.2
Geometrie und Lineare Algebra
Gleichung der Ebene
Eine Ebene E ist auch festgelegt durch einen Punkt A ∈ E und eine Normalenrichtung
−−→
~n. Somit liegt ein Punkt X genau dann in der Ebene E, wenn der Vektor AX orthogonal
zu ~n ist.
−−→ →
AX · −
n =0
⇔
−−→ →
−→ −
OX · −
n − OA· →
n =0

 
 

nx
ax
x
nx
 y  ·  ny  −  ay  ·  ny  = 0
nz
az
z
nz
|
{z
}

⇔
konstant
Somit erhält man die Gleichung der Ebene:
E : nx x + ny y + nz z + c = 0.
Die Koordinaten eines beliebigen Punktes X(x, y, z) der Ebene E erfüllen eine lineare
Gleichung.
Umgekehrt bilden die Koeffizienten bei den Variablen x, y, z die Koordinaten eines Normalenvektors von E.
Beispiel 5.4.3.
Bestimmen Sie aus der Parameterdarstellung der Ebene E die Gleichung von E.
  

x
3 + 3s − 5t
E :  y  =  −6s − 4t 
z
6 − 10s − 2t
In welchen Punkten schneidet E die x-Achse?
Beispiel 5.4.4.
Liegen die Punkte A(0, 2, 2), B(4, 1.5, 4.5) auf der Ebene E : 2x + 3y − 3z + 1 = 0?
89
UZH
MA S410
Geometrie und Lineare Algebra
Beispiel 5.4.5.
BestimmenSie die
der
 Gleichung

 Ebene E, welche durch den Punkt P (4, 2, 1) und die
x
2+t
Gerade g :  y  =  1 − 3t  geht.
z
3+t
5.4.3
Abstand eines Punktes von einer Ebene
Man wählt einen beliebigen Punkt A ∈ E. Der Abstand d = d(P, E) eines Punktes P
−→
von der Ebene E ist dann gleich der Länge der Orthogonalproketion von AP auf den
Normalenvektor ~n und berechnet sich folgendermassen.
−→
1
AP · ~n ~n · p~ − ~n · ~a
=
=
(nx px + ny py + nz pz + reelle Zahl)
d = d(P, E) =
|~n|
|~n|
|~n]
Man muss also die Koordinaten des Punktes P in die Ebenengleichung einsetzen und
durch den Betrag des Normalenvektors dividieren.
Die Grösse d hat ein Vorzeichen mit folgender Bedeutung:
1. d = 0:
P ∈E
2. d > 0:
P ∈
/ E, aber im Halbraum, in den der Normalenvektor ~n zeigt
3. d < 0:
P ∈
/ E, im Halbraum, in entgegengesetzter Richtung zu ~n
Beispiel 5.4.6.
Ein Lichtstrahl geht vom Punkt P (4, 5, −1) nach Q(−7, 8, −9) und wird dazwischen einmal an der Ebene E : x + 3y − 2z − 7 = 0 reflektiert.
Bestimmen Sie den Reflexionspunkt.
90
UZH
MA S410
5.5
Geometrie und Lineare Algebra
Kugel und Kreis
Ein Punkt X liegt genau dann auf der Kugel k im Raum (beziehungsweise auf einem
Kreis k in der Ebene), wenn der Abstand zum Mittelpunkt M gleich dem Radius r ist.
Dies kann vektoriell sehr einfach geschrieben werden.
X∈k
−−→
|M X| = r
⇔
Bezeichnen wir den Ortsvektor des Punktes X mit ~x und denjenigen von M mit m,
~ so
hat die Kugelgleichung (bzw Kreisgleichung) die Form
X∈k
⇔
|~x − m|
~ =r
Jeder Punkt X(x, y, z) der Kugel k mit Mittelpunkt M (mx , my , mz ) und Radius r erfüllt
dann die Kugelgleichung
(x − mx )2 + (y − my )2 + (z − mz )2 = r2
Ebenso erfüllt jeder Punkt X(x, y) auf dem Kreis k mit Mittelpunkt M (mx , my ) und
Radius r die Kreisgleichung
(x − mx )2 + (y − my )2 = r2
Beispiel 5.5.1.
Bestimmen Sie die Durchstosspunkte der Kugel mit Mittelpunkt M (3, 1, −2) und Radius
r = 7mit der
 Geraden g, die durch den Punkt P (1, 1, 2) in Richtung
4
~g =  −3  geht.
2
Die Tangentialebene T an eine Kugel k mit Mittelpunkt M und Radius r im Punkt P ∈ k
kann folgendermassen beschrieben werden:
X∈T
⇔
−−→ −−→
P X ⊥ MP
⇔
−−→ −−→
P X · MP = 0
Beispiel 5.5.2.
Bestimmen Sie auf der Kugel k mit Mittelpunkt M (1, −2, 3) und Radius r = 3 die Punkte
P (3, 0, ?). Berechnen Sie nun die Gleichung der Tangentialebe an k im tieferen der beiden
Punkte.
91
UZH
MA S410
Geometrie und Lineare Algebra
92
Kapitel 6
Matrizenalgebra
Das Studium linearer Gleichungssysteme und ihrer Lösungen ist eine der wichtigsten Aufgaben der linearen Algebra. Lineare Gleichungssysteme treten in vielen Anwendungen auf,
und zwar nicht nur in der Mathematik sondern auch in Physik, Biologie, Wirtschaft, Soziologie und im Ingenieurwesen. Gleichungssysteme werden Platz sparend in rechteckigen
Anordnungen geschrieben, den Matrizen und Vektoren.
6.1
Matrizen
Beispiel 6.1.1.
Oft werden Daten in Tabellen festgehalten. Eine Buchhandlung besitze zwei Filialen,
deren Verkaufszahlen (in CHF 100) in den Monaten Juli und August in der folgenden
Anordnung dargestellt sind.
Juli
Filiale
1
Tageszeitungen 6
Zeitschriften
15
Bücher
45
August
Filiale
2
1
8 Tageszeitungen 7
20 Zeitschriften
18
64 Bücher
52
2
9
31
68
Definition 6.1.2.
1. Eine m × n−Matrix ist ein rechteckiges Schema
Spalten (engl. column).

a11 a12 . . . . . . a1n
 a21 a22 . . . . . . a2n
A=
 ... ... ... ... ...
am1 am2 . . . . . . amn
von m Zeilen (engl. row) und n


 = (aij )m×n

m=Zeilenindex, n=Spaltenindex
93
UZH
MA S410
Geometrie und Lineare Algebra


6 8
Bsp: Juli : J =  15 20 
45 64


7 9
August : A =  18 31 
52 68
2. Die Dimension einer Matrix A ist m×n, wobei m die Zeilenzahl und n die Spaltenzahl.
Bsp: J und A haben die Dimension 3 × 2.
3. Eine Matrix heisst quadratisch (engl. square matrix), wenn m = n ist.
Bsp: J und A sind nicht quadratisch.
4. Das Element aij (engl. ij−entry) ist die Zahl in der i−ten Zeile und der j−ten
Spalte.
Bsp: J = (aij ) ist a21 = 15, abera13 ist nicht definiert.
5. Eine Teilmatrix (engl. submatrix) einer gegebenen Matrix erhält man durch Weglassen ganzer Zeilen oder Spalten.
Bsp: Wenn man sich nur für die
von Zeitschriften und Büchern im
Verkaufszahlen
15 20
Monat Juli interessiert: JZB =
.
45 64
6. Die zur Matrix A transponierte Matrix AT (engl. transpose) ist die Matrix, die
aus A entsteht , wenn gilt: aTij = aji
6
15
45
Bsp: J T =
8 20 64
7. Unter einem Vektor versteht man eine (n×1)-Matrix (Spaltenvektor) oder eventuell
eine (1 × n)-Matrix (Zeilenvektor).


w1
 w2 


w=w
~ =  .. 
Spaltenvektor
 . 
wn
v T = v1 v2 . . . vn
Zeilenvektor
94
UZH
MA S410
Geometrie und Lineare Algebra
8. Eine quadratische Matrix D heisst Diagonalmatrix, wenn die Elemente dij = 0
für i 6= j.



D=


d11
0
...
0
0
0 d22 . . .
0
... ... ... 0
0 . . . . . . dnn






Hauptdiagonale
9. Eine quadratische Matrix En heisst Einheitsmatrix, wenn für die Elemente eij von
En gilt:
eij =
1, wenn i = j
0, wenn i 6= j
Die Spalten (bzw. Zeilen) einer Einheitsmatrix heissen Einheitsvektoren.


 
 
 
1 0 0
1
0
0







0 1 0 , e1 =
0 , e2 =
1 , e3 =
0 
Bsp: E3 =
0 0 1
0
0
1
10. Eine quadratische Matrix heisst symmetrisch, wenn A = AT .


1
2 −3 −4
 2
5
6 −7 

Bsp: A = 
 −3 6
8
9 
−4 −7 9 10
11. Eine quadratische Matrix heisst schiefsymmetrisch (engl. skew-symmetric), wenn
A = −AT .


0
1 2
Bsp: A =  −1 0 3 
−2 −3 0
12. Bei der Nullmatrix sind alle Elemente 0.
95
UZH
MA S410
6.2
Geometrie und Lineare Algebra
Rechnen mit Matrizen
Matrizen sind nicht nur praktisch in der Lagerung von Information sondern auch in deren
Verarbeitung. Man kann mit ihnen rechnen ähnlich wie mit den reellen Zahlen.
6.2.1
Addition von Matrizen und skalare Multiplikation
zurück zu Beispiel 1
Betrachten wir wieder unsere Buchhandlung. Sind wir nun an den Verkaufszahlen über
eine Periode von zwei Monaten, Juli und August interessiert, so ist es selbstverständlich,
dass sich die Verkaufszahlen von J und A addieren:

 
 

6 8
7 9
13 17
J + A =  15 20  +  18 31  =  33 51 
45 64
52 68
97 132
Wollen wir aber wissen, wie die Situation aussehen würde, wenn sich die Verkaufszahlen
im Juli verdoppeln und im August halbieren würden, dann erhalten wir:

 

6 8
12 16
2J = 2 ·  15 20  =  30 40 
45
 64
 90
 128

7 9
3.5 4.5
0.5A = 0.5 ·  18 31  =  9 15.5 
52 68
26 34
Definition 6.2.1.
Sind A = (aij ) und B = (bij ) zwei m × n−Matrizen und ist c ein Skalar (reelle Zahl), so
definieren wir
1. Addition von zwei Matrizen: A + B = (aij ) + (bij ) = (aij + bij )
2. skalare Multiplikation: cA = c(aij ) = (caij )
3. Subtraktion: −A = (−aij ) und A − B = (aij ) − (bij ) = (aij − bij )
Eigenschaften
Sind A, B, C alles m × n-Matrizen und sind s, t Skalare, dann gelten die Gesetze.
1. Kommutativgesetz: A + B = B + A
2. Assoziativgesetz : A + (B + C) = (A + B) + C
3. Inverse von A bez. + : −A = (−1)A, dann gilt: A + (−A) = 0m×n
96
UZH
MA S410
Geometrie und Lineare Algebra
4. 1 · A = A
5. 0 · A = 0m×n
6. (st) · A = s(tA) = stA
7. s(A + B) = sA + sB
8. (A + B)T = AT + B T
9. (sA)T = sAT
10. (AT )T = A
Man sagt auch, dass die Menge aller m × n-Matrizen einen Vektorraum bezg̈lich der
Addition über dem Körper der reellen Zahlen bildet.
Beispiel 6.2.2.
Überprüfen Sie alle obigen Eigenschaften mit folgenden Matrizen und Skalaren.
1 2 3
2 −3 4
A=
, B=
,
−3 2 −4
4 5 6
−2 −6 8
C=
, s = 3, t = −2.
3
5 −8
6.2.2
Multiplikation eines Zeilenvektors mit einem Spaltenvektor:
Skalarprodukt

~x · ~y = xT · y =
x1 x2 . . . xn


·

y1
y2
..
.

n
 X

=
xk yk = x1 y1 + x2 y2 + . . . + xn yn

 k=1
yn

Beispiel ~x · ~y = xT · y =

Aber:
1
2 −4

−1
2
y·x =
3 −6
T

2
−2 −1  −1  = 1
3

−2
1 
−3
97
UZH
MA S410
6.2.3
Geometrie und Lineare Algebra
Multiplikation von Matrizen
Sind A eine m × n-Matrix und B eine n × p-Matrix dann ist die Produktmatrix C eine
m × p-Matrix.
Das Element (cij ) , also das Element in der i-ten Zeile und j-ten Spalte der Produktmatrix
berechnet sich aus dem Skalarprodukt der i-ten Zeile von A und der j-ten Spalte von B.
Am×n · Bn×p = Cm×p
A · B = (aij ) · (bjk ) =
n
X
!
aij · bjk
j=1
 
a11 . . . a1n

..
..  · 
A · B =  ...
.
.  
am1 . . . amn


  Pn
Pn
...
b11 . . . b1p
j=1 a1j bj1
j=1 a1j bjp

..
..
..  = 
.
..
.

.   P ..
. P ..
.
.
n
n
bn1 . . . bnp
j=1 amj bjp
j=1 amj bj1 . . .
Beispiel 6.2.3.


1 2
A =  3 4 ,
5 6
B=
−1 1
3 2
⇒
A · B =?
Mit dem folgenden Schema lässt sich das Matrizenprodukt bequem errechnen:
B= −1 1
3 2




1 2

=A·B
A= 3 4 
5 6
Definition 6.2.4.
Ist A eine quadratische n × n-Matrix, dann heisst A invertierbar, wenn es eine quadratische Matrix B derselben Dimension n gibt, sodass gilt: A · B = B · A = En wobei En
die Einheitsmatrix derselben Dimension n ist.
B heisst die Inverse von A. Man schreibt: B = A−1 .
Also gilt:
A · A−1 = A−1 · A = E
98
UZH
MA S410
Geometrie und Lineare Algebra
Beispiel 6.2.5.
Zeigen Sie, dass B die Inverse von A ist, wenn gilt:
3 5
2 −5
B=
, A=
.
1 2
−1
3
Beispiel 6.2.6.


1 4 0
Warum ist die Matrix C =  2 5 0  nicht invertierbar?
3 6 0
Eigenschaften der Matrizenmultiplikation
Es seien A, F m × n-Matrizen, B, G n × r-Matrizen, C eine r × s-Matrix und λ ∈ R eine
beliebige Zahl.
Dann gelten folgende Aussagen:
1. (A · B)C = A(B · C) = ABC
2. A(λB) = (λA)B = λAB
Assoziativgesetz
Multiplikation mit einer Zahl
3. A(B + G) = AB + AG und (A + F )B = AB + F B
Distributivgesetze
4. AE = EA = A , falls A quadratisch
5. (AB)T = B T AT
6. AB 6= BA
Im Allgemeinen gilt kein Kommutativgesetz!
99
UZH
MA S410
6.3
Geometrie und Lineare Algebra
Anwendungen
6.3.1
Beispiel: Gartenbaugeschäft
Ein Gartenbaugeschäft verkauft 3 Sorten Grassamen.
Die Deluxe-Sorte enthält 80% Riedgras und 20% Roggen.
Die Standard-Sorte enthält 60% Riedgras und 40% Roggen.
Die Economy-Sorte enthält 40% Riedgras und 60% Roggen. Ein Kunde möchte eine Mischung kaufen, die 5 kg Riedgras und 3 kg Roggen enthält.
a) Ist dies ohne Abfall möglich?
b) Wie viel von jeder Sorte muss man mischen?
Sorte
Anteil
Riedgras
Anteil
Roggen
Menge in
Kilogramm
Deluxe
80%
Standard
60%
Economy
40%
20%
40%
60%
x1
x2
x3
Vorratsvektor:
~b =
5
3
Anteilsmatrix:
A=
Vektor ~x
−Riedgras
−Roggen
0.8 0.6 0.4
0.2 0.4 0.6

Mengenvektor:
Matrix A

x1
~x =  x2 
x3
2×3-Matrix
−Deluxe
−Standard
−Economy
Man erhält das folgende Gleichungssystem (linear inhomogen):
0.8x1 + 0.6x2 + 0.4x3 = 5 0.2x1 + 0.4x2 + 0.6x3 = 3 Dieses kann einfach in Matrizenform geschrieben werden.
0.8 0.6 0.4
0.2 0.4 0.6
100


x1
5
·  x2  =
3
x3
UZH
MA S410
Geometrie und Lineare Algebra
oder noch kürzer
A
·
~x
=
~b

  
x1
2



x2
5 .
Eine ganzzahlige Lösung ist z.B. ~x =
=
x3
1
c) Nun sei von den 3 Grassamensorten folgender Vorrat in kg vorhanden:
Deluxe 60
Standard 50
Economy 30


60
Vorratsvektor : ~v =  50 
30
Die Keimraten sind in folgender Tabelle festgehalten:
Samenart
Unter feuchten Bedingungen
Unter trockenen Bedingungen
Riedgras
80%
60%
Roggen
70%
40%
Was ist wohl die Keimmatrix K?
Wie viele kg Samen keimen unter den jeweiligen Witterungsverhältnissen?
Der Gesamtvorrat an Riedgras und Roggen ist in Matrizenschreibweise:
A · ~v = u~.
Die Gesamtmenge der Samen, die unter den jeweiligen Witterungsverhältnissen keimen, ist:
Bei feuchtem Wetter:
Bei trockenem Wetter:
In Matrizenschreibweise:
K · ~u = w
~
K · (A · ~v ) = w
~
(Keimmatrix) · (Anteilsmatrix) · (Vorratsvektor) = (Keimvektor)
107
w
~=
heisst: Bei feuchtem Wetter keimen 107 kg, bei trockenem Wetter 74
74
kg.
101
UZH
MA S410
6.3.2
Geometrie und Lineare Algebra
Stochastische Matrizen
Stochastische Matrizen sind im Wesentlichen Übergangsmatrizen, die angeben, wie eine
gewisse Grösse sich von einem Zeitpunkt zum nächsten verändert. Die Matrixelemente
entlang einer Spalte sind nicht negativ und addieren sich zu 1. Die Spaltenvektoren sind
sog. Wahrscheinlichkeitsvektoren.
Beispiel:
Ein Soziologe habe aus Statistiken in Erfahrung gebracht, dass in jedem Jahr 15% der
Stadtbewohner in die Vororte, während 3% der Vorortsbewohner in die Stadt ziehen. Der
Einfachheit halber nehmen wir an, dass die Bevölkerungszahl innerhalb des Einzugsgebiets
der Grossstadt konstant bleiben. Gegenwärtig leben 500 000 Menschen in der Stadt und
700 000 in den Vororten.
a) )Wie wird die Verteilung der Bevölkerung in einem Jahr sein?
b) Wie viele werden es in 2, 10, 100 und 200 Jahren sein?
Aus
Stadt
In die Stadt
In die Vororte
Total
1.00
der Aus den Vororten
1.00
102
UZH
MA S410
6.3.3
Geometrie und Lineare Algebra
Populationsmatrizen: Bevölkerungsentwicklung
Die Individuen einer gewissen Kolonie von Säugetieren habe eine Lebenserwartung von
bis zu drei Jahren. Die Entwicklung der Populationsgrösse hängt von der Fruchtbarkeitsrate und der Sterberate der Tiere ab. Da nur die Weibchen Junge gebären, genügt es, die
Beobachtungen auf diese zu beschränken.
Wir teilen die Weibchen in drei Gruppen ein: jene im Alter von 0 – 1 Jahr, jene von 1 –
2 Jahren und jene von 2 – 3 Jahren. Von den neugeborenen Weibchen überleben 40% bis
zum ersten Geburtstag. Von diesen überleben 50% bis zum zweiten Geburtstag. Die noch
nicht einjährigen haben keine Nachkommen. Die Weibchen der mittleren Altersgruppe
haben im Durchschnitt zwei Nachkommen und jene der ältesten Altersgruppe gebären im
Durchschnitt ein Junges.
x1 , x2 , x3 seien die Anzahl Weibchen in den betreffenden Altersgruppen.
Aus den obigen Angaben lässt sich die Altersverteilung y1 , y2 , y3 innerhalb der Kolonie
für das darauf folgende Jahr berechnen.
Wie lautet die Populationsmatrix A, so dass A · ~x = ~y ?
Berechnen Sie die Verteilung nach 1, 10, 20, 30, 40 Jahren, wenn die momentane Bevölkerung x1 = x2 = x3 = 1000 beträgt.
Auf welche Verteilung wird sich die Bevölkerung schliesslich stabilisieren?
103
UZH
MA S410
6.3.4
Geometrie und Lineare Algebra
Verkehrsfluss
Die untenstehende Figur stellt den Verkehrsfluss durch das Netz von Einbahnstrassen dar.
Die Pfeile geben die Fahrtrichtung an. Die Zahlen über den Strassen nach einer Kreuzung
geben den Anteil des Verkehrs an, der von der Kreuzung her in diese Strasse eintritt.
x1 = 1000, x2 = 2000 sei die Anzahl der Autos, die von links her über die Einfahrten ins
Strassennetz eintreten.
Bestimmen Sie die Anzahl Autos w1 , w2 , w3 , w4 , die das Strassennetz über die Ausgänge
rechts verlassen.
104
UZH
MA S410
6.3.5
Geometrie und Lineare Algebra
Inzidenzmatrizen (Graphen als Matrizen)
Graphen kann man als Matrizen codieren. Hierzu werden die Ecken des Graphen durchnummeriert, sodass eine feste Reihenfolge besteht. Die Nachfolger der j-ten Ecke sind
dann in der jten Spalte der Darstellungsmatrix ersichtlich. So wird zum Beispiel der unten
abgebildete Graph durch die sogenannte Nachfolgematrix (Inzidenzmatrix) dargestellt.


0 0 1
A= 1 1 0 
1 0 0
Teilmengen der Ecken der Graphen werden dann als Vektoren dargestellt. Die Menge
{1, 2} ist zum Beispiel der Vektor
 
1

1 .
v=
0
1. Was bedeutet A · v?
2. Berechnen sie A2 . Was bedeutet A2 · v?
3. Wie finde ich heraus, auf wie vielen Pfaden der Länge 3 ich von der Ecke 3 zur Ecke
1 komme?
4. Wie finde ich heraus, auf wie vielen Pfaden der Länge maximal 3 ich von der Ecke
3 zur Ecke 1 komme?
105
UZH
MA S410
Geometrie und Lineare Algebra
106
Kapitel 7
Lineare Gleichungssysteme
7.1
Das Gauss’sche Eliminationsverfahren
Kleine Gleichungssysteme löst man meistens mit Hilfe des Additionsverfahrens, indem
man in einer mehr oder weniger geschickten Reihenfolge solange Unbekannte eliminiert,
bis die Lösung ersichtlich ist. Hier wollen wir ein Verfahren zeigen, das die Lösungsschritte
systematisiert. Dieses Verfahren heisst Gauss Eliminationsverfahren. Es ist besonders
bei umfangreichen Gleichungssystemen nützlich und kann leicht programmiert werden. In
vielen Taschencomputer ist das Verfahren vorprogrammiert. An einem einfachen Beispiel
lernen Sie dieses Verfahren kennen.
Beispiel 7.1.1.
Gegeben ist ein Gleichungssystem mit 3 Gleichungen und 3 Unbekannten. Links wird das
Rechnen mit den Gleichungen gezeigt, rechts das Rechnen mit der zugehörigen, um die
Konstantenspalte erweiterten Koeffizientenmatrix.
~
A · ~x = b
x1 − 2x2 − x3 = 3
3x1 − 6x2 − 5x3 = 3
2x1 − x2 + x3 = 0
I
II
III
~

(A|b)
1 −2 −1 3
 3 −6 −5 3 
2 −1 1 0
Die Idee ist nun folgende: Die Variable x1 soll in der 2. und 3. Gleichung eliminiert werden.
Auf der rechten Seite heisst dies, dass unter der 1 links oben nur Nullen stehen. Dazu wird
die Gleichung I unverändert gelassen. Die Gleichung II wird durch II − 3 · I und III
durch III − 2 · I ersetzt.
Durch diese Manipulationen wird die Lösungsmenge des Gleichungssystems nicht verändert.
107
UZH
MA S410
Geometrie und Lineare Algebra


x1 − 2x2 − x3 = 3 3
I
1
−2
−1
3x1 − 6x2 − 5x3 = 3 II − 3 · I
 3 −6 −5 3 
2x1 − x2 + x3 = 0 III − 2 · 1
2 −1 1 0


x1 − 2x2 − x3 = 3 I
1 −2 −1 3
−2x3 = −6
II
 0 0 −2 −6 
3x2 + 3x3 = −6 III
0 3
3 −6
Die Gleichungen II und III werden vertauscht, um ein dreieckförmiges System zu erhalten. Auch dadurch wird die Lösungsmenge des Gleichungssystems nicht verändert.


x1 − 2x2 − x3 = 3 3
I
1
−2
−1
3x2 + 3x3 = −6  0 3
II/3
3 −6 
−2x3 = −6
III/(−2)
0 0 −2 −6
In II wird der Koeffizient von x2 normiert, indem wir II durch 3 dividieren. In III wird
der Koeffizient von x3 normiert, indem wir III durch −2 dividieren.


x1 − 2x2 − x3 = 3 I
3
1
−2
−1
x2 + x3 = −2
II
 0 1
1 −2 
III
x3 = 3
0 0
1 3
Alle eben durchgeführten Manipultionen haben die Lösungsmenge des Gleichungssystems
nicht verändert; sie heissen elementare Zeilenoperationen.
Die eben erhaltene Matrix

1 −2 −1 3
 0 1
1 −2 
0 0
1 3

ist in Dreiecksstufenform (engl.: row echelon form, ref).
Die letzte Gleichung gibt das Resultat x3 = 3. Dies kann nun in die oberen Gleichungen
eingesetzt werden. Dies kann auch mit erlaubten Zeilenoperationen durchgeführt werden.
Es bleibt also III unverändert. In II und I eliminieren wir x3 , indem wir II durch II −III
und I durch I + III ersetzen.


x1 − 2x2 − x3 = 3 I + III
1 −2 −1 3
x2 + x3 = −2
II − III
 0 1
1 −2 
x3 = 3
III
0 0
1 3


x1 − 2x2 = 6 I + 2 · II
6
1
−2
0
x2 = −5
 0 1 0 −5 
II
x3 = 3
III
0 0 1 3
108
UZH
MA S410
Geometrie und Lineare Algebra
Nun muss nur noch I verändert werden, um x2 zu eliminieren, indem I durch I + 2 · II
ersetzt wir


x1 = −4 1 0 0 −4
x2 = −5  0 1 0 −5 
x3 = 3 0 0 1 3
Die zuletzt erhaltene Matrix ist in sogenannter reduzierte Dreiecksstufenform (engl.:
reduced row echelon form, rref).
Die Lösung des Gleichungssystems ist also:

 

x1
−4
~x =  x2  =  −5  .
x3
3
Das Gleichungssystem hat genau eine Lösung; die reduzierte Dreiecksstufenmatrix ist
die Einheitsmatrix und rechts davon steht der Lösungsvektor.
Geometrisch kann man 3 lineare Gleichungen als 3 Ebenen im Raum auffassen. Hat das
Gleichungssystem genau eine Lösung, heisst das, dass sich die 3 Ebenen in einem Punkt
schneiden.
Bemerkung 7.1.2.
Zur Lösung dieses Gleichungssystems haben wir jeweils eine der folgenden Zeilenmanipulationen benützt. Man nennt sie
elementare Zeilenoperationen.
1. Vertauschen von zwei Zeilen: Zeilenaustausch
2. Multiplikation einer ganzen Zeile mit derselben nicht verschwindenden Zahl: Skalierung
3. Addition eines Vielfachen einer Zeile zu einer anderen Zeile: Zeilenaddition
109
UZH
MA S410
7.2
Geometrie und Lineare Algebra
Homogene und inhomogene Gleichungssysteme
Ein Gleichungssystem

a11 . . .
 ..
..
 .
.
am1 . . .

a1n
..
.
amn

b1
.. 
. 
bn

b1
 ..  ~
heisst homogen, falls  .  = 0 ist. Anderenfalls ist es inhomogen.
bn
Beispiel 7.2.1.
Lösen Sie das homogene System A~x = ~0 mit
Matrix A.

1
A= 2
3
3 Gleichungen und 3 Unbekannten mit der

2 3
3 1 
2 2
Wir bringen die Matrix auf Dreiecksform und finden, dass das System genau eine Lösung
hat, nämlich ~x = ~0. Diese Lösung heisst triviale Lösung.
Bemerkung 7.2.2.
Ein homogenes, lineares Gleichungssystem ist immer lösbar, da es immer die triviale
Lösung besitzt.
Satz 7.2.3.
1. Ein homogenes Gleichtungssystem hat immer mindestens eine Lösung, nämlich die
triviale Lösung ~x = ~0.
2. Falls ein inhomogenes Gleichungssystem Lösungen hat, so lässt sich der Lösungsraum wie folgt darstellen
→
−
−
−
−
~x = α1 →
x + α2 →
x2 + . . . + α d →
xd +
xs
,
{z
}
|{z}
| 1
Lösung des
spezielle Lösung
homogenen
des inhomogenen
Gleichungssystems
Gleichungssystems
110
α1 , α2 , . . . , αd ∈ R.
UZH
MA S410
Geometrie und Lineare Algebra
Beispiel 7.2.4 (allgemeines Vorgehen zur Berechnung der reduzierten Dreiecksform).
Gleichungssystem mit 3 Gleichungen und 6 Unbekannten:
0x1 + 0x2 + 2x3 − 4x4 − 5x5 + 2x6 = 5 0x1 + 1x2 − 1x3 + 1x4 + 3x5 + 1x6 = −1 0x1 + 6x2 + 0x3 − 6x4 + 5x5 + 16x6 = 7 1. Erweiterte Matrix (A|b)

0 0 2 −4 −5 2
 0 1 −1 1
3 1
0 6 0 −6 5 16

5
−1 
7
2. Ermittle die erste Spalte von links, die nicht aus lauter Nullen besteht: Pivotspalte.
Bringe dann das erste Element, das nicht null ist, durch Zeilenaustausch auf die oberste
Zeile: Pivotposition.
I ↔ II


0 1 −1 1
3 1 −1
 0 0 2 −4 −5 2 5 
0 6 0 −6 5 16 7
3. Mache alle Elemente unterhalb
III − 6 · I

0 1
 0 0
0 0
der Pivotposition durch Zeilenaddition zu Null.
−1 1
3
1
2 −4 −5 2
6 −12 −13 10

−1
5 
13
4. Ignoriere die schon erhaltenen Pivotzeilen und wiederhole die Schritte 2. bis 4. an der
übrig gebliebenen Teilmatrix.
III − 3 · II


0 1 −1 1
3 1 −1
 0 0 2 −4 −5 2 5 
0 0 0
0
2 4 −2
5. Normiere das unterste Pivotelement durch
1/2 · III

0 1 −1 1
 0 0 2 −4
0 0 0
0
Skalierung der Pivotzeile.
111

3 1 −1
−5 2 5 
1 2 −1
UZH
MA S410
Geometrie und Lineare Algebra
6. Mache alle Elemente oberhalb des untersten
Null.
II + 5 · III und I − 3 · III

0 1 −1 1 0
 0 0 2 −4 0
0 0 0
0 1
7. Normiere das zweit unterste Pivotelement
1/2 · II

0 1 −1 1
 0 0 1 −2
0 0 0
0
8. Mache alle Elemente oberhalb des
I + II

0 1
 0 0
0 0
Pivotelementes durch Zeilenaddition zu
−5
12
2

2
0 
−1
durch Skalierung der entsprechenden Zeile.

0 −5 2
0 6 0 
1 2 −1
zweit untersten Pivotelementes zu Null.
0 −1 0 1
1 −2 0 6
0 0 1 2
Das ist die reduzierte Dreiecksform.
In der reduzierten Dreiecksform lautet
0x1 + 1x2 + 0x3
0x1 + 0x2 + 1x3
0x1 + 0x2 + 0x3

2
0 
−1
das zugehörige Gleichungssystem:
− 1x4 + 0x5 + 1x6 = 2
− 2x4 + 0x5 + 6x6 = 0
+ 0x4 + 1x5 + 2x6 = −1
Die Variablen x2 , x3 , x5 gehören zu den Pivotelementen. Sie können leicht berechnet
werden, wenn für die übrigen Variablen irgend eine beliebige Zahl eingesetzt wird. Die
Variablen x1 , x4 , x6 sind frei wählbar.
Setzt man nun
x1 = λ1 ∈ R
x4 = λ2 ∈ R
x6 = λ3 ∈ R
so können die anderen 3 Variablen leicht bestimmt werden.
x2 = λ2 − λ3 + 2
x3 = 2λ2 − 6λ3 + 0
112
UZH
MA S410
Geometrie und Lineare Algebra
x5 = −2λ3 − 1
Als Lösung erhalten wir:



x1
 x2 




 x3 

 = λ1 
~x = 
 x4 




 x5 

x6
1
0
0
0
0
0








 + λ4 






0
1
2
1
0
0








 + λ6 






0
−1
−6
0
−2
1


 
 
 
+
 
 
 
0
2
0
0
−1
0








Definition 7.2.5.
1. x2 , x3 , x5 heissen Basis- oder Grundvariablen der Lösung. Sie gehören zu den
Pivotelemente der Matrix und sind nicht frei wählbar.
2. x1 , x4 , x6 heissen freie Variablen der Lösung. Sie kommen in der Lösung als Parameter vor und sind frei wählbar.
3. Das Gleichungssystem im obigen Beispiel hat unendlich viele Lösungen.
4. Ein Gleichungssystem, das lösbar ist, nennt man konsistent. Umgekehrt heisst ein
Gleichungssystem, das unlösbar ist, inkonsistent.
Beispiel 7.2.6.
Wird die erweiterte Matrix zum untenstehenden Gleichungssystem auf Dreiecksstufenform
gebracht, sieht man, dass das System keine Lösung besitzt.
x1 + 8x2 + 8x3 = 3 3x1 + 2x2 + 6x3 = 2 2x1 + 5x2 + 7x3 = 2 Zusammenfassend stellen wir fest, dass ein lineares Gleichungssystem
• 1 Lösung
• ∞ viele Lösungen
• keine Lösung
haben kann.
Beispiel 7.2.7.
Machen Sie sich diesen Sachverhalt an einem 2×2 Gleichungssystem klar.
Was ist die geometrische Bedeutung?
113
UZH
MA S410
7.3
Geometrie und Lineare Algebra
Rang einer Matrix, Lösbarkeit von Gleichungssystemen
Mit Hilfe des Gaussschen Eliminationsverfahrens haben wir die reduzierte Dreiecksform
einer Matrix bestimmt.
Es gilt der Satz, dass die reduzierte Dreiecksform einer Matrix eindeutig ist; d.h. eine
Matrix kann auf eine und nur eine reduzierte Dreiecksform gebracht werden.
Wir haben auch gesehen, dass Gleichungssysteme 0, 1 oder ∞ viele Lösungen haben
können und dass man das direkt an der reduzierten Dreiecksform ablesen kann.
Definition 7.3.1.
A sei eine m × n Matrix.
1. Unter dem Rang (engl.: rank) einer Matrix A (rang(A)) versteht man die Anzahl
Zeilen in der reduzierten Dreiecksform, die nicht aus lauter Nullen bestehen.
2. Unter dem Rangdefekt (engl.: nullity) (null(A))verstehen wir die Ergänzung des
Rangs zur Anzahl Spalten.
Beispiel 7.3.2.
Bestimmen Sie Rang und Rangdefekt der

1
 2
M =
 3
2
Matrix M.
2
3
1
2
3
1
2
2
1
3
5
3

0
4 

2 
2
Definition 7.3.3.
1.
Rang(A) = Anzahl Pivotelemente in der reduzierten Dreiecksform
= Anzahl der Grundvariablen
= Anzahl linear unabhängiger Zeilen von A
2.
Null(A) = n − Rang(A)
= d
= Anzahl freie wählbarer Variablen
114
UZH
MA S410
Geometrie und Lineare Algebra
Mit Hilfe des Ranges kann man die Lösbarkeit von linearen Gleichungssystemen charakterisieren.
Satz 7.3.4 (Lösbarkeitskriterium). Folgende Bedingungen sind äquivalent:
1. A · ~x = ~b ist konsistent (lösbar)
2. Der Rang der erweiterten Matrix (A|~b) ist gleich dem Rang von A.
3. In der reduzierten Dreiecksform von (A|~b) gibt es keine Zeile, deren einziges nicht
verschwindendes Element sich in der letzten Spalte befindet.
Beispiel 7.3.5.
Lösen Sie das inhomogene Gleichungssystem.
x1 + 8x2 + 8x3 = 3 3x1 + 2x2 + 6x3 = 2 2x1 + 5x2 + 7x3 = 2 Beispiel 7.3.6.
Das Gleichungssystem A~x = ~b habe 4 Gleichungen und 4 Unbekannte.


2 1
0 3 10
 1 2 −3 0 −4 

(A, ~b) = 
 3 −4 2 1 3 
6 −4 5 7 27
Bestimmen Sie die Lösungen.
Beispiel 7.3.7.
Wie hängen die Lösungen des Gleichungssystems A~x = ~b vom Parameter a ab?


a 1 1
A= 1 a 1 
1 1 a
115


1
→
−
b =  1 .
1
UZH
MA S410
7.4
Geometrie und Lineare Algebra
Inverse Matrix
Quadratische Matrizen n × n Matrizen mit Rang n besitzen eine Inverse Matrix. Dies
ergibt sich unmittelbar aus deren Berechnung.
Das folgende Beispiel zeigt die Berechnung der Inversen auf.
Beispiel 7.4.1.
Berechnen Sie die Inverse Matrix von


5 3 4
A =  5 1 5 ,
6 3 5
falls diese existiert, indem Sie simultan 3
Da A · A−1 = E, also

 
5 3 4
x1
 5 1 5  ·  x2
6 3 5
x3
Gleichungssysteme lösen.
 

y1 z1
1 0 0
y2 z2  =  0 1 0  ,
y3 z3
0 0 1
kann man direkt die erweiterte Matrix (A|E) in die reduzierte Dreiecksform bringen und
A−1 steht schliesslich auf der rechten Seite.
122
116
Kapitel 8
Lineare Abbildungen
8.1
Lineare Abbildungen im R2
Die obige Abbildung ist entstanden, indem lineare Abbildungen auf ein Quadrat angewendet wurden.
Die Geometrie hat 2 Aspekte:
1. Wie können die Objekte, die erzeugt werden sollen, beschrieben werden
2. Wie können die erzeugten Objekte verändert (transformiert) werden.
Ein Objekte, das durch mehrere Vektoren erzeugt wird, soll auf ein anderes Objekt in
gewisser Weise abgebildet werden, ohne seine Form ganz zu verlieren. Die Abbildung, die
Vektoren wieder auf Vektoren abbildet, soll ”linear” sein. Was dies heisst, erfahren Sie in
folgendem Einführungsbeispiel und dann in exakter Definition.
Beispiel 8.1.1. Gegeben sei ein kartesisches Koordinatensystem im R2 mit der Standardbasis
1
0
e1 =
, e2 =
.
0
1
Weiter sind 2 Vektoren gegeben:
a1 =
2
1
,
a2 =
117
−2
4
.
UZH
MA S410
Geometrie und Lineare Algebra
Ein beliebiger Vektor
v=
v1
v2
v10
v20
= v1 e1 + v2 e2
werde abgebildet auf den Vektor
0
v =
= v1 a1 + v2 a2 .
Fragen:
1. Welches ist das Bild v’ des Vektors v =
2. Wie kann die Abbildung f : R2 → R2 ,
1/2
1
?
f (v) = v 0 beschrieben werden?
3. Berechnen Sie die Bilder der Basisvektoren und zeichnen Sie in einem Koordinatensystem das Einheitsquadrat und sein Bild.
118
UZH
MA S410
8.2
Geometrie und Lineare Algebra
Wichtige Eigenschaften linearer Abbildungen
Standardbasis e1 =
1
0
,
e2 =
0
1
a11
a21
.
Gegeben zwei Vektoren
a1 =
,
a2 =
a12
a22
.
Die Abbildung f bildet den Vektor v auf den Vektor v’ folgendermassen ab:
f :v=
v1
v2
= v1 e1 +v2 e2
→
0
v =
v10
v20
= v1 a1 +v2 a2 =
Dies kann in Matrizenform einfach geschrieben werden:
a11 a12
v1
0
v = f (v) = Av =
.
a21 a22
v2
v1 a11 + v2 a12
v1 a21 + v2 a22
(∗)
(∗∗)
Die Abbildung f kann auf verschiedene Arten betrachtet werden.
(*) heisst, dass v und v 0 die gleichen Koordinaten haben, einmal in der {e1 , e2 }-Geometrie
und einmal in der {a1 , a2 }-Geometrie. Das Einheitsquadrat ist auf ein Parallelogramm
transformiert worden (falls {a1 , a2 } eine Basis von R2 ist).
Definition 8.2.1. Eine Abbildung f : R2 −→ R2 auf sich heisst linear, wenn gilt für alle
Vektoren u, v ∈ R2 und für alle Zahlen α ∈ R :
1.
f (u + v)
=
f (u) + f (v)
↓
↓
zuerst addieren,
zuerst abbilden,
dann abbilden.
dann addieren.
2.
=
αf (u)
= αf (u)
f (αu)
↓
↓
zuerst abbilden,
zuerst strecken,
dann strecken.
dann abbilden.
Beide Eigenschaften können zusammengefasst werden zu einer mit Linearkombination von
2 Vektoren:
f (αu + βv) = αf (u) + βf (v), α, β ∈ R.
119
UZH
MA S410
Geometrie und Lineare Algebra
Beispiel 8.2.2. Ebenso wird eine lineare Abbildung f : R −→ R im R1 definiert.
Warum ist die Abbildung f (x) = 5x linear, aber g(x) = 5x + 2 nicht?
Satz 8.2.3.
f : R2 −→ R2 ist eine lineare Abbildung ⇐⇒ f kann durch eine Matrix A dargestellt,
werden.
Diese Matrix A heisst die Darstellungsmatrix von f bezüglich der Standardbasis.
Beweis.
=⇒:
Da f linear ist, gilt für jeden Vektorn u =
u1
u2
= u1 e1 + u2 e2 :
f (u) = f (u1 e1 + u2 e2 ) = u1 f (e1 ) + u2 f (u2 )
Die Bilder der Basisvektoren e1 und e2 sind gegeben:
a11
a12
f (e1 ) =
und f (e2 ) =
.
a21
a22
Dann gilt:
f (u) = u1
a11
a21
+ u2
a12
a22
u1
u2
=
u1 a11 + u2 a12
u1 a21 + u2 a22
=
a11 a12
a21 a22
u1
u2
⇐=:
Es gelte für jeden Vektor u =
und für die Matrix A =
a11 a12
a21 a22
f (u) = Au
Dann gilt speziell für die Basisvektoren
a11 a12
1
a11
f (e1 ) = Ae1 =
=
a21 a22
0
a21
und
120
:
= Au
UZH
MA S410
Geometrie und Lineare Algebra
f (e2 ) = Ae2 =
Für jeden Vektor u =
u1
u2
a11 a12
a21 a22
0
1
=
a12
a22
gilt dann wie vorher beschrieben
f (u) = Au =
u1 a11 + u2 a12
u1 a21 + u2 a22
= u1 f (e1 ) + u2 f (e2 )
Sind nun u und v zwei beliebige Vektoren und α und β zwei beliebige reelle Zahlen, so
erhält man die Linearität von f folgendermassen:
f (αu + βv) =
=
=
=
=
u v1 1
A(αu + βv) = A α
+β
u2
v2
αu1 + βv1
A(
)
αu2 + βv2
(αu1 + βv1 )f (e1 ) + (αu2 + βv2 )f (e2 )
αu1 f (e1 ) + βv1 f (e1 ) + αu2 f (e2 ) + βv2 f (e2 )
α u1 f (e1 ) + u2 f (e2 ) + β v1 f (e1 ) + v2 f (e2 )
= αAu + βAv = αf (u) + βf (v)
Damit ist der Satz bewiesen.
Aus dem obigen Satz folgen nun sofort die weiteren Eigenschaften.
Satz 8.2.4.
1. Wird die lineare Abbildung f dargestellt durch die Matrix
a11 a12
A=
,
a21 a22
also f (u) = Au, so ist sie linear und die Spalten von A sind die Bilder der Basisvektoren.
a11
a12
f (e1 ) =
, f (e2 ) =
a21
a22
2. Ist f : R2 −→ R2 eine lineare Abbildung, dann wird der Nullpunkt auf den Nullpunkt abgebildet.
Kontraposition: Ist f (0) 6= 0, dann ist f nicht linear.
121
UZH
MA S410
8.3
8.3.1
Geometrie und Lineare Algebra
Spezielle lineare Abbildungen
Streckungen
Welche Matrix gehört zu derjenigen Abbildung, die die Länge eines jeden Vektors v halbiert und seine Richtung umkehrt?
Wie lautet allgemein die Matrix der Abbildung, die jeden Vektor um den Faktor λ ∈ R
streckt?
M=
λ 0
0 λ
122
UZH
MA S410
8.3.2
Geometrie und Lineare Algebra
Spiegelungen
Spiegelung an der x -Achse in der xy -Ebene
Aus der Zeichnung ist ersichtlich, dass
x0 = x
y 0 = −y
Also lautet die zugehörige
Matrix:
1
0
0 −1
Spiegeln Sie den Punkt P (3,4) an der x -Achse.
Wie lautet die Matrix für die Spiegelung an der y- Achse?
Spiegeln Sie P (3,4) an der y-Achse.
Was passiert, wenn Sie zuerst an der x- und dann an der y-Achse spiegeln? Wie sieht die
Matrix dieser Abbildung aus?
123
UZH
MA S410
8.3.3
Geometrie und Lineare Algebra
Rotationsmatrizen in der xy-Ebene
Welches ist die Darstellungsmatrix einer Rotation um den Ursprung um den Winkel θ?
Wir wissen, dass die Bilder der beiden Basisvektoren die Spalten der Matrix sind.
1
cos θ
0
Der Basisvektor e1 =
wird auf a1 =
abgebildet und e2 =
auf
0
sin θ
1
− sin θ
a2 =
.
cos θ
Damit erhalten wir die Rotationsmatrix
cos θ − sin θ
R0,θ =
sin θ cos θ
R0,θ stellt eine Rotation um den Ursprung um den Winkel θ dar.
Wird ein beliebiger Punkt P (x, y) um den Ursprung 0 um den Winkel θ gedreht, so erhält
man den Bildpunkt P 0 (x0 , y 0 ) folgendermassen in vektorieller Darstellung.
0 x
x
cos θ − sin θ
x
= R0,θ
=
y
sin θ cos θ
y
y0
Beispiel 8.3.1.
1. Bestimmen Sie die Rotationsmatrix zum Winkel 30◦ .
2. Welche Koordinaten hat der um 30◦ um den Ursprung gedrehte Punkt P (3, 4)?
3. Welche Matrix gibt die Rotation um 0◦ wieder? Welche geometrische Bedeutung
hat diese Matrix?
4. Drehen Sie das Dreieck A(7,4), B (-2,5), C (0,6) um -45◦ um den Ursprung.
124
UZH
MA S410
8.4
Geometrie und Lineare Algebra
Scherung in x -Richtung in der xy -Ebene
Eine der prominentesten Anwendungen der Scherung finden wir in der Typografie, nämlich in der Ührung eines Normalbuchstabens in die kursive Form desselben Buchstabens.
Der Buchstabe I soll kursiv geschrieben werden: I
Der oberste rechte Punkt von I sei P (x, y).
Bei der Scherung bleibt der Buchstaben
gleich hoch, d.h. die y-Koordinate von P
verändert sich nicht.
Der kursive Buchstaben wird um einen gewissen Winkel ϕ gegenüber der Vertikalen
geneigt.
Ist m = tan ϕ, so verändert sich die
x -Koordinate um my.
Der neue Punkt P 0 hat dann die Koordinaten:
x0 = x + my
y0 = y
Also lautet die zugehörige Matrix
1 m
0 1
.
Diese Matrix gibt eine Scherung in Richtung x-Achse an.
Welche Matrix gibt eine Scherung in Richtung y-Achse an?
125
UZH
MA S410
8.5
Geometrie und Lineare Algebra
Zusammensetzung von linearen Abbildungen
→ v 0 ∈ R2 :
v 0 = Av
B : v 0 ∈ R2 → v 00 ∈ R2 : v 00 = Bv 0
__________________________________________________________
v 00 = Bv 0 = B(Av)
=
BAv
Matrizenmultiplikation
assoziativ
2
00
2
⇒ C = BA : v ∈ R
→ v ∈R
A : v ∈ R2
Im Allgemeinen ist das Zusammensetzen von linearen Abbildungen nicht kommutativ,
d.h.
AB 6= BA im Allgemeinen
Dies sieht man an folgendem Beispiel
Beispiel 8.5.1. Zwei lineare Abbildungen seien dargestellt durch die zwei Matrizen
1 2
−2 0
A=
, B=
3 0
1 3
.
Sind die beiden zusammengesetzten Abbildungen
C = AB und D = BA gleich?
2
Bestimmen Sie die Bilder von v =
unter den Abbildungen C und D.
−3
Bemerkung 8.5.2. Das Zusammensetzen von 2 Rotationen um den Ursprung ist aber
kommutativ. Es gilt sogar
Rβ · Rα = Rα+β = Rα · Rβ
Beweis?
126
UZH
MA S410
8.6
Geometrie und Lineare Algebra
Rotationsmatrizen im Raum (Computergrafik)
In der Computergrafik ist es eine immer wiederkehrende Aufgabe, einen räumlichen Gegenstand auf dem Bildschirm darstellen. Eine naturgetreue Darstellung vermittelt dem
Betrachter das Gefühl, den Gegenstand wirklich vor sich zu haben. Dazu möchte man um
den Gegenstand herum- oder sogar in ihn hineingehen. Auf dem Bildschirm braucht man
dazu verschiedene Ansichten dieses Gegenstands.
Mathematisch bedeutet dies, dass man den Gegenstand um verschiedene Achsen dreht
und dann auf den Bildschirm (Ebene) projiziert.
Im Raum gibt es, gemäss den Koordinatenachsen drei grundlegende Rotationan, nämlich
1. die Drehung um die x-Achse, in der Nautik Stampfen, in der Aeronautik Neigen
genannt.
2. die Drehung um die y-Achse, in der Nautik Schlingern, in der Aeronautik Rollen
genannt.
3. die Drehung um die z-Achse, in der Nautik und in der Aeronautik Gieren genannt.
Die zugehörigen Rotationsmatrizen sind:


1
0
0
Rx =  0 cos θ − sin θ  ,
0 sin θ cos θ


cos θ 0 sin θ
0
1
0 ,
Ry = 
− sin θ 0 cos θ
127


cos θ − sin θ 0
Rz =  sin θ cos θ 0 
0
0
1
UZH
MA S410
Geometrie und Lineare Algebra
Ebenso gibt es drei grundlegende Projektionen (Orthogonalprojektionen), nämlich
1. die Projektion auf die yz-Ebene entlang der x-Achse, auch Aufriss genannt.
2. die Projektion auf die xz-Ebene entlang der y-Achse, auch Seitenriss genannt.
3. die Projektion auf die xy-Ebene entlang der z-Achse, auch Grundriss genannt.
Die zugehr̈igen Projektionsmatrizen lauten:




0 0 0
1 0 0
Pyz =  0 1 0  , Pxz =  0 0 0  ,
0 0 1
0 0 1
128

Pxy

1 0 0
= 0 1 0 
0 0 0
UZH
MA S410
8.7
Geometrie und Lineare Algebra
Kern und Bild einer Abbildung
Gegeben sei eine lineare Abbildung f , dargestellt durch die Matrix A.
f : u ∈ R2
→
u0 = Au ∈ R2
Definition 8.7.1. Unter dem Kern der Abbildung f versteht man die Menge aller Vektoren v ∈ R2 , die auf den Nullvektor abgebildet werden.
kernA = {v ∈ R2 |Av = 0}
Definition 8.7.2. Das Bild der Abbildung f ist die Menge aller möglichen Vektoren
w ∈ R2 , die als Ausgabe von f (v) = Av entstehen.
bildA = {w ∈ R2 |Av = w}
Die Spalten von A sind die Bilder der Basisvektoren, darum ist das Bild von A der von
den Spaltenvektoren aufgespannte Vektorraum, der Spaltenraum von A.
Beispiel 8.7.3.
1. Welches sind Kern und Bild der Abbildung f , dargestellt durch die Matrix
1
2
A=
2 −1
2. Welches ist der Kern der Orthogonalprojektion auf die e1 -Richtung?
3. Welches sind Kern und Bild der Abbildung g, dargestellt durch die Matrix
1 2
B=
2 4
129
UZH
MA S410
8.8
Geometrie und Lineare Algebra
Fixe Richtungen bei linearen Abbildungen
Beispiel 8.8.1. Die lineare Abbildung, die gegeben ist durch die Matrix
1
0
2
A=
,
0 12
ist nur eine Skalierung mit dem Faktor 21 vom Ursprung aus. Ein Kreis um den Ursprung
wird auf einen konzentrischen Kreis mit halbem Radius abgebildet. Der Einheitskreis wird
auf einen Kreis mit Radius 12 abgebildet.
2
1
2
2
0
0 2
0 2
k : x + y = 1 → k : (x ) + (y ) =
2
Beispiel 8.8.2. Die lineare Abbildung, die gegeben ist durch die Matrix
2 0
B=
,
0 1
streckt in e1 -Richtung und e2 -Richtung verschieden. Ein Kreis um den Ursprung wird nicht
mehr auf einen konzentrischen Kreis abgebildet sondern auf eine Ellipse. Der Einheitskreis
wird auf eine Ellipse mit Halbachsen 2 und 1 abgebildet.
0 2
x
2
2
2
0
k :x +y =1 → k :
+ (y 0 ) = 1.
2
Beim letzten Beispiel sieht man, dass Vektoren in e1 -Richtung und e2 -Richtung die Richtung behalten und nur die Länge verändert werden:
1
2
x
2x
0
B : e1 =
→ a1 =
,
v=
→ v =
= 2v
0 0 0 0 0
0
0
0
e2 =
→ a2 =
w=
→ w0 =
=w
1
1
y
y
Es gilt also folgendes:
1. Die Matrix B bildet gewisse Vektoren v ab auf Bv = λv.
2. Der Wert λ zeigt an, wie der Vektor v gestreckt wird.
Wir werden sehen, dass es bei einer 2 × 2-Matrix meistens 2 Richtungen gibt, die fix
bleiben, und dass diese Richtungen bei symmetrischen Matrizen orthogonal sind.
Solche Vektoren nennt man Eigenvektoren, die zugehörigen λ-Werte Eigenwerte.
130
UZH
MA S410
8.9
Geometrie und Lineare Algebra
Eigenwerte und Eigenvektoren
Die Bedingung welche Eigenwerte λ und Eigenvektoren v erfüllen müssen lautet?
Av = λv.
(8.1)
Mit der Einheitsmatrix kann diese Bedingung auch anders geschrieben werden.
(A − λE)v = 0.
(8.2)
Ein von 0 verschiedener Vektor v ist genau dann ein Eigenvektor von A, wenn das Gleichungssystem (8.2) nichttriviale Lösungen hat.
Der Rang der Matrix A − λE muss kleiner als 2 sein und daher die Determinante = 0.
det(A − λE) = 0
(8.3)
m11 m12
Bemerkung: Die Determinante einer 2 × 2-Matrix M =
ist definiert durch
m21 m22
det M = m11 m22 − m12 m21
Definition 8.9.1.
1. Eine Zahl λ heisst Eigenwert von A, wenn sie Lösung der Gleichung (8.3),(8.2)
oder (8.1) ist.
2. Ein Vektor v(6= 0) heisst Eigenvektor von A zum Eigenwert λ, wenn er (8.1) rsp
(8.2) erfüllt.
Meistens werden die Eigenvektoren auf 1 normiert, d.h. |v| = 1.
Im R2 ist (8.3) eine quadratische Gleichung. Sie heisst charakteristische Gleichung von A,
die linke Seite von (8.3) ist das charakteristische Polynom von A.
Beispiel 8.9.2.
Welches sind die Eigenwerte und Eigenvektoren der Matrix
2 1
A=
?
1 2
131
UZH
MA S410
8.10
Geometrie und Lineare Algebra
Spezielle Fälle
1. Welche Eigenwerte und Eigenvektoren hat die folgende Matrix?
A=
1
2
0
0
1
2
Diese Matrix bestimmt eine Skalierung mit dem Faktor 12 . Also ist jede Richtung
eine Eigenrichtung. Es gibt nur einen Eigenwert λ = 12 . Geometrisch haben wir
schon gesehen, dass jeder Kreis auf einen konzentrischen Kreis abgebildet wird.
2. Was passiert mit einer Rotationsmatrix? Dazu untersuchen wir die Rotation um
90◦ , also die Matrix
R=
0 −1
1 0
Die charakteristische Gleichung heisst dann
λ2 + 1 = 0.
Es gibt keine reellen Eigenwerte und damit auch keine Richtungen, die fix bleiben.
Dies ist aber klar bei einer Rotation um 90◦ .
Besitzt eine Rotation um 180◦ Eigenwerte und Eigenvektoren?
2 2
3. Welche Eigenwerte und Eigenvektoren hat die Matrix C =
?
2 2
Was bedeutet dies?
Bemerkung 8.10.1.
1. Im allgemeinen sieht man der Matrix nicht einfach an, ob sie reelle Eigenwerte hat.
Man kann aber allgemein beweisen, dass jede symmetrische n × n-Matrix reelle
Eigenwerte hat.
2. Ein Eigenwert 0 bedeutet, dass der zugehörige Eigenvektor (bzw. die Eigenvektoren)
den Kern der Matrix bestimmen.
3. Für stochastische n × n-Matrizen könnte man sogar den folgenden Satz beweisen
Satz 8.10.2.
Jede stochastische n × n-Matrix A besitzt den Eigenwert 1.
Zudem gilt für alle Eigenwerte λ, dass |λ| ≤ 1.
132
UZH
MA S410
Geometrie und Lineare Algebra
Beweis für 2 × 2-Matrizen:
Eine stochastische 2 × 2-Matrix A ist von folgender Form
a
1−b
A=
,
1−a
b
wobei 0 ≤ a, b ≤ 1. Es muss nun gezeigt werden, dass
(a) 1 ist ein Eigenwert von A.
(b) Der Betrag des 2. Eigenwerts von A ist ≤ 1.
a−λ 1−b
det(A − λE) = det
= λ2 − (a + b)λ + (a + b − 1) = 0
1−a b−λ
und daraus
1
λ = [a + b ± (a + b − 2)]
2
Damit erhält man die beiden Eigenwerte
λ1 = 1
und
λ2 = a + b − 1 < 1
4. Stationäre Vektoren werden definiert durch
Definition 8.10.3.
Ein Vektor v heisst stationär bezüglich einer n × n Matrix A, falls v Eigenvektor
zum Eigenwert 1 ist, d.h. falls gilt:
A · v = v.
Warum dieser Name? - Iteriert man die Abbildung A n-mal, so erhält man
A2 v = a(Av) = Av = v, ..., An v = v.
Da jede stochastische Matrix einen Eigenwert 1 hat, so ist der zugehörige Eigenvektor ein stationärer Vektor.
133
UZH
MA S410
8.11
Geometrie und Lineare Algebra
Markov Prozesse (stochastische Matrizen)
Beispiel 8.11.1 (Lagerplanung). Ein Elektronik-Geschäft verkauft Videospiele und hat
maximal 300 Spiele auf Lager. Wenn am Ende des Tages, die Zahl der Einheiten welche
noch auf Lager sind ≤ 100 ist, so wird der Lagerbestand auf Beginn des nächsten Tages
wieder auf 300 aufgestockt. Wir nehmen folgende vereinfachte Situation an.
Käufe pro Tag
0
100
200
Wahrscheinlichkeit
0.3
0.4
0.3
Stellen sie die obige Situation graphisch dar. (Wir haben 4 Zustände 300, 200, 100, 0,
welche am Ende des Tages möglich sind.)
Folgende stochastische Matrix stellt also

0.3
0.4
A=
0.3
0
die obige Situation dar.

0 0.3 0.3
0.3 0.4 0.4
.
0.4 0.3 0.3
0.3 0
0
Eine interessante Frage ist die nach der stationären Wahrscheinlichkeitsverteilung des Lagerbestandes am Ende eines Tages. Wir suchen also einen Vektor v = (v0 , v1 , v2 , v3 )T , der
uns den durchschnittlichen Lagerbestand am Ende des Tages angibt, welcher mit den in
der Aufgabe gegebenen Übergangswahrscheinlichkeiten konstant bleibt.
Dies kann man durch Auflösung folgender Gleichung berechnen.
A · v = v.
Wir suchen also zum Eigenwert 1 einen Eigenvektor, falls möglich!
Dazu äquivalent ist das Lösen des homogenen Gleichungssystems:


−0.7
0
0.3 0.3
 0.4 −0.7 0.4 0.4
 · v = 0.
(A − E4 ) · v = 0 oder 
 0.3
0.4 −0.7 0.3
0
0.3
0
−1
134
(8.4)
UZH
MA S410
Geometrie und Lineare Algebra
Lösen wir 8.4 auf, so erhalten wir folgende Lösungsmenge


1.75
3.3333

L = {v ∈ R4 | v = µ · 
3.0833 µ ∈ R.}
1
Die Spaltensumme des v-Vektors soll 1 sein mit lauter positiven Komponenten. Darum
werden die Komponenten des v-Vektors durch die Spaltensumme (9.1666) geteilt. Wir
erhalten das stationäre Lagerbestandsverhälnis


0.19
 0.36 

v=
 0.34 
0.11
Bemerkung 8.11.2. v = (0.19, 0.36, 0.34, 0.11)T ist ein Eigenvektor zum Eigenwert 1.
Somit wird bei jedem Anfangszustand in unserem Lagerhaltungsbeispiel eine stationäre
Verteilung erreicht.
135
UZH
MA S410
8.12
Geometrie und Lineare Algebra
Googles PageRank-Algorithmus
Google’s Erfolg leitet sich zum grössten Teil aus dem PageRank-Algorithmus ab. Er ist
das Herz der Google-Suchmaschine und ordnet alle Dokumente des WWW nach ihrer
”Wichtigkeit” an. Die bedeutendste Website erscheint zu oberst.
Die eigentlichen Erfinder des PageRank-Algorithmus sind die beiden Stanford-Forscher,
Sergey Brin und Larry Page.
Literatur:
David Austin: How Google Finds Your Needle in the Web’s Haystack
(http://www.ams.org./featurecolumn/archive/pagerank.html)
Kurt Bryan & Tanya Leise: The $ 25 000 000 000 Eigenvector. The Linear Algebra behind
Google (http://www.rose-hulman.edu/~bryan/googleFinalVersionFixed.pdf)
In diesen Artikel finden Sie noch weitere lesenswerte Artikel zum Thema.
Einfaches Beispiel eines Webs
Unser Web habe nur 4 Seiten. Ein Pfeil von Seite i zu Seite j bedeutet, dass es einen Link
von i nach j gibt
Bedeutung einer Website: Die Bedeutung der i-ten Website soll eine reelle Zahl xi ∈ R
sein. Je grösser xi je höher wird die Website i rangiert.
Ziel des Googles PageRank-Algorithmus: Berechnung des Vektors x, der die Bedeutung der Websites angibt.


x1
 x2 
4

x=
 x3  ∈ R
x4
Nach was für Kriterien soll die Bedeutung einer Website berechnet werden?
136
UZH
MA S410
Geometrie und Lineare Algebra
1. Eine Website soll umso bedeutender sein, je mehr Links von anderen Seiten auf sie
zeigen.
2. Links von bedeutenderen Websites sollen stärker zählen als solche von unbedeutenderen.
3. Ein Link von einer Website, die sehr viele Links nach Aussen hat (Outlinks), soll
weniger stark zur Bedeutung beitragen (Beliebigkeit).
Prinzip des Google PageRank-Algorithmus:
Jede Website hat genau eine Stimme zur Verfügung. Diese Stimme verteilt sich gleichmästig auf alle Seiten auf die sie zeigt (Outlinks). Dieses Prinzip wird als Web-Democracy
bezeichnet.
Dieses Prinzip führt auf ein lineares Gleichungssystem für den Vektor x.
Die Gleichung für die Bedeutung der Website 1 erhält man wie folgt.
1
x1 = 0 · x1 + 0 · x2 + 1 · x3 + x4
2
Warum? - Die Website 1 erhält keinen Link von sich selbst, von der Website 2 auch keinen,
aber einen von Site 3. Da Site 3 nur einen Outlink hat, nämtlich nach Site 1, erhält die
Website 1 den vollen Wert 1 von Website 3. Von der Website 4 erhält 1 nur eine halbe
Stimme, da Website 4 genau 2 Outlinks hat.
Das komplette lineare Gleichungssystem lautet somit:
x1
x2
x3
x4
= 0 · x1
= 13 · x1
= 13 · x1
= 13 · x1
+ 0 · x2
+ 0 · x2
+ 12 · x2
+ 12 · x2
+
+
+
+
1 · x3
0 · x3
0 · x3
0 · x3
+ 12 x4
+ 0x4
+ 12 x4
+ 0x4
Dieses Gleichungssystem kann in Matrizenform geschrieben werden.


0 0 1 12
 1 0 0 0 
3

x = P x, wobei P = 
 1 1 0 1 .
3
2
2
1
1
0 0
3
2
Die Link-Matrix P ist eine stochastische Matrix, besitzt also den Eigenwert 1. Der gesuchte Bedeutungsvektor x des Webs ist also ein Eigenvektor zum Eigenwert 1 von P .
137
UZH
MA S410
Geometrie und Lineare Algebra
Mit dem Gauss-Algorithmus lösen wir dazu das homogene Gleichungssystem
(P − E)x = 0
und erhalten eine Lösung
 
12
4

x=
9
6
Die Website 1 erhält das höchste Ranking, gefolgt von Website 3, dann kommt Website
4 und auf dem letzten Platz steht Website 2.
Die Link-Matrix P wird noch modifiziert und es kommt eine zweite Matrix S dazu, die
einem rein zufälligen Surfverhalten ohne Links entspricht, d.h. alle Elemente sind N1 , bei
einem Web mit N Websites.
Die Google-Matrix ist eine Überlagerung der beiden Matrizen.
G = αP + (1 − α)S
Ist α = 1, so erhalten wir wie im Beispiel nur die Matrix P . Die Erfinder des PageRankAlgorithmus, Sergey Brin und Larry Page, wählten α = 0.85.
Wählt man α = 0, so hat man ein rein zufälliges Verhalten ohne auf die Links zu achten.
Für das Netz im Einführungsbeispiel erhalten wir die Google-Matrix


0 0 1 21

 1 0 0 0 
3
+0.15 
G = 0.85 
1
1
1


0 2 
3
2
1
1
0 0
3
2

1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4
1
4


0.0375
  0.320833
=
  0.320833
0.320833

0.0375 00.8875 0.4625
0.0375 0.0375 0.0375 

0.4625 0.0375 0.4625 
0.4625 0.0375 0.4625
Auch dies ist eine stochastische Matrix und hat deshalb den Eigenwert 1. Als Eigenvektor
erhält man (gerundet)
 
18
7

x=
14 ,
10
also wieder dasselbe Ranking.
138
Kapitel 9
Graphen und Algorithmen
9.1
Einführung
Das klassische Einführunsproblem der Graphentheorie ist
Das Königsberger Brücken Problem
Die Abbildung zeigt die Stadt Königsberg im 18. Jahrhundert. Die beiden Arme des
Flusses Pregel umfliessen die Insel, den Kneiphof. Es gibt insgesamt 7 Brücken über den
Fluss.
Abbildung 9.1: Königsberg
Ist es möglich, von der Insel aus einen Rundgang durch die Stadt zu unternehmen, wäh139
UZH
MA S410
Geometrie und Lineare Algebra
renddessen man jede Brücke genau einmal überquert und am Schluss zum Ausgangspunkt
zurückkehrt?
Leonhard Euler (1707 Basel - 1783 St.Petersburg) beantwortete 1736 diese Frage mit
einer Methode, welche die moderne Graphentheorie begründete.
Abbildung 9.2: Leonhard Euler
Anwendungen: Optimierungsprobleme auf Graphen
• Gütertransport von Produzenten zu Verbrauchern soll kostenminimal werden
• kostengünstiges Netz von Versorgungsleitungen und kostenminimaler oder grösster
Durchfluss durch das Netz
• kürzeste Wege in Verkehrsnetzen
• Tourenplanung: schnellst mögliche Belieferung von Kunden
• Terminplanung von Projekten
• optimale Energienetze
Oft lassen sich sehr grosse Probleme (z.B. Verkehrsnetze mit Hunderten von Strassen) mit
graphentheoretischen Methoden mit relativ geringem, d.h. polynomialem Rechenaufwand
lösen. Aber es gibt auch sehr schwere Probleme, die wahrscheinlich nur mit exponentiellem Rechenaufwand zu lösen sind.
140
UZH
MA S410
Geometrie und Lineare Algebra
Viele Probleme sind in populärer Form sehr bekannt und wirken eher wie eine Knobelaufgabe. Ihre Anwendungsmöglichkeiten sind heute mit den schnellen Computern aber
enorm.
Aufgabe: Brunnenproblem
Vor langer Zeit in einem fernen Königreich standen drei Häuser in einem Tal und es gab
in der Nähe drei Brunnen und das Wasser war rein und klar. Es war ein friedliches Tal,
solange bis Zwietracht dort einkehrte. Die drei Höfe fielen in Feindschaft und der Streit
wollte kein Ende nehmen. An Versöhnung war nicht zu denken. Die Menschen in den
drei Höfen bestanden darauf, drei direkte Pfade zu den drei Brunnen zu haben. Die Pfade
sollten aber die der Nachbarn nicht kreuzen. Wenn es von jedem Hof aus diese Wege gäbe,
wären alle zufrieden und im Tal könnte Frieden einkehren. Doch bis heute herrscht dort
Streit.
Kann es jemals Frieden geben?
Mit zwei Brunnen ist das Problem einfach! Aber mit drei Brunnen ist es hoffnungslos!
Skizzieren Sie das Problem mit 2 und 3 Brunnen.
Im Kern handelt dieses Problem vom Zeichnen von Figuren in der Ebene ohne mit dem
Stift abzusetzen. Sie kennen wohl aus ihrer Kindheit das Zeichnen der Laterne (auch Haus
des Nikolaus genannt)
Abbildung 9.3: Haus des Nikolaus
Ein praktisches Beispiel dazu ist das Postbotenproblem.: Ein Briefträger muss in seinem Dorf allen Leuten die Post verteilen. Dazu muss er alle Strassen mindestens einmal
durchlaufen. Welcher Weg ist der kürzeste? Kann man diesen Weg in vertretbarer Zeit
berechnen?
141
UZH
MA S410
Geometrie und Lineare Algebra
Ein weiteres Problem ist die Routenplanung, zum Beispiel im GPS.
Abbildung 9.4: GPS
Abbildung 9.5: Verkehrsplan
Ein anderes Beispiel handelt vom Design von Computerchips: Stehen in einem Schaltkreis
die Positionen der einzelnen Komponenten auf der Platine schon fest, können dann die
Verbindungen auf der Oberfläche ohne Kreuzungen verlaufen? Oder eine andere Frage:
Welche Position der Komponenten und der Verdrahtung auf der Platine beansprucht den
geringsten Platz?
142
UZH
MA S410
Geometrie und Lineare Algebra
Abbildung 9.6: Computerchips
Solche angewandten Probleme gehören zusammen mit dem Design effizienter Algorithmen
allesamt zur Graphentheorie.
143
UZH
MA S410
9.2
Geometrie und Lineare Algebra
Grundbegriffe
Eine einfache Struktur auf einer Menge wird erzeugt durch eine binäre Relation. Zwei
Elemente stehen in einer vorgegebenen Beziehung oder eben nicht. Das sind genau die
Graphen. Sie sind die fundamentale Datenstruktur der diskreten Mathematik.
Definition 9.2.1. Ein Graph G(V, E) besteht aus einer endlichen Menge V und einer
Menge E ⊂ V × V .
Die Elemente von V heissen Ecken (Knoten, vertices) und die Elemente von E heissen
Kanten (edges).
Beispiele
1. V = {1, 2, 3, 4, 5}, E = {{1, 2}, {1, 4}, {1, 56}, {2, 3}, {2, 4}, {4, 5}}
2. Graph zum Königsberger Brückenproblem
Abbildung 9.7: Königsberger Brückenproblem
144
UZH
MA S410
Geometrie und Lineare Algebra
Definitionen
1. Ein Graph kann parallele Kanten (Mehrfachkanten) haben.
2. Eine Ecke kann mit sich selbst verbunden sein, eine solche Kante heisst Schlinge.
3. Eine Ecke, von der aus keine Kanten gehen, heisst isolierte Ecke.
4. Ein Graph ohne Mehrfachkanten und ohne Schlingen heisst einfach.
5. Ein Graph kann zusammenhängend oder nicht zusammenhängend sein (dann
besteht er aus mehreren Teilen.
6. Zwei Ecken heissen benachbart (adjazent), wenn sie durch eine Kante miteinander verbunden sind.
7. Zwei Kanten heissen inzident, wenn sie eine Ecke gemeinsam haben.
8. Die Ordnung eines Graphen ist |V | = Anzahl Ecken.
9. Die Grösse des Graphen ist |E| = Anzahl Kanten.
145
UZH
MA S410
Geometrie und Lineare Algebra
10. Der Grad einer Ecke A ist die Anzahl Kanten, die von dieser Ecke ausgehen; er
wird mit d(A) (degree) bezeichnet. Ist d(A) = 0, so ist A eine isolierte Ecke.
Abbildung 9.8: Grad einer Ecke
11. Unter einem vollständigen Graphen Kn mit n Ecken versteht man einen Graphen,
bei dem jede Ecke mit jeder durch eine Kante verbunden ist.
Abbildung 9.9: vollständige Graphen
Wie viele Kanten hat ein vollständiger Graph mit n Ecken?
146
UZH
MA S410
9.3
Geometrie und Lineare Algebra
Über Grade von Ecken
Beispiel: Tennisturniere
Bei einem Tennisturnier spielt jeder gegen jeden einmal. Nach einer gewissen Zeit sind
folgenden Spiele gespielt:
Der Graph ist einfach, denn jeder spielt gegen jeden genau einmal und keiner spielt gegen
sich selbst. Beim jetzigen Spielstand zählen wir nur die gespielten Spiele und nicht die
Ergebnisse.
Es gibt Leute, welche die gleiche Anzahl Spiele gespielt haben. Ist das bei jedem Turnier
so?
Welches sind die möglichen Spielstände bei n Personen?
Abbildung 9.10: mögliche Spielstände
Für n = 2, 3 gibt es jedes Mal mindestens 2 Personen mit der gleichen Anzahl Spiele; also
147
UZH
MA S410
Geometrie und Lineare Algebra
mindestens 2 Ecken mit demselben Grad.
Das gilt sicher nicht, wenn der Graph nicht einfach ist, wie das folgende Beispiel zeigt.
Abbildung 9.11: mögliche Spielstände
Satz 9.3.1. In jedem einfachen Graph gibt es mindestens 2 Ecken mit demselben Grad.
Beweis. Der Graph habe n Ecken (n = |V |) ⇒ 0 ≤ Eckgrad ≤ n − 1
i) Eine Ecke a1 habe den Grad n − 1.
Dann ist a1 mit allen anderen Ecken verbunden und keine Ecke hat den Grad 0.
Auf die n−1 verbleibenden Ecken müssen die Eckgrade 1, 2, ..., n−1 verteilt werden.
Also muss eine Zahl zweimal vorkommen.
ii) Keine Ecke hat den Grad n − 1.
Also müssen die Zahlen 0, 1, 2, ..., n − 2 auf n Ecken verteilt werden.
Damit muss eine Zahl zweimal vorkommen.
Satz 9.3.2. In jedem Graph ist die Summe der Grade der Ecken gleich der doppelten
Anzahl Kanten.
X
d(ai ) = 2|E|
ai ∈V
Beweis. Jede Kante verbindet 2 Ecken. Gibt es q Kanten, so hat es 2q Enden. Damit ist
die Summe der Eckgrade gleich 2q.
Bemerkungen
1. Dieser Satz gilt auch für nicht einfache Graphen, also Graphen mit Schlingen und
Mehrfachkanten.
2. Der zweite Satz ist auch als handshaking lemma bekannt:
In einer Gruppe von Menschen begrüssen sich einige per Handschlag andere nicht.
Notiert man bei jedem , wie viele Hände er geschüttelt hat und addiert die Zahlen,
so erhält man stets eine gerade Zahl.
Aus dem zweiten Satz folgt sofort der nächste.
148
UZH
MA S410
Geometrie und Lineare Algebra
Satz 9.3.3. In jedem Graph ist die Anzahl der Ecken mit ungeradem Grad gerade.
Beweis. Ist die Summe von ungeraden Zahlen gerade, so ist die Anzahl Summanden
gerade.
X
ai ∈V
d(ai ) |{z}
=
n
X
nEcken i=1
d(ai ) =
X
X
d(ai ) +
Ecken ungeraden Grads
d(ai ) = 2m
Ecken geraden Grads
Definition 9.3.4. Zwei Graphen heissen isomorph, wenn der eine durch kontinuierliche
Verformung aus dem anderen hervorgeht.
Mathematisch heisst dies:
Zwei Graphen sind isomorph, wenn es eine bijektive Abbildung f : V → V 0 gibt, so dass
gilt:
{x, y} ∈ E ⇔ {f (x), f (y)} ∈ E 0
Beispiel 9.3.5.
1. Sind die beiden Graphen isomorph?
2. Beschreiben Sie den Isomorphismus für die beiden Graphen.
3. Skizzieren Sie einen Graphen, dessen Ecken die Grade 1, 2, 3, 4 haben. Gibt es einen
einfachen solchen Graph?
149
UZH
MA S410
Geometrie und Lineare Algebra
4. Wie viele Kanten besitzt ein Graph mit n Ecken, wenn alle Ecken denselben Grad
g haben?
Definition 9.3.6.
1. Eine Folge aufeinander folgender Kanten (e1 , e2 , . . . , en ) mit ei = (vi−1 , vi ) ist ein
Kantenzug.
Die Ecken vi (i = 0, ..., n) müssen nicht notwendigerweise verschieden sein.
2. Ein Kantenzug heisst geschlossen, wenn v0 = vn .
3. Ein Weg oder eine Kette ist ein Kantenzug, der jede Ecke höchstens einmal enthält.
4. Ein Kreis ist ein geschlossener Weg v0 = vn .
150
UZH
MA S410
9.4
Geometrie und Lineare Algebra
Bäume
Die Theorie der Bäume stammt ursprünglich aus der Chemie, entwickelt aus dem Studium
der Kohlenwasserstoffverbindungen und anderer Isomere.
Abbildung 9.12: Bäume in der Chemie
Bäume sind die fundamentalen Bausteine der Graphen. Sie ergeben auch die geeignete
Datenstruktur für viele diskrete Probleme, vor allem für Such- und Sortierprobleme.
Definition 9.4.1.
1. Ein Graph heisst ein Baum, wenn er zusammenhängend ist und keine Kreise enthält. Ein Graph, dessen Komponenten Bäume sind, heisst ein Wald.
Abbildung 9.13: Bäume mit höchstens 5 Ecken
2. G(V, E) sei ein zusammenhängender Graph. Ein Untergraph T von G heisst ein
aufspannender Baum (spanning tree), wenn T ein Baum der Ordnung n = |V |
ist.
151
UZH
MA S410
Geometrie und Lineare Algebra
Jeder zusammenhängende Graph besitzt aufspannende Bäume:
Entweder ist G schon ein Baum oder G besitzt einen Kreis. Entfernt man von diesem Kreis
eine Kante, so ist G immer noch zusammenhängend. Entweder haben wir jetzt schon einen
aufspannenden Baum oder wir müssen noch eine Kante eines Kreises entfernen. Auf alle
Fälle sind wir in endlich vielen Schritten fertig.
Satz 9.4.2. Folgende Aussagen sind äquivalent:
1. G(V, E) ein Baum.
2. Je zwei Ecken in G sind durch genau einen Weg verbunden.
3. G ist zusammenhängend und es gilt: |E| = |V | − 1.
in Worten: Ein Baum hat eine Ecke mehr als Kanten.
Weiter gilt für einen Baum T der Ordnung n ≥ 2 und der Gradfolge der Ecken (d1 , d2 , . . . , dn )
der folgende Satz.
Satz 9.4.3. In einem Baum ist die Summe der Grade der Ecken gleich der doppelten
Kantenzahl.
n
X
dk = 2(n − 1)
k=1
Frage: Wie viele aufspannende Bäume besitzt ein Graph? - Schwierigeres Problem
Satz 9.4.4. Satz von Cayley
Der vollständige Graph Kn auf {1, 2, ..., n} mit n ≥ 2 besitzt nn−2 aufspannende Bäume.
152
UZH
MA S410
Geometrie und Lineare Algebra
Frage: Wie findet man in einem Graphen einen aufspannenden Baum oder einen aufspannenden Wald? Wie erkennt man, ob ein Graph zusammenhängend ist?
Ein Algorithmus zur Konstruktion eines aufspannenden Baums ist der folgende.
BREADTH-FIRST-SEARCH (Breitensuche)
1. Wähle beliebige Ecke und gib ihr die Nummer 1: aktuelle Ecke
2. Aktuelle Ecke habe Nummer iund die Nummern 1, ..., r seien vergeben.
Falls r = n: STOP
Sonst: Gib den nicht nummerierten Nachbarn von i die Nummern r + 1, r + 2, . . .
und füge Kanten ein: i(r + 1), i(r + 2), . . .
Falls i + 1 nicht existiert: STOP
Sonst: Gehe zur Eckei + 1, das ist die neue aktuelle Ecke, und iteriere 2.
Beispiele
1. Suchen Sie einen aufspannenden Baum mit dem Breath-First-Search-Algorithmus
2. G ist durch folgende Nachbarschaftslisten gegeben. Wenden Sie den Breath-FirstSearch-Algorithmus an und beantworten Sie damit die Frage, ob G zusammenhängend ist.
153
UZH
MA S410
9.5
Geometrie und Lineare Algebra
Minimal aufspannende Bäume (Minimal Spanning
Tree)
Gegeben sei der Plan eines Kommunikationsnetzes mit Kosten f§r den Leitungsbau. Die
Schaltelemente sind die Ecken, die Verbindungen zwischen den Schaltelementen die Kanten. Die Zahlen §ber den Kanten sind die Kosten. Gesucht ist ein Schaltplan, sodass jedes
Element mit jedem kommunizieren kann und die Kosten f§r den Leitungsbau minimal
werden.
Modellierung durch einen gewichteten Graphen.
Gegeben ist ein zusammenhängender GraphG(V, E) und eine Gewichtfunktion w . Gesucht ist ein aufspannender Baum T mit minimalem Gewicht.
X
w(T ) =
∈ E(T )w(e)
e
Beispiel: Mit Breath-First-Search kann ein aufspannender Baum konstruiert werden. Dieser muss noch nicht optimal sein.
Greedy-Strategy (gierige Strategie)
Arbeite nach folgender Maxime:
Erledige immer als nächstes den noch nicht bearbeiteten fettesten (optimalen) Teilbrocken. Die folgenden beiden Algorithmen arbeiten nach der Greedy-Strategie.
1. Kruskal-Algorithmus Beim Kruskal-Algorithmus wird immer die Kante mit minimalem Gewicht gewählt, aber so, dass keine Kreise entstehen.
154
UZH
MA S410
Geometrie und Lineare Algebra
Abbildung 9.14: Beispiel mit Kruskal-Algorithmus
2. Algorithmus von Prim Sei G(V, E) ein gewichteter zusammenhŁngender Graph
mit n Ecken. (Jeder minimal aufspannende Baum hat also n − 1 Kanten.)
(a) Wähle eine Kante minimalen Gewichts aus (samt den dadurch gegebenen
Ecken). Diese Kanten stellen samt ihren Ecken den Anfangsbaum T dar, der
im folgenden systematisch zu einem minimal aufspannenden Baum ausgebaut
wird.
(b) Solange der aufzubauende Baum T weniger als n − 1 Kanten hat, führe folgendes aus:
Suche unter denjenigen Kanten mit einer Ecke in T und einer Ecke ausserhalb
T eine Kante mit minimalem Gewicht aus, sodass kein Kreis entsteht und füge
sie zu T dazu (samt des dadurch bestimmten Knotens).
Der mit Hilfe von Prims Algorithmus konstruierte Teilgraph T ist ein minimal aufspannender Baum des ursprünglichen Graphen G.
Bemerkungen zum Beweis: Da der Graph endlich ist und bei jedem Teilschritt eine
neue Kante dazu kommt, bricht der Algorithmus nach endlich vielen Schritten ab.
Nach Abbruch des Algorithmus sind n − 1 Kanten konstruiert, also alle n Ecken
benützt. Mit Induktion könnte man jetzt zeigen, dass der konstruierte aufspannende
Baum T minimal ist. Die Konstruktion ist nicht eindeutig.
155
UZH
MA S410
Geometrie und Lineare Algebra
Abbildung 9.15: Beispiel mit Algorithmus von Prim
Abbildung 9.16: Beispiel zu beiden Algorithmen
156
UZH
MA S410
9.6
Geometrie und Lineare Algebra
Kürzeste Wege in Graphen
Optimierungsprobleme auf gewichteten Graphen:
• Strassenplan: in möglichst kurzer Zeit oder mit möglichst wenig Kilometern von A
nach B gelangen
• Verkehrsnetz: Schienennetz, Gewichtung der Kanten können die Fahrkosten, die
Reisezeit, die Entfernung sein. Die Bahnverbindung vonA nach B soll möglichst
billig, möglichst kurz sein.
• Kommunikationsnetz: Übertragungskosten oder Übertragungszeit als Gewicht der
Kanten. Gesucht ist der kostengünstigste Weg eines Datenpakets von einem Knoten
zu einem anderen.
Meistens wird vorausgesetzt, dass der Ausgangsknoten den Graphen vollständig kennt.
Im Schienenverkehr oder im Strassenverkehr kennt man gewöhnlich den ganzen Graphen.
Im Internet ist das nicht immer der Fall: Knotenausfall Überlastung von Kanten.
Kürzeste Wege Problem:
• Der kürzeste Weg zwischen zwei Knoten.
• Die kürzesten Wege zwischen einem Knoten und zu allen anderen Knoten.
• Der kürzeste Weg in einem Graphen, bei dem alle Knoten (ev. genau einmal) besucht
werden.
Abbildung 9.17: Welcher Weg ist der kürzeste?
Gegeben ist ein zusammenhängender Graph G und eine Gewichtsfunktion
w : E → R+ = {x ≥ 0}
Sei u ∈ V gegeben. Für einen Weg P = P (u, v) von u nach v ist die gewichtete Länge
von P :
X
l(P ) =
∈ E(P )w(e)
e
157
UZH
MA S410
Geometrie und Lineare Algebra
Gesucht ist ein kürzester Weg von u nach v, d.h. l(P ) soll minimal werden.
Die Länge eines kürzesten Weges bezeichnet man als den Abstand d(u, v).
Der berühmte Algorithmus von Dijkstra konstruiert, ausgehend von einer fest gewählten Ecke u, einen aufspannenden Baum, dessen Weg von u nach v stets ein kürzester ist
für alle Ecken v des Graphen.
Abbildung 9.18: Edsger Wybe Dijkstra, 1930 - 2002, holländischer Mathematiker, Algorithmus 1959
Wir erläutern den Algorithmus hier an einem Beispiel.
Beispiel zum Dijkstra Algorithmus
1. Startknoten grün
2. Alle Nachbarknoten blau, Abstand vom Startknoten anschreiben
3. Wähle als neuen Startknoten denjenigen mir kürzestem Abstand zum Start: grün
(samt Kante zum vorherigen Startknoten)
4. zurück zu 1. (verbotene Kanten: rot)
158
UZH
MA S410
Geometrie und Lineare Algebra
Abbildung 9.19: Beispiel zum Dijkstra-Algorithmus
Beispiel zum Dijkstra Algorithmus
Abbildung 9.20: Tabelle zum Beispiel
Noch ein Beispiel: Vom Knoten a aus alle kürzesten Wege berechnen.
Abbildung 9.21: noch ein Beispiel
159
UZH
MA S410
9.7
Geometrie und Lineare Algebra
Eulersche Graphen
Beim Königsberger Brückenproblem sucht man einen speziellen Kantenzug. Dieser sollte
die folgenden Eigenschaften besitzen.
1. Der Kantenzug enthält keine Kante doppelt.
2. Der Kantenzug enthält alle Kanten des Graphen.
3. Anfang und Ende des Kantenzugs stimmen überein.
Definition 9.7.1. Eine Tour ist ein Kantenzug nur mit der 1. Eigenschaft; er enthält
also keine Kante doppelt.
Eine Eulertour ist ein Kantenzug mit allen 3 obigen Eigenschaften. Jede Kante des Graphen wird also genau einmal durchlaufen und der Kantenzug ist geschlossen.
Ein Graph mit einer Eulertour heisst auch Eulerscher Graph.
Gibt es beim Königsberger Brückenproblem eine Eulertour?
Abbildung 9.22: Königsberg
Beispiel 9.7.2. Suchen sie in den untenstehenden Graphen geschlossenen Touren und
Eulertouren.
Welche Grade der Ecken kommen in den Graphen vor?
Gibt es Touren mit der Eigenschaft 2, also Kantenzüge, die jede Kante genau einmal
enthalten?
Ergänzen Sie den letzten Graph, so dass eine Eulertour möglich ist.
160
UZH
MA S410
(a)
Geometrie und Lineare Algebra
(b)
(c)
Satz 9.7.3. Ein zusammenhängender Graph ist genau dann eulersch (d.h. es gibt eine
Eulertour), wenn der Grad jeder Ecke gerade ist.
Beweis.
A) Ist der Graph G eulersch, dann ist der Grad jeder Ecke gerade, denn man verlässt
jede Ecke genau so oft wie man wie man hereinkommt!
B) Die andere Richtung lässt sich algorithmisch beweisen. Es handelt sich um den
Algorithmus von Hierholzer, 1973.
Voraussetzung: Sei G(V, E) ein zusammenhängender Graph, dessen Knoten alle geraden Grad aufweisen.
(a) Wähle eine Ecke A, beginne einen Pfad und markiere jede durchlaufene Kante.
Jede so erreichte Ecke kann wieder verlassen werden bis sich der Kantenzug
schliesst, da die Gradzahl jeder Ecke gerade ist. So entsteht ein Kreis.
(b) Vernachlässige nun alle Kanten dieses Unterkreises.
(c) Hat es noch unmarkierte Kanten, so beginnt eine in einer bereits traversierten
Ecke B. Von B aus kann wieder ein Kreis konstruiert werden, der dann in den
zuerst konstruierten eingebaut werden kann.
(d) Konstruiere nun weiter solche Kreise, bis alle Kanten aufgebraucht sind.
Das Resultat ist eine Eulertour.
Bemerkung: Die Komplexität diesses Algorithmus ist linear in der Anzahl Kanten.
Satz 9.7.4. Es sei G(V, E) ein zusammenhängender Graph mit k Knoten ungeraden
Grades. Dann gilt folgendes.
1. Ist k = 0, so gibt es auf G eine Eulertour.
2. Ist k = 2, so gibt es auf G eine Tour, die alle Kanten des Graphen enthält. Man
kann den Graph in einem Zug zeichnen, ohne eine Kante doppelt zu zeichnen.
161
UZH
MA S410
Geometrie und Lineare Algebra
Abbildung 9.23: Algorithmus von Hierholzer
3. Ist k > 2, so gibt es auf G keine Tour, die alle Kanten enthält.
zum Beweis:
1. Dies wurde im letzten Satz mitdem Algorithmus von Hierholzer bewiesen.
2. Verbinde die beiden Ecken ungeraden Grades durch eine zusätzliche Kante. Konstruiere jetzt mit (1) eine Eulertour. Lösche nun die eingefügte Kante.
Abbildung 9.24: zum Beweis (2)
3. klar wegen (1) und (2).
Was passiert, wenn man jede Kante zweimal durchläuft?.
Satz 9.7.5. In jedem zusammenhängenden Graph gibt es einen Kantenzug, der jede
Kante genau zweimal durchläuft.
Beweis: Man zeichnet einfach zu jeder Kante eine zweite parallele Kante. So erhält jede Ecke einen geraden Grad. Wegen des vorherigen Satzes gibt es eine Eulertour. Nun
verschmelzt man die neuen Kanten wieder mit den ursprünglichen und erhält so einen
Kantenzug, der jede Kante genau zweimal durchläuft.
162
UZH
MA S410
Geometrie und Lineare Algebra
Beispiel 9.7.6. Bildergalerie
Meistens sind die Bilder längs Gängen aufgehängt. Auf einem Rundgang durch die Ausstellung möchte man alle Bilder sehen, ohne aber zweimal an denselben Bildern vorbeizukommen. Am Ende mŽchte man wieder beim Eingang ankommen, der zugleich Ausgang
ist. Ist ein solcher Rundgang überhaupt möglich?
Abbildung 9.25: Ausstellungsraum
163
UZH
MA S410
9.8
Geometrie und Lineare Algebra
Hamiltonsche Graphen
Europareise Eine Gruppe Jugendlicher möchte von Berlin aus mit der Bahn alle eingezeichneten Städte genau einmal besuchen und am Schluss wieder nach Berlin zurückkehren. Ist dies möglich?
Abbildung 9.26: Eisenbahn-Netzplan
Bei dieser Reise soll jede Stadt genau einmal besucht werde. Es ist aber egal, ob jede
Eisenbahnstrecke benützt wird oder nicht. Es ist also keine Eulersche Tour gesucht.
Definition 9.8.1. Ein Hamiltonscher Kreis ist ein geschlossener Kantenzug, der jede Ecke des Graphen genau einmal enthält. Ein Graph, der einen Hamiltonschen Kreis
enthält, heisst ein Hamiltonscher Graph.
(a) Hamiltonscher Graph
(b) kein Hamiltonscher Graph
164
UZH
MA S410
Geometrie und Lineare Algebra
Beispiel 9.8.2. Der Netzplan des Dodekaeders besitzt einen Hamiltonzyklus. Suchen Sie
einen solchen Kreis! Im Spiel von Hamilton “Around the World“ soll man solche Touren
finden, die jede Stadt (Ecken) des Dodekaederplans genau einmal besucht.
165
UZH
MA S410
Geometrie und Lineare Algebra
Beispiel 9.8.3. Billige Reise
Jetzt soll die Reise eine Rundfahrt durch die 4 Städte St. Gallen, Zürich, Basel und Bern
sein. Die Kosten sollen minimal werden.
Wie viele Hamiltonsche Kreise gibt es? Welche Reise ist die billigste?
Bemerkung Der obige Graph ist vollständig, d.h. von jeder Ecke gibt es zu jeder Ecke
eine Kante.
Hat ein vollständiger Graph n Ecken, so kann man von einer beliebigen Ecke aus die
Hamiltonsche Reise beginnen, man hat noch n − 1 Ecken zur Auswahl. Bei der nächsten
Ecke sind es noch n − 2 usw. Im Ganzen hat man also (n − 1)(n − 2) · · · 2 × 1 = (n − 1)!
Möglichkeiten.
Ist uns die Richtung, wie der Hamiltonsche Kreis durchlaufen wird egal, so erhält man
nur die Hälfte der Möglichkeiten. Also gilt
Satz 9.8.4.
Kreise.
In einem vollständigen Graph mit n Ecken gibt es
166
(n−1)!
2
Hamiltonsche
UZH
MA S410
Geometrie und Lineare Algebra
In der obigen Reise mit 4 Städten gibt es nur 3 Hamiltonsche Kreise. Unter diesen möchte
man den billigsten finden.
Zahlenbeispiel
Bei 6 Städten gibt es schon 5!2 = 60 Hamiltonsche Kreise.
Aber bei 20 Städte sind es etwa 60 Billiarden Hamiltonsche Kreise. Mit 1 Million Rechenoperationen pro Minute braucht man etwa 2 × 106 Jahre.
Wer interessiert sich dann noch für dieses Problem!
Das ist das berühmte Traveling Salesman Problem (TSP).
Ein Handelsreisender hat Kunden in n Städten{S1 , S2 , . . . , Sn }. Es gebe Strassen von jeder
Stadt zu jeder anderen mit vorgegebenen Längen d(Si , Sj ), der Distanz längs der Kante
SiSj. Welche Route soll er wählen, wenn er jede Stadt genau einmal besuchen will, der Weg
möglichst kurz sein soll und unser Reisender am Schluss zum Anfangspunkt zurückkehren
soll?
Gesucht ist also ein Hamiltonscher Kreis minimaler Länge.
Bemerkung 9.8.5.
• Im Allgemeinen ist es schwierig zu entscheiden, ob ein Graph einen Hamiltonschen
Kreis enthält.
• Bis heute ist kein Algorithmus bekannt, der in polynomialer Zeit einen Hamiltonschen Kreis findet oder ausschliesst.
In polynomialer Zeit bedeutet, dass die Anzahl erforderlicher Rechenschritte höchstens mit einer festen Potenz der Anzahl Knoten und Kanten wächst.
• Ebenso ist nicht bekannt, ob ein Algorithmus existiert, der in polynomialer Zeit den
kürzesten Weg findet. Man hält es auch für unwahrscheinlich, dass überhaupt ein
solcher Algorithmus existiert.
• Das Travelling-Salesman-Problem (TSP), bei dem man durch jeden Knoten genau
einmal geht, ist nicht zu verwechseln mit dem Chinesischen Postbotenproblem, bei
dem jede Kante mindestens einmal durchlaufen wird und der Weg minimale Länge
haben soll.
• Zu diesen beiden Standardproblemen gibt es tausende von Anwendungen, die alle
unter dem Titel Routenplanung bezeichnet werden können:
Das TSP tritt auf in der Routenplanung von Speditionen, der Müllabfuhr, von
Lieferungen, Car-Pooling, beim automatischen Bohren, Löten, Schweissen von Leiterplatten, usw.
167
UZH
MA S410
Geometrie und Lineare Algebra
• Interessante Informationen zum TSP finden Sie im Internet, z.B. unter:
http://www.math.Princeton,edu/tsp/
168
UZH
MA S410
Geometrie und Lineare Algebra
169