1.1.2 Stabkräfte berechnen

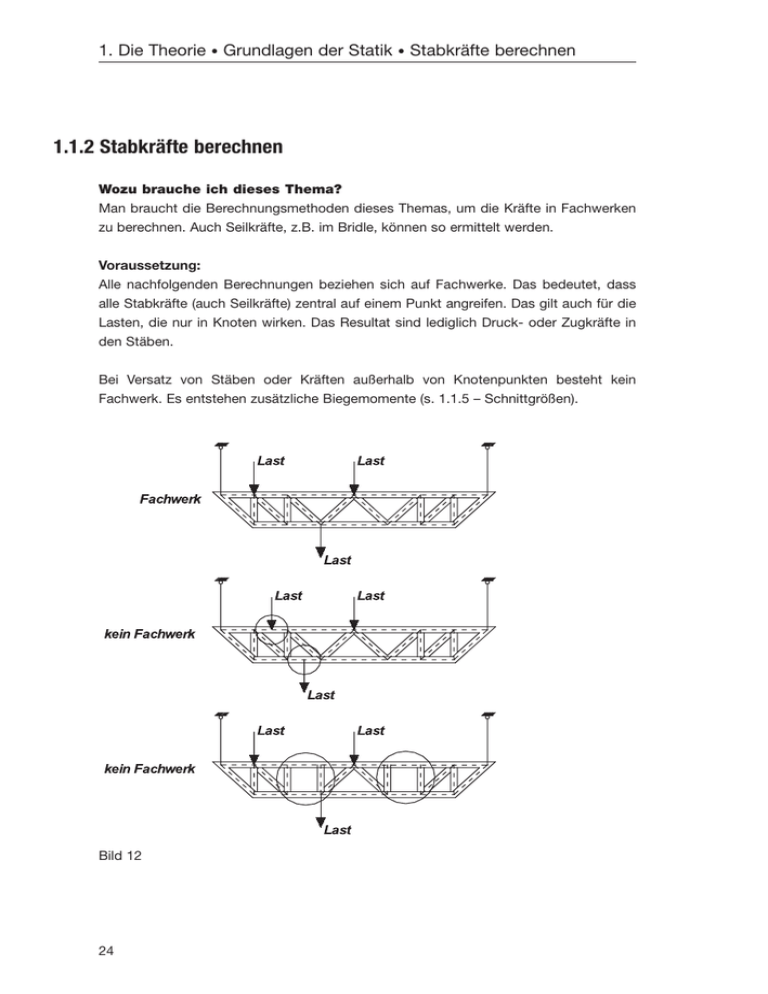
1. Die Theorie • Grundlagen der Statik • Stabkräfte berechnen
1.1.2 Stabkräfte berechnen
Wozu brauche ich dieses Thema?
Man braucht die Berechnungsmethoden dieses Themas, um die Kräfte in Fachwerken
zu berechnen. Auch Seilkräfte, z.B. im Bridle, können so ermittelt werden.
Voraussetzung:
Alle nachfolgenden Berechnungen beziehen sich auf Fachwerke. Das bedeutet, dass
alle Stabkräfte (auch Seilkräfte) zentral auf einem Punkt angreifen. Das gilt auch für die
Lasten, die nur in Knoten wirken. Das Resultat sind lediglich Druck- oder Zugkräfte in
den Stäben.
Bei Versatz von Stäben oder Kräften außerhalb von Knotenpunkten besteht kein
Fachwerk. Es entstehen zusätzliche Biegemomente (s. 1.1.5 – Schnittgrößen).
Bild 12
24
1. Die Theorie • Grundlagen der Statik • Stabkräfte berechnen
Um nun die Stabkraftberechnung kennen zu lernen, greifen wir zu einem Beispiel, das
im Rigging zu Hause ist. Es wird ein Abgriff an einer Traverse mit Rundschlinge untersucht. Es ist wichtig zu wissen, wie groß die Kräfte in den Strängen des Anschlagmittels
sind, um entsprechendes Material auswählen zu können. Natürlich gibt es die
gebrauchsfertigen Tabellen zu den Anschlagmitteln, die die zugehörigen Faktoren der
Belastbarkeit für verschiedene Winkel angeben. Dennoch ist es wichtig zu wissen, wie
sich diese Werte erklären und wo sie herkommen.
Bsp.:
Abgriff einer Traverse mit Rundschlinge
Bild 13
Für diese Anordnung werden nun die Kräfte in den Strängen der Rundschlinge berechnet. Auch für die Stabkraftberechnung gibt es ein schrittweises Lösungsverfahren:
1. Skizze des statischen Systems am Knotenpunkt anfertigen
2. Komponentenzerlegung der „schiefen“ Kräfte
3. Aufstellen und Lösen der Gleichgewichtsbedingungen
25
1. Die Theorie • Grundlagen der Statik • Stabkräfte berechnen
1. Skizze des statischen Systems
Man greift sich für die Skizze stets einen Knotenpunkt mit einer bekannten Kraft heraus.
In unserem Beispiel ist das sehr leicht, weil es nur einen relevanten Knotenpunkt gibt –
den mit der Lastangabe 10,0 kN.
Alle bekannten Kräfte werden in bekannter Richtung eingezeichnet. Alle unbekannten Kräfte werden vom Knotenpunkt weg gezeichnet. Es wird für die unbekannten Kräfte also zunächst angenommen es seien Zugkräfte, die in unserem Beispiel
am Schäkel ziehen.
Bild 14
26
1. Die Theorie • Grundlagen der Statik • Stabkräfte berechnen
2. Komponentenzerlegung der „schiefen“ Kräfte
Als „schiefe“ Kräfte wirken hier nur die Kräfte der Rundschlinge. Sie bestehen jeweils
aus einer X- und einer Y-Komponente. Die bekannte Kraft 10 kN wirkt direkt auf der YAchse und braucht daher nicht zerlegt zu werden. Die Zerlegung selbst funktioniert wie
bereits bei Kapitel 1, „Zusammenfassen von Kräften“, beschrieben.
In unserem Fall haben beide Stränge den gleichen Namen, da beide durch identischen
Winkel die gleiche Kraft aufnehmen.
Für jede unserer Komponenten ergibt sich somit:
sin 55° = Sx / S
cos 55° = Sy / S
Nun löst man die Gleichungen nach Sx und Sy auf:
Sx = sin 55° * S
Sy = cos 55° * S
anders umgestellt:
S = Sx / sin 55°
S = Sy / cos 55°
Zahlenwerte können im Fall der unbekannten Kräfte nicht eingesetzt werden.
Mehr können wir in diesem Schritt nicht tun.
27
1. Die Theorie • Grundlagen der Statik • Stabkräfte berechnen
3. Aufstellen der Gleichgewichtsbedingungen
Der Begriff der Gleichgewichtsbedingungen muss zunächst erläutert werden:
Gleichgewicht bedeutet in der Statik, dass alle Kräfte, die auf einen ruhenden Körper
wirken, zueinander im Gleichgewicht stehen. Das bedeutet, dass alle Kräfte sich gegenseitig kompensieren und in ihrer Gesamtwirkung so erscheinen, als sei keine Kraft
vorhanden. Mathematisch gesehen ist die Summe aller Kräfte gleich null – so als wäre
keine Kraft vorhanden. Würde die Summe der Kräfte nicht gleich null sein, so würde der
Körper beschleunigen. Für eine Aufhängung würde dies heißen, dass der Körper
abstürzt.
Nun aber zurück zu unserer Konstruktion. Wir drücken das Gleichgewicht nun mathematisch als Summe aller auftretenden Kräfte aus. Da es zwei Richtungen gibt (X,Y), gibt
es auch zwei Gleichungen.
ΣFix = 0
ΣFiy = 0
Summe aller Kräfte in X-Richtung ist gleich null
Summe aller Kräfte in Y-Richtung ist gleich null
Jetzt werden alle Kräfte in der Gleichung gelistet. Beginnen wir mit der Y-Richtung, da
bereits eine Kraft in dieser Richtung bekannt ist (10 kN). Für alle Kräfte wird hier das
richtige Vorzeichen angesetzt. Jede Kraft (Pfeil) wird berücksichtigt!
ΣFiy = 0 = 10,0 kN – Sy – Sy
(Sy negativ, weil Pfeile nach unten)
Diese Gleichung wird nach Sy aufgelöst:
<> 0 = 10,0 kN – 2 x Sy
<> 2 * Sy = 10,0 kN
<> Sy = 5,0 kN
Sy ist die Vertikalkomponente unserer Aufhängung. Um an die Kraft im Strang selbst zu
kommen, müssen wir den Zusammenhang zwischen Sy und S herstellen. Dazu können
wir auf die Komponentenzerlegung zurückgreifen. Dort steht:
S = Sy / cos 55°
eingesetzt:
S = 5,0 kN / cos 55° = 8,717 kN
Die zweite Gleichung ΣFix = 0 wird hier nicht mehr benötigt!
28
1. Die Theorie • Grundlagen der Statik • Stabkräfte berechnen
In jedem Strang der Rundschlinge wirkt eine Kraft von 8,717 kN. Man kann das Ergebnis
auch mit dem Programm „Zentrales Kräftesystem V2.0“ überprüfen, indem man alle
Kräfte dort einsetzt und nachsieht, ob wirklich Gleichgewicht herrscht. Das heißt, dass
Fres = 0 sein muss!
Bild 15
Wir haben richtig gerechnet!
29