Untitled

2.3 Beugung von Elementarteilchenstrahlen
13
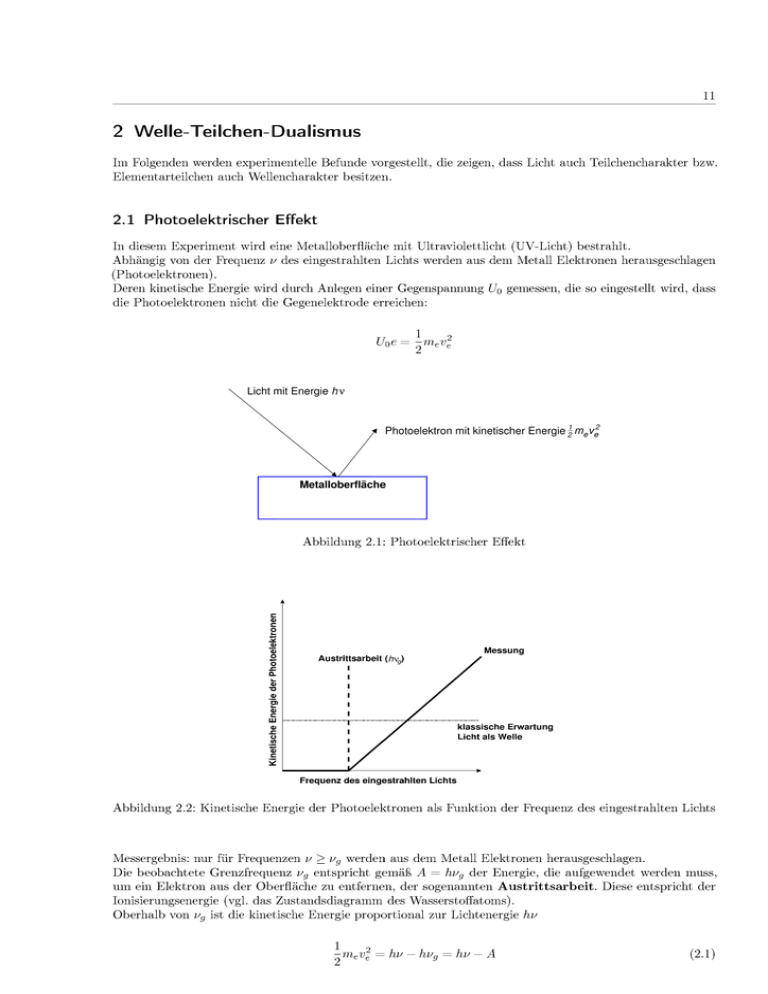
Entgegen der klassischen Erwartung wird beobachtet, dass sich die Wellenlänge des Röntgenstrahls unabhängig von der eingestrahlten Wellenlänge, aber abhängig vom Austrittswinkel β ändert (∆λ > 0).
Abbildung 2.5: Comptoneffekt: Beugung von Röntgenlicht an freien Elektronen eines Metalls
Analog zum Photoelektrischen Effekt gilt die Energiebilanz eines elastischen Stoßprozesses
(2.2)
hν0 = Ekin, e + hν1
Durch die winkelaufgelöste Messung kann zusätzlich die Impulsbilanz (x− und y−abhängig) aufgestellt
werden.
Auch dies entspricht einem elastischen Stoßprozess, wodurch aus dem Compton-Experiment ebenfalls auf den
Teilchencharakter von Licht geschlossen werden muss.
Hierbei wird für das Röntgenlicht die Beziehung p~L = ~~k =
∧
hν
c
· ~ek =
h
λ
· ~ek eingesetzt (mit ~k als Wellenvektor
= Ausbreitungsrichtung des Lichts)
und für das Elektron die klassische Relation p~e = me~ve .
Das Röntgenlicht hat zu Beginn nur eine Impulskomponente in x−Richtung. Sowohl das ausgestrahlte
Röntgenlicht als auch das Elektron haben Impulskomponenten in x− und y−Richtung.
x:
hν1
hν0
=
cos β + me ve cos α
c
c
hν1
sin β + me ve sin α
y: 0=
c
Aus den Gleichungen (2.2 und 2.3) wird eine Beziehung zwischen der Frequenz- bzw. Wellenlängenänderung
des Röntgenstrahls und dem Ausfallwinkel β aufgestellt.
Dabei muss wegen der hohen Geschwindigkeit des Elektrons die relativistische Energie-Impuls-Beziehung
E 2 = E02 + p2e c2 verwendet werden.
Dabei ist E0 die Energie des Elektrons vor der Einwirkung des Röntgenphotons. Es ergibt sich:
⇒
h
1
1
1
=
· (1 − cos β)
−
=
ν1
ν0
∆ν
me c2
h
· (1 − cos β)
bzw. ∆λ = λ1 − λ0 =
me c
(2.3)
Die unter Annahme eines elastischen Stoßprozesses berechnete Wellenlängenverschiebung ∆λ ist, in Übereinstimmung mit den experimentellen Befunden, richtungsabhängig aber wellenlängenunabhängig.
2.3 Beugung von Elementarteilchenstrahlen
Im Folgenden wird sich bei der Definition von Elementarteilchen auf Elektronen beschränkt. Beugungsexperimente werden jedoch auch mit Neutronen durchgeführt.
Im Experiment wird eine Festkörper-Oberfläche mit Elektronenstrahlen beschossen.
Messgröße ist die winkelabhängige Intensität der reflektierten Elektronen, analog zur Röntgenbeugung.
16
3 Aufenthaltswahrscheinlichkeit
3 Aufenthaltswahrscheinlichkeit
3.1 Doppelspaltexperiment mit Elektronen
Das vorige Experiment wird modifiziert, indem der Elektronenstrahl durch zwei parallele Spalten auf den
Messschirm gelenkt wird.
Abbildung 3.10: Beugung eines Elektronenstrahls an einem Doppelspalt.
In der klassischen Erwartung (I) würde nur bei xA und xB Intensität gemessen werden.
Nach Kenntnis des Einzelspaltexperiments (Abschnitt 2.4) würde als Summe der Intensitätsmuster zweier
separater, unabhängiger Spaltdurchgänge das Muster (II) erwartet werden.
Als experimentelles Resultat ergibt sich jedoch das Muster (III), das nicht der Summe zweier Einzeldurchgänge
entspricht.
I. Elektron als klassisches Teilchen
Abbildung 3.11: Erwartetes Messergebnis: zwei scharfe Banden
II. Wechselwirkungsfreie Elektronen als Wellen
Abbildung 3.12: Erwartetes Messergebnis: IAB = IA + IB
III. Messergebnis: Interferenzmuster
17
Abbildung 3.13: Beobachtete Intensitätsverteilung beim Doppelspaltexperiment; ∆x =
D
dλ
Als Resultat der Messung ergibt sich, dass die Elektronendichte eines kombinierten Ereignisses (hier: dem
gleichzeitigen Durchgang eines Elektronenstrahls durch die Spalte A und B) nicht die Summe der Elektronendichten der Einzelereignisse ist.
Dieses experimentelle Ergebnis lässt sich nur mit Hilfe der Quantenmechanik erklären.
In der Quantenmechanik erfolgt die Beschreibung des Aufenthaltsorts eines Elektrons völlig anders als in der
klassischen Physik.
Die Vorstellung, dass zu jedem Zeitpunkt t die Position x (die nächsten Abschnitte beschränken sich auf
eine eindimensionale Ortsdarstellung) des Elektrons eindeutig durch die Funktion x(t) gegeben ist, muss
aufgegeben werden.
Stattdessen kann der Aufenthaltsort nur noch durch eine Wahrscheinlichkeitsfunktion ψ(x, t) angegeben
werden.
Diese Funktion muss die experimentell nachgewiesenen Welleneigenschaften des Elektrons beschreiben. Aus
diesem Grund wird ψ als Wellenfunktion bezeichnet.
4 Einteilchen-Wellenfunktionen
In den nächsten Abschnitten werden ausschließlich Systeme mit einem Teilchen beschrieben, zunächst in einer
Dimension.
Die Symbole für die entsprechenden Einteilchen-Wellenfunktionen sind kleine griechische Buchstaben
(ψ, ϕ, . . . ). Für Mehrelektronenwellenfunktionen werden später griechische Großbuchstaben (Φ, Ψ, . . . ) verwendet.
Es wird zwischen freien Elektronen (im Elektronenstrahl) und gebundenen Elektronen (in Atomen und
Molekülen) unterschieden.
4.1 Freie Teilchen
Auf ein freies Elektron wirkt keine äußere Kraft (dabei wird die Wechselwirkung mit den anderen Elektronen
des Strahls näherungsweise vernachlässigt).
Damit ist gemäß Gleichung 1.8 das Potential V null.
Die Einelektronenfunktionen sind sogenannte ebene Wellen:
ψ(x, t) = Aei(kx−ωt)
(4.1)
Dabei ist
k der Betrag des Wellenvektors ~k
ω = 2πν die Kreisfrequenz
h
h
1
Länge
Bogenmaß
Zeit
i
(analog zu 2.2)
i
Der Wellenvektor gibt die Ausbreitungsrichtung des Elektronenstrahls an. Seine Richtung ist in den vorigen
Abbildungen (2.3,3.1) angegeben.
Der Betrag des Wellenvektors ist von der Wellenlänge des freien Elektrons abhängig. Dies lässt sich aus der
Periodizität der ebenen Welle in der Eulerdarstellung (eiα = cos α + i sin α) direkt ablesen.
2π
(4.2)
λe
Damit ergibt sich mit der de Broglie-Beziehung (2.5) eine direkte Proportionalität zwischen Wellenvektor
und Impuls.
k=
18
4 Einteilchen-Wellenfunktionen
(4.3)
pe = ~k
Die Wellenfront eines Elektronenstrahls (die Verbindungslinie zwischen gleichen Amplitudenwerten der
nebeneinander verlaufenden Elektronenwellen) verläuft senkrecht zu ~k
Abbildung 4.1: Wellenfront und Wellenvektor eines Elektronenstrahls.
Die Phase kx − ωt = konst bewegt sich mit der Phasengeschwindigkeit vp = λν = ωk
Die Phasengeschwindigkeit ist nicht messbar. Sie kann größer als die Lichtgeschwindigkeit sein.
Im Allgemeinen erfolgt die Beschreibung eines Elektrons im Elektronenstrahl nicht durch eine einzelne ebene
Welle, sondern durch eine Gruppe ebener Wellen mit einer Verteilung von k und ω.
Eine solche Gruppe wird als Wellenpaket bezeichnet.
Die Gruppengeschwindigkeit vg = dω
dk = ve ist eine messbare Größe.
4.2 Gebundene Teilchen
Auf das Elektron wirkt eine anziehende Kraft, z.B. die Coulombanziehungskraft durch den Atomkern.
Dadurch resultiert nach (1.8) ein attraktives V (x).
Als Konsequenz hält sich das Elektron bevorzugt in der Nähe des tiefsten Punkts von V (x) auf.
Daraus ergeben sich folgende Bedingungen für gültige Wellenfunktionen ψ(x)
1. ψ(x) muss quadratisch auf Eins normierbar sein.
Z∞
!
ψ ∗ (x)ψ(x) dx = 1
(4.4)
−∞
(dabei ist ψ ∗ (x) die komplex konjugierte Funktion zu ψ(x))
2. ψ(x) muss stetig differenzierbar sein (Ausnahme: Unendlichkeitsstellen des Potentials, z.B. ist im Atom
1
, so dass am Kernort eine Unendlichkeitsstelle existiert).
V ∝ − |x|
3. ψ(x) muss stetig für alle x sein (notwendige Voraussetzung für stetige Differenzierbarkeit)
4. ψ(x) muss eindeutig für alle x sein (notwendige Voraussetzung für Funktionscharakter)
Die letzten drei Bedingungen gelten auch für Wellenfunktionen freier Teilchen.
Beispiele für gültige Einelektronenwellenfunktionen sind
ψ(x) = N e−x
ψ(x) = N e
2
N : Normierungsfaktor
−|x|
4.3 Bornsche Wahrscheinlichkeitsinterpretation
Die Wellenfunktion selbst besitzt keine physikalische Bedeutung.
Nach Max Born ist die Elektronendichte, genauer die Aufenthaltswahrscheinlichkeitsdichte des Elektrons,
die in den Beugungsexperimenten (Abschnitte 2.4,3.1) mit der gemessenen Intensität I verknüpft war, gegeben
durch das Betragsquadrat der Wellenfunktion:
19
4.4 Superpositionsprinzip
I(x) ∝ |ψ(x)|2 = ψ ∗ (x)ψ(x)
(4.5)
h
i
1
Die Aufenthaltswahrscheinlichkeitsdichte hat die Dimension Länge
.
∞
Z
|ψ(x)|2 dx = 1 an, dass sich ein Elektron irgendwo im Raum (hier: auf der x-Achse)
Anschaulich gibt
aufhält.
−∞
Die Aufenthaltswahrscheinlichkeit, das Produkt der Aufenthaltswahrscheinlichkeitsdichte und einem
infinitesimal kleinen Längenelement dx, ist daher dimensionslos.
W (x) = |ψ(x)|2 dx
(4.6)
Anschaulich gibt W (x) dx die Anzahl Elektronen im Längenbereich zwischen x und x + dx an.
4.4 Superpositionsprinzip
Mit Hilfe der Bornschen Wahrscheinlichkeitsinterpretation lässt sich die beim Doppelspaltexperiment (Abschnitt 3.1) beobachtete Abweichung der Gesamtintensität von der Summe der Einzelintensitäten erklären.
Allgemein wird die Wellenfunktion für ein Ereignis AB, das durch Kombination der Einzelereignisse A und
B entsteht, durch eine Linearkombination (Superposition) der Einzelwellenfunktionen zu einer Gesamtwellenfunktion erhalten:
ψAB = ψA + ψB
Dabei sind ψA , ψB die Wellenfunktionen für die Ereignisse/Zustände A und B.
Die Gesamtintensität IAB ergibt sich nach Gleichung 4.5 zu:
∗
∗
∗
IAB ∝ ψAB
ψAB = (ψA
+ ψB
)(ψA + ψB ) =
∗
∗
[ψA
ψ A + ψB
ψB ]
{z
}
|
Summe der Einzelereignisse
∗
∗
+ ψA
ψB + ψ B
ψA
{z
}
|
Interferenz
20
4 Einteilchen-Wellenfunktionen
In Verallgemeinerung des Doppelspaltexperimentes kann ein quantenmechanisches System aus einer Superposition aus beliebig vielen möglichen Zuständen bestehen:
ϕ=
∞
X
(4.7)
c n ψn
n
Dabei sind
ϕ die Gesamtwellenfunktion
cn die Entwicklungskoeffizienten
{ψn } ein Satz von Wellenfunktionen, die je einen Zustand n des Systems beschreiben (daher auch als
Zustandsfunktionen bezeichnet)
Im Sinne einer Reihenentwicklung kann mit diesem Ansatz (4.7) jede beliebige Wellenfunktion als Superposition der Zustandsfunktionen eines quantenmechanischen Operators berechnet werden (siehe späteren
Abschnitt 6). Dies wird später bei der Herleitung des Variationsprinzips ausgenutzt.
Nach der Bornschen Wahrscheinlichkeitsinterpretation muss auch eine solche Gesamtwellenfunktion auf Eins
normiert sein:
Z∞
!
ϕ∗ (x)ϕ(x) dx = 1
−∞
Daraus ergibt sich nach Einsetzen von (4.7)
∞ Z∞
∞ X
X
n
!
c∗n ψn∗ cm ψm dx = 1
m −∞
Quantenmechanische Zustandsfunktionen sind stets orthonormal (siehe Abschnitt 4.7). Das bedeutet, dass
alle Integrale mit verschiedenen Indizes m =
6 n Null sind, im anderen Fall m = n Eins. Daraus ergibt sich als
Forderung an die Entwicklungskoeffizienten, dass ihre Quadratsumme ebenfalls Eins ergibt.
∞
X
n
!
|cn |2 = 1