Ubungen aus Mechanik WS11 - Website von Andreas Windisch.

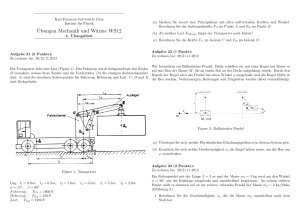
Aufgabe 29 (1 Punkt):
Zu rechnen bis:
Karl-Franzens-Universität Graz
Institut für Physik
Zu lösen:
Übungen aus Mechanik WS11
M. Hopfer, T. Kloiber, S. Kofler, M. Puhr, B. Stremitzer, A. Windisch
4. Übungsblatt
1. Eine Schraubenfeder der Länge l0 = 0.4 m wird unter Einwirkung der Kraft F1 =
10.0 N um die Länge x1 = 2.0 cm gedehnt. Welche Arbeit wird bei einer Dehnung
der Schraubenfeder auf das Zweifache ihrer ursprünglichen Länge benötigt, wenn die
Kraft, die diese Arbeit verrichtet, proportional der Ausdehnung der Feder ist?
2. Eine vertikal hängende Schraubenfeder wird durch eine daran hängende Masse von
1 kg um 2 cm gedehnt. Wie groß ist die aufzuwendende Arbeit, um die vorbelastete
Feder um weitere 3 cm zu dehnen.
Aufgabe 27 (1 Punkt):
Zu rechnen bis:
Zwei Züge befinden sich in einer Entfernung von 75 km. Sie bewegen sich jeweils mit
15 km/h aufeinander zu. Ein Vogel fliegt zwischen den Fronten der beiden Zügen mit Aufgabe 30 (1 Punkt):
einer Geschwindigkeit von 20 km/h hin und her, bis die beiden Züge zusammenprallen. Zu rechnen bis:
Welche Distanz hat der Vogel zurückgelegt, bis er auf unnatürliche Weise stirbt?
Ein Schiff fährt flussaufwärts mit einer Geschwindigkeit v (relativ zum Strom gemessen)
von A nach B. Die Strömungsgeschwindigkeit des Flusses sei u = 6 km/h. Die Reibungskräfte seien proportional zu v 2 . Bei welcher Relativgeschwindigkeit des Schiffes (v 6= 0)
Aufgabe 28 (2 Punkte):
gegenüber des Flusses wird die für die Fahrt aufzuwendende Energie ein Minimum.
Zu rechnen bis:
Ein Block der Masse m1 = 3.70 kg hängt an einem Seil auf einer reibungsfreien schiefen
Aufgabe 31 (1 Punkt):
Ebene, die einen Winkel von 30◦ mit der Horizontalen einschließt. Das Seil führt über eine
Zu rechnen bis:
masselose, reibungsfreie Rolle zu einem zweiten, senkrecht hängenden Block der Masse
Aus welcher Höhe h muss ein Holzklotz auf einer reibungsfreien schiefen Ebene, die in eine
m2 = 2.30 kg. Siehe Abbildung 1. Wie lautet
Loopingbahn übergeht, losgelassen werden, damit er diese vollständig durchläuft (Loopin1. der Betrag der Beschleunigung eines jeden Blocks,
gradius R = 0.2 m)? Die Rotation des Holzklotzes um seine Achse soll unberücksichtigt
bleiben.
2. die Richtung der Beschleunigung des hängenden Blocks?
Aufgabe 32 (1 Punkt):
Zu rechnen bis:
3. Wie groß ist die Zugspannung im Seil?
Wie ändert sich die Beschleunigung für eine Gleitreibungszahl von µG = 0.30?
Ein Fadenpendel mit der Länge L = 3 m und der Masse m1 = 3 kg wird um den Winkel
α = 60◦ aus der Ruhelage ausgelenkt und anschließend losgelassen. An seinem tiefsten
Punkt stößt es elastisch auf an ein zweites, ruhendes Pendel der Masse m2 = 2 kg.(Siehe
Abbildung 2.)
1. Berechnen Sie die Geschwindigkeit v2 , die die Masse m2 unmittelbar nach dem Stoß
hat.
m1
30°
m2
2. Berechnen Sie weiters den Winkel, um den die Masse m2 nach dem Stoß ausgelenkt
wird.
(Benützen Sie keine vorgefertigten Formeln für einen elastischen Stoß, sondern rechnen
Sie alles von Anfang an durch.)
3. Welche kinetische Energie hat das Teilchen nach einer Sekunde?
4. Welche Arbeit W10 leistet das Feld bei der Verschiebung des Teilchens von ~r(t = 0)
nach ~r(t = 1)?
α
L
Aufgabe 35 (1 Punkt):
Zu rechnen bis:
Lösen Sie
1. In welcher Höhe über dem Äquator muss sich ein Satellit befinden, sodass er geostationär ist?
m1
m2
2. Sie sind ein Astronaut in einer Raumfähre und verfolgen einen Satelliten, der repariert
werden muss. Sie befinden sich auf einer kreisförmigen Umlaufbahn mit demselben
Radius wie der Satellit, aber 30 km hinter ihm. Wie können Sie ihn einholen?
(Umlaufdauer der Erde 24h, Gravitationskonstante G = 6.67 · 10−11 m3 /kgs2 , Masse der
Erde M = 5.97 · 1024 kg)
Aufgabe 36 (2 Punkte):
Zu rechnen bis:
Aufgabe 33 (1 Punkt):
Zu rechnen bis:
Berechnen Sie die Felder zu folgenden Potentialen (k, g und m seien konstant):
1. U (~r) = − |~kr|
Eine voll betankte Rakete hat eine Masse von 21000 kg, von denen 15000 kg Treibstoff
sind. In einer Sekunde werden 190 kg Treibstoff verbrannt. Der verbrannte Treibstoff wird
mit einer Geschwindigkeit von 2800 m/s relativ zur Rakete nach hinten ausgestoßen.
Berechnen Sie:
2. U (~r) = k2 ~r2
1. den Schub der Rakete,
3. U (~r) = mgz
2. die bei der Zündung und direkt vor dem Brennschluss (wenn der gesamte Treibstoff
verbraucht ist) auf die Rakete wirkende Nettokraft,
4. U (~r) =
m
ω
2 [(~
· ~r)2 − ω
~ 2~r2 ]
3. die Geschwindigkeit der Rakete in Abängigkeit der Zeit und
4. ihre Endgeschwindigkeit bei Brennschluss.
Aufgabe 34 (1 Punkt):
Zu rechnen bis:
Gehen Sie davon aus, dass die Rakete vertikal nach oben abgefeuert wird. Vernachlässigen
Ein Teilchen mit der Masse m = 3g bewegt sich in einem homogenen, zeitabhängigen Sie außerdem den Luftwiderstand und nehmen Sie an, dass die Erdbeschleunigung mit
9.81 m/s2 konstant ist. Geben Sie eine qualitative Begründung dafür an, dass man die
Kraftfeld
2
−5
Erdbeschleunigung als konstant anehmen kann.
F~ = (45t , 6t − 3, −18t) · 10 N,
(Zeit t in Sekunden) mit den Anfangsbedingungen:
~r(t = 0) = (0, 0, 0) cm,
~r˙ (t = 0) = (0, 0, 6) cms−1 .
1. Was hat der Vorfaktor 10−5 in der Kraft für einen Sinn?
2. Berechnen Sie die Geschwindigkeit des Teilchens nach einer Sekunde.