Lineare Funktionen - Wilhelm-Raabe
Werbung

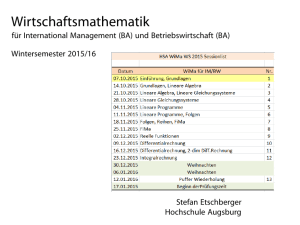
Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Das ganze Leben besteht daraus, dass Dinge voneinander abhängen. Im mathematischen Sinne bezeichnen wir diese Dinge als „Größen“. Es handelt sich also um messbare Größen. Nicht messbare Dinge gibt es auch. Sie können sogar sehr wichtig sein, aber für die Mathematik sind sie nicht brauchbar. Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Auch bei den Abhängigkeiten, die für die Mathematik brauchbar sind, unterscheiden wir verschieden Fälle: Das Körpergewicht eines Menschen ist messbar, seine Körpergröße ist auch messbar, sein Alter ist auch messbar. Berechenbar sind diese Größen ... Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen NICHT ! Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Auch bei den Abhängigkeiten, die für die Mathematik brauchbar sind, unterscheiden wir verschieden Fälle: Wenn man einkauft, muss man für sieben Brötchen mehr bezahlen als für drei. Berechnen kann man diese Größen .... Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Sehr gut ! Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Auch bei den Abhängigkeiten, die für die Mathematik brauchbar sind, unterscheiden wir verschieden Fälle: Wenn mehr bei einer Arbeit mit anfassen, dann ist man schneller fertig. Berechnen kann man diese Größen .... Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Sehr gut ! Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Klassisches Beispiel für voneinander abhängige Größen ist das Kaufen von Speiseeis! Je mehr Kugeln jemand kauft, desto mehr muss er auch bezahlen. Eine Kugel kostet 80 Cent. Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Die Eisdiele macht daraus ein Preisschild: Preistafel: 1 Kugel = 0,80 € 2 Kugeln = 1,60 € 3 Kugeln = 2,40 € 4 Kugeln = 3,20 € jede weitere Kugel kostet 0,80 € Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Schülerinnen und Schüler machen daraus eine Wertetabelle .... Kugeln Preis 1 2 3 4 5 6 0,80 € 1,60 € 2,40 € 3,20 € 4,00 € 4,80 € Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen ... und einen Graphen (Zeichnung): y 7 Preis in Euro 6 5 4 3 2 1 Anzahl_der_Kugeln 1 -1 2 3 4 5 6 7 8 9 10 11 x Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Aus diesem Graphen kann man – genau wie bei der Wertetabelle – alle Eispreise ablesen. Und das geht so: y Die grünen Pfeile zeigen den Preis für vier Kugeln – 7 Preis in Euro 6 5 4 die hellblauen Pfeile zeigen, was sieben Kugeln kosten. 3 2 1 Anzahl_der_Kugeln -1 1 -1 2 3 4 5 6 7 8 9 10 11 x Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Wir merken uns: Es gibt eine Größe, die ich nach Belieben – oder nach vorhandenem Taschengeld – auswählen kann. Das ist die Anzahl der Eiskugeln. Und es gibt eine Größe, die dann berechnet wird. Das ist der Preis. Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Unser Eisverkäufer hat eine Idee: Er bietet jetzt sein Eis auf Wunsch des Kunden mit Sahne an. Wenn man Sahne zu seinem Eis haben möchte, so kostet das 1,00 Euro extra. Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Die Eisdiele macht ein neues Preisschild: Preistafel: 1 Kugel = 0,80 € 2 Kugeln = 1,60 € 3 Kugeln = 2,40 € 4 Kugeln = 3,20 € jede weitere Kugel kostet 0,80 € Mit Sahne 1,00 Euro mehr Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Schülerinnen und Schüler machen daraus eine neue Wertetabelle .... Kugeln Preis 1 2 3 4 5 6 1,80 € 2,60 € 3,40 € 4,20 € 5,00 € 5,80 € Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen ... und einen neuen Graphen (Zeichnung): y 7 Dieser Graph sieht ganz ähnlich aus. Er geht allerdings nicht mehr durch den Nullpunkt des Koordinatensystems, sondern schneidet die Preisachse bei EINS. Preis in Euro 6 5 4 In normalen deutschen Worten heißt das: Wenn man nur Sahne ohne Eis kaufen will, so kostet das einen Euro. 3 2 Ist zwar Unsinn – ist aber möglich! 1 Anzahl_der_Kugeln -1 1 -1 2 3 4 5 6 7 8 9 10 x 11 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Auch aus diesem Graphen kann man – genau wie ohne Sahne alle Eispreise ablesen. Wie es geht, wissen wir schon: y 8 Preis in Euro 7 6,60 Euro 6 5 4 4,20 Euro 3 2 1 Anzahl_der_Kugeln -1 1 -1 2 3 4 5 6 7 8 9 10 11 x 12 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Wir fangen jetzt damit an, aus dem Eisverkauf ein bisschen Mathematik zu machen: Der Gesamtpreis hängt natürlich von der Anzahl an Kugeln ab. Diese Anzahl kann jeder Käufer für sich frei wählen! Anzahl Preis Der Mathematiker sagt: x y Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Nicht wählen kann der Kunde aber, wie teuer eine Kugel ist und was die Sahne kostet. Wir schauen uns das einmal ganz genau an: Zuerst lassen wir den Preis einer Kugel bei 0,80 € -so wie das in Hameln üblich ist – und nehmen verschiedene Preise für die Sahne. Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen y 5 PREIS 4 Und jetzt erkläre bitte: 3 Was unterscheidet diese vier Geraden? Was ist bei den vier Geraden gleich? 2 1 ANZAHL DER KUGELN 1 -1 2 3 4 5 6 7 x 8 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Sie unterscheiden sich nur den Preis der Sahne. Sie verlaufen parallel. Der SAHNEPREIS wird auf der y-Achse angezeigt. Logisch: Wenn man NULL Kugeln kauft, aber Sahne haben möchte, muss man auch nur die Sahne bezahlen. Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Alle Eisdielen haben vereinbart, für Sahne grundsätzlich nur einen Euro zu nehmen. Aber der Kugelpreis ist unterschiedlich: In Hameln – ECE – nimmt man 0,80 € In Berlin – Zeno am Hbf – nimmt man 1,20 € In Amsterdam – Guiseppe an der Damstrat – nimmt 1,75 € Und in Frankreich ist Eis sowieso idiotisch teuer, dort nimmt man überall inzwischen 2,50 € pro Kugel. Da würde ich kein Eis essen! Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen y Wo ist Hameln? Wo ist Frankreich? 5 PREIS 4 3 2 1 ANZAHL DER KUGELN -1 1 -1 2 3 4 5 6 7 x 8 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Auf mathematisch: GESAMTPREIS = EINZELPREIS MAL ANZAHL PLUS SAHNE oder y = m ● x + b Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Gut, jetzt haben wir bereits vieles über lineare Funktionen gelernt. Wir wissen, dass zu einem Wert „x“ ein Wert „y“ errechnet wird. x y Wie dort gerechnet wird, bestimmt die Funktionsgleichung y = m ● x + b Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Bei der Funktionsgleichung y = m ● x + b entscheiden m und b über den Verlauf der Geraden Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen y = m ● x + b „b“ legt fest, wo die Gerade die y-Achse schneidet: Die Gerade schneidet die y-Achse bei dem Wert „+3“. y 5 Also lautet ihre Funktionsgleichung: 4 3 2 y= m●x+3 1 x -7 -6 -5 -4 -3 -2 -1 1 -1 -2 2 3 4 5 6 7 8 9 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Der Wert für „b“ kann in jeder Zeichnung einfach abgelesen werden: y 8 7 y = mx + 7 6 5 4 y = mx + 4 3 2 1 x -7 -6 -5 -4 -3 -2 -1 1 -1 -2 2 3 y = mx + 1 4 y = mx - 2 -3 -4 -5 -6 y = mx - 4 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen y = m ● x + b „m“ legt fest, wie die Gerade verläuft. Ob sie steil oder flach ist. Ob sie steigt oder fällt. Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen y = m ● x + b Wir wollen zuerst zeichnen, dann genau beobachten und dann unsere Beobachtungsergebnisse aufschreiben. Es sei b = -2 und für m wählen wir die Werte -0,5 / +0,5 / -2,5 / +2,5 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Das ergibt dann die Funktionsgleichungen: y y y y = = = = - 0,5 x - 2 + 0,5 x - 2 - 2,5 x - 2 + 2,5 x - 2 Und dazu machen wir eine kleine Wertetabelle: Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Wertetabelle: x y = - 0,5 x - 2 y = + 0,5 x - 2 y = - 2,5 x - 2 y = + 2,5 x - 2 0 -2 2 5 -2 -2 -2 -2 -1 -3 -5 -3 -1 1 3 -7 -15 -7 3 11 -8 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen y y y y y 2 1 x -7 -6 -5 -4 -3 -2 -1 1 -1 -2 -3 -4 -5 -6 -7 2 3 4 5 6 7 8 = = = = - 0,5 x + 0,5 x - 2,5 x + 2,5 x - 2 2 2 2 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen y 2 1 x -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 -1 Ergebnisse : -2 -3 -4 -5 negatives m positives m m>|1| steil - fallend steil - steigend m<|1| flach - fallend flach - steigend -6 -7 y y y y = = = = - 0,5 x + 0,5 x - 2,5 x + 2,5 x - 2 2 2 2 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Wir prüfen gleich am die Geraden von Folie 29 auf ihre Eigenschaften: y 8 7 6 flach – fallend 5 4 steil – steigend 3 2 flach – fallend 1 x -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 flach – steigend -1 -2 -3 -4 -5 -6 steil - fallend Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen – Bestimmung der Funktionsgleichung Gegeben sei der Graph einer Funktion: y 3 2 Zu dieser Geraden gehört eine Funktion -4 -3 der Form 1 x -2 -1 1 -1 y = mx + b -2 -3 -4 -5 2 3 4 5 6 7 8 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen y 1 x -4 -3 -2 -1 1 -1 -2 Hier lesen wir das „b“ einfach ab! -3 -4 -5 2 3 4 5 6 7 8 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Die Funktionsgleichung lautet also: y = mx - 3 Wie groß ist „m“? Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen y 4 Zur Berechnung von3 "m" suche ich 2 f Kreuzungslinien Punkte, die genau auf 1 des Koordinatensystems f llen. fa -7 -6 -5 -4 -3 -2 -1 1 -1 -2 -3 -4 2 3 4 5 6 7 x 8 9 10 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen y 3 2 Hier sind solche Punkte: 1 -9 -8 -7 -6 -5 -4 -3 -2 -1 1 -1 -2 -3 -4 -5 -6 -7 2 x 3 4 5 6 7 8 9 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen y 1 Der Weg zwischen zwei solcher Punkte: -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 -1 -2 2 nach oben: +2 -3 3 nach rechts: +3 -4 -5 -6 x 8 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Berechnung 2 m 3 2 y x3 3 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Woher weiß ich, welche Punkte ich nehmen soll? y Es ist egal! 3 2 1 x -8 -7 -6 -5 -4 -3 -2 Alle Punkte sind geeignet um die-1 Größe m zu berechnen. 1 -1 -2 -3 -4 -5 -6 -7 -8 -9 2 3 4 5 6 7 8 9 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen y -7 -6 -5 -4 -3 -2 x -1 1 2 3 4 -1 -2 -3 -4 -5 -6 -7 6 nach oben: + +6 6 2 m 9 3 9 nach rechts: +9 -8 also: 2 y x3 3 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Es funktioniert sogar rückwärts WAS FÜR DIE DEUTSCHE SPRACHE NICHT GILT: sträwkcür ragos treinoitknuf sE Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen y 3 2 Der Weg zwischen zwei 1 Punkten rückwärts: -5 -4 -3 -2 -1 1 2 3 4 5 -1 -2 -3 -4 12 nach links: -12 -5 6 7 8 8 nach 9 unten: 10 11 -8 x 12 8 2 m 12 3 -6 ALSO: 2 y x3 3 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Dieses Verfahren funktioniert natürlich auch dann, wenn die Gerade nicht durch Punkte mit glatten Werten verläuft. In diesem Fall muss gemessen werden! Wir führen das ganz genau vor. Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen y 7 6 Diese Gerade ist ziemlich schwer zu bearbeiten. 5 4 3 2 1 x -6 -5 -4 -3 -2 -1 1 -1 -2 -3 -4 2 3 4 5 6 7 8 9 10 11 Wir markieren die Punkte, an denen die beiden Achsen geschnitten werden. Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen y 5 4 3,7 cm nach unten: - 3,7 y m x 3,7 3 2 1 x -5 -4 -3 -2 -1 1 -1 -2 2 3 4 5 6,3 cm nach rechts: + 6,3 6 7 -3 ... Und das „m“? -4 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen y 6 3,7 3,7 m 0,6 6,3 6,3 5 4 3,7 cm nach unten: - 3,7 3 2 1 x -5 -4 -3 -2 -1 1 -1 -2 2 3 4 5 6,3 cm nach rechts: + 6,3 6 7 8 -3 y 0,6 x 3,7 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen Die folgenden Folien enthalten Standardaufgaben, die jede/r beherrschen sollte und die auch bei Klassenarbeiten gebräuchlich sind. Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen 1. Zeichne den Graphen der Funktion y = - 0,75 x + 3 Zu dieser Aufgabe gibt es zwei Lösungswege auf den folgenden Folien Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen 1. Zeichne den Graphen der Funktion y = - 0,75 x + 3 Lösungsweg a) Der Graph verläuft durch den Punkt P1 (0/3). Ein weiterer Punkt wird benötigt. Ich wähle x = 4 Und berechne y: Y = -0,75●4 + 3 = 0 (bitte mit TR nachrechnen.) Der zweite Punkt ist also P2 (4/0). Punkte eintragen, Gerade zeichnen, fertig y 4 P1 (0 | 3) 3 2 1 -1 P2 (4 | 0) x 1 -1 2 3 4 5 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen 1. Zeichne den Graphen der Funktion y = - 0,75 x + 3 Lösungsweg b) Der Graph verläuft auch durch den Punkt P1 (0/3). y 4 +4 3 Dann brauche ich ein Steigungsdreieck für die Steigung m = - 0,75. Natürlich ist die Lösung bei beiden Lösungswegen die Gleiche. P1 (0 | 3) Dieses Verfahren ist nur brauchbar, wenn du sofort weißt, dass zu 0,75 der Bruch -2 ¾ gehört. Also 4 nach rechts (+4) und 3 nach unten (-3). Gerade zeichnen, fertig! 2 -3 1 x -1 1 -1 -2 -3 2 3 4 5 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen 2. Vorhanden ist der Graph einer Funktion. Stelle die Funktionsgleichung auf. y 5 4 3 2 1 x -2 -1 1 2 3 4 5 -1 -2 -3 Zu dieser Aufgabe gibt es nur einen Lösungsweg auf der folgenden Folie Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen y 5 b ablesen (grüner Pfeil): b = -2 4 Geeigneten Punkt suchen, Dreieck zeichnen, Werte einfach abzählen und aus den Werten die Steigung m berechnen: 3 2 (auch einfa f ch zählen) +7 1 x -3 -2 -1 1 2 3 4 5 6 m 7 2 1 1,4 5 5 -1 -2 -3 -4 +5 (einfach zählen) Also: y = 1,4 x - 2 Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen 3. Gegeben sind die Punkte A ( -2 / 4 ) und B ( 4 / -5 ). Zeichne die Gerade durch A und B. Gib die Funktionsgleichung an. Zu dieser Aufgabe gibt es einen Lösungsweg auf den folgenden Folien Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen y 5 A 4 3 2 1 x -4 -3 -2 -1 1 2 3 4 5 -1 -2 -3 -4 -5 -6 B 6 Trage die Punkte in ein Koordinatensystem ein. Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen y 6 Zeichne eine Gerade durch die Punkte A und B. 5 A 4 3 2 1 x -4 -3 -2 -1 1 2 3 4 5 -1 Nicht etwa von A nach B – das wäre eine Strecke und damit falsch! -2 -3 -4 -5 -6 -7 B Wilhelm-Raabe-Schule Fachbereich: Mathematik Thema: Lineare Funktionen b bestimmen: b = 1 y 5 A 4 Dreieck zeichnen; Werte auszählen: 3 +4 in x-Richtung 2 -6 in y-Richtung 1 x -4 -3 -2 -1 1 2 3 4 M berechnen: 5 -1 -2 6 6 3 m 1,5 4 4 2 -3 -4 -5 -6 B Also: y = - 1,5 x + 1