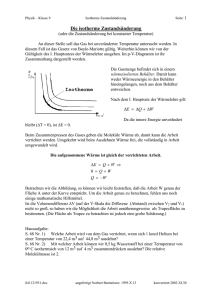
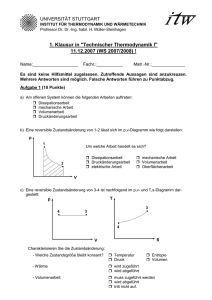
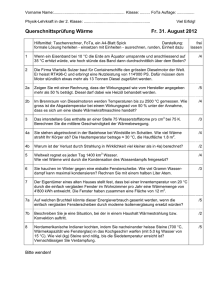
T 300K,p 1,00 10 Pa,V 0525 10 m ,T 1200K, V 1 V 5

Kontrolle Physik Leistungskurs Klasse 12
17.3.2017
1. Hauptsatz, Kreisprozesse
1. Als man früh aus dem Haus gegangen ist, hat man doch versehentlich die Kühlschranktür
offen gelassen. Man merkt es erst, als man nachmittags wieder nach Hause kommt. Wie hat
sich die Temperatur im dem Raum im Vergleich zur geschlossenen Kühlschranktür
verändert? (1)
a) Die Temperatur ist kleiner geworden.
b) Die Temperatur hat sich nicht verändert.
c) Die Temperatur ist gestiegen.
2. (Ph-LK 2011)
Ein einatomiges Gas durchläuft folgenden Kreisprozess:
1
2 Isotherme Kompression
2
3 Isobare Erwärmung
3
4 Isotherme Expansion
4
1 Isobare Zustandsänderung zum Anfangszustand
Dieser Kreisprozess wird mehrfach durchlaufen.
a) Skizzieren sie das p(V)-Diagramm für diesen Kreisprozess. (4)
b) Eine Gasturbine realisiert diesen Kreisprozess mit 2000 Umläufen pro Minute. Es gilt:
T1  300K,p1  1,00 10 5 Pa, V1  0,525 10 3 m3,T3 1200K,
V2 1

V1 5
Geben Sie tabellarisch Druck, Volumen und Temperatur für die Zustände 1 bis 4 dieses
Kreisprozesses an. (4)
c) Ermitteln Sie den Betrag der von dieser Gasturbine in einem Umlauf abgegebenen
Nutzarbeit. (4)
d) Geben Sie die Leistung der Gasturbine an. (3)
3. (LK 2015)
Ein thermodynamischer Kreisprozess besteht aus genau einer isothermen, einer isobaren
und einer isochoren Zustandsänderung des idealen Gases.
Zwei Kreisprozesse, die sich in der Abfolge der Zustandsänderungen unterscheiden, sind
möglich.
a) Skizzieren Sie jeweils ein p(V)-Diagramm für jede der beiden Möglichkeiten. Jeder der
beiden Graphen wird im Uhrzeigersinn durchlaufen. (4)
b) Einer der beiden Prozesse enthält eine Zustandsänderung (a), bei der die Zufuhr von
Wärme ausschließlich zur Erhöhung der inneren Energie des Gases führt.
Die andere enthält eine Zustandsänderung (b), bei der die Volumenarbeit am Gas
ausschließlich zur Abgabe von Wärme führt.
Wenden Sie die Gleichung des ersten Hauptsatzes auf diese beiden Zustandsänderungen
an. (4)
Kennzeichnen Sie die Zustandsänderungen (a) und (b) im jeweiligen Diagramm. (2)
Lösungen
1. c ist richtig.
Man kann den Raum als abgeschlossenes System betrachten. Bleibt die Kühlschranktür
offen, versucht die Regeltechnik im Kühlschrankinneren die Temperatur niedrig zu halten.
Dazu muss der Kompressor für die Erzeugung des Druckes in der Kühlflüssigkeit ständig
arbeiten. Dabei wird die Flüssigkeit erwärmt und gibt über den Wärmetauscher an der
Rückseite die Wärme an die Umgebung ab. Im Kühlschrank dehnt sich die Flüssigkeit aus
und nimmt dabei wieder Wärme auf (Kühlprozess). Da der Wirkungsgrad aber immer unter
100% liegt, nimmt die Flüssigkeit weniger Wärme auf als sie vorher abgibt. Damit ist die
Energiebilanz so, dass der Raum sich langsam erwärmt. Die dazu benötigte Energie wird
über die elektrische Energie zugeführt und wird mit der Zeit teuer.
2.
geg.:
T1  300K
p1  1,00 105 Pa
V1  0,525 103 m3
T3  1200K,
V2 1

V1 5
ges.:
Lösung:
b) Zustand 1: alle Größen sind gegeben
Zustand 2: Das Volumen im Zustand 2 ist nur 1/5 so groß wie das Volumen im Zustand
1, also
V2 
0,525 103 m3
 0,105 10 3 m3
5
Da der Vorgang isotherm verläuft, bleibt die Temperatur erhalten.
Damit wird der Druck aber auf den 5fachen Wert ansteigen.
Zustand 3: Der Druck bleibt gleich (isobar). Die Temperatur steigt nach den gegebenen
Größen auf 1200 K an. Damit dehnt sich aber auch das Volumen auf das 4fache aus.
Zustand 4. Temperatur bleibt gleich (isotherm)
Da die nächste Zustandsänderung isobar zum Anfangszustand verläuft, muss im
Zustand 4 schon der Druck vom Zustand 1 erreicht werden. Das heißt, der Druck fällt
auf ein Fünftel ab. Damit wird sich das Volumen verfünffachen.
Zustand
1
Druck
Volumen
Temperatur
1,00 10 Pa
3
0,525 10 m
300K
2
5,00 105 Pa
0,105 103 m3
300K
3
5,00 10 Pa
0,42 10 m
4
1,00 105 Pa
2,1103 m3
5
5
3
3
3
1200K
1200K
c) Bei der Änderung 3->4 wird dem System Wärme zugeführt. Da der Vorgang
isotherm verläuft, sich die Temperatur also nicht ändert, ist die Änderung der inneren
Energie Null, die gesamte Wärme wird in Volumenarbeit umgewandelt.
Bei der Änderung 1->2 wird dem System Arbeit zugeführt. Die Energie dafür kommt
z.B. aus einem Schwungrad. Da die Temperatur wieder konstant bleibt, muss Wärme
abgegeben werden.
Die Arbeit, die das System nach außen effektiv abgibt, ist die Differenz aus den beiden
Arbeiten. Die im Übergang 3->4 nach außen abgegebene Arbeit wird teilweise im
Schwungrad gespeichert und im Übergang 1->2 dem System wieder zugeführt, kann
also nicht genutzt werden.
Damit ist die Arbeit
W  W3 4  W12
Der zweite Summand ist dabei negativ.
Aus der allgemeinen Gleichung für die Volumenarbeit kann die spezielle Form
V
Wa  e  p  V  ln e
Va
hergeleitet werden.
Damit kann die Gleichung für die angegebene Arbeit aufgestellt werden:
V
V
W  p3  V3  ln 4  p1  V1  ln 2
V3
V1
W  338 J  84,5J
W  253,5J
d) Das ist die Arbeit, die bei einem Umlauf abgegeben wird. Da die Maschine in der
Minute 2000 Umläuft macht, liefert sie
WMin  2000  253,5 J
WMin  507 103 J
WMin  507kJ
Die Leistung ist definiert als Arbeit je Zeit, also
W
t
507kJ
P
60 s
P  8,45kW
P
Antwort:
Die Turbine gibt bei einem Umlauf 253,5 J ab. Sie hat eine Leistung von 8,45 kW.
Vorüberlegung: wie sehen die p-V-Diagramme für die drei Zustandsänderungen aus?
Diese drei Zustandsänderungen sollen einen Kreisprozess bilden. Legt man sich auf der
Isothermen zwei Punkte fest, müssen diese beiden Punkt durch die beiden anderen
Prozesse verbunden werden.
Das wäre die eine Möglichkeit.
Und das die andere.
b) Zustandsänderung (a): Der erste Hauptsatz heißt:
U  Q  W
Da die Zufuhr von Wärme Q ausschließlich zur Erhöhung der inneren Energie führen soll, ist
die Volumenarbeit 0. Es kommt also nur einer der beiden isochoren Zustandsänderungen in
Frage.
Der Hauptsatz wird zu
U  Q
Da die Temperatur ein Maß für die innere Energie ist, muss die Temperatur bei dem
Vorgang größer werden. Das ist im zweiten Prozess die Zustandsänderung 3-1.
Zustandsänderung (b): Die Volumenarbeit am Gas führt zur Abgabe von Wärme. Die innere
Energie soll sich nicht ändern. Der erste Hauptsatz sieht dann so aus:
0Q W
W Q
Die Temperatur bleibt bei diesem Vorgang unverändert, es kann also nur eine
Zustandsänderung auf einer Isothermen sein.
Da am Gas Arbeit verrichtet wird, wird das Volumen kleiner und der Druck größer. Das kann
im ersten Prozess nur die Zustandsänderung 1-2 sein.