Prüfung Physik I 29062011

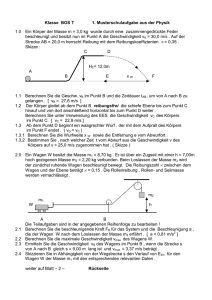
NAME: Matr.Nr.: Stud.‐Richt.: Schriftliche Prüfung aus Physik I (Rechenteil) am 29.6.2011
(6 Beispiele: insgesamt 20 Punkte) 1. Gegeben sei ein homogener dünner Stab der Länge L = 0.5 m und Masse M = 0.8 kg, der 20 cm von einem der beiden Enden drehbar gelagerte sei. Der Stab werde in die horizontale Position gebracht und dann losgelassen. Mit welcher Geschwindigkeit bewegt sich der Stab durch den tiefsten Punkt? (Das Trägheitsmoment eines langen dünnen Stabes bzgl. einer Achse durch den Schwerpunkt ist I = 1/12*M*L2). (3 Punkte)
2. Ein Federpendel mit einer Masse von 0.1 kg werde 20 cm ausgelenkt und dann losgelassen. Im Laufe des Schwingungsvorgangs erreicht das Pendel dabei eine maximale Geschwindigkeit von 0.5 m/s. a) Berechnen Sie die Federkonstante und die Schwingungsdauer des Pendels. b) Berechnen Sie die Zeit nach dem Loslassen, bei der die Momentanauslenkung die Hälfte der Anfangsauslenkung ist, und die zu diesem Zeitpunkt erreichte Momentangeschwindigkeit. (3 Punkte) 3. Auf eine zylindrische Seiltrommel mit der Masse M = 3 kg ist ein masseloses Seil aufgewickelt, an dem eine Masse von m = 0.5 kg hängt. Wenn die Trommel freigegeben wird, beginnt sich das Seil abzuwickeln und die Masse m M
abzusinken. a) Berechnen Sie die Sinkgeschwindigkeit, die die Masse nach einer Höhendifferenz von 3 m erreicht. b) Berechnen Sie die Zeit, die die Masse zum Absinken für diese Strecke benötig. c) berechnen Sie die Seilkraft. m
(4 Punkte) 4. Die g-Saite einer Violine ist 30 cm lang und hat eine Masse von 1 g. Wenn sie ohne Griff
gespielt wird, schwingt die Grundschwingung mit einer Frequenz von 196 Hz. a) Wie weit
vom Saitenende muss der Finger gesetzt werden, um den Ton a (220Hz) zu spielen? b) Mit
welcher Kraft muss man die Saite vorspannen, damit die g-Saite richtig gestimmt ist?
(3 Punkte)
5. Ein kugelförmiger Leiter mit Radius r1 = 6 cm wird mit einer Gesamtladung von +80 nC aufgeladen. Anschließend wird er mit einem zweiten kugelförmigen Leiter mit r2 = 2 cm durch einen dünnen leitenden Draht verbunden. a) Wie groß sind die Ladungen auf den beiden Kugeln? b) Wie groß ist das elektrische Feld der beiden Kugeln direkt an der Kugeloberfläche? c) Wie groß ist das elektrische Potential jeder Kugel? (Nehmen Sie an, die Kugeln seien sehr weit voneinander entfernt, sodass sich ihre elektrischen Felder praktisch nicht gegenseitig beeinflussen, und die Ladung des Verbindungsdrahtes sei vernachlässigbar). (3 Punkte) 6. Berechnen Sie die Kraft (Betrag und Richtung) auf jeden der vier Leiterabschnitte sowie die resultierende Kraft, die der vom Strom I = 15 A durchflossene Leiter (l1 = 20 cm, l2 = 10 cm, l3 = 15 cm, l4 = 20 cm, γ = 45°) im homogenen Magnetfeld von B = 0.3 T erfährt! (4 Punkte) NAME: Matr.Nr.: Stud.‐Richt.: Schriftliche Prüfung aus Physik I (Theoretischer-Teil) am 29.6.2011
(3 Fragen nach Wahl beantworten, bitte genau kennzeichnen!)
1. Oberflächenspannung: Berechnen Sie den Innendruck in einer Seifenblase und in einem
Wassertropfen? Was passiert, wenn man zwei unterschiedlich große Seifenblasen
miteinander verbindet? Wie kommt die Kapillarkraft in dünnen Röhren zustande? Zeigen
Sie quantitativ, dass die Steighöhe in dünnen Röhren höher ist als in dicken? (4 Punkte) 2. Gravitation: Wie hängen die Gravitationskraft und das Gravitationsfeld zusammen, wie die potentielle Energie und das Gravitationspotential? Skizzieren Sie das Gravitationsfeld und die dazugehörigen Äquipotentialflächen für eine punktförmige Masse. Wie ist der Zusammenhang zwischen Gravitationsfeld und Gravitationspotential? Wie groß ist die Gesamtenergie einer Masse im Gravitationsfeld, und wie kann man daraus die Fluchtgeschwindigkeit der Masse berechnen? (4 Punkte) 3. Der Kondensator in nebenstehender Zeichnung sei auf eine Spannung UC aufgeladen und dann werde der Schalter geschlossen. Verwenden Sie das Induktionsgesetz sowie die Definition des elektrischen Stromes um eine Differenzialgleichung für den Strom herzuleiten. Zeigen Sie, dass die Lösung eine harmonische Schwingung ist, und berechnen Sie die Eigenfrequenz dieses Schwingkreises. (4 Punkte) 4. Wie lautet das Ampere’sche Gesetz, und was bedeutet es physikalisch? Welche Überlegungen führen zur Einführung des Maxwell’schen Verschiebungsstroms und damit zur Erweiterung des Ampere’schen Gesetzes zum Ampere‐Maxwell’schen Gesetz. Argumentieren Sie mithilfe eines Kondensators im Wechselstromkreis. Berechnen Sie diesen Verschiebungsstrom innerhalb des Kondensators als Funktion des elektrischen (Wechsel)feldes zwischen den Kondensatorplatten. (4 Punkte)