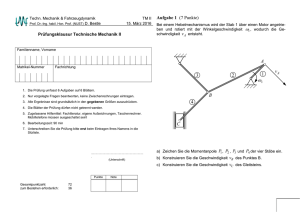
Physik 4 Zusammenfassung

Physik 4 Zusammenfassung
Lukas Wilhelm
3. Januar 2010
Inhaltsverzeichnis
1 Grundlagen
4
1.1
Mathe
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2
Annäherungen
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
1.3
Trigonometrie . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
1.4
Ableitungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
1.5
Dynamik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4
1.6
Bogenlänge
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
1.7
Einheiten
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
2 Elektro
2.1
2.2
4
5
Konstanten
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
2.1.1
Masse eines Atoms . . . . . . . . . . . . . . . . . . . . . . . . . . .
5
2.1.2
Masse eines Elektrons
Ladungen
. . . . . . . . . . . . . . . . . . . . . . . . .
5
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
2.2.1
Begrie
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
2.2.2
Elementarladung . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
2.2.3
Kraft zwischen 2 Ladungen
6
2.2.4
Anzahl Elektronen pro Ladung
2.2.5
Ladungsdichte
2.2.6
Raumladung
2.2.7
Inuenz
. . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . .
6
. . . . . . . . . . . . . . . . . . . . . . . . . . . . .
6
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
7
2.3
Elektrisches Feld
. . . . . . . . . . . . . . . . . . . . . . . . .
7
2.4
Gaussches Gesetz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
2.5
Kondensatoren
8
2.3.1
Elektrisches Potential
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.5.1
Kapazität parallelgeschalteter Kondensatoren
2.5.2
Plattenkondensator . . . . . . . . . . . . . . . . . . . . . . . . . . .
8
2.6
elektrische Arbeit . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
2.7
Elektrischer Strom
2.7.1
. . . . . . . . . . . .
8
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
elektrische Stromdichte . . . . . . . . . . . . . . . . . . . . . . . . .
9
1
2.8
2.7.2
Elektronendichte
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.7.3
Ohmsches Gesetz . . . . . . . . . . . . . . . . . . . . . . . . . . . .
9
2.7.4
spezischer elektrischer Widerstand . . . . . . . . . . . . . . . . . .
10
2.7.5
Widerstand und Leitfähigkeit . . . . . . . . . . . . . . . . . . . . .
10
2.7.6
Klemmenspannung . . . . . . . . . . . . . . . . . . . . . . . . . . .
10
2.7.7
elektrische Leistung
10
. . . . . . . . . . . . . . . . . . . . . . . . . .
9
Magnetostatik . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
10
2.8.1
Lorentz-Kraft . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
10
2.8.2
rechte Hand Daumenregel . . . . . . . . . . . . . . . . . . . . . . .
11
Transformator . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
11
2.10 Wirkungsgrad . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
11
2.9
2.11 magnetisches Feld . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
2.11.1 magnetische Feldstärke eines geraden Leiters
11
. . . . . . . . . . . .
12
2.11.2 magnetischer Fluss . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
2.11.3 magnetische Flussdichte
12
. . . . . . . . . . . . . . . . . . . . . . . .
2.11.4 magnetische Feldkonstante . . . . . . . . . . . . . . . . . . . . . . .
2.12 Induktion
12
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
12
2.13 Wechselstrom . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13
3 Schwingungen
3.1
Allgemein
13
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13
3.1.1
Umdrehungen . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13
3.1.2
harmonische Schwingung . . . . . . . . . . . . . . . . . . . . . . . .
13
3.1.3
Auslenkung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
13
3.1.4
Geschwindigkeit und Beschleunigung . . . . . . . . . . . . . . . . .
14
3.1.5
Federschwingung
14
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
3.2
Masse Feder Schwinger . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
3.3
vertikaler Masse Feder Schwinger . . . . . . . . . . . . . . . . . . . . . . .
14
3.4
mathematisches Pendel . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
14
3.5
Physisches Pendel . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
15
3.5.1
15
3.6
3.7
Trägheitsmomente
. . . . . . . . . . . . . . . . . . . . . . . . . . .
gedämpfte Schwingungen . . . . . . . . . . . . . . . . . . . . . . . . . . . .
15
3.6.1
. . . . . . . . . . . . . . . . . . . . .
15
. . . . . . . . . . . . . . . . . . . . . . . . . . . .
17
geschwindigkeitsproportional
erzwungene Schwingung
4 Wellen
4.1
17
Allgemein
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.1.1
Arten
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
4.1.2
Type . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
17
17
17
4.2
harmonische Wellen
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
17
4.3
Wellengleichung . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
18
4.4
Wellengeschwindigkeiten . . . . . . . . . . . . . . . . . . . . . . . . . . . .
18
4.4.1
tiefes Wasser
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
18
4.4.2
aches Wasser . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
18
2
4.5
Dopplereekt
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
19
4.5.1
optischer Dopplereekt . . . . . . . . . . . . . . . . . . . . . . . . .
19
4.5.2
Schwebung
19
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3
1 Grundlagen
1.1 Mathe
•
mega,
M = 106
•
milli,
m = 10−3
•
mikro,
•
nano,
µ = 10−6
n = 10−9
1.2 Annäherungen
ist ein kleiner Wert
1
=1−
1+
1
=1+
1−
√
1 + 2 = 1 + √
1+=1+
2
1.3 Trigonometrie
G
A
G
A
H
H
A
G
sin
cos
tan
cot
cot(α) =
1
tan(α
sin2 + cos2 = 1
1.4 Ableitungen
Funktion
Ableitung
sin
cos
cos
-sin
1
x
− x12
1.5 Dynamik
Ekin =
4
mv 2
2
1.6 Bogenlänge
gerade Strecke
s = v ∗ ∆t
Umfang Kreis
u = 2πr
folglich:
α
ist der Winkel im Bogenmass, also
π/3
◦
für 60
s = rα
1.7 Einheiten
1N ewton = 1kg
m
s2
2 Elektro
2.1 Konstanten
2.1.1 Masse eines Atoms
S.548
Aran
Anzahl Kernteilchen pro Atom (je nach Element) = zahlengleich der molaren Masse. Tabelle 56
1.66.. ∗ 10−27
mA
mittlere Masse eines Kernteilchens
Masse eines Atoms
mA = Aran u = Aran ∗ 1.660539 ∗ 10−27 kg
Anzahl Atome:
n=
M assegesamt
mAtom
2.1.2 Masse eines Elektrons
9.109 ∗ 10−31
5
2.2 Ladungen
2.2.1 Begrie
Ladungsneutralität
Alle Ladungen summiert sind gleich 0. Position dieser ist egal.
2.2.2 Elementarladung
e = 1.602 ∗ 10−19 C
Qe = −e
Qp = +e
Elektron:
Proton:
2.2.3 Kraft zwischen 2 Ladungen
Q Ladung [C] = [As]
F
r
Kraftwirkung zwischen den Ladungen Q1 und Q2
Abstand
ε0
Feld- oder Inuenzkonstante
er
Einheitsvektor, Richtung dieser Kraft,
F =
F~ =
a2 + b2 = 1
1 q1 · q2
,
4πε0 r2
1 q1 · q2
· e~r
4πε0 r2
ε0 = 8.854 ∗ 10−12
C2
N m2
2.2.4 Anzahl Elektronen pro Ladung
n=
2.2.5 Ladungsdichte
Linienladungsdichte
Flächenladungsdichte
Ladung
Q
=
ElementarladungElektron
Qe
l = Länge
λ=
Q
L
σ=
Q
A
A = Fläche
6
2.2.6 Raumladung
=
%
Q=V%
2.2.7 Inuenz
Wegen der Kraftwirkung einer Ladung, werden andere frei bewegliche Ladungen angezogen oder abgestossen => Ladungstrennung. Inuenzladung ist die dadurch hervorgerufene Ladungsträgerkonzentration. bsp. an der Oberäche eines Metallstücks.
2.3 Elektrisches Feld
Bezeichnung auch E-Feld Einheit: N / C
Q ist die (gesamte) Ladung im Feld.
~
F~ = EQ
~ =
E
~ =
E
1 Q1
~r
4πε0 |r|3
1 Q1
4πε0 r2
Das E-Feld zeigt in eine Richtung (von + zu -). Die Elektronen iessen aber in die
entgegengesetzte Richtung.
2.3.1 Elektrisches Potential
W Arbeit
ϕA
ϕ
elektrisches Potenzial im Punkt A
elektrisches Potenzial (U
Epot
Q
= ϕA − ϕB )
potenzielle Energie, nicht mehr ladungsbezogen
Probeladung
Die potentielle Energie ist gleichbedeutend mit der Arbeit die man aufwenden müss-
te um die Ladung Q von einem beliebigen Bezugspunkt 0 an die betreende Stelle zu
bringen.
Epot = W
ϕA =
7
W
Q
ϕ=
ϕS =
X
Epot
Q
ϕi =
X
1 Qi
4πε0 r
2.4 Gaussches Gesetz
Der elektrische Fluss durch eine beliebige geschlossene Fläche ist gleich der Summe der
eingeschlossenen Ladungen.
Φ=
Z
X
Q
~ A
~=
ε0 Ed
Φ=
Z
%dV
2.5 Kondensatoren
C
Kapazität [F = Farad]
Q
U
C=
2.5.1 Kapazität parallelgeschalteter Kondensatoren
Es liegt an allen die gleiche Spannung.
C=
X
Ci
i
2.5.2 Plattenkondensator
Er
Dielektrizitätskonstante, Permivitätszahl
A
d
A
C = εr ε0
d
U = Ed
C = ε0
1 CU 2
2 d
1
E = CU 2
2
F =
Durchbruchstärke
= Elektrisches Feld bei dem ein Durchbruch stattndet.
8
2.6 elektrische Arbeit
W = QU
aus der Dynamik
W = Fs
2.7 Elektrischer Strom
I=
Q
t
2.7.1 elektrische Stromdichte
j
Stromdichte
n
Elektronendichte
%
Raumladungsdichte
I
A
% = ne
j=
j = nev
2.7.2 Elektronendichte
N
Anzahl der Atome im Volumen V
NA
m
M
%
Avogadro Zahl
Masse
Atommasse
Dichte des Materials (bsp. Kupfer)
n=
N
=
V
m
M nA
V
2.7.3 Ohmsches Gesetz
U = RI
9
=
%Na
m
2.7.4 spezischer elektrischer Widerstand
ρ
spezischer Widerstand des Materials
l
Länge des Leiters
A
Querschnittäche des Leiters
R=ρ
l
A
bsp für Kupfer
ρ = 0.0178Ωmm2 /m)
Kreisäche
A = r2 ∗ π
2.7.5 Widerstand und Leitfähigkeit
%
Widerstand
σ
Leitfähigkeit
σ=
1
%
2.7.6 Klemmenspannung
Die Klemmenspannung ist deniert als die Quellenspannung minus Widerstände im
Stromkreis.
U = U0 − R i I
2.7.7 elektrische Leistung
P = U I[W att]
2.8 Magnetostatik
2.8.1 Lorentz-Kraft
S.467
B
v
Q
Magnetfeld [Tesla =
Vs
]
m2
Geschwindigkeit
Ladung
10
Wenn Kraft auf einen positiven Ladungsträger wirkt, der sich rechtwinklig zur Feldrichtung durch ein Magnetfeld bewegt.
F = QvB
Ladungsträger bewegt sich unter einem beliebigen Winkel zur Feldrichtung:
~
F~ = Q(~v × B)
Wenn Magnetfeld und elektrisches Feld wirkt
~ + ~v × B)
~
F = q(E
2.8.2 rechte Hand Daumenregel
Die technische Stromrichtung geht von + zu -. Die Elektronen iessen aber in Wahrheit
von - zu +.
•
gestreckter Daumen: technische Richtung Strom, entgegen Flussrichtung Elektronen
•
Zeigenger auf gleicher Ebene: Magnetfeld
•
abgespaltener Mittelnger: wirkende Kraft
2.9 Transformator
Uˆ1
maximale Spannung
U1 = Uˆ1 sinωt
beim verlustfreien Transformator gilt:
Uˆ2
N2
=
N1
Uˆ1
das gleiche gilt auch für I
2.10 Wirkungsgrad
η=
PabgebeneLeistung
Pzugef uehrteLeistung
2.11 magnetisches Feld
Bezeichnung auch B-Feld
11
2.11.1 magnetische Feldstärke eines geraden Leiters
S.450
H
magnetische Feldstärke ausserhalb des stromdurchussenen geraden Leiters im Abstand r
H=
I
2πr
2.11.2 magnetischer Fluss
Φ
magnetischer Fluss
BN
Komponente der magnetischen Flussdichte in Richtung Flächennormale
Φ = BN A
2.11.3 magnetische Flussdichte
S.454
B
Flussdichte [T]
µ0
magnetische Feldkonstante
H
magnetische Feldstärke
B = µ0 H
2.11.4 magnetische Feldkonstante
µ0 = 1.256637 ∗ 10−6
Vs
Am
2.12 Induktion
Φ
magnetischer Fluss
U =−
dΦ
d
=−
dt
dt
Z
Wenn sich der Leiter konstant bewegt
U = −Blv
12
A
~ A
~
Bd
2.13 Wechselstrom
Sin Kurve ist in der Realität nicht so schön wie theoretisch gerechnet. Darum gilt dass folgende Werte für Gleichstrom gelten. (Werden für theoretische Berechnungen gebraucht):
Andere Funktionen haben andere Annäherungsfunktionen.
Û
Scheitelwert
U
eektiver Wert
U (t) = Û sin(ωt)
ω = 2πv
auch für I und R:
Û
U=√
2
Normales Stromnetz hat ein v von 50Hz
3 Schwingungen
3.1 Allgemein
3.1.1 Umdrehungen
3.1.2 harmonische Schwingung
w0
v
T
= Kreisfrequenz [rad/s]
Frequenz [Hz] pro Sekunde
Periodendauer
Eine harmonische Schwingung ist periodisch.
2π
= 2πv
T
1
ω0
v= =
T
2π
ω0 =
3.1.3 Auslenkung
x(t) = Rcos(α(t)) = Rcos(ωt)
13
3.1.4 Geschwindigkeit und Beschleunigung
Geschwindigkeit ist die erste Ableitung der Auslenkung, Beschleunigung die zweite Ableitung.
y(t) = Auslenkung
0
y (t) = Geschwindigkeit
y 00 (t) = Beschleunigung
3.1.5 Federschwingung
k
F
Federkonstante
Kraft, die die Änderung
∆l
verursacht.
F
∆l
k=
3.2 Masse Feder Schwinger
y(t) = ŷsin(ω0 t +
wobei
π
) = ŷcos(w0 t)
2
r
ω0 =
c
m
3.3 vertikaler Masse Feder Schwinger
y(t) = Lcos(ω0 t)
mit
r
ω0 =
g
∆l
3.4 mathematisches Pendel
g
Gravitationskraft 9.81
l
Länge von Faden
ϕ(t) = ϕ̂cos(ω0 t)
mit
r
ω0 =
14
g
l
3.5 Physisches Pendel
S. 201
T
Schwingungsdauer
JA
s
Massenträgheitsmoment des Körpers bezüglich der Achse A (Aufhängung)
Abstand Drehpunkt A - Schwerpunkt s
s
T = 2π
JA
mgs
3.5.1 Trägheitsmomente
Wenn
JS
bekannt ist und man das Massenträgheitsmoment
JA
bezüglich einer zur
Schwerpunktachse parallen Achse A berechnen möchte:
JA = JS + ma2
Vollzylinder
JS =
m 2
r
2
3.6 gedämpfte Schwingungen
3.6.1 geschwindigkeitsproportional
ω0
Kreisfrequenz einer ungedämpften Schwingung.
ωd
Kreisfrequenz der gedämpften Schwingung
δ
Abklingkonstante [s
c
Federkonstante [
b
Bremskonstante [
A
τ
−1 ]
N
m]
N
m/s ]
Amplitude [m]
Abklingzeit
•
die Frequenz der gedämpften Schwingung bleibt während dem Schwingungsvorgang
gleich
•
die maximale Auslenkung ist vorhanden bei
oft ignoriert werden.
15
e−δt sin(...) = 1| − 1
und kann darum
•
ϕ0 =
sin kann mit cos ersetzt werden wenn
π
2 . D.h. das Pendel beginnt in der
X-Ebene zu schwingen, nachdem es von rechts losgelassen wird.
y(t) = Ae−δt sin(ωd t + ϕ0 )
b
2m
δ=
ωd =
q
w02 − δ 2
r
ω0 =
1
ϕ
τ=
Dämpfungsgrad
c
m
Wenn es zum Ausklingen mehrere Perioden dauert, spricht man von
einer schwach gedämpften Schwingung =>
D<1
•
= 0 ungedämpfte Schwingung
•
1 gedämpfte Schwingung (viel kleiner als 1)
•
< 1 aperiodisch mit Überschwingung
•
= 1 aperiodischer Grenzfall
•
> 1 aperiodisch mit Kriechbewegung
δ
ω0
D=
p
ωd = ω0 1 − D2
Federkraft
s
Längenänderung durch Kraft F
c=
F
s
16
3.7 erzwungene Schwingung
ωr
Resonanzfrequenz
ω0
Eigenkreisfrequenz
Ar
Resonanzamplitude
D
Dämpfungsgrad
ut
Aufhängepunkt der Feder wird mit Auslenkung u bewegt
p
ωr = ω0 1 − 2D2
u
√ 0
Ar =
2D 1 − D2
u(t) = u0 sin(ωt)
y(t) = A(ω)sin(ωt − φ(ω))
4 Wellen
4.1 Allgemein
4.1.1 Arten
Mechanische Wellen: Wasserwellen, Schallewellen, Erdbebenwellen.
Elektromagnetische Wellen: Radio, Radar, Licht.
Materiewellen (Quantenmechanik)
4.1.2 Type
Transversal: schwingt senkrecht zur Ausbreitungsrichtung.
Longitudinal: Schwingt in Ausbreitungsrichtung. Braucht Medium.
Unterschied: Die Richtung der Auslenkung verglichen mit der Fortpanzungsrichtung
der Welle.
4.2 harmonische Wellen
u
Wellengeschwindigkeit [m/s]
ξ
Amplitude [in Einheit der physikalischen Grösse]
ω
Kreisfrequenz [1/s,rad/s]
k
Wellenzahl [1/m,rad/m]
17
λ
Wellenlänge [m]
v
Frequenz [1/s,Hz]
T
Periodendauer [s]
ϕ0
(Null)-Phasenwinkel, Phasenwinkel zum Zeitpunkt t = 0
u = vλ
λ = ut
ω
k=
u
ξ(x, t) = ξ0 sin(kx − wt + ϕ0 )
k=
2π
λ
4.3 Wellengleichung
ξ¨ Ableitung
nach t,
ξ 00
Ableitung nach x
¨ t) = u2 ξ 00 (x, t)
ξ(x,
ξ(x, t) = ξ0 sin(kx − ωt)
4.4 Wellengeschwindigkeiten
4.4.1 tiefes Wasser
s
u=
gλ
2π
4.4.2 aches Wasser
h
Wassertiefe [m]
r
u=
18
g
h
4.5 Dopplereekt
vB
vom Beobachter wahrgenommene Frequenz
vQ
von der Quelle ausgesendete Frequenz
νB
Geschwindigkeit des Beobachters
νQ
Geschwindigkeit der Quelle
ϑB
Winkel der Bewegungsrichtung des Beobachters zur Verbindungsgeraden zwischen
Quelle und Beobachter
ϑQ
Winkel der Bewegungsrichtung der Quelle zur Verbindungsgeraden zwischen Quel-le
und Beobachter
vB =
u + νB cos(ϑB )
vQ
u − νQ cos(ϑQ )
4.5.1 optischer Dopplereekt
Weil kein Trägermedium vorhanden ist, wird andere Formel benötigt. Es spielt nur die
Relativgeschwindigkeit zwischen Quelle und Beobachter eine Rolle.
v∗
Frequenz im Bezugssystem B
v
Relativgeschwindigkeit
c
Lichtgeschwindigkeit
p
v∗ =
1 − β2
v
1 − βcos(ϑ)
β=
v
c
4.5.2 Schwebung
Überlagerung zweier Schallwellen gleicher Ausbreitungsrichtung ergibt bei geringer Frequenzdierenz eine Schwebung.
vS
v1,2
Schwingungsfrequenz
Frequenz der ersten, zweiten Welle
vS = v1 − v2
19