Wirtschaftstheorie in einem einzigen Satz zusammengefasst: Man

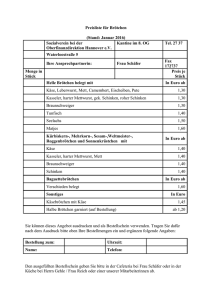
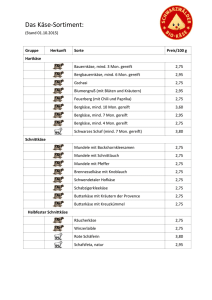
Haushaltstheorie
Wirtschaftstheorie in einem
einzigen Satz
zusammengefasst: Man kann
nicht essen, ohne zu bezahlen.
(Milton Friedman)
Mikroökonomik
Prof. Dr. Hetmar Wilbert
1
Haushaltstheorie
Grenznutzen und Gesetz vom abnehmenden Grenznutzen
Konsummenge
Nutzen
Grenznutzen
Grenznutzen
x
U
GU = ∆U / ∆x
GU * = ( ∆U / ∆x ) *
0
0
10
1
10
(10 + 8) / 2 = 9
8
2
18
(8 + 6) / 2= 7
6
3
24
(6 + 4) / 2= 5
4
4
28
Die Nutzenfunktion stellt Konsum x eines Gutes und damit verknüpften Nutzen U gegenüber. Es wird als
typischer Verlauf angenommen, dass der Nutzen zwar mit zunehmender Konsummenge ansteigt, jedoch diese
Steigerung immer abgebremster verläuft. Kürzer kann man dies mit dem so genannten Grenznutzen
beschreiben, der die Nutzenänderung ∆U zum Ausdruck bringt, wenn der Haushalt eine Einheit mehr
konsumiert (∆x=1) . Offenbar fällt dieser Grenznutzen um so kleiner aus, desto größer die Konsummenge ist, bei
der die Veränderungsbetrachtung startet. Das ist das Gesetz vom abnehmenden Grenznutzen (Gossensches
erstes Gesetz der kardinalen Nutzentheorie). Hoher Konsum bedeutet dann niedrigen Grenznutzen einer
weiteren Konsumeinheit, niedriger Konsum impliziert hohen Grenznutzen einer zusätzlichen Konsumeinheit.
Die ergänzende Asteriskberechnung (*) erlaubt dabei eine Zuordnung des „Grenznutzens der Umgebung“ zu
den x-Stellen, weil ansonsten der Grenznutzen ja auf Intervalle bezogen ist.
Mikroökonomik
Prof. Dr. Hetmar Wilbert
2
Haushaltstheorie
Gesetz des gleichen gewogenen Grenznutzens im Haushaltsoptimum
(∆U/∆Bier) / Preis Bier = (∆U/∆Pizza) / Preis Pizza
Angenommen:
Grenznutzen je
verausgabtem
Euro für Bier
80/5 = 16
>
100/10 = 10
Grenznutzen je
verausgabtem Euro
für Pizza
Konsumanpassungen:
Mehr Bierkonsum und weniger Pizzakonsum
Sinkender Grenznutzen
beim Bier
Nutzenkonsequenzen:
Steigender Grenznutzen
bei Pizza
Denkbares Ergebnis am Anpassungsprozessende:
60/5 = 12 =
120/10 = 12
Eine optimale Aufteilung eines Budgets im Zwei-Güter-Fall ist erreicht, wenn der Grenznutzen je
verausgabter Geldeinheit bei beiden Gütern gleich ist. Das ist das Gossensche zweite Gesetz der
kardinalen Nutzentheorie.
Mikroökonomik
Prof. Dr. Hetmar Wilbert
3
Haushaltstheorie
Indifferenzkurvenkonzept
Wein
6
A
5
4
B
3
C
2
Käse
Wein
Punkt
1
6
A
2
3
B
3
2
C
4
1½
D
D
1
1
2
3
4
5
6
Käse
Eine Indifferenzkurve (ordinale Nutzentheorie) steht für ein bestimmtes Nutzenniveau, was ein Haushalt
über den gemeinsamen Konsum zweier Güter realisieren kann. So kann der Haushalt Wein gegen Käse
substituieren und dabei sein Nutzenniveau beibehalten. Denkbare Möglichkeiten zeigt die Tabelle
(Beispiel!).
Mikroökonomik
Prof. Dr. Hetmar Wilbert
4
Haushaltstheorie
Substitutionsrate und Gesetz der Substitution
Wein
Wein
6
5
4
3
6
Der
Haushalt ist
Wein
bereit, für 1 Käse
mehr auf 1 ½ Wein
zu verzichten.
6/4=
3/2
5
4
B
2
Der Haushalt ist
bereit, für 1 Käse
mehr auf 2/3 Wein
zu verzichten.
3
1
2
1
4/6=
2/3
C
1
1
2
3
4
5
6
Käse
1
1
2
3
4
5
6
Käse
Die Substitutionsrate kann in jedem Punkt der Indifferenzkurve bestimmt werden. Hier ist das für zwei Punkte
gezeigt. Die Substitutionsrate entspricht immer der absolut betrachteten Steigung der Tangente an die
Indifferenzkurve im gerade fokussierten Punkt , die sich als Quotient aus Ordinatenabschnitt und
Abszissenabschnitt der Tangente ermitteln lässt. Die Substitutionsrate gibt die subjektive Tauschbereitschaft
des Haushalts an.
Das Gesetz der Substitution besagt, dass die Substitutionsrate sinkt, wenn fortgesetzt ein zuerst reichlich
konsumiertes Gut (Wein) sukzessive durch ein zunächst knapp konsumiertes Gut (Käse) ersetzt wird.
Mikroökonomik
Prof. Dr. Hetmar Wilbert
5
Haushaltstheorie
Substitutionsrate und Grenznutzen
Ausgangssituation
Käse
Wein
Subjektive Tauschbereitschaft /
Substitutionsrate
⎸∆ Wein / ∆ Käse ⎸:
Das impliziert für das
Grenznutzenverhältnis
∆U/∆Käse / ∆U/∆Wein :
2
3
Für 1 Käse mehr Verzicht
auf 1 ½ Wein
⎸∆ Wein / ∆ Käse ⎸= ⎸⎼ 1 ½ / +1 ⎸
=1½
Bereitschaft, 1 ½ Wein aufzugeben
für 1 Käse mehr, ist gegeben, wenn
∆U/∆Käse / ∆U/∆Wein = 1 ½
3
2
Für 1 Käse mehr Verzicht
auf 2/3 Wein
⎸∆ Wein / ∆ Käse ⎸= ⎸⎼ 2/3 / +1 ⎸
= 2/3
Bereitschaft, 2/3 Wein aufzugeben
für 1 Käse mehr, ist gegeben, wenn
∆U/∆Käse / ∆U/∆Wein = 2/3
Die Substitutionsrate entspricht immer dem Verhältnis der Grenznutzen der beiden Konsumgüter.
Formal gilt dann:
⎸∆ Wein / ∆ Käse ⎸= ∆U/∆Käse / ∆U/∆Wein
Mikroökonomik
Prof. Dr. Hetmar Wilbert
6
Haushaltstheorie
Indifferenzkurvenschar
Wein
6
5
4
3
2
1
1
2
3
4
5
6
Käse
Da eine Indifferenzkurve ein ganz bestimmtes Nutzenniveau repräsentiert, gibt es letztlich beliebig viele
Indifferenzkurven. Oben sind drei solche Indifferenzkurven eingezeichnet. Die mittlere Indifferenzkurve ist die
bislang verwendete Indifferenzkurve. Indifferenzkurven können sich nicht schneiden oder zurückbiegen. Diese
ergäbe logische Probleme. Je weiter weg vom Ursprung eine Indifferenzkurve liegt, desto höher ist das damit
repräsentierte Nutzenniveau. Je näher am Ursprung eine Indifferenzkurve verläuft, desto niedriger ist das
hiermit verknüpfte Nutzenniveau.
Mikroökonomik
Prof. Dr. Hetmar Wilbert
7
Haushaltstheorie
Budgetgerade (bei Budget angenommen 6€)
Wein
5
Käse
(Preis je
Käse sei 1,5€)
4
0
6
I
2
3
II
4
0
III
6
I
3
II
2
Wein
(Preis je
Wein sei 1€)
Punkt
1
1
2
3
III
4
5
6
Käse
Die Budgetgerade zeigt, was ein Haushalt bei gegebenem Budget und gegebenen Preisen für die beiden
Konsumgüter an Kombinationen im gemeinsamen Konsum der beiden Güter realisieren kann. Drei
solcher Kombinationen sind oben einmal dargestellt.
Mikroökonomik
Prof. Dr. Hetmar Wilbert
8
Haushaltstheorie
Das Haushaltsoptimum
Wein
6
5
4
3
2
1
1
2
3
4
5
6
Käse
Oben dargestellt ist einmal die zuvor eingeführte Indifferenzkurvenschar. Zum anderen ist die zuvor
dargestellte Budgetgerade eingezeichnet. Beim Punkt liegt das Haushaltsoptimum, denn hier erreicht der
Haushalt bei gegebenem Budget und gegebenen Preisen gerade noch die Indifferenzkurve mit dem dann
höchstmöglichen Nutzenniveau. Die weiter rechts oben liegende Indifferenzkurve weist zwar ein höheres
Nutzenniveau auf, ist aber bei der gegebenen Budgetrestriktion nicht erreichbar. Die weiter links unten
liegende Indifferenzkurve ist zwar erreichbar (siehe Schnittpunkte), weist aber ein niedrigeres Nutzenniveau
auf als die Optimum erreichbare Indifferenzkurve.
Mikroökonomik
Prof. Dr. Hetmar Wilbert
9
Haushaltstheorie
Das Haushaltsoptimum in formaler Sicht
Die absolute Steigung der Budgetgeraden lässt sich
ermitteln als Quotient aus Ordinaten- und
Abszissenabschnitt. Das ergibt:
Wein
Der Schnittpunkt der
Budgetgeraden mit
der Ordinate ist
ermittelbar als
Budget/Weinpreis (im
Fall 6€/1€=6).
6
Budget/Weinpreis
5
Käsepreis
=
Budget / Käsepreis
4
1,5€
=
Weinpreis
= 1,5
1€
3
Der Schnittpunkt der Budgetgeraden mit
der Abszisse ist gegeben als
Budget/Käsepreis (im Fall 6€/1,5€=4).
2
1
1
2
3
4
5
6
Käse
Im Optimum wird die Budgetgerade zur Tangente an eine Indifferenzkurve (siehe Punkt
). Diese tangierende
Budgetgerade hat dabei als absolute Steigung das Verhältnis der Preise der beiden Konsumgüter (siehe
Ermittlung oben). Gleichzeitig repräsentiert die absolute Steigung einer Tangente an eine Indifferenzkurve
immer die Substitutionsrate der beiden Güter im Tangentialpunkt (siehe oben). Damit gilt, dass der Haushalt
zwecks Nutzenmaximierung eine Konsumsituation herstellt, in der gilt:
⎸∆ Wein / ∆ Käse ⎸= Käsepreis / Weinpreis
Mikroökonomik
Prof. Dr. Hetmar Wilbert
10
Haushaltstheorie
Gesetz des gleichen gewogenen Grenznutzens im Haushaltsoptimum als
Ergebnis der ordinalen Nutzentheorie
Herleitung des Gesetzes
⎸∆ Wein / ∆ Käse ⎸= ∆U/∆Käse / ∆U/∆Wein (Folie weiter oben)
⎸∆ Wein / ∆ Käse ⎸= Käsepreis / Weinpreis (Folie zuvor)
∆U/∆Käse
/ ∆U/∆Wein = Käsepreis / Weinpreis
∆U/∆Käse / Käsepreis = ∆U/∆Wein / Weinpreis
Ein Haushalt handelt hiernach also wieder optimal, wenn er eine solche Konsumsituation wählt, bei der
der Grenznutzen je verausgabter Geldeinheit bei den Gütern gleich ist.
Mikroökonomik
Prof. Dr. Hetmar Wilbert
11
Haushaltstheorie
Änderung des Haushaltsoptimums nach Preisänderung eines Konsumgutes
Wein
Der Schnittpunkt mit
der Ordinate bleibt
unverändert, weil das
Budget und der
Weinpreis unverändert
bleiben sollen.
6
5
Der Schnittpunkt mit der Abszisse wird
kleiner, weil sich gemäß Annahme der
Käsepreis erhöht und der Abszissenabschnitt
durch den Quotienten Budget/ Käsepreis
bestimmt ist (jetzt 6€/3€ = 2).
4
3
2
1
Käse
1
2
3
4
5
6
Wenn der Käsepreis sich verdoppelt (und Budget sowie Weinpreis gleich bleiben), dreht sich die Budgetgerade
im Ordinatenabschnitt (siehe oben) nach links (weil der Abszissenabschnitt kleiner wird). Sie verläuft nunmehr
steiler und erreicht nicht mehr die bisherige Indifferenzkurve sowie das damit verbundene Nutzenniveau. Jetzt
wird eine Indifferenzkurve mit niedrigerem Nutzenniveau gerade noch berührt, und das Optimum (bestmögliche
Nutzenerreichung unter gegebenen Umständen) hat sich verändert (siehe oben). Man erkennt, dass das teurer
gewordene Konsumgut (Käse) nun weniger (nur noch 1 Einheit ) als zuvor (da waren es 2 Einheiten)
konsumiert wird.
Mikroökonomik
Prof. Dr. Hetmar Wilbert
12
Haushaltstheorie
Die typische Nachfragefunktion auf Basis der Haushaltsoptimierung
Käsepreis
3€
1,5€
1
2
Käse
Überträgt man die Ergebnisse der Haushaltsoptimierung der Folie zuvor mit Fokus auf Käsepreis und
Kaufmenge von Käse in ein diesbezügliches Schaubild, erhält man eine spezielle Nachfragefunktion für das
Gut Käse, die im Fall offenbar den typischen Verlauf nimmt, dass die Nachfrage mit steigenden Preis sinkt
(und umgekehrt). Damit ist unter Optimierungsgesichtspunkten des Haushaltsoptimums der typische
Nachfragekurvenverlauf nachgewiesen.
Mikroökonomik
Prof. Dr. Hetmar Wilbert
13
Haushaltstheorie
Änderung des Haushaltsoptimums nach einer Einkommensänderung
Wein
9
Unterstellt ist der Ausgangsfall hinsichtlich der
Preise (1€ Wein, 1,5 € Käse), allerdings soll das
Budget auf 9€ steigen. Die Budgetgerade
verschiebt sich nach außen. Jetzt können z.B.
9 *1 = 9€ Wein oder 6*1,5= 9€ Käse konsumiert
werden. Wie man erkennt , wird jetzt von den
beiden Gütern mehr konsumiert. Im Beispiel
ergeben sich 3*1,5 =4,5€ Ausgaben für Käse und
4,5*1=4,5€ Ausgaben für Wein.
8
7
6
5
4
3
2
1
Käse
1
Mikroökonomik
2
3
4
5
6
Prof. Dr. Hetmar Wilbert
14
Haushaltstheorie
Eine Einkommens-Nachfragefunktion („Engel-Kurve“) auf Basis der Haushaltsoptimierung
Einkommen
9€
6€
2
3
Käse
Überträgt man die Ergebnisse der Haushaltsoptimierung der Folie zuvor nunmehr mit Fokus auf
Einkommen und Kaufmenge von Käse in ein diesbezügliches Schaubild, erhält man eine spezielle
Nachfragefunktion für das Gut Käse, die hier den Verlauf nimmt, dass die Nachfrage mit steigenden
Einkommen zunimmt (und umgekehrt). Damit ist unter Optimierungsgesichtspunkten des
Haushaltsoptimums auch ein Nachfragekurvenverlauf in Abhängigkeit vom Einkommen nachgewiesen.
Mikroökonomik
Prof. Dr. Hetmar Wilbert
15
Haushaltstheorie
Eine genauere Sicht auf Einkommens- und Substitutionseffekte bei einer Preissteigerung von Käse
Wein
1 Substitutionseffekt (Folgen der relativen Preisänderung)
2 Einkommenseffekt (Folgen des Kaufkraftverlusts)
2
„Künstliche“ Budgetgerade
(mit „Budgetausgleich“ ) , die
dem Haushalt ermöglicht,
trotz Preisanhebung bei Käse
sein Nutzenniveau zu halten
(und auf der bisherigen
Indifferenzkurve zu bleiben)
1
Käse
Es kommt durch die Preissteigerung zu einer relativen Verteuerung von Käse und zudem zu einem Verlust an
Kaufkraft. Die Reaktion auf die relative Verteuerung ist der Substitutionseffekt der Preisanhebung, die Reaktion
auf den Verlust an Kaufkraft ist der Einkommenseffekt der Preiserhöhung. Durch eine diesbezügliche
theoretische „Zerlegung“ der Entwicklung von altem zu neuem Haushaltsoptimum lässt sich der Zusammenhang
der Effekte demonstrieren. Offenbar kompensiert im Fall hier der Einkommenseffekt vollkommen den Substitutionseffekt, was Wein anlangt, während bei Käse beide Effekt den Käsekonsum „additiv“ reduzieren.
Mikroökonomik
Prof. Dr. Hetmar Wilbert
16
Haushaltstheorie
Indifferenzkurven bei der Konsum-Freizeit-Entscheidung
Konsum
Freizeit
Arbeitszeit
Der Haushalt kann zwischen Freizeit (und damit Verzicht auf Lohn und Konsum) und Konsum (wofür Lohn
benötigt wird und deshalb Arbeitszeit anfällt) wählen. Es wird unterstellt, dass unterschiedliche
Kombinationen von Freizeit und Konsum dem Haushalt ein gleiches Nutzenniveau bescheren können, was
eine Indifferenzkurve hier zum Ausdruck bringt. Je weiter weg vom Ursprung eine Indifferenzkurve liegt,
desto höher ist das damit repräsentierte Nutzenniveau.
Mikroökonomik
Prof. Dr. Hetmar Wilbert
17
Haushaltstheorie
Budgetgerade bei der Konsum-Freizeit-Entscheidung
Konsum
36
Arbeitszeit
Lohn
(l=10€/h)
Konsum Freizeit
(p=5€/St)
18
180
36
0
12
120
24
6
8
80
16
10
0
0
0
18
Freizeit
Arbeitszeit
24
16
0
6
10
18
18
12
8
0
Die Budgetgerade bringt hier zum Ausdruck, welche Entscheidungsalternativen bei gegebenem Lohnsatz
und gegebenem Preis für den Haushalt bestehen. Vier Alternativen sind in der Tabelle exemplarisch
erfasst.
Mikroökonomik
Prof. Dr. Hetmar Wilbert
18
Haushaltstheorie
Haushaltsoptimum bei der Konsum-Freizeit-Entscheidung
Konsum
54
36
24
16
0
6
10
18
18
12
8
0
Freizeit
Arbeitszeit
Das Haushaltsoptimum liegt dort, wo die Budgetgerade eine Indifferenzkurve berührt. Im Beispiel ergibt
sich das Optimum bei einer Freizeit von 10 Stunden und einer Arbeitszeit von 8 Stunden, welche einen
Lohn von 80€ (beim Lohnsatz 10€/h) erbringt und eine Konsummenge von 16 Stück (beim Preis von
5€/St) erlaubt.
Mikroökonomik
Prof. Dr. Hetmar Wilbert
19
Haushaltstheorie
Budgetgeradenänderung bei der Konsum-Freizeit-Entscheidung
Konsum
54
36
Arbeitszeit
Lohn
(l=15€/h)
Konsum Freizeit
(p=5€/St)
18
270
54
0
12
180
36
6
8
120
24
10
0
0
0
18
Freizeit
Arbeitszeit
24
0
6
10
18
18
12
8
0
Die Budgetgerade verändert sich bei höherem Lohnsatz in der oben gezeigten Weise. Bei gleichem
Schnittpunkt mit der Abszisse wandert der Ordinatenschnittpunkt nach oben.
Mikroökonomik
Prof. Dr. Hetmar Wilbert
20
Haushaltstheorie
Neues Haushaltsoptimum bei der Konsum-Freizeit-Entscheidung nach Lohnsatzänderung
Konsum
54
36
24
16
0
6
10
18
18
12
8
0
Freizeit
Arbeitszeit
Das neue Haushaltsoptimum ist dort, wo die geänderte Budgetgerade wieder eine Indifferenzkurve
berührt. Im Beispiel ergibt sich das neue Optimum bei einer Freizeit von 6 Stunden und einer Arbeitszeit
von 12 Stunden, welche einen Lohn von180€ (beim Lohnsatz 15€/h) einbringt und eine Konsummenge
von 36 Stück (beim Preis von 5€/St) zulässt.
Mikroökonomik
Prof. Dr. Hetmar Wilbert
21
Haushaltstheorie
Die Arbeitsangebotskurve des Haushalts
Lohnsatz
15
10
0
8
12
18
Arbeitszeit
Überträgt man die Lohnsatz-Arbeitszeit-Kombinationen der beiden Optima in ein entsprechendes
Diagramm, ist die Arbeitsangebotskurve des Haushalts gefunden. Im Beispiel steigt die Arbeitszeit mit
zunehmendem Lohnsatz ebenfalls an.
Mikroökonomik
Prof. Dr. Hetmar Wilbert
22