Zur Simulation von Haftreibung und mechanischen Anschlägen

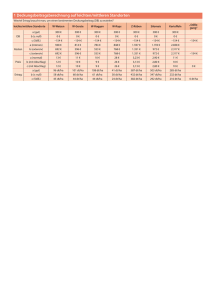
Zur Simulation von Haftreibung
und mechanischen Anschlägen
Heinz A. Gall
Maschinenbau, Berufsakademie in Horb
e-mail: [email protected]
1999
Kurzfassung
Die besonderen Eigenschaften von Zwangskräften liefern einen Ansatz für die Modellierung von Haftreibung und mechanischen Anschlägen. Dabei werden Auslenkung, Geschwindigkeit und Beschleunigung ereignisgesteuert auf feste Werte gesetzt. Dies ist möglich, da die Lösung der Bewegungsgleichung
in Bindungsrichtung bekannt ist, sobald
Zwangskräfte auftreten.
Die Integrationsroutinen müssen dazu über
die Möglichkeit verfügen, einzelne Zustandsgrößen zu setzen, während die anderen Zustandsgrößen weiter integriert werden.
Seit der Version 2 verfügt SIMULINK über
die notwendigen Setzmöglichkeiten. So wird
der beschriebene Ansatz z.B. in der Simulinkdemo „Friction Model with Hard Stops in
Simulink 3“ teilweise realisiert. Leider sind
nicht alle Aspekte des Modellierungsansatzes
berücksichtigt.
Der Beitrag möchte die grundlegenden Gedanken und Hintergründe der Modellbildung
von Haftreibung und mechanischen Anschlägen durch Setzen von Systemzuständen aufzeigen und am Beispiel einer SIMULINKRealisierung verdeutlichen.
1. Einleitung
Bei der Simulation mechanischer Systeme
tritt immer wieder das Problem der harten mechanischen Anschläge auf. Beispielsweise ist
die Steuerkolbenbewegung eines Hydraulikventils oder der Kolbenweg eines Hydraulikzylinders durch Anschläge begrenzt.
Eine einfache, aber wenig vorteilhafte Methode, solche Anschläge zu simulieren, basiert
auf der Vorstellung, daß es sich bei Anschlägen um sehr steife, aber doch nachgiebige Bauteile handelt. Dementsprechend modelliert man
harte Anschlagfedern und entsprechend starke
Anschlagdämpfer. Problematisch ist dann die
Wahl der Feder- und Dämpferkonstanten. Da
diese Parameter nicht direkt aus den technischen Gegebenheiten abgeleitet werden können, erkennt man, daß Anschlag-federn und –
dämpfer oft nur Hilfskonstruktionen sind, um
Anschläge überhaupt simulieren zu können.
Simulationstechnische Schwierigkeiten entstehen auch dadurch, daß das mechanische System durch die harten Federn im Anschlagbereich relativ hochfrequent wird, was z.B. zu
kleinen Integrationsschrittweiten und großen
Rechenzeiten führt.
Die in diesem Beitrag beschriebene Vorgehensweise entspringt einer anderen Anschauung über die physikalische Wirkungsweise von
Anschlägen. Dabei werden keine Aussagen
über die Vorgänge während des Anschlagens
gemacht. Vielmehr betrachtet man das Auftreffen auf einen Anschlag als ein Zustandsereignis.
2. Ein Ausflug in die Technische Mechanik
Ist ein Körper durch materielle Bindungen
mit anderen Körpern verbunden, dann hat man
eine geführte Bewegung. Die Bewegungsfreiheit des Körpers ist durch die starren Verbindungen eingeschränkt.
Rollt z.B. eine Kugel auf einem Tisch, dann
sorgt der materielle Kontakt zwischen Tisch
und Kugel dafür, daß die Kugel nicht in den
Tisch eindringt. Dies geschieht dadurch, daß in
der Bindung eine Zwangskraft erzeugt wird,
die zu jedem Zeitpunkt genau so groß ist, daß
Seite 1
in Richtung der Tischplatte Kräftegleichgewicht herrscht.
3. Anschlagmodellierung
Für die Modellierung mechanischer Anschläge ergibt sich aus der oben beschriebenen
Einsicht folgende Vorgehensweise.
Die Vorstellung, daß in materiellen
Bindungen Zwangs- oder Reaktionskräfte
entstehen, die genau so groß sind, daß sie eine
Bewegung gerade verhindern, kann bei der
Modellbildung von harten Anschlägen verwendet werden.
Man unterscheidet zwei Zustände, in denen
sich das System befinden kann:
a) Freie Bewegung (Fz = 0)
Es wirken keine Anschläge, d.h. keine geometrischen Zwänge. Die Masse bewegt sich
entsprechend der Differentialgleichung (1),
wobei als Kräfte F nur eingeprägte Kräfte Fe in
Erscheinung treten (Gewicht, Feder- und
Dämpferkräfte, Gleitreibung, hydraulische
Druckkräfte, usw.).
b) Erzwungener Stillstand (Fz ≠ 0)
Bild 1: Feder-Masse-System mit Anschlägen
Wird z.B. ein Ventilkolben durch die einwirkenden eingeprägten Kräfte Fe gegen einen
Anschlag gedrückt, dann entsteht zwischen
Ventilkolben und Anschlag eine materielle
Verbindung, die jede Bewegung unterdrückt.
Die Auslenkung x wird in diesem Zustand auf
dem Anschlagswert xa festgehalten. Die Geschwindigkeit ist Null und auch die Beschleunigung verschwindet, solange die einseitige
geometrische Bindung in der Lage ist, Kräftegleichgewicht herzustellen.
Die Beschleunigung wird deshalb zu Null,
weil der Anschlag auf den Kolben eine
Zwangskraft Fz ausübt, die immer genau so
groß ist, daß die Summe aller Kräfte am Kolben gleich Null ist (1).
Beim Übergang von freier Bewegung zum
erzwungenen Stillstand tritt das Zustandsereignis „Stoß“ auf.
Zur Steuerung der Simulation verwendet
man logische Bedingungen, die Auskunft darüber geben, ob gerade ein Stoß eingetreten ist
und ob sich das System im Zustand des erzwungenen Stillstandes befindet oder nicht.
••
m ⋅ x = ∑ F = ∑ Fe + ∑ Fz
Die Masse befindet sich an einem Anschlag.
In der materiellen Bindung treten Zwangskräfte auf, die genau so groß sind, daß die Summe
aller Kräfte gleich Null ist. Solange der Körper
gegen den Anschlag gedrückt wird, bleibt die
Auslenkung x auf dem Anschlagswert xa festgehalten. Die Geschwindigkeit ist Null und es
tritt auch keine Beschleunigung auf. Da somit
die Lösung der Bewegungsgleichung (1) bekannt ist, kann man diese Lösung in das Simulationsmodell einbauen.
(1)
4. Anforderungen an ein Simulationspaket
Da der Anschlag nur Druck- aber keine
Zugkräfte aufbringen kann, wirkt der Anschlag
nur so lange, wie die angreifenden eingeprägten Kräfte Fe den Kolben in Richtung des
Anschlages drücken.
Oft können Begrenzungen dadurch simuliert
werden, daß man den Eingang eines Integrators auf Null setzt und somit eine Zustandsgröße auf dem momentanen Wert festhält. Dies
reicht für die Realisierung der oben dargestellten Anschlagsmodellierung nicht aus. Vielmehr benötigt man Integrationsroutinen, bei
Seite 2
denen einzelne Zustandsgrößen auf vorgebbare
Werte gesetzt werden können. Die nicht gesetzten Zustandsgrößen werden währenddessen
normal weiterintegriert.
Seit MATLAB 5/ SIMULINK 2 steht in
SIMULINK die notwendige Beeinflussungsmöglichkeit der Integratoren zur Verfügung.
Dabei ist zu beachten, daß das Setzen eines
Integrators nicht statisch, in Abhängigkeit eines Zustandes erfolgt, sondern dynamisch, bei
einem Zustandswechsel. Man muß daher dafür
sorgen, daß die gesetzten Integratoren festgehalten werden, solange die entsprechenden
Zustände andauern.
( x ≥ x a ) UND ( ∑ Fe ≥ 0)
6. Realisierung mit SIMULINK
Nachfolgend soll die Realisierung der vorgeschlagenen Anschlagmodellierung mit
SIMULINK 3 aufgezeigt werden.
Eine komfortable Zustandsbehandlung steht
in der Sprache DYMOLA oder mit der SIMULINK-Erweiterung STATEFLOW zur Verfügung.
Bild 1 zeigt das zugrundegelegte mechanische System mit zwei Anschlägen bei x = xa
bzw. bei x = xb. Es wird ein plastischer Stoß
angenommen.
5. Strategie
Will man die vorgeschlagene Anschlagsmodellierung anwenden, dann kommt den
boolschen Setzbedingungen eine zentrale Bedeutung zu. Man muß die Frage beantworten,
unter welcher Bedingung die Auslenkung x auf
den Anschlagswert xa bzw. die Geschwindigkeit auf Null gesetzt werden muß.
1. Erreicht der Körper den Anschlag, dann
tritt das Ereignis „Stoß“ ein. Die Auslenkung x wird auf den Anschlagswert xa und
die Geschwindigkeit wird auf Null gesetzt.
Setztbedingung (dynamisch):
x ≥ xa
( 2)
(3)
3. Ansonsten wird die Bewegungsgleichung
ohne jedweden Eingriff integriert.
In der Simulationssprache ACSL wird die
Ereignissteuerung mit der SCHEDULEOperation bewerkstelligt.
Für einen einseitigen Anschlag beim Auslenkungswert xa und unter der Annahme eines
plastischen Stoßes, kann die Setzstrategie folgendermaßen aussehen:
2. Wird der Körper von den eingeprägten
Kräften gegen den Anschlag gedrückt,
herrscht der Zustand „Erzwungener Stillstand“. Die Auslenkung x wird auf dem
Anschlagswert xa und die Geschwindigkeit
wird auf Null festgehalten. Dies wird durch
das Nullsetzen der Beschleunigung bewerkstelligt. Haltebedingung (statisch):
Die freie Bewegung wird durch folgende
Gleichungen beschrieben
 •
 x = xp
•
1
xp = (−c ⋅ x − d ⋅ xp + c ⋅ x e )
m

(4)
Bild 2 zeigt das SIMULINK-Modell. Alle
für die Anschlagmodellierung notwendigen
Blöcke sind durch Schatten gekennzeichnet.
Für die Integratorbeeinflussung stehen in
SIMULINK zwei Eingriffsmöglichkeiten zur
Verfügung. Die Integratorsättigung (Limit
output) und das externe Setzen (External reset). Dabei ist zu beachten, daß das externe
Setzen dynamisch erfolgt. Man setzt den Integrator also nicht solange ein Zustand andauert, sondern beim Eintreten eines Ereignisses
(Zustandswechsel).
Seite 3
c
d
0
Schaltbedingung
Mux
((u(2)==1)&&(u(1)>=0)) || ((u(2)==-1)&&(u(1)<=0))
1/m
xpp
Beschleunigung
1
s
|u|
Summe der eingeprägten Kräfte Fe
c
Schalter
Anregung
xe
Abs
xp
Geschwindigkeit
x
1
s
Integrator2
Integrator1
Steuersignal: 1...rechter Anschlag erreicht; -1...linker Anschlag erreicht
Bild 2: SIMULINK-Modell mit Anschlägen
Dementsprechend erfolgt die Integratorensteuerung folgendermaßen:
1. Die Auslenkung x wird, durch die Begrenzungen des Integrators2, auf den Anschlagswerten xa bzw. xb festgehalten. Ist
die Auslenkung x in der Sättigung, dann
wird dies durch das Steuersignal am „saturation port“ angezeigt.
2. Mit dem Steuersignal aus dem Integrator2
wird die Geschwindigkeit xp (Integrator1)
dynamisch, d.h. beim Zustandswechsel, auf
Null gesetzt, sobald ein Anschlag erreicht
ist. Da am saturation port auch beim Verlassen der Begrenzung Signalwechsel erfolgen, wird die Betragsbildung (Abs) und
die aufsteigende Flanke benutzt. Dadurch
ist sichergestellt, daß die Geschwindigkeit
nur beim Erreichen eines Anschlages auf
Null gesetzt wird.
3. Damit die Geschwindigkeit xp auch solange auf Null bleibt, solange die Masse gegen
den Anschlag gedrückt wird, hält man die
Beschleunigung xpp (Eingang des Integrators1) auf Null, solange ein Anschlag
wirkt. Schaltbedingung:
[( x ≥ x a ) UND ( ∑ Fe ≥ 0)]
ODER
[( x ≤ x b ) UND ( ∑ Fe ≤ 0)]
(5)
Bild 3 zeigt beispielhaft ein Simulationsergebnis:
Nachdem zur Zeit t = 0.1s die Eingangsgröße
xe einen Sprung von 0 auf 0.1 Meter gemacht
hat, bewegt sich die Masse in Richtung des
rechten Anschlages. Bei x = xa = 0.05m stößt
die Masse plastisch gegen den Anschlag. Da
die Feder die Masse gegen den Anschlag
drückt, bleibt die Geschwindigkeit xp gleich
Null und auch die Beschleunigung xpp verschwindet.
Erst wenn die Eingangsgröße xe bei t = 1,1s
wieder auf Null zurückgeht, löst sich die Masse vom Anschlag. Durch ihr Überschwingen
tippt sie noch am linken Anschlag an, ohne
dort für längere Zeit liegenzubleiben.
Die Simulation zeigt, daß die drei entscheidenden Vorgänge, „Anstoßen und Anliegen“,
„vom Anschlag lösen“ sowie „Antippen“
vom Modell richtig wiedergegeben werden.
7. Teilelastischer Stoß
Soll bei der Simulation berücksichtigt werden, daß der Körper beim Aufprall zurückspringt, dann muß beim Stoß eine Geschwindigkeitsumkehr modelliert werden.
Bild 4 zeigt, durch Schatten gekennzeichnet, die notwendige Erweiterung des SIMULINK-Modells. Die Dead Zone ist erforderlich, damit die Masse nicht unendlich oft und
dabei sehr hochfrequent prellt.
Seite 4
Auslenkung
Xa = 0.05m
Antippen am linken Anschlag
0.04
0.02
0
-0.02
-0.04
plastischer Stoß
am rechten Anschlag
0
0.2
0.4
0.6
Lösen vom
rechten Anschlag
0.8
1
1.2
Xb = -0.02m
1.4
1.6
1.8
2
1.2
1.4
1.6
1.8
2
1.2
1.4
1.6
1.8
2
1
Nullsetzen der Geschwindigkeit
(Stoß)
0.5
0
-0.5
0
Beschl. xpp [m/s 2]
Geschwind. xp [m/s]
Auslenkung x [m]
Bewegungsgrößen
0.2
0.4
0.6
0.8
1
4
2
Beschleunigung auf Null halten
0
-2
0
0.2
0.4
0.6
0.8
1
Zeit [s]
Bild 3: Simulationsergebnisse
c
d
Integrator1
0
Schaltbedingung
Mux
((u(2)==1)&&(u(1)>=0)) || ((u(2)==-1)&&(u(1)<=0))
xpp
1/m
Beschleunigung
c
1
|u|
s
Anregung
xe
Abs
[0]
IC
k
Stoßzahl
Bild 4: SIMULINK-Modell mit elastischem Stoß
Seite 5
Dead Zone
xp
Geschwindigkeit
x
1
s
Integrator2
Auslenkung
Die Stoßzahl k gibt das Verhältnis der Geschwindigkeiten vor und nach dem Stoß an.
v nachher = k ⋅ v vorher
anhalten kann. So kommt eine Masse auf einer
schiefen Ebene nicht vollständig zur Ruhe, da
immer eine kleine Geschwindigkeit erforderlich ist, um der Hangabtriebskraft entgegenzuwirken.
(6)
0.04
0.02
0
-0.02
-0.04
2
Im Gegensatz zur Gleitreibung ist die Haftreibung
eine Zwangskraft. Dementsprechend ist die Haftreibungskraft immer genau so groß, daß
sie den anderen Kräften das
Gleichgewicht hält und damit
jede Bewegung verhindert
(Auslenkung festgehalten, Geschwindigkeit gleich Null). Erst
wenn die anderen am Körper
angreifenden Kräfte von der
Haftreibung nicht mehr gehalten
werden können, tritt eine Bewegung auf.
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
0
0.2
0.4
0.6
0.8
1
Zeit [s]
1.2
1.4
1.6
Analog zum Anschlag läßt
sich daher die Haftreibung als
Zwangskraft modellieren.
Bild 7 gibt das zugehörige SIMULINK-Modell
wieder.
1
0.5
0
-0.5
Beschl. xpp [m/s ]
Geschwind. xp [m/s]
Auslenkung x [m]
Bewegungsgrößen
4
2
0
-2
1.8
Bild 5: Simulationsergebnisse
bei teilelastischem Stoß
2
1. Das Ereignis „Eintritt in die Haftreibung“
tritt nur auf, wenn die Relativgeschwindigkeit Null ist bzw. einen Nulldurchgang hat
(Hit Crossing Block) UND die Summe aller eingeprägten Kräfte kleiner-gleich der
maximal möglichen Haftreibungskraft ist.
Bei einer Stoßzahl von k = 0 handelt es sich
um einen plastischen Stoß. Ist k = -1, dann hat
man einen vollelastischen Stoß. Beim wirklichen Stoß liegt k zwischen 0 und –1.
Für einen teilelastischen Stoß (k = -0,6; tote
Zone = ±0,05 m/s; sonst alles wie für Bild 3) sind
in Bild 5 Simulationsergebnisse dargestellt.
Man erkennt deutlich das Zurückspringen der
Masse und die Geschwindigkeitsumkehr.
•
x=0
UND
∑ Fe ≤ FHaft ,max = µ 0 ⋅ FN
( 7)
8. Haftreibung
Oft wird Reibung durch Schlupfkurven
(Reibkraft über Relativgeschwindigkeit)
modelliert. Die Haftreibung wird dabei durch
einen steilen Kraftanstieg im Bereich kleiner
Geschwindigkeiten nachgebildet (Bild 6).
Neben numerischen Schwierigkeiten durch die
sehr große Verstärkung im Geschwindigkeitsnullpunkt, hat diese Methode den Nachteil, daß
der reibungsbehaftete Körper nicht so richtig
Die Geschwindigkeit xp (Integrator1) wird
in diesem Fall auf Null gesetzt.
2. Solange die Summe der eingeprägten Kräfte betragsmäßig kleiner-gleich der
maximal möglichen Haftreibungskraft
FHaft,max = µ0*FN
ist, befindet sich das System im Zustand
„Verharren in der Haftreibung“. Dabei
sorgt die Haftreibung als Reaktionskraft für
Seite 6
Kräftegleichgewicht. Die Beschleunigung
xpp ist Null.
Dadurch bleibt auch die Geschwindigkeit
xp bei Null stehen. Die Auslenkung x wird
auf dem momentanen Wert festgehalten.
Reibkraft
Geschwindigkeit
3. Tritt keine Haftreibung auf, dann kann z.B.
Gleitreibung als eingeprägte Kraft wirken.
•
FR = −sign( x ) ⋅ µ ⋅ FN
(8)
In Bild 8 sind Simulationsergebnisse dargestellt. Die Anregung springt bei der Zeit
t = 0.1s von Null auf xe = 0.1m. Nach einem
Einschwingvorgang kommt die Masse bei
t = 1,1s in der Haftreibung zur Ruhe. Die Auslenkung entspricht dabei nicht der Anregung!
Die Geschwindigkeit xp ist exakt gleich Null.
Bei t = 1,3s geht die Anregung sprunghaft auf
Null zurück. Die Masse befreit sich aus der
Haftreibung.
Bild 6: Reibkraft eines Hydraulikzylinders
In der Beschleunigung xpp ergeben sich
Nadelimpulse, die das Simulationsergebnis
aber praktisch nicht beeinflussen. Die Peaks
entstehen beim Beginn einer Bewegung, da die
Gleitreibung erst nach einem ersten Integrationsschritt (ab einer Geschwindigkeit xp ≠ 0)
sprunghaft wirkt.
c
Geschwindigkeit
d
Switch
Integrator1
0
xpp
1/m
Gleitreibungsreibungsmodell
Beschleunigung
mue*FN*u(1)
Integrator2
Sign
Gleitreibung
1
s
c
Anregung
xe
Haftreibungsmodell
xp
(u(2)==1)&&(abs(u(1))<=u(3))
Nulldurchgang
Geschwindigkeit
mue0*FN
Schaltbedingung
Max Haftreibung
Geschwindigkeit
Bild 7: SIMULINK-Modell mit Gleit- und Haftreibung
Seite 7
xp
1
s
x
Auslenkung
Xe
0.1
Haftreibung
0
-0.1
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
2
1.8
2
1.8
2
0.5
Haftreibung
0
-0.5
Beschl. xpp [m/s 2]
Geschwind. xp [m/s]
Auslenkung x [m]
Bewegungsgrößen
0.2
-1
0
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
5
Haftreibung
0
-5
0
0.2
0.4
0.6
0.8
1
Zeit [s]
1.2
1.4
1.6
Bild 8: Simulationsergebnisse: Feder-Masse-Schwinger mit Gleit- und Haftreibung
9. Schlußbemerkung
Beim Auftreten von Zwangskräften (materiellen Bindungen und Haftreibung) erfolgt
ein Strukturwechsel im mechanischen System.
Dieser führt dazu, daß die Lösung der Bewegungsgleichungen für die betroffene Größe
bekannt ist. Es herrscht nämlich Ruhe infolge
von Kräftegleichgewicht.
Durch Ereignissteuerung (Setzen und Anhalten von Integratoren) kann diese bekannte
Lösung in die Simulation eingebracht werden.
Bei ersten Versuchen („selbstgestrickte“
setzbare Integrationsroutinen mit fester
Schrittweite) hat sich diese Vorgehensweise
als sehr gutmütig erwiesen. Im Vergleich zu
Anschlagfedern und –dämpfern konnten ex-
trem große (feste) Schrittweiten verwendet
werden (Faktor 1000). Es traten keinerlei
numerische Probleme auf.
Seit es in SIMULINK setzbare Integratoren
gibt, wird die Vorgehensweise an der Berufsakademie in Horb z.B. bei der Simulation von
Hydrauliksystemen erfolgreich eingesetzt.
Auch wenn gelegentlich Warnmeldungen wegen algebraischer Schleifen auftreten, sind die
Erfahrungen sehr positiv.
Abschließend kann festgestellt werden, daß
man mit der vorgestellten Methode über eine
erprobte, funktionierende und leistungsfähige
Vorgehensweise zur Simulation von Haftreibung und harten Anschlägen verfügt.
Seite 8