Lösung Ersatzspannungsquelle

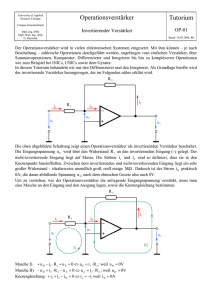
University of Applied
Sciences Cologne
Gleichspannung
Tutorium
Ersatzspannungsquelle
L-ESpQ-01
Campus Gummersbach
Dipl.-Ing. (FH)
Dipl.-Wirt. Ing. (FH)
G. Danielak
Stand: 19.03.2006; R0
Die hier gezeigten Lösungen beziehen sich auf die alten Klausuren von Herrn Dr. Weber, die man sich im
Internet unter den bekannten Adressen herunterladen kann. Sie zeigen verschiedene Lösungswege auf und
beschreiben darüber hinaus das grafische Lösungsverfahren.
Prüfung 2003/1
Aufgabe 5:
ƒ
Bestimmung von R ie
Lastwiderstand entfernen, Spannungsquelle kurzschließen und von der Lastseite her in die
Schaltung hereinschauen.
a
⇐R
ie
b
R ie = R 1 R 2 R 3 =
ƒ
1
1
=
= 15Ω
1
1
1
1
1
1
+
+
+
+
R 1 R 2 R 3 40Ω 120Ω 30Ω
Bestimmung von U 0
Lastwiderstand entfernen, Masche um U 0 legen und U 0 definieren.
a
I1
I2
II)
U R1
U R3
U R2
I)
I3
U0
UQ
b
University of Applied
Sciences Cologne
Gleichspannung
Tutorium
Ersatzspannungsquelle
L-ESpQ-02
Campus Gummersbach
Dipl.-Ing. (FH)
Dipl.-Wirt. Ing. (FH)
G. Danielak
Stand: 19.03.2006; R0
Hierfür gibt es mehrere Lösungsmöglichkeiten, bedingt durch das Legen der Maschen.
Masche I):
− U 0 − U R3 + U Q = 0 ⇔ U 0 = U Q − U R3 = U Q − I 3 ⋅ R 3
− U 0 + U R2 = 0 ⇔ U 0 = U R2 = I 2 ⋅ R 2
Weil R 2 parallel zu R 1 liegt, ist die Spannung an beiden Widerständen gleich
groß, d. h. U R2 = U R1 . Damit kann die II) Masche auch folgendermaßen lauten:
− U 0 + U R1 = 0 ⇔ U 0 = U R1 = I1 ⋅ R 1
In allen Fällen ist das Berechnen des Stroms I 3 unumgänglich, denn um I 2 oder I1 nach der
Stromteilerregel zu berechnen, muss der einfließende Strom I 3 bekannt sein.
Masche II):
Lösung nach Masche I)
a
I3
UQ
b
Der
Widerstand,
mit
dem
die
Spannungsquelle belastet wird, ist der
Gesamtwiderstand R ges . Er setzt sich aus
allen Widerständen zusammen, die an der
Quelle angeschlossen sind und durch die ein
Strom fließt. Dabei muss dieser Strom nicht
unbedingt − so wie hier − der Strom aus der
Quelle sein. Es ist dabei unbedingt wichtig,
dass für diese Formel der Strom aus dem
Pluspol der Quelle herausfließt:
U
UQ
UQ
=
I3 = Q =
R ⋅R
R ges R 3 + R 1 R 2
R3 + 1 2
R1 + R 2
10V
= 166, 6mA
40Ω ⋅120Ω
30Ω +
40Ω + 120Ω
Wenn man die Parallelschaltung bestehend aus R 1 und R 2 durch einen Widerstand R 12
ausdrückt, so fließt durch R 12 der Strom I 3 . Damit liegt R 12 in Reihe zu R 3 , denn er wird vom
gleichen Strom durchflossen. Die Masche (angelegt entgegengesetzt zum Uhrzeigersinn) zur
Bestimmung des Stroms lautet: − U Q + I 3 ⋅ R 3 + I 3 ⋅ R 12 = 0 . Löst man diese Gleichung nach I 3
=
auf, so ergibt sich die oben angegebene Gleichung. Würde man die Stromrichtung in die andere
Richtung wählen − der Strom fließt jetzt durch R 3 von oben nach unten − so erhält man eine
andere Maschengleichung: − U Q − I 3 ⋅ R 3 − I 3 ⋅ R 12 = 0 . Stellt man diese Gleichung nach I 3 um, so
ergibt sich ein negatives Vorzeichen für den gesuchten Strom! Das bedeutet lediglich, dass der
Strom in die entgegen gesetzte Richtung fließt, der Zahlenwert bleibt identisch:
− U Q − I 3 ⋅ R 3 − I 3 ⋅ R 12 = 0 ⇔ U Q = − I 3 ⋅ R 3 − I 3 ⋅ R 12 = − I 3 ⋅ (R 3 + R 12 )
⇔ I3 = −
UQ
R 3 + R 12
=−
UQ
R ⋅R
R3 + 1 2
R1 + R 2
University of Applied
Sciences Cologne
Gleichspannung
Tutorium
Ersatzspannungsquelle
L-ESpQ-03
Campus Gummersbach
Dipl.-Ing. (FH)
Dipl.-Wirt. Ing. (FH)
G. Danielak
Stand: 19.03.2006; R0
Setzt man die Lösung für I 3 in die Gleichung für U 0 ein, so erhält man folgendes Ergebnis:
U 0 = U Q − U R3 = U Q − I 3 ⋅ R 3 = 10V − 166, 6mA ⋅ 30Ω = 10V − 5V = 5V
Lösung nach Masche II)
Für diese Lösung muss erst der Strom I 2 berechnet werden. Das geschieht mit Hilfe der
Stromteilerregel; der einfließende Strom I 3 muss hierfür separat berechnet werden. In diesem
Beispiel wird auf die Lösung aus Masche I) zurückgegriffen.
I2 =
R1
R1
⋅ I3 =
⋅
R1 + R 2
R1 + R 2
UQ
40Ω
10V
=
⋅
= 41, 6mA
R ⋅R
40Ω ⋅120Ω
40Ω + 120Ω
30Ω +
R3 + 1 2
40Ω + 120Ω
R + R2
1442144
3
I3
Die Lösung für I 2 in die Gleichung für Masche II) eingesetzt ergibt:
U 0 = U R2 = I 2 ⋅ R 2 = 41, 6mA ⋅120Ω = 5V
Nach dem Berechnen von U 0 und R ie erfolgt das Ausrechnen der gesuchten Spannung U a sowie
des Stroms I a :
a
Die Gleichungen für I a und U a werden aus dem
Schaltbild der Ersatzspannungsquelle hergeleitet:
Ia
Ia =
Ua
U qe
b
U qe
R ie + R a
=
5V
= 43,47mA
15Ω + 100Ω
U a = I a ⋅ R a = 43,47mA ⋅100Ω = 4,34V
University of Applied
Sciences Cologne
Gleichspannung
Tutorium
Ersatzspannungsquelle
L-ESpQ-04
Campus Gummersbach
Dipl.-Ing. (FH)
Dipl.-Wirt. Ing. (FH)
G. Danielak
ƒ
Stand: 19.03.2006; R0
Grafisches Verfahren
Für das grafische Verfahren benötigt man neben den Werten für U 0 und R ie zusätzlich den
Kurzschlussstrom I 0 . Dieser wird nach folgender Gleichung berechnet:
I0 =
U0
5V
=
= 333, 3mA
R ie 15Ω
Damit zeichnet man zuerst die Quellenkennlinie mit den beiden Punkten U 0 und I 0 ein. Danach
wird die Widerstandgerade für den Lastwiderstand R a eingezeichnet. Dafür benötigt man
wiederum zwei Punkte. Ein Punkt, der bei allen passiven Bauelementen gleich ist, ist der
Ursprung. Den anderen kann man nach dem ohmschen Gesetz U = I ⋅ R berechnen. Man wählt
einfach einen beliebigen Strom I und multipliziert ihn mit dem Widerstandswert für R a :
U = I ⋅ R a = 50mA ⋅100Ω = 5V
Damit ist die Widerstandsgerade definiert. Der Schnittpunkt der beiden Geraden ist der
Arbeitspunkt mit I a und U a .
U
U0
Widerstandsgerade für R a
A
Ua
Quellenkennlinie
1V
Ia
100mA
I0
I
University of Applied
Sciences Cologne
Gleichspannung
Tutorium
Ersatzspannungsquelle
L-ESpQ-05
Campus Gummersbach
Dipl.-Ing. (FH)
Dipl.-Wirt. Ing. (FH)
G. Danielak
Stand: 19.03.2006; R0
Prüfung 2003/3
Aufgabe 5:
ƒ
Bestimmung von R ie
Lastwiderstand entfernen, Spannungsquelle kurzschließen, Stromquelle auftrennen und von der
Lastseite her in die Schaltung hereinschauen.
a
⇐R
ie
b
R ie = (R 1 + R 2 ) R 3 =
ƒ
(R 1 + R 2 ) ⋅ R 3 = (100Ω + 200Ω ) ⋅ 300Ω = 150Ω
R1 + R 2 + R 3
100Ω + 200Ω + 300Ω
Bestimmung von U 0
Lastwiderstand entfernen, Masche um U 0 legen und U 0 definieren. Weil hier zwei Quellen zum
Einsatz kommen − also Strom abgeben − ist die Richtung der Ströme frei wählbar.
U R2
I Q2
a
I2
I Q2
U R3
U R1
I1
I3
U0
U Q1
b
Die Bestimmung der Leerlaufspannung
U 0 erfolgt erst dann, wenn diese
Schaltung so umgeformt wurde, dass sich
die Quellenströme nicht aufteilen,
sondern nur ein einziger Strom fließt.
In diesem Zustand ist das Bestimmen von
I 3 (zur Berechnung von U 0 ) ohne
anwenden der Superposition schwierig.
University of Applied
Sciences Cologne
Gleichspannung
Tutorium
Ersatzspannungsquelle
L-ESpQ-06
Campus Gummersbach
Dipl.-Ing. (FH)
Dipl.-Wirt. Ing. (FH)
G. Danielak
Stand: 19.03.2006; R0
Zum Lösen dieser Aufgabe ist es erforderlich, dass man die Stromquelle in eine Spannungsquelle
umwandelt. Dadurch wird gewährleistet, dass sich kein Strom aus einer der beiden Quellen
aufteilt. Der resultierende Strom fließt somit in einem Strang durch beide Quellen (vgl. Praktikum
Elektrotechnik I 3) und kann auf sehr einfache Art und Weise bestimmt werden.
Umwandeln der Stromquelle in eine Spannungsquelle
I Q2
U R2
I Q2
Der Innenwiderstand einer Stromquelle liegt immer
parallel zu ihr; in diesem Falle ist dies nur der Widerstand
R 2 . Das bedeutet, die Last für die Stromquelle sind alle
Bauelemente unterhalb der beiden Anschlussklemmen C
und D. In dieser Klausuraufgabe ist das die
Reihenschaltung bestehend aus R 3 , U Q1 und R 1 , denn sie
D liegen zwischen C und D.
Wandelt man die Stromquelle in eine Spannungsquelle um, so geht man wie gewohnt vor:
Bestimmung von Ersatzinnenwiderstand und Leerlaufspannung. Weil sich die Last zwischen den
Klemmen C und D befindet, werden beide Größen auf diese Klemmen bezogen. Dadurch heißt der
Ersatzinnenwiderstand R ie ' und die Ersatzspannungsquelle U qe ' .
C
•
Bestimmung von R ie '
Der Erstzinnenwiderstand zwischen C und D ist R 2 , denn die Stromquelle ist aufgetrennt.
R ie ' = R 2
•
Bestimmung von U qe '
Die Leerlaufspannung zwischen C und D ist die Spannung am Widerstand R 2 . Diese wird
berechnet aus I Q2 ⋅ R 2 und fällt in der Richtung von C nach D ab, weil der I Q2 Strom in diese
Richtung fließt.
Die Ersatzspannungsquelle zwischen C und D muss die gleichen Eigenschaften aufweisen, denn
sie soll die Stromquelle ersetzen. Wird bei der Stromquelle die Last angeschlossen, so fließt ein
Teilstrom aus der Quelle von C nach D über die Last. Das bedeutet, dass auch der Strom aus der
Ersatzspannungsquelle von C nach D über die Last fließen muss. Dadurch ergeben sich folgende
Richtungen für die Zählpfeile:
Die Leerlaufspannung fällt bei dieser Schaltung von C
nach D ab, genauso wie bei der Stromquelle. Würde
man eine Last zwischen die Klemmen C und D
anschließen, so würde der Strom aus dem Pluspol der
Ersatzspannungsquelle über die Klemme C zur Klemme
D D und wieder zurück zum Minuspol fließen − analog zur
C
Stromquelle. Damit kann man diese Ersatzschaltung
anstelle der Stromquelle in die Originalschaltung einsetzen.
U qe ' = I Q2 ⋅ R 2
University of Applied
Sciences Cologne
Gleichspannung
Tutorium
Ersatzspannungsquelle
L-ESpQ-07
Campus Gummersbach
Dipl.-Ing. (FH)
Dipl.-Wirt. Ing. (FH)
G. Danielak
Stand: 19.03.2006; R0
U qe '
U Rie'
Hat man die Stromquelle durch eine
Spannungsquelle ersetzt, so ergibt
sich eine neue Schaltung, welche die
gleichen Eigenschaften besitzt wie
die Originalschaltung. Dadurch darf
man jetzt wiederum die Richtung der
Zählpfeile (also der Ströme, denn die
Spannung an einem passiven
Bauelement zeigt immer in die
gleiche Richtung, in die der Strom
fließt) frei wählen. Weil der Strom
aus beiden Quellen in die gleiche
Richtung fließt, ergibt sich ein
resultierender
Strom,
der
entgegengesetzt dem Uhrzeigersinn
fließt. Daraus folgt auch, dass alle
drei hier aufgezeigten Ströme gleich
sind, also:
a
I2
U R3
U R1
U0
I3
I1
U Q1
b
I1 = I 2 = I 3 = I
Mit diesem Ergebnis legt man eine Masche in die Schaltung hinein, so dass alle Spannungen,
welche von Strom I durchflossen werden, berücksichtigt werden:
− U Q1 + U R3 + U Rie' − U qe' + U R1 = 0 ⇔ U Q1 + U qe' = U R1 + U Rie' + U R3
⇔ U Q1 + U qe' = I ⋅ R 1 + I ⋅ R 3 + I ⋅ R ie '
⇔ U Q1 + U qe' = I ⋅ (R 1 + R 3 + R ie ')
⇔I=
⇔I=
U Q1 + U qe'
R 1 + R 3 + R ie '
=
U Q1 + I Q2 ⋅ R 2
R1 + R 2 + R 3
10V + 150mA ⋅ 200Ω
= 66, 6mA
100Ω + 200Ω + 300Ω
Mit dieser Lösung kann man jetzt die Leerlaufspannung U 0 bestimmen, denn sie berechnet sich
aus:
U 0 = U Q1 − U R3 = U Q1 − I ⋅ R 3 = U Q1 −
U Q1 + U qe '
R + R2 + R3
114
4244
3
I
⋅ R 3 = 10V − 66, 6mA ⋅ 300Ω = 10V − 20V = − 10V
Die nachfolgende Rechnung für I a und U a wird mit den hier berechneten Werten genauso wie
immer durchgeführt:
University of Applied
Sciences Cologne
Gleichspannung
Tutorium
Ersatzspannungsquelle
L-ESpQ-08
Campus Gummersbach
Dipl.-Ing. (FH)
Dipl.-Wirt. Ing. (FH)
G. Danielak
Stand: 19.03.2006; R0
a
Ia =
Ia
Ua
U qe
b
U qe
R ie + R a
=
− 10V
= − 33, 3mA
150Ω + 150Ω
U a = I a ⋅ R a = −33, 3mA ⋅150Ω = − 5V
Auch wenn die Werte für I a und U a negativ sind, so
bleiben die Zählpfeile eingezeichnet wie sie sind.
Würde man sie um 180° drehen, so entfällt das negative
Vorzeichen bei I a und U a .
University of Applied
Sciences Cologne
Gleichspannung
Tutorium
Ersatzspannungsquelle
L-ESpQ-09
Campus Gummersbach
Dipl.-Ing. (FH)
Dipl.-Wirt. Ing. (FH)
G. Danielak
ƒ
Stand: 19.03.2006; R0
Grafisches Verfahren
Benötigt wird der Kurzschlussstrom zwischen den Klemmen a und b:
I0 =
U 0 − 10V
=
= − 66, 6mA
R ie 150Ω
Damit zeichnet man zuerst die Quellenkennlinie mit den beiden Punkten U 0 und I 0 ein. Danach
wird die Widerstandgerade für den Lastwiderstand R a eingezeichnet. Dafür benötigt man
wiederum zwei Punkte. Ein Punkt, der bei allen passiven Bauelementen gleich ist, ist der
Ursprung. Den anderen kann man nach dem ohmschen Gesetz U = I ⋅ R berechnen. Man wählt
einfach einen beliebigen Strom I und multipliziert ihn mit dem Widerstandswert für R a :
U = I ⋅ R a = −20mA ⋅150Ω = − 3V
Damit ist die Widerstandsgerade definiert. Der Schnittpunkt der beiden Geraden ist der
Arbeitspunkt mit I a und U a .
−U
U0
Quellenkennlinie
Ua
A
Widerstandsgerade für R a
Ia
I0
2V
10mA
−I
University of Applied
Sciences Cologne
Gleichspannung
Tutorium
Ersatzspannungsquelle
L-ESpQ-010
Campus Gummersbach
Dipl.-Ing. (FH)
Dipl.-Wirt. Ing. (FH)
G. Danielak
Stand: 19.03.2006; R0
Prüfung 2005/3
Aufgabe 2:
ƒ
Bestimmung von R ie
Lastwiderstand entfernen, Spannungsquelle kurzschließen, Stromquelle auftrennen und von der
Lastseite her in die Schaltung hereinschauen.
a
⇐R
ie
b
R ie = (R 1 + R 2 ) R 3 =
ƒ
(R 1 + R 2 ) ⋅ R 3 = (100Ω + 200Ω ) ⋅ 200Ω = 120Ω
R1 + R 2 + R 3
100Ω + 200Ω + 200Ω
Bestimmung von U 0
Lastwiderstand entfernen, Masche um U 0 legen und U 0 definieren. Weil hier zwei Quellen zum
Einsatz kommen − also Strom abgeben − ist die Richtung der Ströme frei wählbar.
U R2
I Q2
a
I2
U R3
U R1
I3
U0
U Q1
I1
I Q2
b
Die Bestimmung der Leerlaufspannung U 0
erfolgt erst dann, wenn diese Schaltung so
umgeformt wurde, dass sich die
Quellenströme nicht aufteilen, sondern nur
ein einziger Strom fließt.
In diesem Zustand ist das Bestimmen von
I 3 (zur Berechnung von U 0 ) ohne
anwenden der Superposition schwierig.
University of Applied
Sciences Cologne
Gleichspannung
Tutorium
Ersatzspannungsquelle
L-ESpQ-011
Campus Gummersbach
Dipl.-Ing. (FH)
Dipl.-Wirt. Ing. (FH)
G. Danielak
Stand: 19.03.2006; R0
Umwandeln der Stromquelle in eine Spannungsquelle
C
I Q2
Bestimmt wird der Ersatzinnenwiderstand R ie ' sowie die
Leerlaufspannung U 0 ' zwischen den Klemmen C und D, denn
zwischen diesen beiden Klemmen liegt die Stromquelle I Q2 mit
U R1
ihrem Innenwiderstand R 1 . Die Last für diese Stromquelle ist die
Reihenschaltung, bestehend aus den Widerständen R 1 , R 2 sowie
der Spannungsquelle U Q1 . Das bedeutet, der Strom muss aus
Knotenpunkt C in die Last hineinfließen und aus D in die Quelle
zurückfließen.
Diese Richtung ist bei der Erstellung der Ersatzspannungsquelle
für die Stromquelle I Q2 zu berücksichtigen.
I Q2
D
•
Bestimmung von R ie '
Der Erstzinnenwiderstand zwischen C und D ist R 1 , denn die Stromquelle ist aufgetrennt.
R ie ' = R 1
•
Bestimmung von U qe '
Die Leerlaufspannung zwischen C und D ist die Spannung am Widerstand R 1 . Diese wird
berechnet aus I Q2 ⋅ R 1 und fällt in der Richtung von C nach D ab, weil der Strom I Q2 in diese
Richtung fließt.
C
U qe '
= I Q2 ⋅ R 1
D
Diese Schaltung wird anstelle der Stromquelle zwischen die Klemmen
C und D eingebaut. Dadurch ist gewährleistet, dass nur ein Strang
existiert, in dem nur ein Strom fließt.
Die Berechnung dieses Stroms ist jetzt sehr einfach.
University of Applied
Sciences Cologne
Gleichspannung
Tutorium
Ersatzspannungsquelle
L-ESpQ-012
Campus Gummersbach
Dipl.-Ing. (FH)
Dipl.-Wirt. Ing. (FH)
G. Danielak
Stand: 19.03.2006; R0
U R2
Für
diese
Schaltung
gilt
wiederum: I1 = I 2 = I 3 = I .
Mit der linken Masche kann der
Strom I berechnet werden;
dieses Ergebnis wird in der
rechten
Masche
für
die
Berechnung von U 0 verwendet.
a
I2
U R3
U Rie'
I3
I1
U0
U Q1
U qe '
b
− U Q1 − U R3 − U R2 − U Rie' + U qe' = 0 ⇔ U qe' − U Q1 = U R2 + U R3 + U Rie'
⇔ U qe' − U Q1 = I ⋅ R 2 + I ⋅ R 3 + I ⋅ R ie '
⇔ U qe' − U Q1 = I ⋅ (R 2 + R 3 + R ie ')
⇔I=
⇔I=
U qe' − U Q1
R 2 + R 3 + R ie '
=
(− I
Q2
⋅ R 1 ) − U Q1
R1 + R 2 + R 3
− 100mA ⋅100Ω − 15V
= − 50mA
100Ω + 200Ω + 200Ω
Das negative Vorzeichen bedeutet lediglich, dass der Strom nicht in die angenommene Richtung,
also von oben nach unten, sondern entgegengesetzt fließt. Mit diesem Ergebnis sowie den
Zählpfeilrichtungen wird weiter gerechnet. Die Leerlaufspannung U 0 wird wie gehabt berechnet:
U 0 = + U R3 + U Q1 = I ⋅ R 3 + U Q1 =
(− I
Q2
⋅ R 1 ) − U Q1
R1 + R 2 + R 3
14
42443
I
⋅ R 3 + U Q1 = −50mA ⋅ 200Ω + 15V = −10V + 15V = 5V
Die nachfolgende Rechnung für I a und U a wird mit den hier berechneten Werten genauso wie
immer durchgeführt:
University of Applied
Sciences Cologne
Gleichspannung
Tutorium
Ersatzspannungsquelle
L-ESpQ-013
Campus Gummersbach
Dipl.-Ing. (FH)
Dipl.-Wirt. Ing. (FH)
G. Danielak
Stand: 19.03.2006; R0
a
Ia =
Ia
Ua
.
U qe
b
U qe
R ie + R a
=
5V
= 29,41mA
120Ω + 50Ω
U a = I a ⋅ R a = 29,41mA ⋅ 50Ω = 1,47V
University of Applied
Sciences Cologne
Gleichspannung
Tutorium
Ersatzspannungsquelle
L-ESpQ-014
Campus Gummersbach
Dipl.-Ing. (FH)
Dipl.-Wirt. Ing. (FH)
G. Danielak
ƒ
Stand: 19.03.2006; R0
Grafisches Verfahren
Benötigt wird der Kurzschlussstrom zwischen den Klemmen a und b:
I0 =
U0
5V
=
= 41, 6mA
R ie 120Ω
Damit zeichnet man zuerst die Quellenkennlinie mit den beiden Punkten U 0 und I 0 ein. Danach
wird die Widerstandgerade für den Lastwiderstand R a eingezeichnet. Dafür benötigt man
wiederum zwei Punkte. Ein Punkt, der bei allen passiven Bauelementen gleich ist, ist der
Ursprung. Den anderen kann man nach dem ohmschen Gesetz U = I ⋅ R berechnen. Man wählt
einfach einen beliebigen Strom I und multipliziert ihn mit dem Widerstandswert für R a :
U = I ⋅ R a = 40mA ⋅ 50Ω = 2V
Damit ist die Widerstandsgerade definiert. Der Schnittpunkt der beiden Geraden ist der
Arbeitspunkt mit I a und U a .
U
U0
Quellenkennlinie
Widerstandsgerade für R a
A
Ua
1V
10mA
Ia
I0
I