schule/physik/11/Material/Zur Vorbereitung EF 2_1
Werbung

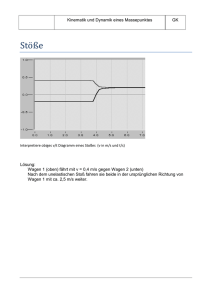
Kinematik und Dynamik eines Massepunktes GK Rotation 1) Notiere die Gleichung für a) Drehimpuls (L=r mv) b) Drehmoment (M= r F) 2) Erhaltungssätze Ohne äußere Krafteinwirkung gilt: a) Energieerhaltung (Evor = E nach) b) Impulserhaltung ( Pvor=Pnach) c) Drehimpulserhaltung (Lvor=Lnach) 3) Pirouette Beim Drehschemelversuch wird eine Person furch äußere Drehmomente zunächst beschleunigt (z.B. ausgestreckter Arm (Radius r) wird durch Kraft F angeschoben). Danach keine äußere Kraft mehr, also Drehimpulserhaltung: Lvor=rmv, m= Masse der Kugel in der Hand). Hand wird angezogen, r verringert sich also, demzufolge muss, damit L konstant bleibt, v größer werden) 4) Kreisel Ein rotierender Kreisel (Fahrrad) bleibt auch was die Richtung angeht, in der gleichen Lage, da der Drehimpuls eine vektorielle Größe ist. Kinematik und Dynamik eines Massepunktes GK Stoße Interpretiere obiges v/t Diagramm eines Stoßes (v in m/s und t/s) Lösung: Wagen 1 (oben) fährt mit etwa v = + 0,4 m/s gegen Wagen 2 (unten, negative Geschwindigkeit, etwa -0,2 m/s, also entgegenkommend) Nach dem unelastischen Stoß fahren sie beide in der ursprünglichen Richtung von Wagen 1 mit ca. 0,25 m/s weiter. GK Physik Jgst: Klausur-Nr. Datum: Geschossgeschwindigkeit Gemäß obiger Apparatur wird eine Kugel der Masse m und der (unbekannten) h Masse m Geschwindigkeit v Masse M Ballistisches Pendel zur Bestimmung der Geschoßgeschwindigkeit Geschwindigkeit v in den Holzklotz mit der Masse M geschossen, der bifilar (an zwei Fäden) aufgehängt ist. Man beobachtet, daß der Schwerpunkt des Holzklotzes um die Höhe h angehoben wird, worauf er wieder zurückschwingt. a) Leiten Sie allgemein den Zusammenhang zwischen Geschoßgeschwindigkeit v und den übrigen meßbaren Größen m, M und h her. b) Berechnen Sie die Geschoßgeschwindigkeit für m = 5 g, M = 500 g, h = 8 cm. c) Mit welcher Geschwindigkeit pendelt der Holzklotz durch die Nulllage? Zusatz: d) Wieviel Energie wird beim Abremsen der Kugel in Wärme umgesetzt? Berechnen Sie den Energieverlust absolut und relativ zur ursprünglichenEnergie. GK Physik Jgst: Klausur-Nr. Datum: Lösung zu a) Das Abbremsen der Kugel erfolgt vollkommen inelastisch. Nach dem Impulssatz gilt: mv M mu (*) wobei u die Geschwindigkeit des Holzklotzes direkt nach dem Einschlagen und Abbremsung der Kugel ist. Nach dem Energiesatz ist dann 1 2 M mgh M mu2 .(**) Einsetzen von u aus (*) in (**) liefert 1 mv M mgh M m M m 2 Mm v 2gh m 2 Lösung zu b) Einsetzen liefert v 2gh Mm 126,5 m s 455,5 km h m Lösung zu c) Wegen (*) gilt mv M mu mv u 125 , ms Mm GK Physik Jgst: Klausur-Nr. Lösung zu d) Die Energien vor und nach dem Stoß sind gegeben durch 1 mv 2 2 Enach M mgh E vor 1 mv 2 M mgh 2 2 1 M m m 2gh M mgh m 2 E M m 1 M m gh m 100,4 J 1 2 M mgh E 2 mv M m gh m 1 2 1 1 E Mm 1 M m 2 mv m2gh 2 m 2 0,99 99 % Datum: GK Physik Jgst: Klausur-Nr. Datum: Impuls- und Energiesatz Auf einer reibungsarmen Fahrbahn stoßen zwei Wagen der Massen m1 und m2 zusammen. Mittels zweier Lichtschranken und zweier Stopuhren werden die Verdunklungszeiten dt1, dt2, dt1’ und dt2’ der auf den Wagen befindlichen Fahnen mit der Breite d vor und nach dem Zusammenstoß bestimmt. dt1 Fahne der Breite d Stoßbereich Wagen der Masse m2 dt2 Fahrbahn Lichtschranke Uhren Protokoll Die Fahnenbreite beträgt jeweils 0,1 m. a) Die Wagen haben auf den Stirnseiten je eine elastische Metallfeder. m1 / kg m2 / kg dt1 / s dt1’ / s dt2 / s dt2’ / s 0,200 0,200 0,137 0,142 0,138 0,140 0,300 0,400 0,201 0,236 0,236 0,313 0,400 0,300 0,291 0,300 0,203 0,237 b) Die Wagen werden über eine Klebstoffmasse beim Stoß zusammengehalten und bewegen sich nach dem Stoß gemeinsam weiter. m1 / kg m2 / kg dt1 / s dt1’ / s dt2 / s 0,200 0,400 0,164 1,091 0,233 0,400 0,200 0,235 0,170 dt2’ / s 1,030 Werten Sie die beiden Experimente hinsichtlich Impuls- und Energieerhaltung aus. LK Physik Jgst: Klausur-Nr. Datum: Lösung Bei Bewegungen nach rechts werden die Zeitdifferenzen positiv und bei Bewegung nach links negativ gerechnet. Mit den Formeln für den Impuls und die kinetische Energie erhält man: m1 / kg 0,200 0,300 0,400 m2 / kg 0,200 0,400 0,300 dt1 / s 0,137 0,201 0,291 dt1’ / s -0,142 -0,201 -0,300 dt2 / s -0,138 -0,236 -0,203 p1 p1' / p2 p2' P=p1+p2 / kg m/s kg m/s / kg m/s / kg m/s / kg m/s 0,146 -0,141 -0,145 0,143 0,001 0,149 -0,149 -0,169 0,128 -0,020 0,137 -0,133 -0,148 0,127 -0,010 dt2’ / s 0,140 0,313 0,237 v1 / m/s 0,730 0,498 0,344 P P'=p1'+p2' / kg m/s / kg m/s 0,002 -0,001 -0,021 0,001 -0,007 -0,004 v1' / m/s -0,704 -0,498 -0,333 v2 / m/s -0,725 -0,424 -0,493 Ekin ' Ekin /J 0,106 0,073 0,060 v2' / m/s 0,714 0,319 0,422 Ekin Ekin /J 0,101 0,058 0,049 0,049 0,212 0,185 Im Rahmen der Meßgenauigkeit bleibt der Impuls erhalten. Die kinetische Energie nimmt um bis zu 20% ab, was durch die Schwingungen der Federn zu erklären ist. m1 / kg 0,200 0,400 m2 / kg 0,400 0,200 dt1 / s 0,164 0,235 dt1’ / s -1,091 dt2 / s -0,233 -0,170 p1 p1' p2 p2' P=p1+p2 / kg m/s / kg m/s / kg m/s / kg m/s / kg m/s 0,122 -0,01833 -0,172 -0,037 -0,050 0,170 0,038835 -0,118 0,019 0,053 dt2’ / s 1,030 v1 / m/s 0,610 0,426 P P'=p1'+p2' / kg m/s -0,055 0,058 / kg m/s 0,005 -0,006 v1' / m/s -0,092 Ekin /J 0,074 0,071 v2 / m/s -0,429 -0,588 Ekin ' /J 0,003 0,003 v2' / m/s 0,097 Ekin Ekin 0,966 0,960 In diesem Experiment bleibt ebenfalls der Gesamtimpuls vor und nach dem Stoß erhalten. Die kinetische Energie nimmt aber um über 90 % ab. Fazit: Der Impuls bleibt bei allen Stoßexperimenten erhalten. Die kinetische Energie geht in Abhängigkeit von der Art des Stoßes mehr oder weniger in andere Energieformen über. LK Physik Jgst: Klausur-Nr. Datum: Aufgabe Auf einer Luftkissenbahn werden zwei ruhende Wagen mit den Massen m1 und m2 durch eine Feder mit der Richtkonstanten D auseinandergedrückt. Der sie zusammenhaltende Faden wird durchgebrannt . Fahne mit Breite d Faden Lichtschranke Fahrbahn Feder mit Richtkonstante D Wagen mit Masse m1 Zur Erinnerung: Hooksche Gesetz: F=-Ds Spannenergie: Espann = ½ D s² Protokoll: Massen Fahnenbreiten Verdunkelungszeit nach dem Stoß Federkonstante: D = 1 N/m Körper 1 0.085 kg 10.0 mm 29.54 ms Körper 2 0.196 kg 10.0 mm LK Physik Jgst: Klausur-Nr. Datum: a) Berechnen Sie die Geschwindigkeiten der beiden Wagen nach dem Durchbrennen des Fadens. b) Berechnen Sie die in der Feder gespeicherte Energie. c) Um wieviel cm wurde die Feder vor Versuchsbeginn zusammengedrückt und welche Kraft mußte dafür aufgewendet werden? LK Physik Jgst: Klausur-Nr. Datum: Lösung zu a) Für die Geschwindigkeit des ersten Wagens gilt v 1 Nach dem Impulssatz gilt Somit ist v 2 d t m1v1 + m2v2 = 0 m1 v1 m2 Lösung zu b) Die in der Feder gespeicherte Energie wird in Bewegungsenergie der Wagen umgewandelt. Somit gilt: E Feder 1 1 1 2 2 m1v 1 m 2 v 2 Ds 2 2 2 2 Lösung zu c) Nach obiger Formel erhält man für den Federweg s s 2 E kin D und gemäß dem Hookschen Gesetz für die benötigte Kraft F Ds D 2 E kin 2 D E kin D Numerische Lösung: m1 m2 d D dt v1 v2 E Feder s F 0,085 0,196 0,01 8 0,02954 kg kg m N/m s 0,34 0,15 0,007 0,04 0,33 m/s m/s J m N LK Physik Jgst: Klausur-Nr. Datum: Peter und Paul sitzen in einem Boot. Das Boot ist nur wenige Meter vom Ufer entfernt. Leider gibt es weder Ruder noch Motor. Wie kann Peter das Boot dennoch ans Ufer bringen, ohne dieses zu ziehen? Löse das Problem allgemein.