U(B,M) - Webarchiv ETHZ / Webarchive ETH

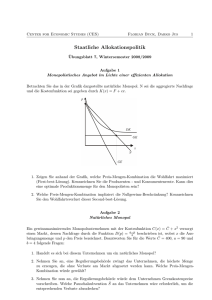
Ökonomie am 1.10.2008
Das Güterangebot von
Unternehmen
1
Hausaufgaben vom 17.9.
1. Opportunitätskosten der
Bildungsausgaben sind die Kosten für
die entgangene Möglichkeit, das Geld
für Militärzwecke auszugeben.
2. Man muss die Präferenzen der Bürger
für Militär und Bildung kennen.
2
Hausaufgaben vom 17.9.
2. Graphische Lösung:
3
Hausaufgaben vom 17.9.

Formal:
Im Optimum muss der Grenznutzen von
Bildung dem Grenznutzen von Militär
entsprechen.
Budget ist gegeben : X  B+M
U(B,M) abgeleitet nach B ergibt UB,
abgeleitet nach M ergibt UM.
Gleichungssystem mit 2 Unbekannten und 2
Gleichungen.
4
Hausaufgaben vom 17.9.

Beispiel:
U(B,M) = B2*M; X = 12
Grenznutzen der Bildung UB = 2*B*M
Grenznutzen des Militär UM = B2
2*B*M = B2  B = 2*M
Budgetrestriktion  B = 12-M
 12-M = 2*M
 12 = 3*M  M = 4; B = 8
5
6
Gewinnmaximierung von
Unternehmen U





Gewinn = Erlös (Umsatz) – Kosten
G = E–K
G(x) = E(x) – K(x)
Notwendige Bed. für Gmax: G‘(x) = 0
Hinreichende Bed. für Gmax: G‘‘(x)< 0
7
Gewinnmaximierung von
Unternehmen U

E(x) = p ∙ x dabei: p fest vorgegeben
=> E‘(x) = p

G‘(x) = E‘(x) – K‘(x) => G‘(x) = 0
=> E‘(x) = K‘(x)
=> p = K‘(x) („Preis=Grenzkosten“Regel)
8
Gewinnmaximierung von
Unternehmen U
Hinreichende Bedingung für Gmax:
G‘‘(x) = E‘‘ (x) – K‘‘(x) < 0

Für fixes p ist E‘(x) = p und E‘‘(x) = 0.
Also: 0 - K‘‘(x) < 0 bzw. K‘‘(x) > 0
Interpretation: die GK müssen ansteigen!
9
Gewinnmaximierung von
Unternehmen U


Grenzerlös bzw. Grenzkosten:
zusätzlicher Erlös bzw. zusätzliche
Kosten, wenn eine weitere Einheit
produziert wird
Approximative Interpretation:
∆E/∆x => E‘(x) für ∆x →0
∆K/∆x => K‘(x) für ∆x →0
10
Gewinnmaximierung von
Unternehmen U
11
Gruppenarbeit No. 1

Bitte lösen Sie mit Ihrer Nachbarin/Ihrem Nachbarn
die folgende Aufgabe:
Eine Firma weist für die Herstellung ihres Produkts X
Gesamtkosten von K(x) = (x-20)² + 160 aus. Der
Stückpreis beträgt 8 Franken. Berechnen Sie die
Grenzkosten und das Gewinnmaximum.
Sie haben 10 Minuten Zeit. Jemand von Ihnen trägt
die Lösung vor.
12
Gruppenarbeit No. 2

Bitte lösen Sie mit Ihrer Nachbarin/Ihrem
Nachbarn die folgenden Aufgaben:
A) Was passiert mit der Angebotskurve von Orangensaft in den
USA, wenn eine Kältewelle über Florida hereinbricht?
B) Was passiert mit der Angebotskurve für Sweatshirts, wenn
Unwetter weltweit die Baumwollernte vernichten?
C) Was passiert mit der Angebotskurve für Sweatshirts, wenn
neue Strickmaschinen entwickelt werden?
Sie haben 10 Minuten Zeit. Jemand von
Ihnen trägt die Lösung vor.
13
14
15
Kostenverläufe

Kosten = Fixkosten + Variable Kosten

Lineare oder s-förmige Kostenverläufe
sind besonders typisch

Es interessieren jeweils die Grenzkosten und die Durchschnittskosten
(totale, variable)
16
Kostenverläufe


Durchschnittskosten: Kosten pro
produzierter Einheit; Quotient aus
Kosten und produzierter Menge
Grenzkosten: Zusätzliche Kosten, wenn
(approx.) eine weitere Einheit produziert
wird; 1. Ableitung der Kostenfunktion
17
Kostenverläufe
18
Kostenverläufe
19
Kostenverläufe



Grenzkosten < Durchschnittskosten:
=> DK sinken
Grenzkosten > Durchschnittskosten:
=> DK steigen
Grenzkosten = Durchschnittskosten:
im Minimum der DK (Betriebsminimum)
20
Kostenverläufe



Positive Skalenerträge: langfristige
totale DK sinken mit zun. Output
Negative Skalenerträge: langfristige
totale DK steigen mit zun. Output
Konstante Skalenerträge: langfristige
DK bleiben konstant bei zunehmendem
Output
21
Kostenverläufe kurz- und langfristig




Bisherige Überlegungen: eher kurzfristig
Kurzfristig: Betriebseinstellung falls
p<VDK (dabei VDK tiefer als DK)
Kurzfristig: Weiterproduktion für
gewisse Zeit falls VDK<p<DK
Langfristig: Marktaustritt falls p<DK
22
Kostenverläufe kurz- und langfristig
23
Kostenverläufe kurz- und langfristig


Kurzfristige Angebotskurve:
ansteigender Ast der GK-Kurve,
oberhalb der VDK
Langfristige Angebotskurve:
ansteigender Ast der GK-Kurve
oberhalb der DK (d.h. ab dem
Betriebsminimum)
24
Determinanten der Kostenverläufe



Verlauf der Kostenfunktion wird durch
Produktionsfunktion bestimmt
Mögliche Produktionsfunktion: f(x,y) = c·xαyβ
(c:Konstante; x,y:Inputfaktoren; α,β:relativer
Beitrag der Inputfaktoren zum Output
(α+β=1)) s-förmiger Kostenverlauf
Bei gegebenen Preisen der Produktionsfaktoren kann für jede Produktionsmenge der
minimale Kostenbetrag bestimmt werden
25
Determinanten der Kostenverläufe

Die Kostenfunktion ist als Menge
derjenigen Kostenbeträge zu
interpretieren, die pro Produktionsmenge jeweils die tiefsten Kosten sind
(Minimalkosten-Kombinationen)
26
Preiselastizität des Angebots PEL-A


Frage: Um wieviel % ändert sich die
angebotene Menge eines Gutes, wenn
der Preis des Gutes um 1% sinkt bzw.
steigt?
PEL-A ist typischerweise positiv
27
Berechnung
 x A ,p = relative Mengenänderung/relative Preisänderung
x
A
,p
x A p

:
A
x
p
A p

x
 xA, p 

p x A
 xA p
x , p 

 p xA
A
(mit dem Differenzenquotienten)
(mit dem Differentialquotienten)
28
Preiselastizität des Angebots PEL-A

Denk-Aufgabe für alle: Erwarten Sie,
dass die PEL-A für Eiscrème insgesamt
oder für Vanilleeis grösser ist?
Begründen Sie Ihre Antwort!
29
Monopol

Gründe für Monopol:
Schlüsselressource im Besitz einer
Firma (Diamanten)/ Staatliche
Regulierung (staatlicher Auftrag oder
Patente bzw. Urheberschutz)/
Kostenstruktur der Industrie
(„natürliches Monopol“)
30
Monopol





Auch hier Annahme der Gewinnmaximierung
Aber: Preis ist kein Datum mehr!
Folglich: E(x) = p(x) ∙ x
Und: E‘(x) = x ∙ p‘(x) + p(x) ∙ 1 („Produktregel“)
Also: x p‘(x) + p(x) = K‘(x) für Gmax
31
Monopol


Beispiel: p(x) = b – ax
=> E(x) = p(x) x = bx - ax²
=> E’(x) = b – 2ax
=> b – 2ax = K’(x)
Dies ist die notwendige Bedingung für
Gmax
32
Monopol
33
Monopol





Hinreichende Bedingung für Gmax:
=> in allgemeiner Form G’’(x) <0
Es ist: G’’(x) = E’’(x) – K’’(x)
Also: E’’(x) < K’’(x)
Im Beispiel: E’(x) = b – 2ax
E’’(x) = -2a
Also: -2a < K’’(x) bzw. K’’(x) > 2a
34
Hausaufgaben für 8.10.2008
1.Ein Monopolbetrieb ist durch einen Erlös
von E = -x(x-60) und Gesamtkosten K(x) =
30x + 100 gekennzeichnet. Bei welcher
Stückzahl erreicht der Betrieb den grössten
Gewinn? Bei welchen fixen Kosten würde er
im Gewinnmaximum weder mit Gewinn noch
mit Verlust arbeiten?
35
Hausaufgaben für 8.10.2008
2. Henry, Bea und Romy betreiben die
einzige Kneipe in einer Stadt. H will so viele
Drinks wie möglich ohne Verlust verkaufen. B
möchte so viel Erlös wie möglich erzielen. R
möchte den maximalen Profit realisieren.
Welche Preis-Mengen-Kombinationen
entsprechen diesen drei Strategien?
Erläutern und begründen Sie Ihre Antworten
anhand von Grafiken.
36
Hausaufgaben für 8.10.2008
3. Brainstorming: Welche Kosten und
Nutzen sind für eine Region mit einem
Energiekonzept verbunden, das die
Nachhaltigkeit betont? Welche nichtmonetären Aspekte müsste man
monetarisieren?
37
Hausaufgaben für 8.10.2008
4. Vorbereiten: Kapitel 3 (Kosten-NutzenAnalyse) => wird nächste Woche in der
Vorlesung besprochen
38