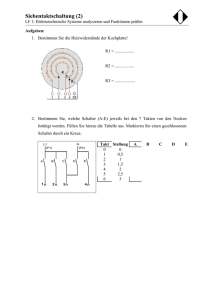
Widerstandsmessung

Torsten Leddig
Mathias Arbeiter
16.November 2004
Betreuer: Dr.Hoppe
Physikalisches Praktikum
3. Semester
- Widerstandsmessung -
1
Aufgaben:
1. Brückenschaltungen
1.1 Bestimmen Sie mit der Wheatstone-Brücke
1.1.1 die Größe eines Widerstandes
1.1.2 den Klemmenwiderstand eines Netzwerkes
1.2 Ermitteln Sie mit einer Wechselstrombrücke die Kapazität eines Kondensators
2. Kondensatorentladung:
2.1 Bestimmen Sie den Isolationswiderstand von mindestens drei Materialien, indem Sie die Funktion U = U (U0 , R, C, t) aufnehmen, aufzeichnen und auswerten
2.2 Ermitteln Sie den Einfluss des endlichen Isolationswiderstandes ihrer Messeinrichtung auf die
Resultate von 2.1, indem Sie die Entladekurve über Luft aufnehmen
zuerst den Widerstand des Drahtes messen
Rdraht = 8.62Ω
maximale Spannung um 2 W nicht zu überschreiten:
1
1.1
Brückenschaltung:
Wheatstone-Brücke
Vorbetrachtung / Formeln:
Die Brücke sollte maximal eine Leistung von P = 2W aufnehmen!
mit
P =
⇒ Umax =
2
Umax
R
√
P · RDraht =
√
2W · 8.62Ω
⇒ Umax = 4.15V
⇒
wir wählen U = 2.75V
Durch den Nullabgleich und aus der kirchhoffschen Maschenregel folgt:
Ux = Ua = U1 = U2 = Ix Rx = Ia Ra = I1 R1 = I2 R2
(1)
aus der kirchhoffschen Knotenregel:
Ix = Ia
(1) + (2)
⇒
I1 = I2
Ix Rx = Ix Ra = I1 R1 = I1 R2
⇒
Ix Rx
I1 R1
=
Ix Ra
I1 R2
2
(2)
⇒ Rx =
R=
ρ·l
A
R1
Ra
R2
⇒
R1
=
R2
Rx =
l1
Ra
l2
ρl1
A
ρ l2
A
(3)
=
l1
l2
(4)
Vergleichswerte:
Rx = 174.8Ω (digitales Multimeter)
RW = 8.2Ω (digitales Multimeter)
C = 10nF (abgelesener Wert)
1.1.1
die Größe eines Widerstandes:
Versuchsaufbau:
Durchführung:
• Schaltung gemäß Versuchsaufbau
• Maximalspannung gemäß Vorbetrachtung beachten
• der Vergleichswiderstand Ra ist so zu wählen, dass er ungfähr in der Größenordnung des zu messenden Widerstandes liegt
• um Inhomogenitäten des Drahtes auszugleichen, ist die Reihenfolge der Widerstände während der
Messung zu variieren
3
Messwerte:
Widerstand Ra in Ω
200
150
160
190
175
Länge l1 in cm
46.7
53.8
52.2
47.9
49.9
Länge l2 in cm
53.3
46.2
47.8
52.1
50.1
Rx aus (4)
175.2
174.7
174.7
174.7
174.3
Länge l1 in cm
53.0
46.0
47.5
51.9
49.9
Länge l2 in cm
47.0
57.0
52.5
48.1
50.1
Rx aus (4)
177.4
176.1
176.8
176.1
175.7
l1 − l2 vertauscht:
Widerstand Ra in Ω
200
150
160
190
175
Rx =
10
P
Rxi
i=1
10
⇒ Rx = 175.6
Fehlerrechnung (im Detail):
Rx = Rx (l1 , l2 , Ra )
¯
¯
¯
¯
¯
¯
¯
¯
¯ ∂Rx ¯
¯
¯
¯ · ul + ¯ ∂Rx ¯ · ul + ¯ ∂Rx ¯ · uR
⇒ uRx = ¯¯
1
2
a
¯
¯
¯
¯
∂l1
∂l2
∂Ra ¯
⇒
¯
¯ ¯
¯ ¯
¯
¯ ul ¯ ¯ ul ¯ ¯ uR ¯
uRx
= ¯¯ 1 ¯¯ + ¯¯ 2 ¯¯ + ¯¯ a ¯¯
Rx
l1
l2
Ra
(für eine Einzelmessung)
¯
¯
¯
¯
¯
¯
¯
¯
¯ u l1 ¯
¯ u l2 ¯
¯ uRa ¯
¯ uRx ¯
uRx
¯
¯
¯
¯
¯
¯
¯
¯
⇒
=¯
+
+
+
Rx
l1 ¯syst. ¯ l2 ¯syst. ¯ Ra ¯syst. ¯ Rx ¯
(für eine Mehrfachmessung)
Fehler durch Mehrfachmessung:
uRx = τ · sRx
v
u
u
sR = t
n
1 X
(Rxi − Rx )2
n − 1 i=1
4
(Standartabweichung der Einzelmessung)
⇒ sR = 1.025Ω
sR
0.013Ω
⇒ sR = √ = √
= 0.324Ω
n
10
(Standartabweichung vom Mittelwert)
Vertrauensbereich: τ9 = 2.262
⇒ uR = 0.324Ω · 2.262
⇒ uR = 0.733Ω
⇒
uR x
Rx
= 0.4%
systematischer Fehler des Lineals:
u l1 ≈ u l2
ul1 = 0.5mm · (10−3 · 530mm) ≈ 1mm
⇒
u l1
≈ 0.2%
l1
systematischer Fehler der Widerstandsdekade:
uRa
= 1%(war gegeben)
Ra
Gesamtfehler:
uRx
= 0.4% + 2 · 0.2% + 1% = 1.8%
Rx
⇒ Rx = (176 ± 4)Ω
Auswertung:
• der durch die Brückenschaltung ermittelte Wert Rx weicht um 0.8Ω vom durch ein digitales Messgerät ermittelten Wert ab
• die Abweichung ist somit insignifikant
• die Wheatstone’sche Brückenschaltung scheint somit sehr gut geeignet zu sein, um unbekannte
Widerstände zu ermitteln
• begünstigt wurde das Experiment dadurch, dass unser Vergleichswiderstand Ra in der Größenordnung des gesuchten Widerstandes lag (die Abweichungen wären sonst höchstwahrscheinlich größer)
5
1.1.2
Klemmwiderstand eines Netzwerkes:
Vorbetrachtung zum Würfel:
⇒ Rw =
Rges =
1
5U
1
6I
=
5
R
6
5
· 10Ω = 8.33Ω
6
Durchführung und Versuchsaufbau analog zu 1.1.1
Messwerte:
Widerstand Ra in Ω
10
9
8
7
6
Länge l1 in m
44.7
47.4
50.3
54.1
57.5
Länge l2 in m
55.3
52.6
49.7
45.9
42.5
RW aus (4)
8.1
8.1
8.1
8.3
8.1
Widerstand Ra in Ω
10
9
8
7
6
Länge l1 in m
55.1
52.4
49.5
46.1
42.3
Länge l2 in m
44.9
47.6
50.5
53.9
57.7
RW aus (4)
8.1
8.2
8.2
8.2
8.2
l1 − l2 vertauscht:
6
⇒ Rx = 8.16Ω
Fehlerrechnung: (analog zu 1.1.1)
⇒
¯
¯
¯
¯
¯
¯
¯
¯
¯ ul ¯
¯ uR ¯
¯ uR ¯
¯ ul ¯
uRw
+ ¯¯ 2 ¯¯
+ ¯¯ a ¯¯
+ ¯¯ w ¯¯
= ¯¯ 1 ¯¯
Rw
l1 syst.
l2 syst.
Ra syst.
Rw
sRw = 0.069Ω
⇒ sRw = 0.0218Ω
⇒ uRw = 0.0218nF · 2.262
⇒ uRw = 0.05Ω
⇒
uR w
Rw
uRw
= 0.6%
Rw
= 0.6% + 2 · 0.2% + 1% = 2.0%
⇒ Rw = (8.2 ± 0.2)Ω
Auswertung:
Rw mit Multimeter
Rw per Rechnung
Rw per Messung
8.2Ω
8.33Ω
(8.2 ± 0.2)Ω
• die gemessenen, und errechneten Werte stimmen sehr genau überein
• die Abweichung ist insignifikant
7
1.2
Kapazitätsermittlung mit Hilfe einer Wechselstrombrücke:
Vorbetrachtung:
Wheatstone-Brücke im Wechselstromkreis:
Zx
Z1
=
Za
Z2
Z = Widerstände im Wechselstromkreis
ZC = χC =
R1
=
R2
daraus ergibt sich für Cx :
Cx =
i
ωCx
i
ωCa
i
ωC
=
Ca
Cx
R2
l2
Ca = Ca
R1
l1
Versuchsaufbau:
Durchführung:
• Schaltung gemäß Versuchsaufbau aufbauen
• die Wheatstone-Brücke kann wie bei den Widerständen angewandt werden
• Berechnung erfolgt gemäß Abschnitt Vorbetrachtung:
Messwerte:
Widerstand Ca in nF
10.7
10.3
10.0
9.7
9.3
Länge l1 in m
49.2
48.5
47.6
46.7
45.7
Länge l2 in m
50.8
51.5
52.4
53.3
54.3
8
Cx aus (4)
11.0
10.9
11.0
11.1
11.1
(5)
l1 − l2 vertauscht:
Widerstand Ca in nF
10.7
10.3
10.0
9.7
9.3
Länge l1 in m
50.3
51.3
52.0
52.8
53.9
Länge l2 in m
49.7
48.7
48.0
47.2
46.1
Cx aus (4)
10.8
10.8
10.8
10.9
10.9
⇒ Cx = 10.93nF
Fehlerrechnung analog zu 1.1
⇒
¯
¯
¯
¯
¯
¯
¯
¯
¯ ul ¯
¯ ul ¯
¯ uC ¯
¯ uC ¯
u Cx
= ¯¯ 1 ¯¯
+ ¯¯ 2 ¯¯
+ ¯¯ a ¯¯
+ ¯¯ x ¯¯
Cx
l1 syst.
l2 syst.
Ca syst.
Cx
sCx = 0.1159nF
⇒ sC = 0.037nF
⇒ uC = 0.037nF · 2.262
⇒ uC = 0.09nF
⇒
uC x
Cx
u Cx
= 0.8%
Cx
= 0.8% + 2 · 0.2% + 1% = 2.2%
⇒ Cx = (10.9 ± 0.3)nF
• die Abweichung zum abgelesenen Wert beträgt 0.9 nF
• damit ist die Abweichung signifikant
9
2
Kondensatorentladung:
Vorbetrachtung:
t
U (t) = U0 e− R C
ln U (t) = lnU0 · −
⇒
als Ausgleichsgerade:
mit
A=−
⇒
1
·t
RC
ln U (t) = lnU0 · A · t
1
Rges C
⇒ Rges = −
(6)
Anstieg
1
AC
(7)
• Bei konstanter Eingangsspannung und unveränderten physikalischen Kondensatoreinstellungen, ist
der Entladevorgang nur vom Widerstand der eingelegten Materialen abhängig
• ist der Widerstand sehr hoch, dauert es lange bis sich der Kondensator entlädt
• dabei ist jedoch zu beachten, dass der Kondensator sich auch über die Luft entladen kann, wenn
ein Material eingelegt ist (siehe Skizze)
• der Gesamtwiderstand berechnet sich somit aus einer Parallelschaltung des Widerstandes der Luft
und des Widerstandes des Materials
• der durch lineare Regression ermittelte Widerstandswert ist demzufolge nicht der Widerstandswert
des Materials, sondern der Gesamtwiderstand von Material und Luft
• bei Materialien mit geringem Widerstand und somit geringer Entladedauer, sind Rges ≈ RM aterial ,
da sich der Kondensator dann fast vollständig über den geringen Widerstand (des Materials) entlädt
• je höher der Widerstand des Materials, desto wichtiger wird es, die Entladung über die Luft mitzuberücksichtigen
⇒
1
1
1
=
+
Rges
RLuf t
RM aterial
⇒ RM aterial =
Rges · RLuf t
RLuf t − Rges
Versuchsaufbau:
10
(8)
2.1
Isolationswiderstand von Luft:
Messwerte:
gegeben: C = 970nF · (1 ± 3%)
Zeit t in s
0.0
100
240
370
785
936
1140
1420
1515
1740
2230
2650
3135
3540
3670
4185
4755
5580
5965
6415
6950
Spannung U in V
988
971
956
943
908
900
883
862
855
841
813
798
780
767
761
748
732
712
702
690
673
ln U
6.90
6.88
6.86
6.85
6.81
6.80
6.78
6.76
6.75
6.73
6.70
6.68
6.66
6.64
6.63
6.62
6.60
6.57
6.55
6.54
6.51
Abbildung 1: Entladekurve für Luft
11
aus linearer Regression:
A = −5.26 · 10−5 Ω−1 F −1
uA
= 10.2%
A
(7) ⇒ Rges1 =
1
−5.26 ·
10−5
Ω−1 F −1
· 970 · 10−9 F
⇒ Rges1 = RLuf t = 19.6GΩ
Fehlerrechnung:
uRLuf t
uA
uC
=
+
RLuf t
A
C
uRLuf t
= 10.2% + 3% = 13.2%
RLuf t
⇒ uRLuf t = 2.0 GΩ
⇒ RLuf t = (20 ± 2) GΩ
2.2
2.2.1
Isolationswiderstand verschiedener Materialien:
Isolationswiderstand von ungewaschenem Stoff:
Messwerte:
gegeben: C = 970nF · (1 ± 3%)
Zeit t in s
0
39
60
87
148
183
229
280
347
Spannung U in V
800
700
650
600
500
450
400
350
300
12
lnU
6.69
6.55
6.48
6.40
6.21
6.11
5.99
5.86
5.70
Abbildung 2: Entladekurve von ungewaschenem Stoff
aus linearer Regression:
A = −2.85 · 10−3 Ω−1 F −1
uA
= 5.6%
A
Rechnung:
(7) ⇒ Rges2 =
(8)
1
−2.85 ·
⇒
10−3
Ω−1 F −1
Runwashed =
· 970 · 10−9 F
= 0.362 GΩ
0.362 GΩ · 19.6GΩ
19.6 GΩ − 0.362 GΩ
⇒ Runwashed = 0.369 GΩ
Fehlerrechnung:
¯
¯ ¯
¯
¯
¯ ¯ ∂Runwashed
¯ ∂Runwashed
· uRLuf t ¯¯ + ¯¯
· uRges ¯¯
uRunwashed = ¯¯
∂RLuf t
∂Rges
uRunwashed
¯ ¯
¯
¯
2
¯ ¯
¯
¯
2
RLuf
Rges
¯ ¯
¯
¯
t
·
u
·
u
=¯
+
¯
¯
R
R
ges
Luf t ¯
¯ ¯ (RLuf t − Rges )2
¯
¯ (RLuf t − Rges )2
uRges
uA
uC
=
+
Rges
A
C
13
uRges
= 5.6% + 3% = 8.6%
Rges
⇒ uRges = 0.0311 GΩ
⇒ uRunwashed =
(19.6 GΩ)2
(0.362 GΩ)2
·
0.0311
GΩ
+
· 2.59 GΩ
(19.6 GΩ − 0.362 GΩ)2
(19.6 GΩ − 0.362 GΩ)2
⇒ uRunwashed = 0.0332 GΩ
Runwashed = (0.37 ± 0.04) GΩ
2.2.2
Isolationswiderstand von gewaschenem Stoff:
Messwerte:
gegeben: C = 970nF · (1 ± 3%)
Zeit t in s
0
12
19
29
42
57
67
80
95
107
124
137
160
175
215
245
290
Spannung U in V
952
900
870
830
780
730
700
660
620
590
550
520
480
450
390
350
300
14
ln U
6.86
6.80
6.77
6.72
6.66
6.59
6.55
6.49
6.43
6.38
6.31
6.25
6.17
6.11
5.97
5.86
5.70
Abbildung 3: Entladekurve von gewaschenem Stoff
aus linearer Regression:
A = −4.01 · 10−3 Ω−1 F −1
uA
= 3.2%
A
Rechnung:
(7) ⇒ Rges3 =
(8)
1
= 0.257 GΩ
−4.01 · 10−3 Ω−1 F −1 · 970 · 10−9 F
⇒
Rwashed =
0.257 GΩ · 19.6GΩ
19.6 GΩ − 0.257 GΩ
⇒ Rwashed = 0.260 GΩ
Fehlerrechnung:
uRwashed
uRwashed
¯
¯ ¯
¯
¯
¯ ¯ ∂Rwashed
¯ ∂Rwashed
¯
¯
¯
· uRLuf t ¯ + ¯
· uRges ¯¯
=¯
∂RLuf t
∂Rges
¯ ¯
¯
¯
2
¯
¯ ¯
¯
2
RLuf
Rges
¯
¯ ¯
¯
t
+
·
u
·
u
=¯
¯
¯
Rges
RLuf t ¯
¯ (RLuf t − Rges )2
¯ ¯ (RLuf t − Rges )2
¯
uRges
uA
uC
=
+
Rges
A
C
uRges
= 3.2% + 3% = 6.2%
Rges
15
⇒ uRges = 0.016 GΩ
⇒ uRwashed =
(19.6 GΩ)2
(0.257 GΩ)2
·
0.016
GΩ
+
· 2.59 GΩ
(19.6 GΩ − 0.257 GΩ)2
(19.6 GΩ − 0.257 GΩ)2
⇒ uRwashed = 0.017 GΩ
Rwashed = (0.26 ± 0.02) GΩ
16