formelsammlung - j2mcl

FORMELSAMMLUNG
Luftfahrzeugtechnik
Erstellt vom Berufskolleg für Technik und Medien Mönchengladbach
für Fluggerätemechaniker Fachrichtung A/B/C
konvertiert aus dem ursprünglichen Works-Format
Formelsammlung
Luftfahrzeugtechnik
Seite 1
BK
Inhaltsverzeichnis
1
Basisgrößen, Einheiten, Umrechnungen
5
1.1
1.2
1.3
Basisgrößen und Vorsätze
Längen und Geschwindigkeiten
Druck und Durchflußmengen
5
5
5
2
Algebra
6
2.1
2.2
2.3
Addition, Subtraktion
Multiplikation, Division
Potenzen und Wurzel
6
6
6
3
Winkelfunktion
7
3.1
3.2
3.3
Sinus, Cosinus
Tangens, Cotangens
Sinus- und Cosinussatz
7
7
7
4
Prozent und Zinsrechnung
8
4.1
4.2
4.3
Prozentrechnung
Zinsrechnung
Zinseszinsrechnung
8
8
8
5
Längenberechnung
9
5.1
5.2
5.3
Längenteilung
Umfang, Bogenlängen
Regelmäßige Vielecke
9
9
11
6
Flächenberechnung
13
6.1
6.2
6.3
Pythagoras
Eckige Flächen
Runde Flächen
13
14
16
7
Volumenberechnung
18
7.1
7.2
7.3
7.4
Einfache Körper
Spitze Körper
Abgestumpfte
Kugel
18
19
20
20
8
Längen und Verschnitte
22
8.1
8.2
8.3
8.4
8.5
Längen gebogener Werkstücke
Einspannlänge
Mindestbiegeradien
Zuschnittlängen gebogener Rohre
Verschnitt
23
23
24
24
24
9
Kinematik
25
9.1
9.2
9.3
Gleichförmige Bewegung
Durchschnittsgeschwindigkeit
Drehbewegung
25
26
27
Formelsammlung
Luftfahrzeugtechnik
Seite 2
9.4
9.5
9.6
Beziehnung zwischen Drehbewegung und geradliniger Bewegung
Gleichmäßig beschleunigte Bewegung
Zusammengesetzte Bewegung
27
28
30
10
Masse und Kraft
31
10.1
10.2
10.3
10.4
10.5
10.6
10.7
10.8
Masse
Dynamisches Grundgesetz
Kraft als Vektor
Kräftezusammensetzung
Kräftezerlegung
Reibung
Fliehkraft
Federkraft
31
31
31
32
33
34
35
35
11
Drehmoment, Hebel und Auflagekräfte
36
11.1
11.2
11.3
Drehmoment
Hebel
Auflagekräfte
37
37
37
12
Schwerpunktbestimmung
38
12.1
12.2
12.3
Einfache Körper
Zusammengesetzte Körper
Schwerpunkt eines Flugzeugs
38
38
39
13
Kräfte am Flugzeug
40
13.1
13.2
13.3
Kräfte beim Start
Kräfte während des Fluges
Flugmechanik
40
41
53
14
Arbeit, Energie und Leistung
45
14.1
14.2
14.3
14.4
Arbeit
Energie
Energieumwandlung
Leistung
45
47
48
49
15
Festigkeit
50
15.1
15.2
15.3
15.4
15.5
15.6
15.7
15.8
15.9
Zugspannung, Druckspannung
Scherspannung
Zulässige Spannung und Sicherheitszahl
Dehnung, Elastizität
Biegemoment
Widerstandsmomente
Biegespannung
Torsionsspannung
Kesselspannung
50
51
51
52
53
54
55
55
56
16
Druck, Hydrostatik
57
16.1
16.2
Kraft, Fläche und Druck
Wandler
57
58
Formelsammlung
Luftfahrzeugtechnik
Seite 3
17
Hydrodynamik
59
17.1
17.2
17.3
Ausfluß aus Gefäßen
Strömungen
Dynamische und kinematische Viskosität
59
60
61
18
Aerostatik
62
18.1
18.2
Atmosphäre
Statischer Auftrieb
62
64
19
Aerodynamik
65
19.1
19.2
19.3
19.4
19.5
19.6
19.7
19.8
19.9
19.10
Kontinuitätsgleichung
Bernoullische Gleichung
Machzahl
Korrektur der Bernoullischen Gleichung
Dynamischer Auftrieb, Kräfteverteilung
Luftvolumenstrom
Widerstand
Widerstandsbeiwerte
Reynoldszahl
Widerstandsbeiwerte und Interferenzwiderstand
65
65
67
67
68
69
70
71
72
73
20
Tragflächen- und Profilgrößen
74
20.1
20.2
20.3
20.4
20.5
Tragflächengeometrie
Flügelstreckung, Seiten-, Dicken-, und Wölbungsverhältnis
Kraftangriffspunkt und Auftriebsbeiwert
Profiltiefe und mittlere aerodynamische Flügeltiefe
Meßprotokoll
74
75
75
76
76
21
Thermodynamik
77
21.1
21.2
21.3
21.4
Wärmedehnung
Wärme, Energie
Wärmemischung
Luftfeuchtigkeit
77
78
81
83
22
Triebwerke
85
22.1
22.2
22.3
22.4
Kolbentriebwerke
Strahltriebwerke
Wirkungsgrade
Kreisprozeß
85
89
91
92
23
Instrumente
96
23.1
23.2
23.3
23.4
23.5
23.6
23.7
23.8
Temperatur, Höhe und Geschwindigkeit
Kreisel
Driften, Kippen
Kompaß, Kompaßfehler
Flugzeugmagnetismus bzw. Deviation
Elektromagnetische Wellen
Entfernungsmessung
Frequenzbereiche
96
99
100
102
107
112
113
114
Formelsammlung
Luftfahrzeugtechnik
Seite 4
1 Baisisgrößen, Einheiten und Umrechnungen
1.1 Basisgrößen und Vorsätze
Basisgröße
Länge
Masse
Einheit
Meter
Kilogramm
m
kg
Kurzzeichen
Piko
Nano Mikro
p
10
µ
n
-12
10
-9
10
-6
Strom Temperatur Lichtstärke
Zeit
Sekunde Ampere
s
A
Kelvin
Candela
K
cd
Milli
Zenti
Dezi
Hekto
Kilo
Mega
Giga
m
c
d
h
k
M
G
-3
10
10
-2
10
-1
10
2
10
3
10
6
10
9
1.2 Längen und Geschwindigkeiten
Einheit
m
ft
NM
1m
1
3,2808
5,4 10
-4
1 ft
0,3048
1
1,65 10
-4
1 NM
1852
6076
1
KTS
m/s
km/h
1 KTS
1
0,514
1,852
1 m/s
1,944
1
3,6
1 km/h
0,54
0,277
1
Einheit
l/h
1.3 Drücke und Durchflußmengen
Einheit
bar
1 bar
1
1 Pa
10
1 hPa
10
1 psi
Pa
3
5
-5
-3
-2
6,9 10
Formelsammlung
hPa
psi
14,5
1 cuft/min 1700
10
10
1
10
100
1
14,5 10
68,9
1
3
6,9 10
-2
-5
14,5 10
-3
Luftfahrzeugtechnik
kg/h
1 usg/h
1 lb/h
3,785
0,454
Seite 5
2 Algebra
2.1 Addition, Subtraktion
2a + a
2 ab + 3 ab
= 3a
= 5 ab
14 a - 5 c - 8 a
= 5a - 5c
2a - 5a
= -2 a
Vertauschungsregel:
a + b = c
Klammerregel:
(a + b) + c
b+ a = c
=
a + (b + c)
a + b + c
2.2 Multiplikation, Division
4a 2b 3
10 a 5 a
= 24 ab
= 2
Vorzeichenregel:
6 a 2 = 3a
-4 a 2 a
= -2
( +a )
(-a)
(-a)
( +a )
= - ab
= +ab
= - ab
( +b )
( +b )
(-b)
(-b)
= +ab
2.3 Potenzen und Wurzeln
Potenzen
c = a
a
a = Basis (Grundzahl)
n = Exponent (Hochzahl)
c = Potenzwert
n
a =c
a ... a
Wurzeln
n
n
a = Wurzelwert
n = Wurzelexpont
c = Radikant
n
a b =
a = a
1
n
Formelsammlung
a
n
a
b
b
=
a
b
0
a = 1
Luftfahrzeugtechnik
n
c= a
Seite 6
3 Winkelfunktion
3.1 Sinus und Cosinus
Hypotenuse c
Gegenkathete
Sinus α =
Hypotenuse
β
α
Gegenkathete
a
Ankathete b
Cosinus α =
Ankathete
Hypotenuse
oder
Sin α =
a
c
oder
Cos α =
b
c
3.2 Tangens und Cotangens
Hypotenuse c
Gegenkathete
Tangens α =
Ankathete
β
α
Gegenkathete
a
Ankathete b
Cotangens α
=
Ankathete
Gegenkathete
oder Tan α =
a
b
oder Cot α =
b
a
3.3 Sinussatz und Cosinussatz
β
c
γ
α
a
b
Sinussatz:
Cosinussatz:
Formelsammlung
a
b
c
sin α = sin β = sin γ
a2 = b2 + c 2 - 2 b c cos α
Luftfahrzeugtechnik
Seite 7
4 Prozent- und Zinsrechnung
4.1 Prozentrechnung
p = Prozentsatz in %
G = Grundwert
P = Prozentwert
p =
100 P
G
p gibt den Zahlenwert der Hundertstel an
G ist der Wert, auf den sich die Prozentrechnung bezieht
P ist der Teil des Grundwerts, der dem Prozentsatz entspricht
4.2 Zinsrechnung
Z
K
p
n
=
=
=
=
Zins
Kapital
Zinssatz in %
Zeit
Zins für n Jahre
Z =
K p n
100
Zins für n Monate
Z =
K p n
100 12
Zins für n Tage
Z =
K p n
100 360
4.3 Zinseszinsrechnung
K0
Kn
n
m
p
w
W
=
=
=
=
=
=
=
Anfangskapital
Endekapital
Anzahl der Jahre
Anzahl der Zinszahlungen pro Jahr
Zinssatz in %
Wachstumsrate
Wachstumsfaktor
K
mn
w =
= K0
p
mn
{1 + m 100 }
p
100
W = w + 1
Formelsammlung
Luftfahrzeugtechnik
Seite 8
5 Längenberechnung
5.1 Längenteilungen
n = Teilungszahl (Lochzahl)
p = Teilung (Lochabstand)
L = Gesamtlänge
l 1/2 = Randabstände
l1
p
p
L
Teilungszahl:
n=
l2
L - (l1 + l 2 )
+1
p
p=
Teilung:
L - (l1 + l2 )
n-1
L = p (n - 1) + (l1 + l2 )
Gesamtlänge:
p = Teilung (Kreisteilung)
p
d
p
π
p = dn
Teilung:
5.2 Umfang und Bogenlängen
Kreisumfang
d
d = Durchmesser
U = d π
Umfang:
Formelsammlung
Luftfahrzeugtechnik
U =2rπ
Seite 9
lB
Kreisbogenlänge
α
d = Durchmesser
α = Mittelpunktswinkel
d
Bogenläge l B
d π α
360
lB =
Ellipsenumfang
d
D,d = Durchmesser
D
D+d
2
U = π
Umfang:
2
U =π
2
2 (R + r )
Gestreckte Längen
s
D
D
= Außendurchmesser
d
= Innendurchmesser
d
dm
d m = mittlerer Durchmesser
l
m
= gestreckte Länge (Umfang)
D+d
2
mittlerer Durchmesser:
dm =
mittlerer Länge (Umfang):
l m = dm π
Formelsammlung
Luftfahrzeugtechnik
Seite 10
5.3 Regelmäßige Vielecke
Dreieck
D
d
l
h
=
=
=
=
D
h
Umkreisdurchmesser
Inkreisdurchmesser
Seitenlänge
Höhe
d
l
Durchmesser:
D =
2 d
Seitenlänge:
l = 1,73 D
Umfang:
U =
Höhe:
h = 0,866 l
l n
Quadrat:
D = Umkreisdurchmesser
d = Inkreisdurchmesser
SW = Schlüsselweite (Seitenlänge)
D = e = Eckenmaß
Formelsammlung
D
l
SW
d
Durchmesser:
D = 1,414 d
Seitenlänge:
l = 0,707 D
Umfang:
U =
Luftfahrzeugtechnik
l n
Seite 11
D
Sechseck:
β
D = Umkreisdurchmesser
d = Inkreisdurchmesser
SW = Schlüsselweite
D = e = Eckenmaß
α
SW
l
d
h
Durchmesser:
D = 1,155 d
Seitenlänge:
l = 0,5 D
Umfang:
U =
Höhe:
h = 0,866 l
Achteck:
l n
β
D = Umkreisdurchmesser
l = Seitenlänge
SW = Schlüsselweite
D = e = Eckenmaß
D
SW
h
α
l
SW = 0,924 D
Schlüsselweite:
Formelsammlung
Seitenlänge:
l = 0,383 D
Umfang:
U =
Luftfahrzeugtechnik
l n
Seite 12
6 Flächenberechnung
6.1 Pythagoras
Pythagoras
Satz des Pythagoras:
Das Hypotenusenquadrat ist gleich der Summe der beiden Kathetenquadrate.
C
A3
c = Hypotenuse
Die Hypotenuse liegt dem
rechten Winkel gegenüber.
b
2
A2 =a
2
A3 =b
2
Formelsammlung
a
c
B
A
a, b = Katheten
Die Katheten bilden
den rechten Winkel.
A1 =c
A2
A1
2
2
Satz des Pythagoras:
c =
2
a + b
Hypotenuse:
c =
a + b
Kathete:
a =
c - b2
Kathete:
b =
c2 - a
Luftfahrzeugtechnik
2
2
2
2
Seite 13
6.2 Eckige Flächen
e
Quadrat (h = l)
l = Seitenlänge
h = Höhe
h
l
Fläche:
A = l
2
Rhombus (Raute)
l = Seitenlänge
h = Höhe
h
l
l
A =
Fläche:
l h
e
Rechteck
l = Seitenlänge
h = Höhe
h
l
A =
Fläche:
Formelsammlung
Luftfahrzeugtechnik
l h
Seite 14
Dreieck
l = Seitenlänge
h = Höhe
h
l
A =
Fläche:
l2
Trapez
l = Seitenlänge
h = Höhe
l h
2
h
lm
l1
A =
Fläche:
l1 + l2
2
h
D
Sechseck:
β
D = Umkreisdurchmesser
d = Inkreisdurchmesser
SW = Schlüsselweite
D = e = Eckenmaß
α
SW
Formelsammlung
Luftfahrzeugtechnik
d
h
A =
Fläche:
l
l h
2
n
Seite 15
6.3 Runde Flächen
Kreis:
d
d = Durchmesser
d2 π
A =
4
Fläche:
Kreisring:
dd
D, d = Durchmesser
D
2
2
A = (D - d )
Fläche:
π
4
lB
Kreisausschnitt (Sektor)
α
d
d = Durchmesser
d
α = Mittelpunktswinkel
2
d π α
A =
4 360
Fläche:
Formelsammlung
d
Luftfahrzeugtechnik
Seite 16
lB
Kreisabschnitt (Segment)
h
d = Durchmesser
r = Radius
α = Mittelpunktswinkel
α
d
r
l = Segmentlänge
h = Segmenthöhe
l
l B r - l (r - h)
2
Fläche:
A=
oder:
A=
Segmentlänge
l= 2 2 h r-h2
Segmenthöhe
h= r-
2 l h
3
2
2
r -l /4
Ellipse:
d
D,d = Durchmesser
r
R,r = Radien
D
R
π D d
4
Fläche:
A =
oder:
A = π R r
Formelsammlung
Luftfahrzeugtechnik
Seite 17
7 Volumenberechnung
7.1 Einfache Körper
Prisma ( Würfel )
l
= Seitenlänge
b = Breite
f
h
A
e
h = Höhe
Volumen (Würfel l=b=h):
b
l
V =
V =
A h
l
3
Zylinder
d = Durchmesser
h = Höhe
h
A
d
2
d π
V =
4
Volumen:
h
d
Hohlzylinder
D, d = Durchmesser
h = Höhe
h
A
D
π 2 2
V = 4 (D - d ) h
Volumen:
Formelsammlung
Luftfahrzeugtechnik
Seite 18
7.2 Spitze Körper
Pyramide
l = Seitenlänge
b = Breite
h = Höhe
h
hb
hl
b
l
Volumen:
V =
A
l b h
3
Kegel
d = Durchmesser
h = Höhe
s = Mantelhöhe
s
h
A
d
Mantelfläche:
AM = π r s
Volumen:
1 d π
V =
3
4
2
Formelsammlung
Luftfahrzeugtechnik
h
Seite 19
7.3 Abgestumpfte Körper
b2
Pyramide
l = Seitenlänge
b = Breite
h = Höhe
l2
h
Ag
b1
l1
Volumen:
Ad
V = h3 (A g + A g A d + A d )
d
Kegelstumpf
Ad
s
D, d = Durchmesser
h = Höhe
s = Mantelhöhe
h
Ag
D
Volumen:
2
2
h π
V = 12 (D + d + D d)
7.4 Kugel
Kugel:
d
d = Durchmesser
Volumen:
Formelsammlung
V =
Luftfahrzeugtechnik
π d3
6
Seite 20
s
Kugelabschnitt:
d = Durchmesser
h = Abschnitthöhe
s = Abschnittdurchmesser
h
d
r
V = π h 2 ( d2 - h )
3
Volumen:
s
Kugelausschnitt:
h
d = Durchmesser
h = Abschnitthöhe
s = Abschnittdurchmesser
d
r
Volumen:
V =
d1
d2
Kugelschicht:
d = Kugeldurchmesser
h = Abschnitthöhe
d = Abschnittdurchmesser
π d2
h
6
h
d
r
1/2
Volumen:
Formelsammlung
2
2
2
V = π h (3 r 1 + 3 r 2 + h )
6
Luftfahrzeugtechnik
Seite 21
8 Längen und Verschnitte
8.1 Längen gebogener Werkstücke (gestreckte Längen)
a u. b = gerade Längen
L 1/2 = Schänkellängen
t = Materialstärke
α = Biegewinkel
β = Öffnungswinkel
R = Biegeradius
NF = neutrale Faser
α
β
b
L2
R
NF
R+t
t
a
L1
L
Abwicklungslänge:
gestreckte Länge:
Zuschnittlänge:
L = L1 + L 2 - V
Ausgleichswert:
V = 2(R + t) - (R + 3 ) 2
Ausgleichswert (Faustformel):
V =R + t
2
t
π
8.2 Einspannlänge
b
Der Abstand zwischen Oberwange und Biegewange
muß 1,2 t sein, da sonst
das Blech gequetscht wird.
1,2 t
t
b = L1 - R
2
Einspannlänge:
Formelsammlung
Luftfahrzeugtechnik
Seite 22
8.3 Mindestbiegeradien beim Kantbiegen von Blechen LN 9003
Blechdicke
Werkstoff
0,3
0,4 0,5
0,6 0,8
1
1,2 1,5
2
2,5
3
R mindestens (mm)
1.0334.7
0,6 0,6 0,6
0,6 1,0 1,0
1,2
1.1274.2
0,6 0,6 1,0
1,0 1,2 1,6
2,0 2,5
1.4544.9
0,6 0,6 0,6
0,6
1.5074.4
0,6 1,0 1,0
1.7734.4
1,0 1,0 1,2
1,6
2,0
2,5 3,0
1,6 2,0
2,5
1,2 1,6
2,0 2,5 3,0 4,0
6,0
8,0
0,6 1,0 1,0
1,2 1,6
2,0 2,5 3,0 4,0
6,0
8,0
2.0034.1
0,6 0,6 1,0
1,0 1,6
1,6 2,5 3,0 4,0
4,0 6,0
2.0224.2
0,6 0,6 1,0
1,0 1,6
1,6 2,5 3,0 4,0
4,0 6,0
2.1964.2
0,6 1,0
1,6 2,5
2,5 3,0
4,0
W3050.2
0,6 0,6
0,6 0,6
0,8 1,0 1,2 1,6
2,0 2,5
W3116.5
1,0 1,2
1,6 2,0
2,5 3,0 3,0 5,0
6,0 8,0
3.1364.1
0,6 0,6
0,6 1,0
1,2 1,6 2,0 3,0
4,0 5,0
3.1364.5
1,0 1,6
2,0 2,5
3,0 4,0 5,0 8,0
10
3.1364.4
0,6 0,8
1,0 1,6
2,0 2,5 3,0
4,0
5,0 6,0
3.3524.1
0,6 0,6
0,6 0,8
1,0 1,2 1,6 2,0
2,5 3,0
3.3214.1
0,6 0,6
0,6 0,8
1,0 1,6 2,0 2,5
3,0 4,0
3.3214.5
0,6 1,0
1,0 1,6
2,0 2,5 3,0 4,0
5,0 6,0
3.3214.7
0,6 1,0
1,2 2,0
2,0 3,0 4,0 5,0
6,0 8,0
3.4374.1
0,6 0,6
0,6 0,8
1,0 1,2 1,6 2,0
2,5 4,0
3.4374.7
1,6 2,0
2,5 4,0
5,0 6,0 8,0 10
12
Formelsammlung
Luftfahrzeugtechnik
12
16
Seite 23
8.4 Zuschnittlängen gebogener Rohre (gestreckte Längen)
L1
D
90° Rohrbogen
R
L2
D = Rohrdurchmesser
R = Biegeradius
NF = neutrale Faser
NF
L1
R
R/2 R/2
P
L2
Zuschnittlänge
Zuschnittlänge:
L = L1 + L 2 - R
2
Biegelänge (Faustformel):
L = 1,5 R
B
8.5 Verschnitt von Blechen
AV
A w = Werkstückfläche
AV
AB = Bruttofläche
A V = Verschnitt
A1
A2
A V= AB - A W
Verschnitt:
A V% =
Verschnitt in %:
Formelsammlung
A3
Luftfahrzeugtechnik
A V 100 %
AW
Seite 24
BK
9 Kinematik
9.1 Gleichförmige Bewegung
BK
BK
s
s = Strecke
t 1/2 = Zeit
t1
t2
s
t
Geschwindigkeit:
v=
oder:
∆s
v= ∆
t
Grapische Darstellung gleichförmiger Bewegung
s in m
4
v in m/s
4
v1
v2
3
v1 3
∆s
2
v3
∆t
1
v2 1
0
0
1
2
2
3
4
Weg-Zeit-Diagramm
t in s
v3
"A" = s
0
0
1
2
3
4
t in s
Geschwindigkeit-Zeit-Diagramm
Anmerkung:
Je steiler der Anstieg der Geraden im Weg-Zeit Diagramm ist, um so größer ist
die Geschwindigkeit.
Im oben dargestellen Diagramm h.d.: v1 > v2 > v3
Formelsammlung
Luftfahrzeugtechnik
Seite 25
9.2 Durchschnittsgeschwindigkeit
Bewegt sich ein Flugzeug oder ein anderes Fahrzeug mit unterschiedlichen
Geschwindigkeiten v1 , v2 , v3 ,...,vn in den entsprechenden Zeitintervallen, so
ist für die gesamte Strecke bzw. Zeit die Durchschnittsgeschwindigkeit vm von
Bedeutung. Zwischenstops bzw. Unterbrechungen können mit einbezogen
werden. Die Geschwindigkeit ist in dem Zeitintervall vi = 0.
v in m/s
s in m
4
4
3
v3
2
v2
v2 3
v4
2
vm
1
v1
0
0
1
2
3
4
t in s
Weg-Zeit-Diagramm
vm
v4 1
v1
v3
0
0
1
2
3
4
t in s
Geschwindigkeit-Zeit-Diagramm
n
Σ si
Durchschnittsgeschwindigkeit:
vm =
i=1
n
Σ ti
i=1
vm =
oder:
v1 t 1 + v2 t 2 + ... + vn t n
t 1 + t 2 + ... + t n
Anmerkung:
Zur Bestimmung der Einzelwege si bzw. des Gesamtweges s eignet sich das
Geschwindigkeit-Zeit-Diagramm.
Denn die Fläche unterhalb des Graphens im v-t-Diagramm entspricht dem
zurückgelegten Weg s in dem Zeitintervall ∆t.
.
Die Rechteckflächen v t im oben dargestellten v-t-Diagramm entsprechen
den Einzelwegen s. Die Summe der Einzelflächen ergibt den Gesamtweg.
Formelsammlung
Luftfahrzeugtechnik
Seite 26
9.3 Drehbewegung
d = Durchmesser in m
r = Radius in m
ϕ = Drehwinkel
n = Drehzahl in 1/min:
v u = Umfangsgeschwindigkeit
ω = Winkelgeschwindigkeit
ϕ
t1
r
vu
t0
ω
n
d
d π n
60 1000
Umfangsgeschwindigkeit in m/s:
vu =
Winkelgeschwindigkeit in rad/s
ω = 2 π n
60
v= ω r
Umfangsgeschwindigkeit in m/s:
9.4 Beziehung zwischen Drehbewegung und geradliniger Bewegung
vu
v = Geschwindigkeit
vu = Umfangsgeschwindigkeit
v = vu
Geschwindigkeit in m/s:
oder:
Formelsammlung
d
v
v=
Luftfahrzeugtechnik
d π n
60 1000
Seite 27
9.5 Gleichmäßig beschleunigte Bewegung
BK
BK
Mönchengladbach
Mönchengladbach
t 0/1/2 = Zeit
v0/1/2 = Geschwindigkeit
s
t0
v0 = 0
s = Strecke
Beschleunigung:
t1
v1
<
t2
v2
<
Geschwindigkeitszunahme pro Zeiteinheit
a =
Beschleunigung:
∆v
∆t
Graphische Darstellung gleichmäßig beschleunigter Bewegung:
v in m/s
s in m
4
4
a2
3
∆v
a1
2
2
∆t
a3
1
1
0
0
1
2
3
3
4
t in s
0
0
Geschwindigkeit-Zeit-Diagramm
1
2
3
4
t in s
Weg-Zeit-Diagramm
v = a t
Geschwindigkeit in m/s:
Ist bereits eine Anfangsgeschwindigkeit vorhanden, so folgt:
v = v0 + a t
Geschwindigkeit in m/s:
Formelsammlung
Luftfahrzeugtechnik
Seite 28
Verzögerung:
Geschwindigkeitsabnahme pro Zeiteinheit
∆v
∆t
a = -
Verzögerung:
v in m/s
4
a2
3
Graphische Darstellung der
Verzögerung imm v-t-Diagramm
∆v
2
1
a1
∆t
0
t in s
0
1
2
3
4
Geschwindigkeit-Zeit-Diagramm
Die Strecken lassen sich u.a. mit Hilfe des v-t-Diagramms berechnen.
Strecke mit v und t:
s =
v t
2
Strecke mit a und t:
s =
a 2
t + v0 t
2
Gesamtstrecke:
s = Σ si
n
i =1
Radialbeschleunigung:
r = Radius in m
v = Umfangsgeschwindigkeit
ω = Winkelgeschwindigkeit
v2
t1
ω
v1
t1
r
v1 = v2
v1 = v2
Radialbeschleunigung:
Formelsammlung
2
ar = ω r
Luftfahrzeugtechnik
V
ar = r
2
Seite 29
9.6 Zusammengesetzte Bewegung
Durch Überlagerung verschiedener Einzelbewegungen entsteht eine zusammengesetzte (resultierende) Bewegung.
2 Komponenten
vv = Vertikalgeschwindigkeit
vH = Horizontalgeschwindigkeit
v
v
V
R
α
vR = Resultierende Geschwindigkeit
v
Vektorielle Addition:
v = vv +
Resultierende Geschwindigkeit:
v =
√ vv2
H
vH
+
vH2
3 Komponenten
vSW = Seitenwind,
vst = Steiggeschwindigkeit
vF
= Fluggeschwindigkeit (Eigengeschwindigkeit)
vR
= Resultierende Geschwindigkeit
v = vst + vSW + vF
Vektorielle Addition:
Resultierende Geschwindigkeit:
Formelsammlung
Luftfahrzeugtechnik
2
2
2
v = √ vSW
+ vF + vst
Seite 30
BK
Mönchengladbach
10 Masse und Kraft
10.1 Masse
Die Masse m eines Körpers ist das Maß für die Stoffmenge. Die Basiseinheit
der Masse im SI-System ist das kg.
Die Dichte ρ eines Stoffes ist die auf eine Volumeneinheit bezogene Masse.
m=V ρ
Masse:
10.2 Dynamisches Grundgesetz
Wird einer Masse m die Beschleunigung a zuteil, dann ist eine Kraft F erforderlich, die gleich dem Produkt aus der Masse m und der Beschleunigung a ist.
F= m a
Kraft:
Eine besondere Kraft ist die Gewichtskraft. Die allgemeine Beschleunigung a
ist bei der Gewichtskraft die Erdbeschleunigung g.
Fg = m g
Gewichtskraft:
10.3 Kraft als Vektor
Die Kraft läßt sich als Vektor (Kraftpfeil) darstellen:
BK
Mönchengladbach
Widerstandskraft F W
Formelsammlung
Luftfahrzeugtechnik
Schubkraft F S
Seite 31
10.4 Kräftezusammensetzung
Die Resultierende ergibt sich aus der vektoriellen Addition der Einzelkräfte.
Mit Hilfe eines Kräftemaßstabes (KM) läßt sich die Resultierende graphisch
ermitteln.
F4
F3
F2
F4
F1
F1
F3
F2
FR
Kräftemaßstab (Beispiel):
500 N
n
Resultierende Kraft:
FR = Σ Fi
oder:
F R = F 1 + F2 + ... + Fn
i=1
Die Resultierende (Betrag) eines Kräfteparallelogramms läßt sich auch mit Hilfe
des Cosinus-Satzes berechnen.
F1
α
Resultierende Kraft:
FR
F2
FR =
2
2
F 1 + F 2 + 2 F1 F 2 cos α
Bilden F1 und F2 einen rechten Winkel, so kann man den Pythagoras anwenden
Formelsammlung
Luftfahrzeugtechnik
Seite 32
10.5 Kräftezerlegung
Graphisch läßt sich eine Kraft, ähnlich wie bei der Zusammensetzung, in Einzelkräfte zerlegen, wenn deren Kraftrichtungen (Wirklinien) bekannt sind.
Sind die Richtungen bekannt, so zieht man die Wirkungslinien durch den Kraftangriffspunkt (KAP) der zu zerlegenden Kraft und konstruiert das Parallelogramm.
Fs
Fs
KAP
Fs
Fs
Fs = Seilkraft
Fg
Fg = Gewichtskraft
Fg
F s1 = Fg - Fs2
Resultierende Kraft:
Stehen die Einzekräfte senkrecht aufeinander und ist der Winkel α bekannt,
dann lassen sich die Einzelkräfte wie folgt berechnen.
FHab = Hangabtriebskraft
FN
= Normalkraftkraft
Fg
= Gewichtskraft
α
Fg
FN
FHab
Hangabtriebskraft:
F Hab = Fg sin α
Normalkraft:
F N = F g cos α
Formelsammlung
Luftfahrzeugtechnik
Seite 33
10.6 Reibung
Bei der Reibung muß man zwischen Haft-, Gleit- und Rollreibung unterscheiden.
F = wirksame Kraft
FN = Normalkraft
FR
FR = Reibkraft
SP
F
v
v
F
FR
FN = FG
FN
Gekennzeichnet sind die Reibungskräfte durch die unterschiedlichen
Reibungszahlen:
µHaft , µGleit und µRoll
µHaft > µGleit > µRoll
F R = µ FN
Reibkraft:
Bewegt sich ein Körper auf einer schiefen Ebene, so ist die Normalkraft nicht
gleich der Gewichtskraft, wie im oberen Beispiel. Sie ist abhängig von dem
Neigungswinkel α.
F
= wirksame Kraft
Fg = Gewichtskraft
F N = Normalkraftkraft
FHab = Hangabtriebskraft
FR = Reibkraft
F
FR
α
α
Fg
FN
F Hab
F R = µ Fg cos α
Reibkraft:
Formelsammlung
Luftfahrzeugtechnik
Seite 34
10.7 Fliehkraft
Die Fliehkraft ist abhängig von der Masse m im Schwerpunkt (SP) und der
Radialbeschleunigung ar (s. S. 27).
2r = d
FF
FF
SP
ω
m
= Fliehkraft
= Schwerpunkt
= Winkelgeschwindigkeit
= Masse
FF
m
m
SP
SP
ω
FF = m a r
Fliehkraft:
2
FF = m ω r
oder:
2
FF = m v
r
10.8 Federkraft
Die elastische Verlängerung der Schraubenfeder ist der wirkenden Kraft
proportional.
F in N D
1
∆ s = Federweg
D = Federkonstante
FFed = Federkraft
D
2
D
3
∆s
F Fed
Federkennlinie
F Fed = D ∆ s
Federkraft:
Formelsammlung
s in mm
Luftfahrzeugtechnik
Seite 35
BK
11 Drehmoment, Hebel und Auflagekräfte
Mönchengladbach
11.1 Drehmoment
Bei einem Drehmoment stehen Hebelarm (r) und Wirklinie der Kraft senkrecht
aufeinander.
d
r
F
M
=
=
=
=
Durchmesser
Hebelarm
Kraft
Drehmoment (Vektor)
r
d
M
F
M= F r
Drehmoment:
11.2 Hebel
Hebelgesetz:
Summe aller linksdrehenden Momente = Summe aller rechtsdrehenden Momente.
F2
r
= Hebelarme
1,2
F
= Kräfte
F1
1,2
Quadrant
r2
r1 > r2
F1 r1 = F2 r2
Hebelgesetz:
Formelsammlung
r1
Luftfahrzeugtechnik
Seite 36
11.3 Auflagekräfte
Auflagekräfte werden mit Hilfe des Drehmomenten- und Kräftegleichgewichtes
ermittelt. Der Drehpunkt kann dabei frei gewählt werden. Es empfiehlt sich jedoch
ihn an einem Auflagepunkt (z.B. Hauptfahrwerk oder Wälzlager A) zu legen. Die
Summe der Auflagekräfte = der Summe der übrigen Kräfte (Gewichtskräfte).
BK
Mönchengladbach
s H,B = Hebelarme
Fg
= Gewichtskraft
FH,B = Auflagekräfte (Fahrwerk)
Fg
FHF
F BF
sH
A,B = Lager
l 1,2,... = Hebelarme
F 1,2,... = Gewichtskräfte der
Triebwerksmodule
F A,B = Auflagekräfte
sB
B
A
FB
F1
FA
F2
l1
l2
F4
F3
lB
l3
l4
n
n
1
1
Kräftegleichgewichtsbedingung:
Σ Fgi = Σ F Auf i
Momentengleichgewichtsbedingung:
Σ M re = Σ M
Auflagekraft Bugfahrwerk:
FBF =
Auflagekraft Lager B:
Formelsammlung
FB =
li
Fg s H
sB
F2 l 2 + F3 l 3 + F 4 l 4 - F 1 l 1
lB
Luftfahrzeugtechnik
Seite 37
BK
12 Schwerpunktbestimmung
Mönchengladbach
12.1 Einfache Körper
Befindet sich ein Körper im Momentengleichgewicht, so wird er in seinem
Schwerpunkt gestützt bzw. gelagert.
Bei geometrisch bestimmten Figuren ist der Schwerpunkt leicht zu finden.
Es bietet sich hier eine zeichnerische Lösung an,
12.2 Zusammengesetzte Körper
Zusammengesetzte Körper werden ähnlich wie bei den Auflagekräften über
die Momentengleichgewichtsbedingung berechnet.
Bezugskante
F1
x1
F3
F2
x2
x
x3
F1,2,3 = Einzelkräfte
x 1,2,3 = Einzelkoordinaten
n
ΣM
Koordinate des Schwerpunktes:
x =
1
n
Σ Fgi
1
oder:
Formelsammlung
x
=
F1 x 1 + F 2 x 2 + F
F Ges
Luftfahrzeugtechnik
3
x
3
Seite 38
12.3 Schwerpunkt eines Flugzeugs
Wie im vorherigen Beispiel läßt sich auch der Schwerpunkt von Flugzeugen
mit der Momentengleichgewichtsbedingung berechnen.
BL
m Fuel = Kraftstoffmasse
m Nutz= Nutzlast
x 1,2,... = Koordinaten (Hebelarme)
f
= zulässiger Schwerpunktsbereich
Bezugskante
f
BK
Mönchengladbach
m Nutz
x1
x2
x3
x4
m Fuel
m BL
m Nutz
m Nutz
x5
x
Koordinate des Schwerpunktes:
x =
Σ (m x)
Σm
In den meisten Flughandbüchern sind Tabellen bzw. Diagramme (Beladungsdiagramme) mit denen ebenfalls der Schwerpunkt ermittelt werden kann.
Beladungsmasse
m in kg
vorderen Fluggäste
und Besatzung
Grundmasse +
Σ Beladungsmasse
Kraftstoff
hinteren Fluggäste
und Nutzlast
Beladungsmoment M in Nm (da Nm)
Formelsammlung
Zulässiger
Schwerpunktbereich
Grundmoment + Σ Beladungsmomente
Luftfahrzeugtechnik
Seite 39
BK
13 Kräfte am Flugzeug
Mönchengladbach
13.1 Kräfte beim Start
F Sch
FB
Fw
FR
=
=
=
=
Schubkraft
Beschleunigungskraft
Luftwiderstand
Rollwiderstand
Fa
Fg
= Auftriebskraft
= Gewichtskraft
BK
Fa
Fw
FSch
FB
FRB
FRH
Fg
F B + F W + F RH + F RB
F Sch
Horizontalkräfte:
13.2 Kräfte während des Fluges (Horizontalflug)
Fa
Fg
FH
= Auftriebskraft
= Gewichtskraft
= Höhenleitwerkskraft
F Sch = Schubkraft
F w = Luftwiderstand
BK
Fa
Fw
FH
FSch
Fg
la
Vertikalkräfte:
Vertikalmomente:
Formelsammlung
l
H
Fa = F g + F H
Luftfahrzeugtechnik
F a l a = FH ( l H + la )
Seite 40
13.3
Flugmechanik
Begriffsbestimmung :
T
=
Schubkraft
L
=
Auftrieb
D
=
Luftwiderstand
A
=
Beschleunigung
W
=
Gewicht, Gewichtskraft
MTW = Maximales TO-Gewicht
n
=
Belastungszahl (Lastvielfache)
γ
=
Steigwinkel
TAS
=
True Air Speed (wahre Luftgeschwindigkeit)
RC
=
Rate of Climb (Steiggeschwindigkeit)
H
=
Höhe
TRUE AIR SPEED TAS
∆H
γ
RATE OF CLIMB RC
AIR DISTANCE
Formelsammlung
Luftfahrzeugtechnik
Seite 41
Schub:
T = D + W sin γ
Auftrieb:
L = W cos γ
∆H
Air Distance
Climb Gradient:
tan γ =
Climb Gradient:
tan γ =
Für kleine Winkel:
tan γ ~
~ sin γ
Climb Gradient:
sin γ =
T - D
W
Climb Gradient mit Beschleunigung:
sin γ =
T - D
W
Rate of Climb:
RC =
∆H
Steigzeit
Rate of Climb mit v = TAS :
RC = v
Formelsammlung
Luftfahrzeugtechnik
T - D
W
a
- g
a
T - D
- v g
W
Seite 42
Begriffsbestimmung :
FF
β
ω
v
=
=
=
=
Fliehkraft
Querneigungswinkel
Winkelgeschwindigkeit des Kurvenfluges
Bahngeschwindigkeit
Lastvielfache:
n =
L
W
Fliehkraft:
FF = m r ω2
oder:
2
FF = m vr
oder:
FF = W tan β
Formelsammlung
Luftfahrzeugtechnik
Seite 43
√
Resultierende Kraft:
FR = m
oder:
F = cos
β
R
bzw.:
F = cos
β
R
v
4
g2 + r2
m g
W
Auftriebsverlust:
oder:
∆ Fa = FR - Fa
FR = m
√
Lastvielfache im Kurvenflug:
n =
Querneigung:
tan β =
Lastvielfache im Kurvenflug:
n =
Formelsammlung
Luftfahrzeugtechnik
( √ g2
1 +
v
v
4
v
+ r2
)
- g
4
r 2 g2
2
r g
√1 +
2
tan β
Seite 44
BK
14 Arbeit, Energie und Leistung
Mönchengladbach
14.1 Arbeit
Die Arbeit W ist das Produkt aus Kraft und Weg. Kraft und Weg müssen dabei
parallel bzw. auf einer gemeinsamen Geraden liegen.
W= F s
Arbeit:
Die Einheit der Arbeit wird in J angegeben. 1J = 1 N 1 m
Es gibt verschiedene Formen von Arbeit. So gibt es, um nur einige zu nennen,
z. B. die Hubarbeit und die Federspannarbeit.
Hubarbeit:
Das Flugzeug steigt um die Höhe h. Dabei wird Hubarbeit verrichtet.
Auftriebskraft Fa = Hubkraft F Hub
Höhe h = Hubweg s
BK
Mönchengladbach
2
h
F a = F Hub
BK
Mönchengladbach
1
W= F h
Hubarbeit:
Formelsammlung
Luftfahrzeugtechnik
Seite 45
Die Arbeit W läßt sich im Kraft-Weg-Diagramm darstellen.
Im unten dargestelltem Beispiel sind die Kräfte eines Flugzeuges beim
Start (s. S. 38) eingezeichnet. Zur Überwindung der Kräfte FR, FB und FW
entlang des Weges s muß vom Triebwerk Schubarbeit W (Fläche unterhalb
des Graphens FR +FB + FW ) verrichtet werden.
F in kN
1200
Fg
Fa
900
F Sch
F R + F B+ F W
600
FR + FB+ FW
FSch
300
FB
FW
FR
s in m
0
0
600
300
900
Kraft-Weg-Diagramm
1200
Federspannarbeit:
Beim Spannen einer Feder wird Federspannarbeit verrichtet.
F in N
D
1
D
2
F=Ds
D
W=F
s
2
3
s in mm
Kraft-Weg-Diagramm
s2
W= D
2
Federspannarbeit:
Formelsammlung
Luftfahrzeugtechnik
Seite 46
14.2 Energie
Die Arbeit ist ein zeitlich ablaufender Vorgang. Ist der Vorgang vollzogen, so
wird keine Arbeit mehr verrichtet. Die Arbeit kann man also nicht speichern.
Energie hingegen ist ein Zustand, der nicht abläuft. Energie läßt sich (im Prinzip unbegrenzt) speichern. Energie hat aber auch die Fähigkeit Arbeit zu verrichten (gespeicherte Arbeitsfähigkeit).
Die Einheit der Energie wird auch in J angegeben. 1J = 1 N 1 m
Energie kann in verschiedenen Formen auftreten und ist unter bestimmten
Voraussetzungen umwandelbar. Man unterscheidet aber grundsätzlich
zwischen Lageenergie (potentielle) und Bewegungsenergie (kinetische).
Potentielle Energie:
GS
Gewerbliche Schulen
Fg
h
MSL = Bezugsebene
Lageenergie:
E p = Fg h
oder:
Ep= m g h
Man bezeichnet die Energie einer Körpermasse, bezogen auf eine bestimmte
Bezugsebene als Energie der Lage bzw. als potentielle Energie.
Die vorher verrichtete Hubarbeit (s.S. 40) ist gleich der Zunahme der potentiellen
Energie.
Formelsammlung
Luftfahrzeugtechnik
Seite 47
Massen die sich bewegen, besitzen Bewegungsenergie.
Kinetische Energie:
GS
v
Gewerbliche Schulen
2
Ek = m v
2
Bewegungsenergie:
Man bezeichnet die Energie der Bewegung auch als kinetische Energie.
14.3 Energieumwandlung (Energieerhaltung)
Wie bereits erwähnt kann man unter bestimmten Voraussetzungen Energieformen umwandeln. So läßt sich z.B. potentielle Energie in kinetische Energie
umwandeln. Die beiden folgenden Beispiele verdeutlichen die Umwandlung.:
Epot
v=0
h
Ekin
Ekin
v>0
Epot
v=0
h
v>0
Die Beispiele zeigen, daß potentielle Energie (nach Verrichten der Hubarbeit)
in kinetische Energie umgewandelt wird.
v2
m g h = m 2
Energieumwandlung:
Formelsammlung
Luftfahrzeugtechnik
Seite 48
14.4 Leistung
Die Leistung P ist das Verrichten von Arbeit pro Zeiteinheit. Es ist also der
Quotient aus Arbeit und Zeit . Oder:
Wenn in der Zeit t die Arbeit W verrichtet wird, errechnet sich daher die Leistung
P in dieser Zeit aus der Gleichung:
P= W
t
Leistung:
Die Einheit der Leistung wird in Watt angegeben. 1W = 1 J
/1s
WS
Aachen
2
h
F a = F Hub
WS
Aachen
1
P=
Hubleistung:
FHub h
t
Leistung als Funktion von Kraft und Geschwindigkeit:
s
t
Leistung:
P=F
oder:
P = F v
Formelsammlung
Luftfahrzeugtechnik
Seite 49
15 Festigkeit
15.1 Zugspannung, Druckspannung
2
Den Quotienten aus Belastung in N und Fläche in mm bezeichnet man als
Spannung.
σ =
Spannung:
F
A
Man unterscheidet zwischen Zugspannung und Druckspannung.
Rm =
σ =
FD =
Fz =
A =
l0 =
σz =
σD =
σzul =
ν =
Bruchfestigkeit
Spannung
Druckkraft
Zugkraft
Querschnitt
Ausgangslänge
Zugspannung
Druckspannung
zulässige Spannung
Sicherheitszahl
FZ
A
FD
l0
A
FZ
FD
Zugspannung:
σz =
Fz
A
Druckspannung:
σD =
FD
A
Formelsammlung
Luftfahrzeugtechnik
Seite 50
15.2 Scherspannung
Die Scherspannung wird ähnlich berechnet wie die Zug- und Druckspannung.
2
Es ist der Quotient aus Belastung in N und Scherfläche in mm .
τ
τB
Fs
As
=
=
=
=
F
A
τ =
Scherspannung:
Scherspannung
Scherfestigkeit = 0,8 R
m
Scherkraft
Scherfläche
Fs
As
Fs
τzul = zulässige Spannung
ν = Sicherheitzahl
Fz
Fz
(A z )
Fs
Fs
τ =
Fs
As
zulässige Zugspannung:
σ zul =
Rm
ν
zulässige Scherspannung:
τ zul =
Scherspannung:
15.3 zulässige Spannung, Sicherheitszahl
Formelsammlung
Luftfahrzeugtechnik
τB
ν
Seite 51
15.4 Dehnung, Elastizität
Feste Körper verhalten sich ähnlich wie Federn. Werden sie elastisch verformt,
so erhalten sie nach der Entlastung wieder ihre ursprüngliche Form.
FZ
Stab ist wieder entlastet
Stab ohne Belastung
l0
l 0 = Ausgangslänge
∆ l = Verlängerung
Fz = Belastung
l0
l0
∆l
FZ
Stab ist belastet
Als Dehnung bezeichnet man den Quotient aus Verlängerung durch Ausgangslänge.
ε =
Dehnung:
∆l
l0
Zwischen Belastung (Spannung) und Verlängerung (Dehnung) gilt folgende
Beziehung:
Die elastische Dehnung ist der vorhandenen Spannung proportional.
Rm
Ez = Elastizitätsgrenze
Rm = Bruchgrenze
Z = Zerreißgrenze
E = Elastizitätsmodul
(Proportionalitätsfaktor)
Z
Ez
K
r
a
f
t
elastischer Bereich
Verlängerung
plastischer Bereich
∆l
σ = Ε ε
Spannung:
Formelsammlung
Luftfahrzeugtechnik
Seite 52
15.5 Biegemoment
Das Biegemoment Mb ist das im Bauteil (Rumpf,...) auftretende Moment,
welches den angreifenden äußeren Drehmomenten das Gleichgewicht hält.
x
M b = Biegemoment
Fq = Querkraft
Fq
Mb
FA
FB
+
x
la
F H = Höhenleitwerkskraft
F a = Auftriebskraft
Fg
F g = Gewichtskraft
lH
FH
Fa
LU
+
Fq -
Mb
M b = - (M g + M H +...)
Biegemoment:
Formelsammlung
Luftfahrzeugtechnik
Seite 53
15.6 Widerstandmoment
Welches Biegemoment Mb = Σ Mi von den inneren Kräften aufgebracht werden
kann, hängt vom Werkstoff des Balkens und von seinem Widerstandsmoment ab.
Biegewiderstandsmomente:
z
Wb = πd
32
z
3
d
d
z
4
z
Wb =
D-d
4
10 D
D
W yb = π r
8
y
SP
z
z
3
4r
3π
d =d 2r
W zb=
0,1902
Wb =
b h
r
3
b
z
z
h
2
6
B
z
z
b
Wb = B H
h H
3
6H
b h
3
b
Formelsammlung
Luftfahrzeugtechnik
Seite 54
15.7 Biegespannung (Randfaserspannung)
Die Biegespannung bzw. Randfaserspannung ist der Quotient aus dem
Biegemoment und dem Widerstandsmoment.
x
Schnittstelle
Biegeachse
Neutrale
Faser
Mb
σb=
Biegespannung:
Mb
Wb
15.8 Torsionsspannung (Verdrehspannung)
Torsionsspannung am Rumpf können u.a. durch Böen, Ruder- und Leitwerkskräfte
verursacht werden.
FSL = Seitenleitwerkskraft
FR = Ruderkräfte
F B = Böenkräfte
FSL
h
Drehachse
FR
FR
l
Böe (F B )
M Tor
W pol
Torsionsspannung:
σ Tor =
Torsionsmoment durch Querruder:
M Tor = F R l
polares Widerstandsmoment:
D-d
W pol = π
16 D
4
Formelsammlung
Luftfahrzeugtechnik
4
Seite 55
15.9 Kesselspannung
Kesselspannung am Rumpf tritt durch den Differenzdruck zwischen Kabine und
Atmosphäre auf.
Druckfläche A l = D l
2 π
Druckfläche Aq = D 4
Schnittfläche A s = l s
Schnittfläche A s = D π s
p = Differenzdruck
F = Kräfte durch Differenzdruck
F = p A l(q)
p
F
F
P
Druckfläche A l
F
s
Schnittfläche Asl
D
FP
p
l
P
F
Druckfläche A q
p
p
F
Schnittfläche A sq
Kesselspannung L:
σL = p
Kesselspannung Q:
σQ= p
Formelsammlung
Luftfahrzeugtechnik
D
2s
D
4s
Seite 56
BK
16 Druck, Hydrostatik
Mönchengladbach
16.1 Kraft, Fläche und Druck
Druck ist der Quotient aus Kraft und Fläche. D.h. die Gesamtkraft ist auf eine
Flächeneinheit bezogen.
F
F
F
F
F
F
F
F
F
F
F
A = 1m x 1m
F
F
F
F
F
F
A = 1m
2
Flächeneinheit
p =
Druck:
2
Druckeinheit: 1 N/m = 1 Pa
F
A
5
1bar = 10 Pa
Der Druck ist eine skalare Größe und ist damit nicht richtungsgebunden.
Er breitet sich in alle Richtungen gleichmäßig aus.
hydrostatischer
Druck
∆h
p
Der hydrostatische Druck ist von der Höhendifferenz ∆h abhängig.
p = ρ g ∆h
hydrostatischer Druck:
Formelsammlung
Luftfahrzeugtechnik
Seite 57
16.2 Kraft, Wandler
Kraft:
F = p A
Kraft:
Kraftwandler
F
= Kräfte
1/2
A
= Flächen
1/2
p
= Druck
A1
F2
F1
A2
p
Kräfteverhältnis:
F1
A1
=
F2
A2
oder:
F1 A 2 = F 2 A 1
Druckwandler
p
= Drücke
1/2
A
= Flächen
1/2
F
= Kraft
p1
A
F1
p2
A2
A1
Druckverhältnis:
p1
A2
=
p2
A1
oder:
p
Formelsammlung
Luftfahrzeugtechnik
1
A
1
= p
2
A
2
Seite 58
BK
17 Hydrodynamik
Mönchengladbach
17.1 Ausfluß aus Gefäßen
Volumenstrom durch Bodenöffnung:
Q
A
h
g
µ
=
=
=
=
=
Volumenstrom
Öffnungsquerschnitt
Spiegelhöhe der Flüssigkeit
Erdbeschleunigung
Kontraktionszahl
h
A
Kontraktionszahl für:
gut abgerundete Düsen µ = 0,97
µ = 0,62
scharfkantige Düsen
Q
Volumenstrom:
Q =Aµ
Bodenausflußgeschwindigkeit:
v = µ
2gh
2gh
Volumenstrom durch Seitenöffnung:
Q = Volumenstrom
b = Breite der Ausflußöffnung
h u = Abstand Fluidspiegel bis untere Kante
der Ausflußöffnung
h o = Abstand Fluidspiegel bis obere Kante
der Ausflußöffnung
h m = Abstand Fluidspiegel bis Mitte
der Ausflußöffnung
Volumenstrom:
Formelsammlung
Q
Q = 23 µ b ( hu
2 g h u - ho
Q =Aµ
Volumenstrom (kleine Öffnung):
Luftfahrzeugtechnik
ho
hu
2 g hu )
2 g hm
Seite 59
17.2 Strömungen
Turbulente Strömung
v
V
A St
cw
ρ
=
=
=
=
Anströmgeschwindigkeit
Stirnfläche
Widerstandsbeiwert
Dichte
A St
Wirbel (Rotationsenergie)
Für turbulente Strömung wird folgende Formel verwendet:
2
Fw = c w 1 ρ v A St
2
Strömungswiderstand:
laminar
turbulent
Umschlagpunkt
v1
v0
v1
v0
laminar
turbulent
v2
Die Grenze (bzw. Übergang) zwischen laminarer und turbulenter Strömung wird
durch die Reynoldssche Zahl Rekrit bestimmt.
Re =
Reynoldssche Zahl:
l vρ
η
Die Reynoldssche Zahl ist u.a. von der Geschwindigkeit (v = variabel)
abhängig. Die anderen Größen sind m.o.w. konstant.
Im oberen Beispiel ( Profil ) ist bis zum Umschlagpunkt die Geschwindigkeit
verhältnismäßig klein. Die Strömung ist laminar (Re < Rekrit). Zur Berechnung
der Reibung kann die Formel FRI = η A v/d verwendet werden.
Ab dem Umschlagpunkt ist die Geschwindigkeit groß. Die Strömung ist
turbulent ( Re > Rekrit ). Zur Widerstandsberechnung muß die Formel
2
FW = cW 1/2 ρ v A verwendet weden.
5
Für das obere Profil (Luft) liegt die kritische Reynoldszahl bei: Rekrit = 5 10 .
Formelsammlung
Luftfahrzeugtechnik
Seite 60
17.3 dynamische und kinematische Viskosität
Die Viskosität oder Zähigkeit ist eine wichtige Materialkonstante. Sie ändert
sich mit der Temperatur.
dynamische Viskosität:
v = Geschwindigkeit,
FRI = innere Reibkraft,
A
= Fläche des Körpers, d = Grenzschichtdicke
η = F RI d
dynamische Viskosität:
A
v
kinematische Viskosität:
ρ = Dichte
ν = η
ρ
kinematische Viskosität:
kinematische
Zähigkeit
2
in m bei
s
Normalluftdruck
Stoffe und
Temperatur
Ethanol
Benzol
Glyzerin
Wasser
Wasser
Wasser
Luft
Luft
Luft
Sauerstoff
bei 20 °C
bei 20 °C
bei 20 °C
bei 0 °C
bei 20 °C
bei100 °C
bei 0 °C
bei 20 °C
bei100 °C
bei 20 °C
1,5
0,74
850
1,79
1,01
0,28
13,2
16,9
181
18
-6
10
-6
10
-6
10
-6
10
-6
10
-6
10
-5
10
-5
10
-5
10
-6
10
Stoffe und
Temperatur
kinematische
Zähigkeit
2
in m bei
s
Normalluftdruck
Motorenöl bei 10 °C
Motorenöl bei 20 °C
Motorenöl bei 50 °C
Motorenöl bei 80 °C
Motorenöl bei 100°C
Motorenöl bei 120°C
Motorenöl bei 150°C
800
380
80
20
10
3
0,5
-6
10
-6
10
-6
10
-6
10
-6
10
-6
10
-6
10
kinematische Viskosität in Abhängigkeit der Temperatur
Umrechnung: 10
Formelsammlung
-6
2
m /s
=
1 Zentistokes = 1 cSt = 0,01 St
Luftfahrzeugtechnik
Seite 61
BK
18 Aerostatik
18.1
Mönchengladbach
Atmosphäre
Internationale Standard Atmosphäre ISA:
In der ISA wurden die atmosphärischen Verhältnisse festgelegt, welche etwa
in einer geographischen Breite von 45° in Meereshöhe (MSL) herschen.
Dabei wurden drei Werte wie folgt definiert:
Temperatur ϑ
:
15° C
3
Dichte ρ
:
1,225 Kg/m
Luftdruck p
:
1013,25 hPa
Der Luftdruck entspricht der Gewichtskraft der Luftsäule bezogen auf ihre
Grundfläche.
Da die Luftsäule über der Grundfläche mit zunehmender Höhe immer kürzer wird,
der Luftdruck mit zunehmender Höhe abnehmen.
Für die folgenden Berechnungen ist die Höhe H in km einzusetzen.
muß auch
Der Luftdruck nimmt nach folgender Funktion ab:
Luftdruck:
p = 1013,25 (1 - 0,0226 H)
5,25
Der Luftdruck der Atmosphäre ist relativ geringen Schwankungen unterworfen.
Sie liegt bei 5 % vom Mittelwert.
Nach einer ähnlichen Funktion nimmt die Dichte ab:
Dichte:
ρ = 1,225 (1 - 0,0226 H)
4,25
Die Dichte der Atmosphäre schwankt um ca. 20 % um den Mittelwert.
Formelsammlung
Luftfahrzeugtechnik
Seite 62
Die Temperatur nimmt bis zur Tropopause nach ISA 6,5° pro 1000 m linear
ab und bleibt ab 11 km mit - 56,5 ° konstant.
Die Temperatur nimmt bei 0% Luftfeuchtigkeit nach folgender Funktion ab:
T = 15°C - 6,5
Temperatur (trocken):
H
Die Temperatur ist großen Schwankungen in der Atmosphäre unterworfen.
Die Werte der verschiedenen Größen können entweder nach den obigen
Formeln errechnet, Zahlentafeln entnommen oder in Diagrammen (s.u.)
abgelesen werden.
ICAO - Normalatmosphäre mit standardisierten Werten
Höhe in km
Höhe in km
12
12
10
10
8
8
6
6
4
4
2
2
0
0
1050 950 850 750 650 550 450 350 250 150
1,2
1,1
1,0
0,9
0,8
0,7
0,6
0,5
0,4
Druck p in hPa, Dichte ρ in kg/m
Formelsammlung
15
0,3
5
-5
-15
-25
Temperatur
-35
-45 -55
-65
T in ° C
3
Luftfahrzeugtechnik
Seite 63
18.2
Auftrieb
Statischer Auftrieb:
Jeder eingetauchte Körper (in Gas oder Flüssigkeit) erfährt eine nach oben
gerichtete Auftriebskraft, die ebenso groß ist wie die Gewichtskraft der von
ihm verdrängten Gas- oder Flüssigkeitsmenge.
m
VL
= Masse der verdrängten Luft
Fa
m = Nutzlast
L
m = Masse der Hülle
m
H
G
Nutzlast
= Füllgasmasse
mg = m
L
+ mH + mG
Fg
schwebt:
Fa = Fg
steigt:
Fa > Fg
Formelsammlung
Luftfahrzeugtechnik
Seite 64
BK
19 Aerodynamik
19.1
Mönchengladbach
Kontinuitätsgleichung
Bei Flüssigkeiten oder Gasen sind die durch verschiedene Querschnitte einer
Leitung je Zeiteinheit durchtretenden Volumen gleich.
v
= Geschwindigkeiten
d1
A = Querschnitte Q = Volumenströme
v1
A1
v2
A2
d2
Q2
Q1
19.2
Bernoullische Gleichung
2
pges = 1 ρ v + p
2
0
Gesamtdruck:
oder:
1 ρ v 2 + p = konstant
2
0
oder:
1 ρ v2 + p = 1 ρ v2 + p
2
2
1
2
1
2
Formelsammlung
Luftfahrzeugtechnik
Seite 65
Differenz der statischen Drücke:
v1
v
v1
ρ
L
ρ
Fl
∆h
p
=
<
=
=
=
=
Geschwindigkeiten
v2
Dichte der Luft
Dichte der Meßflüssigkeit
Differenzhöhe
statischen Drücke
Luft
ρ
v2
L
p
p
2
1
∆h
Meßflüssigkeit
Differenzdruck:
∆p = p1- p2
Differenzdruck:
2
2
∆ p = 1 ρ ( v2 - v 1 )
2
hydrostatischer Druck:
∆ p = ρ Fl g ∆ h
Durchflußgeschwindigkeit v1:
2∆p
v1 =
Durchflußgeschwindigkeit:
Formelsammlung
ρ
L
Luftfahrzeugtechnik
A1 2
- 1
A2
( )
Seite 66
19.3
Machzahl
Die Machzahl (M) zeigt das Verhältnis der Fluggeschwindigkeit v zur Schallgeschwindigkeit a:
M =
Machzahl:
v
a
Berechnung der Schallgeschwindigkeit a:
κ = Adiabatenexponent (für Luft κ =1,4)
R = Gaskonstante (für Luft R = 287 J/kg K)
T = absolute Temperatur (in K)
Schallgeschwindigkeit:
a =
oder
a = 20,1
19.4
κ R T
T
Korrektur der Bernoullischen Gleichung
Die Änderung der Dichte infolge der Änderung des dynamischen Druckes, die
sogenannte Kompressibilität, macht es erforderlich die Bernoullische Gleichung
(ab etwa v = 100 m/s) zu korrigieren:
p + q + ∆q
0
Gesamtdruck (korrigiert):
pges =
oder
pges = p 0 + q 1 + 1 M 2
4
Formelsammlung
Luftfahrzeugtechnik
Seite 67
19.5
Auftrieb
Beim Tragflügel kann Auftrieb nur dann entstehen, wenn in Vertikalrichtung eine
Impulsstromänderung (∆v) auftritt. Um eine solche hervorzurufen, muß der Tragflügel Luft nach unten ablenken. Der Flügel ist also gezwungen, um sein eigenes
Fallen zu verhindern, an seiner Stelle Luft nach unten zu leiten.
F a = Auftriebskraft
Fa
v0
v0
v
∆v
Q
ρL
=
=
=
=
ca =
A =
∆v
Geschwindigkeiten
Geschwindigkeitsänderung
Volumenstrom
Dichte der Luft
Auftriebsbeiwert
Auftriebsfläche
v
dynamischer Auftrieb:
Fa = Q ρ ∆v
2
1
Fa = ca 2 ρ v A
oder:
19.5
1
Kräfteverteilung
F a = Auftriebskraft
F w = Widerstandskraft
F R = Resultierende
FN
F N = Normalkraft
α = Anströmwinkel
Fa
v0
Profilsehne
α
Formelsammlung
FR
Fw
Luftfahrzeugtechnik
Seite 68
19.6
Luftvolumenstrom
Ablenkung und sekundlich abgelenktes Luftvolumen:
Das sekundlich durch den Tragflügel verarbeitete Luftvolumen Q kann auf Grund
folgender vereinfachten (idealisiert) Annahme bestimmt werden:
Man betrachtet die vom Flügel beeinflußte Luft scharf begrenzt durch einen über
die Spannweite b errichteten Kreisquerschnitt und rechnet mit einer über den
ganzen Querschnitt konstante Ablenkung. In Wirklichkeit ist die Ablenkung an der
Flügelwurzel am größten und klingt mit zunehmender Entfernung ab.
bewegtes bzw. abgelenktes
Luftvolumen
=b
Ablenkung:
∆ v = 2π c a vo λ
abgelenktes Luftvolumen:
Q =
Formelsammlung
Luftfahrzeugtechnik
π 2
b
4
v
Seite 69
19.7
Widerstand
Während im luftleeren Raum alle Körper unter Einfluß der Schwerkraft gleich
schnell und gleichmäßig beschleunigt fallen, trifft dies im Luftraum nicht zu.
Diese gegen die Bewegungsrichtung gerichtete Kraft ist der Luftwiderstand.
Bis auf den Reibungswiderstand sind alle anderen Widerstandskräfte Druckkräfte.
vo
Stirnfläche A
Maßgebend für die Widerstandskraft ist die Stirnfläche A und der dynamische Druck q. Hinzu
kommt noch der Widerstandsbeiwert cw. Er beinhaltet u.a.
die Widerstandsart, er gibt also an, um welchen Widerstand es sich handelt.
Folgende Widerstände werden unterschieden:
Reibungswiderstand F
R
Formwiderstand FF
Induzierter Widerstand F I
Interferenzwiderstand FIn
Schockwellenwiderstand F
S
Nicht jeder Widerstand läßt sich einfach berechnen, so z.B. der Schockwellenwiderstand im Überschallbereich.
Die berechenbaren Widerstände werden mit folgender Gleichung berechnet:
2
1
Fw = cw 2 ρ v A
Widerstand:
Das gilt für turbulente Stömungszustände.
Laminare Strömung (Reibungswiderstand) wird berechnet: s. K. 17.5 (S. 75 )
Formelsammlung
Luftfahrzeugtechnik
Seite 70
19.8
Widerstandsbeiwerte
Formwiderstand:
Der Formwiderstandsbeiwert kann, sofern das Dickenverhältnis bekannt ist, dem
Diagramm entnommen werden.
cw
0,8
0,7
0,6
0,5
Profile
0,4
0,3
0,2
0,1
0,05
0,1 0,2
0,3
0,4
0,5
0,6 0,7
0,8
0,9
1,0
1,1 1,2
d
t
Formwiderstandsbeiwerte in Abhängigkeit des Dickenverhältnisses
Induzierter Widerstand:
Der Widerstandsbeiwert des induzierten Widerstandes kann wie folgt berechnet
werden:
Beiwert des induzierten Widerstandes:
Formelsammlung
Luftfahrzeugtechnik
cwi =
c 2a
π λ
Seite 71
19.9 Reynoldszahl (Kutter)
Widerstandsbeiwert laminar:
c f lam =
Widerstandsbeiwert turbulent:
c f tu =
Widerstandsbeiwert Übergang:
(Re xu = 3 10 6 )
Formelsammlung
Luftfahrzeugtechnik
1,328
√Re
0,455
2,58
(log Re)
8700
c f = c f tu Re
Seite 72
19.10 Widerstandsbeiwerte und Interferenzwiderstand
Reibungswiderstand:
cwi
0,008
0,007
turbulent
0,006
0,005
0,004
0,003
0,002
laminar
0,001
0,0005
10
5
10 6
10
7
10
8
Re
der Reynoldschen Zahl (nach Dubs).
Interferenzwiderstand:
der Interferenzwiderstand ist die Differenz zwischen dem Gesamtwiderstand und
der Summe der Einzelwiderstände.
b
a
Fw1
Fw2
Fw ges
Fw3
Σ Fwi
< Fw ges
∆ Fint = F
Interferenzwiderstand:
Formelsammlung
Luftfahrzeugtechnik
w ges
-
n
Σ Fw i
i=1
Seite 73
BK
20 Tragflächen- und Profilgrößen
20.1
Mönchengladbach
Tragflächengeometrie
Begriffsbestimmung:
b
= Spannweite
t
= Profiltiefe (mittlere Segmenttiefe)
t Sp = Flügelspitzentiefe
t w = Flügelwurzeltiefe
KP
A = Flügelfläche
n = Anzahl der Segmente
= Kraftangriffspunkt
MAC = Mittlere aerodynamische Flügeltiefe
s
= Abstand zum Kraftangriffspunkt
KP
c ai
= Auftriebsbeiwert der Segmente
ϕ = Pfeilungswinkel
∆ b = Segmentbreite
s
KP
Längsachse
∆b
Segmente
tw
ϕ
KP
t/4-Linie
ti
8
5
6
7
2
3
4
s
1
D
MAC
i
b
t = Profiltiefe f = Wölbung d = Profildicke
x d = Dickenrücklage xf = Wölbungsrücklage
xd
r = Nasenradius
xf
Skelettlinie
d f
r
Formelsammlung
Sehne
t
Luftfahrzeugtechnik
Seite 74
20.2
Flügelstreckung, Seiten-, Dicken-, und Wölbungsverhältnis
Flugelstreckung Λ:
2
Λ = b
A
Flügelstreckung:
Seitenverhältnis λ:
Seitenverhältnis:
λ =
1
δ =
d
t
ω =
f
t
Λ
Dickenverhältnis δ:
Dickenverhältnis:
Wölbungsverhältnis ω:
Wölbungsverhältnis:
20.3
Kraftangriffspunkt und Auftriebsbeiwert
mittlerer Auftriebsbeiwert cA:
c
mittlerer Auftriebsbeiwert:
A
=
∆ b Σ ( c ai t i )
A
=
∆ b Σ ( c ai t i s i )
c
A
A
Abstand zum Kraftangriffspunkt sKP:
Abstand zum Kraftangriffspunkt:
Formelsammlung
Luftfahrzeugtechnik
s
KP
Seite 75
20.4
Profiltiefe und mittlere aerodynamische Flügeltiefe
Profiltiefe ti:
ti =
mittlere Profiltiefe:
tw
t sp
( b - s i ) + t sp
2
tw
t sp
( b - sKP ) + t sp
2
n ∆b
mittlere aerodynamische Flügeltiefe MAC:
MAC =
mittlere aerodyn. Flügeltiefe:
20.5
n ∆b
Meßprotokoll (empfohlen)
Nr.
c ai
ti
c ai t i
in
m
si
c ai
in
m
t i si
1
2
3
4
5
6
7
8
Σ
Formelsammlung
Luftfahrzeugtechnik
Σ
Seite 76
BK
21 Thermodynamik
21.1
Mönchengladbach
Wärmedehnung
Länge, Fläche, Volumen:
y
x, y, z =
l x,y,z =
o
=
∆l
∆ϑ
=
α
=
γ
Koordinaten
Ausgangslängen
Verlängerung
Temperaturdifferenz
Wärmedehnungszahl
= Wärmedehnungszahl
lyo
ly
z
lxo
lx
lz
l zo
x
Länge:
∆ l = l 0 α ∆ϑ
Längendehnung:
l = l0 + ∆l
Neue Länge:
Fläche:
Flächendehnung:
∆ A = A 0 2 α ∆ϑ
Neue Fläche:
A = A0 + ∆ A
Volumen:
Volumendehnung:
∆ V = V 0 γ ∆ϑ
Neues Volumen:
V = V0 + ∆ V
Formelsammlung
Luftfahrzeugtechnik
Seite 77
21.2
Wärme, Energie
Wärme ist eine Energieform. Wärmemenge ist die Energiemenge zum Erwärmen
einer Materialmenge.
Wärmemenge:
Q
c p,v
m
= zu- bzw. (abgeführte) Wärmemenge
= spezifische Wärmekapazität (bei konst. Druck bzw. Volumen)
= Masse
m ϑ1
ϑ
∆ϑ
ϑ
1
ϑ
2
T
1
m
ϑ2
ϑ2
= Temperaturdifferenz
= Temperatur vor der Erwärmung
= Temperatur nach der Erwärmung
Wärmezufuhr
= absolute Temperatur in K
Q = m c ∆ϑ
Wärmemenge:
Wärmestromdichte:
q = c
Wärmestromdichte:
∆ϑ
Innere Energie:
U = m cv T
innere Energie:
spezifische innere Energie:
u = cv T
innere Energie:
Formelsammlung
Luftfahrzeugtechnik
Seite 78
Enthalpie:
Enthalpie ist die Energiemenge, die nötig ist, um eine Materialmenge in den
durch p, V und T gekennzeichneten Zustand zu bringen.
D
D
A
h
p
= Durchmesser
= Querschnitt
1,2,3
1,2,3
T
= Temperatur
R
κ
s
p 3 V3 T3
= Druck
= Volumen
1,2,3
p 2 V2 T2
= Hub
V
1,2,3
p 1 V1 T1
h3
h2
h1
= Gaskonstante
= Isentropenexponent
Enthalpie:
H = m cp T
Enthalpie:
spezifische Enthalpie:
h = cp T
innere Enthalpie:
Gaskonstante Rs:
R s = cp - cv
Gaskonstante:
Isentropenexponent (Adiabatenexponent):
c
κ = cp
v
Isentropenexponent:
Formelsammlung
Luftfahrzeugtechnik
Seite 79
Zustandsänderungen:
p V = m Rs
allgemeine Zustandsgleichung:
p
Gasgleichung:
V
= konstant
T
p
oder:
1
V
T1
V1
Isobare Zustandsänderung (p = konstant):
T1
p
isotherme Zustandsänderung (T = konstant):
Stoffe
Wasserstoff
Stickstoff
Sauerstoff
Luft
CO
CO 2
Methan
Helium
1
V
p1
Isochore Zustandsänderung (V = konstant):
T
T1
1
p
=
V
2
T2
V2
=
T2
p
1 =
=
2
2
V
2
p2
T2
R in
J
kg K
c p in
J
kg K
4123,0
296,7
260,0
287,0
14250
998
920
1005
10125
743
660
718
269,9
188,8
518,6
2078,0
1010
835
2180
5200
743
646
1662
3123
c v in
J
kg K
Stoffwerte einiger Gase
Formelsammlung
Luftfahrzeugtechnik
Seite 80
21.3
Wärmemischung
Begriffsbestimmung:
p1/2
R
T1/2
ρLuft
ϑm
ϑ1
ϑ2
cp
Q1/2
m1/2
=
=
=
=
=
=
=
=
absoluter Luftdruck (Leitungsdruck) (Pa)
Gaskonstante der Luft (RL = 287Nm/kg K)
absolute Temperatur (K)
Dichte der Luft [ f(p,T)]
Temperatur nach der Mischung (°C)
Temperatur der heißen Luft (°C)
Temperatur der kalten Luft (°C)
spezifische Wärmekapazität bei konst. Druck (kNm/K)
3
= Volumenstrom m /s (heiße/kalte Luft)
= Massenstrom kg/s (heiße/kalte Luft)
Gasgleichung zur Bestimmung der Dichte siehe Seite 104
Mischungstemperatur:
ϑm =
Σ ( m c ϑ)
Σ ( m c)
Mischungstemperatur:
ϑm =
Σ ( m ϑ)
Σ(m )
oder:
ϑm =
m1 c1
ϑ1
m1 c1
+ m2 c2 ϑ2
+ m2 c2
.
Massenstromverhältnis:
m2
ϑ1 - ϑm
. =
ϑm - ϑ 2
m1
Volumenstromverhältnis:
Q2 ρ1 ( ϑ1 - ϑm )
=
Q1 ρ2 ( ϑm - ϑ 2 )
Formelsammlung
Luftfahrzeugtechnik
Seite 81
m2
Temperatur der heißen Luft:
ϑ1 =
Temperatur der kalten Luft:
ϑ2 = ϑm -
Mittlerer Druck nach der Mischung:
Kritisches Druckverhältnis :
m1
(ϑm - ϑ2 ) + ϑm
m1
m2
(ϑ1 - ϑm )
p1 Q 1 + p 2 Q 2
pm =
Q1 + Q2
p h < 1,89 p k
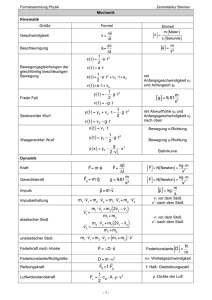
COCKPIT
DUCT
Wärmemischung
FWD CABIN
MID CABIN
AFT CABIN
CONDITIONED
AIR MANIFOLD
TO CARGO
COMPARTMENT
TRIM AIR VALVES
TRIM AIR MANIFOLD
PACK
2
Formelsammlung
PACK
1
Luftfahrzeugtechnik
FROM TRIM AIR
PRESS REG VALVE
Seite 82
21.4 Luftfeuchtigkeit
Begriffsbestimmung:
p =
pD =
pDS =
ρD =
ρDS =
ϕ =
x =
realer Luftdruck (Kabinendruck, Leitungsdruck)
Wasserdampfdruck
Sättigungsdampfdruck
Dichte des Wasserdampfs in der Luft
Sättigungskonzentration (Dichte)
relative Luftfeuchtigkeit
Wassermasse je kg Luft
ϕ pDS
x = 0,622
p - ϕ pDS
Wassermasse:
oder:
x = 0,622
ϕ =
relative Luftfeuchtigkeit
p
p -
x
0,622 + x
D
p
D
p
p
D
p
ϕ = pD
oder:
DS
ρ
ϕ = ρD
oder:
DS
Formelsammlung
Luftfahrzeugtechnik
Seite 83
Zustandsänderungen ( bezogen auf 1 kg ):
isochor
isobar
isotherm
ohne T
V1 = V2
p1 = p2
p 1 V1 = p 2 V 2
ohne p
V1 = V2
V1
V2
=
T1
T2
T1 = T2
ohne V
p1
p2
=
T2
T1
p1 = p2
isentrop
polytrop
κ
κ
p 1 V 1 = p 2 V2
κ−1
κ−1
T 1 V1 = T 2 V2
p2
T2
p 1 = T1
0
-W =
c v (T 2 -T 1 )
∆U =
zugeführte
c p (T 2 -T 1 )
c
(T -T )
Wärme
v 2 1
W
0
V2
V1
p2
R T ln
p1
p2
p V ln
p1
V2
p V ln
V1
R T ln
Arbeit W
0
technische
Arbeit W t
R (T2 -T 1)
V (p -p )
1
2
( )
κ −n
κ−1 W
R (T -T )
2 1
R (T -T )
2 1
n -1
p1 V2 T2
− 1)
κ−1 ( T
1
p1 V2 T2
( − 1)
n -1
T1
1 (p V - p V )
κ−1
2 2
n
n-1
c v (T 2 -T 1 )
κ−1
1 1
1 (p V - p V )
n -1
κ W
W
0
1
p2
T2
p 1 = T1
( )
T1 = T2
n-1
n-1
T 1 V1 = T 2 V 2
κ
κ−1
Änderung
q =
c v (T 2 -T 1 )
der inneren
c v (T 2 -T 1 )
Energie
p (V2 -V 1 )
n
n
p 1 V1 = p 2 V2
2 2
1 1
n W
p - V - Diagramme
p
p
2
1
V
isochor
Formelsammlung
V
1
V
2
isobar
V
1
V
2
isotherm
Luftfahrzeugtechnik
V
1
V
2
isentrop, polytrop
Seite 84
22 Triebwerke
22.1
Kolbentriebwerke
Begriffsbestimmung :
d
d = Zylinderdurchmesser
z = Zylinderzahl
o.T.
s = Hub
F = Kolbenkraft
Fpi = Pleulstangenkraft
s
FN = Seitenkraft (Normalkraft)
FT = Tangentialkraft
Frad = Radialkraft
u.T.
l = Pleulstangenlänge
r = Kurbelradius
α = Kurbelwinkel
β = Pleulstangenwinkel
λ Pl = Pleulstangenverhältnis
n = Drehzahl
p m = mittlerer Verbrennungsdruck
v m = mittlere Kolbengeschwindigkeit
pm
vm
FN
l
F pi
F
β
vu
α
FT
r
n
F pi
F rad
Abmessungen des Motors:
Pleulstangenverhältnis:
λ Pl = r
Kurbelwinkel:
sin α =
l sin β
r
oder:
sin α =
sin β
λ Pl
Pleulwinkel:
sin β =
r sin α
l
Formelsammlung
l
Luftfahrzeugtechnik
Seite 85
s =
Kolbenhub:
Kolbenweg vom OT:
30 Vm
n
s K = r (1 - cos α ) + l (1 - cos β )
Kräfte, Momente:
Kolbenkraft:
F = p
Pleulstangenkraft:
F Pl =
Seitenkraft:
FN = F tan β
Tangentialkraft:
FT =
Radialkraft:
F rad =
Drehmoment:
M = FT r
maximales Drehmoment:
M max =
Formelsammlung
Luftfahrzeugtechnik
A
F
cos β
F sin (α + β)
cos β
F cos (α + β)
cos β
F max r
cos β
Seite 86
Begriffsbestimmung :
d = Zylinderdurchmesser
z = Zylinderzahl
s = Hub
V h = Hubvolumen je Zylinder
V H = Gesamtvolumen
Vc = Verdichtungsraum
n = Drehzahl
ε = Verdichtungsverhältnis
PL = Hubraumleistung
P I = induzierte Leistung
Pe = effektive Leistung
L = Luftbedarf in kg Luft/ kg Kraftstoff
F F = Kraftstofffluß in kg/h
be = spezifischer Kraftstoffverbrauch
η = Wirkungsgrad
η m = mechanischer Wirkungsgrad
OT
Vc
s
d
Leistung des Viertaktmotors:
VH p m n
induzierte Leistung:
Pi =
effektive Leistung:
Pe = Pi η m
Hubraumleistung:
Pe
PL = V
H
1200
Weitere Kenngrößen:
Liefergrad:
λL =
m zu
m th
oder:
λL =
Vzu ρ zu
V h ρ th
Luftverhältnis:
L
λ =
L min
Formelsammlung
Luftfahrzeugtechnik
Seite 87
Leistungsgewicht:
FG
PG = P
e
Verdichtungsverhältnis:
ε =
2
π
d
s z
=
Gesamtvolumen:
VH
spezifischer Kraftstoffverbrauch:
be =
Formelsammlung
Luftfahrzeugtechnik
Vh + VC
VC
4
FF
Pe
Seite 88
22.2
Strahltriebwerke
Begriffsbestimmung und Größen:
N1/2 =
A =
Drehzahlen
Stirnfläche (Heißluft)
n
=
Anzahl der Verdichterstufen
ε
mo =
Massendurchsatz (v = 0) in kg/s
m
=
=
Nebenstromverhältnis
Massendurchsatz in kg/s
∆p =
πi =
Differenzdruck (Düse-Umgebung)
Stufendruckverhältnis (Mittelwert)
Massenstrom:
m0 = mK + mH
Massenstrom ZTL:
ε =
Nebenstromverhältnis:
mK
mH
Heißstrom:
m H0 =
bzw.:
mH =
1+ ε
m
1+ ε
ε
m K0 = m 0
Kaltstrom:
1+ ε
ε
1+ ε
mK = m
bzw.:
2
m = m 0 (1 + 0,2 M )
Staustrahleffekt:
Formelsammlung
m0
Luftfahrzeugtechnik
κ
κ−1
Seite 89
Druckverhältnis:
p
n
π = π i = p3
1
Druckverhältnis:
Schubkraft:
F s = m (o) (c - v)
Schubkraft TL:
Schubkraft ZTL:
Fs = m H(0) (c H - v) + m K(0) (c K - v)
oder:
Fs =
m (0)
1+ ε
(c H - v) + ε (c K - v)
statischer Schub:
Ist das Druckverhältnis p6 zu p0 größer oder gleich 1,8 ,so wird auch statischer
Schub erzeugt.
F s st = ∆ p
statischer Schub:
A
Gesamtschubkraft:
F Ges =
Gesamtschub:
Fs st + F s
spezifischer Schub:
Fsp =
spezifischer Schub:
Formelsammlung
Luftfahrzeugtechnik
F Ges
mo
Seite 90
22.3
Wirkungsgrade
ηV
ηth
ηAuf
ηVad
ηTad
ηG
ηin
ηGb
ηa
ηm
= Verbrennungswirkungsgrad
= thermischer Wirkungsgrad
= Aufheizgrad
= Verdichterwirkungsgrad (bezogen auf adiabatischen Kreisprozeß)
= Turbinenwirkungsgrad (bezogen auf adiabatischen Kreisprozeß)
= Gütegrad
= innerer Wirkungsgrad
= Gebläsewirkungsgrad
= äußerer Wirkungsgrad
= mechanischer Wirkungsgrad
η th = 1 -
thermischer Wirkungsgrad:
T2
T3
κ −1
κ
=1 - ( 1 )
π
oder:
η th
Aufheizgrad:
η Auf =
T4
T3
η Auf η Tad -
( η Vad )
1
Gütegrad:
ηG =
innerer Wirkungsgrad:
η in = η th η m η Vad η Tad η V
2
ηa = c
(v) +1
äußerer Wirkungsgrad (TL):
Formelsammlung
η Auf - 1
Luftfahrzeugtechnik
Seite 91
äußerer Wirkungsgrad (ZTL):
ηa =
2
2
( cvK + 1) + ε1v ( ccH -- vv
K
2
+
)
2
2
( cvH + 1) + εv ( ccK -- vv
H
2
)
η ges = η in η a
Gesamtwirkungsgrad:
optimale Geschwindigkeit (ZTL):
v =
22.4
2 + c2
√ ε + 1 √ ε cK
H
(√ ε + 1
2
√ ε c K2 + c H2 - √ ε (c H - c K ) )
ε2 c K + ε ( c H + c K) + c H
Kreisprozeß
Verdichterarbeit:
W tV = W κ
Verdichterarbeit (technische):
κ −1
κ
W tV = c p T2 ( π
oder:
Verdichteraustrittstemperatur:
Formelsammlung
Luftfahrzeugtechnik
T3 = T2
p3
p2
- 1)
κ−1
κ
( )
Seite 92
Verdichterarbeit:
p2V 2
κ−1
κ−1
(
p3 κ
p2 ) - 1
Verdichterarbeit (Gasarbeit):
W =
oder:
R
( T3 - T2 )
W =
κ−1
Verdichterleistung:
P V = m H W tV
Leistungsbedarf:
P
P Vind = η V
Vad
Leistungsbedarf des Gebläses (Fan) wird mit den gleichen Formel berechnet.
Brennkammer:
lu
lu
= Heizwert
= 42700 kJ/kg
Kraftstoffbedarf:
m Krst =
m H cp
lu
( T4 - T3 )
Turbine:
Leistungsbedarf:
P T = P Vind + P Gbind
oder:
P T = m H W tT η Tad η m
Formelsammlung
Luftfahrzeugtechnik
Seite 93
Turbinenarbeit:
Turbinenarbeit:
W tT =
PT
η Tad η m
mH
Turbinenarbeit ist die Arbeit, die dem Verdichter, Gebläse, Pumpen usw.
zugeführt wird.
κ−1
Turbinenarbeit:
Turbinenaustrittsdruck:
Turbinenaustrittstemperatur:
W tT = c p T4 1 - (
p5 κ
p4 )
W tT
= p4 ( 1 c p T4
p5
T5 = T4
p5
p4
)
κ
κ−1
κ−1
κ
( )
Düse:
2
Energie in der Düse:
Düsenaustrittsdruck:
Düsenaustrittstemperatur:
Formelsammlung
cH
= T5
2 cp
p 6 = p5
T6 = T5
Luftfahrzeugtechnik
κ
1 -(
p 6 κ−1
p5 )
2
cH
( 1 - 2 cp
p6
p5
T5
κ−1
κ
)
κ−1
κ
( )
Seite 94
Geschwindigkeiten:
mittlere Kolbengeschwindigkeit:
vm = s n
maximale Kolbengeschwindigkeit:
v max ~
~ 1,6 v m
Formelsammlung
Luftfahrzeugtechnik
30
Seite 95
23 Instrumente
23.1
Temperatur, Höhe und Geschwindigkeit
Begriffsbestimmung :
TAT =
SAT =
∆ϑ T =
HT =
HO =
ϑISA =
Total Air Temperature
Static Air Temperature
Temperaturdifferenz
tasächliche Höhe
gemessene Höhe
Standardtemperatur
a =
Schallgeschwindigkeit
IAS = Indicated Airspeed
CAS = Calibrated Airspeed
EAS = EquivalentAirspeed
TAS = True Airspeed
ISA-Standardwerte:
Normaldruck
Normaldichte
Normaltemperatur
po = 1013,25 hPa
3
ρo = 1,225 Kg/m
ϑo = 15°C
Höhenformeln s. Seite 58-59
Temperaturen:
2
Gemessene Temperatur:
TAT = SAT (1 + 0,2 M )
Gemessene Temperatur:
TAT = SAT + ∆ϑ T
Temperaturerhöhung:
2
∆ϑ T = 2v c
p
Temperaturfehler des Höhenmessers:
0
ALT
9
1
x 1000
x 10000
8
2
7
3
6
30000
5
tatsächliche Höhe:
1
H T = H o (1 - 273 ∆ϑ H )
Temperaturabweichung:
∆ϑ H = ϑISA − ϑ T
4
1013.2
1
.5
2
VS
4
0
.5
4
1
2
Formelsammlung
Luftfahrzeugtechnik
Seite 96
Machzahl:
110
400
350
M 0.38
120
300
Machzahl:
TAS
M= a
oder:
M=
130
250
140
225
200
180
160
∆p
pH
2
a
Airspeed Indicator
κ R T
Schallgeschwindigkeit:
a=
oder:
a = 20,1
T
Geschwindigkeiten:
IAS =
Indicated Airspeed:
Calibrated Airspeed:
p
2 ∆p
H
CAS = IAS - Systemfehler
Equivalent Airspeed:
EAS = CAS - Kompressibilitätsfehler
Equivalent Airspeed:
EAS = CAS
Formelsammlung
Luftfahrzeugtechnik
1
1 + 0,25 M
2
Seite 97
TAS = EAS - Dichtefehler
True Airspeed:
ρ
o
ρ
True Airspeed:
TAS = EAS
oder:
TAS = K
Faktor:
K = 2 R = 23,96
H
∆p
p TH
H
TAS = 445
HÖHE
DENSITY CORRECTION = 120KT
EAS = 325
COMPRESSIBILITY
CORRECTION = - 10KT
CAS = 335
IAS = 333
BK
POSITION ERROR
CORRECTION = +2KT
FL 200
TAS = EAS = CAS = 332
IAS = 333
BK
MSL
POSITION ERROR
CORRECTION = - 1KT
250
300
350
400
450
AIR SPEED (KTS)
Formelsammlung
Luftfahrzeugtechnik
Seite 98
23.2
Kreisel
Begriffsbestimmung :
H = Drehimpuls des Rotationskörpers
M = Moment, mit dem der Kreisel
präzediert
MS =
Störmoment
ωX =
ωY =
Winkelgeschwindigkeit
des Rotationskörpers
Winkelgeschwindigkeit
des Störmoments
ωZ = Winkelgeschwindigkeit,
mit der der Rotationskörper
präzediert
Y
CRS
123 NM
225 KT
270
ωy
Ms
270
V
O
R
1
ωx
N
S
ωz
090
ADF 1
X
ADF 2
Z
Kurskreisel
H
M
Drehimpuls:
H = Mx t
oder:
H = J ωx
Trägheitsmoment: (Kreisscheibe)
J = 12
Winkelgeschwindigkeit:
ωx = 2 π n
Rotationsenergie:
E = 12
Formelsammlung
Luftfahrzeugtechnik
m
J
R
2
2
ωx
Seite 99
Kreiselgleichung:
M = ωy
Kreiselgleichung:
M = Kreuzprodukt ( M =
ωy
H
kreuz H )
Moment:
x - Komponente
y - Komponente
z - Komponente
x = i ( y1 z2 - y2 z1 )
y = -j ( x1 z2 - x2 z1 )
z = k ( x1 y2 - x2 y1 )
23.3 Driften, Kippen
Driftwinkel und Kippwinkel durch Zeitveränderung:
Driftwinkel:
Kippwinkel:
sin ϕ =
sin κ =
sin γ sin β
2
2
2
1 - cos β sin β (1 - cos γ )
sin β cos β (1 - cos γ )
(1 - sin β) 2 (sin γ)
2
λ = Längengrad
∆λ = Differenz der Längengrade
βΜ = mittlerer Breitengrad
ϕ° = zulässige Abweichung
βM =
mittlerer Breitengrad:
Formelsammlung
Luftfahrzeugtechnik
βA + βB
2
Seite 100
λ = + λ von West nach Ost
λ = − λ von Ost nach West
Vorzeichenregel:
Driftwinkel durch Zeitveränderung und Ortsveränderung:
γ = t 15° + (+- ∆λ )
Zeit-und Ortswinkel:
Zeit- und Ortswinkel in die obige Gleichug Driftwinkel einsetzen.
Nachstellzeit:
t n = ϕ°
Nachstellzeitraum in min:
4
sin β
Kardanfehler (Neigungsfehler) :
Begriffsbestimmung:
κ = wahrer Kurs
κ’ = angezeigter Kurs
∆κ = Kardanfehler
γ = Querneigungswinkel
Fehleranzeige durch Querneigung:
tan ∆κ =
Fehleranzeige:
tan κ (1 - cos γ )
2
1 + tan κ cos γ
Wahrer Kurs bei Querneigung:
tan κ =
Formelsammlung
(
1 - cosγ
2 cos γ tan ∆κ
2
)
-
1
cos γ
Luftfahrzeugtechnik
+
(
1 - cosγ
2 cos γ tan ∆κ
)
Seite 101
23.4
Kompaß, Kompaßfeheler
Begriffsbestimmung :
T =
Totalintensität (der Erdfeldlinien)
ϑ =
Inklination (Ein- bzw. Austrittswinkel der Feldlinien zur Erdoberfläche)
Horizontalintensität (Horizontalkomponente)
Z = Vertikalintensität (Vertikalkomponente)
ZH =
Komponente von Z quer zur geneigten Kompaßnadel
ZV =
Komponente von Z senkrecht zur geneigten Kompaßnadel
FG =
Gewichtskraft
FF = Fliehkraft
a = Abstand Schwerpunkt-Drehachse
b = Abstand Angriffspunkt-Drehachse
Querneigungswinkel der Kompaßnadel
γ =
ϕ =
Kompaßabweichung
ω = Winkelgeschwindigkeit des Kurvenfluges
v = Bahngeschwindigkeit
H =
N
Η
KAP
Τ
N
Gewichte
S
Ζ
SP
FG
ϑ
b
a
Momentengleichgewicht:
a FG = b Z
Vertikalkomponente Z:
Z = T sin ϑ
Abstand a:
a =
Formelsammlung
Luftfahrzeugtechnik
b T sin ϑ
FG
Seite 102
Querneigungsfehler:
Durch eine Querneigung des Flugzeuges (im Kurvenflug) kommt die sonst
unwirksame Vertikalkomponente Z auf der Totalintensität T zur Wirkung und
übt auf die Kompaßnadel ein ablenkendes Drehmoment aus. Man setzt
voraus, daß die Drehachse der Kompaßnadel parallel zur Hochachse des
im Kurvenflug immer der Fall ist, da sich das Kompaßsystem nach dem Scheinlot einstellt.
Flugzeugs liegt, was
N
ϕ
90°
ΖH
NN
Ζ γ
SP
γ
S
ΖV
b
Querneigungskomponente ZH :
Z H = Z sin γ
mit:
Z = T sin ϑ
Querneigungskomponente ZH :
Z H = T sin ϑ sin γ
Drehmoment:
M = ZH b
Die Vertikalkomponente ZV hat keinen Einfluß auf die Magnetnadeln, da sie mit
Drehachsenrichtung des Magnetsystems übereinstimmt.
Formelsammlung
Luftfahrzeugtechnik
der
Seite 103
Fliehkraftfehler:
Die beim Fliegen einer Kurve auftretende Fliehkraft wirkt auch auf das Magnetsystem des Kompasses. Sie greift im Schwerpunkt (SP) der Nadel an und
ist stets, vom Kurvenkrümmungsmittelpunkt ausgehend, nach außen gerichtet.
Die Fliehkraft übt ein Drehmoment auf die Nadel aus.
Der Fliehkraftfehler tritt nur bei Kompassen auf, bei denen das Inklinationsmoment durch Verlagerung des Schwerpunktes kompensiert wurde.
N
ϕ
FF
90°
SP
S
N
γ
a
Fliehkraft F F :
F F = m ω 2 r cos γ
oder:
F F = m ω v cos γ
oder:
F F = FG sin γ
Neigungswinkel:
Drehmoment:
Formelsammlung
tan γ
=
v ω
g
M = FF a
Luftfahrzeugtechnik
Seite 104
Summenfehler:
Bei jedem Kurvenflug, der richtig geflogen wird, wirken Querneigungs- und
Fliehkraftfehler gleichzeitig. Die Summe dieser beiden Fehler nennt man
Summenfehler, oder allgemein Kompaßdrehfehler.
N
γ
FF
ZH
ϕ
FF
90°
SP
N
Η
ΖH
γ
S
b
a
Bei voller Kompensation des Inklinationsmoments durch Gewichte sind
folgende Momente gleich:
FF a = ZH b
Drehmoment:
Mit
Summenfehler:
Formelsammlung
Rechtskurve:
tan ϕ =
γ = +γ
und
Linkskurve:
γ= - γ
2 sin ϑ sin γ cos κ
2 sin ϑ sin γ sin κ
cos ϑ
Luftfahrzeugtechnik
Seite 105
Kurskorrektur:
Ist der Fehler ϕ bekannt, so kann der Beendungswinkel (für nördliche Kurse)
κ
ϕ
N
γ
bestimmt werden.
κ
b
a
Rechtskurve
κ
ϕ
κ
N
γ
b
Linkskurve
a=0
κ = κ + ϕ
Beendungswinkel:
Bei
Formelsammlung
Luftfahrzeugtechnik
ϕ Vorzeichen beachten !
Seite 106
Kurskorrektur mittels eines Nomogramms:
Querneigungswinkel γ = 7,5°
Inklination ϑ = 66,5°
360
330
300
16
10
30 32
22 25
270
240
0
5
10
16
35
-
5
22
300
060
34
20
R
0
+
20
30
34
34
30
30 25
35 32
22
+
20
090
270
30
34
-
240
120
150
35
22
32 30 25
210
180
060
16
10
5
0
L
0
20
090
5
b
10
16
120
150
180
κ = κ + ϕ
Beendungswinkel:
Achtung:
030
330
30
35
25 30 32
210
360
030
Für südliche Kurse ändern sich die Vorzeichen.
Sink- und Steigfehler:
Mit
Sink- und Steigfehler:
Formelsammlung
steigen:
α = +α
tan ϕ =
und sinken:
α= - α
sin ϑ sin α cos κ
sin ϑ sin α sin κ
cos ϑ
Luftfahrzeugtechnik
Seite 107
23.5
Flugzeugmagnetismus bzw. Deviation
Jedes Flugzeug bsitzt einen Eigenmagnetismus und das dazugehörige magnetische Feld, das die
Kompaßanzeige stört, wenn keine geeigneten
Gegenmaßnahmen ergriffen werden.
Begriffsbestimmung:
P
Q
R
δ
δP
= Längsfeld
= Querfeld
= Hochfeld
= Ablenkung
= Längsfeldfehler
wirkt parallel zur Flugzeuglängsachse
wirkt parallel zur Flugzeugquerachse
wirkt parallel zur Flugzeughochachse
(Deviation)
δQ = Querfeldfehler
δR = Hochfeldfehler (bei Quer- und Längsneigung)
Gemessene Fehler bei Ausrichtung des Lfz :
δN =
δS =
δO =
δW =
A =
B =
C =
D =
nach Norden
nach Süden
nach Osten
nach Westen
Einbau und Aufstellungsfehler
Beiwert der magnetischen Längswirkung
Beiwert der magnetischen Querwirkung
Beiwert der magnetischen Hochwirkung (bei Quer- und Längsneigung)
Komponenten der Feldlinien
Formelsammlung
Luftfahrzeugtechnik
Seite 108
Längsfeld P
δP
Querfeld Q
N
δQ
κ
H
H
W
H
κ
N
κ
H
Q
O W
O
P
P sin κ = H sin δ P
Q cos κ = H sin δQ
S
S
Kräfte im Längsfeld:
P sin κ = H sin δ P
Kräfte im Querfeld:
Q cos κ = H sin δ Q
Winkelumrechnung von ° in rad:
δ
(rad)
1
= 57,3 δ°
Da die Ablenkung selten größer als 5° ist, kann der Sinus vom Winkel δ gleich
dem Winkel δ gesetzt werden:
Gleichsetzung:
sin δ = δ (rad)
Ist der Winkel δ klein, so kann auch H’ gleich H gesetzt werden. Dadurch ändert
Kräftegleichgewicht.
sich das
1
Kräfte im Längsfeld:
Formelsammlung
P sin κ = H 57,3 δ°P
Luftfahrzeugtechnik
Seite 109
1
Q sin κ = H 57,3 δ°Q
Kräfte im Längsfeld:
Umstellung nach δ°Q ergibt:
Längsfeldfehler:
P
sin κ
δ°P = 57,3
H
Querfeldfehler:
δ°Q = 57,3
Q
cos κ
H
Beiwerte:
Beiwert C:
Q
C = 57,3 H
Beiwert B:
P
B = 57,3 H
Einbau-, Längsfeld- und Querfeldfehler zusammen:
Gesamtfehler ohne Hochfeld:
δ° = A + B sin κ + C cos κ
Bestimmung der Beiwerte:
Einbau- oder Aufstellfehler:
Beiwert B:
Beiwert C:
Formelsammlung
A =
( δ N) + ( δ S) + ( δ W) + ( δ O)
4
B =
( δ W) - ( δ O)
2
C =
( δ N) - ( δ S)
2
Luftfahrzeugtechnik
Seite 110
Gesamte Deviation:
δ° = A + (B + D sin α ) sin κ + (C + D sin γ ) cos κ
Kompensierbericht
Flugzeug-Kennzeichen: D - EABC
Kompaß-Muster:
Magnet
Flugzeuglage:
Rollage
Kompensiert am:
4.05.99
15°
10°
Deviation
5°
0°
+
5°
10°
mw
Kurs
15°
000°
030°
060°
060°
090°
090°
120°
120°
150°
150°
180°
180°
210°
210°
240°
240°
270°
270°
300°
300°
330°
330°
360°
δ (N)+ δ (S)+ δ (O)+ δ (W)
A=
A=
Formelsammlung
Kompaß
Kurs
000°
030°
A=
Deviation
4
δ ( )+δ( )+δ( )+δ( )
4
B=
B=
δ (O) − δ (W)
2
δ( ) − δ( )
2
B=
Luftfahrzeugtechnik
C=
δ (N) − δ (S)
C=
2
δ( ) − δ( )
2
C=
Seite 111
23.6
Elektromagnetische Wellen
Begriffsbestimmung :
C = Ausbreitungsgeschwindigkeit
λ
f
ε
µ
ε
µ
0
0
r
0
= Wellenlänge
= Frequenz
= elektrische Feldkonstante (ε0 = 8,85 pF/m)
= magnetische Feldkonstante (µ0 = 1,26 µH/m)
= Permittivitätszahl
= Permeabilitätszahl
Ausbreitungsgeschwindigkeit:
c = f λ
Ausbreitungsgeschwindigkeit:
c =
1
Feldstärke:
E =
380 h
λ r
oder:
E = E max sin ϑ
Formelsammlung
Luftfahrzeugtechnik
√ ε r ε0 µ r µ 0
l sin
ϑ
Seite 112
23.7
Entfernungsmessung DME
Begriffsbestimmung :
R =
H =
D =
Schrägentfernung
Höhe
Bodenentfernung
T =
Laufzeit (µs)
t
=
tt =
Rücklaufzeit (µs)
Verzögerunszeit µs ( t t = 50 µs )
Laufzeit:
T = 2 t + 50 t
Entfernung:
R =
c
( T - 50 )
2
Entfernung:
D =
√
Meßfehler:
F = R-
Formelsammlung
Luftfahrzeugtechnik
2
R - H
√
2
2
2
R - H
Seite 113
23.8 Frequenzbereiche
Formelsammlung
Luftfahrzeugtechnik
Seite 114