Übungen zur 7. Klasse

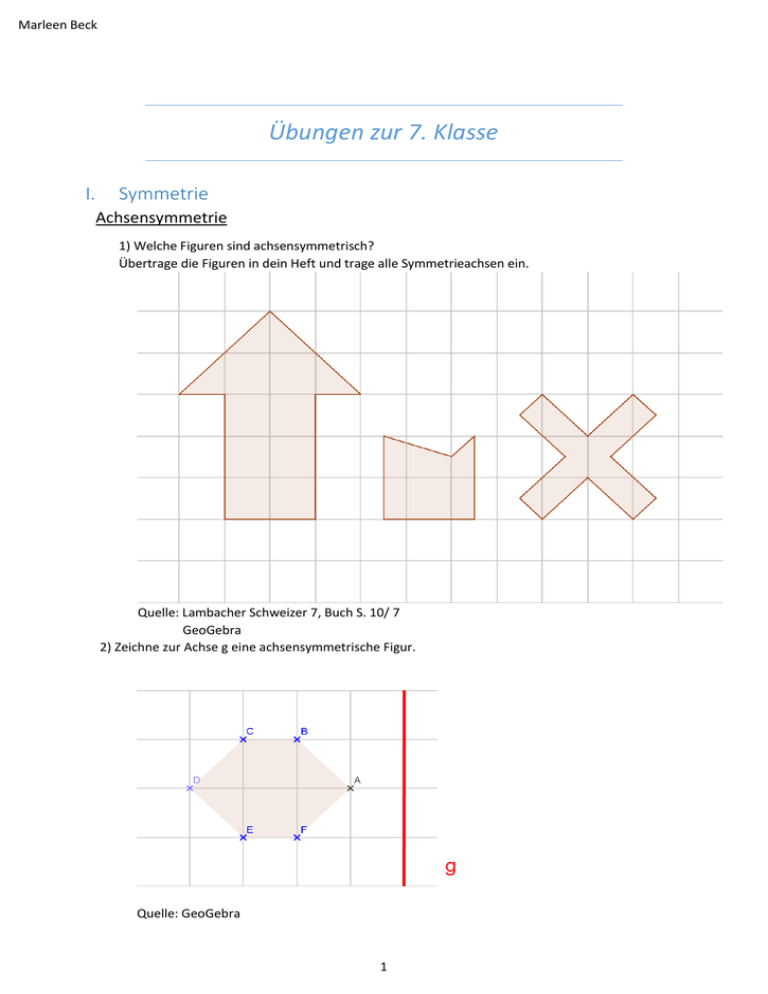
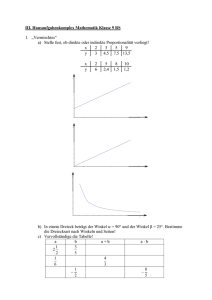
Marleen Beck
Übungen zur 7. Klasse
I.
Symmetrie
Achsensymmetrie
1) Welche Figuren sind achsensymmetrisch?
Übertrage die Figuren in dein Heft und trage alle Symmetrieachsen ein.
Quelle: Lambacher Schweizer 7, Buch S. 10/ 7
GeoGebra
2) Zeichne zur Achse g eine achsensymmetrische Figur.
Quelle: GeoGebra
1
Marleen Beck
Konstruieren von Spiegelpunkten und Achse
3) Konstruiere zu den beiden gegebenen Punkten (1|3), P` (3|1) die Symmetrieachse a.
Quelle: Lambacher Schweizer, Buch S. 14/2
Mittelsenkrechte, Winkelhalbierende und Lote
4) Zeichne ein Dreieck ABC mit A (0|1), B (4|1) und C(3|5). Konstruiere
a) die Mittelsenkrechte m von [AC]
b) das Lot l zur Strecke [AB] durch C
c) die Symmetrieachse von ∡ABC
Quelle: Lambacher Schweizer, S. 18/ 6
Punktsymmetrie
5) Übertrage die Figur sowie das Symmetriezentrum Z in dein Heft. Konstruiere das
Spiegelbild des Dreiecks bei der Punktspiegelung am Zentrum Z.
2
Marleen Beck
Symmetrische Vierecke
6)
a) Welche Eigenschaften hat ein (allgemeines) Parallelogramm, die ein (allgemeines)
gleichschenkliges Trapez nicht hat? Welche Eigenschaften haben sie gemeinsam?
b) Welche besonderen Vierecke besitzen gleich lange Diagonalen?
c) Welche besonderen Vierecke besitzen Diagonalen, die sich halbieren?
Quelle: http://www.strobl-f.de/ueb71.pdf
II. Winkelbetrachtung
Scheitelwinkel und Nebenwinkel
1) Bestimme alle Winkel, wenn =40° und = 80°.
Quelle: Lambacher Schweizer 7, Buch S.39/ 3
GeoGebra
Stufenwinkel und Wechselwinkel
2) In der nebenstehenden Figur sind 𝑔2 ‖𝑔3 .
a) Nenne alle Stufenwinkel
b) Nenne alle Wechselwinkel
Berechne die übrigen Winkel, wenn  = 50°
http://www.realmath.de/Neues/Klasse7/parallelen/parallueb.html
3
Marleen Beck
Winkelsumme im Dreieck
3) Berechne den fehlenden Winkel  , wenn =20° und =75° groß ist.
Quelle: Lambacher Schweizer 7, Buch S. 44/ 3
GeoGebra
Winkelsumme im Vieleck
4) Ergänze die fehlenden Winkel oder verbessere falls nötig.
Ecken
5
4
3
III.





45°
106°
223°
54°
107°
137°
88°
23°
100°
24°
92°
-
Winkelsumme
Terme
1) Berechne die Werte der Terme.
a) T1 (x, y)=  5  y  (6x)
für a) x = 3 und y = 2
b) x= 2 und y = 4
5
b) T2 (a, b) = (a3)  (b3)  6
2
für a) a = 0,5 und b = 3
b) a= -3 und b = 3
2) Aus einem Quadrat mit der Seitenlänge 6 cm wird ein Rechteck gemacht, indem eine Seite
x cm verkürzt wird und die angrenzende Seite um x cm verlängert wird.
Stelle einen Term zur Berechnung der Rechteckfläche auf.
1
3) Gegeben ist der Term T(x) = 2x + 2
a) Fertige eine Wertetabelle für die Werte von -4 bis 2 an.
b) Veranschauliche die durch den Term gegebenen Zuordnung durch einen Graphen.
4
um
Marleen Beck
IV. Termumformungen
1) Berechne durch Zusammenfassen der positiven und negativen Glieder
a) x + 3x + 7,5x
b) 15x−7,25x −5x
c) −23y + 6y − 11y
1
3
d) 14y − 18,25y − 3 y + 39y
2) Vereinfache so weit wie möglich. Gib dabei jeweils an, welches Rechengesetz du verwendest.
a) 7x + 4y −12x + 8y
b) 289a −15²a − 727a + 34b −694b
𝑥
c) -5y - 2 + 83x – 12,7y
5
6
d) 0,75a- 6 + 5 – 0.25a
3) Vereinfache
a) x²⋅x⋅x²
c) 4d⋅3d²⋅ (-) 0,25−
b) a3  a2 (2a)2
d) -x3 (-x2)  (-x)2
4) Fasse soweit wie möglich
a) 4p2 23(-q)-3(p2)  (-q)
b) 3b³ + (-3b)3
c) 4,5x²y ⋅(-6x2+2x3y)
5) Übertrage ins Heft und setze Klammern so, dass das Gleichheitszeichen zu Recht steht.
a) 2b – 5b -12a = 2b -5b + 12a
b) -4c + 2d – 3e = -4c -2d – 3e
c) 2f – g + f – 3g = 2f – g – f + 3g
6) Fasse so weit wie möglich zusammen.
a) -3a – [(a -2b) + ( -7a2+ 5b)]
b) 2,6x – [ - 6,3y – (7,2y + 4,8x) + 0,2x]
7) Schreibe als Produkt
a)
b)
c)
d)
6a + 6b
12v2 – 32uv
8t3 -12t2
48a2b3- 36 a3b2
8) Multipliziere die Summen aus und vereinfache, falls möglich.
a) (3x+5y +1)  (2x+4)
b) (3+ a + 2b)  (a+4)
c) (2+ a + 2b)  (2a +1 + b)
5
Marleen Beck
9) Zeige, dass die Terme (1) (2k-4r)2 und (2) (2k-4r)  (2k + 4r) nicht äquivalent sind.
6