Grundwissen 7. Klasse I. Symmetrie

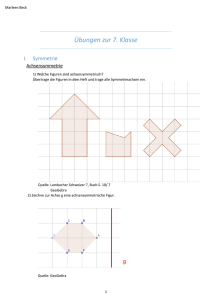
Marleen Beck
Grundwissen 7. Klasse
I.
Symmetrie
1. Achsensymmetrie
Die Punkte P und P‘ sind achsensymmetrisch bzgl. der Symmetrieachse a.
Sind Figuren zueinander achsensymmetrisch, so kannst du folgende Eigenschaften
erkennen:
 Die Strecke zwischen Punkt und Bildpunkt wird von der Symmetrieachse
senkrecht halbiert
 Strecke und Bildstrecke sind gleich lang
 Zueinander symmetrische Kreise besitzen den gleichen Radius
 Winkel und dazu symmetrischer Winkel sind gleich groß,
ihre Drehrichtung ist entgegengesetzt

Zueinander symmetrische Geraden sind parallel oder sie schneiden sich auf
der Achse, z. B. 𝑔‖𝑔′, h und h‘ schneiden sich im Punkt F = F‘.

Achsenpunkte und nur diese sind von Punkt und Bildpunkt gleich weit
′
̅̅̅̅̅̅
entfernt ̅̅̅̅̅
𝐴1 𝑃 = 𝐴
1𝑃
Punkte auf der Achse nennt man auch Fixpunkte

2. Konstruieren von Spiegelpunkten und Achse
a) Konstruieren von Spiegelpunkte
̅̅̅̅)
Wähle zwei beliebige Punkte Q und R auf der Achse a. Die Kreise k1 (R; r=𝑅𝑃
̅̅̅̅
und k2 (Q; r= 𝑄𝑃 ) schneiden sich in P und P’.
b) Konstruieren der Symmetrieachse
Zeichne zwei Kreise durch P und P’ mit beliebigem (genügend großem),
aber gleich großem Radius. Durch die Schnittpunkte S1 und S2 der Kreise
ist die Achse a eindeutig festgelegt.
1
Marleen Beck
3. Mittelsenkrechte, Winkelhalbierende und Lote
Man kann diese mit Hilfe der Achsenspiegelung konstruieren
 Mittelsenkrechte zu [AB]
Die Kreise um A und B mit gleichem (genügend großem) Radius
schneiden sich in zwei Punkten, die die Mittelsenkrechte m eindeutig
festlegen.
 Winkelhalbierende 𝜔𝛼
Der Kreis um S mit beliebigem Radius schneidet die Schenkel in
den Punkten G und G’.
Die Symmetrieachse, die G auf G’ abbildet und S fest lässt (S  a)
ist die Winkelhalbierend
 Lot errichten
Man erhält das Lot l zu einer Geraden g durch einen Punkt P, indem
man um P einen Kreis mit einem beliebigen Radius zeichnet, der die
Gerade g in zwei Punkten A und B schneidet. Anschließend konstruiert
man die Symmetrieachse zu diesen Punkten.
 Lot fällen
Ein Kreisbogen um den Punkt P, der nicht auf der
Geraden g liegt, schneidet g in den Punkten A und B. Zwei
weitere Kreisbögen mit gleichem Radius um die
Punkte A und B schneiden sich in dem Punkt P‘.
Man nennt die Länge der Lotstrecke von P zur Gerade g
Abstand des Punktes P von der Geraden g.
2
Marleen Beck
4. Punktsymmetrie
Die Punkte P und P‘ sind punktsymmetrisch mit Symmetriezentrum (oder
Spiegelzentrum) Z, wenn sie durch eine Drehung von 180° um Z aufeinander
zur Deckung kommen
Es gilt:
̅̅̅̅̅
a) [PP‘] wird durch Z halbiert. ̅̅̅̅
𝑃𝑍 =𝑃𝑍′
b) Zueinander punktsymmetrische Geraden sind parallel (g║g‘), Strecken sind gleich lang und parallel
̅̅̅̅̅ ; [CA]║[C’A‘]), Winkel sind gleich groß und haben den gleichen Drehsinn (α = α‘).
̅̅̅̅ =𝐶′𝐴′
(𝐶𝐴
.
Konstruktion des Zentrums
Man verbindet zueinander symmetrische Punkte der Figur. Das
Symmetriezentrum Z ergibt sich als Schnittpunkt zweier
solcher Verbindungsgeraden.
Konstruktion des Zentrums bei nur zwei gegebenen Punkten P
und P‘
Man verbindet die zwei Punkte durch die Gerade g. Dazu konstruiert
man die Symmetrieachse zu den Punkten. Der Punkt der
Symmetrieachse, der die Gerade schneidet ist das Symmetriezentrum Z.
Aus jeder Figur lässt sich durch eine Punktspiegelung an einem Zentrum
Z eine punktsymmetrische Figur erzeugen. Dazu konstruiert man zu
jedem Punkt seinem Spiegelpunkt.
3
Marleen Beck
Konstruktion der Spiegelpunkte
Um einen Punkt A am Zentrum zu spiegeln, zeichnet man die
Halbgerade [AZ und einen Kreis um Z mit Radius r=𝐴𝑍. Dieser
Kreis schneidet [AZ im Punkt A`
Konstruktion einer Tangente
Gegeben sind ein Kreis mit dem Mittelpunkt M und ein Kreispunkt
B. Die Tangente des Kreises durch den Punkt B erhält man, indem
man im Punkt B das Lot zur Geraden MB konstruiert. Der
gemeinsame Punkt von Kreis und Tangente heißt Berührpunkt.
Eine Gerade kann mit einem Kreis zwei Punkte, einen einzigen Punkt oder keinen Punkt gemeinsam
besitzen.
Sekante
Tangente
Passante
4
Marleen Beck
5. Symmetrische Vierecke
a) Punktsymmetrische Vierecke
Parallelogramm
Ein Parallelogramm ist ein Viereck bei dem die
gegenüberliegenden Seiten parallel sind.
Es gilt:
 Seiten, die gegenüberliegen sind gleich lang
 Winkel, die gegenüberliegen sind gleich groß
 Die Diagonalen halbieren sich
b) Achsensymmetrische Vierecke mit einer Achse
Achsensymmetrisches Trapez
Ein achsensymmetrisches Trapez ist ein Viereck bei dem die
Mittelsenkrechte von zwei gegenüberliegenden Seiten die
Symmetrieachse ist.
Es gilt, dass Schenkel und Diagonalen gleich lang sind.
Drachenviereck
Ein Drachenviereck/Drache ist ein Viereck mit einer Diagonale als
Symmetrieachse
Hier gilt, dass die Diagonalen senkrecht zueinander sind.
c) Achsensymmetrische Vierecke mit zwei Achsen
Rechteck
Ein Rechteck ist ein Viereck bei dem alle vier Winkel 90°
betragen.
Es gilt, dass die Mittelsenkrechte die Symmetrieachsen sind
und diese stehen aufeinander senkreckt und halbieren sich
gegenseitig. Ein Rechteck ist auch eine punktsymmetrische
Figur.
Raute
Eine Raute ist ein Viereck bei dem alle vier Seiten gleich lang sind.
Es gilt, dass die Diagonalen die Symmetrieachsen sind und sie aufeinander
senkreckt stehen und sich gegenseitig halbieren. Die Raute ist auch eine
punktsymmetrische Figur.
5
Marleen Beck
d) Achsensymmetrische Vierecke mit vier Achsen
Das Quadrat
Ein Rechteck mit vier gleich langen Seiten heißt Quadrat
Es gilt:
 Es ist auch ein Rechteck und eine Raute und somit ist
es auch eine punktsymmetrische Figur
 Es besitzt vier gleich lange Seiten mit vier 90°- Winkel
 Die Mittelsenkrechten und Diagonalen sind die
Symmetrieachsen
Übersicht über symmetrische Vierecke
6
Marleen Beck
II.
Winkelbetrachtung
1. Scheitelwinkel und Nebenwinkel
Winkel an einer Geradenkreuzung:
Je zwei gegenüberliegende Winkel werden als Scheitelwinkel
bezeichnet. Welche gleich groß sind.
Je zwei nebeneinander Winkel werden als Nebenwinkel bezeichnet,
sie ergänzen sich zu 180°.
In der Figur sind 𝛼 𝑢𝑛𝑑 𝛾 Scheitelwinkel, ebenso 𝛽 𝑢𝑛𝑑 𝛿.
𝛼 𝑢𝑛𝑑 𝛽 sind Nebenwinkel, ebenso 𝛾 𝑢𝑛𝑑 𝛿, 𝑢𝑛𝑑 𝛾 sowie
und 𝛿 𝑢𝑛𝑑 𝛼.
2. Stufenwinkel und Wechselwinkel
Werden zwei Geraden g und h von einer anderen Geraden geschnitten, so nennt man die jeweils
gleich gefärbten Winkel an der Geraden Stufenwinkel (F-Winkel) bzw. Wechselwinkel (Z-Winkel).
Wir betrachten nun Stufen- und Wechselwinkel an zwei parallelen Geraden g und h.
Die Stufenwinkel sind hier gleich groß.
Die Wechselwinkel sind hier gleich groß.
7
Marleen Beck
3. Winkelsumme im Dreieck
Winkelsumme im Dreieck
Die Summe der Innenwinkel im Dreieck betragt 180°:
α + β + γ = 180°
Beispiel: α = 45°, γ = 72°, dann ist
β = 180° − α − γ = = 180° − (45° + 72°) = 63°
Bezeichnung für Dreiecke:
Spitzwinkliges Dreieck
Jeder Winkel ist spitz.
rechtwinkliges Dreieck
Ein Winkel ist ein rechter.
stumpfwinkliges Dreieck
Ein Winkel ist stumpf.
4. Winkelsumme im Vieleck
Satz von der Winkelsumme in Vielecken:
Die Winkelsumme in einem n-Eck beträgt: (n-2)  180°.
Insbesondere beträgt die Winkelsumme im Viereck 360°.
III.
Terme
1. Terme mit Variablen
In Termen können auch Variablen auftreten, z.B.
a+b
4x+2
y2 – 7  y
Die Variablen sind Stellvertreter für Zahlen oder für Größen sind die Variablen.
8
Marleen Beck
2. Berechnen von Termwerten
Erst wenn alle Variablen durch Zahlen bzw. Größen ersetzt sind, kann man den Wert eines Terms
berechnen.
Wenn die gleiche Variable mehrmals in einem Term auftritt wie z. B. y (y + 3), so muss man für sie
jeweils die gleiche Zahl bzw. Größe einsetzen.
Treten in einem Term wie z. B. 3x2 + 4y – 2 verschiedene Variablen auf, so können für diese
unterschiedliche, aber auch die gleichen Zahlen bzw. Größen eingesetzt werden.
Für die Termberechnung gelten die bekannten Regeln:
1. Es wird zuerst berechnet, was in der Klammer steht.
2. Vor den Punktrechnungen Multiplizieren und Dividieren kommt Potenzieren.
3. Die Punkrechnungen kommen vor den Strichrechnungen Addieren und Subtrahieren.
3. Aufstellen und Interpretieren von Termen
Schritte beim Aufstellen des Terms
1. Untersuchung des Sachverhaltes an konkreten Beispielen und Suche nach einer
Gesetzmäßigkeit.
2. Einführung von Variablen und Beschreibung der gefundenen Gesetzmäßigkeit durch einen
Term
Beispiel: (Quelle: Lambacher Schweizer 7, S. 59 Bsp.2)
a) Stelle einen Term zur Berechnung des Oberflächeninhaltes des Prismas auf,
das man nach dem Netz bauen kann.
b) a = 6,5 cm, b = 12 cm
Berechne den Oberflächeninhalt.
Lösung:
a) Oberflächeninhalt: O (a; b) = 6a2 + 8ab
b) O (6,5cm; 12cm)
= 6 (6,5cm)2 + 8  6,5cm  12cm
= 877,5cm2
Term interpretieren
Wenn du einen Term interpretieren oder Aussagen über ihn machen sollst,
musst du erst überlegen, welche Bedeutung die Variablen haben.
Zum Beispiel beschreibt a  b den Flächeninhalt eines Rechtecks,
wenn a und b die Seitenlängen sind.
9
Marleen Beck
4. Zuordnung: Variablenwert - Termwert
Es wird durch Terme, wie z.B. T(x) = x2 – 1 jedem Variablenwert x ein eindeutig bestimmter Termwert
zugeordnet. Verschiedene Variablenwerten können gleiche Termwerte zugeordnet werden, z. B. gilt:
T (2) = T (-2) = 3
Es können aber umgekehrt niemals einem Variablenwert durch einen Term zwei verschiedene
Termwerte zugeordnet werden. Die durch den Term beschriebene Zuordnung ist eindeutig.
Die Zuordnung lässt sich durch eine Wertetabelle beschreiben
x
T(x)
-2
3
-1,4
0,96
-1
0
0
-1
1
0
1,5
1,25
Jedes Zahlenpaar aus Variablenwert und zugeordnetem Termwert
bestimmt einen Punkt im Koordinatensystem.
Die Menge dieser Punkte nennt man Graph der Zuordnung.
IV.
Termumformungen
Für alle rationale Zahlen a, b, c gilt:
Kommunikativgesetz (KG) (Vertauschungsgesetz) der Addition und der Multiplikation:
ab=ba
a+b=b+a
In einer Summe oder in einem Produkt darf man die Summanden bzw. Faktoren vertauschen, ohne
dass sich der Wert der Summe bzw. des Produkts ändert.
2
5
2
5
(-3,5)  7 = 7  (-3,5)
Beispiele: 14,7 + 5 = 5 + 14,7
Assoziativgesetz (AG) (Verbindungsgesetz) der Addition und der Multiplikation:
a + (b + c) = (a + b) + c
a  (b  c) = (a  b)  c
In einer Summe oder einem Produkt mit mehreren Gliedern darf man beliebig Klammern setzen oder
weglassen, ohne dass sich der Wert der Summe bzw. des Produkts ändert.
Beispiele: (11,4 + 83,5) + 6 = 11,4 + (83,5 + 6)
[3  (41,8  11,9]) = [(3  41,8)  11,9]
10
Marleen Beck
Distributivgesetz (DG) (Verteilungsgesetz) für die Multiplikation einer Summe oder Differenz
mit einer Zahl: (a + b)  c = a  c + b  c
(a - b)  c = a  c – b  c
Du kannst jeden Summanden bzw. den Subtrahenden mit der Zahl multiplizieren und
anschließend die Produkte addieren bzw. subtrahieren, ohne dass sich der Wert des Terms
ändert.
Beispiele: (14,2 + 8,03)  5 = 14,2  5+ 8,03  5
(31 – 0,5)  4,1 = 31  4,1- 0,5  4,1
Umgekehrt kannst du aus einer Summe oder einer Differenz von Produkten, die einen
gemeinsamen Faktoren enthalten, diesen Faktor „ausklammern“.
Beispiele: 12  4 + 0,5  4 – 87  4 = (12 + 0,5 - 87)  4 = (-74,5)  4 = -298
10ab-35ac + 5a= 5a  (2b-5c+1)
1. Gleichwertige Terme
„Zwei Terme, die bei jeder möglichen Ersetzung der Variablen durch Zahlen jeweils den gleichem
Termwert ergeben, nennt man gleichwertig oder äquivalent. Man darf zwischen ihnen ein
Gleichheitszeichen setzen. Durch Anwendung der Rechengesetzte kann man einen Term in einen
äquivalenten Term umformen.“ (Lambacher Schweizer 7, S. 75)
1
2
𝑇1 (x) = x ( 𝑟y+ x) und 𝑇2 (x) = 0,5xy + 𝑥 2 sind äquivalent.
T1 (a) = 2𝑎2 -4 und 𝑇2 (a) = 2a – 4 sind nicht äquivalent.
2. Umformungen in Produkten
Potenzen mit gleicher Basis kann man multiplizieren, indem man die gemeinsame Basis mit der
Summe der Exponenten potenziert.
Beispiel: a5 a7  a3 = a5+7+3= a14


Potenzen potenziert man, indem man die Basis mit dem Produkt der Exponenten potenziert,
Beispiel: (a2)3  a23= a6
Enthalten Termen bereits Potenzen, so kann es nützlich sein, die Potenzen zunächst als
Produkte zu schreiben und anschließend Termumformungen durchzuführen.
Beispiel: a5 : a3 =
𝑎5
𝑎3
=
𝑎 ∙ 𝑎 ∙ 𝑎 ∙ 𝑎 ∙𝑎
𝑎 ∙ 𝑎 ∙𝑎
=
𝑎 ∙ 𝑎 ∙ 1 ∙ 1 ∙1
1 ∙ 1 ∙1
= a2
3. Umformungen in Summen
„Zwei Produkte, in denen genau die gleichen Variablen in jeweils gleicher Potenz auftreten, nennt
man gleichartig. Sie werden addiert (subtrahiert), indem man die Zahlenfaktoren vor den Variablen
addiert (subtrahiert) und die gemeinsamen Variablen beibehält.“ (Lambacher Schweizer 7, S.82)

Mithilfe der Rechenregel für Potenzen lassen sich Produkte vereinfachen. Nutze dabei das
Kommunikativgesetz der Multiplikation und fasse sowohl Zahlen als auch Variable zusammen.
1
8
1
8
1
8
Beispiel: (4ac)2  c2f2 = 4ac  4ac  c2f2 = 4  4   a  a  c  c  c2  f2 = 2  a2  c4  f2 = 2a2c4f2

In Summen lassen sich nur gleichartige Terme zusammenfassen, d.h. solche, die sich nur durch
einen Zahlenfaktor unterscheiden. Sie werden addiert oder subtrahiert, indem man die
Zahlenfaktoren addiert oder subtrahiert, das Variablenprodukt bleibt dabei unverändert.
11
Marleen Beck
Beispiel: 2u2z + 4uz2 – 3,5u2z = -1,5 u2z + 4uz2 (dieser Term kann nicht weiter zusammengefasst,
sondern nur als Produkt geschrieben werden)
Klammerregel
Die Klammern können weggelassen
werden, falls ein Plus vor der
Klammer steht.
Ist ein Minus vor der
Klammer, so ändert man die
Vorzeichen in der Klammer und lässt
die Klammern und das
Minuszeichen vor der Klammer weg
a + (b+ c) = a + b +c
a + (b- c) = a + b - c
3k + (5+2k) = 3k + 5 + 2k =5k + 5
7r+(𝑠 2 -3,5) = 7r + s2 – 3,5
a - (b +c) = a-b-c
a - (b-c) = a- b +c
𝑥 2 -(2𝑥 2 +𝑦 2 ) = 𝑥 2 − 2𝑥 2 − 𝑦 2 = -𝑥 2 -𝑦 2
-2u - (u𝑣 2 − 2u) = -2u -u𝑣 2 +2u = -uv2
4. Anwendungen des Distributivgesetzes
Mit Hilfe des Distributivgesetzes können Produkte in Summen umgeformt werden. (Siehe DG)
Beispiel: 2x (-4+6u) = 2x  (-4) + 2x  6u = -8x +12ux
„Eine Summe wird mit einem Term multipliziert, indem man jeden Summanden mit dem Term
multipliziert und die dabei entstehenden Produkte addiert.“ (Lambacher Schweizer 7, S. 86)


Man spricht vom Ausmultiplizieren, wenn Produkte mit Hilfe des Distributivgesetzes in Summen
umgeformt werden
Beispiel: -4 (-s -5f) = -4 (-s) – (-4)  5f = 4s + 20f
Man spricht vom Ausklammer oder Faktorisieren, wenn Summen durch die Anwendung des
Distributivgesetzes in Produkte umgeformt werden
Beispiel: 5x + 5y = 5  (x + y)
5. Multiplizieren von Summen
„Zwei Summen werden multipliziert, indem man jeden Summanden der ersten Summe mit jedem
Summanden der zweiten Summe multipliziert und die dabei entstehenden Produkte addiert:
(a + b)  ( x + y) = a  x + a  y + b  x + b  y = ax + ay + bx + by
(Lambacher Schweizer 7, S. 90)
Häufig spricht man vom Ausmultiplizieren oder Auflösen der Klammern.
 Steht ein Minuszeichen vor der Klammer, so kann der Term ohne Klammer geschrieben werden,
wenn alle Vorzeichen in der Klammer abgeändert werden. Umgekehrt kannst du auch (-1)
ausklammern.
Beispiele: 2 – (3a -2c + 0,5) = 2- 3a +2c – 0,5 = 1,5 -3a + 2c
3a- 2b+ 0,4 = -(-3a +2b -0,4)
Quellen:
Prof. August Schmid& Prof. Dr. Ingo Weidig, Lambacher Schweizer 7,2011, Klett Verlag
Bayern
GeoGebra für alle Bilder (selbstgemacht)
12