Formelsammlung Physik II Schrewe

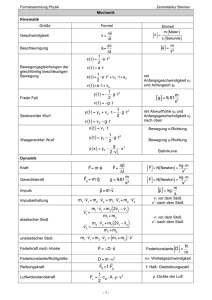
Hochschule Hannover
Fakultät II - Maschinenbau und Bioverfahrenstechnik
Vorlesung: Physik I + II
Formelsammlung
KINEMATIK
Translation

Verschiebung:
s

 ds
v
Geschwindigkeit:
dt


 dv d 2 s
Beschleunigung:
a

dt dt 2
Drehwinkel:
Winkelbeschleunigung:

d

dt


 d d 2

 2
dt
dt

Gleichförmige
Winkelgeschwindigkeit
 


   t
  const.
 0
Gleichförmige Beschleunigung
 

 1
v  a t
a  const.
s  a t2
2
Gleichförmige Winkelbeschleunigung
 1
 

   t2    t
  const.
2
1
Umdrehungszeit:
T
n
2 r
v
 2 r n
Bahngeschwindigkeit:
T
dN
dt
2

 2  n
Τ
n
Winkelgeschwindigkeit:

Winkelgeschwindigkeit:
Gleichförmige Geschwindigkeit
 

s  v t
v  const.
a0
Drehzahl:
Rotation

v2
 v    2  r
r
Bahngröße = Radius · Winkelgröße:
s  r 
v  r 
a  r 


Zerlegung einer beliebigen Beschleunigung in die Tangential- ( T ) - und die Normalkomponente ( N )


dv
dv

aT  T
aN  N
a  aT  T  a N  N
dt
dt
vy
v
v
aT  x  a x   a y  z  a z
a N  a 2  aT2
v
v
v
Zentripetalbeschleunigung:
ar 
DYNAMIK
Translation
Masse:
Kraft:
Impuls:
Arbeit:
Leistung:
Bewegungsenergie:
m


 dp
F  ma 
dt


p  mv
 
dW  F  ds
 
W   F  ds

dW  ds  
F
Fv
dt
dt

1
Etrans   m  v 2
2
P
Rotation
Trägheitsmoment:
Drehmoment:
Drehimpuls:
Arbeit:
Leistung:
Bewegungsenergie:
J   mi  ri 2   r 2  dm
i

  
 dL
M  r  F  J  
dt
  

L  r  p  J 
 
dW  M  d
 
W   M  d
 d
 
dW
P
M
M
dt
dt
2
1
E rot   J  
2
Prof. Dr. U. J. Schrewe, Physik I + II: Formelsammlung - 2012
Seite 1
Hochschule Hannover
Fakultät II - Maschinenbau und Bioverfahrenstechnik
Vorlesung: Physik I + II
Formelsammlung
Feder- Drehfederkräfte, elastische Verformungsarbeit
Rotation
Translation
Federkonstante:
D
Winkelrichtgröße:
D*




Federkraft:
F  D  s
Drehfedermoment:
M  D* 
1
1
Verformungsarbeit:
Wel  D  s 2
Verformungsarbeit:
Wel  D *   2
2
2
Reibungskräfte, Reibungsarbeit
H
R
Haftreibungszahl:
Gleitreibungszahl:
G
Rollreibungszahl:
Haftreibungskraft:
FH ,max   H  FN
FG   G  FN
FR   R  FN
Gleitreibungskraft:
Rollreibungskraft:
Gleitreibungsarbeit: WG  FG  s   G  FN  s
Rollreibungsarbeit: WR  FR  s   R  FN  s
Gravitationskräfte, potentielle Energie im Gravitationsfeld
Gravitationskonstante:
G = 6,672 59(85) 10-11 N m2 kg-2

M m
M m
Gravitationskraft:
potentielle Energie: E (r )  G 
F G 2
r
r
-2
Masse der Erde:
ME
Erdradius:
RE
Erdbeschleunigung: g = 9,81 m s

M 
Gewichtskraft:
potentielle Energie: E (h)  m  g  h
Fg  m   G  2E   m  g
RE 

Erhaltungssätze

F
Ohne äußere Kräfte:
0
i
i
Ohne äußere Drehmomente:

p
i

M
gilt Impulserhaltung:
i
0
gilt Drehimpulserhaltung:
i
i
0
i
0

L
i
Bei konservativen Kräften gilt (mechanische) Energieerhaltung:
kin
kin
E ges  E pot  E trans
 E rot
Bei nicht-konservativen Kräften (z.B. Reibung) gilt keine (mechanische) Energieerhaltung:
(ein Teil der mechanischen Energie wird z. B. in Wärme oder Verformungsenergie, Q, umgewandelt):
kin
kin
E ges  E pot  Etrans
 E rot
Q

Wirkungsgrad:
E ges  Q
E ges
Wnutz
E ges

Gleiten, Rotieren, Rollen
Gleiten:
 
 

v (r )  v (r )  v S
Geschwindigkeit des Schwerpunktes:

vS
Rotieren:
 
 
v (  r )  v ( r )
Geschwindigkeit des Schwerpunktes:

vS  0
Rollen:

 
vS  r  

v Kontakt  0
Geschwindigkeit des Schwerpunktes:
Verschiebung des Schwerpunktes:
Beschleunigung des Schwerpunktes:

 
s S  r 

 
aS  r 
Prof. Dr. U. J. Schrewe, Physik I + II: Formelsammlung - 2012
Seite 2
Hochschule Hannover
Fakultät II - Maschinenbau und Bioverfahrenstechnik
Vorlesung: Physik I + II
Formelsammlung
ANWENDUNGEN
Trägheitsmomente
Wird ein Körper der Masse m um eine Achse gedreht, deren Abstand zum Schwerpunkt S gleich h ist,
gilt:
J ges  m  h 2  J S ,
wobei JS das Trägheitsmoment bezüglich des Schwerpunktes bezeichnet (Steinerscher Satz).
Trägheitsmoment geometrischer Körper:
J  k mr2
Hohlzylinder (Ring): k = 1; Vollzylinder (Scheibe): k = 1/2; Vollkugel: k = 2/5; Hohlkugel: k = 1/3;
dünner Stab: Drehpunkt Mitte k = 1/12, Drehpunkt Ende: k = 1/3;
Trägheitsmoment flacher Körper (Ausdehnung in x- und y-Richtung): J z  J x  J y
Zentrifugalkraft:
Trägheitskräfte im beschleunigten Bezugssystem


D’Alembertsches Prinzip:
Ftr  m a

v2
F  m
Corioliskraft:
r
Geschwindigkeit zum Zeitpunkt t = 0:
Geschwindigkeit zum Zeitpunkt t:
Ausströmungsgeschwindigkeit:

 
F  2  m    v r
Raketengleichung

v0
Masse zum Zeitpunkt t = 0: m0

v (t )
Masse zum Zeitpunkt t:
m(t )

u aus
m



v (t )  u aus  ln 0  v0
m(t )
Geschwindigkeit der Rakete:
Zentraler elastischer Stoß

Vor dem Stoß:
Geschwindigkeit der Masse m1 ist v1 , Geschwindigkeit der Masse m2 ist

Nach dem Stoß:
Geschwindigkeit der Masse m1 ist u1 , Geschwindigkeit der Masse m2 ist
2m 2
2m1

 m  m1 

 m  m2 
 v2
 v1  2
u1 
 v1
u2 
 v2  1
m1  m2
m1  m2
m1  m2
m1  m2

v2 .

u2 .
Zentraler vollkommen unelastischer Stoß:


Vor dem Stoß: Geschwindigkeit der Masse m1 ist v1 , Geschwindigkeit der Masse m2 ist v 2 .


Nach dem Stoß: Geschwindigkeit der Masse m1 ist u , Geschwindigkeit der Masse m2 ist u .

u
m1
m2


 v1 
 v2
m1  m2
m1  m2
Verformungsarbeit beim vollkommen unelastischen Stoß: WQ



1
1
1
m 1  v 12  m 2  v 22  m 1  m 2   u 2
2
2
2


m1 
m2  p1  p 2
1
2
  E kin
 
WQ  E kin
 1 
 1 
m

m
m

m
m1  m2
1
2 
1
2 


W Q 
Prof. Dr. U. J. Schrewe, Physik I + II: Formelsammlung - 2012
Seite 3
Hochschule Hannover
Fakultät II - Maschinenbau und Bioverfahrenstechnik
Vorlesung: Physik I + II
Formelsammlung
MECHANIK DEFORMIERBARER KÖRPER
Allgemeine Größen
F
m
p

Druck:
V
A
p
1  V V

Kompressibilität (Flüssigkeit):  

 V V

p
Dichte:
Kompressionsmodul:
Feste Körper
F
A
l

l
F A
E
l l
  E 

Zugspannung:
Dehnung:
Elastizitätsmodul:
Hooksches Gesetz:
Druck durch Säule h:
Oberflächenspannung:
Innendruck einer Kugel:
FS
A
x
 
l
F A
G S
x l
  G 

Scherspannung:
Scherung:
Schub-oder Torsionsmodul:
Scherungsgesetz:
Flüssigkeiten
p ( h)   g h  p 0
Auftrieb:
Fa  V g
W F
2   cos  K


Steighöhe in der Kapillare: h 
A 2l
rg
2
4
p
Innendruck der Seifenblase: p 
r
r
Gase
Gesetz von Boyle-Mariotte: p V  const.
Gesetz von Gay-Lussac:
Allgem. Gasgesetz:
p V  n  R  T
alternativ:
Anzahl der Mole:
n
Gaskonstanste:
23
1
Boltzmann-Konst.: k B  1,380 658 (12) 10 J K Avogadro-Konst.:
Gaskonstante = Boltzmann-Konst. · Avogadro-Konst.
R  kB  N A
Kompressibilität (Gase)
1

p
C
T
V
p V  n  k B  N A  T
pT  
R  8,314 510 (70) J mol 1 K 1
N A  6,022 1367(36) 10 23 mol 1
Barometrische Höhenformel: p (h)  p0  e

0
p0
 g h
 p0  e

h
7,988 km
Strömende Flüssigkeiten (und Gase)
Q  V  v  A  const.
Kontinuitätsgleichung:
Bernoulli-Gleichung:
Gesetz von Torricelli: Wenn v konstant ist, gilt:
Viskosität (): (A = Fläche, z = Schichtdicke)
Hagen-Poiseuillesches Gesetz:
p    g  y  12   v 2  const.
p( y )  p( y 0 )    g   y  y 0 
v A
F  
.
z
   p1  p2   r 4
Q  V 
.
8l
Prof. Dr. U. J. Schrewe, Physik I + II: Formelsammlung - 2012
Seite 4
Hochschule Hannover
Fakultät II - Maschinenbau und Bioverfahrenstechnik
Vorlesung: Physik I + II
Formelsammlung
SCHWINGUNGEN
Allgemeine Größen
Ungedämpfter Oszillator:
Gedämpfter Oszillator
Periodische Erregung:
0
e
a
Eigenkreisfrequenz:
Eigenkreisfrequenz:
Erregerkreisfrequenz:
:
f0
fe
fa
1 2


f
T
Schwingungsdauer:
Eigenfrequenz:
Eigenfrequenz:
Erregerfrequez:
Ungedämpfte Schwingung
xt   A  sin  0 t   
Harmonische Differentialgleichung:
x   02  x  0
Lösung:
Federpendel:
m x  D x  0
Eigenkreisfrequenz:  0 
D*
J
g
l 
sgs0
Eigenkreisfrequenz:  0 
l
mgd
J   mgd   0
Eigenkreisfrequenz:  0 
J
2
2
max
max
1
1
 const.  E kin t   E pot (t )  E kin  E pot  2 m v max  2 D x max
J   D *   0
Drehpendel:
Mathematisches Pendel:
Physikalisches Pendel:
Energieerhaltung (Federpendel):
E ges
D
m
Eigenkreisfrequenz:  0 
E kin t   E ges  sin 2  0 t   
Kinetische Energie:
E pot t   E ges  cos 2  0 t   
Potentielle Energie:
E kin  E pot  12 E ges
Energiemittelwerte:
Gedämpfte Schwingung (Geschwindigkeitsabhängige Dämpfung)
x  2  x   02 x  0
Abklingkonstante:

Charakteristische Gleichung für :  2  2     02  0
beim Federpendel:

Differentialgleichung:
Schwingfall:
Bedingung:
 2   02
Anfangsbedingung: x(t  0)  x 0 und x t  0   0 :
Lösung:
    i   e
 e2   02   2

 
x(t )  x 0  e   t 
sin  e t   cos e t 

e
x (t )   x 0  e
Anfangsbedingung: x(t  0)  0 und x t  0  x 0 :
b
2m
x(t ) 
x 0
e
 t
 02
 sin  e t 
e
 e   t  sin  e t 



x (t )  x 0  e   t  cos e t  
sin  e t 
e


Prof. Dr. U. J. Schrewe, Physik I + II: Formelsammlung - 2012
Seite 5
Hochschule Hannover
Fakultät II - Maschinenbau und Bioverfahrenstechnik
Vorlesung: Physik I + II
Formelsammlung
Aperiodischer Grenzfall:
Bedingung:
 2   02
Lösung:
Anfangsbedingung: x(t  0)  x 0 und x t  0   0 :
x(t )  x 0  e
Bedingung:
 2   02
Anfangsbedingung: x(t  0)  x 0 und x t  0   0 :
  
 1   t 
x (t )   x 0  e   t   2  t
Anfangsbedingung: x(t  0)  0 und x t  0  x 0 :
Kriechfall:
 t
x(t )  x 0  t  e   t
x (t )  x 0  e   t  1   t 
    i  
Lösung:
 2   2   02
      t     t 
x(t )  x 0  e   t 
e 
e 
2
 2

2
2
 
x (t )   x0  e   t
 e  t  e  t
2
x
x(t )  0  e   t  e  t  e  t
2

Anfangsbedingung: x(t  0)  0 und x t  0  x 0 :



      t     t 
x (t )   x 0  e   t 
e 
e 
2
 2

Gedämpfte Schwingung (Geschwindigkeitsunabhängige Dämpfung)
Differentialgleichung:
Fallunterscheidung:
Anfangsbedingung:
Lösung (für 0   t  2 ):
Amplitudenabnahme:
 FN  D  a
 FN   D  a
m x   FN  D x  0
m x  D  x  a   0
m x  D  x  a   0
x(t  0)  x 0 und
x t  0   0


x(t )  ( x 0  a)  sin   0 t    a für:
2



x(t )  ( x 0  a)  sin   0 t    a für:
2

x( )  x(0)  2a
x(2 )  x( )  2a
für:
für:
x  0
x  0
x  0
x  0
x(2 )  x(0)  4a
Erzwungene Schwingung mit sin-förmiger Erregung
Differentialgleichung:
Beispiel: Federpendel mit periodischer Kraft: F (t )  Fa  sin  a t 
m x  b x  D x  Fa  sin  a t 
Mit:  
b
0 
2m
D
m
fa 
Fa
m
folgt:
Komplexe Lösung:
 2  2     02  f a  sin  a t 
 02   a2   z 0  i 2   a  z 0  f a  e i
Amplitude:
x 0  a ,  0 ,   
Charakteristische Gleichung für komplexe :
Phasenverschiebung:

0
fa
2
0
  a2
 0  a ,  0 ,    arctan
  2  
2
2
a
2  a
 02   a2
Prof. Dr. U. J. Schrewe, Physik I + II: Formelsammlung - 2012
Seite 6
Hochschule Hannover
Fakultät II - Maschinenbau und Bioverfahrenstechnik
Vorlesung: Physik I + II
Formelsammlung
Amplitudenverstärkung

1
0
tritt eine Amplitudenverstärkung auf.
2
Die Resonanzfrequenz  R ist der Wert von  a , bei dem die Amplitudenüberhöhung maximal wird:
Bei kleiner Dämpfung:
 R2   02  2  2
x0max  x0 a  R , 0 ,   
Die Resonanzamplitude ist:
Die Amplitudenüberhöhung ist:
fa
4    4
2
2
0
4

x0max x0 a  R , 0 ,  
0,5


2
4
x00
x0 a  0, 0 ,  
   
   
 0   0 
fa
2
   
2      
 0   0 
4
2
0
Gekoppelte Schwingungen
Harmonische Differentialgleichungen mit Koppelung:
J 1  D* 1  D  1  2   0
J 2  D* 2  D  1   2   0
Gleichsinnige Schwingung: Differentialgleichung für  1   2 :
Eigenkreisfrequenz  0 :
Gegensinnige Schwingung: Differentialgleichung für  1   2
Eigenkreisfrequenz:  1 :
Für die Anfangsamplituden:
Amplitude:  1  a sin  0 t   a  sin  1 t 
 2  a sin  0 t   a  sin  1 t 
0 
D*
J
J 1  2    D*  2 D   1  2   0
1 
D*  2 D 
J
 1 t  0   2 t  0  0
gilt:
Geschwindigkeit: 1  a 0 cos 0 t   a 1 cos 1 t 
2  a 0 cos 0 t   a 1 cos 1 t 
Für gleichsinnige Schwingung mit Anfangsgeschwindigkeiten:

Amplitude:  1  0  sin  0 t 
Geschwindigkeit:
0

 2  0  sin  0 t 
0
 1 t  0   2 t  0   0
gilt:
1  0 cos 0 t 
2  0 cos 0 t 
Für gegensinnige Schwingung mit Anfangsgeschwindigkeiten:

Amplitude: 1  0  sin 1 t 
Geschwindigkeit:
1

2   0  sin 1 t 
1
J 1  2   D* 1   2   0
 1 t  0   2 t  0    0
gilt:
1  0 cos 1 t 
2  0 cos 1 t 
Prof. Dr. U. J. Schrewe, Physik I + II: Formelsammlung - 2012
Seite 7
Hochschule Hannover
Fakultät II - Maschinenbau und Bioverfahrenstechnik
Vorlesung: Physik I + II
Formelsammlung
Für Schwebungsschwingungen
mit Anfangsgeschwindigkeiten:
 1 t  0   0 und  2 t  0  0
Amplituden (Näherungslösung):
     0
  0
 1  0   sin 1
t  cos 1
1 
2
2
Geschwindigkeiten:
  0
  0

 1   0   cos 1
t  cos 1
2
2

gilt:
 0 
  0
  0 
  cos 1
t  sin 1
t
1 
2
2


t

2 

t

 2   0   sin

1   0

2
t  sin
1   0 
2
t

Wellen
Wellen:
Wellenfunktion einer nach rechts laufenden Welle: y ( x, t )  y1 ( x  vt )
Wellenfunktion einer nach links laufenden Welle: y ( x, t )  y1 ( x  vt )
Gesamtwellenfunktion:
y ( x, t )  y1 ( x  vt )  y 2 ( x  vt )
y ( x, t )  A  sin(k x   t )
dE 1
Übertragene Leistung durch harmonische Welle:
P
  2 A 2 v
dt 2

 
Interferenz: y1  A sin( k x   t ) u. y 2  A sin( k x   t   ) : y1  y 2  2 A cos  sin(k x   t  )
2
2
Stehende Wellen:
Für die Randbedingungen: y n ( x  0)  0 und y n ( x  l )  0
folgt:
2
2l
oder:  n 
knl 
 l  n 
Wellenfunktionen:
y n  x, t   2 An cos n t   sin k n x 
n
n
Harmonische Welle:
Wellengleichung:
2 y  2 y
 
x 2 F t 2
oder:
2 y 1 2 y


x 2 v 2 t 2
Geschwindigkeit:
v
Prof. Dr. U. J. Schrewe, Physik I + II: Formelsammlung - 2012
F

Seite 8
Hochschule Hannover
Fakultät II - Maschinenbau und Bioverfahrenstechnik
Vorlesung: Physik I + II
Formelsammlung
Formelzeichen und Einheiten
A
A
b

a
Fläche
Amplitude
Reibungskonstante
Beschleunigung
1 m2
1m
1 kg s-1
1 m s-2
D
Federkonstante
1 N m-1
D*
Winkelrichtgröße
1 kg m2 s-2
D
Koppelungskonstante
1 N m-1
E
Elastizitätsmodul
1 N m-2
E

F
Energie
1 J = 1 N m = 1 kg m2 s-2
Kraft
1 N = 1 kg m s-2
f
Frequenz
1 s-1
g
Erdbeschleunigung
9,81 m s-2
G
Torsionsmodul
1 N m-2
G
Gravitationskonstante
6,672 59(85) 10-11 N m2 kg-2
J
Trägheitsmoment
1 kg m2
Wellenzahl
1 m-1
Boltzmann-Konstante
1,380 658(12) 10-23 J K-1
Drehimpuls
1 kg m2 s-1
m

M
Masse
1 kg
Drehmoment
1 kg m2 s-2
n
Drehzahl
1 s-1
N
Zahl der Umdrehungen
1
NA

p
Avogadro-Konstante
6,022 1367(36) 1023 mol-1
Impuls
1 kg m s-1
p
Druck
1 Pa =1 N/m2
P
Leistung
1 J s-1 = 1 N m s-1 = 1 kg m2 s-3
Q
Wärmeenergie
1 J = 1 N m = 1 kg m2 s-2
Q  V
Volumenstrom
1 m3 s-1
R
allgemeine Gaskonstante
8,314 510(70) J mol-1 K-1
r oder R
Radius
1m
k
2

kB

L
Prof. Dr. U. J. Schrewe, Physik I + II: Formelsammlung - 2012
Seite 9
Hochschule Hannover
Fakultät II - Maschinenbau und Bioverfahrenstechnik
Vorlesung: Physik I + II
Formelsammlung

s
Verschiebung
1m
t
Zeit
1s
T
Umdrehungszeit oder Schwingungsdauer
1s
T

v
Temperatur
1 K (0 K = - 273,15°C)
Geschwindigkeit
1 m s-1
W
Arbeit
1 J = 1 N m = 1 kg m2 s-2

Winkelbeschleunigung
1 s-2

Abklingkonstante
1 s-1

Phasenkonstante
1

Dehnung
1

Scherung
1
 (oder  )
Oberflächenspannung
1 J m-2 = 1 N m-1 = 1 kg s-2

Kompressionsmodul
1 Pa = 1 N m-2 = 1 kg m-1 s-2

Kompressibilität
1 Pa-1= 1 m2 N-1 = 1 m s2 kg-1

Wirkungsgrad
1

Viskosität
1 Pa s = 1 kg s-1 m-1
H
Haftreibungszahl
1
G
Gleitreibungszahl
1
R
Rollreibungszahl
1

Massenbelegung
1 kg m-1

Dichte
1 kg m-3

Zugspannung
1 N m-2 = 1 kg m-1 s-2

Scherspannung
1 N m-2 = 1 kg m-1 s-2
Drehwinkel
1 (Umrechnung: 360° = 2)

Winkelgeschwindigkeit (allgemein)
1 s-1
0
Eigenkreisfrequenz ohne Dämpfung
1 s-1
 e   02   2
Eigenkreisfrequenz mit Dämpfung
1 s-1
a
Erregerkreisfrequenz
1 s-1
 R   02  2  2
Resonanzfrequenz
1 s-1




Prof. Dr. U. J. Schrewe, Physik I + II: Formelsammlung - 2012
Seite 10