Schulmathematik: Zahlen

Arbeitsunterlagen zur Vorlesung
Schulmathematik: Zahlen
........
(1)
Historisches
Zur geschichtlichen Entwicklung der Zahlen
(2)
Systematisches ......
Skizze einer systematischen Behandlung der Zahlbereiche
(3)
Didaktisches
Diskussion ausgewählter didaktischer Konzepte für die Schule
(4)
Zahlentheoretisches .....
Begriffe und Sätze der elementaren Zahlentheorie für die Schule
.......
Franz Schoberleitner
Schulmathematik Zahlen
I Literaturliste:
A.
Schulbücher
Alle in Österreich approbierten AHS-Lehrbücher für Mathematik enthalten
entsprechende Abschnitte zu den Themen der Vorlesung.
B.
Bücher zum fachlichen bzw. fachdidaktischen Hintergrund
REISS I SCHMIEDER, Basiswissen Zahlentheorie. Eine Einführung in Zahlen und
Zahlbereiche, Springer Verlag 2005
PADBERG/DANCKWERT/STEIN, Zahlbereiche. Eine elementare Einfiihrung,
Spektrum Akademischer Verlag 1995
PADBERG, Didaktik der Bruchrechnung, Spektrum Akademischer Verlag 1995
PADBERG, Didaktik der Arithmetik, BI-Wissenschaftsverlag 1986
EBBINGHAUS u.a., Zahlen, Springer Verlag 1992
EVES, An introduction to the history of mathematics, Saunders College Publishing
1989
SCHEID, Zahlentheorie, BI-Wissenschaftsverlag 1994
SCHEID, Elemente der Arithmetik und Algebra, BI-Wissenschaftsverlag 1991
COURANTIROBBINS, Was ist Mathematik?, Springer Verlag 1992
ENZENBERGER, Der Zahlenteufel. Ein Kopfkissenbuch für alle, die Angst vor der
Mathematik haben, dtv 62045, 1999
TASCHNER., Der Zahlen gigantische Schatten. Mathematik im Zeichen der Zeit,
vieweg 2004
CONWAYIGUY, The book of numbers, Springer Verlag 1996
I
I
Schulmathematik Zahlen
1. Historisches
2
Vorüberlegungen zur Geschichte des Zahlbegriffs
1.
Was sind Zahlen ?
1 , 2, 3, 4, ......
zusätzlich - 4, %, 43, i, ......
Mann auf der Straße:
Schüler der Oberstufe:
Mathematik-Lehrer:
????
In der Mathematik gibt es keine wirkliche Definition des Begriffs "Zahl"....
Versuch:
''Zahlen sind Objekte, mit denen man rechnen kann ..."
Einwand: Man kann z.B. auch mit Polynomen, Vektoren usw. rechnen (d.h. addieren,
multiplizieren, ....).
Diese Denkweise fuhrt zu den algebraischen Strukturen ....
Antwort auf die Frage gibt wohl am besten die historische Entwicklung:
Zahlen sindjene Objekte, die man im Lauf der Zeit als solche bezeichnet hat .....
Der Weg dahin war oft langwierig und verschlungen und alles andere als einfach. Diese
Entwicklung spiegelt sich wider in der Lerngeschichte der Schüler.
Typische Situation im MU:
Bei der Einführung der komplexen Zahlen stellen Schüler (sich oder dem Lehrer) die
Frage:
Sind diese eigenartigen Objekte denn wirklich Zahlen ??
2.
Drei Aspekte beim Thema "Zahlen":
\
Darstellung
von Zahlen
Zahlbegriff
)
Operieren
Schulmathematik Zahlen
I Überblick:
A.
I. Historisches
Systeme zur Darstellung natürlicher Zahlen
Rein additive Systeme
Basis: b
Symbolefür: 1, b, b2, b3, .......
Darstellungssysfem: Symbole werden additiv verwendet.
Beispiele:
-
ägyptisches System
babylonisches System (für Zahlen < 60)
frühes griechisches System
römisches System (späte Ergänzung: „Subtraktionsprinzipb')
.
B.
Multiplikativ - additive Systeme
Basis: b
2 Arten von Symbolen:
(1)
(2)
fir:
für:
1, 2, 3, ....., b-1
b, b2, b3, ....
Darstellungssystem:
Symbole aus (1) werden als Faktoren für Symbole aus (2) verwendet.
Beispiel:
traditionelles chinesisch-japanisches System
Basis: b
Symbolefür:
Darstellungssystem: Symbole werden additiv verwendet.
Beispiele:
griechisches (ionisches) System
(b=10; als Symbole wurden die Buchstaben des Alphabets und drei
Sonderzeichen verwendet)
hebräisches / syrisches / koptisches System
Hindu- Brahmi- System
frühes arabisches System
3
Schulmathematik Zahlen
D.
I . Historisches
Stellenwertsysteme
Basis: b
Symbole für: 0, 1, 2, ....., b-I
Darstellungssystem :
Die Zeichenfolge a,a,.ia,-2 ....aiao bezeichnet die Zahl N
Beispiele:
= anb,+a,_lb"-'+...+alb+ao
babylonisches System (b=60)
System der Mayas (b=20)
indisch-arabisches System (b=10)
Dualsystem, Hexagesimalsystem, ....
1
10
I
st i c h
i
wo
100
n
e
1000
Fessel
Strick
Lotuspflanze
stehender Finger
..
2
100 000
1 000 000
k
Kaulquappe
T
Gott
I.
Y 2I'iI E%%K ee e nnn
rinn 1 1 1 1
g
@
Japan / China:
111
1. Historisches
Schulmathematik Zahlen
Griechenland:
I
a
alpha
2
3
ß
beta
4
5
6
E
6
obsolete
7
8
5
zeta
?
9
e
eta
theta
Y
'
gamma
delta
epsilon
digamma
10
20
30
40
50
60
70
80
90
K
iota
kappa
L
A
lambda
P'
mU
V
nu
C
0
xi
omicron
7r
pi
obsolete
koppa
100
200
300
400
500
600
P
U
7
U
<b
X
700
J!
800
900
obsolete
W
Mesopotamien:
Indien / Arabien:
-==
-i
FFd7'7?
;? 3 8 Y < 7 G)
1
(,
f
(/
L/ 3
O
2
4 64 8 9
1 2 3 4. 6 ? $ 9
1 7 5
Indisch (Brahrni) 3. Jh. V. Chr.
Indisch (Gwalior] 8. Jh. n. Chr.
Westarabisch (Gebar) 11. Jh.
0
Evrap5isch15.Jh.
0
Europ3isch (D"„)
I S 3 4 5 6 7 8 9 O
16. Jh.
Neuzeit (Grotesk) 20. Jh.
rho
sigma
tau
upsilon
phi
chi
psi
Omega
sampi
Schulmathematik Zahlen
1. Historisches
6
Natürliche Zahlen
(1)
In allen Hochkulturen gab es die natürlichen Zahlen .......
Große Unterschiede gab es bei der Darstellung dieser Zahlen und (damit zusammenhängend) bei den Algorithmen für die Rechenoperationen.
Der Ursprung aller mathematischen Betätigung ist das Zählen (dadurch entstehen die
natürlichen Zahlen) und das Operieren mit natürlichen Zahlen (Addition, Subtraktion,
Verdoppeln, Halbieren, Multiplizieren, Dividieren)
(2)
Reflexionen über Eigenschaften der natürlichen Zahlen (Unendlichkeit; Strukturelle
Eigenschaften wie Kommutativitätsgesetze usw.) sind dabei zunächst völlig im
Hintergrund.
Vgl. die Situation des Kindes (in der Vorschul- und Volksschulzeit):
Fragen wie: „Was ist die größte Zahl?" beziehen sich auf Zahlennamen und nicht auf
die Zahlen selber!
Die antiken Griechen gaben eine Definition des Begriffs "Zahl":
Euklid:
"Zahl ist die aus Einheiten zusammengesetzte Menge. "
Beachte:
1 ist keine Zahl, sondern die Einheit, aus der die Zahlen gebildet werden.
Bruchzahlen
Zu den natürlichen Zahlen kamen sehr früh (bei Ägyptern, Babyloniern, Griechen) die
Bruchzahlen (positive rationale Zahlen).
Anfänglich verwendeten alle antiken Hochkulturen nur „natürliche Brüche", die in der
alltäglichen Praxis notwendig waren,
2.B.:
112, 3 , 1 4 I , ...
und die ,,Komplementärbrüche" 213, 314, .. .
Das ist bei den primitiven Völkern der Gegenwart noch heute der Fall.
(Auch in unserer täglichen Praxis:
Niemand kauft 117 kg Wurst, Getränke werden in Halben, Vierteln und Achteln bestellt, ....)
I . Historisches
Schulmathematik Zahlen
1
Die Ägypter hatten Zeichen für alle „Stainmbrüche" (der Form -).
n
Alle anderen Brüche mussten als Summe von verschieclenen Stumrnbrüchen dargestellt werden.
Diese Darstellung ist nicht eindeutig. Welcher Darstellung der Vorzug gegeben wurde, ist nicht
klar. Denkbar ist:
möglichst kleine Zahl von Summanden
(I)
(2)
möglichst großer ,,HauptbruchG
2
eine
n
Darstellung als Summe von Stammbrüchen enthalten (z.B. im Papyrus Rhind für alle
ungeraden Zahlen von 3 bis 101). Wie diese Tabellen erstellt worden sind, ist völlig ungeklärt.
Zum konkreten Rechnen verwendete man Tabellen, die für Brüche der Form
-
Mit Hilfe dieser Tabellen konnte man Vielfache von Brüchen berechnen; denn das
Multiplizieren wurde zurückgeflihrt auf Verdoppeln und Addieren.
Die Darstellung von Brüchen als Summe von Stammbrüchen hat sich lange gehalten.
Beispiel:
Nach Plinius macht Europa etwa 113 + 118 der ganzen Erde aus, Asien etwa 114 + 1/14, Afrika
etwa 115 + 1/60.
Bemerkung:
Die Darstellung von Brüchen als Summe verschiedener Stammbriiche ("ägyptische
Darstellung") ist ein altes Thema der Zahlentheorie.
Leonardo von Pisa gab einen (naheliegenden) Algorithmus zur Auffindung einer solchen
Darstellung an. (Dabei wird Schritt fir Schritt der jeweils größtmögliche Stammbruch
bestimmt.)
Allerdings liefert diese Verfahren manchmal "unschöne" Darstellungen:
4
17
1
5
1
29
---+-+-
Für Brüche der Form
1
1233 + 3039345
1
während auch
2
(n ungerade) gibt es stets folgende Darstellung (mit 2
n
-
Summanden):
2 =-+1
1
n k k.n
-
mit
n+l
k =2
Die Tabelle im Papyrus Rhind enthält aber zum Teil andere Darstellungen.
Schulmathematik Zahlen
I . Historisches
Erst 1985 wurde gezeigt:
Für jedes z besitzen fast alle Brüche der Form
z
eine Darstellung als Summe von
n
-
höchstens 2 verschiedenen Stammbrüchen.
Babylonier:
Nach der Entwicklung des sexagesimalen Positionssystems (in altbabylonischer Zeit) wurden
Stammbrüche in diesem System dargestellt (analog zu unseren Dezimalzahlen).
Man verwendete entsprechende Tabellen als Rechenhilfe.
Allgemeine Brüche konnten durch Multiplikation dieser Werte im Sexagesimalsystem
dargestellt werden.
Griechen:
Sie verwendeten fur praktische Zwecke vielfach an ägyptische und babylonische Vorbilder
angelehnte Darstellungsweisen und Methoden.
In der ,,theoretischen Mathematik" werden Brüche durch Proportionen ersetzt.
Denn konsequenterweise betrachteten die griechischen Mathematiker Brüche nicht als Zahlen,
sondern als Verhältnisse von Zahlen. (Denn die Einheit ist nicht teilbar ....)
Das Buch V111 von Euklids Elementen behandelt ausfihrlich und systematisch die Theorie der
Proportionen.
Schulmathematik Zahlen
I
I . Historisches
9
I
Irrationale Zahlen
Für die griechische Mathematik (und erst recht für ihre Vorläufer) waren ,,ZahlenGdas, was wir
heute als natürliche Zahlen bezeichnen. Zusätzlich betrachteten sie Zahlenverhältnisse und
hatten damit im Wesentlichen unsere positiven rationalen Zahlen zur Verfügung.
Die so genannten „PythagoräerUmachten im 5.Jahrhundert vor Christus die Entdeckung, dass
es Strecken gibt, deren Länge nicht durch eine ,,Zahlcc(in ihrem Verständnis) ausgedrückt
werden kann: die Länge der Diagonale des Einheitsquadrates ist keine rationale Zahl.
Aus heutiger Sicht kann dieser Sachverhalt auf verschiedene Weise formuliert werden:
Satz: (in drei äquivalenten Formulierungen)
1
sodass x2 = 2
(1)
Es gibt keine rationale Zahl
(2)
fi
ist eine irrationale Zahl
(3)
fi
ist eine unendliche nicht periodische Dezimalzahl
X,
Beweis (nach EUKLID, Ca. 300 v.Chr.):
Angenommen, es gibt eine rationale Zahl x mit x 2 = 2
a
Dann besitzt x eine Darstellung x = -, sodass a und b teilerfremd sind, der Bruch
b
also nicht gekürzt werden kann. Insbesondere sind a, b nicht beide gerade.
X
2
=2
U
a 2 = 2b2
3
a 2 ist gerade a
U
a ist gerade
3 es
gibt ein k
E
N , sodass a = 2k
4 k 2 = 2b2
U
b2 = 2k2
b2 ist gerade
3
b ist gerade
Es müsste also sowohl a als auch b gerade sein. Das widerspricht der Annahme.
Also ist die Annahme falsch, und das Gegenteil ist wahr.
I . Historisches
Schulmathematik Zahlen
Wichtig ist folgende Erkenntnis:
Sobald eine einzige Zahl (etwa &)als irrational erkannt worden ist, kann man sofort eine
unendliche Menge irrationaler Zahlen angeben:
Fiir alle rafionalenZahlen r, s (+ 0) ist die Zahl
X =r
+ s.&
irrational
Beweis:
ES
gilt:
x=r+s.&
X-r
&=S
Wäre
X
rational, dann auch die Zahl
X-r
-; wir
wissen aber, dass
& irrational ist!
S
Bemerkung:
Es ist also klar, dass es zumindest so viele irrationale Zahlen gibt wie rationale. Aber in
Wirklichkeit gibt es „viel mehr"!
Alle Zahlen der Form X = r + s.& treten als Lösungen von quadratischen Gleichungen mit
rationalen Koeffizienten auf, sind also algebraische Zahlen. Nach CANTOR ist die Menge der
algebraischen Zahlen abzählbar, die Menge aller reellen Zahlen aber nicht. Es gibt also
überabzählbar viele nicht algebraische irrationale Zahlen. Diese heißen transzendent.
Für die griechische Mathematik war die ,,Entdeckung der irrationalen Zahlenc' ein wichtiger
Einschnitt:
Es zeigt sich, dass nicht alles durch (natürliche) Zahlen und ihre Verhältnisse beschrieben
werden kann. Die griechische Mathematik gab in der Folge der Geometrie den Vorzug vor
der Arithmetik.. .
Diese Entdeckung ist kein Ergebnis praktischer Handlungen oder empirischer Versuche,
sondern nur dem denkenden Verstand zuzuschreiben: sie ist eine wesentlich mathematische
Erkenntnis und zeigt die Überlegenheit der Mathematik über die materielle Wirklichkeit!
PLATO (der selbst kein Mathematiker war, aber die Mathematik sehr hoch schätzte) sagt in
seinen „Gesetzenu:
„Lieber Kleinias, ich habe ja wohl auch erst selbst recht spät etwas darüber vernommen und
musste mich über diesen Umstand sehr verwundern. Es kam mir vor, als wäre das gar nicht bei
Menschen möglich, sondern eher nur etwa beim Schweinevieh. Und da schämte ich mich, nicht
nur für mich selbst, sondern für alle Hellenen. "
Schulmathematik Zahlen
1. Historisches
11
Negative Zahlen
(1)
Babylonische Texte aus der Zeit 620 - 440 v.Chr. enthalten Zahlenreihen mit einer
zusätzlichen Charakterisierung ( durch die Silben tab und lal).
Die meisten Historiker interpretieren diese als + und - . Es handelt sich bei den
Zahlenreihen um Pegelstände eines Flusses, Längen eines Tages usw.
Genaugenommen werden hier nicht um positive und negative Zahlen verwendet,
sondern "hinzuzufügende" und "abzuziehende" Zahlen (zu bzw. von einem Mittelwert).
(2)
Aus einem chinesischen Rechenbuch (2.Jhdt. V. Chr.)
5 Garben einer guten Ernte vermindert um 11 sind 7 Garben einer schlechten Ernte.
7 Garben einer guten Ernte vermindert um 25 sind 5 Garben einer schlechten Ernte.
Zu lösen ist (in unserer Darstellungsweise) das lineare Gleichungssystem
Da die symbolische Verwendung von Unbekannten noch nicht geläufig war, schrieb
man die Koeffizienten in ein Schema folgender Art:
Dann wurde eine Regel zum Berechnen der Lösung verwendet, die in etwas der
heutigen Determinantenmethode entspricht.
In diesem Zusammenhang wurden algebraische Regeln wie "minus mal minus gibt
plus" angegeben......
(3)
In ähnlicher Weise findet man Regeln zum Umgang mit negativen Zahlen bei
DIOPHANT (3.Jhdt. n. Chr., Alexandria), BRAHMAGUPTA (um 600 n.Chr., Indien)
u.a..
Negative Zahlen kommen nicht als Lösung von Aufgaben vor, sondern nur in Zwischenschritten.
Islamische Mathematiker des Mittelalters, die große Fortschritte beim Lösen von
quadratischen Gleichungen machten, geben jeweils nur positive Lösungen an.
Schulmathematik Zahlen
(4)
I . Historisches
Das erste bekannte Beispiel mit einer akzeptierten negativen Lösung findet sich bei
LEONARDO von PISA (1 170 - 1250):
Die Aufgabe handelt von 4 Personen, die die Geldbeträge X,,xz, xj, ~q besitzen und
eine Geldbörse mit dem Betrag b finden. Der Text fuhrt (in moderner Darstellung!) auf
folgendes Gleichungssystem:
X, t b = 2(x2 t X,)
X, t b = 3(x3 t x 4 )
Leonardo schreibt dazu: "Ich werde zeigen, dass diese Aufgabe unlösbar ist, wenn nicht
zugestanden wird, dass der erste Partner Schulden hat. "
L. gibt dann eine spezielle Lösung an: X, = -I, X, = 4, X, = 1, X , = 4, b = 11
(Da das Gleichungssystem homogen ist, kann eine Unbekannte beliebig festgesetzt
werden.)
(5)
Die italienischen und deutschen Mathematiker der Renaissance arbeiten durchwegs
auch mit negativen Lösungen von Gleichungen, versehen diese allerdings mit
Attributen wie Jikitv, Jingiert, falsch, erdichtet, negativ, ....
Im Lauf der Zeit wurden aus diesen abwertenden Attributen termini technici; man
gewöhnte sich einfach an das Vorkommen negativer Zahlen.
(6)
Trotzdem traten immer wieder „theoretische Probleme" mit negativen Zahlen auf:
ARNAULD in einem Brief an Leibniz:
Es besteht (aufgrund der Rechenregelnfür negative Zahlen) die Proportion
(+I) : (-1) = (-1) : (+I)
Wie aber kann sich das Größere zum Kleineren verhalten wie das Kleinere zum
Größeren ?
Leibniz sieht das Problem und rät zur ,,Toleranz" ......
WALLIS (1 6 16 - 1703) hat folgendes „Ordnungsproblern".
Es gilt:
(I)
(2)
Je kleiner eine Zahl ist, umso größer ist ihr Kehrwert.
Der Kehrwert von 0 ist Unendlich
Also muss der Kehrwert von Zahlen, die kleiner als 0 sind, gröJer als Unendlich sein!
-I ist der Kehrwert von - I also : -I größer als Unendlich.
Schulmathematik Zahlen
I . Historisches
13
Komplexe Zahlen
Eine der großen Herausforderungen für die italienischen Mathematiker des 16. Jahrhunderts
war die Lösung von Gleichungen dritten und vierten Grades.
CARDANO gab in seiner "Ars magna" (1 545) ein "Rezept" zur algebraischen Bestimmung
einer Lösung einer Gleichung 3.Grades an. In heutiger Darstellung lautet dieses so:
Die Gleichung
X
3
+ m.x = n
besitzt die Lösung
Die Entdeckungsgeschichte dieser Formel ist ziemlich abenteuerlich; um sie rankt sich eine der
berühmtesten Prioritätenstreitigkeiten in der Mathematik-Geschichte.
Jede Gleichung der Form x3 + a.x2 + b.x + C = 0 kann mit Hilfe der Substitution y = X
+ -a3
auf die obige Form gebracht werden. Damit ist jede Gleichung dritten Grades mit dieser
Formel lösbar.
Allerdings beinhaltet die Formel von CARDANO eine Schwierigkeit:
Es ist möglich, dass in dieser Formel Quadratwurzeln aus negativen Zahlen auftreten, obwohl
die schließlich zu berechnende Lösung reell ist! ("Casus iweduzibilis '7
BOMBELLI hat um 1560 diesen Fall erstmals in voller Konsequenz behandelt und formal mit
Wurzeln aus negativen Zahlen gerechnet, ohne allerdings die Zwischenergebnisse deuten zu
können.
Die Gleichung
x3 = 15x + 4
besitzt offenbar die reelle Lösung
Die Formel von CARDANO liefert allerdings:
ES gilt
formal:
Also erhält man:
(i2+~-iy
X
=
=
+2+J-121
(Z+fl)-(-2+a)
=
4
X
=4 .
Schulmathematik Zahlen
I . Historisches
Der Anlass für die Verwendung komplexer Zahlen liegt also nicht bei den quadratischen
Gleichungen (deren komplexe Lösungen man ja einfach ignorieren kann!), sondern in der
Tatsache, dass bei der Ermittlung von reellen Lösungen einer Gleichung 3. Grades komplexe
Zwischenergebnisse auftreten können ("Casus irreduzibilis").
Wie man leicht zeigen kann, gilt:
Der "Casus irreduzibilis" tritt genau dann ein, wenn eine Gleichung 3. Grades genau drei
reelle Lösungen besitzt.
Schon bald erwiesen sich die komplexen Zahlen als hilfreich in den verschiedensten Bereichen
der Mathematik, vor allem in der sich rasch entwickelnden Analysis. Die Erklärung, was
komplexe Zahlen eigentlich sind, bereitete aber lange Zeit große Schwierigkeiten:
R. DESCARTES (1 596- 1656) meinte sinngemäß:
Man kann sich bei jeder Gleichung so viele Wurzeln "einbilden":wie der Grad angibt, nur
entspricht diesen manchmal keine reelle Größe.
G. LEIBNIZ (1646- 1716)
Imaginäre Zahlen sind "einefeine und wunderbare Zuflucht des göttlichen Geistes, beinahe
ein Amphibium zwischen Sein und Nichtsein. "
L. EULER (1 707- 1783)
" .... ist klar, dass die Quadratwurzeln von Negativ-Zahlen nicht einmal unter die möglichen
Zahlen gerechnet werden konnen;folglich müssen wir sagen, dass dieselben ohnmögliche
Zahlen sind L....] undgemeiniglich imaginäre oder eingebildete Zahlen genannt werden, weil
sie bloß allein in der Einbildung stattjnden. "
C.F. GAUSS (1 777-1 855) bringt als einer der ersten Licht in das Dunkel:
"Sowie man sich das ganze Reich der reellen Größen durch eine unendliche gerade Linie
denken kann, so kann man das ganze Reich aller Größen, reeller und imaginärer, sich durch
eine unendliche Ebene sinnlich machen, worin jeder Punkt, durch Abszisse a und Ordinate b
bestimmt, die Größe a + b.i gleichsam repräsentiert. "
""Hatman diesen Gegenstand bisher aus einem falschen Gesichtspunkt betrachtet und eine
geheimnisvolle Dunkelheit dabei gefunden, so ist das großteils den wenig schicklichen
Benennungen zuzuschreiben. Hätte man + 1, - 1 f i nicht positive, negative und
imaginäre (oder gar unmögliche) Einheit, sondern etwa direkte, inverse und laterale Einheit
genannt, so hätte von einer solchen Dunkelheit kaum die Rede sein konnen. "
Schulrnathernatik Zahlen
1. Historisches
15
I Systematische Grundlegung der Zahlenbereiche im 19. Jahrhundert
(1)
HAMILTON charakterisiert 1833 die komplexen Zahlen als Paare reeller Zahlen:
Er fasst die komplexe Zahl z = a + b.i als Zahlenpaar (a, b) auf und definiert die
beiden Rechenoperationen
Addition:
Multiplikation:
(a,,bl)@(a2,b2):=(al
+ a 2 , b l+ b 2 )
(al,bl)@(a2,b2):=(al.a2
- b l b 2 , a 2 b l+al.b2)
Auf diese Art sind die komplexen Zahlen und ihre Rechenoperationen ohne das
,,Mysteriumu einer Zahl i mit der Eigenschaft i2 = -1 definiert.
Modern gesprochen, hat HAMILTON den Vektorraum R2 so mit einer Multiplikation
versehen, dass ein Körper entsteht.
Die Untersuchungen HAMILTONs ergaben weiterhin:
In R~ ist es nicht möglich, eine umkehrbare Multiplikation einzuführen, wohl aber in
R ~Dies
. führt auf die von HAMILTON entdeckten Quaternionen.
(2)
Um die Mitte des 19,Jahrhunderts spürten einige der Ehrenden Mathematiker die
dringende Notwendigkeit, die reellen Zahlen streng zu begründen. Bis dahin lag der
gesamten Mathematik so etwas wie eine ,,Intuition der reellen Zahlenc' zugrunde, die in
etwa der Vorstellung von den Punkten der Zahlengeraden entspricht.
Alle Definitionsversuche der reellen Zahlen gingen von den als gesichert geltenden
rationalen Zahlen aus.
DEDEKIND definierte die reellen Zahlen als „Schnitte der rationalen Zahlen"
CANTOR verstand unter einer reellen Zahl eine ,,Äquivalenzklasse von
Fundamentalfolgen rationaler Zahlen".
Weitere berühmte Definitionen stammen von WEIERSTRASS und MERAY.
Eine ganz andere Vorgangsweise wählte HILBERT (um 1900):
Er formulierte eine lange Liste von Axiomen (in heutiger Diktion: Körperaxiome,
Axiome der Anordnung, Vollständigkeitsaxiom) und bezeichnet ein System von
Objekten, das alle diese Axiome eriullt, als Menge der reellen Zahlen.
(3)
Am Ende des 19. Jahrhunderts taten einige an den Grundlagen der Mathematik und der
Logik forschende Mathematiker einen letzten Schritt: Sie versuchten zu definieren, was
die natürlichen Zahlen sind. Am berühmtesten ist das Axiomensystem von PEANO.
Ein systematischer Aufbau der ganzen und der rationalen Zahlen wurde in der Folge
von vielen Mathematikern durchgeiuhrt. Dies wurde aber nicht mehr als große
wissenschaftliche Leistung angesehen, sondern eher als Anwenden von modernen
algebraischen Denkweisen auf ein im Grunde bereits gelöstes Problem.
Schulmathematik Zahlen
(4)
I . Historisches
In den 60-er Jahren des 20.Jahrhunderts wurde schließlich eine Art von Zahlen in der
Mathematik etabliert, über deren Existenz man 150 Jahre lang gestritten hatte und die
schließlich um 1850 aus der „strengen Mathematik" eliminiert worden waren: die
unendlich kleinen und die unendlich großen Zahlen.
ROBINSON konstruierte einen Erweiterungskörper der reellen Zahlen, die
hyperreellen Zahlen. Diese können als späte Rechtfertigung jener infinitesimalen
Größen betrachtet werden, mit denen große Mathematiker wie LEIBNIZ und EULER
höchst erfolgreich gearbeitet hatten, ohne wirklich erklären zu können, was denn das für
Zahlen seien.
Schulmathematik Zahlen
IZahlbereiche:
2. Systematisches
17
Übersicht über Axiomensvsteme und Konstruktionen
Axiome der
Mengenlehre
V
Konstruktion von N
PEANO-Axiome
für N
+-+
(Def. von +, . <)
I
Konstruktion von Z
o:*
s(n):=nu{n}
/
(Äquivalenzklassen von
Paaren natürl. Zahlen)
i
Konstruktion von Q
(Äquivalenzklassen von
Paaren ganzer. Zahlen)
I Konstruktion von R I
(Cauchy-Folgen,
Dedekind-Schnitte, .. .)
T
Konstruktion von C
(Paare reeller Zahlen)
+-+
Körperaxiome
Ordnungsaxiome
Vollständigkeit
I
Schulmathematik Zahlen
2. Systematisches
18
~ahlenbereiche- Skizze einer exakten Fundierung
h.
Axiomatische Charakterisierung. der Natürlichen Zahlen
Ausgehend von der intuitiven Vorstellung von natürlichen Zahlen beschrieb G. PEANO 1899
die natürlichen Zahlen durch folgendes Axiomensystem:
Die Begriffe „natürliche Zahl ", „ 0 " und „Nachfolger " treten dabei als undefinierte
Grundbegriffe der Theorie auf.
(I)
(2)
(3)
(4)
(5)
0 ist eine natürliche Zahl
Der Nachfolger einer natürlichen Zahl ist eine natürliche Zahl
0 ist nicht Nachfolger einer natürlichen Zahl
Verschiedene natürliche Zahlen haben verschiedenen Nachfolger.
Wenn 0 die Eigenschaft E besitzt
und wenn aus der Tatsache, dass eine natürliche Zahl n die Eigenschaft E
besitzt, stets folgt, dass auch der Nachfolger von n die Eigenschaft E hat,
dann hat jede natürliche Zahl die Eigenschaft E.
Etwas formaler ausgedrückt:
Das Tripel (0, N, S ) heißt PEANO-System, falls gilt:
(1)
(2)
(3)
OEN
S : N + N ist injektiv, und es gilt: S(N)
O E E ~ NA S ( E ) c E
E=N
N\(O}
Man kann zeigen, dass durch die PEANO-Axiome die Menge N bis auf Isomorphie eindeutig
charakterisiert ist.
Mit anderen Worten: Alle PEANO-Systeme sind zueinander isomorph.
Definition der Rechenoperationen:
Die Addition wird - aufbauend auf der Nachfolgerfunktion S - rekursiv definiert:
Die Multiplikation wird dann mit Hilfe der Addition rekursiv definiert:
I
Schulmathematik Zahlen
2. Systematisches
Man kann zeigen:
(I)
Die Addition ist kommutativ und assoziativ und besitzt 0 als neutrales Element.
(2)
Die Multiplikation ist kommutativ und assoziativ und besitzt I :=S(O) als
neutrales Element.
(3)
Es gelten folgende „Kürzungsregeln":
n+x=n+y
n.x=n.y
x=y
x = y , falls n f O
3
Definition einer Ordnungsrelation in N:
Man kann zeigen, dass dadurch tatsächlich eine Ordnungsrelation in N definiert ist und dass
diese mit den Rechenoperationen verträglich ist („Monotonie der Addition und der
Multiplikation")
1 2.
Konstruktion der Ganzen Zahlen
Der algebraischen Konstruktion von Z aus N liegt folgende Idee zugrunde:
Jede ganze Zahl (im naiven Gmndverständnis) kann als Differenz zweier natürlicher Zahlen
dargestellt werden, wobei diese Darstellung natürlich nicht eindeutig ist (,,differenzengleiche
Paare")
Man definiert daher zunächst eine Äquivalenzrelation fur Zahlenpaare aus N X N , welche bei
Differenzbildung die selbe ganze Zahl erzeugen.
Man sieht leicht, dass dadurch eine Äquivalenzrelation definiert ist.
Definition:
I
Jede Äquivalenzklasse z = [(a, b)]:= {(X,y ) u + y = b + X ) mit
Die Menge aller ganzen Zahlen wird mit Z bezeichnet.
U,b t
N heißt ganze Zahl.
Schulmathematik Zahlen
2. Systematisches
Geometrische Veranschaulichung:
Definition der Rechenoperationen:
Addition:
[(a, b)l @ [(C, d ) l := [(a + C, b + d)l
Multiplikation:
[(a, b)] 8[(C, d)] := [(a.c + b.d, a.d + b.c)]
Motivation:
( a - b)(c - d ) = (ac + bd) - (ad + bc)
Man muss zeigen, dass diese Definition unabhängig von den gewählten Repräsentanten der
Äquivalenzklassen ist!
Es gilt:
( Z , 8 , 8 ) ist ein Integrititätsring, d.h. ein kommutativer, nullteilerfreier Ring mit Eins.
Definition einer Ordnungsrelation in Z:
Einbettung von N in Z:
Gemäß der durchgefihrten Konstruktion von Z (als Äquivalenzklassen von Paaren natürlicher
Zahlen) kann nicht gelten: N c Z
Allerdings kann N in Z eingebettet werden (sodass in Z eine zu N strukturgleiche Teilmenge
entsteht) mit Hilfe der Funktion
Schulmathematik Zahlen
2. Systematisches
h besitzt die „strukturerhaltenden" Eigenschaften:
Also kann h(N) C Z mit N identifiziert werden.
(Wir unterscheiden in Hinkunft nicht mehr zwischen den Rechenoperationen in N und Z.)
1 3.
I
Konstruktion der Rationalen Zahlen
Jede rationale Zahl kann als Quotient zweier ganzer Zahlen geschrieben werden (und kann also
als Paar ganzer Zahlen aufgefasst werden), wobei diese Darstellung nicht eindeutig ist
("Kürzen und Erweitern").
Man definiert daher eine Äquivalenzrelation in Z X Z \ (0) :
(a, b)
- (C,d )
e a.d = b.c
(a,b,c,d
E
Z, b + O,d z 0 )
Man sieht leicht, dass dadurch eine Äquivalenzrelation definiert ist.
Definition:
I
Jede Äquivalenzklasse r = [(a,b)] := ((X,y) a.y = b.x ) mit a, b E 2,b # 0 heißt rationale
Zahl. Die Menge aller rationalen Zahlen wird mit Q bezeichnet.
Geometrische Veranschaulichung:
Schulmathematik Zahlen
2. Systematisches
Definition der Rechenoperationen:
Addition:
[(U,b)] C
3
I [(C,d)] := [(a.d + b.c, b.d)]
Multiplikation:
[(a, b)] C3 [(C,d)] := [(a.c, b.d)]
Motivation:
Rechenregeln für das Bruchrechnen
Man muss zeigen, dass diese Definition unabhängig von den gewählten Repräsentanten der
Äquivalenzklassen ist!
Es gilt:
(Q, 9,
B) ist ein Körper.
Einbettung von Z in Q:
Analog zur Einbettung von N in Z kann Z in Q eingebettet werden, und zwar mit Hilfe der
Funktion
h:
Z + Q
2 -+
[(z,l>l
welche die erforderlichen strukturerhaltenden Eigenschaften besitzt.
Also kann h(Z) c Q mit Z identifiziert werden.
(Wir unterscheiden in Hinkunft nicht mehr zwischen den Rechenoperationen in Z und Q.)
1 4.
Axiomatische Charakterisierung der Reellen Zahlen
Definition:
R ist ein vollständiger angeordneter Körper
Genauer:
R ist eine Menge mit den Verknüpfungen ,,+" und „ ." und der Relation ,,
", I
sodass gilt:
(I)
(R, +, .) ist ein Körper
(2)
„< "
(3)
ist eine lineare Anordnung auf R, die mit „+" und „ ." verträglich ist.
Vollständigkeit:
Jede nicht leere nach oben beschränkte Teilmenge von R besitzt ein Supremum.
I
2. Systematisches
Schulmathematik Zahlen
Es gilt der folgende Satz:
R ist @is auf Isomorphie) durch diese Axiome eindeutig bestimmt, d.h.: alle vollständigen
angeordneten Körper sind zueinander isomorph.
Detailierte Formulierung der Axiome:
(1)
X
+( y+ z ) = ( X +y ) + z
x+y= y+x
und
und
x.(y.z) = (x.y).z
x.y = y.x
Assoziat ivgesetze
Komrnutativgesetze
es existieren Zahlen 0 und 1, sodass für alle X gilt:
x+O=x
und
x.1 = X
Zu jedem
Zu jedem
X
X
existiert eine Zahl ( - X ) , sodass X + ( - X )
# 0 existiert eine Zahl X - ' , sodass x.x?
x.(y + z ) = x.y
(2)
=0
X,
Distributivgesetz
y gilt genau eine der drei Beziehungen:
X<Y
x=y
Aus
< y und y < z folgt:
Aus X <y folgt:
Inverse Elemente
=1
+ x.2
Für je zwei Zahlen
X
Neutrale Elemente
Y<X
X
<z
x+z< y+z
x.z < y.z falls z > 0
Trichotomiegesetz
Transitivitätsgesetz
Monotoniegesetze
Ausgehend von der durch dieses Axiomensystem festgelegten Menge R können die
Zahlenmengen N, Z und Q als Teilmengen von R bestimmt werden:
(1)
Eine Menge T
R heißt induktiv, falls gilt:
0ET
(a)
(b)
x~T=x+l€T
N:= Durchschnitt aller induktiven Teilmengen von R
(2)
Z:= ,,kleinster" Unterring von R, der 1 enthält
(3)
Q:= „kleinsteru Unterkörper von R, der 1 enthält
Schulmathematik Zahlen
1 5.
2. Systematisches
24
Konstruktion von R mittels Fundamentalfolgen (nach G. CANTOR)
Idee:
Jede reelle Zahl kann als Grenzwert einer Folge rationaler Zahlen aufgefasst werden.
Zur Konstruktion von R betrachtet man daher zunächst Folgen in Q (,,rationale Folgen").
Zwei Fragen sind dann zu klären:
(1)
Wann konvergiert eine solche Folge ?
(Man benötigt ein Kriterium, das den Grenzwert nicht explizit enthält, da dieser ja nicht
in Q liegen muss!)
(2)
Welche Folgen konvergieren gegen denselben Grenzwert ?
(Alle diese Folgen bestimmen ja dann dieselbe reelle Zahl!)
Exakte Vorgangsweise:
Sei M die Menge aller Folgen in Q.
(1)
Eine Folge
(X,) E
M heißt Fundamentalfolge (bzw. Cauchy-Folge), falls gilt:
V & > O 3 k ~ N ' d n , m > k :Ix, - x , ~ < E
(2)
Zwei Fundamentalfolgen
Nullfolge ist, d.h.
(X, ), (Y,)E
V &> 0 3k
tN
M heißen äquivalent, falls
V n > k : Ix,
(X, - Y,) eine
- y,l < E
Definition:
Eine reelle Zahl ist eine Äquivalenzklasse von Fundamentalfolgen in Q.
Die Menge aller reellen Zahlen wird mit R bezeichnet.
Als nächstes müssen Addition, Multiplikation und Ordnung definiert werden.
Definition:
Seien X, y reelle Zahlen.
Sei (X,) ein Repräsentant für X,
ein Repräsentant für y
I
Schulmathematik Zahlen
2. Systematisches
Zu zeigen ist dann:
Summe und Produkt von Fundamentalfolgen sind Fundamentalfolgen
Addition, Multiplikation und Ordnung sind repräsentantenunabhängig
(R,@,@) ist ein Körper
Durch ,,<" ist tatsächlich eine Anordnung des Körpers definiert, die mit Addition und
Multiplikation verträglich ist.
Es gilt das Vollständigkeitsaxiom
(1)
(2)
(3)
(4)
(5)
1 6.
Konstruktion von R mittels DEDEKIND-Schnitten
Diese Konstruktion wurde 1872 von R. DEDEKIND angegeben. Die Gmndidee dazu findet
sich bereits in der Proportionenlehre des EUDOXUS (4.Jahrhundert v.Chr.), die im 5.Buch der
Elemente des EUKLID überliefert ist. DEDEKIND präzisierte diese Ansätze, fihrte sie weiter
und entwickelte daraus eine dem heutigen mathematischen Standard entsprechende Theorie der
reellen Zahlen.
Idee:
Jeder Punkt s der Zahlengerade „zerschneidetcbdiese in zwei „TeilecL,die in diesem Punkt s
,,aneinander stoßen".
Diese „Teile" sind Mengen U, 0 mit bestimmten typischen Eigenschaften:
(1)
(2)
(3)
(4)
U und 0 sind nicht leer
Rede rationale Zahl liegt in genau einer der beiden Mengen
Jedes Element von U ist kleiner als jedes Element von 0
0 hat kein kleinstes Element (oder: U hat kein größtes Element)
Ein Paar (U,O) von Mengen rationaler Zahlen mit den Eigenschaften (1) bis (4) heißt Schnitt.
Beispiele für Schnitte:
Jede rationale Zahl r „erzeugtu einen Schnitt:
U={xtQlxr} O={XEQ~X>~}
Andererseits wird nicht jeder Schnitt auf diese Art erzeugt, 2.B. der folgende:
O = { X € Qx~ > ~ A x ~ > ~ } U = Q\O
2. Systematisches
Schulmathematik Zahlen
Definition:
Eine reelle Zahl ist ein Schnitl (in Q). R ist die Menge aller Schnitte (in Q)
Als nächstes müssen Addition, Multiplikation und Ordnung für Schnitte definiert werden.
Schließlich kann (mit einigem Aufwand) gezeigt werden, dass diese Konstruktion zu einem
vollständigen angeordneten Körper fuhrt.
7.
Konstruktion von C
Vorü berlegungen:
In R besitzen viele quadratische Gleichungen keine Lösung, z.B. die Gleichung x2 + 1 = 0
Wir versuchen daher, einen Körper C zu konstruieren, der folgende Eigenschaften hat:
(1)
(2)
(3)
C ist ein Erweiterungskörper von R
C enthält ein Element i (P R) mit der Eigenschaft: i2 + 1 = 0
C ist der „kleinsteGKörper mit den Eigenschaften (1) und (2)
Wenn C ein Körper ist, der R und das Element i enthält, müssen auch alle Elemente der Form
z = X + i.y (mit X,y E R) in C liegen. Weiteres Bilden von Summen und Produkten fuhrt
wegen der Eigenschaft
i2 + 1 = 0 zu Elementen derselben Form.
Es ist also nahe liegend, „Zahlenu der Form z = X + i.y (mit X,y E R) zu betrachten und mit
ihnen so zu rechnen, wie man es mit Binomen gewohnt ist - mit der zusätzlichen Regel:
.2
1 =-I
Definition:
C := { ~ + i .x~, yl ~ R )
Es gilt folgender Satz:
(C,@,@)ist ein Körper, der (R,+, . ) als Unterkörper enthält
2. Systematisches
Schulmathematik Zahlen
C wurde eingeführt, damit gewisse Gleichungen, welche in R keine Lösung besitzen,
Lösungen in einer „größeren Zahlenmenge" bekommen.
Satz:
(1)
Jede quadratische Gleichung mit Koeffizienten aus C besitzt in C mindestens eine
Lösung.
(2)
Fundamentalsatz der Algebra:
Jede algebraische Gleichung (mit Koeffizienten aus C) besitzt in C mindestens eine
Lösung.
(3)
Jede algebraische Gleichung n-ten Grades (mit Koeffizienten aus C) besitzt in C genau
n Lösungen, wenn man ihre "Vielfachheit" beachtet.
Genauer:
Zu jedem Polynom der Gestalt
existieren Zahlen al,.....,an
E
f (2) = an.zn+ an-,.z n-1
+ .....+ a,
C , sodass gilt:
f(z) =an.(z-a,).(z-a,)
.....( z - a n )
Bemerkung:
(1) ist elementar zu beweisen, man kann die Lösungen ja explizit angeben. (2) ist eine reine
Existenzbehauptung; es ist i.A. unmöglich, Formeln für die Lösung anzugeben. Der Beweis
von (2) wird meist mit fortgeschrittenen Methoden der Funktionentheorie geführt.
(3) ist eine relativ einfache Folgerung aus (2), die mit der Methode des Abspaltens von
Linearfaktoren zu beweisen ist.
In Bezug auf das Lösen von Gleichungen hat C also wesentlich angenehmere Eigenschaften als
R. Allerdings haben komplexe Zahlen eine Eigenschaft nicht mehr, die reelle Zahlen besitzen:
man kann sie nicht anordnen.
Satz:
Der Körper (C,+, . ) kann nicht angeordnet werden, d.h. es gibt keine Anordnung "<", so dass
gilt:
(I)
(2)
fur jedes z E C gilt genau eine der Beziehungen: z < 0, z = 0, 0 < z
es gelten die Monotoniegesetze:
z >0A W >0
z + W > 0 A z.w > 0
Schulmathematik Zahlen
[ 8.
2. Systematisches
28
Alternative Konstruktion von C (nach HAMILTON)
Man fasst komplexe Zahlen als Paare reeller Zahlen auf, geht also von R2 aus.
R2 ist ein Vektorraum mit einer Addition und einer skalaren Multiplikation. Man versucht
nun, in diesem Vektorraum eine Multiplikation 8 "." so einzuführen, dass gilt:
(1)
(2)
(R2,+,B) ist ein Körper
(1,O) ist das neutrale Element dieser Multiplikation
Dies gelingt mit folgender Definition:
( x , , ~ l ) @ ( x 2 , ~ 2:=) ( ~ I ~ ~ - Y I . Y ~ ~ ~ I . Y ~ + ~ ~ . Y I )
In dieser Definition enthalten ist:
( 0 , l ) ( 0 1 = (-10)
was der Aussage:
.2
I = -1
entspricht.
Man kann sich leicht überzeugen, dass (R2,+,B) tatsächlich ein Körper ist, der isomorph zu
(C,+, . ) ist.
Die Abbildung
h:
R2
(X,y )
--+ C
-+ X + i.y
ist ein Körperisomorphismus
1.1 Erweiterung zur
zahlengeraden
j
Lies auf d e m T h e r m o m e t ~ rd i e Temperatur ab.
j
Hbhenangaben auf einer Landkarte bexlehen slch Immer auf den
Meerospicgel (0 m). I n Israel glbt es Gegenden. die sogar unter dem
Meeresspiegel liegen. Such* a u f d u b n d k i r t e drr ibtr M m r . d e n
S e r aenezareth und d i e S t a d t Jeru%alem u n d o l b d i e Meeres.
h o h e n an.
a) W i r v i e l M e t e r ilbrr d e m i b t e n M e e r 11egt h r u s a l r n i ?
b) FilefJt dw Jordan v o m m t e n M6.r z u m See G e n e r a n t h o d e r
umgekehrt? Welchen H d h e n u n t e r r c h l r d ü b e n v l n d e t e r dabei?
0 Auf der Erde hat man eine Hdchsttempcrstur von +6B 'C und eine
Tlefinemperatur von -92 'C gemessen. Berechne d e n T r m p r a t u r .
untenchled.
Warmcgrade werden mit einem Plus (i).
Kbitegiade mit einem Minuszeichen (-) kenntlich gemacht. Diese Zeichen heißen Vonelchon einer
W
Zatii.
W i r v l e l G r a d Ober bxw. u n t e r n u l l b e t r a g e n d i r Temperaturen?
b) -31 +C'
a) +9', -12'
Klppe ein Thermometer nach rechts: Die Skala mit den Kdrltograden
liegt links. rechts liegt d ~ eSkaia mit den Wlrmcgraden. Du srhdltst
einen nach links erwcitenen Zahlenstrahi.
Eine Zehlrngerade entsteht. wenn ein Zahlenstrahl nach links iiber
null hinaus erweitert wird.
.
Schulden auf clnem Bankkonto werden mlt einem Minus angezeigt
4) W a l b d e u t e t *In K o n l o r t r n d v o n 100 C b m . -300 0
b l WIo v l e l O r l d wrdr a b ~ ~ h o b e nmnn
.
sich d e r K o n t o s t a n d
v o n 250 C a u f -7S0 C p r l n d e r t hat?
C) Wie v l e l G e l d wrdr a u f r l n K o n t o Obrnvl*srn, mnn d e r
f t ü h e n K o n t o s t a n d 4 5 0 C b e t r u g und drr n e u * 450 C
betrllgtl
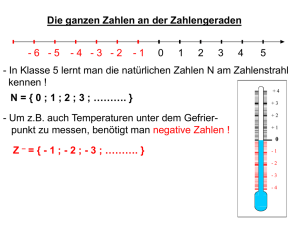
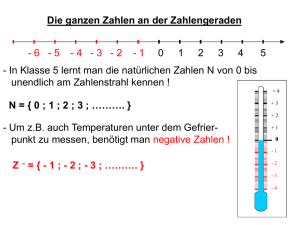
B s r r l c h n e d i e m a r k l e r r e n P u n k t e d e r Zahl*ngeradrn.
a)
-1 0 + l
v o n n u l l m l t d e m Von8lchan Plus g i k e n n c 8 l c h n r t .
W l h l e *In* veelpnete E i n h r l t u n d n l c h n r a u f einer Zahlrng r r a d r n d i e folgenden p a n n n Zahlen .In:
0 Mrnuel hat bei clnem Spiel 13 Plus- und 5 Minuspunkts erhalten, tcins
Schwester Anja 10 Plus- u n d 8 Minuspunkte.
W r r v o n b e l d e n h a t b r s s r r a b g r s d n l t f r n ? Berechne d e n
ßunkteunterschled.
D e Zahl -3 hegt glelch wei! links von null wie +3 rechts von null
Erganit man d e naturlichen Zahlen 0. 1. 2, 3.
der Null durch die iiegat~vprZaliien - 1 . -2. -3.
ganzan Zahlen
(0. .1. *2, . 3 . . .
1
vibckmnt.
Skhu lsi, d a s dk
vd üabyionkr
dle Zohl 0 rrrrsdrtui
dk Römw m k r nlcht.
Waiwchefnlich
p l w r n dle Ngrrtlnr
i a h l u i m i n d l u i &r
dle A m b a In M f n r l alter m c h Ewwpa.
*er
G war ZUMCM
whwierlg. q t h
&U
+7. tll.-3,-15. 41,-20,+14,-9.
Menge der
nat5lichen Zahlen:
*I
&t.
durch Spiegelung a n
50 erhalt maii die
Faist man die ganzen Zahlen mit einer geschwungeneri Klammer
zusammen, 10 erhalt man die Menge der ganzen Zahlen,
r l e wird mit Z benannt.
Walfisch Moby kennt von seinen Taucherpcditionen nur
neprtive Meereshbhen u n d zwar ganz brtrllchtllche Dleimai
brginnt e r seine Erkundungen In -100 m und taucht auf
-700 m, tp)iter noch auf -1 100 m. um dann wieder a u f -200 rn
zu steigen.
s e n c h n e M o b y r g r a n d l o s r i b u c h l r l n t u n u I n jeder
d e r d m l E t a p p r n u n d k r n n r r l c h n e sie m i t d e m e n t rpruchenden Vonrichen.
Zahlur N *urtrhen vd
mlt Rna N ruhnen.
Sie d l m olr symbol
fD.Schuidm tind f*
8
L.
Vi
3.
Co
g
P:
Cr
j
4
1.2 Ordnung der
ganzen Zahlen
j
Gegenzahlen
tp Zelchne auf drr Zahlengeraden folgende Zahlen ein:
+3 und -3, *5 und - 5 ,
Welche bcrondcrr
Lage haben
+3 u n d -3
zueinander 7
0
i @ Weiche Temperatur i s t h(iher7
a) +3' oder +8: b) +2' oder -4' c) -5' oder -9'7
j
Q)
Oante Z a h l e h d l e sich nur durch das V o m l c h e n
untenchelden, h e i i i e n .Ininder e n t g e g e n g n e t n
(Gegemahlen).
Weicher Kontostand rit gröoer?
a) 120 € oder E0 <. b) -30 C oder 10 €. CI
-200 € oder -50 € 7
Ganze Zahlen lassen sich auf d u
Eine Zahl und ihre Gegenzahl liegen auf der Zahlcngeradrn
symmetrisch zur zahl O.
I l e g t a u f der Z8hlmng.raden w e l t e r Ilnks.
-3
-1 0 +1
+4
Wlr wollen allgemein die Gegenzahl einer Zahl a mit
< + l oder -4 r rl
d! -10 s -8 oder -10 < -8
a) + 3 s -5 oder +3 > -5
bl -2 < -6 oder - 2 , -6
a1 +3
-5
C ] -4
- lbedeutet d i e G*genrahl v o n s.
,ein.
+7
.2
b) -2
13
CI
-20
is
-i
-3
(p Ordne die folgenden ganren Zahlen.
k l e i n s t r n Zahl.
al r 2 , -1. -7. +31
-12
-4
d) 0
-7
-10
0
Bestlmme W jeder d e r angegebenen Zahlen dir Cegrniahi:
Beginns m i t der
b) +44. -91. +74, -53
C) -20. 0,+30. -30. -100
0 Wmiche Aussage i s t wahr?
al Jede po<~tive
ganze Zahl ist gi0ßet als jede negative Zahl
b) Jede ganze Zahl hat einen Vorglnger und Nachfolger
cl Die grdßere von zwei ganzen Zahlen liegt auf der Zahleiigeraden
weiter rechts.
dlO 5s: kleiner ali jede negative Zahl
L
Q)
+
Gib r u l r d e r Z a h l d e n Vorglnger an: + I . 0, -7, -101, - 1 000
b) Glb z u jeder Z a h l den Nachfolger an: +B. -1. .E. -100, -2 1
Kannst du da5 auch
m i t einer Ungleichung
ausdrucken?
+
f,,g
d,..
1-18
1
I
I
1
0
+ll
I
'
-
-2
- (- 8)
+2
1-27
1 - 9 8
I
I
I
I
I
I
+2
+5
-B
D l e Gegenzahl d e r Gegen-hi ist
urcprüngllche Zahl:
(- a)
-
I
-12
il
B c d e v h m p e n des
Mlnusnlchenr:
I s t In b) d i e Z a h l
27
"
Q)
Subtraktlons.
zcichen:
geradenein.
a
*IT
und kleiner als t4,
Welche ganzen Zahien werden durch d i e Ungleichung
beschrisbcn?
al + l < x < + 7
C) - B 5 x < . l
c! - 5 s r ,; 2
b i - 3 ~ ~ c . 4 d!-13<i 8
{)-I6 x , .-6
46
0
(p Für welche ganze Zahlen g i l t
1. blsle sind kleiner als -2 und großer als -1 1.
CI
sie liege? 2wirchcn - 4 irnd +4,
dl sie sind rnlridesten3 $0 g i o f l wtc -5 und hochltens ro groO wie
1
1
I
fD Gegeben ist die Zahl r . Zelchne i h m Gegenzahl - a auf d e r Zahlen.
Weiche Zahl l i e g t genau i n d e r M i t t e v o n
b) -6 und + 2,
a) -1 und 3.
C ) -10 und - 27
9 ai sie sind großer als -6
a
-a
Etvtimme von der
Zahl die G.genzrhl.
davon wieder die
Gegenzahl.
(
j Q) J)
j
bezeichnen
-
Q) War I s t n c h t i g ?
Q) Setze < oder
-8
Beatlmme d l e Gagenrahl:
a) ( 4 ) * -3
Die Gegenzahl von + 3 ist -3.
(-3). *3
Dir Gegenzahl von -3 1st +3.
-
a
b)
0
10-7s)
-e-e--
Vonelchen:
-5 (minus 5)
a eine negative Zahl?
Gib d r e l z a h l e n Mr x an. so dar* .J
L
- x nigativ, b l -
X
p o s i t i v ire.
Welche Aussagen s i n d r l c h t i q ?
a) Eine Zahl und ihre GegenzaN haben von ü d e n s e h n a f l a n d
b)- z ist Immer rlne negative Zahl
C) +9 1st dasselbe wle
(-9)
-
j
--
Ci.(jrnzahllalch.n:
8 ( G . p m u h 1 von 8 )
x (G-hl
von X)
I
1.3 ~ d d i t i o nv o n
ganzen Zahlen
,
FV die folgenden
Übungen benötigst du
eincn Zahlenteppich und
I eine Spielftgur von
einem Brettspiel
-
~cliiilibewcgungcirkbnstcn dtircli <)Ulilc Zalilcrr ddrgestcli: werdcn
1
;
;
:
;
-
;
C
.'l
-
bedeutet elne
i,ineni Znl~lcniepl,~~li
\ i l i c i <,aiize Zalilcii i i i Feldern eiiigetr,i(ii?!i
rrlniieri u n s an die t>Q!ei:< b?i.L11111~
Zdhlellgerade
Atlf
.... ...-.- . - ..
Zohlcnteppich ous-
.
ter der Zahl (-3) kannst d u d l r n l c h r n u r e l n e n Punkt a
der Zahlengeraden. s o n d e r n auch e l n e B e w e g u n g v o n
3 Schritten n a c h I l n k s a u f d e r Zahlenperaden v o r i t e l l e n .
.. - .
,,
wciterc Aufgaben
-.
.
. ..
.
..'.
-
1
0
a) Vom F e l d fr2) gehe 3 Schritte nach rechts.
b) Vom Feld (-1) gehe 4 Schrltte nach links.
A u f welchem Feld s t e h t dadurch d i e Splelflgur7
Welche B e w e g u n g v o n null ausgehend b e d e u t e t d i e Zahl
a) (+I), b ) 1-9). C) 07
0 Selner
t ~ l l *dl@
Z a h l a) (4,b) (+6J.
Zahlengeraden dar.
0
C)
- - . -
---.- -..
Q)
Jcde ßewegu~ignur iici Znliletiqcradeii kann m a n
durch etnen Pfoql versnschsullchcn.
Die L l n g e des Pfeiles g l b t d i e Anzahl d i r Schrltte an, d l e
4 Schritre nach Iinkr
1
0
)
\-H444
I
L.-_
--.-.-P-
''i
.
Zeichne auf einer Zahlengeraden 3 Pfeile ein. d i e Bewegungen
revgen: n) 7 Schrltte nach links. b ) 3 Schritte nach rechts.
z
PI:
1
U0
e
Eine Schrittbewegung verlduh vom Punkt (-5) zum Punkt (.3).
Zelchne d e n r u g c h ö r l g e n H a l l e i n und beschreibe i h n d u r c h
eine ganze Zahl.
-4
-3
-2
0
-1
+2
*1
-3
r4
+5
+6
i
Beschreibung von Bewegungen durch die
Addition
@)
Glb d e n Startpunkt. d e n Pfell u n d d e n Zielpunkt der darg e i t r l l t e n B e w e g u n g an.
-2
-1
0
+l
+2
*3
.
Z e ~ c h n *a u f der Zahlengeraden folgende Schrlttbewegungen
vorn angegebenen
Startpunkt m i t slnern P f e l l ein:
al Gehe vom Piinki ( - 3 ) 7 Schrtlte nach rechts
b l Gehe vorn Punkt ( - 2 ) 6 Schr8tte nach liriks
< I Gehe vorn Puiikl i-I ) 3 Scliiitte nach links
@
20
geraden d e n zugehörigen H e l l e l n u n d b * s c h n l b e i h n m i t einer
q a n t e n Zahl.
-----.--~--.----.,..-....,.
,
8
Ein. 8rwegunQ verlluft il von (+2) nach (+9). b) von i r 4 ) nach (-4).
Cl von ( - 0 nach (-71, d l von (-9) nach (-2). Zelchne a u f einer Zahlen.
.-.* ...-., .- ..,
Pfeile -I¶ der gleichon Urige u n d glelcher Richtung
stellen dieselbe Bewegung dar: Es w o r d e n gleich viele
Schritte i n dieselbo Rlchtung gemacht.
0
!
Wrlche p a n n n Zahlen wcrd.n d u r c h d l e m a r k l c r t r n P u n k t e u n d
eing*zelchneten Pfelle a u f d e r Z e h l e n g e r a d i n darq.stellt7
-5
Welche Schrittbewegungen a u f d e r Zahlengeraden werdcn
durch die elngezeichneten Pfeile dargestellt7
/
\
(-1) als P u n k t u n d ais Pfeil a u f
0
7
bedeutet e i n
Bewegungen auf der Zahlengeraden
kannst du einen
3 Schrtttc nach rechts
...
.
Wie viele Schritte i n welcher Rlchtung fiihren
a) v o m Feld (-5) a u f Feld (+alt b) v o m Feld (+C) a u f Feld (-5).
C l v o m Feld 1-12) auf Feld ( - 4 ) . d) vom Feld (-3) auf Feld (-9))
+5
t4
.
.
.-
+6
.. .. .
*7
-
Verqlriche m i t der A d d i t l o n natilriicher Znhlrn: 2 r 5
Du lleI~$l
bcr 1.21 u ~ > yd ? l ~ I5 SfImtlc ,,,>,I! rv<!;l\ I),, C,,, . w q t
I
.a
:7
!.>CI,
:.7i
r9
Eine Bewegung out
Addition ousdriicken
!
j Q)
Berchnlb: die dargestellte Bewegung durch r l w Addltlon.
0 Füll* d i e Additlonrtabelle aus:
b)
dl
03) Wekhe
Rechenregeln
d l t Additlon ganzer Zahlen kannsf du aus
folgenden Rechnungen ablelnn? Schreibe sie mir Viriabltn auf!
iür
/
@
.I
Gib das ZI.1 folgrnder Bewrgungen auf der Zahlengeraden an
und schnlbe dle xugehbrlge Addltlon an.
E
1
%<
I
5 nach llnks
5 nach rechts
7 nach links
r (-5)
0 Suche die unbekannte Zahl
5 Schrinc
nach links
Ziel
Stan
1-31
(-8)
und
4 Schrllit
nach rechts
ZImI
14)
Welche Bewegung wird durch dle Addltlon dargestellt?
Wie lautet daher dar Ergebnls?
J ) (-3) r ( 4 )
0 ( + I ) + (-6)
e) (-12) + 1-2)
b ) (-81 t (-31
d) ( - 5 ) + (-7)
f ) (-7) + ( + 2 )
-
.
Vbrlei)r Start
und Schritibewegungl
. .
i
Q)
b 9
;@
i
\
+ (-8
C) (-101
(t14)
d l ( + T ) + (-121
e) (-8)
+ (-9)
!I (-61
+ l+ll)
CI 1-30]
+ (-20)
d) 1-10) + (+30)
e l (t15) t (-25)
f) (-151 + (+25)
Oberprilfe dar V~rtaurchungsgesetzder Additlon ganzer Zahlen:
a) ( i 3 ) t 1-8)
b) 1-4) + (+9)
C) 1-7) t (-5)
1-8) + i * 3 )
(+9) + 1-4)
(-51 + (-7)
i
C..„.,
,'
'.
Addieren Sv nach,
,1.2)
+ 1.-
C)
= I - 8)
-
-
t 4
1-5 = 1-11)
-
-
-
Setrr ein und Ubtrpnife so das Verbindungagertfi
ge1etz) der p n r e n Zahlen: a + Ib r C) i (a + bj + c
Ai
a
= 1-31, b
.
1.51.
n) a
1-71
i
(-71, b
C
1-8)
I+&) t 1-6)
(-2) + 1-3)
4
2
1-3) =
(-51
[ A S S O ~ , ~ ~ ~ ~ .
..
11)
al Addiere zur Zahl Ir301 forllaulend 30 lange die Zalrl (-. b,$ d u 0
iirilerichreiicri W i r hei13t d l r t r s t r Zahl unter O?
b l Addicrc z i i r Zahl (-301 fortiaufe,id so lange dio Zaid L - : ii.5 d , , o
iibers<hrcnie<i Wie helflt die erste Zahl Uber O ?
vischrncrgcbnisse au!l
L--
Rechne inr Kopl:
)LI
(-9)+ (+GI.
I 51
-1-111 < l i i l O l (-61. ( - 7 ) . . i 2 l * ( . 3 1
~ + 7 ~ + 1 - 5 1 + l - 4 ~ + 1 ~ 3 i * ~~ - )l 2i ~- l 4 1 ~ 1 ~ 8 . :I . ~
: 5 ~1 *+( l G~I
1 b B i
0Welche Zahl muss z u l ~ t z noch
t
addierf werden.
Ergebnls (-101 rein soll?
Berechne:
a) (-20) + (+I51
b) (151 + (-201
t
(-6) *
Meiiiore Znlile.. kbiiiien .\.i,lere!nt . d c < ~ d < l ; c ii.>erdcn
l
Berechne
1-31 + (+I31 .-GI
2 ) 1-8) + ( + 3 )
I . 6 ) . 31
U1 ( + 9 I 1-11 1-51
+I( t 2 1 t I 91 + 13.
-5)
0 1.10) I - J b.71
' I 1-11 + (-8) 1-91
- ::
a)
Berechne:
a) (110) + 1-13)
-91
-12)
X:
b) 1-31 + r = (+3)
a) (+31 + x 1.11
(-4) r X = 0
-
Dia Addition zweier ganzer Zahlen kann man durch .In.
Bewegung auf der Zahlengeraden verinschaulieh*n:
und
--
(*I21
Kenn +in* Summe von 2 Zahlen kleiner I r i n .Ir einer der b c t d r n
Summanden? Wenn 1. glb * I n Zahlenbeisp~elan.
d)
StaR
C) 1-91
Kann r l n e Summe von 2 Zahlen k k l n e r sein a b Jeder d r r b e ~ d e n
Summanden? Wenn ja, gib ein Belsp/el an.
1
Umgekehrl kannst du dir unter der Addition von zwel ganzen Zahlen
eine Bewegung vorstellen
j
,.-
63)
*
b l (4) 1-61
( - 2 ) t 1-2)
+
l+4)
7 nach rechts
:
T,.$
al 1-5) + 0
0 + (-51
a) 1-20) + ( + S I
+
bl (+40) + (-26)
( + ? I + (+4) t 1t71
+
-
(-231 + 1.2) + (-:J1
I
= (-10)
(-10)
t iz
Benchne fiir die Startzahlrn (-2) und 1,s).
wenn das
Um wie viei
unrerrcheiden rlch ote
beiden Siarl,ahlen.
um wre viei die
FrQebntrie'
.
,..-
-
@
Anwendingen der Addition
-
In einigen Jahren hast du w a h r ~ h e i n l ~ cein
h Konto auf elner
Bank Du kannst dann:
Geld abheben (Lastschr
m Zustindsllnderungen
Benchne d e n neuen Kontostand:
(+35) C
t
Peter liest am Morgen, am Mittag und am Abend am Thermometer die
Lufttemperatur ab. Ergänze dle Beschnlbung.
Alter
(-62) f
+
1
1
F
i
Lastrchrlft
I
I
Neuer
1
B
Benchne den n w e n Kontostand:
r l dr?e h t r r a k h i n D.1-r.
r M M i p RDVI wird dn V a .
ilthan s(l Mmir dir h h i
*#M
(L I.U-1 Und dii W.
iIchqn + drd miln mgg*l.rtrn.
-
O h werden mehrere Kontohwegungrn hintereinander durchgef0hn.
I e r u h n e d e n neuen Kontostand:
Zu111nd
12.00 Uhr
Zustand
I
&OO
(-8)'
uhp
4
(+)l3'
(+5)'
(+5)'
rn
Zu~tand
18.00 Uhr
+
1. Ablesung + Andtrunq 2. Abiesung
1. Ablesunp Anderung 2 Ableiung
(+10)'
1+1Y
C&\.
1-
2
(4.7)'
(+4)'
I
-
(-3)
+ (+10)
(-12)
+ (+4)
+I20
470
INeuer Kontonand
MaRlna liest zweimal am Tag die Temperatur ab. FUlle dle Rbelle aus.
3
-12
Gutschrift
Lastschrlh
Nwsr Kontonand
Q) Benchne d e n nmuen Kontostand:
(17)
I
1
Q)
Um 7 Uhr betrug die Temperatur -2 'C. Wahrend des Tages stieg sie um
5 'C. wdhrend der Nacht sank sie um B 'C Welche Rmperatur h a t t e
es am nschrten Morgen7
Q)
Gib dle Rmperdturinderung an:
a)
b)
e)
4
1. Ablesung
+3'
-2"
+ S V 0 '
-12'
-5'
g)
-16.
2.Ablesung
c8'
+9'
-2'
+4'
-11'
-9'
C)
d)
-7'
Q)
Du k
m auf
zwel Arten rechnen:
In der anppcbcncn
Ralhnfolgr oder
Indem du wrai dle
I(mtobe*npvp.n
I
.
m
F
Bmmchne dle fehlende Kontobmwegung, ist ms elnc Gutschrift
oder elne L a r h c h d h ?
~ n n n f a u t .
Schulmathematik Zahlen
3. Didaktisches: Ergänzungen
Lehrbuchauszug: Erber / Ottenschläger u.a., Zum Beispiel Mathematik 3, 2001
-
..
sap?
;:E
P2 t -+
Y) C
S K X
C0
-f n7
P".
5:;
,-
L + -
agg
C
.
1
2ss
g$S
*:Ti$
-E::
6z
8
34
t Q) E q d n z e ZU einem magischen Quadrat:
1.5 Multiplikation von
ganzen Zahlen
j
2 -3 -4
0
[0
a) S e h e d l e Zahlen
1. 0, -1, -1. -3, 4 ein,
so dass d l e Summe aller
z a h l e n e n t l a n g j e d e r Seite
glelch gmr3 Ist.
5 -6
3 - 3 2
Q)
b) Setze d l e Zahlen
2, 0, -1, 4, 4 eln,
sa dass d l e Summe
w a a g n c h t u n d senkrecht
gleich g m 0 Ist.
Die Multipllkatlon poslliver Zahlen entspricht der Multiplikation
natrirlicher Zahlen. Berechne:
(+3) . (+4)
(112)
(+5) , ( r 7 ) r
.t
t
3 . 4 . 1 2
t
t
t
5 . 7 1
WIa aber m v l t l p l l t l e r t m a n n e g a t l v e Zahlen)
Dazu betrachten wir ein Reihe von Multiplikationen. In denen ein
Faktor gleich bleibt und der andere jeweils um 1 kleiner wtrd.
sind dle Ergebnisse
r12, r9. * 6 . *3. 0.
d m müssen die
-3+5=7
Beginne bei -3 und
zdhle 5 vombrtr:
-3
0
2
-3t5.2
oder: -3 + 5
(-31 + (CS) = (+2)
/
:
'
1
!
'
Brnchne:
(1)-3+9
-5r9
b)-9iil
-10+3
C) - 8 + 6
-9e13
d)-1319
-11+20
E)-20117
-16+19
Benchne:
a)5-9
3-5
b)7-11
0-6
0-2-7
4-11
d)-4-9
-8-12
e)8-21
6-14
8-10-7
j @
3-Sr?
Beginne bei 3 u n d
zahle 6 zurOci:
-;
: :
:
- 1
-2 - K-m-- 2 oder: 3 - 6 =
(+3) - ( r 6 )
-
(+3)+(d)i(-3)
j
i
1
\
Deshalb hat man In der Mathematik festgelegt.
enchne:
a) 7 - 4 - 8
niichsten Ergrbnissc
Fdllt d i r a n den E q e b n l s r e n e t w a s ruf7
Wir setzen die Ergebnisse im gleichen Sinn f o n
b) 3 - 8 - 7
5 - 11 -7
Benchne:
a) 6 - 9 t 4 - 8
3-713-11
Berechne:
a) 5 - 9 - 7 + 1 0 - 3
9-1?+4-8-7
C)
6-7
4-9t3
1-13r8
p o t l t l v e Z a h l n e g a t l w Zahl 8 negatlve Zahl
n e g i t i v e Zahl. p o s l t l v a Z a h l negatlve Zahl
n e g i U v e Zahl. m p a t l v a Zahl iposltlve Zahl
b) 9 - 1 2 - 7 * 4
Q)
b)-217-9+3-8
-7-9+8+3-6
8enchne:
a) - 1 0 i 1 5 - 1 3 t . 4 - 8 r 6
6-llt3-7+13-10+0
b) 5 - 2 5 + 1 0 - 2 0 + 3 5 - 1 5
1 7 - 3 0 + 8 - 1 5 + 13-25
C) 3 - 5 4 7 - 8 + 3 .
10-15-8-7+4
Benchne:
a) ( 1 4 ) . (4)
( + 4 ) . (-5)
4
C) - 3 - 8 r 1 4 - 9 - 6 + 7
-6+10-9+4-1018
d) - 1 5 - 1 5 + 2 5 - 8 r 2 0 - 1 0
10-45+15+8-12r25
I -
Benchne:
8) ( + 5 ) . (c7)
(-3) . ( t 7 )
l+9) . (-5)
(-12). (-3)
b) (-2). (+7)
(-2) . (-7)
( + Z l . (-71
b) (-17). (+2)
1 1 -5)
(-3) (-9)
( t 2 0 ) . (+?)
.
C
1
1
(-1). (*I)
( * l ) 1-1)
C) 4
( I )
5
- 7
(16) ( 4 )
(-12) ( t l O )
d) (-3)
li21
1-3) ( - 1 )
(-31 0
d) (-51 1-51
( t 8 1 (-7)
1-11)
. (+91
1-131 (-1)
Achte auf die
Vwxelchcnregeln.
alles andere bleibt
Q)
A
Fülle die Multlplikatlonstabclle aus.
b)
M
1.6 Division von
ganzen Zahlen
--
-
(ip Die Division ist die Umkehrung dar Multiplikation.
j
@
/,
Was b e w i r k t dle Multlpllkatlon e h e r Zahl m i t
bewlrkt die Multiplikation elner Zahl m l t (-1)7
a) (+6).( + I )
b) (+6) (-1)
C)
(4)
, (+I)
(4), (-1)
0 .( + I )
0 . (-1)
.
j
Benchne:
a - 4 - 3 - 2
(+6) (-4). ( +3)
(-1) (-6) ( t 7 )
(+6). (-24)
(-4) = (-12)
nepstlve Zahl : posltlva Zahl
b ) (13) (-7)
, (t2)
C)
(-1) (-8) (-9)
( + I > ) ,(-1) , (-4)
(t3)
( r 4 ) . (-5) , (-3)
(-15) , ( + 4 ) . (-1)
(-5)
(-6)
Dla Basb p l b t an, welche Zahl ,,mit sich selbst"
multipllrlert w l d . DIa Hochzahl g l b t an, wie o f t dar
Schnlbe k i l n e r als Potenz
7 7 7 7 7
.
(-6) (-6) (-6) . (-6)
Bonchno don Wert der Potenz:
a) 5'
b) 10'
ci 34
d) (-7j2
8'
53
- 2
Q) Berechne das Produkt:
a) 2 . 3'
b) 3 . 4 '
o
4.2'
d) s . i l
(4 . 2)3
3 (-2)'
.
e) (-2)'
(-lP
e) 2 . 5'
2
-
negatlva Zahl
,
Q)
Unhnchelden $Ich dle Vonelchutregeln der Olvlslon von
denen der Multlpllkatlon?
Q)
Beruhne:
ai ( + X ) : (4)
(-32) : J 4 1
(-32) : (+4)
S t a t t 4 . 4 schreibt man kurzer 4' und sagt "4 hoch 2" oder ,.4 zum
Quadrat". Statt 4 , 4 . 4 schreibt man k0rzer 4' und sagt "4 hoch 3-.
(3 412
weil
weil
posltlve Zahl r posltlva Zahl = porltlva Z i h l
Q,
(2 . 3 ) '
(-3). (-5) = (+15)
Deshalb hat man In der Mathematik irrtgelegt:
Benchne den FIYcheninhalt *Ines Quadrats u n d das Volumen
eines WOriels m i t der SeltenliYnge 4 cm.
3 3
(c7). (4) (+211
.
Potenzschreibweise
1
j
weil
well
E q l n z s genauso:
(-24) : ( 4 )
(-12) : (-4)-
(-1). (+E)
(-1). (-7)
(-1) , (-5)
Multlpllxlert man aine Zahl m l t (-1).
so e r h l l t man dle Geaeniahl.
iI)
: (+3) (+T)
5:5
- 3
1
(+Y)? Was
b) (-24) : (+6)
(+24) : (-6)
(-24) : (-6)
C) (+36) : (-9)
(-60) : (+5)
5
. -5)
Berechne u n d m u l t l p l l z l e n zur probe:
a) (+I21 : (+4)
b) (-32) : (+8)
C 2
7 :- 3
(-20) : (+5)
(+35) : (-7)
- 5 - 1
1
:- 3
(-30) : (-6)
( + X ) : (+3)
- 2 :1
(145) . (c9)
(-65) . (CS)
@
Benchne u n d f ü h n dle Pmbe durch:
a) 0 : (+7)
b) (-5) : ( + I )
0 : (-3)
(+5) : (-1)
Benchne:
8) - 2 :2
:- 3
- 3 6 :- 2 :- 6
C)
d) (-18) , (+2)
(-18) : (-3)
(r18) . (-6)
d) (190): (-6)
(+7)
(-72). (-4)
( ~ 9 6 :1(-12)
(-84)
E r l m n dlch:
5 I0
~IMIOS.
Es gibt k r l n Zahl.
dir mlt 0 rnuttiplirirri
(-8) : (+E)
(-4) (-4)
B tqtbtl
b) (+28) : (-7) : (+4)
(+60) : (-5) : (-4)
Benchne zuerst den W r r t der Potenz u n d d l v l d l a n dann:
a) 2' : (-2)
b) 6' : (-12)
C) (-4)' : (-8)
2' : (-4)
31 : (-9)
(-2? : (+4)
(Di) Such* dl* Unbekannte x durch Umkehrung der Rechcnoperation:
a) (-2) . K = (-8)
b) (+3) , X = (-27)
C) x : (-6) m (-7)
X
. (+7) a (-56)
X
:- 2
-
(-9)
(+48) . x
n
(-8)
@ Wegen d n VeRauKhungs. und Verblndung%gesttzeikannst du dte
- -,
@
-
-
F U h n sowelt mdglich folgende Rechnungen aus u n d ver.
glelche dle Ergebnisse:
a ) (-6) + (+3)
C) (-6) - (+3)
e) (-6) (+3)
g) 1-6): (+3)
<+ 3) + (-6)
(+31 - (-6)
(+3). (-6)
(+3) : (-6)
.
Reihenfolge der Summanden beliebig vertauschen.
Ycrtausche b1
. d h s m Rechnungen voriallhaft:
1) (-13) + (4)
+ (-7) + (+13)
b) ( 4 ) + (-15) + (-25) r (+T41
(-18) + (-26) + (-14) + (-12)
(-9) + (-17) + 1-21) + (+7)
@ Fasse alle Summinden u n d alle Subtrahenden rusammen:
a) 1 3 - 2 4 - 1 6 + 8 + 9
Wende dar Vertollunprgeset. an:
b) (+7) 1-21) (+5) , (-21)
C) l+48) : (+3) + (-42) . 1.3)
b) (+19), (-12) (+19) 1-10)
d) (-63). (-7) + (+63); (-7)
.
FOr alle ganran Zahlan 8 u n d b g1Ik
a + b r b * i
Vertiuschungsgeseh
i.b-b.a
(Komrnutativgeseb)
-
F ü h n soweit m(lp.llch
glelche die Ergebnisse:
a 1-24 + I
+- 2
(-24) + 1(+6) + (-2))
glelen k a m man die
M I t l g k r l t *Inu
nuh.ng.wtiu fP all.
i a h l m nlcht herleiten.
E: 1st auch wmögllch.
r l n R8chrngue?z fP
unendlich viel* Zahlen
-
b) [(-24) (+6)1 - (-2)
1-24) [(+G) (-2)l
-
- folgende Rechnungen aus u n d ver.
I(-24) . ( 4 1 . (-2)
C)
-
-
(IP Beachte dle Reihenfolge der Rerhenoperationen:
U)
(-7)
+ 3 . (-8)
b) (-4) : (+2) + 1
.
(-24) . 1(+6) (-2)1
d) I(-24) : (+6)1: (-2)
(-24) : [(+W : (-2)l
b)22-9-17+28-44
-
2
1-12 : 6
d) (-7). (-2) 4 (-9): 3
C
-
e) 27 1-2). (-6)
f) (+)E) : (4) 5
9) (-9)+ ( 4 4 ) : (-6)
h) (-20) (+36) : (-9)
-
-
@ S e m In der Rachenrchlsng.
naci1.1nander
- (-3) (-61
(-21) : (-3)
- (+B) (-1)
- (+15) (-3)
(-45)
(-7) +
k) (-13)
I) (+45)
I)
j)
,
,
/
1, -2 u n d 8 ein1
in der
Mathematik sind
duhalb üemlse. dle
allpsmelne Wltlgkelt
zelprn, sehr gefmgtl
FOr alle ganzen Zahlen a, b u n d C pllt:
(a+b)+cma+(b+c)
V~rblndungsgas~tz
(Asaoalatlvges~hl
@
Zahlen k a m man Jede
Addltlon und
MulHpllkaHm ausfhren
ud bekommt als
Ergebnii w i c d v clne
m t ( C l l c k Zahl. MI?
garuen Zahlen 1st auch
Jede SlibtmMlon
mogllch. Dol g(lt Jedoch
nicht fP Jede ballebigr
Führe folgende Rechnungen aus u n d vergleiche die Prgebnlase:
a) ((-7) + (+5)1 , 14)
b) (-6) [(+SI + (-!')I
(-7). (-4) + (45) . (-4)
(-6). (+5) + (-6) . (-7)
.
+
(6)-1+3)
4 -1
,
-
- )
(+4*
-18
e) Multlpllzien man eine Zahl mit 5 und addien 12, so erhalt man 2
b) Addlen man zu einer Zahl 4 und multlplizirn mit 3. so erhhlt man -9
C) Dlvldien man eine Zahl durch 4 und subtrahlen 7. ro erhdli man -!0.
POr alle ganzen Zahlmn a. b u n d C gllt:
(a+b).c.a.c+b,c
Varteflungsgesih
a.(b+c).a.bca.c
(DlstrlbutlvgaseM
I
/
j
ZUSAMMENFASSUNG
DIe ganzen Zahlen kOnnen Z u s t l n d e (m Punkte a u t d i r
Avch klganian Zahlen gllt: Punkt- vor S t i l c h M n u n g .
Wenn auch Potmnzan vorkommen. so muss man SI-w a r s t
boruhnmn.
I
-
-
Findest du einen
Zussmmrnhing
zwischen der
Start- uqd Endzahl,
I
II
Beachte die Vorrangregeln u n d berechne:
a) 1-2) + (-3) + (-2) (-3)
d) (-3) . l 3+ (+I91
b) (+6) - (-5) . (+2) i(-8). 1+2)
e) (-4) : 1-11 3 l
C ) 12-10
(-2)-30
1) (-512 ; (-5) - (-20)
-
II
Die Subtrsktlon einer ganzen Zahl Ist dle Addltlon der
Qagenzahl.
FUr dle Multipllkatlon u n d D l v l r i o n galten d i e
Vonmlch*nregeln:
G a k h V m e l c h e n ergeben eIn posltlves Ergebnis.
v*rschledene Vonelchen argeben *In ~ p a t l v m sErp*bnls.
1-3)
- (-2) * (-3) + I+Z)
.
1-3). 1-21 (+6l
1-3) , I +2) 1-6)
'I
3. Didaktisches: Ergänzungen
Schulrnaihematik Zahlen
.
[ Spiel zur Einffihrung des Addierens und Subtrahierens ganzer Zahlen
Spielsteine:
@@.
@ @
.
•
00000000
Operationen:
(schwarze Steine)
(rote Steine)
(Befehle auf Kärtchen, die gezogen werden ....)
Hinzufugen von Steinen:
Wegnehmen von Steinen:
Regel:
Jederzeit dürfen gleich viele schwane und rote Steine aus dem Spiel oder in das Spiel
genommen werden ("Reduzieren" bzw. "Erweitern")
Beispiele (Ikonische Ebene)
Formale Rechnung: (Symbolische Ebene)
(+3) + (+2) = (+5)
(+3)
-
(+4)
(-2) + (+4)
= (-1)
= (+2)
(- 1) - (-3) = (+2)
(+3) - (-1) = (+4)
38
Schulmathematik Zahlen
3. Didaktisches: Ergänzungen
39
I Wichtige Eigenschaften der reellen Zahlen
I Dichtheit von Q in R:
Sei A
(Ä
B. Dann gilt:
= Menge
A liegt dicht in B a Ä = B
aller Häufungspunkte von A = Menge aller Grenzwerte von Folgen in A)
Der Satz: „ Q liegt dicht in R " bedeutet:
In jeder Umgebung einer reellen Zahl gibt es zumindest eine rationale Zahl
Jede reelle Zahl lässt sich beliebig genau durch rationale Zahlen approximieren
Davon zu unterscheiden ist die folgende wichtige Eigenschaft von Q:
Zwischen zwei verschiedenen rationalen Zahlen liegen unendlich viele weitere rationale
Zahlen.
Äquivalente Fassungen der Vollständigkeit von R:
A. Jede nicht leere, nach oben beschränkte Teilmenge von R besitzt ein Supremum
Wenn eine (nicht leere) Teilmenge von R eine obere Schranke besitzt, dann besitzt sie auch
eine kleinste obere Schranke.
B. Sind A, B nicht leere Teilmengen von R,sodass
dann existiert eine reelle Zahl C,sodass
alb
JUr alle a E A, b E B
a l c i b füralle a € A , b € B
C. Jede Intewallschachtelung besitzt einen inneren Punkt
zusammen mit dem Archimedischen Axiom:
Zu jeder positiven reellen Zahl a gibt es eine natürliche Zahl n mit n > a
D. Jede Cauchy-Folge ist konvergent.
zusammen mit dem Archimedischen Axiom
Schulmathematik Zahlen
3. Didaktisches: Ergänzungen
40
Algebraische und transzendente Zahlen
Definition:
Sei a eine reelle Zahl.
b
a heißt rational, wenn es ganze Zahlen a,b gibt, sodass a = - bzw. a.a - b = 0
a
a heißt irrational, wenn a nicht rational ist.
a heißt algebraisch, wenn es eine Polynomfunktion f mit ganzzahligen Koeffizienten gibt,
sodass f(a) = 0
a heißt transzendent, wenn a nicht algebraisch ist.
Beispiele:
fi
ist irrational, aber algebraisch (da
&? Lösung der Gleichung
x2-2=0 ist)
il
1+ - ist algebraisch
('0
e ist irrational
e ist transzendent
(Hermite 1873)
ist irrational
n ist transzendent
(Lambert 1767)
(Lindemann 1882)
7~
I ..Konstuierbare Zahlen"
Seit der griechischen Antike sind ,,Konstruktionsprobleme mit Zirkel und Linealc' intensiv
studiert worden. Dahinter steht die Auffassung, dass Geraden und Kreise die eigentlichen
Objekte der Geometrie sind.
Die Verwendung der Werkzeuge „Zirkelccund „Lineal" ist dabei sehr eingeschränkt:
Mit dem Lineal kann eine Gerade durch zwei bereits vorhandene Punkte gezeichnet
werden.
Mit dem Zirkel kann ein Kreis gezeichnet werden, wenn sein Mittelpunkt und ein Punkt der
Kreislinie bereits vorhanden sind.
I
Schulmathematik Zahlen
3. Didaktisches: Ergänzungen
(Das Lineal hat keine Markierungen, kann also nicht zum Messen verwendet werden. Der
Zirkel kann nicht zum Übertragen von Längen verwendet werden.)
3 klassische Probleme:
(1)
DreiteilungdesWinkls:
Ein gegebener Winkel ist „mZuL" in drei gleich große Winkel zu teilen
(2)
Würfelverdoppelung:
Aus der Seitenlänge eines Würfels ist „mZuL" die Seitenlänge eines Würfels mit
doppeltem Volumen zu konstruieren.
(3)
Quadratur des Kreises:
Zu einem gegebenen Kreis ist „mZuL" ein flächengleiches Quadrat zu konstruieren.
Im 19. Jahrhundert konnte gezeigt werden, dass alle drei Probleme unlösbar sind.
Zum Beweis werden die geometrischen Konstruktionsprobleme in algebraische Probleme
übersetzt.
Man verwendet ein kartesisches Koordinatensystem und betrachtet die Koordinaten jener Punkte,
die in endlich vielen Schritten aus den Endpunkten einer Einheitsstrecke konstruiert werden
können. (Neue Punkte entstehen dabei als Schnittpunkt zweier Geraden, als Schnittpunkte eines
Kreises mit einer Geraden oder als Schnittpunkte zweier Kreise.)
Auf diese Weise erhält man die Menge der „konstruierbaren Zahlencc.
Klarerweise ist jede rationale Zahl konstruierbar; es gibt aber eine große Klasse von irrationalen
Zahlen, die ebenfalls konstruierbar sind.
Jede konstruierbare Zahl ist algebraisch.
Es gilt:
Beispiele:
ist algebraisch und sogar konstruierbar
G
7~
ist algebraisch (als Lösung der Gleichung x3-2 = 0), aber nicht konshvierbar
(und damit
6) ist transzendent, also nicht konstruierbar
cos(20°) ist nicht konstruierbar.
Schulmathematik Zahlen
3. Didaktisches: Ergänzungen
42
I Die Euler'sche Zahl e
1
(1) Stetige Verzinsung
Ein Gedankenexperiment nach L.EULER, das im Kern auf J. BERNOULLI zurückgeht:
Ein Kapital Kwerde zu einem Zinssatz von jährlich 100% verzinst.
Sei K r sein Wert nach 1 Jahr.
Wir betrachten verschiedene Möglichkeiten der Verzinsung:
Ganzjährige Verzinsung (arn Jahresende) :
K' = K.2
Halbjährige Verzinsung (mit jeweils 50% pro Halbjahr
und Zinseszinsen):
K' = K.1,5.1,5 = K.2,25
Vierteljährige Verzinsung (mit jeweils 50% pro Halbjahr
und Zinseszinsen):
K'= K.1,25~= K.2,44
Allgemein: n Verzinsungsperioden (wie oben)
Man erkennt schnell (der Beweis ist aber lästig!), dass K r größer wird, wenn man die Anzahl
der Verzinsungsperioden vergrößert.
(d.h.: Die Folge
X,
=
L)"
1+ -
ist streng monoton wachsend)
Es stellt sich nun die Frage:
Kann man durch immer weiteres Verkürzen der Verzinsungsperiode das Kapital K r beliebig
groJ machen, oder existiert ein Grenzwert ?
Tatsächlich existiert ein solcher, und er wird EULER zum Gedenken mit e bezeichnet:
Interpretation:
Die Zahl e gibt an, um welchen Faktor ein Kapital bei kontinuierlicher („stetiger'7 Verzinsung
und einem Jahreszinssatz von 100% nach einem Jahr anwächst.
P
..-
Bei einem Jahreszinssatz von p % und „stetiger Verzinsung" beträgt dieser Faktor e loO
Die ,,stetige Verzinsung" ist ein interessantes Gedankenexperiment ohne praktische Bedeutung.
Es wird daraus nicht klar, warum die Zahl e eine so wichtige Rolle in der Mathematik spielt.
3. Didakiisches: Ergänzungen
Schulmathernatik Zahlen
(2)
Ableitung der Exponentialfunktionen
Zur Berechnung der Ableitung vereinfachen wir zunächst den Differenzenquotienten:
Damit gilt:
f
'(X)
= lim
f
(X
+ h) - f
(X)
h
h+O
= ax.limh+O
ah - 1
h
Ohne den verbleibenden Grenzwert zunächst berechnen können, lässt sich feststellen:
Die Ableitung einer Exponentialfunktion ist wieder die Funktion selbst, multipliziert mit einer
Konstanten, die nur von der Basis abhängt.
a h -1
f(x)=ax
f'(x)=aX.ca
wobei C, = lim h+O
h
Dieser Faktor
C,
kann interpretiert werden als Steigung der Tangente an der Stelle
X =0
Für konkrete Werte von a lässt sich C , näherungsweise mit dem Taschenrechner bestimmen
durch Einsetzen „sehr kleiner" Werte fur h .
Man erhält 2.B.:
C,
N
0,69
C, N
1,10
Welche Basis muss eine Exponentialfunkfion haben, dass diese Konstante den Wert 1 hat ?
Diese Basis erhält die Bezeichnung e . Aufgrund obiger Überlegungen ist plausibel, dass eine
solche Zahl e existiert und einen Wert zwischen 2 und 3 hat.
Dieser Zugang zeigt eine zentrale Bedeutung der Zahl e fur die Mathematik:
e ist die Basis jener Exponentialfunktion, die mit ihrer Ableitung identisch ist.
Mit folgender Überlegung kann die Zahl e näherungsweise berechnet werden:
Aus
eh -I
lim h-tO
h
=
1 folgt:
e h -1
h
-
N
1
1 fur kleine h . Setzt man: h = - und
n
-
denkt sich n „sehr groß", dann gilt:
-
e" -1
1
-
-
1
also
e
N
(l+
:)"
Schulmathematik Zahlen
3. Didaktisches: Ergänzungen
44
I Die Kreiszahl n
Das Symbol n wurde von L. EULER eingeführt (als Abkürzung für „perimeter"), die Zahl
selbst ist seit den Anfangen der Mathematik erforscht (und mystifiziert) worden.
(1) n in der Elementargeometrie:
Üblicherweise wird die Zahl n definiert als Verhältnis zwischen Umfang und Durchmesser
eines Kreises.
(Dazu muss zuerst gesichert sein, dass dieses Verhältnis vom Durchmesser unabhängig ist,
d.h. f i r jeden Kreis gleich groß ist!)
Damit gilt für den Umfang des Kreises kiarerweise: U = d.n = 2rn
Die Zahl n taucht in der Folge in vielen weiteren Formeln auf, 2.B.:
Kreisfläche:
A
= r2.n
Kugelvolumen:
Kugeloberfläche:
0 = 4r .n
Bemerkung: Diese drei Formeln wurden - unter anderen! - erstmals von ARCHIMEDES
mit Hilfe der Exhaustionsmethode bewiesen. Heute verwendet man am besten
Integralrechnung.. .
(2) n in der Analysis
In der Analysis werden Winkel im Bogenmaß gemessen; also sind wichtige besondere
Winkel Teile oder Vielfache von n .
Grund fur die Verwendung des Bogenmaßes (neben seiner „NatürlichkeitG)sind die sich
ergebenden einfachen Ableitungsregelnfür die Winkelfunktionen.
.f (X)= sin(x)
f '(X) = lim
h+O
sin(x + h) - sin(x)
h
= lim
h-0
sin(x).cos(h) + cos(x).sin(h) - sin(x)
h
Schulmathematik Zahlen
3. Didakiisches: Ergänzungen
= COS(X).
lim*
h-tO
+ sin(x). lim cos(h) - l
h
h-tO
h
Misst man Winkel im Bogenmaß, dann (und nur dann!) gilt:
lim
h+O
f '(X)
Also folgt:
cos(h) - 1
=O
h
= cos(x)
Um die Schwierigkeiten bei einer exakten Definition von r in der Elementargeometrie zu
umgehen, verwendet man oft andere Definitionen, die natürlich von der Idee her der
Geometrie entstammen:
(Flächeninhalt des Einheitskreises)
0
?
1
1
r := 2.j =dr
(Umfang des Einheitskreises)
0
r
-
2
ist die kleinste positive Nullstelle der Funktion
(3) Numerische Berechnung von
7c
„Vorgriechische" Kulturen verwendeten verschiedene Werte für r ,vermutlich ohne klare
Vorstellung davon, dass es sich nur um Näherungswerte handelt.
1
8
Babylonier:
7c
= 3-
Bibel:
r = 3 (?)
= 3,125
Sehr gute Näherungswerte finden sich auch bei Chinesen, Indern und Arabern.
3. Didakiisches: Ergänzungen
Schulmathematik Zahlen
10
1
Erster systematischer Berechnungsversuch von ARCHIMEDES liefert: 3- < n < 3 71
7
.... lnhalt des Kreises mit Radius I
K
An ....Inhalt des umgeschriebenen regulären n-Ecks
I, .... Inhalt des eingeschriebenen regulären n-Ecks
Es gilt:
In < K < An
An I
kann beliebig klein gemacht werden
(1)
(2)
Die Berechnung der Zahlen I, und An erfolgt
rekursiv mit Hilfe von Formeln:
I
n
An+'„
A. startet mit n=6 und rechnet bis n = 96
Die Ergebnisse von Archimedes wurden später - im Wesentlichen mit derselben Methode weiter verbessert. LUDOLF van CEULEN berechnete n auf 35 Stellen genau.
Berechnung von n mit Hilfe von Reihenentwicklungen:
Berühmtes Beispiel:
Für x = l erhältman:
n
1 1
-=I--+---+
4
3 5
1
7
.......
Diese Reihe ist besonders „schön", konvergiert aber sehr langsam. Es gibt aber sehr rasch
konvergierende Reihendarstellungen von n.
(4) Zahlentheoretische Ergebnisse über n:
ist irrational.
n ist transzendent
7~
(LAMBERT, 1767)
(LINDEMANN, I 882)
Schulmathematik Zahlen
3. Didaktisches: Ergänzungen
(5) Berühmte Formeln, die n enthalten:
Formel von VIETA (1 579):
Formel von WALLIS (1655):
2n.2n
.......
1.3 3.5 5.7 ""'(2n-1)(2n+l)
n - 2.2 4.4 6.6
- - ---
2
Formel von GREGORY (1671) und LEiBNIZ (1674):
Formel von EULER (1734) für die Summen reziproker Potenzen:
(Anmerkung: <(2k) =
"
n=i
,
1
ist für jedes k ein rationales Vielfaches von n2*)
n
Formel von RAMANUJAN (19 14):
9801
= 3,14159273 ...
1 103.&
Mit jedem weiteren Summand steigt die Zahl der korrekten Nachkommastellen um etwa 8.)
(Schon der erste Summand liefert einen sehr guten Wert:
I Wichtige Definitionen und Sähe der elementaren Zahlentheorie
I
Definition: (Teilbarkeit in N)
1
a heißt Teiler von b (geschrieben: a b)
Q
es existiert ein n E N , sodass a.n = b
Einige Sätze über Teilbarkeit:
(1)
a l a ~ l l a
fur alle a
(2)
alb
A
blc 3 a l c
für alle a , b , c ~
N
(3)
alb
A
a/c
E r alle a, b, C E N
(4)
a b 3 a (b.c)
1
al(b+c)
1
E
N
für alle a, b, C E N
Einige Teilbarkeitsregeln (für im Dezimalsystem dargestellte Zahlen)
Eine Zahl n ist teilbar durch
2
4
8
3
9
5
e
e
e
e
e
e
die letzte Ziffer von n ist durch 2 teilbar
die durch die letzten zwei Ziffern von n dargestellte Zahl ist durch 4 teilbar
die durch die letzten drei Ziffern von n dargestellte Zahl ist durch 8 teilbar
die Ziffernsumme von n ist durch 3 teilbar
die Ziffernsumme ist durch 9 teilbar
die letzte Ziffer von n ist 0 oder 5
Definition:
Eine natürliche Zahl p heißt Primzahl, wenn p größer als 1 ist und nur die Teiler 1 und p
besitzt. Jede andere natürliche Zahl heißt zusammengesetzt.
Fundamentalsatz der Zahlentheorie:
Jede natürliche Zahl n (>I) lässt sich als Produkt von Primzahlen darstellen, und diese
Darstellung ist (abgesehen von der Reihenfolge der Faktoren) eindeutig.
4. Zahlentheoretisches
SchuImathematik Zahlen
Satz:
Es gibt unendlich viele Primzahlen.
Formulierung von EUKLID:
Es gibt mehr als jede vorgelegte Menge von Primzahlen.
Kanonische Primfaktonerlegung:
Sei p,, p,, ....... die Folge der Primzahlen in aufsteigender Reihenfolge.
Dann kann jede natürliche Zahl n dargestellt werden in der Form
Definition: ggT, kgV
Seien a, b E N ; T ( a ) := Menge der Teiler von a; V ( a ):= Menge aller Vielfachen von a
ggT(a,b ) := größtes Element von T ( a )nT(b) heißt größter gemeinsamer Teiler von a und b
kgV(a,b) := kleinstes Element von V ( a )n V ( b ) heißt kleinstes gemeinsames Vielfaches
Mit Hilfe der kanonischen Primfaktorzerlegung können ggT und kgV sehr einfach ermittelt
werden:
n
mit ci = min{ai, b,)
npid
'
mit di = max{ai,bi}
m
Dann gilt:
ggT(a, b)
=
piC'
i=l
m
kgV(a, b)
=
i=l
Allerdings ist die Ermittlung der kanonischen Primfaktorzerlegung fur große natürliche Zahlen
mit großem Rechenaufwand verbunden.
Schulmathernatik Zahlen
4. Zahlentheoretisches
Euklidischer Algorithmus zur Ermittlung des ggT:
Seien a,b E N mit a > b
Man bildet folgende Kette von Divisionen mit Rest, so lange, bis Rest 0 auftritt:
= b.q,
+
r,
(0 < r, < b)
b = r,.q2
r, = r2.q3
USW.
+
+
r2
(0 < r2 < r,
r3
(0 < r3 <r2)
a
...
n -
Dann gilt:
-
n
+
0
ggT(a, b ) = rn
I Lineare dio~hantischeGleichungen
1
Gegeben ist eine Gleichung der Form
(*)
Gesucht:
a.x + b.y = C
mit a, b,c E Z
Zahlenpaare ( X , y) E z2,
die diese Gleichung (*) erfüllen
(,,Lösungen der diophantischen Gleichung (*) ")
I
(Analog fur lineare Gleichungen mit drei oder mehr Variablen ...)
Beispiele:
(1)
Eine Klasse mit 25 Schülern wird fur eine Gruppenarbeit in Vierer- und Dreiergruppen
eingeteilt. Ist das möglich? Auf welche Arten ist das möglich?
(2)
Bleistifte einer bestimmten Sorte gibt es nur in Packungen zu 3 Stück und zu 10 Stück.
Welche Anzahl von Bleistiften kann man kaufen, wenn man nur ganze Packungen
erhält?
Schulmathematik Zahlen
4. Zahlentheoretisches
(3)
Ein fiktives Land hat nur Münzen zu 5 GE und zu 10 GE.
Welche Geldbeträge kann man mit diesen Münzen zahlen, wenn auch Herausgeben
möglich ist ?
Ein anderes fiktives Land hat nur Münzen zu 3 GE und zu 10 GE.
Welche Geldbeträge kann man zahlen, wenn auch Herausgeben möglich ist ?
(4)
Für ein Konzert gibt es Karten zu 10 €, 16 € und 24 E.
20 Personen kauften je eine Karte und zahlten insgesamt 300 C.
Wie viele Karten jeder Kategorie sind gekauft worden ?
Satz:
(I)
(*) besitzt genau dann Lösungen, wenn d := ggT(a, b) ein Teiler von C ist.
(2)
Wenn
(X,,
y,) eine Lösung von (*) ist, dann ist die Lösungsmenge gegeben durch
a
-k.-)I
d
Beispiel:
4 x + 3 y = 25
Die Gleichung besitzt eine Lösung, da ggT(4,3) = I
Hat man etwa die Lösung (1, 7) bereits gefunden,
so liegen alle weiteren auf der Geraden mit der
Pararneterdarstellung
~
E
Z