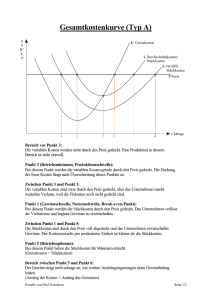
Mathematikskript
Werbung

Skript Mathematik Inhaltsverzeichnis 1 Folgen und Reihen..................................................................................................... 1 1.1 Arithmetische Folgen und Reihen.................................................................................... 1 1.2 Geometrische Folgen und Reihen.................................................................................... 2 1.3 Aufgaben .................................................................................................................... 3 2 Zins- und Zinseszinsrechnung ................................................................................... 4 2.1 Einfache Verzinsung ..................................................................................................... 4 2.2 Zinseszinsrechnung ...................................................................................................... 5 2.3 Gemischte Verzinsung................................................................................................... 6 2.4 Unterjährige und stetige Verzinsung ............................................................................... 6 2.5 Aufgaben .................................................................................................................... 7 3 Rentenrechnung ........................................................................................................ 8 3.1 Vorschüssige konstante Zeitrenten ................................................................................. 8 3.2 Nachschüssige konstante Zeitrenten ............................................................................... 9 3.3 Renten mit unterjährigen Rentenzahlungen ................................................................... 10 3.4 Aufgaben .................................................................................................................. 11 4 Tilgungsrechnung.................................................................................................... 12 4.1 Ratentilgung .............................................................................................................. 12 4.2 Annuitätentilgung ....................................................................................................... 13 4.3 Aufgaben .................................................................................................................. 14 5 Investitionsrechnung .............................................................................................. 15 5.1 Kapitalwertmethode.................................................................................................... 15 5.2 Methode des internen Zinsfußes ................................................................................... 16 5.3 Aufgaben .................................................................................................................. 17 6 Untersuchung von Funktionen mit einer unabhängigen Variablen........................... 18 6.1 Das Differential einer Funktion ..................................................................................... 18 6.2 Extremwertbestimmung .............................................................................................. 19 6.3 Krümmung und Wendepunkte...................................................................................... 20 6.4 Untersuchung einiger ökonomischer Funktionen ............................................................. 21 6.4.1 Die Preis-Absatz-Funktion und die Erlösfunktion .......................................................... 21 6.4.2 Kostenfunktionen .................................................................................................... 22 6.4.3 Gewinnfunktionen ................................................................................................... 23 6.5 Aufgaben .................................................................................................................. 24 7 Untersuchung von Funktionen mit mehreren unabhängigen Variablen ................... 26 7.1 partielle Differentation ................................................................................................ 26 7.2 Extremwertbestimmung .............................................................................................. 27 7.3 Extremwerte unter Berücksichtigung von Nebenbedingungen........................................... 27 7.3.1 Lösung von Extremwertaufgaben durch Variablensubstitution ....................................... 27 7.3.2 Multiplikatorregel von LaGrange ................................................................................ 29 8 Aufgaben................................................................................................................. 29 1 1 FOLGEN UND REIHEN Eine Zahlenfolge ist eine Abbildung, die jeder natürlichen Zahl n Є N eine reelle Zahl an Є R zuordnet. Die einzelnen Glieder einer Zahlenfolge lassen sich also durchnummerieren, und die Zahl n stellt den laufenden Zähler (Zählindex) dar, d.h. sie beschreibt, um das wievielte Glied der Folge es sich handelt (n = 1: erstes Glied a1; n = 2: zweites Glied a2; .....). Von besonderem Interesse für finanzmathematische Problemstellungen sind spezielle Zahlenfolgen, bei denen gewisse charakteristische Eigenschaften (konstante Differenzen bzw. Quotienten aufeinanderfolgender Glieder) zwischen den Folgegliedern besteht. Wir unterscheiden dabei 2 Hauptgruppen Folgen, bei denen das Folgeglied aus seinem Vorgänger durch Addition bzw. Subtraktion einer konstanten Größe entsteht. Folgen, bei denen das Folgeglied aus seinem Vorgänger durch Multiplikation bzw. Division einer konstanten Größe entsteht. => Arithmetische Folgen => Geometrische Folgen 1.1 Arithmetische Folgen und Reihen Eine Zahlenfolge wird arithmetisch genannt, wenn die Differenz aufeinanderfolgender Glieder an +1 = an + d konstant ist: n = 1,2,3,... Die Bildungsformel für das n-te Glied: Die Summe aller Glieder dieser Folge ist die arithmetische Reihe ∞ a1 + a2 + a3 + ... = ∑ an n =1 Bildet man die Summe aus den jeweils ersten n Gliedern einer Folge erhält man die Teil- oder Partialsummen. n sn = a1 + a2 + a3 + ... + an = ∑ ai i =1 Die Bildungsformel für die n-te Teilsumme: (Die Partialsummen ergeben wieder eine neue Folge s1, s2, s3,...) Grenzwertuntersuchung für arithmetische Folgen: a1 = 0 ; d = 5 a1 = 100 ; d = -2 Der Grenzwert hängt ab von 2 Übung: Gegeben sei die Folge 1, 3 5 , 2 , , 3 , ... 2 2 Beschreiben Sie die Folge. Wie viele Glieder hat die Folge, wenn die Summe 914,5 beträgt? 1.2 Geometrische Folgen und Reihen Eine Zahlenfolge wird geometrisch genannt, wenn der Quotient aufeinanderfolgender Glieder a n +1 = q ⋅ a n konstant ist: n = 1,2,3,. Die Bildungsformel für das n-te Glied: Die Bildungsformel für die n-te Teilsumme: Grenzwertuntersuchung für geometrische Folgen: Die Berechnung des Grenzwertes einer allg. Zahlenfolge kann sehr kompliziert werden, weswegen wir uns mit einigen Sachverhalten Begnügen: Beispiele: Folge Grenzwert a1 = 3 ; q = 2 a1 = -3 ; q = 2 a1 = 100 ; q = 4/5 a1 = 100 ; q = -4/5 a1 = 3 ; q = -2 Übung: Gegeben sei die Folge 80 , 40 , 20 , ... Beschreiben Sie die Folge. Wie viele Glieder hat die Folge, wenn die Summe 158,75 beträgt? 3 1.3 Aufgaben 1. Bestimmen Sie die Werte des jeweils 15. Gliedes der folgenden endlichen arithmetischen Reihen sowie deren Summen: a) 110 + 114 + 118 + . . . + a15 b) 783 + 762 + 741 + . . . + a15 2. Wie groß ist die Summe der natürlichen Zahlen von 1 bis 300? 3. Berechnen Sie für die geometrische Folge 7, 14, 28, . . . das elfte Glied und die Summe der ersten elf Glieder. 4. Berechnen Sie den Wert der neungliedrigen Reihe 5. Wie viele dreistellige Zahlen gibt es, die durch sechs teilbar sind? 6. Bestimmen Sie für die Reihe 230 + 245 + 260 + . . . + an die zugehörige Anzahl von Gliedern, wenn der Wert dieser Reihe 27.960 beträgt. 7. Stellen Sie eine unendliche geometrische Reihe mit dem Anfangswert 70 und dem Quotienten 0,25 auf und bestimmen Sie den Grenzwert für n ∞. 8. Nach einer einmaligen Einzahlung von 7.000 Euro zeigt ein Sparbuch in den nächsten vier Jahren folgende Entwicklung: ein Jahr nach Einzahlung: zwei Jahre nach Einzahlung: drei Jahre nach Einzahlung: vier Jahre nach Einzahlung: 7.385,00 7.791,17 8.219,68 8.671,76 170 + 510 + 1.530 + . . . + a9 . € € € € Welche Folge liegt vor und wie groß sind die charakteristischen Werte dieser Folge 9. Bestimmen Sie das allgemeine Folgeglied an und geben Sie an, ob es sich evtl. um eine arithmetische oder geometrische Folge handelt. a) 1 1 1 1 1 , , , , ,..... 3 6 12 24 48 b) 12,0,−12,−24,−36,..... 1 1 1 1 c) 1, , , , ,..... 2 3 4 5 d ) 2,4,6,8,10,..... e) 3 3 3 3 3 , , , , ,..... 2 4 8 16 32 f ) 1,7,17,31,49,71,... 10. Gegeben ist eine geometrische Reihe, mit dem letzten Glied an = 88.578,05. Das Vorletzte Glied ist an-1 = 80.525,5. Die Summe der Reihe beträgt 474.358,55. Bestimmen Sie das erste Glied dieser Reihe. 4 2 ZINS- UND ZINSESZINSRECHNUNG Abkürzungen: K = Kapital t = Anzahl der Zinstage Zt = Zinsen für die Zeit t Kt = Kapital zum Zeitpunkt t p = Zinssatz i = Zinsrate = p/100 2.1 Einfache Verzinsung Zinsen sind die Vergütung für das Überlassen eines Kapitals in einer bestimmten Zeit (Zinsperiode). In der Regel beträgt die Zinsperiode ein Jahr (dies wird unsere generelle Annahme sein), üblich sind aber durchaus auch andere Perioden der Verzinsung wie ½ Jahr, ¼ Jahr, 1 Monat usw. Nach der „deutschen“ Methode wird das Jahr mit 360 Tagen, jeder Monat mit 30 Tagen berechnet. z.B.: vom 18.08.01 bis 25.11.01 => 3 ∙ 30 Tage + 7 Tage = 97 Tage Zinsformel: z= K ⋅ p ⋅t 100 ⋅ 360 Sparraten Beispiel: Im Verlauf eines Jahres sollen regelmäßig zu Monatsbeginn r = 100 € gespart werden. Der Zinssatz beträgt 6%. Welcher Betrag R ist nach 1 Jahr verfügbar? 5 Wären die Sparraten jeweils zu Monatsende eingezahlt worden, ergäbe sich folgende Rechnung: Sparraten können auch zu anderen Perioden vereinbart werden, wie z.B. jedes ½ Jahr oder ¼ Jahr. Mit den folgenden Formeln können bei jährlich erfolgenden m Zahlungen (im Abstand von 1/m Jahr) der Höhe r das Kapital zum Jahresende berechnet werden. vorschüssige Einzahlung: m +1 R vor = r ⋅ m + ⋅ i 2 nachschüssige Einzahlung: m −1 R nach = r ⋅ m + ⋅i 2 2.2 Zinseszinsrechnung Abkürzungen n – Anzahl der Zinsperioden K0 – Anfangskapital Kn - Endkapital q=1+i - Aufzinsungsfaktor Im Gegensatz zur einfachen Verzinsung, bei der die Zinsen nach einer Periode ausgeschüttet werden, wird der Zinsgewinn bei der Zinseszinsrechnung dem Kapital zugerechnet und in den kommenden Perioden mitverzinst. Beispiel: Am Anfang des Jahres 01 werden 10.000 € zu einem Zinssatz von 8% für 10 Jahre angelegt. Allgemein : • • • Ein Unternehmen beabsichtigt, anlässlich seines Jubiläums in 5 Jahren einem gemeinnützigen Verein 40.000 € zur Verfügung zu stellen. Welcher Betrag hat es heute bei einer Bank anzulegen, wenn diese eine Verzinsung von 6,5% bietet. Ein Student kauft abgezinste Sparkassenbriefe mit einer Laufzeit von 5 Jahren im Nennwert von 1.000 €, wofür er 745 € bezahlen muss. Zu welchem Zinssatz erfolgt die Verzinsung? Eine Person spart für ein Auto, das seiner Vorstellung nach 20.000 € kosten soll. Er verfügt über 12.000 €, die er zu 5,75% anlegen kann. Wie lange muss er sparen? 6 2.3 Gemischte Verzinsung Auf welchen Betrag wächst ein Kapital von 2000 € an, das bei 6%iger Verzinsung vom 10.03.01 bis 19.07.05 angelegt wird? Allgemein: 2.4 Unterjährige und stetige Verzinsung Zinszahlungen können nicht nur jährlich, sondern auch in kürzeren Zeitabschnitten (halbjährlich, vierteljährlich, monatlich) vereinbart werden. Ist m die Anzahl unterjähriger Zinsperioden der Länge 1/m Jahre, so entsprechen diesem kürzeren Zeitraum anteilige Zinsen in Höhe von z=K⋅ i m i K 1, m = K 0 ⋅ 1 + m Kapital nach 1 Jahr: K n,m Kapital nach n Jahren: m i = K 0 ⋅ 1 + m m ⋅n Beispiel: Ein Kapital von 10.000 € wird über 3 Jahre bei 6% Verzinsung (nominal) p.a. angelegt: jährliche Verzinsung (m = 1): halbjährliche Verzinsung (m = 2): vierteljährliche Verzinsung (m = 4): monatliche Verzinsung (m = 12): effektiver Zinssatz Der Jahreszinssatz, der bei einmaliger jährlicher Verzinsung den gleichen Endkapitalbetrag ergibt wie die m-malige unterjährige Verzinsung mit dem relativen Zinssatz p/m , nennt man den effektiven Zinssatz peff m p eff i 1 + = 1 + 100 m => Für das Beispiel betragen die effektiven Zinssätze: stetige Verzinsung m i lim 1 + = e i m→∞ m ⇒ K n = K 0 ⋅ e in 7 2.5 Aufgaben 11. Berechnen Sie den Zinsbetrag bei einfacher Verzinsung für einen Kapitalbetrag von 8.450,00 €, der vom 10. April bis 25. September desselben Jahres bei einer jährlichen Verzinsung von 5,75 % erreicht wird. 12. Welches Endkapital ergibt sich für ein mit jährlich 6,25 % verzinstes Anfangskapital in Höhe von 17.670,00 € nach Ablauf von vier Jahren? a) bei einfacher Verzinsung b) bei Wiederanlage von Zinsen 13. Eine Sparerin legt am Jahresbeginn bei einer Bank 8.200 € zu 6,0 % Zinsen an. Auf welche Summe ist der eingezahlte Betrag 12 Jahren angewachsen? 14. Einem Kind wird bei seiner Geburt von einem Paten ein Geldbetrag von 1.500 Euro geschenkt. Der Betrag darf vom Sparkonto erst bei Vollendung des 18. Lebensjahres abgehoben werden. Auf welchen Betrag ist das Geschenk bei einer Verzinsung von 6,5 % angewachsen? 15. Ein Kapital von 3.800 Euro wird 4 Jahre lang mit 5 %, danach 5 Jahre lang mit 6 % und anschließend noch 6 Jahre mit 7 % verzinst. Auf welchen Betrag wird es insgesamt anwachsen? 16. Auf welche Summe wachsen 4.500 Euro zu 7 % Zinsen in 8 Jahren an bei a) jährlicher, b) vierteljährlicher, c) monatlicher Zinszahlung? 17. Bestimmen Sie den Zeitraum, in welchem 6.500 Euro bei 6,5 % iger Verzinsung auf den doppelten Betrag anwachsen. 18. Bestimmen Sie den Zinssatz, zu dem ein Kapitalbetrag von 38.000 Euro auszuleihen ist, damit er sich in 12 Jahren verdreifacht. 19. Welches Kapital ergibt sich, wenn ein Betrag von 7.500 Euro bei 6,25 % iger Verzinsung vom 20.06.1992 bis 10.05.1997 angelegt wird? 20. Ein Zerobonds ist ein festverzinsliches Wertpapier, das nach n Jahren zum Nominalbetrag zurückgezahlt wird. Während der gesamten Laufzeit werden keine Zinsen gezahlt. Bestimmen Sie den Ausgabepreis eines Zerobonds bei einer Laufzeit von 12 Jahren und einem Jahreszinssatz von 7 % bei einem Rückzahlungsbetrag von 40.000 Euro. 21. Eltern wollen für spätere Ausbildungszwecke ihres Kindes einen Betrag von 50.000 Euro zur Verfügung haben. Welches Kapital müssen sie zu Beginn des 5. Lebensjahres dieses Kindes bei einer Bank anlegen, wenn diese 8 % Zinsen einräumt und der vorgesehene Betrag mit Vollendung des 18. Lebensjahres bereitstehen soll? 22. Eine reiselustige Person plant eine größere Reise in vier Jahren. Welchen Betrag muss sie jetzt sparen, wenn die Reisekosten mit 16.000 Euro veranschlagt werden und der jetzt bereitzustellende Betrag eine Verzinsung von a) 5,75 % Zinsen b) 7,50 % Zinsen c) 9,25 % Zinsen erbringt? 23. Welcher Unterschied im Endkapital ergibt sich bei einer zehnjährigen Kapitalanlage in Höhe von K0 (z.B. 30.000 Euro), wenn anstelle einer jährlichen Verzinsung von 6,5 % eine monatliche Verzinsung treten würde? 24. Bestimmen Sie den effektiven Jahreszinssatz, wenn der Jahreszinssatz 8 % beträgt und eine viermalige Verzinsung pro Jahr stattfindet. 25. Welcher Endwert ergibt sich, wenn ein Anfangskapital von 35.000 Euro bei stetiger Verzinsung mit einer Zinsintensität von 9 % zwölf Jahre lang angelegt wird? 8 3 RENTENRECHNUNG Die Rentenrechnung befasst sich mit der Fragestellung, mehrere regelmäßige Zahlungen zu einem Wert zusammenfassen bzw. mit dem umgekehrten Problem, einen gegebenen Wert unter Beachtung anfallender Zinsen in eine bestimmte Anzahl von (Renten-) Zahlungen aufzuteilen. 3.1 Vorschüssige konstante Zeitrenten Beispiel: Eine 30jährige Person hat eine Lebensversicherung abgeschlossen. Es ist vorschüssige Prämienzahlung vereinbart. Welchem Endwert und welchem Barwert entsprechen diese Versicherungsleistungen (unter Zugrundelegung von 5,5% Zinsen), wenn die Versicherung auf das Endalter 63 Jahre abgeschlossen worden ist und die jährliche Versicherungsprämie 2.400 € beträgt? Berechnung des Rentenendwertes Der Rentenendwert ist die Summe aller aufgezinsten Rentenbeträge. Berechnung des Barwerts Der Rentenbarwert entspricht einem auf Zinseszins angelegten Kapitalbetrag, der eine n-malige vorschüssige Rentenzahlung R bis zur Aufzehrung des Kapitals ermöglicht. Berechnung des Kontostandes zum Zeitpunkt m Nach m (mit m < n) Rentenzahlungen beläuft sich das noch nicht aufgezehrte Kapital auf: 9 3.2 Nachschüssige konstante Zeitrenten Hierbei erfolgen die Zahlungen jeweils am Jahresende: Berechnung des Rentenendwertes Berechnung des Barwerts Berechnung des Kontostandes zum Zeitpunkt m , 10 3.3 Renten mit unterjährigen Rentenzahlungen Entsprechen die Rentenperioden nicht einem Jahr, so müssen die Formeln modifiziert werden. Dies ist in der Praxis von großer Bedeutung, denn häufig ist jährliche Verzinsung (mit einem Zinssatz p) bei monatlichen, viertel- oder halbjährlichen Rentenperioden vereinbart. Aus den unterjährigen Zahlungen muss ein jährlicher Rentenbetrag berechnet werden. Dies geschieht mittels der Sparratenformel. A. Ermittlung des Endwertes (Ansparphase) Beispiel: Eine monatliche Rente beträgt 2.000 €. Die jährliche Verzinsung liegt bei 6%, und die Rentendauer 10 Jahre. Wie hoch ist der Rentenendwert? Ermittlung der Jahresrente und daraus den Endwert B. Aufzehrung des Barwertes Beispiel: Welche monatliche Rentenleistung kann ein Anfangskapital von 100.000 € sicherstellen, wenn eine Verzinsung von 6 % und eine Anspruchsdauer von 10 Jahren vorliegen? Ermittlung der Jahresrente und daraus den konformen Rentenbetrag: 11 3.4 Aufgaben 26. Vergleichen Sie die Formel zur Berechnung des Barwertes der vorschüssigen und der nachschüssigen Rente. Worin besteht der Unterschied und wie ist er zu erklären? 27. Auf welchen Betrag wachsen jährliche Einzahlungen in Höhe von 2.500 Euro in 14 Jahren an, wenn eine Verzinsung von 7 % zugrunde gelegt wird? 28. Eine Rente aus einer Unfallversicherung wird 25 Jahre lang in Höhe von 4.800 Euro am Jahresende gezahlt. Mit welchem Betrag könnte sich der Berechtigte bei einer Verzinsung von 6,5 % sofort abfinden lassen? 29. Jemand möchte in 4 Jahren über 18.000 Euro verfügen. Welchen Betrag muss diese Person jährlich zurücklegen, um bei einer Verzinsung von 6 % über diesen Betrag zu verfügen? 30. Ein Studium wird mit einer Dauer von 5 Jahren veranschlagt. Über welchen Betrag kann ein Student jährlich verfügen, wenn ihm ein Kapitalbetrag in Höhe von 28.000 Euro zu Studienbeginn überlassen wird, der mit 7,5 % Zinsen angelegt werden kann (bei vorschüssiger Verfügbarkeit)? 31. Eine nachschüssige Rente in Höhe von 8.000 Euro ist zwölfmal zu zahlen. Welcher Barwert ist dafür erforderlich und welcher Kontostand ergibt sich nach 5 Jahren bei einer Verzinsung zu 9 %? Welche Resultate erhält man bei vorschüssiger Zahlungsweise? 32. Welchen Betrag müssen Sie 30 Jahre lang vorschüssig sparen, um über eine jährliche Summe von 25.000 Euro für die Dauer von 20 Jahren (vorschüssig) zu verfügen? Der Zinssatz in der Sparphase beträgt 6 %; in der anschließenden „Rentenphase“ beträgt er 5,5 %. 33. In eine Kapitallebensversicherung werden monatlich vorschüssig 100,00 € einbezahlt. Wie hoch ist die Auszahlung nach 30 Jahren bei einer Verzinsung von 7% jährlich? 34. Eine Unterstützungskasse verfügt über ein Kapital in Höhe von 2.000.000 Euro. Wie lange kann die Kasse jährliche Ansprüche in Höhe von 200.000 Euro zahlen, wenn eine Verzinsung von 6,5 % gewährleistet ist? Über welches Kapital verfügt die Unterstützungskasse nach sieben Jahren? 35. Ein Grundstück wird zu einem Preis von 350.000 Euro erworben. Die Bezahlung erfolgt durch konstante Ratenzahlung (Rentenzahlung) in 10 Jahren. Wie groß ist der jährliche Ratenbetrag bei nachschüssiger Ratenzahlung, wenn ein Zinssatz von 8 % zugrunde gelegt wird? 36. Für die Sicherstellung eines jährlichen Anspruchs in Höhe von 15.000 Euro wird ein Kapitalbetrag von 120.000 Euro verzinslich angelegt. Wie groß ist der noch nicht aufgezehrte Kapitalbetrag bei einer jährlichen Verzinsung von 7 % nach 8 Jahren? 37. Ein Bausparer schließt einen Bausparvertrag über 100.000 Euro ab. Welcher Betrag ist jährlich vorschüssig einzuzahlen, damit das Bausparguthaben in 10 Jahren auf 40 % der Bausparsumme bei einem jährlichen Guthabenzins von 3 % anwächst? 38. Welche Rentenleistung kann ein Anfangskapital von 150.000 Euro sicherstellen, wenn eine jährliche Verzinsung von 7 % und eine Anspruchsdauer von 15 Jahren vorliegen? a) Wie groß ist das Kapital nach 5 Jahren bei jährlich vorschüssiger Leistung b) Wie groß ist das Kapital nach 5 Jahren bei jährlich nachschüssiger Leistung c) Wie hoch ist die monatliche vorschüssige Rente d) Wie hoch ist die monatliche nachschüssige Rente 39. Bestimmen Sie für die monatliche nachschüssige Rente von 1.500 Euro den Rentenbar- und Rentenendwert mit Hilfe des konformen Rentenbetrages, wenn die Rentendauer 20 Jahre beträgt und eine jährliche Verzinsung von 7 % vorliegt. 40. Welche Verzinsung muss bei einem vorhandenen Kapitalbetrag von 150.000 Euro erreicht werden, damit eine Jahresrente von 9.375 Euro davon finanziert werden kann? 12 4 TILGUNGSRECHNUNG Bei der Tilgungsrechnung (oder auch Anleihenrechnung) geht es um die Bestimmung der Rückzahlungsraten für Zinsen und Tilgung eines aufgenommenen Kapitalbetrages (Darlehen, Hypothek, Kredit). Es können aber auch andere Bestimmungsgrößen wie Laufzeit oder Effektivverzinsung gesucht sein. Grundbegriffe: o Annuität = Gesamtzahlungsbetrag, bestehend aus Tilgungs- und Zinsrate o Tilgungsplan = Tabellarische Darstellung der Annuitäten im zeitlichen Verlauf Annahme: o die Annuitätenzahlung erfolgt am Periodenende Abkürzungen: S0 - Kreditbetrag, Anfangsschuld Sk - Restschuld am Ende der k-ten Periode Tk - Tilgung in der k-ten Periode Zk - Zinsen in der k-ten Periode Ak - Annuität in der k-ten Periode (Ak = Tk + Zk) 4.1 Ratentilgung Beispiel: Für den Bau einer Lagerhalle wird ein Darlehen in Höhe von 100 T€ aufgenommen. Der Zinssatz für das Darlehen beträgt 6%, die Laufzeit 5 Jahre. Das Darlehen soll in gleichbleibenden Tilgungsraten zurückbezahlt werden. Die (jährliche) Annuität wird jeweils zum Ende des Jahres fällig. Bei dieser Form sind die jährlichen Tilgungsraten konstant: Tk = S0 = const. n Die Annuitäten sind nicht konstant: Ak = Tk + Z k Die Restschuld Sk nach k Perioden stellt eine arithmetische Folge mit dem Anfangsglied S0 und der Differenz d =− S0 dar. n k S k = S 0 ⋅ 1 − n Die Zinsen, die für die jeweilige Restschuld Sk-1 zu bezahlen sind, betragen Z k = S k −1 ⋅ k −1 p p = S 0 1 − ⋅ 100 n 100 13 4.2 Annuitätentilgung Im Gegensatz zur Ratentilgung, bei der die jährlichen Annuitäten fallen, sind die jährlichen Annuitäten bei der dieser Tilgungsart konstant. Die Leistung des Gläubigers besteht in der Bereitstellung des Kreditbetrages S0 zum Zeitpunkt 0, die demzufolge mit ihrem Barwert übereinstimmt. Der Barwert aller Zahlungen des Schuldners ist gleich dem Barwert einer nachschüssigen Rente mit gleichbleibenden Raten r in Höhe der gesuchten Annuität A, daher folgende Beziehung: n S0 = A⋅ q (q − 1) n q −1 n q −1 n q (q − 1) A = S0 ⋅ Weitere Formeln: Tilgung: Tk = T1 ⋅ q k −1 Restschulden: Sk = S0 − T1⋅ Zinszahlungen: Z k = S0 ⋅ Laufzeit: n= mit T1 = A − S 0 ⋅ p 100 k k q −1 q −1 = S 0 ⋅ qk − A ⋅ q −1 q −1 p k −1 k −1 − T1 q −1 = A − T1⋅ q 100 ( ) ln A − ln( A − (q − 1) S 0) ln A − ln( A − i ⋅ S 0) = ln q ln q Unterjährige Vereinbarungen bei vorgegebenen Jahreszinssatz Beispiel: Eine Schuld von 50.000 € soll bei 9% Verzinsung pro Jahr innerhalb von 6 Jahren mit konstanten monatl. Raten zurückgezahlt werden. Wie groß ist die monatl. Rate a zu wählen? jährliche Annuität: Und daraus die monatliche Annuität: 14 4.3 Aufgaben 41. Berechnen Sie den Tilgungsbetrag bei Ratentilgung, wenn sich der Kreditbetrag auf 72.000 Euro beläuft und die Tilgung nach 12 Jahren beendet sein soll. 42. Wie groß ist bei Ratentilgung eines Kredites von 84.000 Euro der Kreditbetrag nach sechs Jahren, wenn eine Kreditdauer von 8 Jahren vereinbart ist? 43. Bestimmen Sie die bei Ratentilgung eines zu 7,5 % zu verzinsenden Kredites von 40.000 Euro die bei jährlicher Tilgung von 4.000 € a) im siebten Jahr, b) insgesamt anfallenden Zinsen. 44. Stellen Sie einen Tilgungsplan für eine Annuitätentilgung eines Kredites von 120.000 Euro mit einer Laufzeit von sechs Jahren und einer Verzinsung von 7,5 % auf. 45. Bestimmen Sie den Betrag der Annuität bei Annuitätentilgung, wenn der Kreditbetrag 35.000 Euro, die Tilgungsdauer 12 Jahre und der Zinssatz 7 % betragen. 46. Ein Unternehmen ist in der Lage, eine jährliche nachschüssige Annuität von 90.000 Euro für ein Darlehen über 750.000 Euro aufzubringen. Bestimmen Sie näherungsweise die Tilgungsdauer bei einer Darlehensverzinsung von 9 %. 47. Ein Unternehmen hat einen Kredit in Höhe von 1.800.000 Euro aufgenommen. Wie groß ist die Restschuld nach sechs Jahren, wenn Annuitätentilgung bei einer Verzinsung von 8,5 % mit einer Laufzeit von 15 Jahren vereinbart worden ist? 48. Stellen Sie einen Tilgungsplan für die ersten 5 Jahre bei Vorliegen folgender Darlehensvereinbarungen auf: Kreditbetrag: 380.000,00 €, Zinssatz: 8,5 %, Laufzeit: 18 Jahre, Annuität: konstant 49. Ein Kredit in Höhe von 120.000 Euro wird für eine Dauer von 18 Jahren gewährt, wonach er vollständig zurückgezahlt sein soll. Welche jährlich konstante (nachschüssige) Leistung für Zins und Tilgung ist aufzuwenden, wenn ein fester Zinssatz von 7 % für die gesamte Dauer vereinbart ist? Bestimmen Sie den Zinsbetrag für das 8. Jahr, die Tilgung für das 10. Jahr und den Restkreditbetrag nach 12 Jahren. Stellen Sie einen Tilgungsplan für die ersten drei Jahre auf. 50. Ermitteln Sie näherungsweise die Laufzeit eines Darlehens, für welches bei einem Zinssatz von 9,0 %, eine Annuität von 11,0 % zu zahlen ist. 51. Ein Bauspardarlehen in Höhe von 60.000 Euro mit einem Jahreszinssatz von 5 % wird in jährlich nachschüssigen Annuitäten in Höhe von 7.200 Euro getilgt. Bestimmen Sie näherungsweise den Zeitraum, in dem das Bauspardarlehen vollständig zurückgezahlt sein wird. 52. Eine Person benötigt zum Kauf eines Einfamilienhauses einen Kredit, den sie bis in 20 Jahren in gleichmäßigen monatlichen Raten getilgt haben möchte. Der Bankzinssatz beträgt 5%. a) Wie hoch ist die monatliche Belastung bei einer Kreditsumme von 150.000€ ? b) Die Person kann monatlich maximal 1200€ aufbringen. Wie hoch kann die Kreditsumme höchstens sein? 15 5 INVESTITIONSRECHNUNG Die Investitionsrechnung stellt Modelle, Methoden und Verfahren zur Beurteilung der Wirtschaftlichkeit von Investitionen bereit. 5.1 Kapitalwertmethode Bei dieser Methode werden alle mit einer Investition verbundenen zukünftigen Einnahmen und Ausgaben einander gegenübergestellt. Da zu unterschiedlichen Zeitpunkten fällige Zahlungen nur dann vergleichbar sind, wenn man sie auf einen festen Zeitpunkt bezieht, geht man hierbei so vor, dass alle Einnahmen und Ausgaben mittels eines festgelegten Kalkulationszinssatzes auf den Zeitpunkt Null abgezinst werden. => Berechnung der Barwerte. Abkürzungen: Ek (zu erwartende) Einnahmen zum Zeitpunkt k, Ak (zu erwartende) Ausgaben zum Zeitpunkt k, Ck Barwerte der Einnahmenüberschüsse k = 1,2,3,....,n k = 1,2,3,....,n Bedeutung der Ergebnisse: n ∑C k >0 die Investition ist vorteilhafter als die Anlage zum Kalkulationszinssatz p k =0 die Investition erbringt eine Verzinsung in Höhe von p k <0 die Verzinsung von p wird von der Investition nicht erreicht k =1 n ∑C k =1 n ∑C k =1 Bsp.: Einnahmen- und Ausgabenplan für eine Investition, Kalkulationszinssatz 8% Jahr k 0 Einnahmen Ausgaben Ek Ak - € 435.000 € 1 150.000 € 45.000 € 2 180.000 € 60.000 € 3 210.000 € 80.000 € 4 190.000 € 70.000 € 5 170.000 € 65.000 € n Kapitalwert der Investition ∑C k =1 k Einnahmen überschüsse Ek - Ak Barwerte der Einnahmenüberschüsse Ck 16 5.2 Methode des internen Zinsfußes Bei dieser Methode wird ermittelt, mit welchem Zinssatz sich die ursprünglichen Anschaffungsausgaben während der Nutzungsdauer einer Investition verzinsen. Dieser als interne Zinsfuß p bezeichnete Wert ist bei einem Kapitalwert der Investition von Null gegeben, d.h. n ∑C k =0 k =1 Beispiel: Jahr k 0 Einnahmen Ausgaben Ek Einnahmen überschüsse Ak - € Ek - Ak 48.200 € - 48.200 € 1 48.000 € 23.000 € 25.000 € 2 56.000 € 26.000 € 30.000 € 17 5.3 Aufgaben 53. Eine Unternehmung steht vor der Entscheidung, eine Erweiterungsinvestition durchzuführen oder zu unterlassen. Zur Fundierung ihrer Entscheidung hat sie eine Planung der zu erwartenden Mehreinnahmen und Mehrausgaben durch diese Investition vorgenommen. Welche Entscheidung ist bei einer Mindestverzinsung von 9 % zu treffen, wenn die Planung der Investitionseinnahmen und –ausgaben zu folgenden Werten geführt hat: Zeitpunkt 54. Einnahmen Ausgaben 0 0 850.000 1 250.000 50.000 2 300.000 60.000 3 320.000 70.000 4 310.000 80.000 5 290.000 100.000 Drei Investitionsobjekte führen zu folgender Einnahmenreihe und zu folgenden Ausgabereihen: Zeitpunkt Einnahmen jeweils Ausgaben Alternative 1 Alternative 2 Alternative 3 0 0 450.000 320.000 230.000 1 150.000 20.000 55.000 70.000 2 170.000 25.000 60.000 100.000 3 200.000 30.000 65.000 110.000 4 180.000 35.000 70.000 120.000 Welche Investition erweist sich bei Zugrundelegung eines Kalkulationszinsfußes von 9,5 % als vorteilhafter? 55. Gegeben sei eine Investition mit folgenden zu erwartenden Einnahmen und Ausgaben: Zeitpunkt Einnahmen Ausgaben 0 0 30.000 1 14.000 5.000 2 8.000 3.000 3 17.000 7.000 4 21.000 4.000 a) Ermitteln Sie den Kapitalwert der Investition bei einem Kalkulationszinsfuß von 8,5 %. b) Bestimmen Sie den Kapitalwert bei einem Kalkulationszinssatz von p = 11 und p = 12. Welcher interne Zinssatz ergibt sich unter Berücksichtigung dieser Werte näherungsweise 18 6 UNTERSUCHUNG VON FUNKTIONEN MIT EINER UNABHÄNGIGEN VARIABLEN 6.1 Das Differential einer Funktion Die Sekante durch die Punkte ( x0 , f(x0)) und (x0 + ∆x , f(x0 + ∆x)) besitzt den Anstieg, der durch den Tangens des Winkels αS definiert ist tan α S = ∆y f ( x0 + ∆x) − f ( x0 ) = ∆x ∆x (Differenzquotient) Um die Steigung im Punkt x0 zu ermitteln, wird ∆x immer weiter verkleinert, d.h. x0 wird angenähert: Daraus ergibt sich: ∆y f ( x0 + ∆x) − f ( x0 ) = lim ∆x → 0 ∆x ∆x → 0 ∆x lim (Differentialquotient) Der Differentialquotient wird auch erste Ableitung der Funktion f(x) im Punkt x0 bezeichnet. Ableitungsregeln -> siehe Formelsammlung Beispiele: f ( x) = 3 x 2 f ( x) = 3 x 2 + 4 x 3 + 7 f ( x) = (2 x + 1) 2 f ( x) = x −1 x +1 19 6.2 Extremwertbestimmung Schema zur Bestimmung von Extremwerten einer n-mal differenzierbaren Funktion y=f(x) a) Bestimmung von f’(x) b) Lösung der Gleichung f’(x)=0 a. Hat die Gleichung keine Lösung, so existiert kein Extremwert. b. Existieren die Lösungen xi, so ist Schritt c) durchzuführen. c) Bestimmung von f’’(x) d) Prüfung des Vorzeichens der zweiten Ableitung an den Stellen xi a. Falls f’’(xi)<0 liegt ein Maximum an dieser Stelle b. Falls f’’(xi)>0 liegt ein Minimum an dieser Stelle c. Falls f’’(xi)=0 ist Schritt e) durchzuführen e) Sukzessive Bestimmung von höheren Ableitungen und Prüfung dieser Ableitungen an den Stellen xi solange, bis f(n)(xi)≠0 a. Ist n gerade und f(n)(xi)>0 , so liegt bei xi ein Minimum b. Ist n gerade und f(n)(xi)<0 , so liegt bei xi ein Maximum c. Ist n ungerade, so existiert kein Extremwert. Es liegt ein (Wende-) Sattelpunkt vor. d. Gibt es keine Ableitung, für die f(n)(xi)≠0 ist, so ist eine eindeutige Aussage nicht möglich. f ( x) = x 4 − 8 x 2 + 16 Beispiele: f ( x) = x 4 f ( x) = 0,2 x5 − x 3 + 1 Randmaxima und –minima Funktionen in den Wirtschaftswissenschaften haben durchweg einen begrenzten Definitionsbereich. Wirtschaftsfunktionen werden meist durch die Produktionsmenge 0 und Kapazitätsgrenzen beschränkt. 500 450 400 350 300 250 200 150 100 50 0 0 1 2 3 4 5 6 7 8 9 10 Beispiel: K(x) = x³-10x²+37x+72 , die Kapazitätsgrenze liegt bei x0 = 10 Bei einem begrenzten Definitionsbereich kann es vorkommen, dass Extremwerte einer Funktion am Rande des Definitionsbereichs liegen, obwohl die erste Ableitung dort nicht verschwindet. Diese Extremwerte bezeichnet man als Randmaxima bzw. Randminima. 20 6.3 Krümmung und Wendepunkte Von besonderem Interesse sind die Grenzen zwischen konkaven und konvexen Bereichen einer Funktion. => Wendepunkte. Im Wendepunkt ändert sich die Krümmung der Kurve. Die Funktion f(x) sei an der Stelle x0 dreimal differenzierbar. Ist f’’(x0) = 0 und f’’’(x0)≠0 , so hat die Funktion bei x0 einen Wendepunkt. 100 80 60 40 20 4, 5 3, 5 2, 5 1, 5 -20 0, 5 -0 ,5 -1 ,5 -2 ,5 -3 ,5 -4 ,5 0 -40 Überträgt man die Extremwertbedingungen auf die erste Ableitung einer Funktion , so hat man demnach die Bedingungen für Wendepunkte. Wenn für eine n-mal differenzierbare Funktion f(x) an der Stelle x0 für ungerades n gilt f’’(x0) = f’’’(x0) = ... = f(n-1)(x0) = 0 und fn(x0) ≠ 0 so besitzt f(x) an der Stelle x0 einen Wendepunkt. Bei geradem n Extremstelle. Ist darüber hinaus auch f’(x0) = 0 , so besitzt die Funktion bei x0 einen Wendepunkt mit horizontaler Tangente, der als Sattelpunkt bezeichnet wird. Beispiel: f ( x) = x 3 − 12 x + 28 f ( x) = 0,2 x 5 − x 3 + 1 f ( x) = x 5 f ( x) = x 4 Exkurs: Nullstellenbestimmung Es gibt mehrere Verfahren zur näherungsweisen Bestimmung von Nullstellen, z.B. Polynomdivision oder Intervallschachtelung. Ein von Newton entwickeltes Verfahren benutzt zur Nullstellenbestimmung die erste Ableitung einer Funktion. Gegeben sei eine differenzierbare Funktion f(x). Ferner sei eine Genauigkeitsschranke c gegeben. a) Setze i =1 b) Bestimme xi +1 = xi − f ( xi ) . Gehe zu c). f ' ( xi ) c) Berechne f(xi+1). Falls f(xi+1) = 0 gehe zu f). Falls f(xi+1) ≠ 0 gehe zu d). d) Falls I f(xi+1) I < c ist die Näherung ausreichend, gehe zu f), andernfalls gehe zu e). e) Setze i = i+1 und gehe zu b). f) Ende Beispiel: f(x) = x³-1,75x²+2x-3,5 21 6.4 Untersuchung einiger ökonomischer Funktionen 6.4.1 Die Preis-Absatz-Funktion und die Erlösfunktion a) Betrachtung eines Monopolisten Wird ein Produkt auf einem Markt nur von einem Anbieter angeboten, dann liegt ein Angebotsmonopol vor. Der Preis p, den der Monopolist setzt, bestimmt die abgesetzte Menge (bzw. die von ihm auf dem Markt angebotene Menge den Preis). Die Preisabsatzfunktion des Monopolisten, die die Beziehung zwischen Preisen und Mengen ausdrückt, hat dann in der Regel eine fallende Tendenz. Beispiel: p = -20x+200 Die Fragestellung lautet, mittels welcher wirtschaftlichen Aktivität (d.h. bei welchem Wert der unabhängigen Variablen) der größtmögliche Erlös erzielt werden kann. Grenzerlös E’ Der maximale Erlös wird erreicht wenn gilt E’ = 0 und E’’ < 0 b) Betrachtung bei vollständiger Konkurrenz Bei vollständiger Konkurrenz geht man davon aus, dass auf dem Markt eines Gutes der einzelne Anbieter den Preis nicht beeinflußen kann. Es wird also p = const. unterstellt. Zu diesem Preis kann der Anbieter praktisch jede beliebige Menge Absetzen. Beispiel: p = constant Bei dieser Betrachtungsweise wird deutlich, dass der Erlös theoretisch unbegrenzt mit der abgesetzten Menge steigt. Die Differentation macht hier zur Bestimmung des maximalen Erlöses keinen Sinn, da E’ = p. Den maximalen Erlös kann der Anbieter an der Kapazitätsgrenze realisieren, d.h. es handelt sich um ein Randmaximum. 22 6.4.2 Kostenfunktionen Bei folgenden Überlegungen wird ein s-förmiger Kurvenverlauf unterstellt. Geht man von einem linearen Kostenverlauf aus, können mit der Differentialrechnung keine Extremwerte berechnet werden. Beispiel: K = x³-10x²+37x+72 Gesamtkosten ( K ) 500 450 400 Kosten 350 300 250 200 150 100 50 0 0 1 2 3 4 5 6 7 8 9 10 Menge x Natürlich interessieren bei der Betrachtung der Kosten die Minimalstellen. Dabei macht es wenig Sinn, die Gesamtkosten auf Extremstellen zu untersuchen, da die Kosten üblicherweise mit der produzierten Menge steigen. D.h. die Minimalkosten liegen bei der Produktionsmenge 0 und die Maximalkosten bei der Kapazitätsgrenze. Interessante Punkte sind unter Anderem der geringste Kostenanstieg, die geringsten Stückkosten, das Betriebsoptimum und das Betriebsminimum. Kf – Fixkosten. Kosten, die unabhängig von der produzierten Menge entstehen. kf - Fixe Stückkosten. Fixkosten verteilt auf die produzierte Menge. kv - Variable Stückkosten. Kosten, die direkt einer produzierten Einheit zugerechnet werden können. KV - Variable Kosten. Die variablen Stückkosten multipliziert mit der produzierten Menge. K – Gesamtkosten. Die Summe aus Fixkosten und variablen Kosten. k - Stückkosten (Durchschnittskosten). Die Gesamtkosten verteilt auf die produzierte Menge K’ - Grenzkosten (Differentialkosten). Zusätzliche Kosten pro Mengeneinheit oder momentaner Kostenanstieg. Wenn K’’ = 0 und K’’’ > 0 dann liegt bei dieser Menge der geringste Kostenanstieg. (Dies ist der Wendepunkt von K !) k’ - Ableitung der Stückkosten. Wenn k’ = 0 und k’’ > 0 dann liegt bei dieser Menge der geringste Anstieg der Stückkosten. Diese Menge wird als Betriebsoptimum bezeichnet. kv’ - Ableitung der variablen Stückkosten. Wenn kv’ = 0 und kv’’ > 0 dann liegt bei dieser Menge der geringste Anstieg der variablen Stückkosten. Diese Menge wird als Betriebsminimum bezeichnet. Wenn der Produktpreis diese Kosten unterschreitet, kann kein Deckungsbeitrag mehr erzielt werden, die Produktion müsste eingestellt werden. Der zum Betriebsminimum gehörige variable Stückpreis wird als "kurzfristige Preisuntergrenze" bezeichnet. So kann ein Betrieb bei schwankenden Marktpreisen für die hergestellten Güter den Preis vorübergehend bis zu dieser Preisgrenze hinunterschrauben, um von der Konkurrenz nicht vom Markt verdrängt zu werden. Auf eine Deckung der fixen Kosten wird dabei verzichtet. 23 6.4.3 Gewinnfunktionen a) Gewinnmaximum eines Monopolisten Der Monopolist wird den Preis setzen, bei dem er den größtmöglichen Gewinn realisiert (bzw. die entsprechende Menge anbieten). Notwendige Bedingung für ein Gewinnmaximum ist G’ = E’ – K’ = 0 bzw. E’ = K’ Notwendige Bedingung für die Existenz eines Gewinnmaximums ist also die Übereinstimmung von Grenzerlös und Grenzkosten. Hinreichende Bedingung für ein Gewinnmaximum ist G’’ = E’’ – K’’ < 0 bzw. E’’ < K’’ 600 500 Erlös ( E ) 400 Gesamtkosten ( K ) Grenzerlös (E') 300 Preisabsatzfunktion Grenzkosten ( K' ) 200 100 0 0 1 2 3 4 5 6 7 8 9 10 Die Schnittpunkte von E und K sind die Nutzenschwelle bzw. die Nutzengrenze, zwischen diesen Grenzen liegt die Gewinnzone. Die Produktionsmenge, bei der der maximale Gewinn realisiert werden kann, liegt beim Schnittpunkt von E’ und K’. Der zu dem Gewinnmaximum gehörende Preis p kann über die Preisabsatzfunktion ermittelt werden. Beispiel: p = -20x+200 K = x³-10x²+37x+72 b) Gewinnmaximum bei vollständiger Konkurrenz 500,0 450,0 400,0 350,0 300,0 Erlös ( E ) 250,0 Gesamtkosten ( K ) 200,0 Preis 150,0 Grenzkosten ( K' ) 100,0 50,0 0,0 0 1 2 3 4 5 6 7 8 9 10 Wird p = const. unterstellt, dann ist E = px und E’ = p, d.h. der Grenzerlös ist gleich dem Preis. Anstelle von E’ = K’ ergibt sich p = K’, und anstatt E’’ < K’’ muss K’’ > 0 gelten. Bei vollständiger Konkurrenz ist also für die Erreichung eines Gewinnmaximums die Übereinstimmung von Preis und Grenzkosten notwendige Bedingung. Beispiel: p = 40 K = x³-10x²+37x+72 24 6.5 Aufgaben 56. 57. 58. Bestimmen Sie die erste, zweite und dritte Ableitung folgender Funktionen: 12 + 12 x 3 3 x a) y= d) y = a3 x 3 + a2 x 2 + a1 x + a0 2x + 3 x2 − 1 b) y= e) y = e3 x c) y=4 x f) y = ln x 2 Bestimmen Sie die Nullstellen für folgende Funktionen. Verwenden Sie dazu das NewtonVerfahren, Polynomdivision und die Mitternachtsformel (evtl. mit Substitution). a) y = x 3 −5 x 2 + 4 x d) y = x 4 − 13 x 3 + 51x 2 − 67 x + 28 mit der doppelten Nullstelle x1/2 = 1 Untersuchen Sie b) y= y = x 3 − 7,5 x 2 + 12 x + 8 c) y = x 6 − 18 x 4 + 81x 2 2 3 x − 4 x 2 + 6 x − 1 auf Extremwerte und Wendepunkte, und bestimmen 3 Sie die Bereiche, in denen die Funktion konkav bzw. konvex ist. y= 1 3 1 2 3 x − x − x die Nullstellen, Extremwerte und Wendepunkte. 6 2 2 59. Bestimmen Sie für 60. Bestimmen Sie für die Umsatzfunktion U(x) = -0,01x² + 42x das Umsatzmaximum und den dazu gehörenden Verkaufspreis. Ermitteln Sie daraus die Funktion des Stückumsatzes und überprüfen Sie diese auf Extremwerte. 61. Es gelte die Preis-Absatz-Funktion p = -0,02x + 12 . Bestimmen Sie die zugehörige Umsatzfunktion, die umsatzmaximale Absatzmenge und den größtmöglichen Umsatzbetrag. 62. Eine quadratische Kostenfunktion mit K = 1,15x² + 62100 ist gegeben. Bestimmen Sie die Ausbringungsmenge, bei welcher die Stückkosten ein Minimum erreichen. Wie groß ist der zugehörige Stückkostenbetrag? 63. Es gelte die Kostenfunktion K= 1 x ³ − 21x ² + 1570 x + 25200. Bestimmen Sie die Funktion der 10 Stückkosten, der variablen Stückkosten und der Grenzkosten. 64. Welche Maßnahme hat ein Unternehmen für die Erzielung eines Gewinnmaximums zu ergreifen, wenn die Preis-Absatz-Funktion p = -0,02x + 12 und die Kostenfunktion K = 3x + 500 gelten ? 65. Ermitteln Sie für die Gewinnfunktion G ( x) = − 1 2 x + 180 x − 50325 den Stückgewinn. 12 Untersuchen Sie die gebildete Funktion auf mögliche Extrempunkte. Stellen Sie die Stückgewinnfunktion und die Grenzgewinnfunktion grafisch dar. 66. Für die Produktion eines Gutes, das zu einem konstanten Preis von p = 53 abgesetzt wird, existiert die Kostenfunktion K = 2x² + 5x + 242. Bestimmen Sie a) die Erlösfunktion, b) die Grenzerlösfunktion, c) die Grenzkostenfunktion, d) die Durchschnittskostenfunktion, e) die Gewinnfunktion, f) die gewinnmaximale Ausbringungsmenge, g) die Ausbringungsmenge mit maximalem Stückgewinn, h) die Nutzenschwelle und die Nutzengrenze, i) Stellen Sie E und K grafisch dar. 67. Für eine Einproduktunternehmung lautet die Kostenfunktion K = 6x + 40 und die Preisabsatzfunktion p = 30 – 2x. Bestimmen Sie a) die Grenzkostenfunktion, b) die Durchschnittskostenfunktion, c) die Erlösfunktion, d) die Grenzerlösfunktion, e) den Bereich positiver Gewinne, f) die gewinnmaximale Ausbringungsmenge, g) Stellen Sie E, G und K grafisch dar. 68. Die Gesamtkosten eines Betriebes hängen von der Ausbringungsmenge ab und werden durch eine ganzrationale Funktion dritten Grades beschrieben. Der Verkaufspreis je ME (Mengeneinheit) beträgt 100 GE (Geldeinheiten). Die Fixkosten betragen 1820 GE. Kostendeckung wird bei einer Ausbringungsmenge von 70 ME erzielt. Bei 40 ME betragen die 25 Stückkosten 65,5 GE und bei 50 ME die variablen Kosten 1500 GE. Bestimmen Sie die Gleichung der Gesamtkostenfunktion. 69. Die Gesamtkostenfunktion ist gegeben durch K ( x) = 1 13 x ³ − x ² + 60 x + 1820 . Der 25 5 Verkaufspreis je ME beträgt 100 GE. Erstellen Sie eine Wertetabelle für 0 ≤ x ≤ 80 und zeichnen Sie das Schaubild der Kostenfunktion, der Umsatzgeraden und der Gewinnkurve. Berechnen Sie den maximalen Gewinn. Berechnen Sie die Nutzenschwelle, wenn die Nutzengrenze bei einer Ausbringungsmenge von 70 ME liegt. Bestimmen Sie das Betriebsminimum. Aus Wettbewerbsgründen muss der Betrieb den Verkaufspreis senken. Die Nutzenschwelle liegt jetzt bei einer Ausbringungsmenge von 25 ME. Berechnen Sie den neuen Verkaufspreis. 70. Ein Betrieb erzielt für sein Produkt einen Verkaufserlös von 22 GE je ME. Die Gesamtkosten sind durch eine ganzrationale Funktion dritten Grades bestimmt. Die fixen Kosten betragen 20 GE. Bei einer Ausbringungsmenge von 2 ME entstehen Kosten von 44 GE, bei einer Ausbringung von 1 ME tritt ein Verlust von 15 GE auf. Bei 4 ME betragen die Stückkosten 13 GE. Bestimmen Sie den Funktionsterm der Gesamtkostenfunktion. 71. Die Gesamtkostenfunktion ist gegeben durch: K ( x) = x ³ − 8 x ² + 24 x + 20 . Der Verkaufserlös beträgt 22 Ge je ME. Berechnen Sie die Nutzengrenze, wenn die Nutzenschwelle bei einer Ausbringung von 2 ME liegt. Berechnen Sie den maximalen Gewinn. Berechnen Sie das Betriebsoptimum mit einem Näherungsverfahren. Welcher Erlös p1 muss pro ME erzielt werden, wenn bei einer Ausbringung von 5 ME ein Gewinn von 60 GE erzielt werden soll? 26 7 UNTERSUCHUNG VON FUNKTIONEN MIT MEHREREN UNABHÄNGIGEN VARIABLEN 7.1 partielle Differentation In der anschaulichen Interpretation entspricht die Bestimmung der ersten Ableitung einer Funktion mit einer unabhängigen Variablen y = f(x) der Bestimmung der Steigung der Kurve. Da diese Steigung davon abhängt, welchen Wert x annimmt, ist auch die erste Ableitung wieder eine Funktion von x, d.h. y’ = f’(x). Bei einer Funktion mit zwei unabhängigen Variablen z = f(x,y) ist die Bestimmung einer Steigung nicht mehr eindeutig möglich: z = f(x,y) entspricht in einem x-y-z Koordinatensystem einer Fläche im Raum. Die Steigung auf einer solchen Fläche hängt nun nicht nur von x und y ab, sondern auch von der Richtung, in der man sich bewegt. Um dennoch Aussagen über die Steigung der Funktionsfläche in Abhängigkeit von Ort und Richtung zu erhalten, kann man folgendermaßen vorgehen: In der Funktion z = f(x,y) wird die Variable y durch eine Konstante y1 ersetzt. Die dadurch entstehende Funktion z = f(x,y1) = za(x) hängt nur noch von der Variablen x ab. Wird die Variable x durch eine Konstante x1 ersetzt, so hängt die Funktion z = f(x1,y) = zb(y) nur noch von y ab. Die Funktionen za(x) und zb(y) können, da sie nur Funktionen einer Variablen sind, nach x bzw. y differenziert werden. Gegeben sei die Funktion z = f(x,y). Existieren für alle (x,y) Є D(f) die Grenzwerte: lim ∆x →0 f ( x + ∆x, y ) − f ( x, y ) = f ' x ( x, y ) = z ' x ∆x und lim ∆y →0 f ( x, y + ∆y ) − f ( x, y ) = f ' y ( x, y ) = z ' y ∆y so heißt die Funktion partiell differenzierbar nach x und nach y. Eine Funktion mit zwei unabhängigen Variablen z = f(x,y) besitzt somit zwei partielle Ableitungen erster Ordnung. Höhere Ableitungen Die partiellen Ableitungen erster Ordnung können nun wiederum partiell nach den unabhängigen Variablen differenziert werden. Das ergibt die partiellen Ableitungen zweiter Ordnung der Funktion. Da jede der n partiellen Ableitungen erster Ordnung wieder nach jeder der n Variablen differenziert werden kann, gibt es insgesamt n² partielle Ableitungen zweiter Ordnung. Beispiel: f(x,y) = x³ y³ f(x,y) = x³+x²y+xy²+y³ 27 7.2 Extremwertbestimmung Schema zur Untersuchung einer Funktion z = f(x,y) auf Extremwerte a) Bestimmung von f’x und f’y b) Lösung des Gleichungssystems f’x = 0 und f’y = 0 für x und y. a. Hat das Gleichungssystem keine Lösung, so existiert kein Extremwert. b. Existieren die Lösungen (xi, yi) so ist Schritt c) durchzuführen. c) Bestimmung von f’’xx, f’’yy, f’’xy d) Vergleich von f’’xx , f’’yy und (f’’xy)² a. Falls f’’xx * f’’yy > (f’’xy)² , so liegt an der Stelle (xi,yi) ein Extremwert, weiter mit Schritt e) b. Falls f’’xx * f’’yy < (f’’xy)² , so liegt an der Stelle (xi,yi) kein Extremwert, sondern ein Sattelpunkt. c. Falls f’’xx * f’’yy = (f’’xy)² , so ist keine verbindliche Aussage über die Stelle (xi,yi) möglich. e) Für f’’xx < 0 folgt ein Maximum an der Stelle (xi,yi). Für f’’xx > 0 folgt ein Minimum an der Stelle (xi,yi). Beispiel: f(x,y) = x³+3x²y-3xy²-21x+y³-3y Extremwerte bei Funktionen mit mehr als zwei unabhängigen Variablen Für Funktionen mit mehr als zwei unabhängigen Variablen sind Maximum und Minimum ähnlich definiert wie bei zwei unabhängigen Variablen. Notwendige Bedingung für die Existenz eines Extremwertes einer stetig partiell differenzierbaren Funktion ist das verschwinden aller partiellen Ableitungen erster Ordnung nach allen unabhängigen Variablen. Auf die hinreichende Bedingung wird hier verzichtet. Es sei auf die Literatur verwiesen. Beispiel: z = x²+y²+v²+4x-2y-10v+27 7.3 Extremwerte unter Berücksichtigung von Nebenbedingungen Bei zahlreichen Wirtschaftswissenschaftlichen Anwendungen sind Extremwerte einer Funktion mit mehreren unabhängigen Variablen unter Berücksichtigung von Nebenbedingungen zu bestimmen. Für die Lösung derartiger Probleme, bei der die Nebenbedingungen in Gleichungsform gegeben sind, bieten sich zwei Möglichkeiten an: Die Variablensubstitution und die Multiplikatorregel nach LaGrange. 7.3.1 Lösung von Extremwertaufgaben durch Variablensubstitution Für die Lösung einer Extremwertaufgabe unter Beachtung einer Nebenbedingung durch Variablensubstitution löst man die Nebenbedingung nach einer Variablen auf und ersetzt diese Variable dann in der auf Extremwerte zu untersuchenden Funktion entsprechend. Dadurch erhält man eine Funktion mit einer unabhängigen Variablen. Beispiel: Ein Kraftwerk erzeugt Strom aus der Verbrennung von Kohle (r1) ME und Erdgas (r2) ME. Der Preis je ME Kohle beträgt q1 = 4 GE und für Erdgas q2 = 12 GE. Die Produktionsfunktion für die erzeugte Strommenge (Output) lautet: f(r1,r2) = 20r10,25 r20,75. Die benötigte Strommenge liegt derzeit bei 80 EE. Wie lautet die Minimalkostenkombination für die Produktionsfaktoren? (Wie ändert sich die Situation bei einem Strombedarf von 120 EE?) 28 Sind die Produktionsfaktoren substituierbar, dann wird man eine vorgegebene Produktionsmenge mit der Faktorkombination herstellen, die die geringsten Kosten verursacht. Sind q1 und q2 die Preise der beiden Produktionsfaktoren, dann ergibt sich für die Kosten die zu minimierende Funktion (=Zielfunktion) K = q1r1 + q2r2. Für unser Beispiel K = 4r1 + 12r2 . Zu beachten ist, dass die Bedingung des benötigten Strombedarfs x eingehalten wird x = f(r1,r2). Für unser Beispiel 80 = 20r10,25 r20,75 . Kurz: Minimiere K = 4r1 + 12r2 unter Einhaltung der Nebenbedingung 80 = 20r10,25 r20,75 . Wird r1 in der Nebenbedingung in Abhängigkeit von r2 ausgedrückt, r1 = f(r2) , erhält man die Isoquante. Isoquanten sind Kurven, auf der alle Faktorkombinationen liegen, die zu der selben Produktionsmenge (Output) führen. 4 80 = 256 r2 − 3 r1 = 0 , 75 20r2 Die so isolierte Variable wird nun in der Zielfunktion substituiert, man erhält K = q1f(r2 )+ q2r2. Für unser Beispiel: −3 K = 4 ⋅ 256 r2 + 12 r2 => Minimum bei r1 = 4 und r2 = 4 und K = 64 Alle Faktorkombinationen, die zu einem bestimmten Kostenbetrag führen, q1r1 + q2r2 = c , liegen auf einer Geraden (Isokostengerade) r1 = − q2 c r2 + . Für unse Beispiel r1 = −3r2 + 16 q1 q1 10 9 r1 = 256 r2 8 −3 7 6 5 4 3 2 r1 = −3r2 + 16 1 0 3 3,2 3,4 3,6 3,8 4 4,2 4,4 4,6 4,8 Im Isoquantendiagramm ist eine Minimalkostenkombination als Tangentialpunkt von Isoquante und Isokostengerade zu erkennen. Beispiel 2: Für ein Unternehmen sollen Konservendosen aus Blech in Form eines Kreiszylinders hergestellt werden. Die Dosen sollen eine Füllmenge von 330 ml beinhalten und unter dem Gesichtspunkt des minimalen Materialverbrauchs hergestellt werden. Der m² Weißblech kostet 3,78 €. Wie viel kostet das Material für eine Dose? 29 7.3.2 Multiplikatorregel von LaGrange Bei Anwendung der Multiplikatorregel werden die Nebenbedingungen mit einem Faktor λ (LaGrangescher Multiplikator) multipliziert und dann zu der auf Extremwerte zu untersuchenden Funktion addiert. Die daraus entstandene erweiterte Funktion wird auf Extremwerte untersucht. Auch die LaGrangeschen Multiplikatoren stellen dabei unabhängige Variablen dar. Vorgehensweise a) Bestimmung der Zielfunktion und der Nebenbedingungen (Achtung NB = 0) b) Erstellen der Lagrange Funktion c) Bildung der Ableitungen z = f ( x, y ) + λ ⋅ g ( x, y ) z 'λ , f ' x , f ' y . Die Ableitungen werden gleich Null gesetzt, es entsteht ein LGS, das eindeutig gelöst werden kann. Beispiel: 8 72. AUFGABEN Bilden Sie für folgende Funktionen die partiellen Ableitungen erster Ordnung. a) 73. z = x3 + y 3 b) z = ax b y c c) z = ax 2 + by 2 Untersuchen Sie die folgenden Funktionen auf Extremwerte a) 74. Es soll z = f(x,y) = -x² - y² + 9 unter Berücksichtigung der Nebenbedingung g(x,y) = x + y = 2 minimiert werden. z = x3 + 3 x 2 y + 3 xy 2 − 48 x z = 2 x 2 y + 2 xy 2 + 2 xy + b) 2 3 y + y2 − 4 y 3 Für ein Unternehmen, das zwei Güter in den Mengen x1 und x2 herstellt, gilt die Gewinnfunktion 2 2 G ( x1 , x2 ) = 14 x1 + 28 x2 − x1 − 2 x2 + x1 x2 . Bestimmen Sie den Produktionsplan mit dem größten Gewinn. 75. Es wird ein Produktionsprozeß betrachtet, bei dem ein Gut mit zwei Produktionsfaktoren r1 und r2 hergestellt wird. Die Produktionsfunktion lautet x=5r12r2. Die Kosten werden gegeben durch K=6r1+12r2. Bestimmen Sie die Minimalkostenkombination für die Produktion von 80 Einheiten eines Gutes. 76. Für ein Unternehmen sollen Plastikbecher in Form eines Kreiszylinders, der oben geöffnet ist, hergestellt werden. Die Becher sollen eine Füllmenge von 250 ml beinhalten und unter dem Gesichtspunkt des minimalen Materialverbrauchs hergestellt werden. Welche Maße haben der Radius und die Höhe des Bechers? 77. Untersuchen Sie die Funktion z = x² + 2xy unter der Nebenbedingung y = -1,5x + 6 auf Extremwerte a) mittels des Ansatzes von LaGrange und B) durch Substitution. 78. Untersuchen Sie die Funktion z = 4 x 3 + xy − y + 2 unter der Nebenbedingung y = xy + 3 x auf Extremwerte. 79. Es soll f(x,y,z) = x²+y²+z2 unter Berücksichtigung der Nebenbedingung g(x,y,z) = 2x+y-z = 1 minimiert werden. 80. Untersuchen Sie die folgende Funktion auf Extremwerte. z = ( x − y )3 + 12 xy