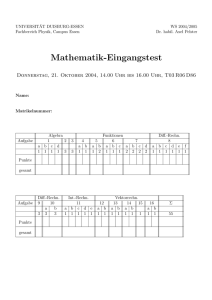
Unverbindlich geplanter Inhalt 01. Woche: 06.04.2011 Aufbau des

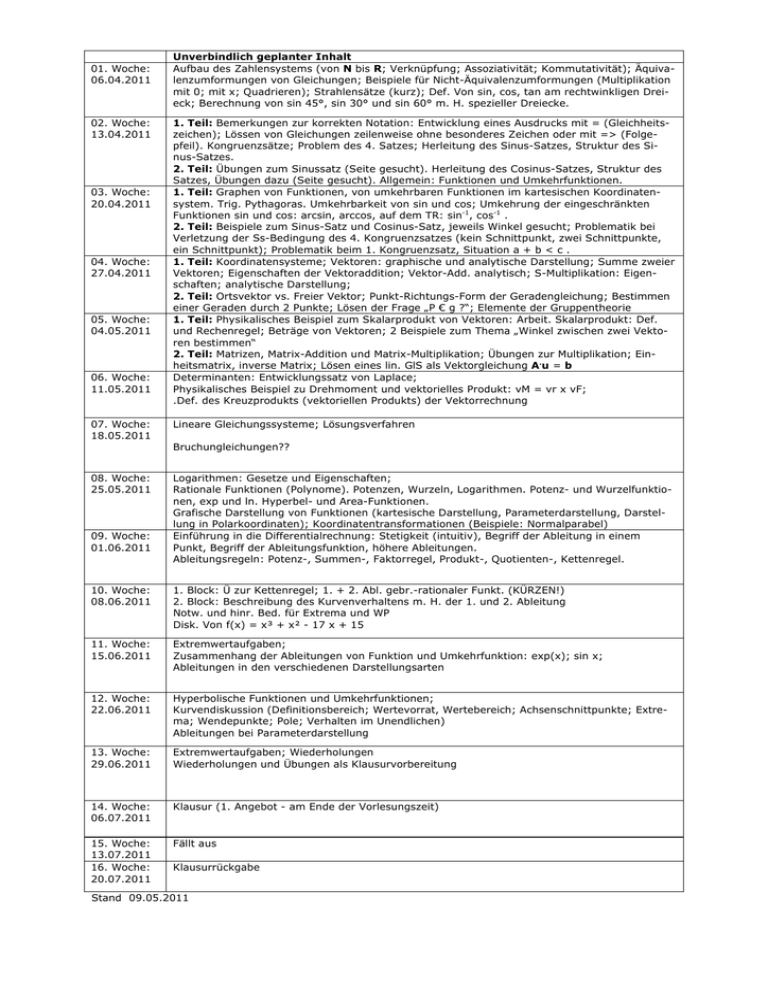
01. Woche:
06.04.2011
02. Woche:
13.04.2011
03. Woche:
20.04.2011
04. Woche:
27.04.2011
05. Woche:
04.05.2011
06. Woche:
11.05.2011
07. Woche:
18.05.2011
Unverbindlich geplanter Inhalt
Aufbau des Zahlensystems (von N bis R; Verknüpfung; Assoziativität; Kommutativität); Äquivalenzumformungen von Gleichungen; Beispiele für Nicht-Äquivalenzumformungen (Multiplikation
mit 0; mit x; Quadrieren); Strahlensätze (kurz); Def. Von sin, cos, tan am rechtwinkligen Dreieck; Berechnung von sin 45°, sin 30° und sin 60° m. H. spezieller Dreiecke.
1. Teil: Bemerkungen zur korrekten Notation: Entwicklung eines Ausdrucks mit = (Gleichheitszeichen); Lössen von Gleichungen zeilenweise ohne besonderes Zeichen oder mit => (Folgepfeil). Kongruenzsätze; Problem des 4. Satzes; Herleitung des Sinus-Satzes, Struktur des Sinus-Satzes.
2. Teil: Übungen zum Sinussatz (Seite gesucht). Herleitung des Cosinus-Satzes, Struktur des
Satzes, Übungen dazu (Seite gesucht). Allgemein: Funktionen und Umkehrfunktionen.
1. Teil: Graphen von Funktionen, von umkehrbaren Funktionen im kartesischen Koordinatensystem. Trig. Pythagoras. Umkehrbarkeit von sin und cos; Umkehrung der eingeschränkten
Funktionen sin und cos: arcsin, arccos, auf dem TR: sin-1, cos-1 .
2. Teil: Beispiele zum Sinus-Satz und Cosinus-Satz, jeweils Winkel gesucht; Problematik bei
Verletzung der Ss-Bedingung des 4. Kongruenzsatzes (kein Schnittpunkt, zwei Schnittpunkte,
ein Schnittpunkt); Problematik beim 1. Kongruenzsatz, Situation a + b < c .
1. Teil: Koordinatensysteme; Vektoren: graphische und analytische Darstellung; Summe zweier
Vektoren; Eigenschaften der Vektoraddition; Vektor-Add. analytisch; S-Multiplikation: Eigenschaften; analytische Darstellung;
2. Teil: Ortsvektor vs. Freier Vektor; Punkt-Richtungs-Form der Geradengleichung; Bestimmen
einer Geraden durch 2 Punkte; Lösen der Frage „P € g ?“; Elemente der Gruppentheorie
1. Teil: Physikalisches Beispiel zum Skalarprodukt von Vektoren: Arbeit. Skalarprodukt: Def.
und Rechenregel; Beträge von Vektoren; 2 Beispiele zum Thema „Winkel zwischen zwei Vektoren bestimmen“
2. Teil: Matrizen, Matrix-Addition und Matrix-Multiplikation; Übungen zur Multiplikation; Einheitsmatrix, inverse Matrix; Lösen eines lin. GlS als Vektorgleichung A.u = b
Determinanten: Entwicklungssatz von Laplace;
Physikalisches Beispiel zu Drehmoment und vektorielles Produkt: vM = vr x vF;
.Def. des Kreuzprodukts (vektoriellen Produkts) der Vektorrechnung
Lineare Gleichungssysteme; Lösungsverfahren
Bruchungleichungen??
08. Woche:
25.05.2011
09. Woche:
01.06.2011
Logarithmen: Gesetze und Eigenschaften;
Rationale Funktionen (Polynome). Potenzen, Wurzeln, Logarithmen. Potenz- und Wurzelfunktionen, exp und ln. Hyperbel- und Area-Funktionen.
Grafische Darstellung von Funktionen (kartesische Darstellung, Parameterdarstellung, Darstellung in Polarkoordinaten); Koordinatentransformationen (Beispiele: Normalparabel)
Einführung in die Differentialrechnung: Stetigkeit (intuitiv), Begriff der Ableitung in einem
Punkt, Begriff der Ableitungsfunktion, höhere Ableitungen.
Ableitungsregeln: Potenz-, Summen-, Faktorregel, Produkt-, Quotienten-, Kettenregel.
10. Woche:
08.06.2011
1. Block: Ü zur Kettenregel; 1. + 2. Abl. gebr.-rationaler Funkt. (KÜRZEN!)
2. Block: Beschreibung des Kurvenverhaltens m. H. der 1. und 2. Ableitung
Notw. und hinr. Bed. für Extrema und WP
Disk. Von f(x) = x³ + x² - 17 x + 15
11. Woche:
15.06.2011
Extremwertaufgaben;
Zusammenhang der Ableitungen von Funktion und Umkehrfunktion: exp(x); sin x;
Ableitungen in den verschiedenen Darstellungsarten
12. Woche:
22.06.2011
Hyperbolische Funktionen und Umkehrfunktionen;
Kurvendiskussion (Definitionsbereich; Wertevorrat, Wertebereich; Achsenschnittpunkte; Extrema; Wendepunkte; Pole; Verhalten im Unendlichen)
Ableitungen bei Parameterdarstellung
13. Woche:
29.06.2011
Extremwertaufgaben; Wiederholungen
Wiederholungen und Übungen als Klausurvorbereitung
14. Woche:
06.07.2011
Klausur (1. Angebot - am Ende der Vorlesungszeit)
15. Woche:
13.07.2011
16. Woche:
20.07.2011
Fällt aus
Klausurrückgabe
Stand 09.05.2011