Geraden / Kreise / Dreiecksberechnungen

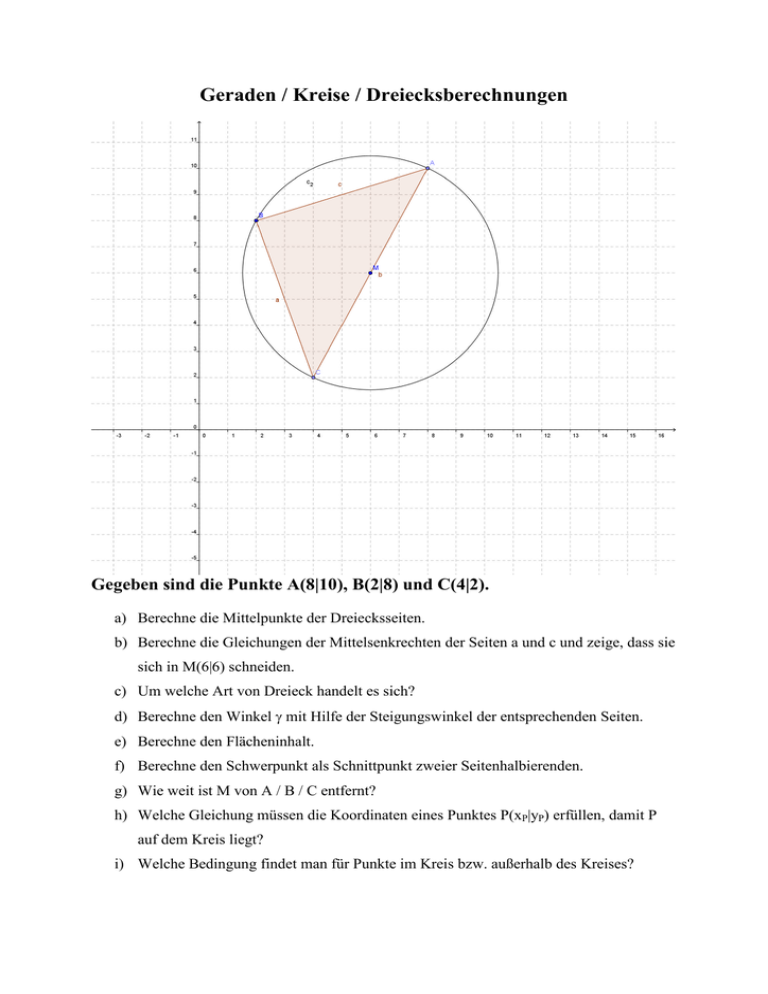
Geraden / Kreise / Dreiecksberechnungen
Gegeben sind die Punkte A(8|10), B(2|8) und C(4|2).
a) Berechne die Mittelpunkte der Dreiecksseiten.
b) Berechne die Gleichungen der Mittelsenkrechten der Seiten a und c und zeige, dass sie
sich in M(6|6) schneiden.
c) Um welche Art von Dreieck handelt es sich?
d) Berechne den Winkel mit Hilfe der Steigungswinkel der entsprechenden Seiten.
e) Berechne den Flächeninhalt.
f) Berechne den Schwerpunkt als Schnittpunkt zweier Seitenhalbierenden.
g) Wie weit ist M von A / B / C entfernt?
h) Welche Gleichung müssen die Koordinaten eines Punktes P(xP|yP) erfüllen, damit P
auf dem Kreis liegt?
i) Welche Bedingung findet man für Punkte im Kreis bzw. außerhalb des Kreises?
Inhalte
Wir haben das erste Kapitel über Geraden durch, von Kapitel II die Unterkapitel 1 und 2.
Beim Steigungswinkel gibt es kleines Taschenrechnerproblem: er gibt bei fallenden
Funktionen statt z.B. 120° den negativen Winkel -60° an; aber das kann man ja leicht
umrechen.
Wichtig:
- Aufstellen von Geraden aus 2 Punkten bzw. Steigung und 1 Punkt.
- Steigungswinkel
- senkrechte Geraden (mg mh = -1)
- Länge und Mitte von Strecken
- Dreiecksberechnungen
später dann:
- Kreise
- Tangenten
Hier die Lösungen zum Arbeitsblatt:
a) Ma(3|5), Mb(6|6), C(5|9)
1
b) Mittelsenkrechten sind m a : y  x 4,
m c : y 3x 24
3
Gleichsetzen ergibt den gewünschten Punkt.
c) Da der Kreis ein Thaleskreis ist, ist das Dreieck rechtwinklig.
d) AC hat die Steigung 2, also Steigungswinkel 63,4°, BC hat die Steigung -3, StW. –71,6°,
daraus erhält man = 180° - 63,4° - 71,6° = 45°, also ist das Dreieck auch noch
gleichschenklig.
e) a  36 4  40 [LE], damit der Flächeninhalt 20 [FE] (Längen-, bzw.
Flächeneinheiten).
2 2
f) Der Schwerpunkt ist Schnittpunkt zweier Seitenhalbierenden: S(4 | 6 ) .
3 3
g) AM BM CM  20
h) (6 - xP)² + (6 - yP)² = 20
i
)… >20f
ü
ra
uße
r
ha
l
b,… <20f
üri
nne
r
ha
l
b.