Tutoriumsblatt 8

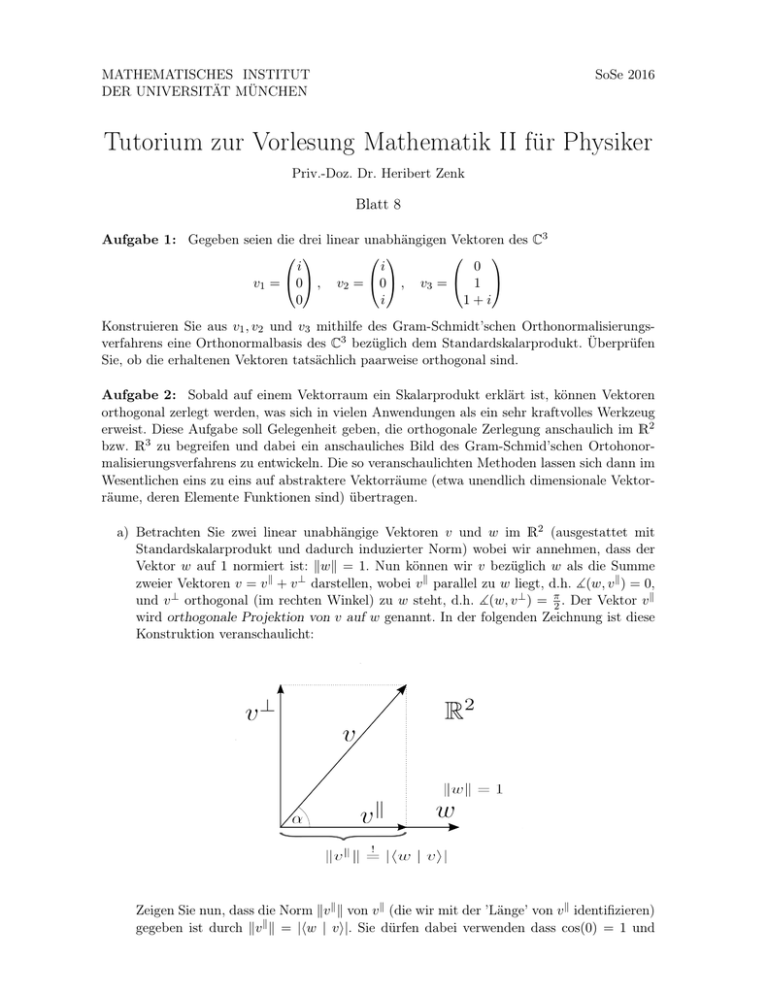
MATHEMATISCHES INSTITUT
DER UNIVERSITÄT MÜNCHEN
SoSe 2016
Tutorium zur Vorlesung Mathematik II für Physiker
Priv.-Doz. Dr. Heribert Zenk
Blatt 8
Aufgabe 1: Gegeben seien die drei linear unabhängigen Vektoren des C3
 
 


i
i
0
v1 = 0 , v2 = 0 , v3 =  1 
0
i
1+i
Konstruieren Sie aus v1 , v2 und v3 mithilfe des Gram-Schmidt’schen Orthonormalisierungsverfahrens eine Orthonormalbasis des C3 bezüglich dem Standardskalarprodukt. Überprüfen
Sie, ob die erhaltenen Vektoren tatsächlich paarweise orthogonal sind.
Aufgabe 2: Sobald auf einem Vektorraum ein Skalarprodukt erklärt ist, können Vektoren
orthogonal zerlegt werden, was sich in vielen Anwendungen als ein sehr kraftvolles Werkzeug
erweist. Diese Aufgabe soll Gelegenheit geben, die orthogonale Zerlegung anschaulich im R2
bzw. R3 zu begreifen und dabei ein anschauliches Bild des Gram-Schmid’schen Ortohonormalisierungsverfahrens zu entwickeln. Die so veranschaulichten Methoden lassen sich dann im
Wesentlichen eins zu eins auf abstraktere Vektorräume (etwa unendlich dimensionale Vektorräume, deren Elemente Funktionen sind) übertragen.
a) Betrachten Sie zwei linear unabhängige Vektoren v und w im R2 (ausgestattet mit
Standardskalarprodukt und dadurch induzierter Norm) wobei wir annehmen, dass der
Vektor w auf 1 normiert ist: kwk = 1. Nun können wir v bezüglich w als die Summe
zweier Vektoren v = v k + v ⊥ darstellen, wobei v k parallel zu w liegt, d.h. ](w, v k ) = 0,
und v ⊥ orthogonal (im rechten Winkel) zu w steht, d.h. ](w, v ⊥ ) = π2 . Der Vektor v k
wird orthogonale Projektion von v auf w genannt. In der folgenden Zeichnung ist diese
Konstruktion veranschaulicht:
Zeigen Sie nun, dass die Norm kv k k von v k (die wir mit der ’Länge’ von v k identifizieren)
gegeben ist durch kv k k = |hw | vi|. Sie dürfen dabei verwenden dass cos(0) = 1 und
cos( π2 ) = 0 gilt. Wenn Sie noch die Bedeutung des Kosinus im rechtwinkligen Dreieck
aus der Schule kennen (’Kosinus gleich Ankathete durch Hypotenuse’), können Sie sich
den Zusammenhang kv k k = |hw | vi| auch mithilfe der Zeichnung geometrisch überlegen.
Wie sieht die Konstruktion aus, wenn α > π2 ist (in diesem Fall dürfen sie verwenden,
dass cos(π) = −1 gilt)?
b) Geben Sie für die Vektoren v und w aus Aufgabeteil a) mithilfe obiger Konstruktion
eine anschauliche Erklärung des Gram-Schmidt’schen Orthonormalisierungsverfahrens.
c) Betrachten Sie nun drei linear unabhängige Vektoren u, v und w im R3 und versuchen
Sie nun auch hier alle Schritte der Orthonormalisierung dieser drei Vektoren nach GramSchmidt geometrisch nachzuvollziehen. Auch im R3 gilt die obige Konstruktion, wobei
die orthogonale Projektion eines Vektors auf einen Einheitsvektor in der von diesen
beiden Vektoren aufgespannten Ebene zu verstehen ist.
Bemerkung: Bemerkenswert ist, dass für orthogonale Zerlegungen letztlich das Konzept eines
Winkels zwischen zwei Vektoren – das nur in euklidischen Vektorräumen Sinn macht – nicht
gebraucht wird, da sinnvolle Definitionen von Orthogonalität und Parallelität genügen: Zwei
Vektoren v, w 6= 0 in einem Vektorraum V über dem Körper K = R oder K = C mit Skalarprodukt h· | ·i heißen parallel, wenn es ein λ ∈ K gibt, sodass v = λw und orthogonal wenn
hw | vi = 0. Ist w ∈ V zu 1 normiert (kwk = 1), so lässt sich ein beliebiges v ∈ V in die
Summe eines zu w parallelen und eines zu w orthogonalen Anteils zerlegen: v = v k + v ⊥ mit
v k = hw | viw und v ⊥ = v − hw | viw.
Aufgabe 3: Gegeben sei die selbstadjungierte Matrix


2 −1 −1
A = −1 2 −1 ∈ M3 (R).
−1 −1 2
Finden Sie eine Orthonormalbasis des R3 bestehend aus Eigenvektoren von A.