WS 10/11 - mv.uni

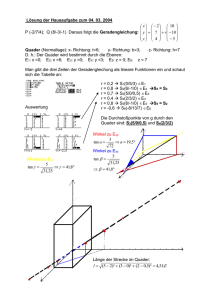
E RGEBNISSE
TM I,II UND ETM I,II
Lehrstuhl für Technische Mechanik, TU Kaiserslautern
WS 10/11, 26.02.2011-28.02.2011
1. Aufgabe:
( TMI)
q0
C
x2
α
z2
l
x1
A
G
z1
l
B
l
Das dargestellte masselose Tragwerk mit einem Gelenk in G ist in A, B und C gelenkig gelagert. Im oberen Bereich wird das Tragwerk durch eine lineare Streckenlast mit Maximalwert q0
belastet.
a) Ermitteln Sie die Lagerreaktionen in A, B und C.
b) Berechnen Sie die Verläufe von Normal-, Querkraft und Biegemoment (N, Q, M) im
Rahmenabschnitt oberhalb des Gelenks G in Abhängigkeit der Koordinaten x1 und x2 .
c) Skizzieren Sie die Verläufe von Normal,- Querkraft und Biegemoment (N, Q, M) im
Balken AB. Geben Sie ausgezeichnete Werte an.
Gegeben: q0 , l, α = 30◦ .
√
(2 3 + 3)q0 l
√
a) A =
12( 3 + 1)
√
(2 3 + 3)q0 l
√
By =
12( 3 + 1)
q0 l
√
Bx =
6(1 + 3)
q0 l
√
C=
3(1 + 3)
√
q0 l
(2 3 + 3)q0 l
√
√
b) Gx =
Gy =
6(1 + 3)
6( 3 + 1)
Schnittgrößen x1
√
(2 3 + 3)q0 l
√
N(x1 ) = −
6( 3 + 1)
q0 l
√
Q(x1 ) = −
6(1 + 3)
q0 lx1
√
M(x1 ) = −
6(1 + 3)
Schnittgrößen x2
q0 l
√
N(x2 ) = −
6(1 + 3)
√
q0 x22
(3 + 2 3)q0 l
√
Q(x2 ) =
− q0 x2 +
2l
6(1 + 3)
√
q0 l2
q0 x32 q0 x22 (3 + 2 3)q0 lx2
√
√
−
+
−
M(x2 ) =
6l
2
6(1 + 3)
6(1 + 3)
N
Gx
x
l
2l
Q
A
x
l
A − Gy
M
2l
Al
x
l
c)
2l
2. Aufgabe:
( TMI)
3
l
2
l
g
l
2
R
l
2
F
a
l
y
x
µ0
Eine homogene Scheibe der Masse m mit konstanter Dicke und den angegebenen Abmessungen
befindet sich auf einer horizontalen Fläche. An der Scheibe sind zwei Räder mit vernachlässigbaren Dimensionen angebracht. Das linke Rad ist blockiert, während das rechte Rad frei rollen
kann.
Ermitteln Sie:
l
a) für den Abstand a =
die Lage (xS , yS ) des Schwerpunktes im angegebenen Koordi2
natensystem,
b) für F = 0 den maximalen Abstand a so, dass die Scheibe nicht nach links kippt,
l
c) für a = die maximale Kraft F , damit die Scheibe nicht nach rechts rutscht. Der Haft2
koeffizient zwischen Rad und Boden ist µ0 .
l
Gegeben: m, l, R = √ , µ0 , g
2 π
a)
b)
c)
xs =
20
l
13
(1)
ys =
31
l
26
(2)
a=l
F max
(3)
25
mg
= 26
1
1+
µ0
(4)
3. Aufgabe:
( TMI)
F
45◦
q0
B
r
C
A
r
r
r
r
2
r
2
Gegeben ist das skizzierte Rahmen- und Bogensystem, welches durch eine lineare Streckenlast
und die Einzelkraft F belastet wird.
Bestimmen Sie mit Hilfe des Prinzips der virtuellen Verrückungen
a) die vertikale Lagerkraft Av sowie das Einspannmoment MA ,
b) das Schnittmoment im Punkt C.
Lösungswege ohne das Prinzip der virtuellen Verrückungen werden nicht berücksichtigt!
Gegeben: r, q0 , F =
√
2q0 r.
7
a) Av = q0 r, MA = q0 r 2 .
6
1
b) MC = q0 r 2
2
4. Aufgabe:
(TMII)
a − 2δ
nur c)
a−δ
p
h>l
l
z
E, ν, αT
y
x
a
a
starr
Ein homogener, elastischer Quader (Kantenlänge der Grundfläche a, Höhe l, Elastizitätsmodul E, Querkontraktionszahl ν, Wärmeausdehnungskoeffizient αT ) soll in einen starren Kasten
eingepasst werden. Die Grundfläche des Kastens ist in x-Richtung um δ und in y-Richtung
um 2δ kleiner als die Abmessungen des Quaders. Die Seitenflächen des Quaders können reibungsfrei an den Innenwänden des Kastens gleiten.
a) Der Quader wird zunächst abgekühlt, um ihn in den Kasten einzusetzen. Wie groß muss
die Temperaturdifferenz ∆T sein, damit der Quader gerade spannungsfrei in den Kasten
passt?
b) Der Quader erwärmt sich nun im starren Kasten wieder auf seine ursprüngliche Temperatur (∆T = 0). Berechnen sie die Längenänderung ∆lz des Quaders in z-Richtung (in
Bezug auf seine ursprüngliche Länge l). Die Höhe h des Kastens ist groß genug, damit
der verformte Quader nicht über den Rand quillt.
c) Welcher Druck p (in z-Richtung) muss auf den Quader im Kasten aufgebracht werden,
damit die Längenänderung in z-Richtung komplett verschwindet?
Hinweis: Alle Teilaufgaben können unabhängig voneinander gelöst werden.
Gegeben: a, l, E, ν, αT .
a) ∆T = −
2δ
aαT
b) ∆lz = 3δ
c) p = 3E
l ν
a1−ν
δ
ν
a 1 − ν − 2ν 2
5. Aufgabe:
(TMII)
2mT0
1111
0000
0000
1111
0000
1111
0000
1111
0000
1111
mT0
t
x
r
l
Der Flügelholm (Länge l, Schubmodul G, Kreisringquerschnitt mit Radius r und Dicke t ≪ r)
im Inneren einer Flugzeugtragfläche wird durch ein linear veränderliches Torsionsmoment pro
Längeneinheit mT (x) mit mT (0) = 2mT0 und mT (l) = mT0 belastet. Die Verbindung zum
Rumpf kann als feste Einspannung betrachtet werden.
a) Geben Sie die Funktion mT (x) an.
b) Ermitteln Sie das aus mT (x) resultierende Torsionsmoment MT (x) im Holm.
c) Berechnen Sie das Torsionsträgheitsmoment IT des gegebenen Querschnitts.
d) Um welchen Winkel ϑ verdreht sich das Ende des Flügels gegenüber dem Rumpf?
e) Wie groß ist die maximal auftretende Schubspannung τ max , und wo tritt sie auf?
Skizzieren Sie den Mohrschen Kreis für diesen Spannungszustand.
Gegeben: mT0 , G, l, r, t.
x
mT0
a) dmT (x) = 2 −
l
2
x
3
b) MT (x) =
− 2x + l mT0
2l
2
c) θ =
l2 mT0
3πr 3 tG
e) τ max =
3 lmT0
4 πr 2 t
τ
τmax
σ
−τmax
6. Aufgabe:
(TMII)
EA
a
2
EI
F
a
2
q0
A
a
Das dargestellte System aus einem dehn- und schubstarren Rahmen (Biegesteifigkeit EI) und
einem Stab (Dehnsteifigkeit EA) wird duch die konstante Streckenlast q0 sowie eine Einzelkraft F belastet.
a) Ermitteln Sie die Stabkraft S.
b) Berechnen Sie die vertikale Verschiebung des Punktes A.
Gegeben: q0 , F = q0 a, EI, EA.
a) S =
b) fc =
q0 a3
3
4 8 2 EI
a −
3
EA
3
q0 a3
a
4 8 2 EI 2EA
a −
3
EA
7. Aufgabe:
( ETMII)
g
x4
ϕ5
m
r
ϕ4
r
m
x5
x1
x2
m1
m2
m3
x3
Das dargestellte System besteht aus drei Massen (m1 , m2 und m3 ), zwei homogenen Walzen
und zwei masselosen Umlenkrollen, welche durch undehnbare Seile miteinander verbunden
sind.
a) Bestimmen Sie die kinematische Beziehunge für x3 in Abhängigkeit von x1 und x2
(x3 = x3 (x1 , x2 )).
b) Zeichnen Sie alle Freikörperbilder und stellen Sie die kinetischen Gleichungen auf.
c) Bestimmen Sie die Masse m3 so, dass die Masse m2 in Ruhe bleibt. Wie groß ist in
diesem Falle die Beschleunigung ẍ3 ?
Gegeben: m1 = m, m2 =
m
, r, g.
8
a) x3 = 4x1 + x2
b)
S1 − m1 g − m1 ẍ1 = 0
↑
(1)
S1
x1
m1
m1 g, m1 ẍ1
S2 − m2 g − m2 ẍ2 = 0
↑
(2)
S2
x2
m2
m2 g, m2 ẍ2
↑
S3 − m3 g + m3 ẍ3 = 0
S3 , m3 ẍ3
m3
x3
m3 g
(3)
↑
x
M:
S4 + S5 − S1 − mg − mẍ4 = 0
S5 r − S4 r − θ4 ϕ̈4 = 0
S4
(4)
(5)
S5
x4
m
r
ϕ4
Θ4 ϕ̈4
S1 , m g m ẍ4
↑
x
M:
S5 − S2 − S3 − mg + mẍ5 = 0
S3 r − S2 r − θ5 ϕ̈5 = 0
(6)
(7)
S5 , m ẍ5
ϕ5
T5
r
m
x5
S2
S3
mg
c)
m3 =
17m
40
(8)
die Beschleunigung von Masse m3 :
ẍ3 =
4g
9
(9)
8. Aufgabe:
(ETMII)
Das dargestellte Stangengetriebe besteht aus einer Kurbel BC, einer Schwinge AF und einer
Schubstange DE. Die Kurbel wird mit der konstanten Geschwindigkeit ω1 angetrieben.
a) Skizzieren Sie die Richtungen der Geschwindigkeitsvektoren für die Punkte C, D und E.
b) Bestimmen Sie die Lagen der Momentanpole der Kurbel BC und der Schwinge AF .
Berechnen Sie in Abhängigkeit von ω1 für die skizzierte Lage :
c) den Geschwindigkeitsvektor für im Punkt C,
d) die Winkelgeschwindigkeit ω2 der Schwinge AF und den Geschwindigkeitsvektor im
Punkt E,
e) den Beschleunigungsvektor im Punkt C und die Winkelbeschleunigung ω̇2 der Schwinge
AF .
Gegeben: ω1 , α, c, d, r.
a) Geschwindigkeitsvektoren:
(vD ist hier die Geschwindigkeit der Schwinge im Punkt D während vC die Geschwindigkeit der Kurbel in C bezeichnet!)
b) Momentanpole:
Der Momentanpol der Kurbel BC befindet sich im Punkt B.
Der Momentanpol der Schwinge AF befindet sich im Punkt A.
c) Geschwindigkeitsvektor ~vc im Punkt C:


ω1 · r
~vC =  0 
0
(1)
d) Winkelgeschwindigkeit ω2 der Schwinge AF und den Geschwindigkeitsvektor ~vE der
Schubstange DE:
r
ω2 = ω1 · · sin α
c

0



r·d


~vE =  −ω1 ·
· tan α 


c
0
(2)
e) Beschleunigungsvektor ~aC der Kurbel im Punkt C und die Winkelgeschwindigkeit ω̇2 :


0
~aC =  −ω12 · r 
(3)
0
Die Winkelbeschlaunigung ω̇2 ergibt sich zu:
ω̇2 = ω1 ω2 ·
r
· cos α.
c
(4)
9. Aufgabe:
( ETMII)
A
11111
00000
00000
11111
11111
00000
g
2R
R
ϕ
M
y
m
C
R
S
x
B
11111111111111111111111111
00000000000000000000000000
Ein in A drehbar gelagerter Stab der Masse m wird mit der Auslenkung um den Winkel ϕ
aus der Ruhe losgelassen. Er trifft im Punkt B mit seiner unteren Kante (Punkt C) auf den
homogenen, dünnwandigen Hohlzylinder der Masse M (Radius R). Der Hohlzylinder befindet
sich zunächst in Ruhe und rollt nach dem inelastischen Stoss (e = 0, 75) ohne zu gleiten los.
Berechnen Sie:
(A)
a) das Massenträgheitsmoment des Stabes ΘS bezüglich A und das Massenträgheitsmo(S)
ment des Hohlzylinders ΘH bezüglich seines Schwerpunktes,
b) die Winkelgeschwindigkeit des Stabes ωS und den Geschwindigkeitsvektor des Stabes ~vC
kurz vor dem Stoss,
c) kurz nach dem Stoss: die Winkelgeschwindigkeit des Stabes ωS∗ , den Geschwindigkeits∗
vektor des Stabes ~vC∗ im Punkt C, die Winkelgeschwindigkeit des Hohlzylinders ωH
und
∗
den Geschwindigkeitsvektor des Hohlzylinders ~vB im Punkt B,
d) die Stosskräfte in A.
Gegeben: m; R; ϕ = 60◦ ; e = 0, 75; M =
3
m; g.
4
(A)
a) ΘS = m R2
2
R
R2
(S)
ΘH = M
= M R2
+
2
2
r
g
b) ωS = −
2R


2RωS
c) ~vC∗ =  0 
0
r
1 g
ω̄S∗ =
2 R
r
g
1
∗
ω̄H
=
2 R


−1
p
1
∗
~v¯B =
gR  1 
2
0
d) Kraftstoss in A
Ây = 0
r
Âx = 3m
gR
2